016-二叉搜索树（C++实现）

016-二叉搜索树（C++实现）

1. 二叉搜索树概念

二叉搜索树又称二叉排序树，它可以是一颗空树，或是满足下列性质的二叉树：

• 若它的左子树不为空，则左子树上的所有节点的键值小于根节点的值

• 若它的右子树不为空，则右子树上的所有节点的键值大于根节点的值

• 它的左右子树也为二叉搜索树

其中，二叉树中每个节点包括三个成员：数据、左子树指针、右子树指针。

2. 二叉搜索树操作

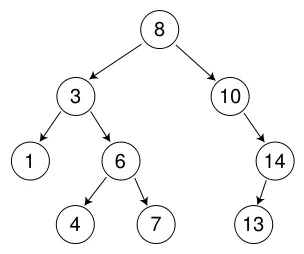
2.1 二叉搜索树的查找

1. 从根节点开始查找，比较需要查找的值和根节点的值的大小
2. 如果相等，返回当前节点
3. 如果比根小，进入左子树
4. 如果比根大，进入右子树
5. 进入子树后继续循环上面的1~4步，直到为空
6. 如果直到nullptr还没找到，返回空

这种查找最多只需要查找树的高度次。

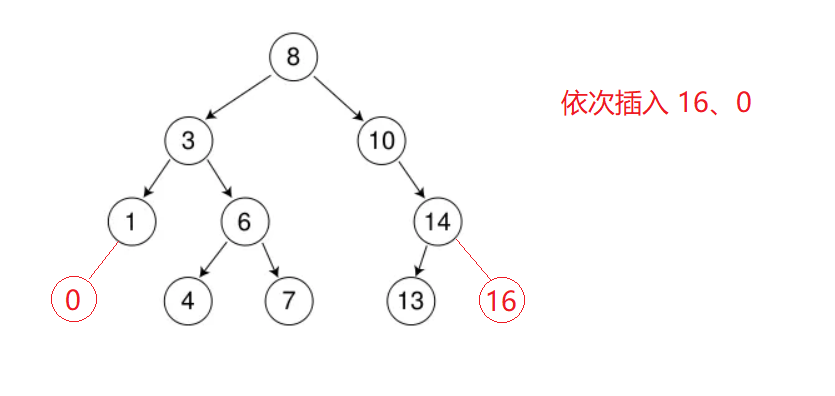
2.2 二叉树的插入

1. 树为空，新增节点，作为树的根节点
2. 树不为空，对比当前树根节点与插入的值的大小
3. 这里不考虑新插入的值与根节点相等的情况，如果新的值已经存在于树中，将不插入
4. 如果小于根节点，进入左子树
5. 如果大于根节点，进入右子树
6. 进入子树后循环1~5步，过程中如果碰到与根节点相同的情况，不插入，除此之外，到最后一定会找到空子树，此时新增节点插入即可。

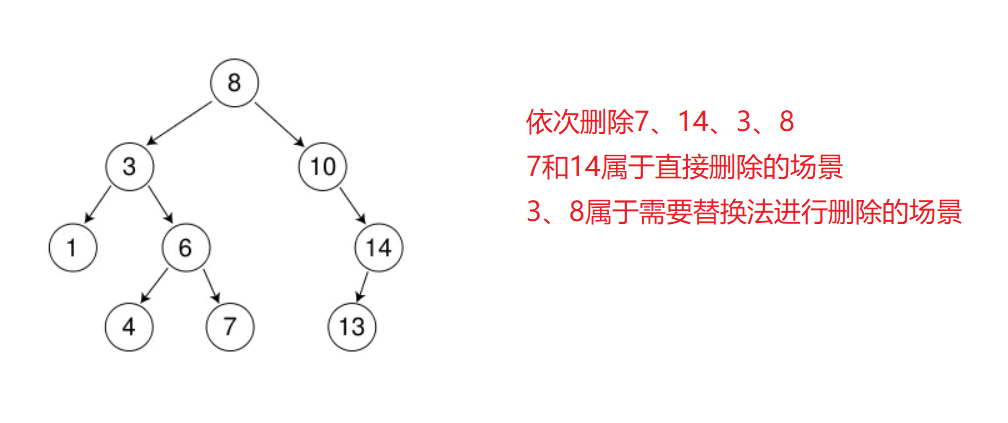
2.3 二叉树的删除

1. 首先查找该节点是否在二叉树中。
2. 如果不存在，直接返回。
3. 如果存在，将会有下面四种情况：
   • 要删除的节点无左右子树：直接删除
   • 要删除的节点有左子树，无右子树：让该节点的父节点指向该节点的左子树，然后删除节点
   • 要删除的节点有右子树，无左子树：让该节点的父节点指向该节点的右子树，然后删除节点
   • 要删除的节点有左右子树：找到左子树中最大的节点，或右子树中最小的节点，将该节点的值赋给要删除的节点，然后处理删除该节点的问题。

3. 二叉树的具体实现

这里学习二叉树只是为了了解二叉树的工作原理，为了方便，这里只实现增删查三个接口，不实现迭代器，后续在学习AVL树和红黑树时将会具体的实现迭代器和其他接口。

// BSTree.hpp

#pragma once

#include <iostream>

template <typename T>
struct BSTNode
{
	BSTNode(const T& data = T()): _pLeft(nullptr), _pRight(nullptr), _data(data)
	{}
	BSTNode<T>* _pLeft;
	BSTNode<T>* _pRight;
	T _data;
};

template <typename T>
class BSTree // binary search tree
{
private:
	using Node = BSTNode<T>;

	// 递归删除二叉树
	void _destroyTree(Node* root)
	{
		if (root == nullptr) return;
		_destroyTree(root->_pLeft);
		_destroyTree(root->_pRight);
		delete root;
	}

	// 递归查找节点
	Node* _find(Node* root, const T& data)
	{
		if (root == nullptr) return nullptr;
		if (root->_data == data) return root;
		_find(root->_pLeft);
		_find(root->_pRight);
	}

	// 删除指定节点
	void _erase(Node* father, Node* child)
	{
		// 如果要删除的节点是根节点，需要特殊处理（此时father为nullptr）
		if (child->_pLeft && child->_pRight) // 两个孩子都存在
		{
			// 找到左子树中最大的节点,替换当前节点，删除该节点。
			Node* delFather = child;
			Node* del = child->_pLeft;
			while (del->_pRight)
			{
				delFather = del;
				del = del->_pRight;
			}

			// 替换
			child->_data = del->_data;
			
			// 由于del是child左子树中最大的节点，所以它没有右孩子，只需要将左孩子连接到父节点即可
			// 如果del的父节点是child，那么del是父节点的左孩子，否则del是父亲的右孩子
			if (delFather == child) delFather->_pLeft = del->_pLeft;
			else delFather->_pRight = del->_pLeft;

			delete del;
		}
		else if (child->_pLeft) // 只存在左孩子
		{
			if (father == nullptr) _root = child->_pLeft;
			else if (child->_data < father->_data) father->_pLeft = child->_pLeft;
			else father->_pRight = child->_pLeft;
			delete child;
		}
		else if (child->_pRight) // 只存在右孩子
		{
			if (father == nullptr) _root = child->_pRight;
			else if (child->_data < father->_data) father->_pLeft = child->_pRight;
			else father->_pRight = child->_pRight;
			delete child;
		}
		else // 左右孩子都不存在
		{
			if (father == nullptr) _root = nullptr;
			else if (child->_data < father->_data) father->_pLeft = nullptr;
			else father->_pRight = nullptr;
			delete child;
		}
	}

	// 递归实现中序遍历
	void _InOrder(Node* root)
	{
		if (root == nullptr) return;
		_InOrder(root->_pLeft);
		std::cout << root->_data << " ";
		_InOrder(root->_pRight);
	}
public:
	BSTree(): _root(nullptr)
	{}

	~BSTree()
	{
		_destroyTree(_root);
	}

	// 找到返回节点指针，没找到返回nullptr
	Node* find(const T& data)
	{
		_find(_root, data);
	}

	// 插入成功返回true，失败返回false
	bool insert(const T& data)
	{
		// 树为空，直接插入
		if (_root == nullptr)
		{
			Node* node = new Node(data);
			_root = node;
			return true;
		}

		Node* father = nullptr; // 用于记录父节点，方便后续插入
		Node* cur = _root; // 寻找插入位置，找到为nullptr时插入为father的子节点
		while (cur)
		{
			// 如果已经存在data，则不插入
			if (cur->_data == data) return false;

			// 记录当前节点
			father = cur;

			// data小于该节点，进入左子树，大于该节点进入右子树
			if (cur->_data > data) cur = cur->_pLeft;
			else cur = cur->_pRight;
		}

		// cur碰到nullptr，插入到father的子节点，比father小插入到左孩子，比father大插入到右孩子
		Node* node = new Node(data);
		if (father->_data > data) father->_pLeft = node;
		else father->_pRight = node;

		return true;
	}

	// 删除成功返回true，失败返回false
	bool erase(const T& data)
	{
		// 树为空，直接返回，删除失败
		if (_root == nullptr) return false;

		// 查找data在树中的位置
		Node* father = nullptr;
		Node* cur = _root;
		while (cur)
		{
			// 当前节点为要删除的节点
			if (cur->_data == data)
			{
				_erase(father, cur); // 将删除逻辑封装成一个函数
				return true;
			}

			father = cur;

			// 要删除的节点比当前节点小，进入左子树，否则进入右子树
			if (cur->_data > data) cur = cur->_pLeft;
			else cur = cur->_pRight;
		}

		// 没有找到要删除的节点，删除失败
		return false;
	}

	// 为了测试代码，这里实现一个中序遍历
	void InOrder()
	{
		_InOrder(_root);
		std::cout << std::endl;
	}
private:
	Node* _root;
};

测试代码：

// test.cc

#pragma once

#include "BSTree.hpp"

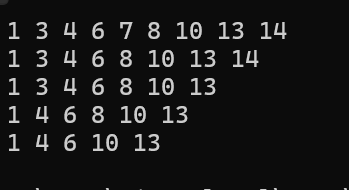
int main()
{
	int arr[] = { 8,3,10,1,6,14,4,7,13 };
	BSTree<int> t;
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
	{
		t.insert(arr[i]);
	}
	t.InOrder();

	t.erase(7);
	t.InOrder();

	t.erase(14);
	t.InOrder();

	t.erase(3);
	t.InOrder();

	t.erase(8);
	t.InOrder();

	return 0;
}

运行结果：

4. 二叉搜索树的应用

1. K模型：即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。
   • 如给定一个单词word，判断该单词是否拼写正确，假设在二叉搜索树中存着词库中所有拼写正确的单词
   • 在二叉树搜索中检索该单词，查到即为拼写正确，否则拼写错误
2. KV模型：每个关键码Key都有与之对应的Value，即<Key, Value>键值对。
   • 给定一个单词word，查找中文意思，假设在二叉搜索树以<单词, 意思>的形式存着词库中所有的单词和意思的对应。
   • 在二叉树搜索中检索该单词，查到返回Value即为意思，否则单词在词库中不存在。

5. 二叉搜索树的性能分析

插入和删除都必须先查找，所以查找的效率代表了二叉搜索树的整体效率。

对有N个节点的二叉搜索树，二叉搜索树的最多需要查找的次数就是查找到最深的节点，此时查找的次数为二叉树的高度次，高度越深，次数越多。

对于一棵二叉搜索树，插入节点的顺序不同，将会得到不同结构的二叉树。

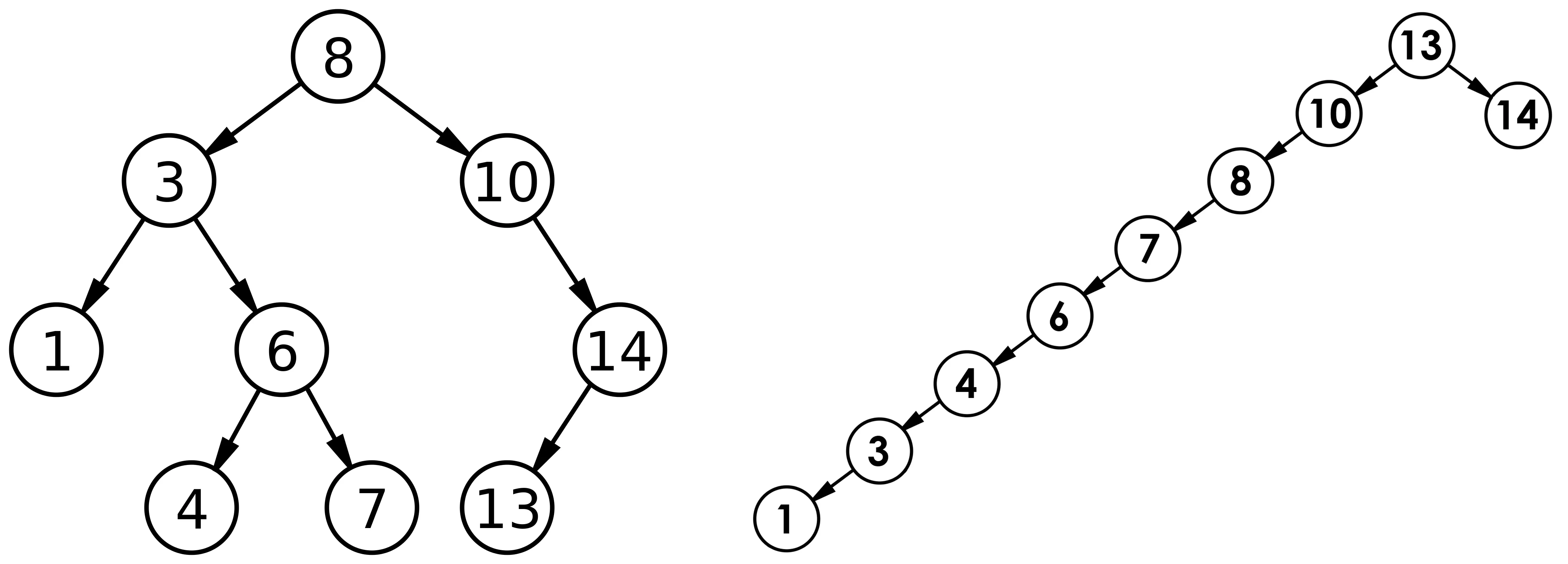
最理想的情况下，二叉树为完全二叉树，此时最差比较次数为 l o g 2 N log_2N log2N，即查找的时间复杂度为O(N)。

最差的情况下，即以升序或降序的顺序插入二叉树，该二叉树将退化为类似链表的结构，此时最差比较次数为N次，即查找的时间复杂度为O(N)。

在最差的情况下，二叉搜索树的性能将会退化，那么能否改进？让其无论如何插入都能接近完全二叉树的结构？后续章节将会介绍AVL树和红黑树，这两种解决方案可以改进上述问题。