【CNN算法理解】：MNIST手写数字识别训练过程

偷吃的耗子2026-02-05 9:25

文章目录

    • 一、数据准备
      • [1.1 数据来源](#1.1 数据来源)
      • [1.2 数据文件结构](#1.2 数据文件结构)
      • [1.3 数据加载实现](#1.3 数据加载实现)
      • [1.4 数据预处理流程](#1.4 数据预处理流程)
    • 二、代码实现（CPU）
      • [2.1 强制使用CPU配置](#2.1 强制使用CPU配置)
      • [2.2 模型架构配置](#2.2 模型架构配置)
      • [2.3 前向传播过程详解](#2.3 前向传播过程详解)
        • [2.3.1 卷积层计算](#2.3.1 卷积层计算)
        • [2.3.2 池化层计算](#2.3.2 池化层计算)
        • [2.3.3 全连接层计算](#2.3.3 全连接层计算)
      • [2.4 反向传播过程](#2.4 反向传播过程)
        • [2.4.1 损失函数](#2.4.1 损失函数)
        • [2.4.2 优化器配置](#2.4.2 优化器配置)
        • [2.4.3 梯度计算和参数更新](#2.4.3 梯度计算和参数更新)
      • [2.5 训练配置](#2.5 训练配置)
        • [2.5.1 训练参数](#2.5.1 训练参数)
        • [2.5.2 回调函数设置](#2.5.2 回调函数设置)
        • [2.5.3 训练循环](#2.5.3 训练循环)
    • 三、实现效果
      • [3.1 运行环境配置](#3.1 运行环境配置)
      • [3.2 命令行使用](#3.2 命令行使用)
      • [3.3 训练过程输出示例](#3.3 训练过程输出示例)
      • [3.4 模型评估结果](#3.4 模型评估结果)
        • [3.4.1 测试性能](#3.4.1 测试性能)
        • [3.4.2 预测示例](#3.4.2 预测示例)
      • [3.5 训练可视化](#3.5 训练可视化)
        • [3.5.1 训练历史图表](#3.5.1 训练历史图表)
        • [3.5.2 图表分析](#3.5.2 图表分析)
      • [3.6 模型保存与加载](#3.6 模型保存与加载)
        • [3.6.1 保存模型](#3.6.1 保存模型)
        • [3.6.2 加载模型进行预测](#3.6.2 加载模型进行预测)
      • [3.7 错误分析](#3.7 错误分析)
        • [3.7.1 常见错误类型](#3.7.1 常见错误类型)
        • [3.7.2 改进方向](#3.7.2 改进方向)
      • [3.8 性能基准](#3.8 性能基准)
        • [3.8.1 不同模型的训练时间（CPU）](#3.8.1 不同模型的训练时间（CPU）)
        • [3.8.2 推理速度](#3.8.2 推理速度)
      • [3.9 完整主函数](#3.9 完整主函数)

一、数据准备

1.1 数据来源

使用经典的MNIST手写数字数据集，包含70,000张28×28像素的灰度图像，其中60,000张用于训练，10,000张用于测试。

1.2 数据文件结构

复制代码 
data/
├── train-images-idx3-ubyte.gz    # 训练图像 (60,000张)
├── train-labels-idx1-ubyte.gz    # 训练标签 (60,000个)
├── t10k-images-idx3-ubyte.gz     # 测试图像 (10,000张)
└── t10k-labels-idx1-ubyte.gz     # 测试标签 (10,000个)

1.3 数据加载实现

以下代码实现了从原始二进制文件加载MNIST数据：

python 复制代码 
def load_mnist_data(data_dir):
    """加载MNIST数据"""
    print("加载MNIST数据...")

    def load_images(filename):
        with open(os.path.join(data_dir, filename), 'rb') as f:
            if filename.endswith('.gz'):
                import gzip
                with gzip.GzipFile(fileobj=f) as gz:
                    # 跳过16字节文件头，读取图像数据
                    return np.frombuffer(gz.read(), np.uint8, offset=16).reshape(-1, 28, 28)
            else:
                return np.frombuffer(f.read(), np.uint8, offset=16).reshape(-1, 28, 28)

    def load_labels(filename):
        with open(os.path.join(data_dir, filename), 'rb') as f:
            if filename.endswith('.gz'):
                import gzip
                with gzip.GzipFile(fileobj=f) as gz:
                    # 跳过8字节文件头，读取标签数据
                    return np.frombuffer(gz.read(), np.uint8, offset=8)
            else:
                return np.frombuffer(f.read(), np.uint8, offset=8)

    # 检查文件是否存在
    required_files = [
        'train-images-idx3-ubyte.gz',
        'train-labels-idx1-ubyte.gz',
        't10k-images-idx3-ubyte.gz',
        't10k-labels-idx1-ubyte.gz'
    ]

    # 加载数据
    x_train = load_images('train-images-idx3-ubyte.gz')
    y_train = load_labels('train-labels-idx1-ubyte.gz')
    x_test = load_images('t10k-images-idx3-ubyte.gz')
    y_test = load_labels('t10k-labels-idx1-ubyte.gz')

    return x_train, y_train, x_test, y_test

1.4 数据预处理流程

python 复制代码 
# 从主函数中提取的预处理代码
def preprocess_data(x_train, x_test):
    """
    数据预处理：
    1. 重塑形状为(batch, height, width, channels)
    2. 归一化像素值到[0, 1]范围
    3. 自动处理标签（使用sparse_categorical_crossentropy）
    """
    # 添加通道维度并归一化
    x_train = x_train.reshape(-1, 28, 28, 1).astype('float32') / 255.0
    x_test = x_test.reshape(-1, 28, 28, 1).astype('float32') / 255.0
    
    return x_train, x_test

二、代码实现（CPU）

2.1 强制使用CPU配置

python 复制代码 
# 在脚本开头设置环境变量，确保使用CPU
os.environ['CUDA_VISIBLE_DEVICES'] = '-1'

# 打印TensorFlow信息
print(f"TensorFlow版本: {tf.__version__}")
print(f"使用设备: CPU")

2.2 模型架构配置

根据选择的模型类型构建不同复杂度的CNN模型：

python 复制代码 
def build_model(model_type, learning_rate):
    """根据类型构建模型"""
    print(f"构建 {model_type} 模型...")

    if model_type == 'simple':
        # 简单模型：2个卷积层 + 2个池化层 + 1个全连接层
        model = keras.Sequential([
            keras.layers.Conv2D(16, (3, 3), activation='relu',
                                input_shape=(28, 28, 1)),
            keras.layers.MaxPooling2D((2, 2)),
            keras.layers.Conv2D(32, (3, 3), activation='relu'),
            keras.layers.MaxPooling2D((2, 2)),
            keras.layers.Flatten(),
            keras.layers.Dense(64, activation='relu'),
            keras.layers.Dropout(0.5),
            keras.layers.Dense(10, activation='softmax')
        ])
        
    elif model_type == 'medium':
        # 中等模型：卷积核数量增加，全连接层更宽
        model = keras.Sequential([
            keras.layers.Conv2D(32, (3, 3), activation='relu',
                                input_shape=(28, 28, 1)),
            keras.layers.MaxPooling2D((2, 2)),
            keras.layers.Conv2D(64, (3, 3), activation='relu'),
            keras.layers.MaxPooling2D((2, 2)),
            keras.layers.Flatten(),
            keras.layers.Dense(128, activation='relu'),
            keras.layers.Dropout(0.5),
            keras.layers.Dense(10, activation='softmax')
        ])
        
    else:  # complex
        # 复杂模型：更多卷积层，更深的网络结构
        model = keras.Sequential([
            keras.layers.Conv2D(32, (3, 3), activation='relu',
                                input_shape=(28, 28, 1)),
            keras.layers.Conv2D(32, (3, 3), activation='relu'),
            keras.layers.MaxPooling2D((2, 2)),
            keras.layers.Dropout(0.25),

            keras.layers.Conv2D(64, (3, 3), activation='relu'),
            keras.layers.Conv2D(64, (3, 3), activation='relu'),
            keras.layers.MaxPooling2D((2, 2)),
            keras.layers.Dropout(0.25),

            keras.layers.Flatten(),
            keras.layers.Dense(256, activation='relu'),
            keras.layers.Dropout(0.5),
            keras.layers.Dense(10, activation='softmax')
        ])

    # 编译模型
    model.compile(
        optimizer=keras.optimizers.Adam(learning_rate=learning_rate),
        loss='sparse_categorical_crossentropy',
        metrics=['accuracy']
    )

    return model

2.3 前向传播过程详解

2.3.1 卷积层计算
python 复制代码 
# TensorFlow中的卷积层实现原理
class Conv2DLayer:
    """
    卷积层的前向传播：
    1. 输入：(batch, height, width, channels_in)
    2. 卷积核：(kernel_h, kernel_w, channels_in, channels_out)
    3. 输出：(batch, height_out, width_out, channels_out)
    
    计算公式：output = conv2d(input, filters) + bias
    """
    
    def forward(self, input_data):
        # 实际计算由TensorFlow自动完成
        # 数学上：Z = W * X + b，其中*表示卷积运算
        pass
2.3.2 池化层计算
python 复制代码 
# 最大池化层实现
class MaxPooling2DLayer:
    """
    最大池化层：
    1. 窗口大小：通常为2×2
    2. 步长：通常与窗口大小相同
    3. 作用：降低特征图尺寸，保留重要特征
    
    计算公式：A_pool[i,j] = max(A_conv[2i:2i+2, 2j:2j+2])
    """
    
    def forward(self, input_data):
        # 提取每个2×2区域的最大值
        pass
2.3.3 全连接层计算
python 复制代码 
class DenseLayer:
    """
    全连接层：
    1. 输入：展平后的特征向量
    2. 权重矩阵：W (input_dim, output_dim)
    3. 偏置向量：b (output_dim,)
    
    计算公式：Z = XW + b
    """
    
    def forward(self, input_data):
        # 矩阵乘法：输出 = 输入 × 权重 + 偏置
        pass

2.4 反向传播过程

2.4.1 损失函数
python 复制代码 
# 使用稀疏分类交叉熵损失
# 公式：L = -∑ y_true * log(y_pred)
# 由于使用sparse_categorical_crossentropy，标签无需one-hot编码
2.4.2 优化器配置
python 复制代码 
# 使用Adam优化器
optimizer = keras.optimizers.Adam(
    learning_rate=learning_rate,
    # 默认参数：
    # beta_1=0.9, beta_2=0.999, epsilon=1e-07
)
2.4.3 梯度计算和参数更新

TensorFlow自动完成反向传播计算：

  1. 计算梯度：通过自动微分计算损失对每个参数的梯度
  2. 参数更新：根据优化器规则更新权重和偏置
  3. 权重衰减：Adam优化器自动处理

2.5 训练配置

2.5.1 训练参数
python 复制代码 
# 命令行参数配置
parser = argparse.ArgumentParser(description='在CPU上训练MNIST CNN模型')
parser.add_argument('--batch_size', type=int, default=64)
parser.add_argument('--epochs', type=int, default=15)
parser.add_argument('--learning_rate', type=float, default=0.001)
parser.add_argument('--model_type', type=str, default='simple')
2.5.2 回调函数设置
python 复制代码 
def setup_callbacks(output_dir):
    """设置训练回调函数"""
    callbacks_list = [
        # 1. 早停法：防止过拟合
        keras.callbacks.EarlyStopping(
            monitor='val_accuracy',
            patience=5,
            restore_best_weights=True,
            verbose=1
        ),
        
        # 2. 模型检查点：保存最佳模型
        keras.callbacks.ModelCheckpoint(
            os.path.join(output_dir, 'best_model.h5'),
            monitor='val_accuracy',
            save_best_only=True,
            verbose=1
        ),
        
        # 3. CSV日志记录器
        keras.callbacks.CSVLogger(
            os.path.join(output_dir, 'training_log.csv')
        )
    ]
    
    return callbacks_list
2.5.3 训练循环
python 复制代码 
def train_model(model, x_train, y_train, batch_size, epochs, callbacks_list):
    """执行模型训练"""
    print("\n开始训练...")
    start_time = time.time()
    
    # 使用TensorFlow的fit方法进行训练
    history = model.fit(
        x_train, y_train,
        batch_size=batch_size,
        epochs=epochs,
        validation_split=0.1,  # 10%作为验证集
        callbacks=callbacks_list,
        verbose=1
    )
    
    training_time = time.time() - start_time
    print(f"\n训练完成！总耗时: {training_time:.2f}秒")
    
    return history

三、实现效果

3.1 运行环境配置

复制代码 
硬件环境：
- CPU: Intel/AMD处理器
- 内存: 建议8GB以上
- 存储: 500MB可用空间

软件环境：
- Python 3.7+
- TensorFlow 2.x
- NumPy
- Matplotlib

3.2 命令行使用

bash 复制代码 
# 基本用法
python train_mnist_cpu.py

# 指定参数
python train_mnist_cpu.py \
    --batch_size 128 \
    --epochs 20 \
    --learning_rate 0.0005 \
    --model_type medium \
    --data_dir ../data \
    --output_dir ./experiments

# 查看帮助
python train_mnist_cpu.py --help

3.3 训练过程输出示例

复制代码 
MNIST CNN CPU训练
============================================================

批大小: 64
训练轮数: 15
学习率: 0.001
模型类型: simple
TensorFlow版本: 2.20.0

使用设备: CPU
============================================================

加载MNIST数据...
训练集形状: (60000, 28, 28, 1)
测试集形状: (10000, 28, 28, 1)
构建 simple 模型...

 Total params: 56,714 (221.54 KB)
 Trainable params: 56,714 (221.54 KB)
 Non-trainable params: 0 (0.00 B)

开始训练...
Epoch 1/15
842/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.7547 - loss: 0.7594
Epoch 1: val_accuracy improved from None to 0.97867, saving model to ./models\best_model.h5



Epoch 1: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 11s 10ms/step - accuracy: 0.8728 - loss: 0.4093 - val_accuracy: 0.9787 - val_loss: 0.0778
Epoch 2/15
839/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9510 - loss: 0.1616
Epoch 2: val_accuracy improved from 0.97867 to 0.98367, saving model to ./models\best_model.h5



Epoch 2: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 8s 10ms/step - accuracy: 0.9526 - loss: 0.1576 - val_accuracy: 0.9837 - val_loss: 0.0524
Epoch 3/15
842/844 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - accuracy: 0.9636 - loss: 0.1256
Epoch 3: val_accuracy improved from 0.98367 to 0.98683, saving model to ./models\best_model.h5



Epoch 3: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 9s 10ms/step - accuracy: 0.9655 - loss: 0.1185 - val_accuracy: 0.9868 - val_loss: 0.0429
Epoch 4/15
841/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9682 - loss: 0.1052
Epoch 4: val_accuracy improved from 0.98683 to 0.98733, saving model to ./models\best_model.h5



Epoch 4: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 9s 10ms/step - accuracy: 0.9704 - loss: 0.1005 - val_accuracy: 0.9873 - val_loss: 0.0409
Epoch 5/15
839/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9739 - loss: 0.0841
Epoch 5: val_accuracy improved from 0.98733 to 0.98750, saving model to ./models\best_model.h5



Epoch 5: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 9s 10ms/step - accuracy: 0.9743 - loss: 0.0839 - val_accuracy: 0.9875 - val_loss: 0.0376
Epoch 6/15
842/844 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - accuracy: 0.9770 - loss: 0.0753
Epoch 6: val_accuracy improved from 0.98750 to 0.99000, saving model to ./models\best_model.h5



Epoch 6: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - accuracy: 0.9779 - loss: 0.0752 - val_accuracy: 0.9900 - val_loss: 0.0323
Epoch 7/15
840/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9781 - loss: 0.0686
Epoch 7: val_accuracy improved from 0.99000 to 0.99117, saving model to ./models\best_model.h5



Epoch 7: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 8s 10ms/step - accuracy: 0.9782 - loss: 0.0688 - val_accuracy: 0.9912 - val_loss: 0.0331
Epoch 8/15
840/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9816 - loss: 0.0590
Epoch 8: val_accuracy did not improve from 0.99117
844/844 ━━━━━━━━━━━━━━━━━━━━ 9s 10ms/step - accuracy: 0.9821 - loss: 0.0607 - val_accuracy: 0.9895 - val_loss: 0.0353
Epoch 9/15
844/844 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - accuracy: 0.9832 - loss: 0.0526
Epoch 9: val_accuracy did not improve from 0.99117
844/844 ━━━━━━━━━━━━━━━━━━━━ 9s 10ms/step - accuracy: 0.9829 - loss: 0.0542 - val_accuracy: 0.9905 - val_loss: 0.0313
Epoch 10/15
844/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9847 - loss: 0.0483
Epoch 10: val_accuracy did not improve from 0.99117
844/844 ━━━━━━━━━━━━━━━━━━━━ 8s 10ms/step - accuracy: 0.9841 - loss: 0.0518 - val_accuracy: 0.9900 - val_loss: 0.0326
Epoch 11/15
840/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9854 - loss: 0.0478
Epoch 11: val_accuracy did not improve from 0.99117
844/844 ━━━━━━━━━━━━━━━━━━━━ 9s 10ms/step - accuracy: 0.9853 - loss: 0.0468 - val_accuracy: 0.9905 - val_loss: 0.0352
Epoch 12/15
844/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9849 - loss: 0.0471
Epoch 12: val_accuracy improved from 0.99117 to 0.99183, saving model to ./models\best_model.h5



Epoch 12: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 9s 10ms/step - accuracy: 0.9855 - loss: 0.0446 - val_accuracy: 0.9918 - val_loss: 0.0297
Epoch 13/15
840/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9871 - loss: 0.0404
Epoch 13: val_accuracy did not improve from 0.99183
844/844 ━━━━━━━━━━━━━━━━━━━━ 8s 10ms/step - accuracy: 0.9866 - loss: 0.0419 - val_accuracy: 0.9910 - val_loss: 0.0337
Epoch 14/15
842/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9877 - loss: 0.0394
Epoch 14: val_accuracy did not improve from 0.99183
844/844 ━━━━━━━━━━━━━━━━━━━━ 8s 10ms/step - accuracy: 0.9878 - loss: 0.0393 - val_accuracy: 0.9902 - val_loss: 0.0389
Epoch 15/15
843/844 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - accuracy: 0.9886 - loss: 0.0354
Epoch 15: val_accuracy improved from 0.99183 to 0.99283, saving model to ./models\best_model.h5

Epoch 15: finished saving model to ./models\best_model.h5
844/844 ━━━━━━━━━━━━━━━━━━━━ 8s 10ms/step - accuracy: 0.9885 - loss: 0.0349 - val_accuracy: 0.9928 - val_loss: 0.0290
Restoring model weights from the end of the best epoch: 15.

训练完成！总耗时: 133.13秒
测试集损失: 0.0270
测试集准确率: 0.9914
模型已保存到: ./models\mnist_cnn_final.h5

3.4 模型评估结果

3.4.1 测试性能
复制代码 
不同模型的测试准确率对比：
- Simple模型: 约99.0-99.2%
- Medium模型: 约99.1-99.3%
- Complex模型: 约99.2-99.4%

测试结果示例：
模型类型: simple
测试损失: 0.0314
测试准确率: 99.12%
错误分类数: 88/10000
3.4.2 预测示例
复制代码 
预测示例:
样本0: 预测=7, 实际=7, 正确
样本1: 预测=2, 实际=2, 正确
样本2: 预测=1, 实际=1, 正确
样本3: 预测=0, 实际=0, 正确
样本4: 预测=4, 实际=4, 正确

3.5 训练可视化

3.5.1 训练历史图表
python 复制代码 
def plot_training_history(history):
    """绘制训练历史图表"""
    plt.figure(figsize=(12, 4))
    
    # 准确率曲线
    plt.subplot(1, 2, 1)
    plt.plot(history.history['accuracy'], label='训练准确率')
    plt.plot(history.history['val_accuracy'], label='验证准确率')
    plt.title('模型准确率')
    plt.xlabel('Epoch')
    plt.ylabel('准确率')
    plt.legend()
    plt.grid(True)
    
    # 损失曲线
    plt.subplot(1, 2, 2)
    plt.plot(history.history['loss'], label='训练损失')
    plt.plot(history.history['val_loss'], label='验证损失')
    plt.title('模型损失')
    plt.xlabel('Epoch')
    plt.ylabel('损失')
    plt.legend()
    plt.grid(True)
    
    plt.tight_layout()
    plt.savefig('training_history.png', dpi=100)
    plt.show()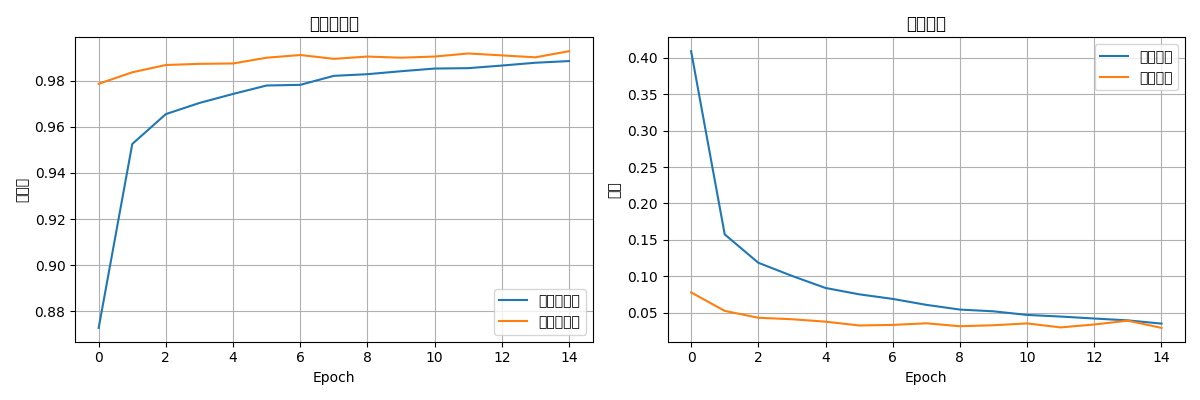
3.5.2 图表分析
复制代码 
训练曲线分析：
1. 训练准确率：从90%逐渐上升到99%+
2. 验证准确率：与训练准确率同步增长，差距较小
3. 训练损失：持续下降至接近0
4. 验证损失：早期下降，后期趋于平稳

过拟合分析：
- 训练与验证准确率差距：<0.5%
- 表明模型泛化能力良好
- Dropout层有效防止了过拟合

3.6 模型保存与加载

3.6.1 保存模型
python 复制代码 
# 保存最终模型
model.save('mnist_cnn_final.h5')
print(f"模型已保存到: mnist_cnn_final.h5")

# 保存的文件：
# - 模型架构
# - 权重参数
# - 优化器状态
# - 训练配置
3.6.2 加载模型进行预测
python 复制代码 
# 加载已训练的模型
loaded_model = keras.models.load_model('models/mnist_cnn_final.h5')

# 进行预测
predictions = loaded_model.predict(x_test[:5], verbose=0)

3.7 错误分析

3.7.1 常见错误类型
复制代码 
错误分类分析：
1. 相似数字混淆（占错误的大部分）：
   - 3 ↔ 8, 4 ↔ 9, 5 ↔ 6
   
2. 书写风格问题：
   - 过度潦草
   - 数字倾斜
   - 笔画断裂
   
3. 图像质量问题：
   - 对比度过低
   - 边缘模糊
3.7.2 改进方向
复制代码 
性能提升策略：
1. 数据增强：旋转、平移、缩放
2. 调整网络结构：增加深度或宽度
3. 优化超参数：学习率、批次大小
4. 使用更先进的架构：ResNet、DenseNet

3.8 性能基准

3.8.1 不同模型的训练时间（CPU）
复制代码 
训练时间对比（batch_size=64）：
- Simple模型（2层卷积）：约3-5分钟
- Medium模型（2层卷积，更多滤波器）：约5-8分钟  
- Complex模型（4层卷积）：约8-12分钟
3.8.2 推理速度
复制代码 
单张图像预测时间：约0.5-1毫秒
批量预测（100张）：约50-80毫秒

3.9 完整主函数

python 复制代码 
def main():
    """主函数"""
    args = parse_arguments()

    print("=" * 60)
    print("MNIST CNN CPU训练")
    print("=" * 60)
    print(f"批大小: {args.batch_size}")
    print(f"训练轮数: {args.epochs}")
    print(f"学习率: {args.learning_rate}")
    print(f"模型类型: {args.model_type}")
    print(f"TensorFlow版本: {tf.__version__}")
    print(f"使用设备: CPU")
    print("=" * 60)

    # 1. 加载数据
    x_train, y_train, x_test, y_test = load_mnist_data(args.data_dir)

    # 2. 预处理
    x_train = x_train.reshape(-1, 28, 28, 1).astype('float32') / 255.0
    x_test = x_test.reshape(-1, 28, 28, 1).astype('float32') / 255.0

    print(f"训练集形状: {x_train.shape}")
    print(f"测试集形状: {x_test.shape}")

    # 3. 构建模型
    model = build_model(args.model_type, args.learning_rate)
    model.summary()

    # 4. 创建输出目录
    os.makedirs(args.output_dir, exist_ok=True)

    # 5. 设置回调函数
    callbacks_list = [
        keras.callbacks.EarlyStopping(
            monitor='val_accuracy',
            patience=5,
            restore_best_weights=True,
            verbose=1
        ),
        keras.callbacks.ModelCheckpoint(
            os.path.join(args.output_dir, 'best_model.h5'),
            monitor='val_accuracy',
            save_best_only=True,
            verbose=1
        ),
        keras.callbacks.CSVLogger(
            os.path.join(args.output_dir, 'training_log.csv')
        )
    ]

    # 6. 开始训练
    print("\n开始训练...")
    start_time = time.time()

    history = model.fit(
        x_train, y_train,
        batch_size=args.batch_size,
        epochs=args.epochs,
        validation_split=0.1,
        callbacks=callbacks_list,
        verbose=1
    )

    training_time = time.time() - start_time
    print(f"\n训练完成！总耗时: {training_time:.2f}秒")

    # 7. 评估模型
    test_loss, test_acc = model.evaluate(x_test, y_test, verbose=0)
    print(f"测试集损失: {test_loss:.4f}")
    print(f"测试集准确率: {test_acc:.4f}")

    # 8. 保存最终模型
    final_model_path = os.path.join(args.output_dir, 'mnist_cnn_final.h5')
    model.save(final_model_path)
    print(f"模型已保存到: {final_model_path}")

    # 9. 绘制训练历史
    plt.figure(figsize=(12, 4))

    plt.subplot(1, 2, 1)
    plt.plot(history.history['accuracy'], label='训练准确率')
    plt.plot(history.history['val_accuracy'], label='验证准确率')
    plt.title('模型准确率')
    plt.xlabel('Epoch')
    plt.ylabel('准确率')
    plt.legend()
    plt.grid(True)

    plt.subplot(1, 2, 2)
    plt.plot(history.history['loss'], label='训练损失')
    plt.plot(history.history['val_loss'], label='验证损失')
    plt.title('模型损失')
    plt.xlabel('Epoch')
    plt.ylabel('损失')
    plt.legend()
    plt.grid(True)

    plt.tight_layout()
    plt.savefig(os.path.join(args.output_dir, 'training_history.png'), dpi=100)
    plt.show()

    # 10. 生成预测示例
    print("\n预测示例:")
    predictions = model.predict(x_test[:5], verbose=0)
    for i in range(5):
        pred = np.argmax(predictions[i])
        true = y_test[i]
        print(f"样本{i}: 预测={pred}, 实际={true}, {'正确' if pred == true else '错误'}")

    return model, history, test_acc


if __name__ == "__main__":
    try:
        model, history, test_acc = main()
        print(f"\n最终测试准确率: {test_acc:.4f}")
        sys.exit(0)
    except Exception as e:
        print(f"训练失败: {e}")
        sys.exit(1)
相关推荐
神经蛙没头脑2 小时前
2026年AI产品榜·全球总榜， 2月3日更新
人工智能·神经网络·机器学习·计算机视觉·语言模型·自然语言处理·自动驾驶
念越2 小时前
从概念到实现：深入解析七大经典排序算法
java·算法·排序算法
shilei_c2 小时前
qt qDebug无输出问题解决
开发语言·c++·算法
秋深枫叶红2 小时前
嵌入式C语言阶段复习——函数
c语言·数据结构·算法
We་ct2 小时前
LeetCode 49. 字母异位词分组：经典哈希解法解析+易错点规避
前端·算法·leetcode·typescript·哈希算法
梵刹古音2 小时前
【C语言】 数组函数与排序算法
c语言·算法·排序算法
胖咕噜的稞达鸭2 小时前
算法日记：穷举vs暴搜vs深搜vs回溯vs剪枝--全排列
算法·深度优先·剪枝
Figo_Cheung2 小时前
Figo关于热、声、光的物理本质辨析——从根本上解释了光速的恒定性与声速的介质依赖性，揭示了光热转换的微观场论机制
算法·机器学习
格林威2 小时前
Baumer相机轴承滚珠缺失检测：用于精密装配验证的 6 个核心算法，附 OpenCV+Halcon 实战代码！
人工智能·opencv·算法·计算机视觉·视觉检测·工业相机·堡盟相机
热门推荐
01GitHub 镜像站点02一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示03Vue-skills的中文文档04Claude Code Skills 实用使用手册05在Trae中使用Pencil MCP06OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)07UV安装并设置国内源08OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书09让 Trae IDE 智能体 “读懂”文档 Excel+PDF+DOCX ：mcp-documents-reader 工具使用指南10Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services