PyTorch参数更新方法

核心结论：参数更新是模型 "学习" 的核心，SGD 是基础方法，而 Momentum、AdaGrad、RMSProp、Adam 等优化方法能解决 SGD 的不足，让模型学得更快、更稳，实际应用中优先选 Adam 或 RMSProp。本文只是居于PyTorch的代码应用，具体原理查看以往文章

https://blog.csdn.net/weixin_65875490/article/details/157514923?spm=1011.2124.3001.6209https://blog.csdn.net/weixin_65875490/article/details/157514923?spm=1011.2124.3001.6209

一、核心目标

参数更新的目的是让模型的损失函数越来越小（预测越来越准），核心逻辑是 "沿着损失函数的负梯度方向调整参数"------ 梯度就像 "导航"，告诉参数该往哪个方向动才能让误差变小。

二、常用更新方法（通俗理解 + 特点）

1. SGD（随机梯度下降）：基础款

原理：直接沿着当前梯度方向调整参数，步长由学习率控制。
特点：简单易理解，但有明显缺点 ------ 容易在最优解附近 "震荡"，收敛速度慢，还可能陷入局部最优或鞍点（梯度为 0，训练停滞）。
适用场景：简单模型或作为基准对比。

2. Momentum（动量法）：带 "惯性" 的 SGD

原理：模拟物理中的 "动量"，不仅考虑当前梯度，还会累积历史梯度的方向，就像滚雪球一样，沿着正确方向加速，遇到小波动时不容易跑偏。
特点：缓解震荡，收敛速度比 SGD 快，能有效避开鞍点。
适用场景：大部分场景，尤其适合损失函数表面起伏较大的情况。

import torch
import numpy as np
import matplotlib.pyplot as plt

def gradient_descent(X, optimizer, n_iters):
"""
执行梯度下降优化过程并记录每一步的参数变化
参数:
X: 初始参数 (torch.Tensor)
optimizer: 优化器 (torch.optim.Optimizer)
n_iters: 迭代次数 (int)
返回:
X_arr: 每一步参数的变化轨迹 (numpy.ndarray)
"""
X_arr = [X.detach().numpy().copy()] # 初始化轨迹记录列表
for epoch in range(n_iters):
# 计算目标函数 y = X^T * W * X（二次型）
y = (X ** 2) @ w
y.backward() # 反向传播计算梯度
optimizer.step() # 更新参数
optimizer.zero_grad() # 清空梯度
X_arr.append(X.detach().numpy().copy()) # 记录当前参数
return np.array(X_arr) # 返回完整轨迹数组

定义初始参数和超参数

X = torch.tensor([-7.0, 2.0], dtype=torch.float32, requires_grad=True)
w = torch.tensor([[0.05], [1.0]], dtype=torch.float32, requires_grad=True)
lr = 1e-2 # 学习率
n_iters = 500 # 迭代次数

普通梯度下降 (SGD)

X_clone = X.clone().detach().requires_grad_(True)
optimizer_sgd = torch.optim.SGD([X_clone], lr=lr)
X_arr1 = gradient_descent(X_clone, optimizer_sgd, n_iters)

动量法 (Momentum)

X_clone = X.clone().detach().requires_grad_(True)
optimizer_momentum = torch.optim.SGD([X_clone], lr=lr, momentum=0.9)
X_arr2 = gradient_descent(X_clone, optimizer_momentum, n_iters)

绘制优化轨迹

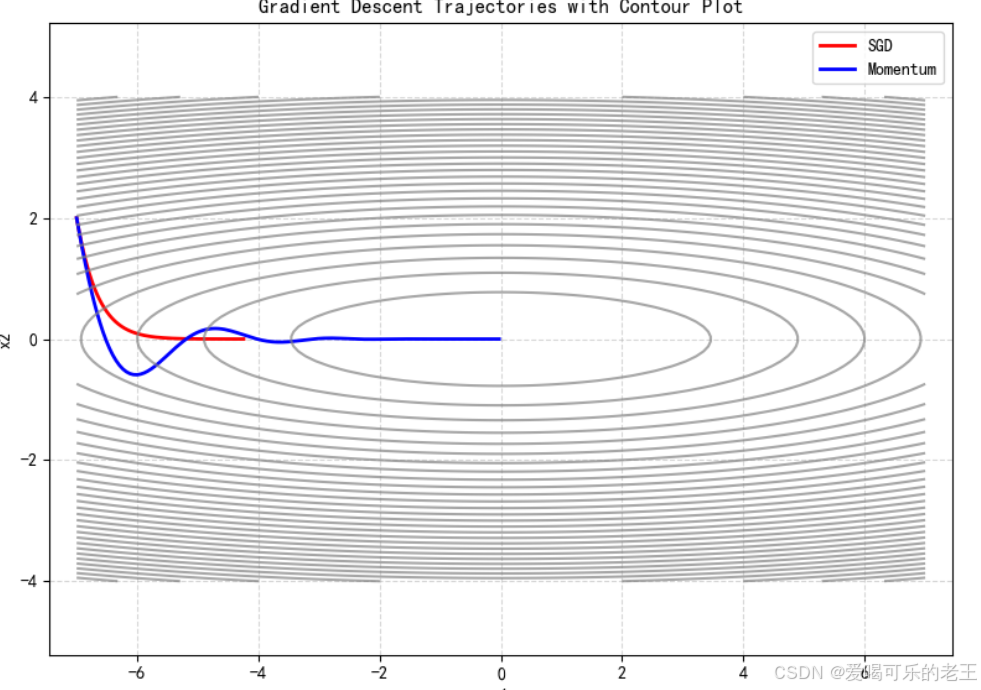
plt.figure(figsize=(8, 6))
plt.plot(X_arr1[:, 0], X_arr1[:, 1], "r-", label="SGD", linewidth=2)
plt.plot(X_arr2[:, 0], X_arr2[:, 1], "b-", label="Momentum", linewidth=2)

绘制目标函数的等高线

x1_grid, x2_grid = np.meshgrid(np.linspace(-7, 7, 100), np.linspace(-4, 4, 100))
y_grid = w.detach().numpy()[0, 0] * x1_grid2 + w.detach().numpy()[1, 0] * x2_grid2
plt.contour(x1_grid, x2_grid, y_grid, levels=30, colors="gray", alpha=0.7)

图形美化

plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Gradient Descent Trajectories with Contour Plot")
plt.legend()
plt.grid(True, linestyle="--", alpha=0.5)
plt.axis("equal") # 保持坐标轴比例一致
plt.tight_layout()
plt.show()

3. 学习率衰减：动态调整 "步长"

原理：学习率是参数更新的 "步长"------ 太大容易跑过最优解，太小收敛太慢。学习率衰减就是让前期用大步长快速接近最优解，后期用小步长精准收敛。

常见类型：

1）等间隔衰减：每隔固定 epoch（比如 20 轮），学习率按比例（比如 0.7）下降。

torch.optim.lr_scheduler.StepLR(optimizer, step_size, gamma)来实现学习率的等间隔衰减。
optimizer：要实现学习率衰减的优化器step_size:间隔
gamma：衰减的比例

例如，使学习率每隔 20 epoch 衰减为之前的 0.7:

复制代码

#等间隔衰减
import torch 
import numpy as np
import matplotlib.pyplot as plt

#从（-7，2）出发
X = torch.tensor([-7, 2], dtype=torch.float32, requires_grad=True)
w = torch.tensor([[0.05], [1.0]], requires_grad=True)
lr = 0.9 #初始学习率
n_iters = 1000 #迭代次数

optimizer = torch.optim.SGD([X], lr=lr) #创建优化器
scheduler_lr = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.7) #学习率衰减
X_arr = X.detach().numpy().copy() #拷贝，避免修改原数据，记录优化过程
lr_list = [] #记录学习率
for epoch in range(n_iters):
    y = X**2 @ w
    y.backward() #反向传播
    optimizer.step() #更新参数
    optimizer.zero_grad() #清空梯度
    # X.detach().numpy()表示获取张量的值，并转换为NumPy数组
    X_arr = np.vstack([X_arr, X.detach().numpy()])#记录优化过程
    lr_list.append(optimizer.param_groups[0]["lr"]) #记录学习率
    scheduler_lr.step() #更新学习率
    
plt.rcParams["font.sans-serif"] = ["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"] = False #显示负号
fig,ax = plt.subplots(1,2,figsize=(12,4))
x1_grid, x2_grid = np.meshgrid(np.linspace(-7, 7, 100), np.linspace(-2,2, 100)) #生成等值线
y_grid = w.detach().numpy()[0, 0] * x1_grid**2 + w.detach().numpy()[1,0] * x2_grid**2
ax[0].contour(x1_grid, x2_grid, y_grid, levels=30, colors="gray")
ax[0].plot(X_arr[:, 0], X_arr[:, 1], "r")
ax[0].set_title("梯度下降过程")
ax[1].plot(lr_list,"k")
ax[1].set_title("学习率衰减")
plt.show()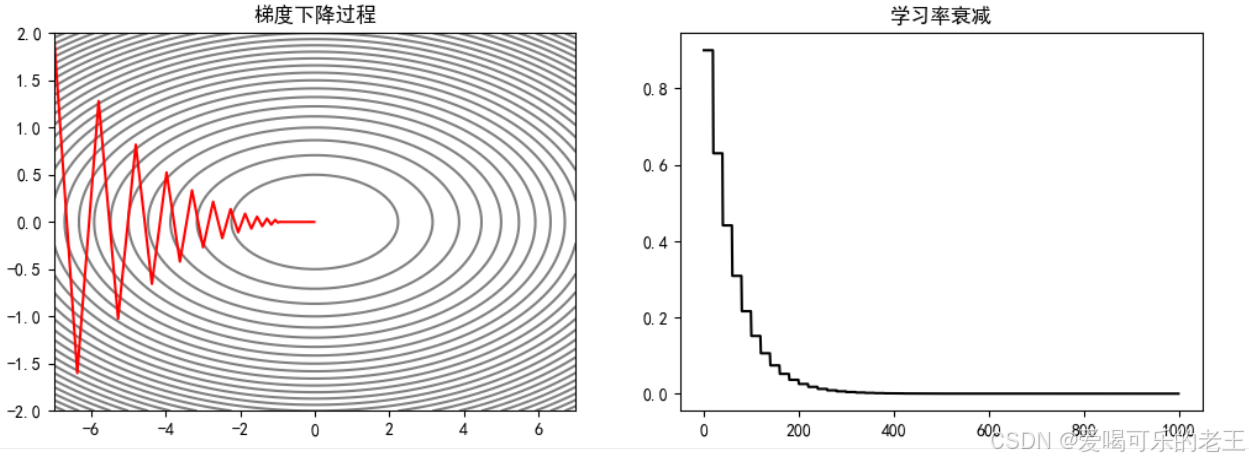

2）指定间隔衰减：在特定 epoch（比如 10、50、200 轮）触发衰减。

可以通过 torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones, gamma)来实现学习率的指定间隔衰减。
optimizer：要实现学习率衰减的优化器milestones：指定衰减的间隔
gamma：衰减的比例

例如，使学习率在 epoch 达到[10,50,200]时衰减为之前的 0.7:

复制代码

#指定间隔衰减
import torch 
import numpy as np
import matplotlib.pyplot as plt

#从（-7，2）出发
X = torch.tensor([-7, 2], dtype=torch.float32, requires_grad=True)
w = torch.tensor([[0.05], [1.0]], requires_grad=True)
lr = 0.9 #初始学习率
n_iters = 1000 #迭代次数

optimizer = torch.optim.SGD([X], lr=lr) #创建优化器
scheduler_lr = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[10,50,200], gamma=0.7) #学习率衰减
X_arr = X.detach().numpy().copy() #拷贝，避免修改原数据，记录优化过程
lr_list = [] #记录学习率
for epoch in range(n_iters):
    y = X**2 @ w
    y.backward() #反向传播
    optimizer.step() #更新参数
    optimizer.zero_grad() #清空梯度
    # X.detach().numpy()表示获取张量的值，并转换为NumPy数组
    X_arr = np.vstack([X_arr, X.detach().numpy()])#记录优化过程
    lr_list.append(optimizer.param_groups[0]["lr"]) #记录学习率
    scheduler_lr.step() #更新学习率
    
plt.rcParams["font.sans-serif"] = ["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"] = False #显示负号
fig,ax = plt.subplots(1,2,figsize=(12,4))
x1_grid, x2_grid = np.meshgrid(np.linspace(-7, 7, 100), np.linspace(-2,2, 100)) #生成等值线
y_grid = w.detach().numpy()[0, 0] * x1_grid**2 + w.detach().numpy()[1,0] * x2_grid**2
ax[0].contour(x1_grid, x2_grid, y_grid, levels=30, colors="gray")
ax[0].plot(X_arr[:, 0], X_arr[:, 1], "r")
ax[0].set_title("梯度下降过程")
ax[1].plot(lr_list,"k")
ax[1].set_title("学习率衰减")
plt.show()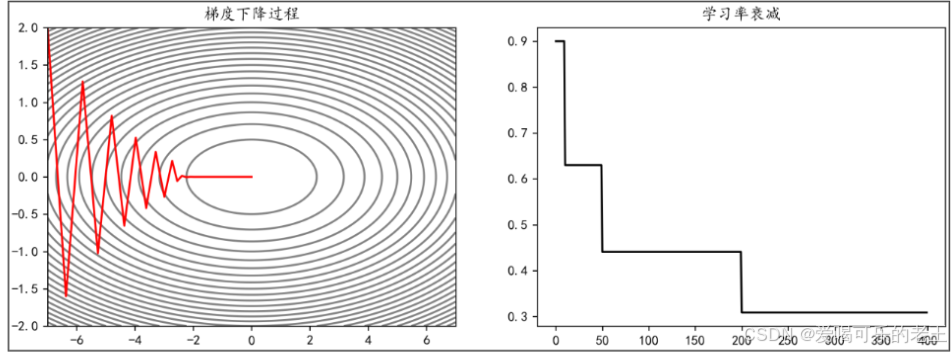

3）指数衰减：学习率按指数函数逐步减小，衰减更平滑。

可以通过 torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma)来实现学习率的指数衰减。
optimizer：要实现学习率衰减的优化器
gamma：底数，学习率←学习率×gamma

例如，使学习率以 0.99 为底数，epoch 为指数衰减:

复制代码

#指数衰减
import torch 
import numpy as np
import matplotlib.pyplot as plt

#从（-7，2）出发
X = torch.tensor([-7, 2], dtype=torch.float32, requires_grad=True)
w = torch.tensor([[0.05], [1.0]], requires_grad=True)
lr = 0.9 #初始学习率
n_iters = 1000 #迭代次数

optimizer = torch.optim.SGD([X], lr=lr) #创建优化器
scheduler_lr = torch.optim.lr_scheduler.ExponentialLR(optimizer,  gamma=0.99) #学习率衰减
X_arr = X.detach().numpy().copy() #拷贝，避免修改原数据，记录优化过程
lr_list = [] #记录学习率
for epoch in range(n_iters):
    y = X**2 @ w
    y.backward() #反向传播
    optimizer.step() #更新参数
    optimizer.zero_grad() #清空梯度
    # X.detach().numpy()表示获取张量的值，并转换为NumPy数组
    X_arr = np.vstack([X_arr, X.detach().numpy()])#记录优化过程
    lr_list.append(optimizer.param_groups[0]["lr"]) #记录学习率
    scheduler_lr.step() #更新学习率
    
plt.rcParams["font.sans-serif"] = ["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"] = False #显示负号
fig,ax = plt.subplots(1,2,figsize=(12,4))
x1_grid, x2_grid = np.meshgrid(np.linspace(-7, 7, 100), np.linspace(-2,2, 100)) #生成等值线
y_grid = w.detach().numpy()[0, 0] * x1_grid**2 + w.detach().numpy()[1,0] * x2_grid**2
ax[0].contour(x1_grid, x2_grid, y_grid, levels=30, colors="gray")
ax[0].plot(X_arr[:, 0], X_arr[:, 1], "r")
ax[0].set_title("梯度下降过程")
ax[1].plot(lr_list,"k")
ax[1].set_title("学习率衰减")
plt.show()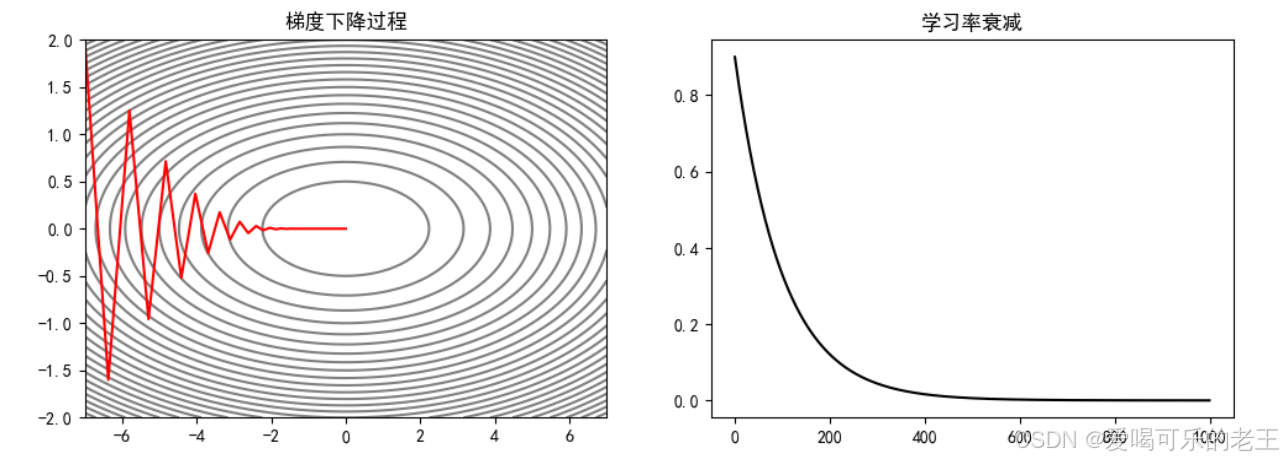

4. AdaGrad（自适应梯度）：给每个参数 "定制步长"

原理：为每个参数单独调整学习率 ------ 频繁更新的参数（梯度大），步长自动变小；不常更新的参数（梯度小），步长自动变大。
特点：适合稀疏数据（部分参数频繁更新），但缺点是学习率会一直减小，后期可能完全停止更新。

5. RMSProp：改进版 AdaGrad

原理：解决 AdaGrad 学习率持续下降的问题，不累积所有历史梯度，而是逐渐 "遗忘" 早期梯度，只关注近期梯度的变化。
特点：学习率更稳定，收敛速度快，是常用的优化方法之一。

6. Adam：集大成者

原理：融合了 Momentum（动量）和 RMSProp（自适应步长）的优点，既考虑历史梯度方向，又为每个参数定制步长，还会对梯度进行修正。
特点：收敛快、稳定性强，几乎适用于所有场景，是实际应用中的首选。

import torch
import numpy as np
import matplotlib.pyplot as plt

def adam_manual(X, lr, betas, n_iters):
"""
手动实现Adam优化算法
参数:
X: 初始参数 (torch.Tensor)
lr: 学习率 (float)
betas: Adam超参数(beta1, beta2) (tuple)
n_iters: 迭代次数 (int)
返回:
X_arr: 每一步参数的变化轨迹 (numpy.ndarray)
"""
X_arr = [X.detach().numpy().copy()] # 初始化轨迹记录列表
V = torch.zeros_like(X) # 一阶矩估计
H = torch.zeros_like(X) # 二阶矩估计
beta1, beta2 = betas
复制代码
```
  for epoch in range(n_iters):
      # 计算梯度
      grad = 2 * X * w.T
      grad.squeeze_()

      # 更新一阶矩估计和二阶矩估计
      V = beta1 * V + (1 - beta1) * grad
      H = beta2 * H + (1 - beta2) * grad ** 2

      # 偏差校正
      V_hat = V / (1 - beta1 ** (epoch + 1))
      H_hat = H / (1 - beta2 ** (epoch + 1))

      # 更新参数
      X.data -= lr * V_hat / (torch.sqrt(H_hat) + 1e-8)

      # 记录轨迹
      X_arr.append(X.detach().numpy().copy())

  return np.array(X_arr)
```
def gradient_descent(X, optimizer, n_iters):
"""
使用优化器进行梯度下降
参数:
X: 初始参数 (torch.Tensor)
optimizer: 优化器 (torch.optim.Optimizer)
n_iters: 迭代次数 (int)
返回:
X_arr: 每一步参数的变化轨迹 (numpy.ndarray)
"""
X_arr = [X.detach().numpy().copy()] # 初始化轨迹记录列表
for _ in range(n_iters):
# 计算目标函数
y = (X ** 2) @ w
y.backward() # 反向传播
复制代码
```
      optimizer.step()  # 更新参数
      optimizer.zero_grad()  # 清空梯度

      # 记录轨迹
      X_arr.append(X.detach().numpy().copy())

  return np.array(X_arr)
```
定义初始参数和超参数

X = torch.tensor([-7.0, 2.0], dtype=torch.float32, requires_grad=True)
w = torch.tensor([[0.05], [1.0]], dtype=torch.float32, requires_grad=True)
lr = 1e-1 # 学习率
n_iters = 1000 # 迭代次数

标准梯度下降 (SGD)

X_clone = X.clone().detach().requires_grad_(True)
optimizer_sgd = torch.optim.SGD([X_clone], lr=lr)
X_arr_sgd = gradient_descent(X_clone, optimizer_sgd, n_iters)
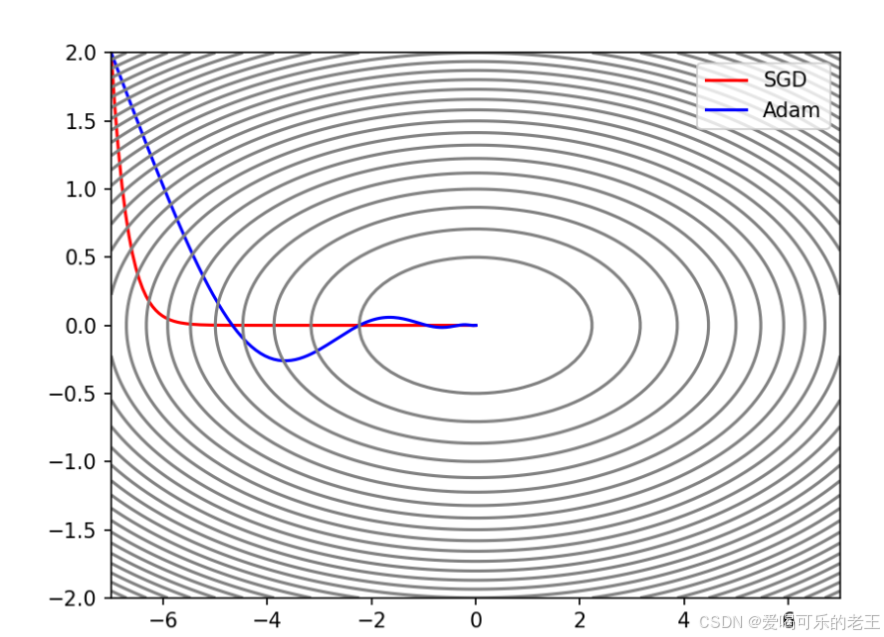
plt.plot(X_arr_sgd[:, 0], X_arr_sgd[:, 1], "r", label="SGD")

PyTorch内置Adam优化器

X_clone = X.clone().detach().requires_grad_(True)
optimizer_adam = torch.optim.Adam([X_clone], lr=lr, betas=(0.9, 0.999))
X_arr_adam_builtin = gradient_descent(X_clone, optimizer_adam, n_iters)
plt.plot(X_arr_adam_builtin[:, 0], X_arr_adam_builtin[:, 1], "b", label="Adam (Built-in)")

手动实现的Adam优化器

X_clone = X.clone().detach().requires_grad_(True)
X_arr_adam_manual = adam_manual(X_clone, lr=lr, betas=(0.9, 0.999), n_iters=n_iters)
plt.plot(X_arr_adam_manual[:, 0], X_arr_adam_manual[:, 1], c="orange", linestyle="--", linewidth=3, alpha=0.7, label="Adam (Manual)")

绘制目标函数的等高线

x1_grid, x2_grid = np.meshgrid(np.linspace(-7, 7, 100), np.linspace(-4.5, 4.5, 100))
y_grid = w.detach().numpy()[0, 0] * x1_grid ** 2 + w.detach().numpy()[1, 0] * x2_grid ** 2
plt.contour(x1_grid, x2_grid, y_grid, levels=30, colors="gray", alpha=0.5)

图形美化

plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Optimization Trajectories Comparison")
plt.legend()
plt.grid(True, linestyle="--", alpha=0.5)
plt.axis("equal") # 保持坐标轴比例一致
plt.tight_layout()
plt.show()

三、通俗总结

新手入门：先试 Adam，大部分场景都能搞定；
对比实验：用 SGD 做基准，再用 Momentum 或 RMSProp 对比效果；
关键技巧：搭配学习率衰减，让模型后期收敛更精准；
核心逻辑：好的更新方法都是在 "快速接近最优解" 和 "精准收敛" 之间找平衡。

PyTorch参数更新方法

一、核心目标

二、常用更新方法（通俗理解 + 特点）

1. SGD（随机梯度下降）：基础款

2. Momentum（动量法）：带 "惯性" 的 SGD

定义初始参数和超参数

普通梯度下降 (SGD)

动量法 (Momentum)

绘制优化轨迹

绘制目标函数的等高线

图形美化

3. 学习率衰减：动态调整 "步长"

4. AdaGrad（自适应梯度）：给每个参数 "定制步长"

5. RMSProp：改进版 AdaGrad

6. Adam：集大成者

定义初始参数和超参数

标准梯度下降 (SGD)

PyTorch内置Adam优化器

手动实现的Adam优化器

绘制目标函数的等高线

图形美化

三、通俗总结