【刘二大人】PyTorch深度学习实践笔记 —— 第四集：反向传播（凝练版）

Lecture 4: Backpropagation (反向传播)

文章目录

[Lecture 4: Backpropagation (反向传播)](#Lecture 4: Backpropagation (反向传播))
- [1. 核心动机：为什么需要反向传播？](#1. 核心动机：为什么需要反向传播？)
- - （1）深度神经网络是什么样子的：
  - （2）如何神经网络解决求梯度问题
- [2. 理论基础：计算图 (Computational Graph)](#2. 理论基础：计算图 (Computational Graph))
- - [2.1 两个过程](#2.1 两个过程)
  - [2.2 链式法则与局部梯度](#2.2 链式法则与局部梯度)
- [3. 详细实例推导：双层神经网络 (Complex Example)](#3. 详细实例推导：双层神经网络 (Complex Example))
- - [Step 1: 前馈 (Forward) 构建计算图](#Step 1: 前馈 (Forward) 构建计算图)
  - [Step 2: 反向传播 (Backward) 计算梯度](#Step 2: 反向传播 (Backward) 计算梯度)
- [4. PyTorch 实现细节](#4. PyTorch 实现细节)
- - [4.1 核心数据结构: Tensor](#4.1 核心数据结构: Tensor)
  - [4.2 完整代码实现](#4.2 完整代码实现)
  - [4.3 常见坑点 (Pitfalls)](#4.3 常见坑点 (Pitfalls))
- [5. 课后作业](#5. 课后作业)
- - [作业 1: 扩展到二次模型](#作业 1: 扩展到二次模型)
  - [作业 2: 手动推导](#作业 2: 手动推导)

1. 核心动机：为什么需要反向传播？

在第三讲中，我们学习了梯度下降算法。对于简单的线性模型（如 y = w ⋅ x y = w \cdot x y=w⋅x），我们可以手动推导损失函数对权重的导数公式（ ∂ L o s s ∂ w \frac{\partial Loss}{\partial w} ∂w∂Loss）。

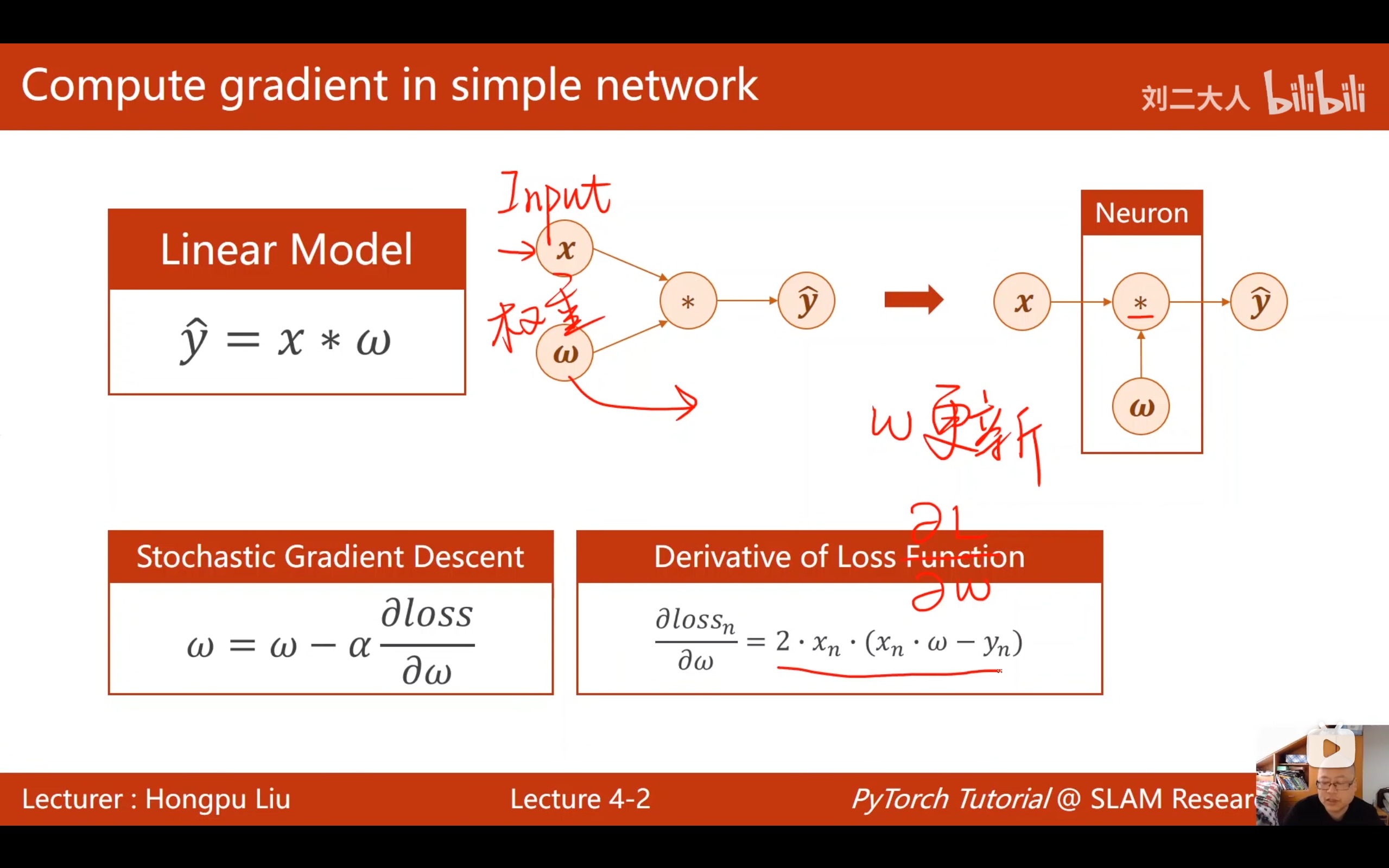
（1）深度神经网络是什么样子的：

深度神经网络不只是多个神经元线性叠加，如果都是线性叠加，那么最后的预测值y与所有特征也只会是线性关系 ，就处理不了非线性问题 了。

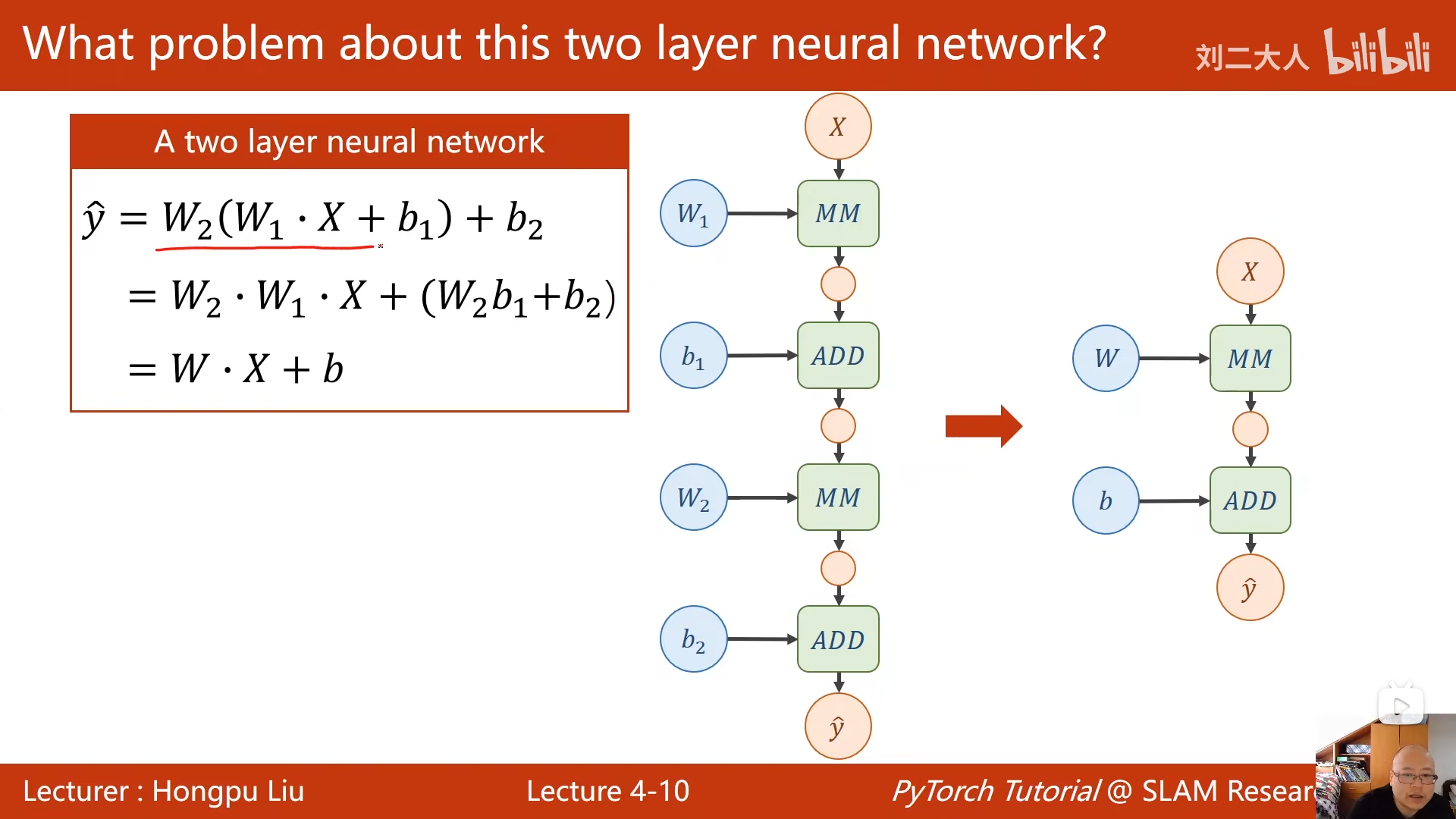
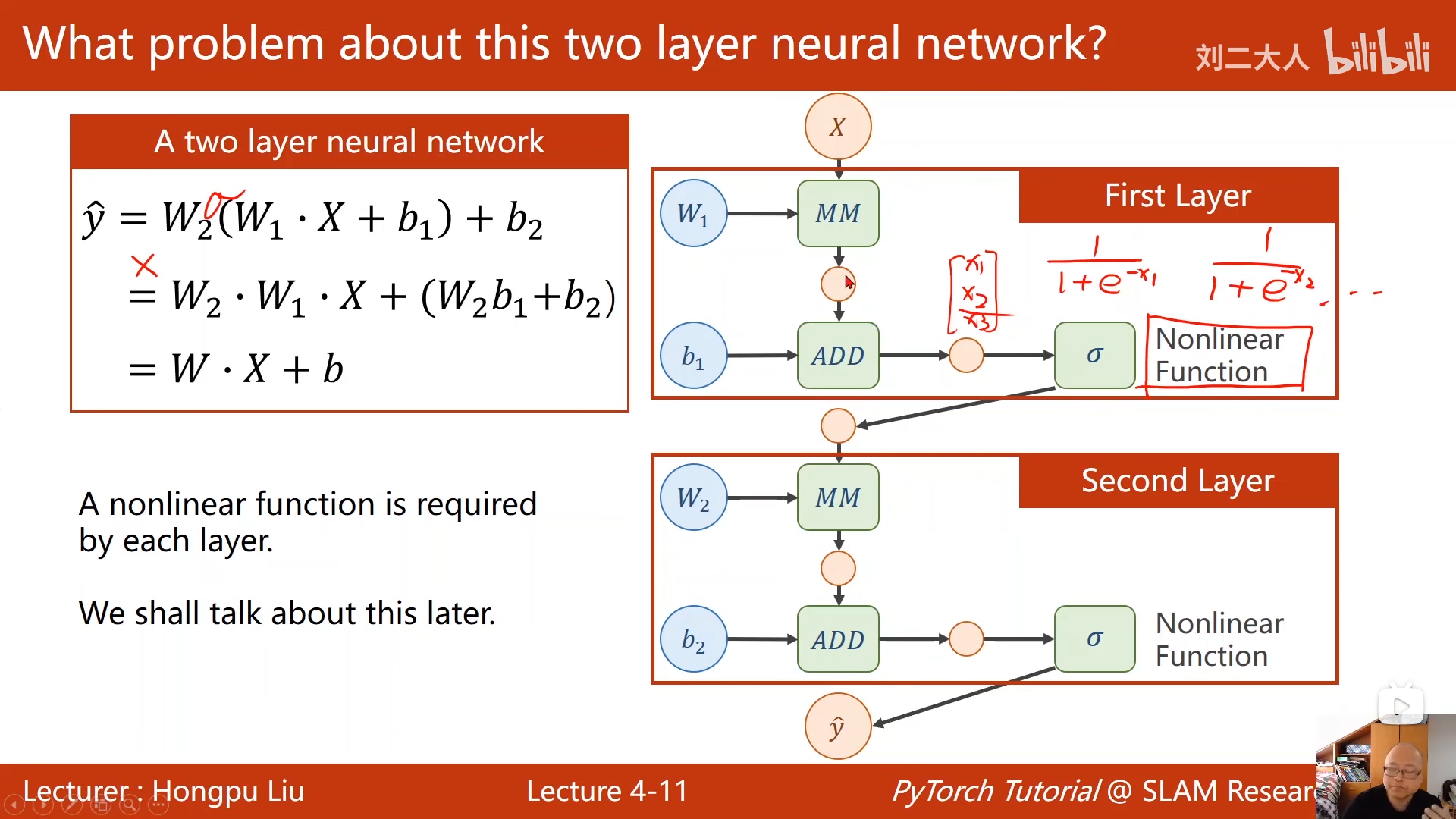
要解决这个问题，每个神经元在接收前层所有神经元传递的y值时，都需要经过激活函数 （非线性函数）的处理。通过这种方式，激活函数让深度神经网络从线性模型变为非线性模型，从而能够拟合现实中复杂的非线性关系。

所以神经网络是由许多带激活函数的神经元 编织的，每个神经元在不断接受前一层神经元们的线性组合 ，然后输出他们的**非线性形态（激活）**到下一层。

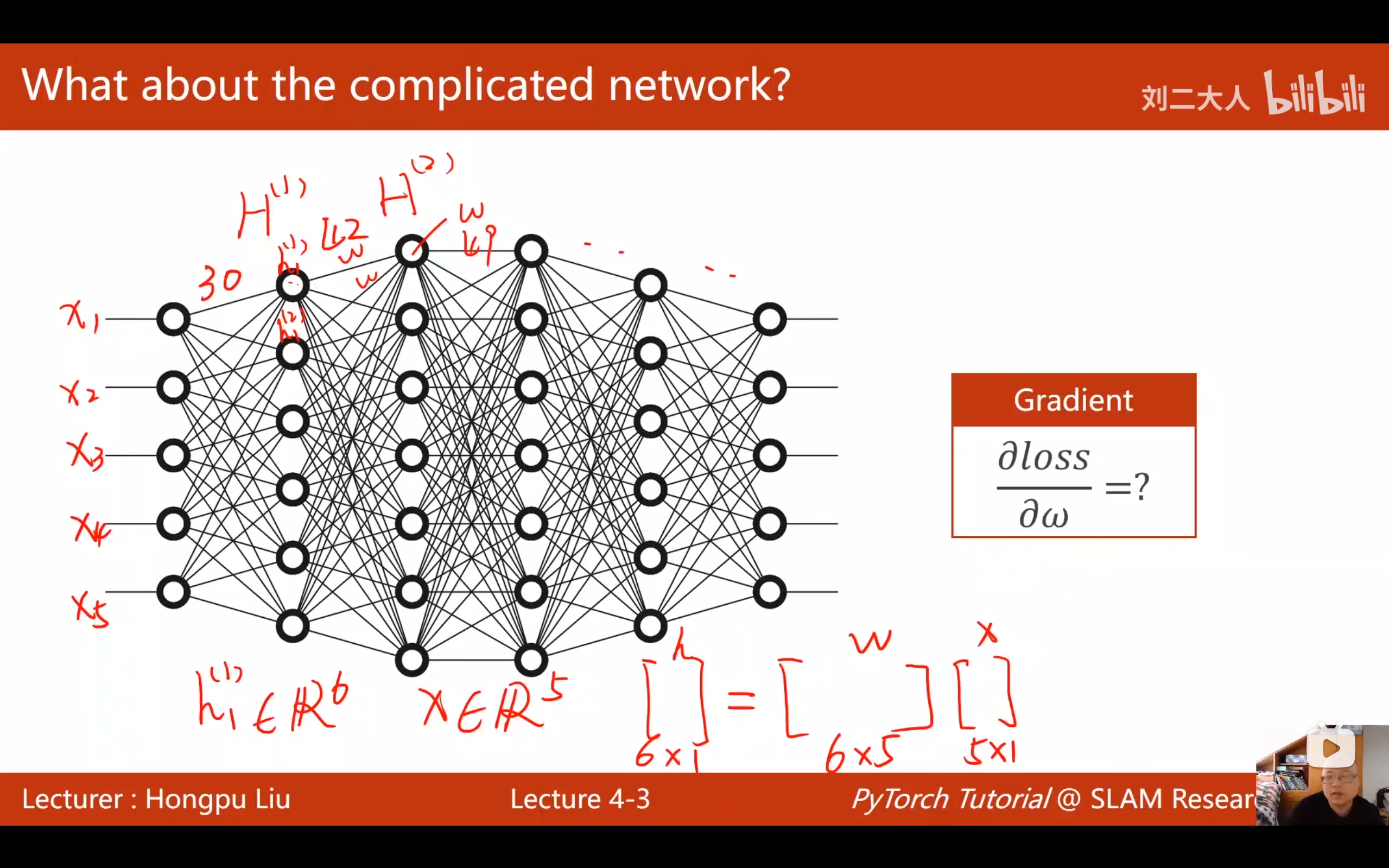
（2）如何神经网络解决求梯度问题

然而，深度学习模型（Deep Neural Networks） 通常非常复杂，求如何求解每一个神经元的参数梯度就变成了问题

之前我们在推导简单线性模型时，根据关系式一步步写出这个参数梯度表达式 ，但是这种方法在负责咋的神经网络不适合，因为要先从这个神经元开始求出Loss的表达式 ，然后再对这个神经元不断求偏导，公式非常的多，而且复杂，最后带入xy计算会变得麻烦。

不如直接从一开始就带入数字 计算具体的Loss数值，求偏导时也带入数值，直接计算，这种方法其实就是反向传播。他和前一种方法的本质是直接带入数字 ，减少多余计算。

2. 理论基础：计算图 (Computational Graph)

反向传播的核心思想是将复杂的数学运算分解为一系列简单的原子操作，并用图（Graph）的形式表示。

2.1 两个过程

前馈 (Forward) : 输入数据 x x x，经过一系列运算节点，最终计算出预测值 y ^ \hat{y} y^ 和损失 L o s s Loss Loss。
反馈 (Backward) : 从 Loss 开始，利用链式法则 (Chain Rule) ，沿着图的反方向传播梯度，直到计算出所有叶子节点（权重 w w w）的梯度。

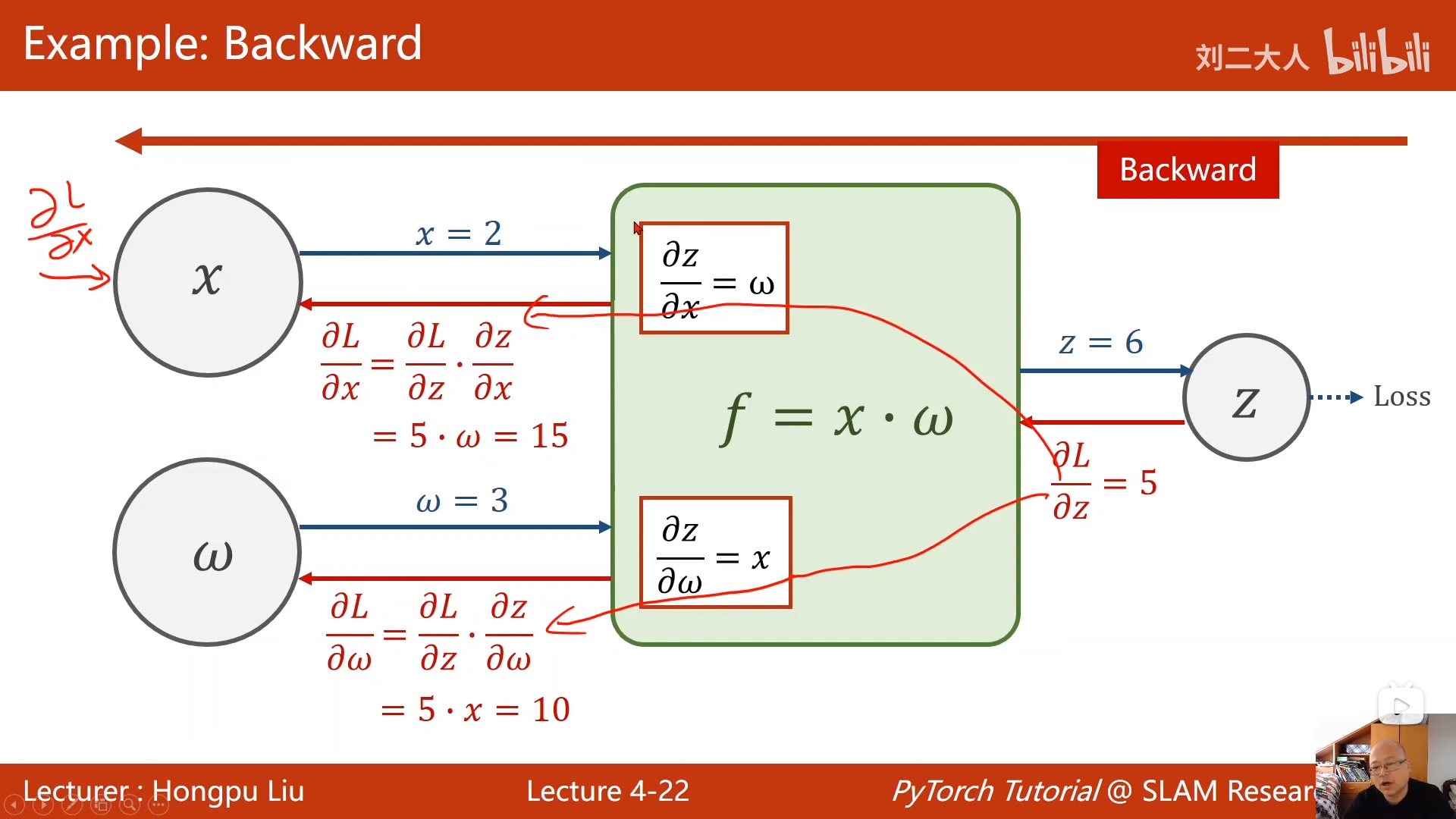
2.2 链式法则与局部梯度

在计算图中，每一个节点（Operation）只需要关注自己的局部梯度。

假设某节点运算为 z = f ( x , y ) z = f(x, y) z=f(x,y)：

在该节点，我们可以很容易求出局部导数 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z 和 ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z。
反向传播时，我们会从上游节点接收到一个全局梯度 ∂ L ∂ z \frac{\partial L}{\partial z} ∂z∂L。
根据链式法则，我们可以将梯度传递给下游：
- 传给 x x x 的梯度： ∂ L ∂ x = ∂ L ∂ z ⋅ ∂ z ∂ x \frac{\partial L}{\partial x} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial x} ∂x∂L=∂z∂L⋅∂x∂z
- 传给 y y y 的梯度： ∂ L ∂ y = ∂ L ∂ z ⋅ ∂ z ∂ y \frac{\partial L}{\partial y} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial y} ∂y∂L=∂z∂L⋅∂y∂z

核心优势：无论图多么复杂，每个节点只负责"接收上游梯度，乘以局部梯度，分发给下游"。

3. 详细实例推导：双层神经网络 (Complex Example)

为了展示反向传播的真正威力，我们来看一个包含隐藏层 和激活函数的复杂例子。

模型结构:

输入: x x x
隐藏层: z = w 1 ⋅ x + b z = w_1 \cdot x + b z=w1⋅x+b
激活函数: h = ReLU ( z ) h = \text{ReLU}(z) h=ReLU(z) (如果 z > 0 , h = z z>0, h=z z>0,h=z; 否则 h = 0 h=0 h=0)
输出层: y ^ = w 2 ⋅ h \hat{y} = w_2 \cdot h y^=w2⋅h
损失: L = ( y ^ − y ) 2 L = (\hat{y} - y)^2 L=(y^−y)2

初始数值:

数据: x = 2 , y = 0 x=2, y=0 x=2,y=0
权重: w 1 = 3 , b = − 2 , w 2 = 1 w_1=3, b=-2, w_2=1 w1=3,b=−2,w2=1

Step 1: 前馈 (Forward) 构建计算图

我们需要算出损失 L L L。

线性节点 (Linear) : z z z
- z = w 1 ⋅ x + b = 3 ⋅ 2 + ( − 2 ) = 4 z = w_1 \cdot x + b = 3 \cdot 2 + (-2) = 4 z=w1⋅x+b=3⋅2+(−2)=4
激活节点 (ReLU) : h h h
- h = ReLU ( 4 ) = 4 h = \text{ReLU}(4) = 4 h=ReLU(4)=4 (因为 4 > 0 4 > 0 4>0)
输出节点 (Linear) : y ^ \hat{y} y^
- y ^ = w 2 ⋅ h = 1 ⋅ 4 = 4 \hat{y} = w_2 \cdot h = 1 \cdot 4 = 4 y^=w2⋅h=1⋅4=4
损失节点 (Loss) : L L L
- L = ( y ^ − y ) 2 = ( 4 − 0 ) 2 = 16 L = (\hat{y} - y)^2 = (4 - 0)^2 = 16 L=(y^−y)2=(4−0)2=16

Step 2: 反向传播 (Backward) 计算梯度

我们的目标是求出所有参数 w 1 , w 2 , b w_1, w_2, b w1,w2,b 的梯度。我们将从 L L L 开始，一步步往回推。

1. Loss 对 y ^ \hat{y} y^ 的梯度

∂ L ∂ y ^ = 2 ( y ^ − y ) = 2 ( 4 − 0 ) = 8 \frac{\partial L}{\partial \hat{y}} = 2(\hat{y} - y) = 2(4 - 0) = \mathbf{8} ∂y^∂L=2(y^−y)=2(4−0)=8
(这是一个全局梯度，将传给上一层)

2. 求 w 2 w_2 w2 的梯度 (Output Layer)

根据链式法则: ∂ L ∂ w 2 = ∂ L ∂ y ^ ⋅ ∂ y ^ ∂ w 2 \frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial w_2} ∂w2∂L=∂y^∂L⋅∂w2∂y^
局部梯度: ∂ y ^ ∂ w 2 = h = 4 \frac{\partial \hat{y}}{\partial w_2} = h = 4 ∂w2∂y^=h=4
最终梯度 : 8 ⋅ 4 = 32 8 \cdot 4 = \mathbf{32} 8⋅4=32

3. 求 h h h 的梯度 (传递给隐藏层)

根据链式法则: ∂ L ∂ h = ∂ L ∂ y ^ ⋅ ∂ y ^ ∂ h \frac{\partial L}{\partial h} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial h} ∂h∂L=∂y^∂L⋅∂h∂y^
局部梯度: ∂ y ^ ∂ h = w 2 = 1 \frac{\partial \hat{y}}{\partial h} = w_2 = 1 ∂h∂y^=w2=1
传递梯度 : 8 ⋅ 1 = 8 8 \cdot 1 = \mathbf{8} 8⋅1=8

4. 求 z z z 的梯度 (过激活函数)

根据链式法则: ∂ L ∂ z = ∂ L ∂ h ⋅ ∂ h ∂ z \frac{\partial L}{\partial z} = \frac{\partial L}{\partial h} \cdot \frac{\partial h}{\partial z} ∂z∂L=∂h∂L⋅∂z∂h
局部梯度 (ReLU导数): 因为 z = 4 > 0 z=4 > 0 z=4>0, 导数为 1 1 1。
传递梯度 : 8 ⋅ 1 = 8 8 \cdot 1 = \mathbf{8} 8⋅1=8

5. 求 w 1 w_1 w1 和 b b b 的梯度 (Hidden Layer)

对于 w 1 w_1 w1 :
- ∂ L ∂ w 1 = ∂ L ∂ z ⋅ ∂ z ∂ w 1 \frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial w_1} ∂w1∂L=∂z∂L⋅∂w1∂z
- 局部梯度: ∂ z ∂ w 1 = x = 2 \frac{\partial z}{\partial w_1} = x = 2 ∂w1∂z=x=2
- 最终梯度 : 8 ⋅ 2 = 16 8 \cdot 2 = \mathbf{16} 8⋅2=16
对于 b b b :
- ∂ L ∂ b = ∂ L ∂ z ⋅ ∂ z ∂ b \frac{\partial L}{\partial b} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial b} ∂b∂L=∂z∂L⋅∂b∂z
- 局部梯度: ∂ z ∂ b = 1 \frac{\partial z}{\partial b} = 1 ∂b∂z=1
- 最终梯度 : 8 ⋅ 1 = 8 8 \cdot 1 = \mathbf{8} 8⋅1=8

总结 :

通过反向传播，我们一次性算出了三个参数的梯度：

∇ w 1 = 16 \nabla w_1 = 16 ∇w1=16
∇ b = 8 \nabla b = 8 ∇b=8
∇ w 2 = 32 \nabla w_2 = 32 ∇w2=32

更新参数时，我们将沿着梯度的反方向调整它们。

4. PyTorch 实现细节

PyTorch 的核心竞争力在于其动态计算图 (Dynamic Computational Graph)。我们通过编写普通的代码来构建图，每一行计算都会动态地在内存中建立图结构。

4.1 核心数据结构: Tensor

Tensor (张量) 是 PyTorch 中的基本数据单元。

data: 保存张量本身的数值（权重值）。
grad: 保存损失函数对该张量的梯度（也是一个 Tensor）。
grad_fn: 指向创建该 Tensor 的函数（用于反向传播）。
is_leaf: 指示是否为叶子节点（用户创建的节点，如权重）。

关键属性 : requires_grad=True

默认创建的 Tensor requires_grad=False。
必须显式设置为 True，PyTorch 才会跟踪其运算并构建计算图。

4.2 完整代码实现

python 复制代码

import torch

# 1. 准备数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# 2. 定义权重 (这是一个 Tensor)
# requires_grad=True: 告诉 PyTorch 我们需要对 w 求导
w = torch.Tensor([1.0]) 
w.requires_grad = True 

def forward(x):
    # w 是 Tensor, x 会被自动广播为 Tensor
    # 这一步不是简单的数字乘法，而是在构建计算图的一个乘法节点
    return x * w 

def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

# 3. 训练过程
print("Predict (before training)", 4, forward(4).item())

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        # --- Build Computation Graph ---
        l = loss(x, y) # l 是一个 Tensor，代表当前的计算图
        
        # --- Backward ---
        # 自动计算所有 requires_grad=True 的叶子节点的梯度
        # 计算结果存入 w.grad 中
        l.backward() 
        
        # --- Update ---
        # ⚠️ 关键点 1: w.grad.data
        # 梯度本身也是 Tensor，我们只需要它的数值
        # ⚠️ 关键点 2: w.data
        # 更新权重时，不能直接用 w = w - ... 否则会建立新的计算图节点
        # 我们这里只是想修改数值，不希望此操作被记录到图中，所以用 .data
        w.data = w.data - 0.01 * w.grad.data
        
        # ⚠️ 关键点 3: 梯度清零
        # w.grad 会累加 (Assign Add)，如果不清零，下次 backward 会加上这次的梯度
        w.grad.data.zero_()
        
    print(f"Epoch {epoch}: Loss={l.item()}") # .item() 取出标量数值

print("Predict (after training)", 4, forward(4).item())

4.3 常见坑点 (Pitfalls)

梯度累加:
- PyTorch 设计上，.backward() 产生的梯度是累加到 .grad 里的。
- 原因: 有时候通过不同的路径计算 Loss，或者在多任务学习中，需要聚合多个 Loss 的 gradient。
- 后果 : 如果不手动清零 (w.grad.data.zero_())，梯度会越来越大，导致训练发散。
计算图导致的内存泄漏:
- 错误写法: sum_loss += loss
- 问题: loss 是一个 Tensor，且包含整个计算图的历史。直接累加会把每一轮的计算图都连接起来，导致内存爆炸。
- 正确写法: sum_loss += loss.item() (取 python 标量值，脱离计算图)。
计算图是动态的:
- 每次执行 l = loss(x, y) 和 l.backward()，计算图被创建，反向传播后（默认）被释放。
- 如下一次循环，会创建全新的图。

5. 课后作业

作业 1: 扩展到二次模型

实现一个非线性模型: y = w 1 x 2 + w 2 x + b y = w_1 x^2 + w_2 x + b y=w1x2+w2x+b

需要训练三个参数： w 1 , w 2 , b w_1, w_2, b w1,w2,b。

提示:

定义三个 Tensor，均设为 requires_grad=True。
前馈函数改为: return w1 * x**2 + w2 * x + b。
backward 会自动计算三个参数的梯度。

作业 2: 手动推导

使用 x = 1 , y = 2 x=1, y=2 x=1,y=2 的例子，手动推导上述二次模型的梯度计算过程，画出计算图。