线性回归是机器学习中最基础、最经典的模型,看似只是"画一条直线",背后却藏着正态分布、极大似然估计、最小二乘法等统计核心思想。本文从简单线性回归出发,拆解底层原理,再延伸到多元线性回归实战,帮你彻底搞懂线性回归的来龙去脉。
一、起点:简单线性回归------用一条直线拟合关系
简单线性回归的核心是:用一条直线描述自变量 x 和因变量 y 的线性关系,比如用"体重"预测"血压收缩压"、用"身高"预测"体重"。
1. 数学模型
简单线性回归的公式非常直观:
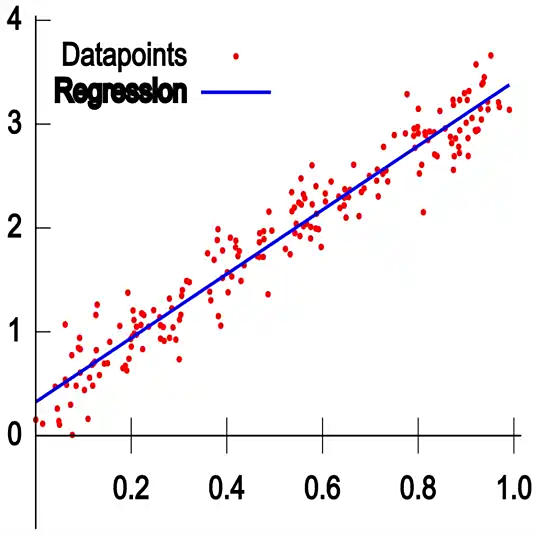
• y:因变量(真实值,如血压收缩压)
• x:自变量(特征,如体重)
• :权重(斜率),表示 x 每增加1个单位,y 的平均变化量
• :偏置(截距),表示 x=0 时 y 的基础值
• :误差项,真实值与预测值的偏差
2. 关键假设:误差项服从正态分布
为什么线性回归能成立?核心假设是:误差项服从均值为0、方差
的正态分布,即:
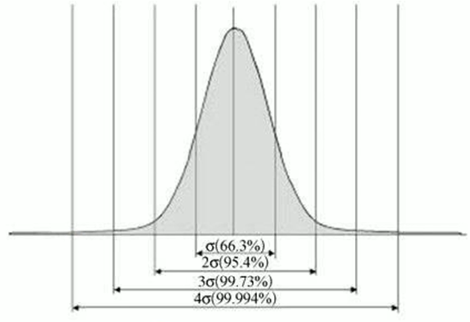
这个假设的合理性:
-
误差是多种微小随机因素的叠加(如测量仪器误差、个体差异波动),根据中心极限定理,大量独立随机变量的和近似服从正态分布;
-
正态分布的数学性质简洁,方便后续用极大似然估计求解参数。
基于此,给定 x 时,y 的分布也服从正态分布:
二、原理推导:从极大似然估计到最小二乘法
我们的目标是找到最优的和 b,让模型预测尽可能接近真实值。这个过程可以通过极大似然估计推导,最终等价于最小二乘法。
1. 极大似然估计(MLE):让"观测到当前数据"的概率最大
极大似然估计的核心思想:找到一组参数,使得当前观测到的所有数据出现的概率最大。
对于 m 个独立样本,
,...,
,似然函数(所有样本出现的联合概率)为:
由于误差服从正态分布,单个样本的概率密度函数为:
代入似然函数,取对数(将乘法转为加法,简化计算),得到对数似然函数:
2. 最小二乘法:极大似然估计的等价目标
要最大化对数似然函数,由于前半部是
常数,只需最小化后半部分:
这就是最小二乘法(OLS)的目标函数:所有样本的预测误差平方和最小。
简单来说:在误差服从正态分布的假设下,极大似然估计等价于最小二乘法。
3. 最小二乘法的闭式解
对目标函数关于 和 b 求偏导,令导数为0,可直接解出最优参数:
其中 、
分别是 x 和 y 的均值。
三、延伸:多元线性回归------多特征的线性拟合
实际场景中,影响因变量的因素往往不止一个,比如预测血压收缩压,需要考虑"体重、年龄"等多个特征,这就是多元线性回归。
1. 数学模型
多元线性回归是简单线性回归的扩展,公式为:
• ,
,...,
:m个自变量(特征,如体重、年龄)
•,
,...,
:每个特征对应的权重
• 误差项仍服从
,原理与简单线性回归一致。
写成矩阵形式更简洁:
其中 X 是 m*n 的特征矩阵, 是 n*1 的权重向量。
2. 多元线性回归的闭式解
同样通过最小二乘法,可推导出矩阵形式的闭式解:
其中 包含权重
,
,
和偏置 b(需在 X 中添加一列全1向量)。
四、实战:用多元线性回归预测血压收缩压
下面通过Python实战,用"体重、年龄"两个特征预测血压收缩压,完整演示多元线性回归的流程。
1. 数据准备
我们使用包含"体重、年龄、血压收缩压"的CSV数据集:
python
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.model_selection import train_test_split
# 读取数据
df = pd.read_csv("多元线性回归.csv", encoding="gbk")
print("数据集前5行:")
print(df.head())
print("\n数据集描述性统计:")
print(df.describe())2. 模型训练与参数求解
python
# 划分特征和目标
X = df[["体重", "年龄"]] # 特征:体重、年龄
y = df["血压收缩"] # 目标:血压收缩压
# 划分训练集和测试集(可选,用于评估泛化能力)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练多元线性回归模型
model = LinearRegression(fit_intercept=True) # fit_intercept=True表示包含偏置b
model.fit(X_train, y_train)
# 输出模型参数
print("\n===== 多元线性回归模型结果 =====")
print(f"系数(体重, 年龄): {model.coef_}")
print(f"截距: {model.intercept_:.2f}")
print(f"回归方程: 血压收缩压 = {model.intercept_:.2f} + {model.coef_[0]:.2f}*体重 + {model.coef_[1]:.2f}*年龄")3. 模型评估与预测
python
# 模型预测
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# 评估指标
train_r2 = r2_score(y_train, y_train_pred) # 训练集R²:拟合优度,越接近1越好
test_r2 = r2_score(y_test, y_test_pred) # 测试集R²:评估泛化能力
train_rmse = np.sqrt(mean_squared_error(y_train, y_train_pred)) # 训练集均方根误差
test_rmse = np.sqrt(mean_squared_error(y_test, y_test_pred)) # 测试集均方根误差
print("\n===== 模型评估 =====")
print(f"训练集R²得分: {train_r2:.4f}")
print(f"测试集R²得分: {test_r2:.4f}")
print(f"训练集RMSE: {train_rmse:.2f}")
print(f"测试集RMSE: {test_rmse:.2f}")
# 示例预测:体重80kg,年龄40岁
sample = pd.DataFrame({"体重": [80], "年龄": [40]})
predicted = model.predict(sample)
print("\n===== 示例预测 =====")
print(f"当体重为80kg,年龄为40岁时,预测血压收缩压为: {predicted[0]:.2f} mmHg")
4. 结果解读运行代码后,会得到:
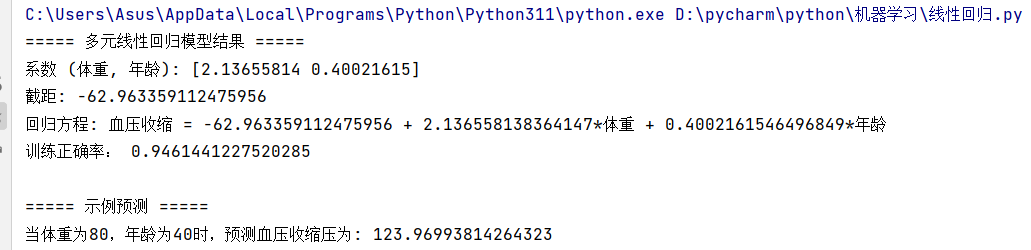
五、线性回归的优缺点与适用场景
优点
-
可解释性强:权重直接反映特征对目标的影响程度(如体重每增加1kg,血压收缩压平均增加多少);
-
计算高效:闭式解直接求解,无需迭代,训练速度快;
-
理论基础扎实:基于正态分布和极大似然估计,统计性质明确。
缺点
-
假设严格:要求特征与目标线性相关、误差服从正态分布、无多重共线性;
-
对异常值敏感:异常值会大幅影响最小二乘法的结果;
-
无法拟合非线性关系:需通过特征工程(如多项式特征)扩展。
适用场景
• 特征与目标存在明显线性关系的场景(如血压预测、房价预测);
• 对模型可解释性要求高的领域(如医疗分析、金融风控);
• 作为基线模型,对比复杂算法(如决策树、神经网络)的效果。
六、总结
线性回归从"一条直线"出发,背后是正态分布的误差假设、极大似然估计的参数求解逻辑,最终落地为最小二乘法的直观目标。从简单线性回归到多元线性回归,不仅是特征数量的增加,更是对线性关系建模能力的扩展。
掌握线性回归的底层原理,不仅能熟练应用模型解决实际问题,更能为理解复杂机器学习算法(如逻辑回归、神经网络)打下坚实基础。