STM32F769I-EVAL板载数字麦克风采集到的音频信号如下图所示:
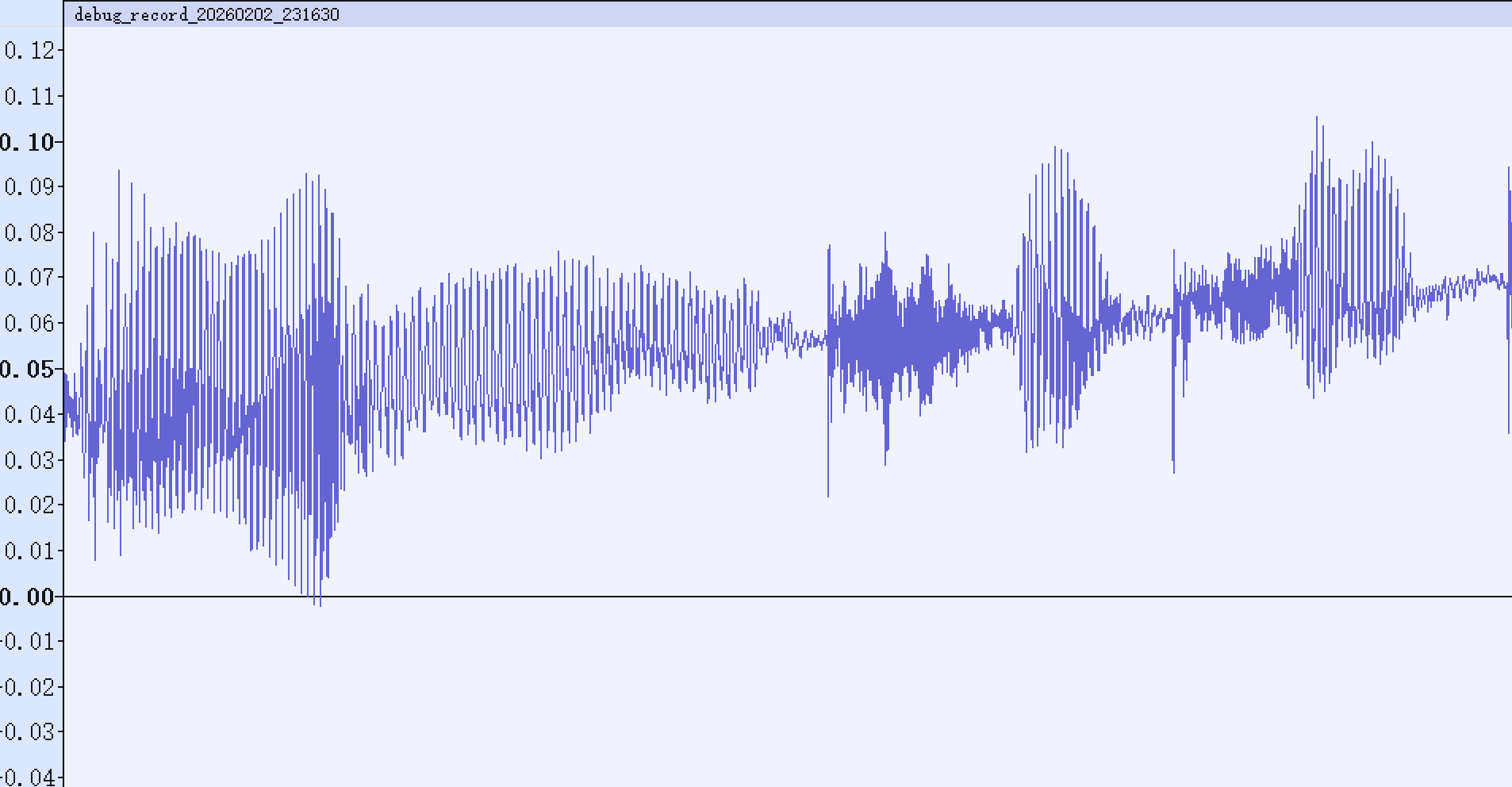
理想的音频信号应当围绕 0 轴对称分布。但可以明显看到,当前信号整体向正半轴偏移,存在明显的直流偏置( DC Offset)。这个会对静音检测和后续的音频处理带来影响。
由于直流信号频率为 0Hz,因此最直接、最有效的手段是:使用高通滤波器滤除直流分量。
1 FIR高通滤波器分析
FIR(Finite Impulse Response) 有限冲激响应滤波器,是数字信号处理(DSP)中最基础、最常用的滤波器类型之一。 FIR的输出信号是当前输入信号和过去一段时间的信号,通过一组固定的系数进行加权求和得到的:
:滤波器的输出信号
:滤波器的输入信号
:滤波器的系数
:滤波器的阶数
:当前的时间索引
形象理解:想象一个滑动窗口,窗口里的每一个采样点都乘以一个权重(系数),然后把这些乘积加起来,得到当前的输出值。窗口会随着时间向前移动,新的采样点进入窗口,旧的采样点离开窗口。
FIR可以轻易实现低通、高通、带通等各种复杂的频率特性,但我们的需求是过滤0HZ直流分量,这需要非常陡峭的滤波器,也就是需要非常高的阶数,计算量会非常大。
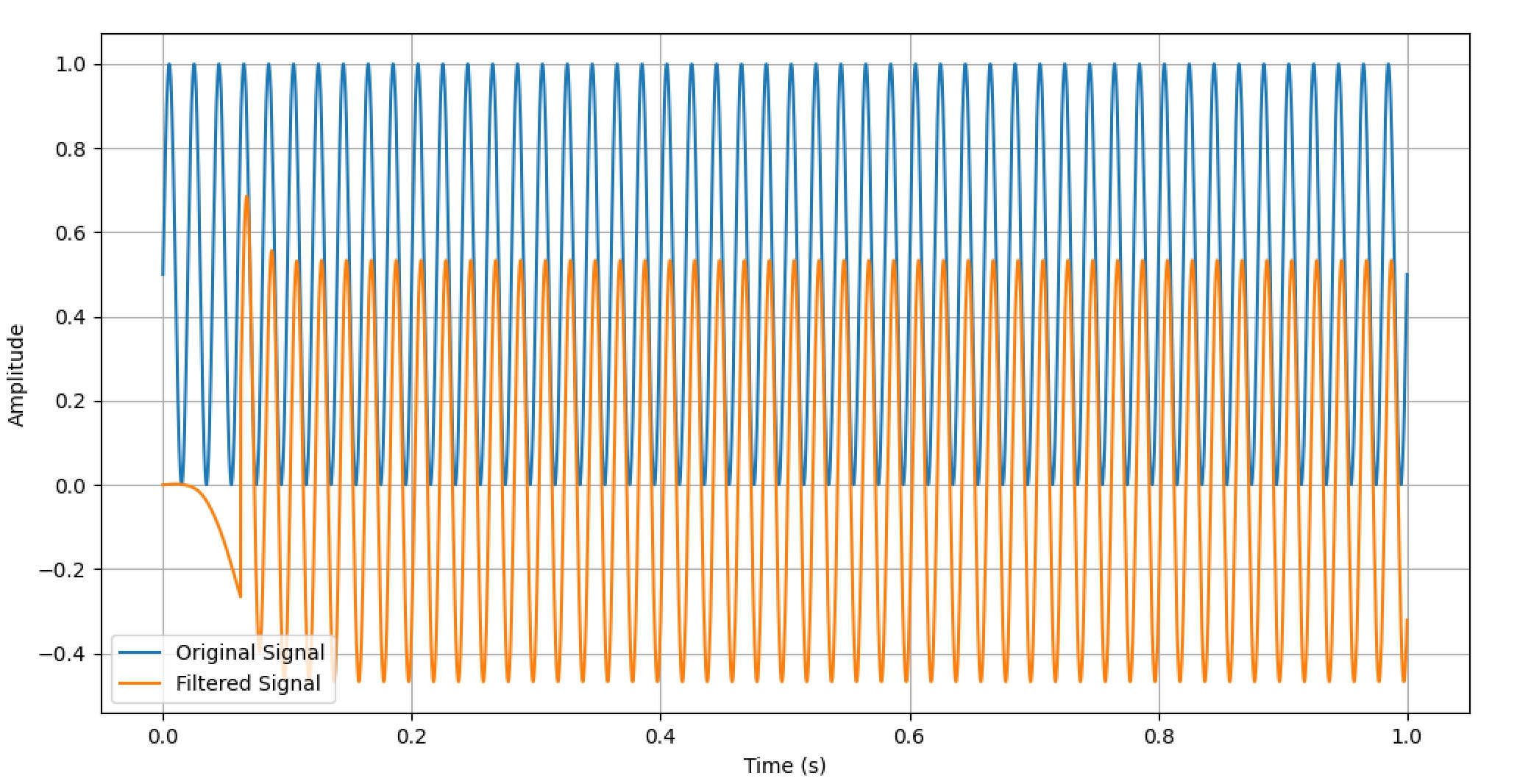
接下来我们用python的scipy.signal库来设计一个高通FIR滤波器。测试信号是一个50Hz的正弦波,加上一个DC偏置。滤波器的截止频率设置为10Hz,采样率为16kHz,测试下来滤波器的阶数需要达到2001阶,才能较好地滤除直流分量。
python
import numpy as np
from scipy.signal import firwin, lfilter
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as plt
# 参数
cutoff_frequency = 10 # 截止频率10Hz
sampling_rate = 16000 # 采样率16kHz
num_taps = 2001 # 滤波器阶数
# 计算FIR高通滤波器系数
filter_coeffs = firwin(num_taps, cutoff=cutoff_frequency, fs=sampling_rate, pass_zero=False)
# 时间轴
t = np.linspace(0, 1, sampling_rate)
# 生产带DC偏置的50Hz信号
signal = 0.5 * np.sin(2 * np.pi * 50 * t) + 0.5
# 应用FIR高通滤波器
filtered_data = lfilter(filter_coeffs, 1.0, signal)
# 渲染结果
plt.figure(figsize=(12, 6))
plt.plot(t, signal, label='Original Signal')
plt.plot(t, filtered_data, label='Filtered Signal')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()原始信号和输出信号波形对比:
2 IIR高通滤波器分析
IIR(Infinite Impulse Response) 无限冲激响应滤波器,是数字信号处理(DSP)中另一种常用的滤波器类型。与FIR滤波器不同,IIR滤波器具有反馈回路,其输出信号不仅依赖于当前和过去的输入信号,还依赖于过去的输出信号。
IIR最大的优势时用极小的计算量实现极陡峭的滤波效果。因为它有反馈回路,可以通过少量的系数实现复杂的频率特性。
通用差分方程为:
在工程实践中,最常用的是 二阶 IIR(Biquad):
ARM 库为了计算效率,将反馈项的符号定义为加法形式:
关键提示:这种定义差异意味着:当你使用 Python (scipy.signal) 或 MATLAB 生成系数后,必须将
和
取反 才能填入 ARM 的 coeffs 数组,否则滤波器会因正反馈而发散(导致输出无穷大)。
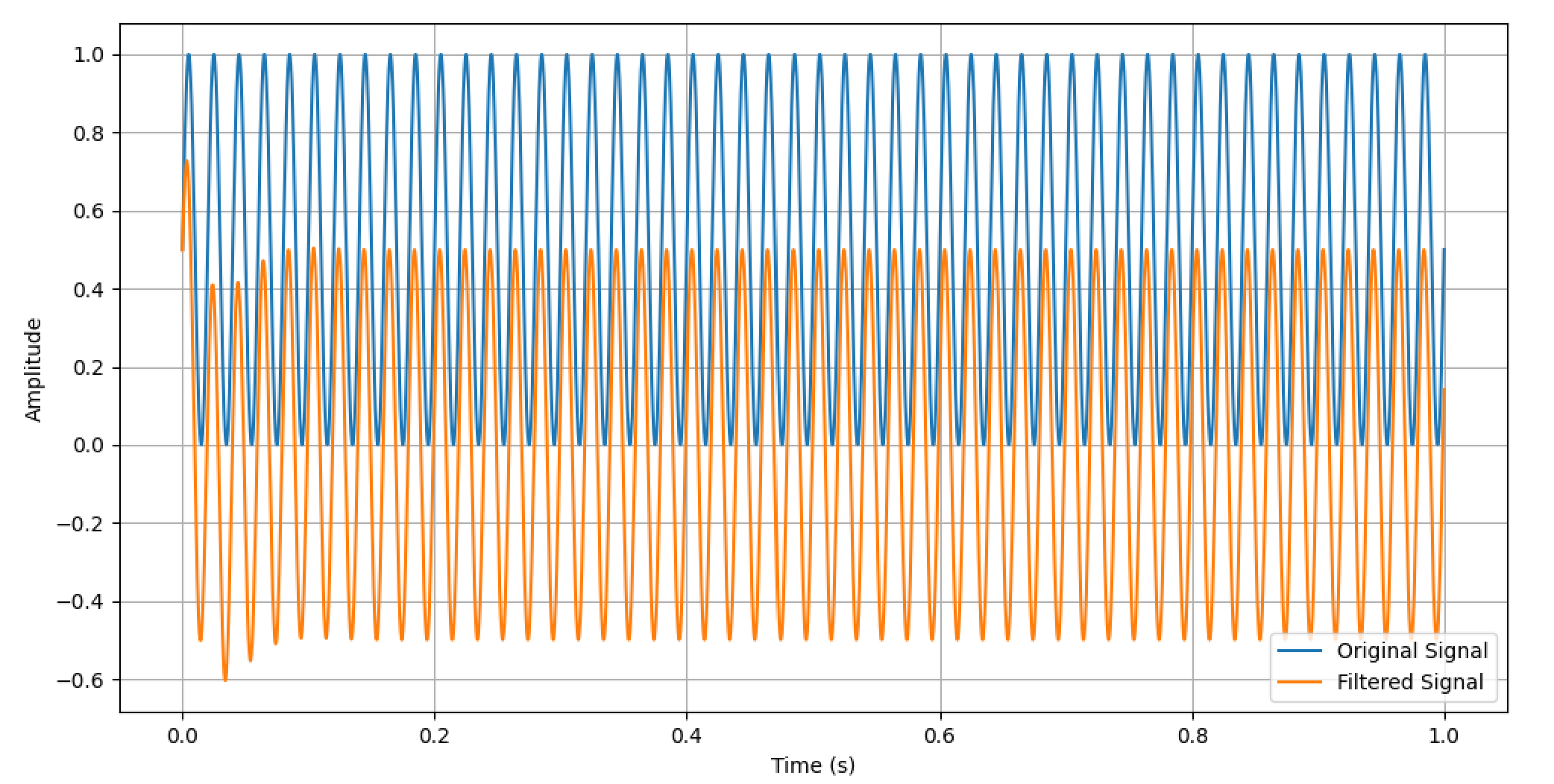
接下来我们用python的scipy.signal库来设计一个高通IIR滤波器。测试信号是一个50Hz的正弦波,加上一个DC偏置。滤波器的截止频率设置为10Hz,采样率为16kHz,测试下来只需要2阶的IIR滤波器,就能较好地滤除直流分量。
python
import numpy as np
from scipy.signal import butter, lfilter
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as plt
# 参数
cutoff_frequency = 10 # 截止频率10Hz
sampling_rate = 16000 # 采样率16kHz
num_taps = 2 # 滤波器阶数
# 时间轴
t = np.linspace(0, 1, sampling_rate)
# 生产带DC偏置的50Hz信号
signal = 0.5 * np.sin(2 * np.pi * 50 * t) + 0.5
# 设计IIR高通滤波器
# b,a即为滤波器系数
b, a = butter(num_taps, cutoff_frequency, btype='highpass', fs=sampling_rate)
print(f"IIR 系数 b (分子): {b}")
print(f"IIR 系数 a (分母): {a}")
# 应用IIR高通滤波器
filtered_data = lfilter(b, a, signal)
# 渲染结果
plt.figure(figsize=(12, 6))
plt.plot(t, signal, label='Original Signal')
plt.plot(t, filtered_data, label='Filtered Signal')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)
plt.show()原始信号和输出信号波形对比:
3 设计IIR滤波器
接下来,我们用python scipy库设计一个二阶IIR高通滤波器。
import scipy.signal as signal
import numpy as np
# 参数
cutoff_frequency = 10 # 截止频率10Hz
sampling_rate = 16000 # 采样率16kHz
num_taps = 2 # 滤波器阶数
# 设计IIR高通滤波器
# 输出sos格式,每一行是[b0, b1, b2, a0, a1, a2]
sos = signal.butter(num_taps, cutoff_frequency, btype='highpass', fs=sampling_rate, output='sos')
print(sos)
# ARM CMSIS-DSP要求顺粗:[b0, b1, b2, -a1, -a2], (注意 a0 被略过,a1/a2 取反)
arm_coeffs = [sos[0][0], sos[0][1], sos[0][2], -sos[0][4], -sos[0][5]]
# 打印滤波器系数为 C 语言数组格式 float16
print("const float iir_highpass_biquad_coeffs[5] = {")
for i, coeff in enumerate(arm_coeffs):
end_char = "," if i < len(arm_coeffs) - 1 else ""
print(" {:.6f}{}".format(np.float16(coeff), end_char))
print("};")sos 矩阵的结构为:
其中通常已被归一化为 1。
前面提到,CMSIS-DSP 的二阶 IIR(Biquad)因此,在将 sos 系数转换为 CMSIS-DSP 使用的格式时,需要对 sos 中的 和
取反,最终输出给 ARM DSP 的系数顺序为:
4 使用ARM DSP 库实现高通滤波器
ARM DSP 库是 ARM 公司为其 Cortex-M 处理器系列开发的一套高性能数字信号处理函数库。它提供了丰富的 DSP 算法和数学函数,涵盖了滤波器设计、傅里叶变换、矩阵运算、统计分析等多个领域。ARM DSP 库经过高度优化,能够充分利用 Cortex-M 处理器的硬件特性,如 SIMD 指令集和浮点运算单元,从而实现高效的计算性能。
4.1 在 STM32 工程中集成 DSP 库
以 STM32F779I-EVAL(Cortex-M7 核心)为例,介绍两种常见的集成方式:
方法一:通过 STM32CubeMX 快速集成
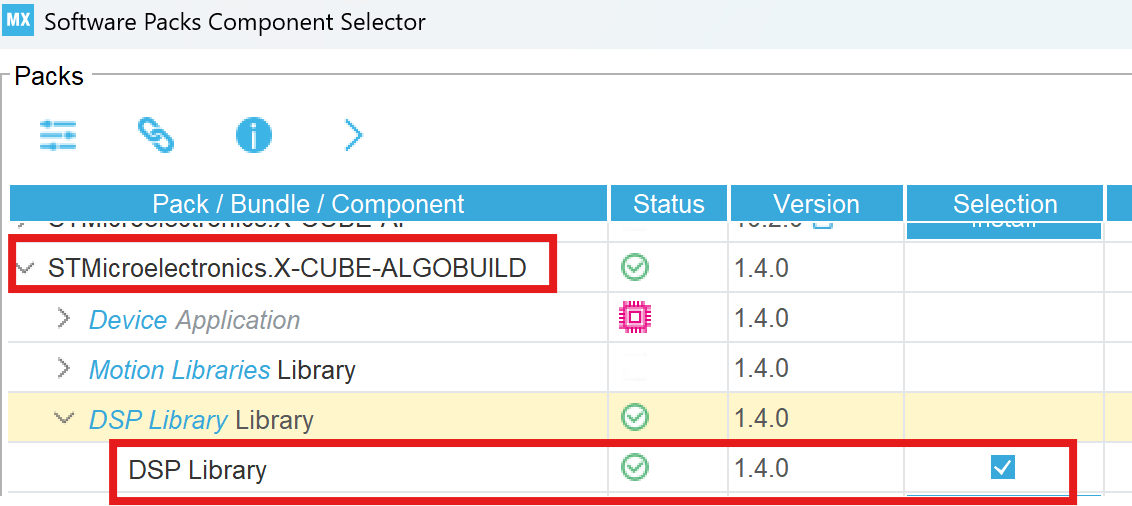
- 打开组件选择
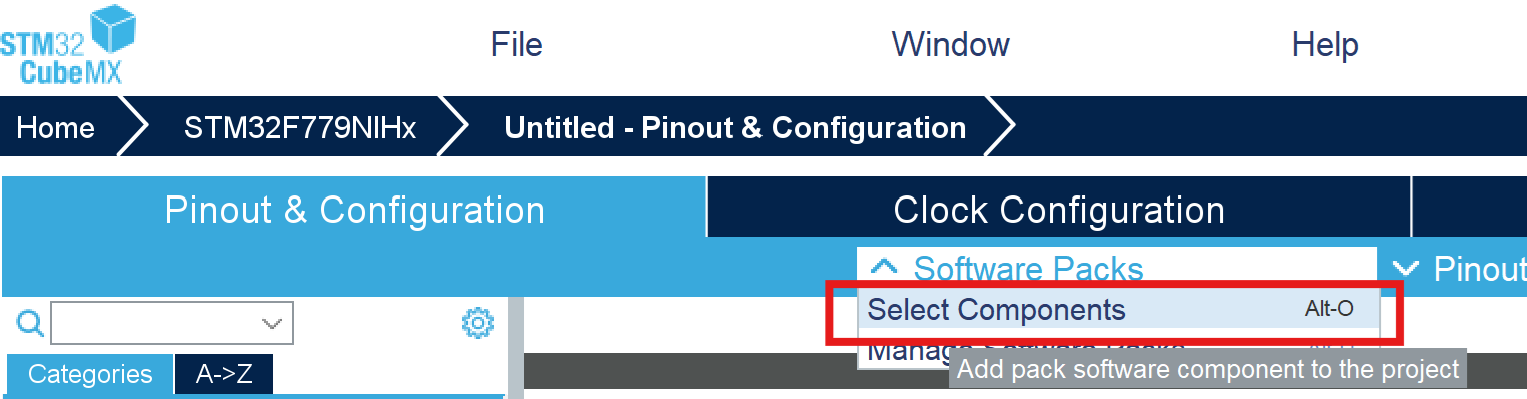
- 勾选DSP Library
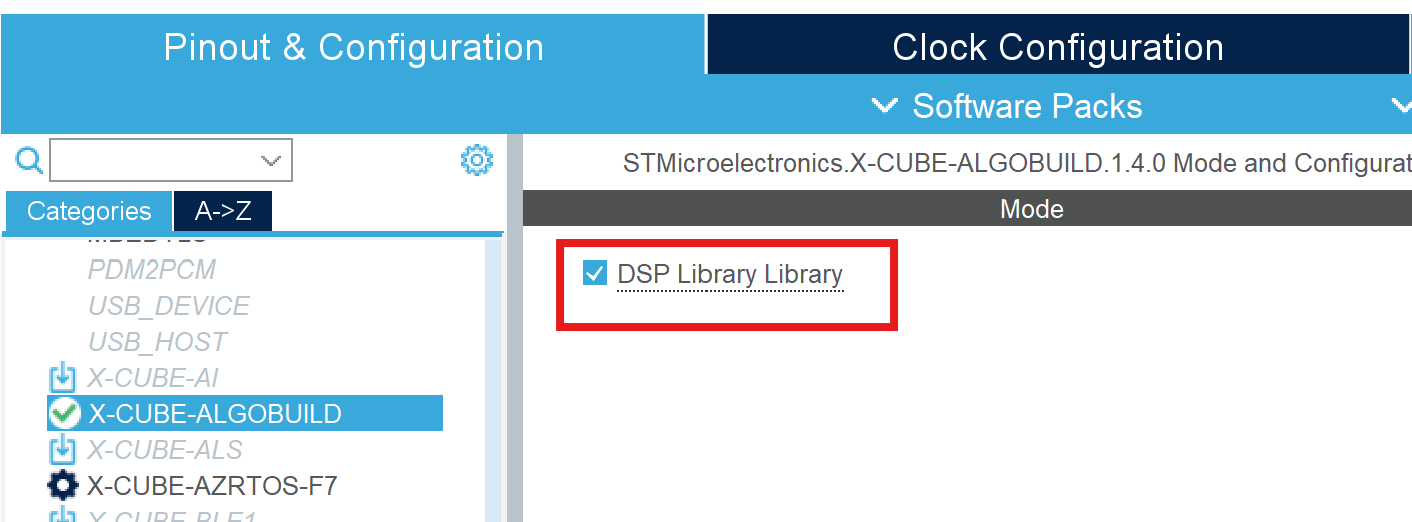
- 回到CubeMX主页面,勾选DSP Library Library
方法二:手动移植库文件
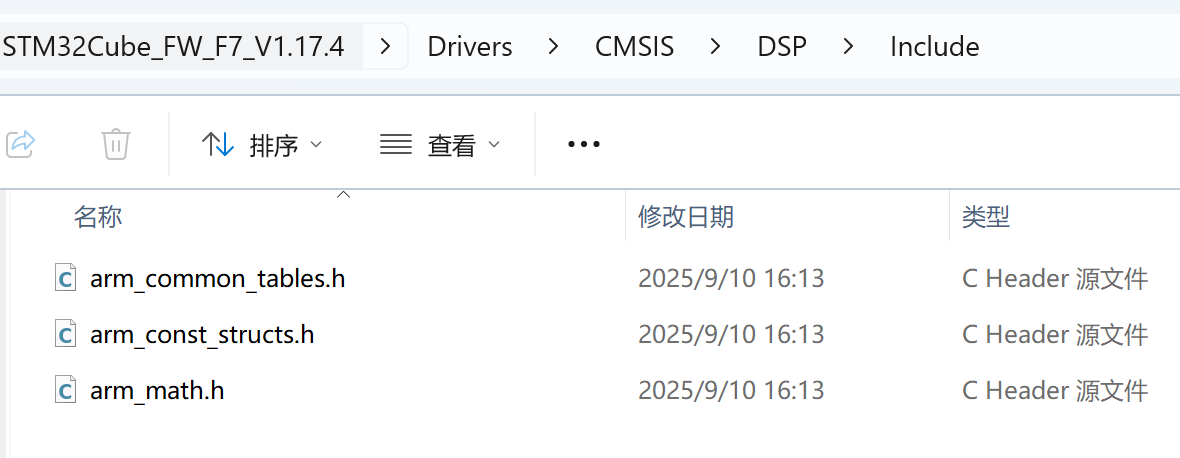
- 拷贝头文件:从 STM32Cube 固件包中提取 Include 文件夹下的所有 .h 文件。
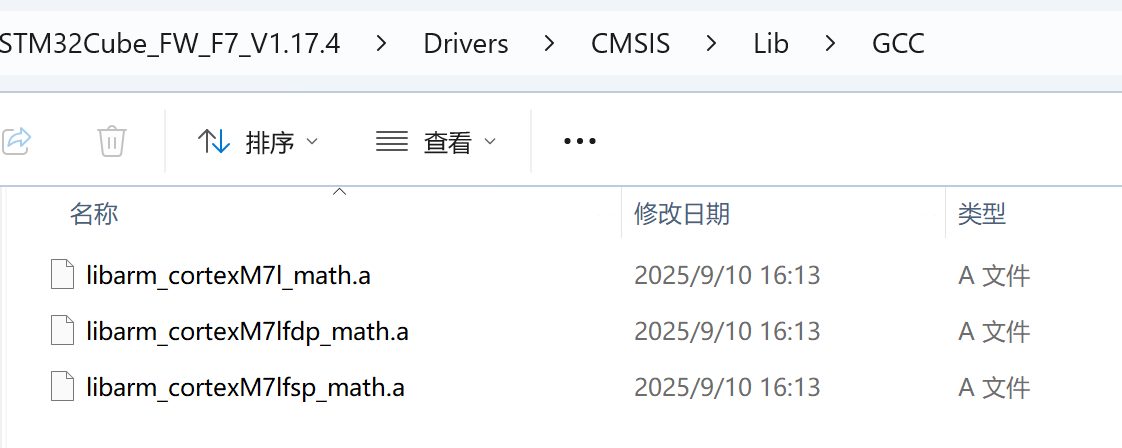
- 拷贝静态库 (.lib/.a):根据你的工具链(MDK-ARM 用 .lib,GCC 用 .a)选择对应的编译库。
- 配置路径:
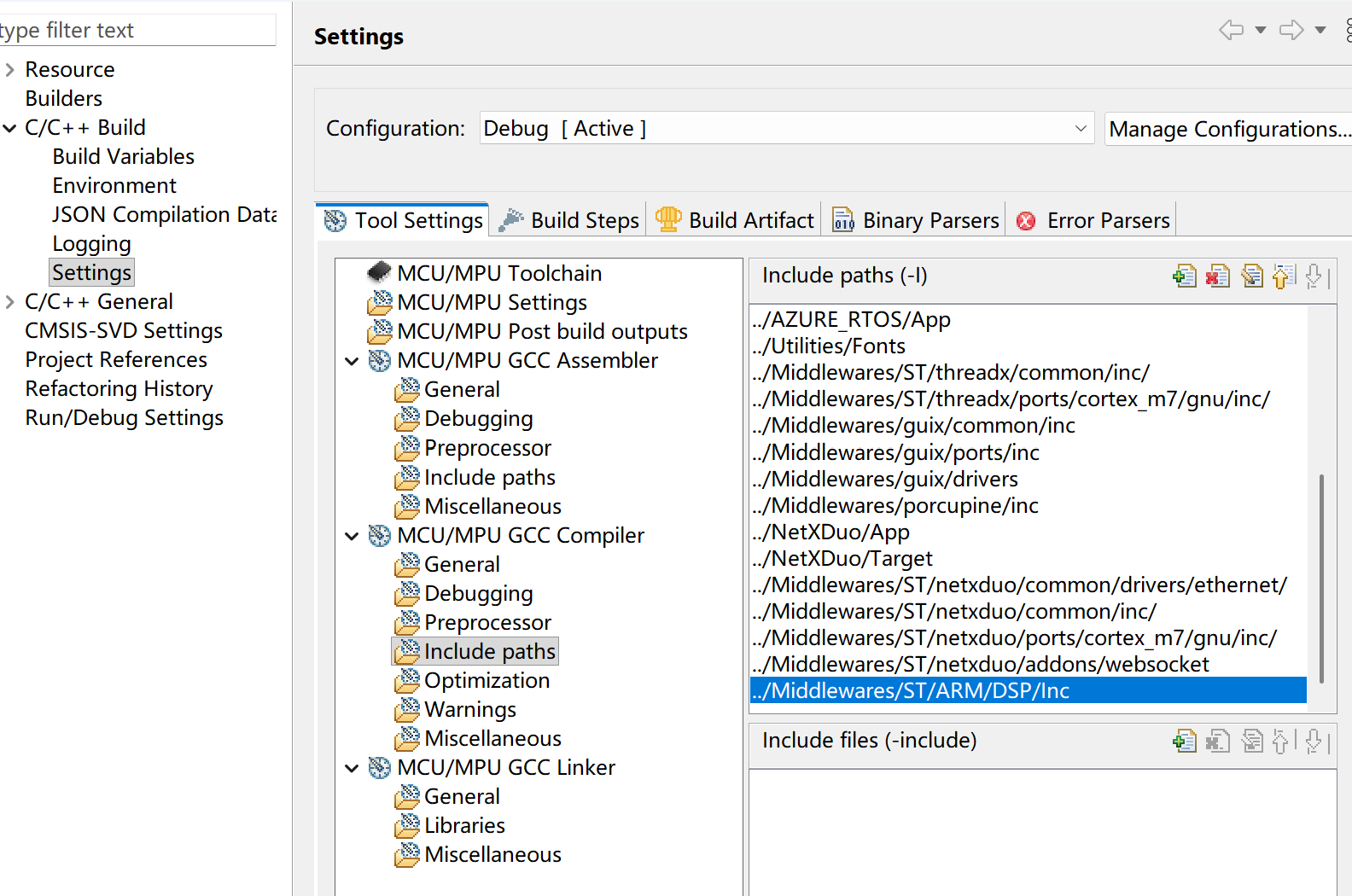
- 配置宏定义:
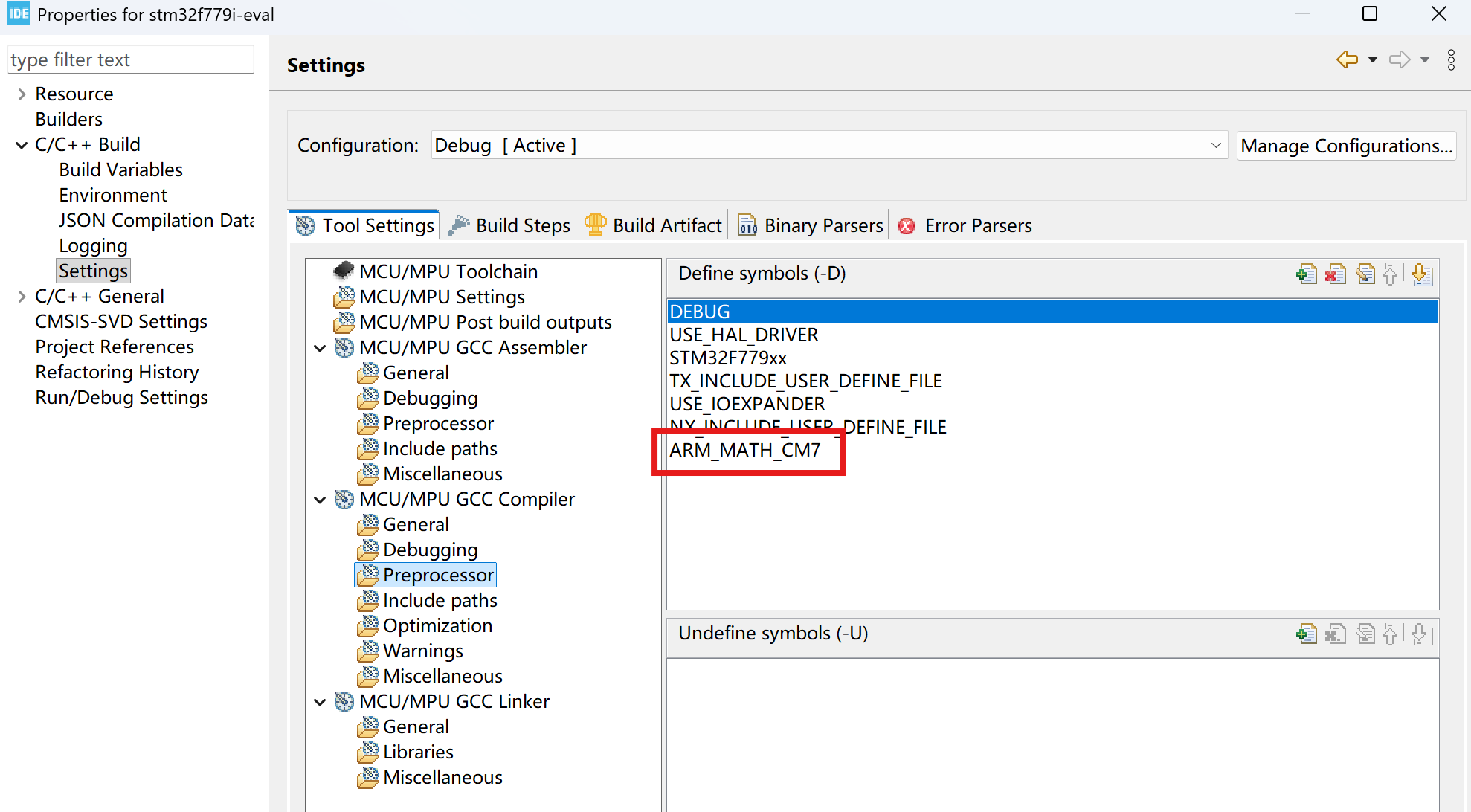
- 启用浮点数:
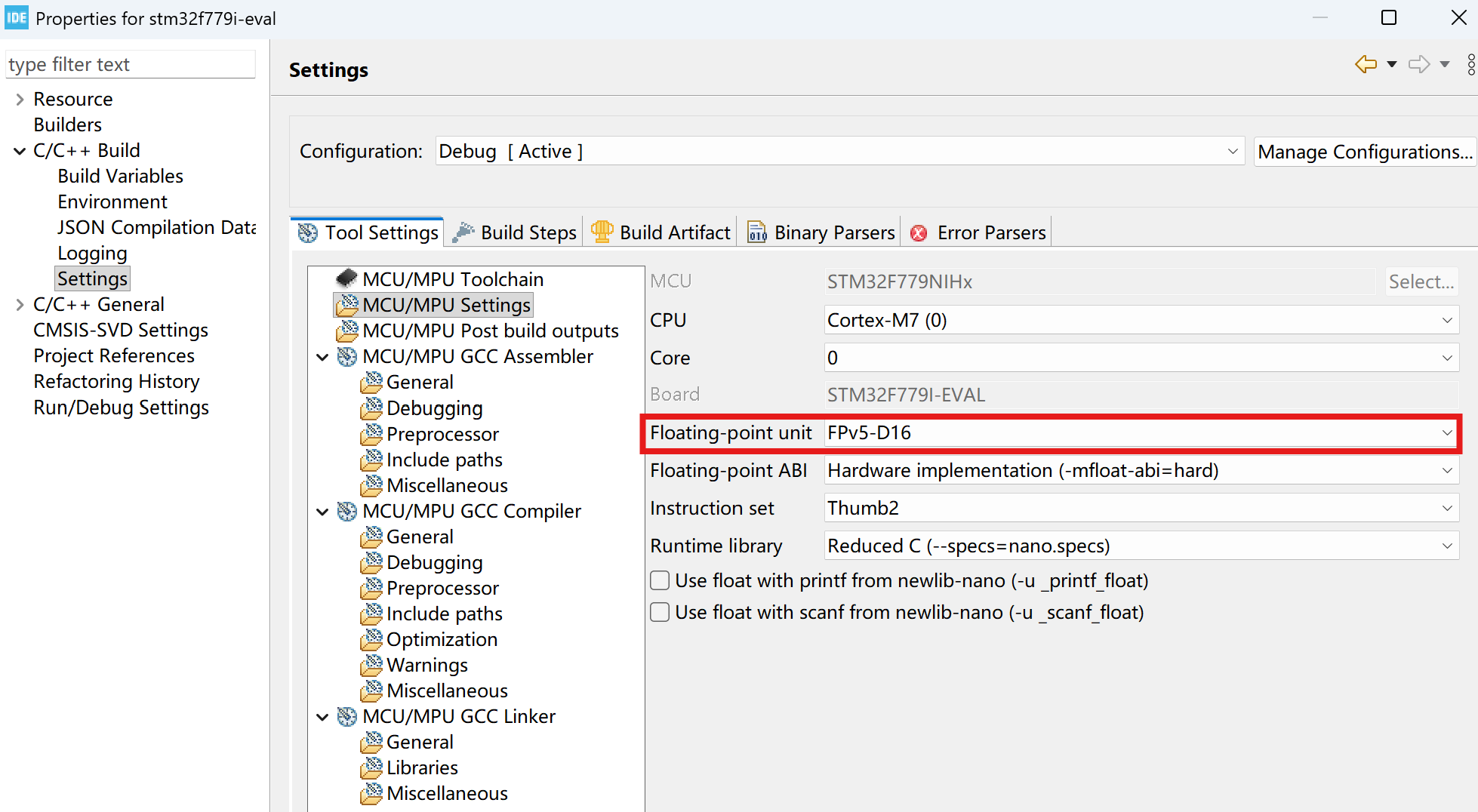
4.2 代码实现
cpp
#include "arm_math.h"
#define LENGTH_SAMPLES 512
#define BLOCK_SIZE 32
#define NUM_STAGES 1 /* IIR阶数:1个二阶节即可实现优异的去直流效果 */
static float32_t Input_f32[LENGTH_SAMPLES];
static float32_t Output[LENGTH_SAMPLES];
/* IIR 状态缓冲大小为 4 * NUM_STAGES */
static float32_t iirStateF32[4 * NUM_STAGES];
/*
* IIR 高通系数 (由 Python 设计,截止频率约 20Hz @ 16kHz)
* CMSIS-DSP 格式: {b0, 0, b1, b2, a1, a2}
* 注意:a1, a2 已经按照 arm_math 库要求进行了取反处理
*/
const float32_t iirCoeffs32[5 * NUM_STAGES] = {
0.997070,
-1.994141,
0.997070,
1.994141,
-0.994629
};
// 定义滤波器实例为全局,避免反复初始化丢失历史状态
arm_biquad_casd_df1_inst_f32 IIR_S;
/**
* @brief 初始化滤波器 (在系统启动时调用一次)
*/
void filter_init(void) {
arm_biquad_cascade_df1_init_f32(&IIR_S, NUM_STAGES, (float32_t *)iirCoeffs32, iirStateF32);
}
int8_t iir_highpass_filter() {
uint32_t i;
// 使用 CMSIS-DSP 优化过的 Biquad 级联函数
// 每次处理 BLOCK_SIZE 个点
for(i = 0; i < LENGTH_SAMPLES; i += BLOCK_SIZE) {
arm_biquad_cascade_df1_f32(&IIR_S, &Input_f32[i], &Output[i], BLOCK_SIZE);
}
return 0; // 假设 0 为 SUCCESS
}5 应用高通滤波器到音频信号
为了验证滤波器的有效性,我们将设计好的 IIR 高通滤波器应用到带有直流偏移(DC Offset)的音频信号中。
下图展示了滤波后的音频信号:
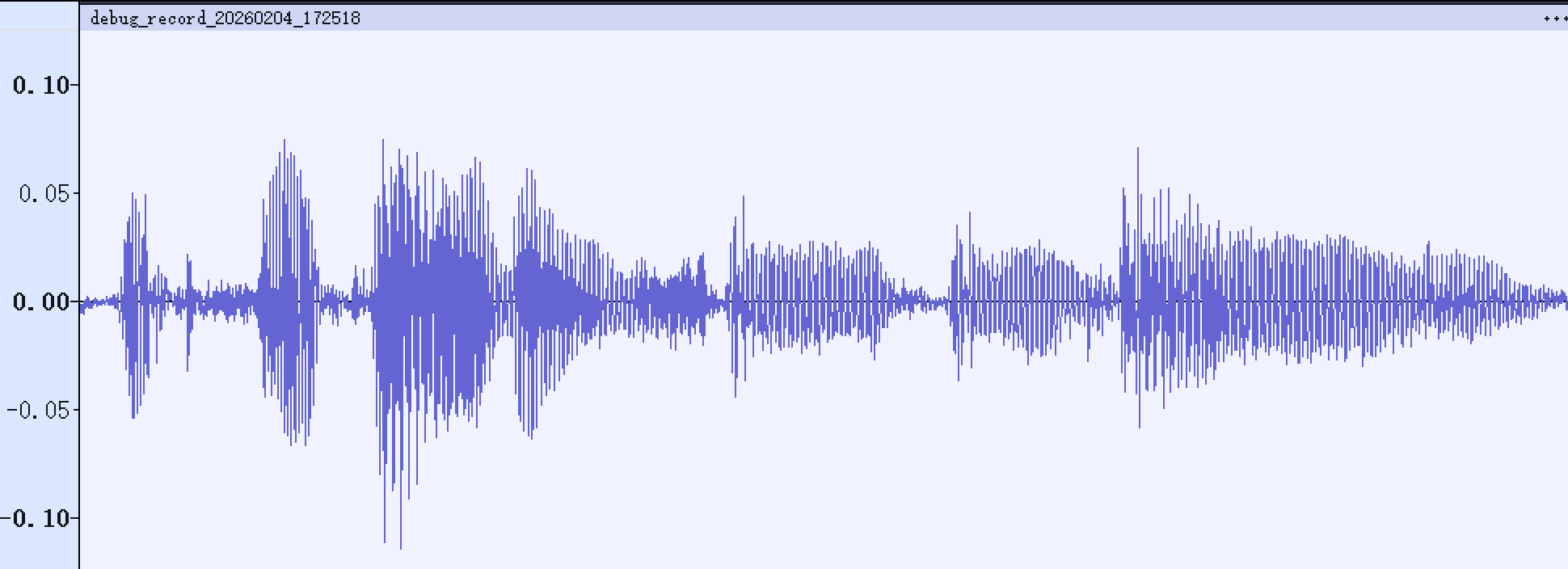
可以看到直流偏移被去除了。