比赛链接:Dashboard - Codeforces Round 1064 (Div. 2) - Codeforces
A:

思路:
看看字符串和最后一个字符不同的字符数有多少个即为答案,代码略。
B:

思路:
简单解释一下题意,就是有 个标签页,然后你可以让你的鼠标移动到任意固定位置,看需要多少次能把标签页都关闭(关闭的时候只能点击每个标签页最右边的
,最开始鼠标在最左边的标签页的左边),然后标签页的长度
,其中
为当前标签页的个数。
其实只要理解题意就好很多了,我们当 的时候,我们只需要把鼠标移动到最左边标签页的
即可,这样就是1次操作。否则这时候屏幕一定是满的,就需要点击最右边标签页的
,让标签页个数下降,直至出现
,这样就可能出现2次操作。
需要注意的是,当 的时候,这时候只需要 1 次操作即可。
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve(){
ll a,b,n,x;
cin>>a>>b>>n;
ll ans=1;
if(b*n>a&&a!=b){
ans++;
}
cout<<ans<<'\n';
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}C:

思路:
从宏观的角度思路合并的过程,我们合并 次相当于加
次数,比较直观的一个贪心策略:把当前的最小值和左右两边较小的值合并。
为什么这个策略是对的,我们就需要单独考虑这个最小值作为被合并项对于答案的贡献了。
由于小的值和大的值合并之后,就合并为较大的那个值,所以之后无论任何策略,想和最小值合并,就要先合并到最小值的邻居位置,这样的话就会导致最小值的邻居位置值不会比最开始的较小邻居值小,且小的值无论如何都要被合并,不会对未来的最优解有影响。
根据这个贪心策略,我们每次算的统计下来其实本质上等效于 (因为每个值除了一个最大值的元素外都有可能被选为最小值,所以本质上就是相邻值的最大值之和减去不可能的最大值就是答案)。
根据公式,代码如下:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
typedef long long ll;
ll a[N];
int n;
void solve(){
cin>>n;
ll ma=0,sum=0;
for(int i=0;i<n;i++)
cin>>a[i];
for(int i=0;i<n;i++){
sum+=max(a[i],a[(i+1)%n]);
ma=max(ma,a[i]);
}
ll ans=sum-ma;
cout<<ans<<'\n';
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}D:

思路:
感觉可以这么思考,我们要求的是有多少个不同的 的个数,而每一种可能的
内部中的每个元素都是在每个
集合中的一个众数,和数组中某个元素的出现次数有关系,和大小没有关系,所以我们就要从每个数的出现次数来考虑这道题。
对于一个数 而言,假设考虑把
这个数避免成为
内部的一个元素,也就是不会成为任何一个集合
内的一个唯一最大值(数学符号简单表示就是
,简单描述就是覆盖
),那么最起码需要满足:
而若想覆盖所有元素,就需要满足:
有了这个思路,我们就需要考虑如何去写这道题了,由于其只关系方案数,而方案数只和选取为 中的元素个数有关系,和是什么没有关系,所以我们就可以考虑用状态转移来获得最终结果。
比如 ,考虑加入 4 的时候,其实有5种情况,
加入1个4、2个4 ... 5个4,而每种情况只要满足
其实都可以和其他可能去组合,最终让 4 加入集合中。
刚开始的时候肯定是啥都没有,然后一点点加入集合考虑,所以我们可以这么设置,设 为考虑
的时候,在数组中
的元素个数总和为
时候的方案数。
有以下转移方式:
我们考虑第 个元素的时候,有考虑
是否出现在
的可能,如果
不出现在
中,那么就是
,否则就要考虑
出现后带来的可能组合,然后和
的元素个数总和为
时候的方案数结合一下。
这个DP由于只关心相邻两个数之间,所以其实可以优化一下,消去考虑 这一维,变成以下递推式:
AC代码如下:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int N=5050;
ll dp[N],cnt[N];
int n;
void solve(){
cin>>n;
for(int i=0;i<=n;i++)
cnt[i]=dp[i]=0;
dp[0]=1;
for(int i=1;i<=n;i++){
int x;
cin>>x;
cnt[x]++;
}
ll ma=0;
for(int i=1;i<=n;i++)
ma=max(ma,cnt[i]);
for(int i=1;i<=n;i++){
if(cnt[i]){
for(int j=n;j>=cnt[i];j--){
dp[j]=(dp[j]+cnt[i]*dp[j-cnt[i]]%mod)%mod;
}
}
}
ll ans=0;
for(int i=ma;i<=n;i++)
ans=(ans+dp[i])%mod;
cout<<ans<<'\n';
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}E:
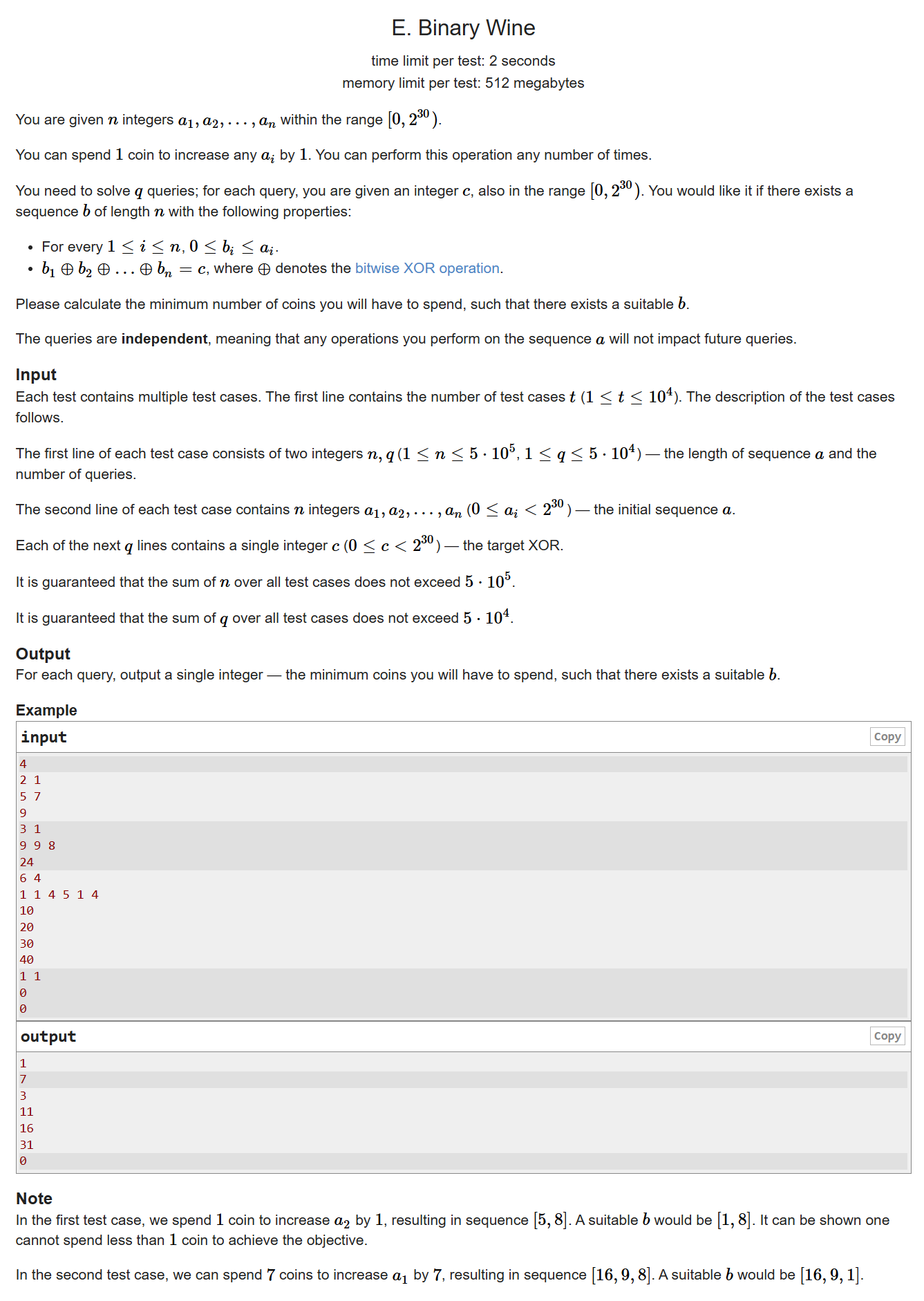
思路:
这道题和二进制有关系,从二进制的角度考虑,对于 而言,从最高位开始考虑,假设当前处理的是二进制第
位,我们设一个数
来表示
的二进制第
位有多少个 1 。因此我们可以容易求出来
以及
,初始化
,然后有以下几种情况:
(1) 的时候,由于这一位数组贡献的位数比
多,完全可以替代
的更低位,这时候就结束遍历,把当前得到的
输出。
(2) 的时候,这一位正好可以贡献,占住即可。
(3) 的时候,这时候需要找一个最接近
的
,这时候就花费了
硬币,然后让
,并让对应的
。
然后如果直接查询+遍历整个数组的话时间复杂度为 ,会超时,所以就需要有这么一个想法:其实只考虑数组最大的30个元素即可。
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+100;
int a[N],b[N];
int n,q;
bool cmp(int a,int b){
return a>b;
}
void solve(){
cin>>n>>q;
for(int i=1;i<=n;i++)
cin>>a[i];
sort(a+1,a+1+n,cmp);
int len=min(32,n);
while(q--){
int c;
cin>>c;
for(int i=1;i<=len;i++)
b[i]=a[i];
int ans=0;
for(int i=29;i>=0;i--){
int cnt=((c>>i)&1);
for(int j=1;j<=len;j++){
if((b[j]>>i)&1)
cnt--;
}
if(cnt<0)
break;
else if(cnt>0){
int add=1e9,mod=1<<i;
int id=1;
for(int j=1;j<=len;j++){
if(add>mod-b[j]%mod){
id=j;
add=mod-b[j]%mod;
}
}
ans+=add;
b[id]=b[id]-b[id]%mod+mod;
}
}
cout<<ans<<'\n';
}
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}