【C++学习笔记】图论-最短路径Dijkstra算法

前言

这是放假以来的第二篇博文，最近可能月更吧。

作者也是学图论了awa
注意：由于作者刚刚学数论，有错误请友善指正，让我也纠正一下思路错误。

最短路径是什么

Q&A

Q：最短路径到底指什么？

A：一个加权图中从点u到点v经过的边的权值和最小值。

Q：学习最短路径需要什么前置知识？

A：会建图即可。

DJ克斯特拉（Dijkstra）

思考过程

Dijkstra到底是个啥？能吃吗？嗯，真香！它的实现思路是什么？请看图解（注意，因为作者太粗心，漏掉了点5又懒得改，所以请忽略点5。）

我们先建立一个数组dis，dis $i$ 代表从1号点到i号点的最短路径，初始dis $1$ 为0，因为初始点距离自己的最短路径就是0。其他值均赋值一个很大的数，我们暂时叫它INF。

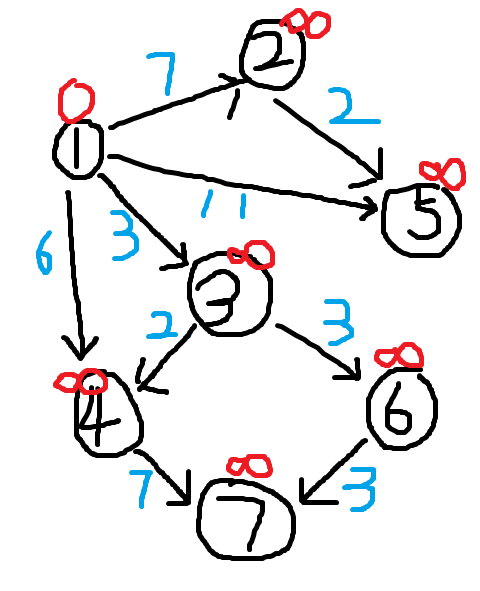
初始我们从某个地方弄来一张图

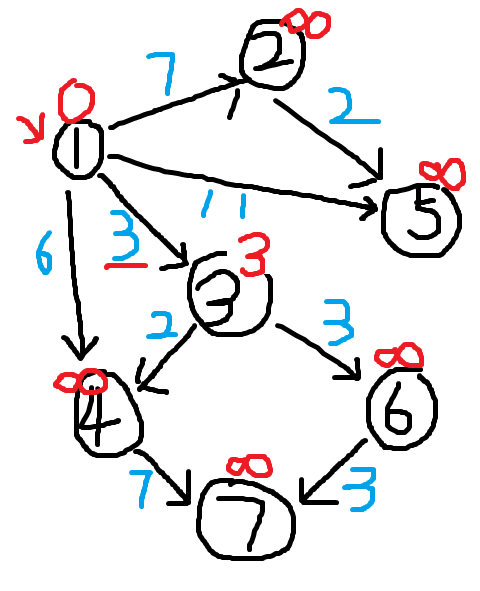
然后我们从初始点1开始，这个初始点也叫做源点，我们找连接这个点的所有边中，权值最小的那一条，也就是边【1,3】，然后我们发现，dis $3$ 的值可以更新为dis $1$ +边【1,3】的权值，那么我们将它更新为3。

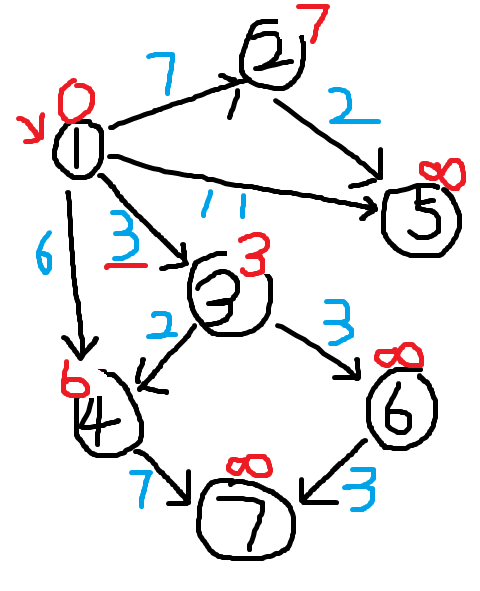
接着我们同样更新点1连接的另外两个点dis $2$ 和dis $4$ 。我们通过点1更新它连接的其他点的dis值，这个操作叫做松弛。我们松弛结束后，应将点1标记，表示它已经松弛过了。

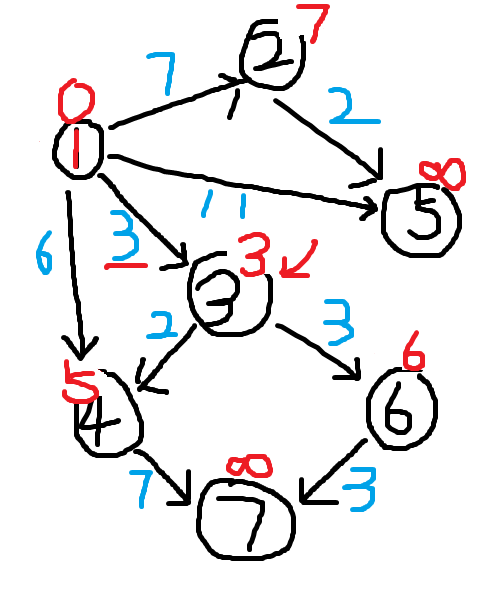
我们在未标记的点中找到dis值最小的那一个，对该点进行松弛操作，发现点4的值比dis $3$ +边【3,4】的权值要大，更新dis $4$ 的值为5。点6同理。将点3标记。

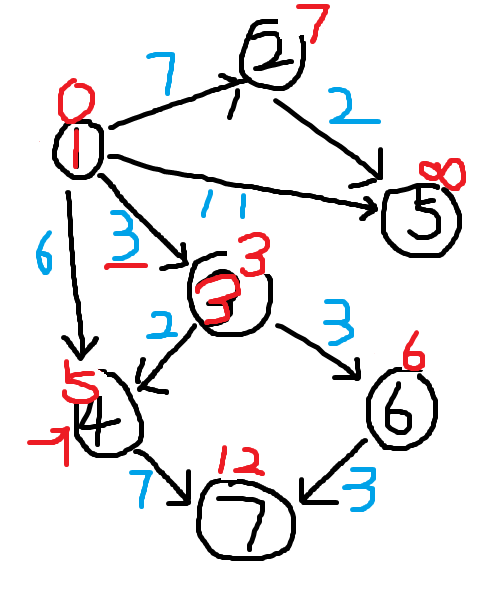
我们继续在未标记的点中找dis值最小的那一个，我们找到了4，对点4进行松弛，将dis $7$ 更改为dis $4$ +边【4,7】，也就是12。将点4标记。

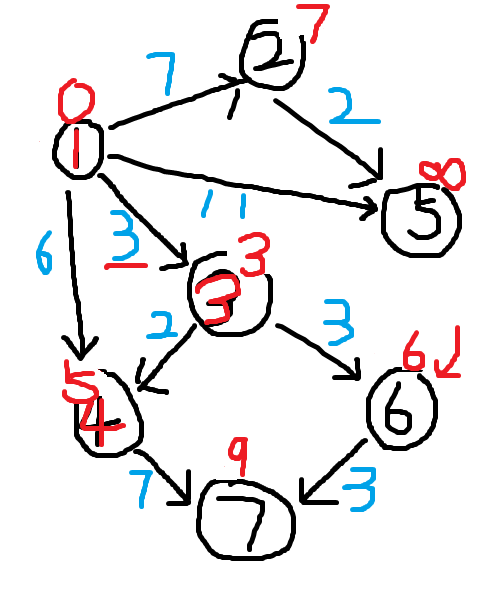
找到未标记的、dis值最小的点6，对该点进行松弛，将dis $7$ 的值改为9。

代码

后面的步骤就不画了，大家都理解了吗？接下来直接上代码。

cpp 复制代码

int n,m,s,t,d[2501];
bool vis[2501];
struct e{
    int t,d;
};
vector<e> g[2501];

其中n代表点的个数，m代表边的条数，s代表起始点（源点），t代表目标点，d就是dis数组，vis记录是否已经对该点进行松弛，g是邻接表，存储了图。

cpp 复制代码

void dijkstra(){
    memset(d,127,sizeof(d));
    memset(vis,0,sizeof(vis));
    d[s]=0;
    for(int i=1;i<=n;i++){
        int k=0,t=1e9;
        for(int j=1;j<=n;j++){
            if(t>d[j]&&vis[j]!=1)t=d[j],k=j;
        }
        vis[k]=1;
        for(int i=0;i<g[k].size();i++){
            int v=g[k][i].t;
            if(d[v]>d[k]+g[k][i].d){
                d[v]=d[k]+g[k][i].d;    
            }
        }
    }
}

先初始化，将除源点外的d值都赋为很大的值（memset是用字节存储，所以int内的最大值为127）。同时将vis统统设为0，表示未访问。然后遍历n次（因为要遍历所有的点），每次找到d值最小且未标记的那个点，然后对该点连接的所有其他点进行松弛操作。

cpp 复制代码

int main(){
    cin>>n>>m>>s>>t;
    for(int i=1;i<=m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        g[u].push_back(e{v,w});
        g[v].push_back(e{u,w});
    }
    dijkstra();
    cout<<d[t]<<endl;
    return 0;
}

读入数据，建图，运用函数，最后输出即可。

优化

以上算法的时间复杂度是O(n^2)，对于一些较大的数据会超时，那我们应该怎么优化呢？因为每一次循环都需要找到dis值最小且未访问的值，所以很容易想到堆（优先队列）。

优化后的代码：

cpp 复制代码

struct node{
    int dis,pos;
    bool operator <(const node &x)const{
        return x.dis<dis;
    }
};
priority_queue<node> q;

先建一个优先队列

cpp 复制代码

void dijkstra(){
    memset(d,127,sizeof(d));
    memset(vis,0,sizeof(vis));
    d[s]=0;
    q.push(node{0,s});
    while(q.size()){
        int k=q.top().pos;q.pop();
        if(vis[k])continue;
        vis[k]=1;
        for(int i=0;i<g[k].size();i++){
            int v=g[k][i].t;
            if(d[v]>d[k]+g[k][i].d){
                d[v]=d[k]+g[k][i].d;
                q.push(node{d[v],v});
            }
        }
    }
}

优先队列存储了dis值和该点，每次队头都是最小的dis值且未被访问的点，大大减少了不必要的循环。

结语

老天爷！手已经打废了！点个赞+收藏+关注吧！

Dijkstra虽然没有SPFA好用，但是也是必不可少的一份子，另外，这个算法无法解决有负环的图哦！所以要谨慎看题！不要像我一样被硬控20mins

下次我会发一个SPFA和Bellman算法的，再见喽！