借助Matlab有限元工具pde进行静态结构有限元分析

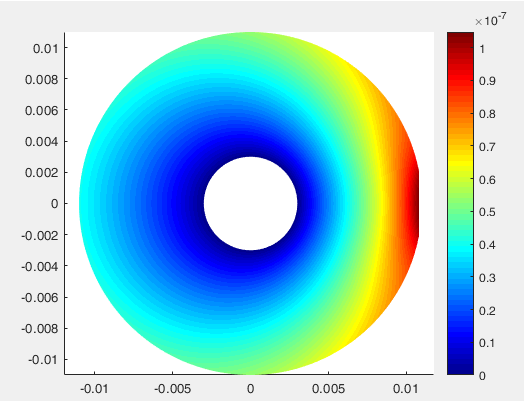
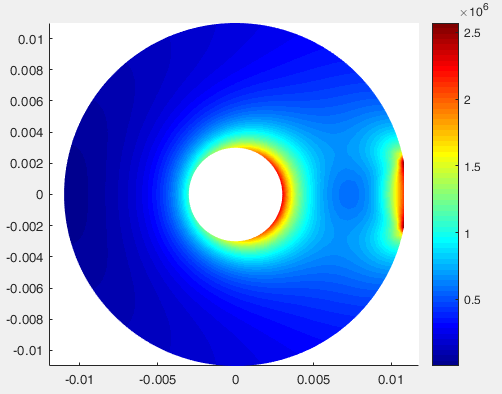
本次学习通过Matlab中的有限元工具进行静态结构有限元分析，假设分析的模型为：

在右端受到5N的力。

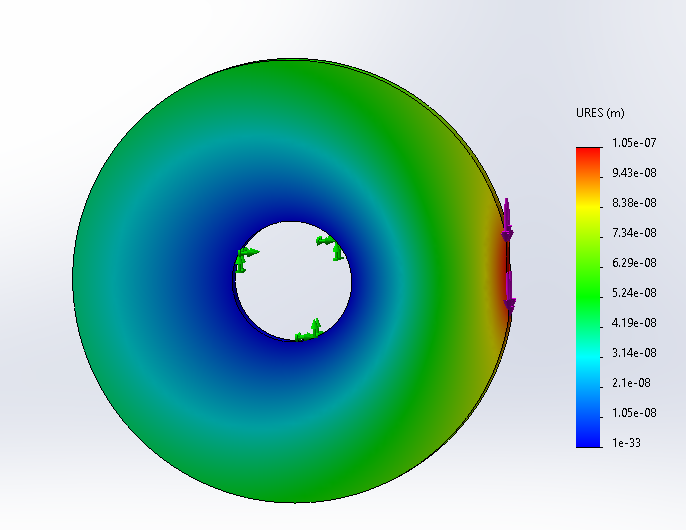
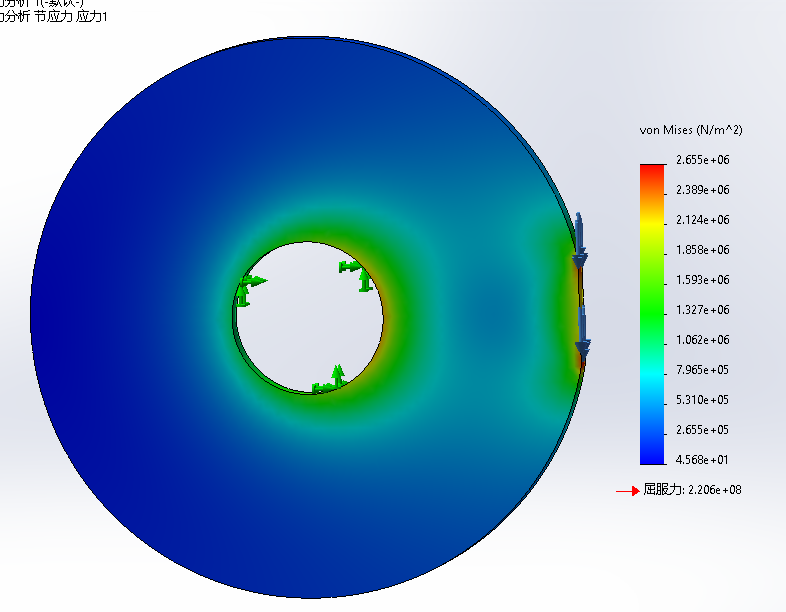
Matlab分析的代码及含义：

clc

clear

tic

% 创建 PDE model

model = createpde('structural', 'static-planestress');

% 创建需要计算的几何区域

circle = 1, 0., 0., 11e-3';

square = 3, 4, 10.8e-3, 12.9e-3, 12.9e-3, 10.8e-3, -3e-3, -3e-3, 3e-3, 3e-3';

circle2 = 1, 0., 0., 3e-3';

circle = circle; zeros(length(square) - length(circle), 1);

circle2 = circle2; zeros(length(square) - length(circle2), 1);

gm = circle, square,circle2;

sf = 'cir-sq-cir2';

ns = char('cir', 'sq','cir2')';

g = decsg(gm, sf, ns);

% 应用几何到模型

geometryFromEdges(model, g);

% pdegplot(model, 'EdgeLabels', 'on');

% 生成网格

generateMesh(model, 'GeometricOrder', 'quadratic', 'Hmax', 0.5e-3);

% pdeplot(model);

% 定义材料属性

structuralProperties(model, 'YoungsModulus', 210e9, 'PoissonsRatio', 0.28);

% 定义固定的约束边界条件

structuralBC(model,'Edge',6,7,8,9, 'Displacement', 0;0); % 固定位移约束

% 定义载荷

structuralBoundaryLoad(model, 'Edge', 1, 'SurfaceTraction', 0;-5e6/4.1761226); % 施加Y方向力，单位N/m^2

% 模型求解

results = solve(model);

M = results.Displacement.Magnitude;

XY = (results.Mesh.Nodes)';

toc

mean(M(XY(:,1) == 10.8e-3))

%

figure(1);

pdeplot(model, 'XYData', results.Displacement.Magnitude,'ColorMap','jet');

axis equal

%

figure(2);

pdeplot(model, 'XYData', results.VonMisesStress,'ColorMap','jet');

axis equal

计算结果：