速通DeepSeek论文mHC：给大模型装上物理阀门的架构革命

文章目录

1、前言
[2、背景：从残差连接到 mHC 的演进之路](#2、背景：从残差连接到 mHC 的演进之路)
- [2.1 没有残差连接的世界：梯度消失](#2.1 没有残差连接的世界：梯度消失)
- - [2.1.1 反向传播详解](#2.1.1 反向传播详解)
- [2.2 残差连接：那个救命的"1"](#2.2 残差连接：那个救命的"1")
- [2.3 矩阵变换的几何本质：不停地"扭曲"空间](#2.3 矩阵变换的几何本质：不停地"扭曲"空间)
- - [2.3.1 具体理解](#2.3.1 具体理解)
  - [2.3.2 为什么扭曲有用？](#2.3.2 为什么扭曲有用？)
- [2.4 HC（超连接）：打破信息瓶颈](#2.4 HC（超连接）：打破信息瓶颈)
- - [2.4.1 信息瓶颈问题](#2.4.1 信息瓶颈问题)
  - [2.4.2 HC 的做法](#2.4.2 HC 的做法)
  - [2.4.3 HC 的致命问题](#2.4.3 HC 的致命问题)
- [2.5 核心矛盾与 mHC 的诞生](#2.5 核心矛盾与 mHC 的诞生)
[3、核心创新：mHC 流形约束超连接](#3、核心创新：mHC 流形约束超连接)
- [3.1 核心思想](#3.1 核心思想)
- [3.2 为什么这么设计](#3.2 为什么这么设计)
- - [3.2.1 解耦"记忆容量"与"计算成本"](#3.2.1 解耦"记忆容量"与"计算成本")
  - [3.2.2 解决训练不稳定性](#3.2.2 解决训练不稳定性)
  - [3.2.3 引入物理与几何的先验](#3.2.3 引入物理与几何的先验)
4、关键数学概念
- [4.1 双随机矩阵：完美的任务分配](#4.1 双随机矩阵：完美的任务分配)
- - [4.1.1 普通矩阵（乱套了）](#4.1.1 普通矩阵（乱套了）)
  - [4.1.2 双随机矩阵（完美守恒）](#4.1.2 双随机矩阵（完美守恒）)
- [4.2 核心公式 Eq.6：mHC 的"宪法"](#4.2 核心公式 Eq.6：mHC 的"宪法")
- [4.3 非负性约束的重要性](#4.3 非负性约束的重要性)
- [4.4 什么是凸组合（Convex Combination）](#4.4 什么是凸组合（Convex Combination）)
- - [4.4.1 线性组合 vs 凸组合](#4.4.1 线性组合 vs 凸组合)
  - [4.4.2 mHC 为什么选凸组合](#4.4.2 mHC 为什么选凸组合)
- [4.5 Softmax：把任意数字变成概率分布](#4.5 Softmax：把任意数字变成概率分布)
- - [4.5.1 Softmax 公式](#4.5.1 Softmax 公式)
  - [4.5.2 为什么 Softmax 不够用](#4.5.2 为什么 Softmax 不够用)
  - [4.5.3 Sinkhorn 的优势](#4.5.3 Sinkhorn 的优势)
[5、Sinkhorn-Knopp 算法：矩阵平衡术](#5、Sinkhorn-Knopp 算法：矩阵平衡术)
- [5.1 一句话解释](#5.1 一句话解释)
- [5.2 手动演算示例](#5.2 手动演算示例)
- [5.3 为什么不用 Softmax？](#5.3 为什么不用 Softmax？)
6、残差连接层的数据流
- [6.1 数据形式](#6.1 数据形式)
- [6.2 三个关键映射矩阵](#6.2 三个关键映射矩阵)
7、三大工程优化策略
- [7.1 算子融合 (Kernel Fusion)](#7.1 算子融合 (Kernel Fusion))
- - [7.1.1 问题背景](#7.1.1 问题背景)
  - [7.1.2 解决方案](#7.1.2 解决方案)
- [7.2 选择性重计算 (Selective Recomputing)](#7.2 选择性重计算 (Selective Recomputing))
- - [7.2.1 问题背景](#7.2.1 问题背景)
  - [7.2.2 两种极端方案](#7.2.2 两种极端方案)
  - [7.2.3 mHC 的聪明做法](#7.2.3 mHC 的聪明做法)
- [7.3 DualPipe 通信重叠](#7.3 DualPipe 通信重叠)
- - [7.3.1 问题背景](#7.3.1 问题背景)
  - [7.3.2 DualPipe 的做法](#7.3.2 DualPipe 的做法)
  - [7.3.3 最终效果](#7.3.3 最终效果)
8、三代架构对比
9、深层追问：为什么这些架构创新能让模型学得更好？
- [9.1 工厂类比](#9.1 工厂类比)
- [9.2 更丰富的输入信息](#9.2 更丰富的输入信息)
- [9.3 更有效的梯度回传](#9.3 更有效的梯度回传)
- [9.4 约束本身也是一种"知识"](#9.4 约束本身也是一种"知识")
10、实验结果与核心突破
- [10.1 实验配置](#10.1 实验配置)
- [10.2 关键指标](#10.2 关键指标)
- [10.3 核心突破](#10.3 核心突破)
11、总结
- [11.1 关键公式推导脉络](#11.1 关键公式推导脉络)
- [11.2 一句话概括](#11.2 一句话概括)
- [11.3 后续发展](#11.3 后续发展)

🍃作者介绍：25届双非本科网络工程专业，阿里云专家博主，深耕 AI 原理 / 应用开发 / 产品设计。前几年深耕Java技术体系，现专注把 AI 能力落地到实际产品与业务场景。

🦅个人主页：@逐梦苍穹

📕所属专栏：🌩 专栏① ：人工智能； 🌩 专栏② ：速通人工智能相关论文

🐼GitHub主页：https://github.com/XZL-CODE

✈ 您的一键三连，是我创作的最大动力🌹

论文标题 : mHC: Manifold-Constrained Hyper-Connections
arXiv : https://arxiv.org/abs/2512.24880 (2025年12月31日提交)
通讯作者: 梁文锋（DeepSeek 创始人兼 CEO）

1、前言

DeepSeek 最新发布的 mHC（Manifold-Constrained Hyper-Connections，流形约束超连接）论文，做了一件非常有意思的事情：给大模型的"神经网络"装上了符合物理守恒定律的"智能阀门"。

用一句话概括：mHC 把大模型的"单车道"升级成了"多车道高速公路"，并给每条车道装上了流量控制系统，让信息流巨大但绝不拥堵失控。

这篇文章将带你彻底搞懂：

残差连接为什么重要，没有它会怎样
HC（超连接）解决了什么问题，又带来了什么麻烦
mHC 如何用数学手段（双随机矩阵 + Sinkhorn-Knopp 算法）把问题解决
为什么这些"复杂的变换"能让模型学得更好

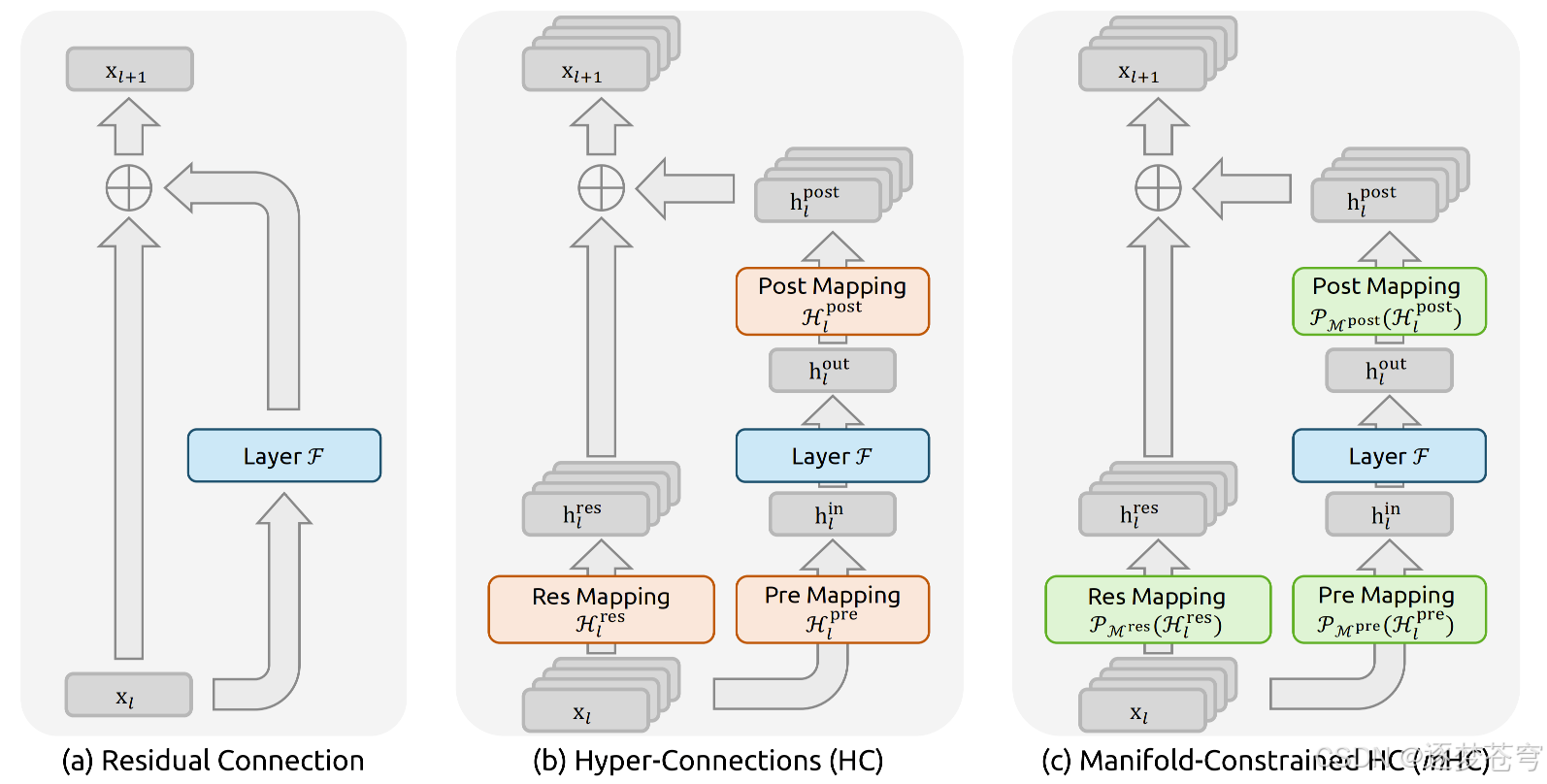
2、背景：从残差连接到 mHC 的演进之路

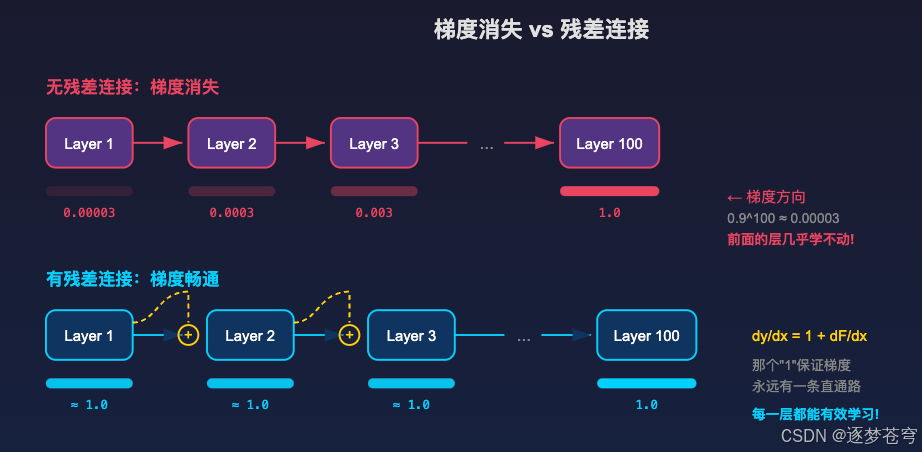
2.1 没有残差连接的世界：梯度消失

在残差连接发明之前（2015 年以前），深层神经网络面临一个致命问题。

假设网络有 100 层，每层做一个变换 F F F。没有残差的话，信号是串行嵌套的：

输出 = F 100 ( F 99 ( ... F 2 ( F 1 ( x ) ) ... ) ) \text{输出} = F_{100}(F_{99}(\dots F_2(F_1(x))\dots)) 输出=F100(F99(...F2(F1(x))...))

训练神经网络靠的是反向传播 -- 从最后一层往回算梯度，告诉每一层"你该怎么调整参数"。根据链式法则，梯度要把 100 个导数连乘。只要每个导数稍微小于 1（比如 0.9），连乘 100 次：

0.9 100 ≈ 0.0000265 0.9^{100} \approx 0.0000265 0.9100≈0.0000265

梯度几乎归零，前面的层根本收不到有效的学习信号 -- 这就是梯度消失。

实际后果 ：2015 年以前，网络超过 20 层就基本训不动了。何恺明等人的实验表明，56 层的网络反而比 20 层的更差 -- 这不是过拟合，是根本没学会。

2.1.1 反向传播详解

很多人对"反向传播"概念模糊，这里详细解释一下：

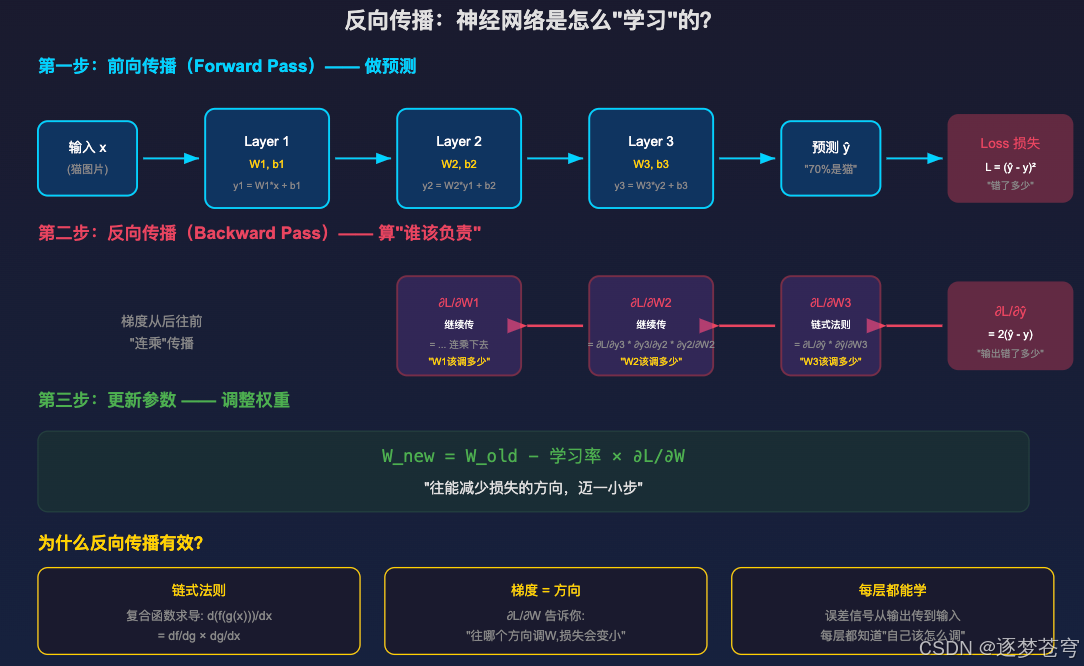
前向传播：数据从输入层流向输出层，每一层做变换，最后得到预测结果和损失值（Loss）。

反向传播：从 Loss 开始，根据链式法则，一层一层往回算"这个参数对 Loss 的影响有多大"（也就是梯度）。得到梯度后，按照"负梯度方向"调整参数，让 Loss 变小。

为什么需要反向传播？ 因为神经网络有百万甚至数十亿个参数，没法穷举哪个参数组合最好。反向传播是高效的"指引"------告诉每个参数"你该往哪个方向调、调多少"。

2.2 残差连接：那个救命的"1"

2015 年，ResNet 提出了一个极其简单但深刻的改动 -- 残差连接：

y = x + F ( x ) y = x + F(x) y=x+F(x)

就是在每一层的输出上，把输入直接加回去。

为什么这个简单的加法能解决问题？对 x x x 求导：

∂ y ∂ x = 1 + ∂ F ∂ x \frac{\partial y}{\partial x} = 1 + \frac{\partial F}{\partial x} ∂x∂y=1+∂x∂F

关键在那个 "1" 。不管 F F F 的梯度多小多烂，梯度至少有一条直通高速路（恒等映射），永远不会归零。这就是为什么 ResNet 能训练 152 层甚至 1000 层的网络。

一句话：残差连接不是让模型变聪明，而是让深层网络"能训练"。它解决的是生存问题，不是能力问题。

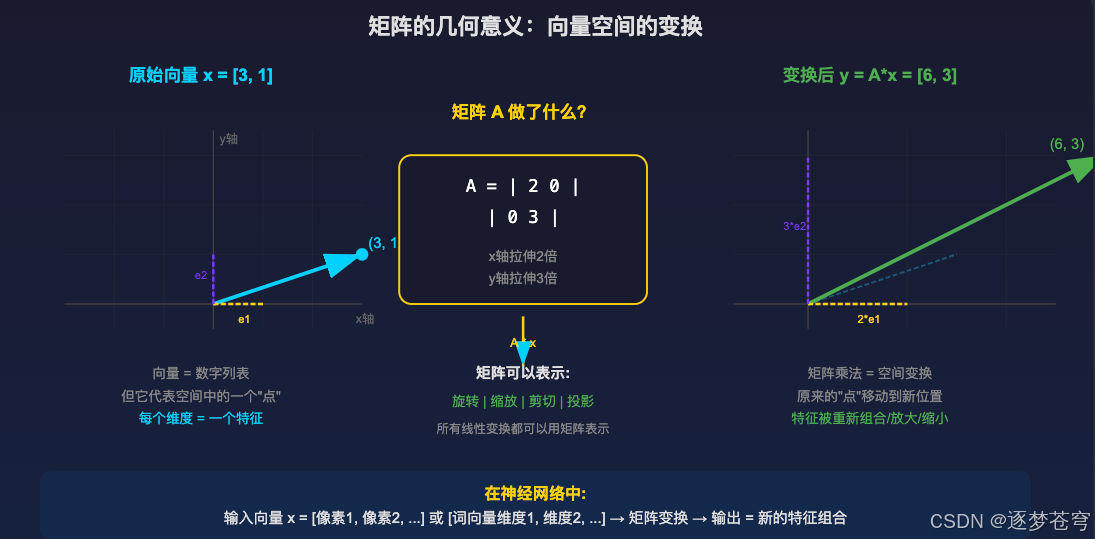
2.3 矩阵变换的几何本质：不停地"扭曲"空间

要理解神经网络为什么能学习，首先要理解矩阵变换的本质是什么。

矩阵的变换，其实就是不停地在"扭曲"空间。

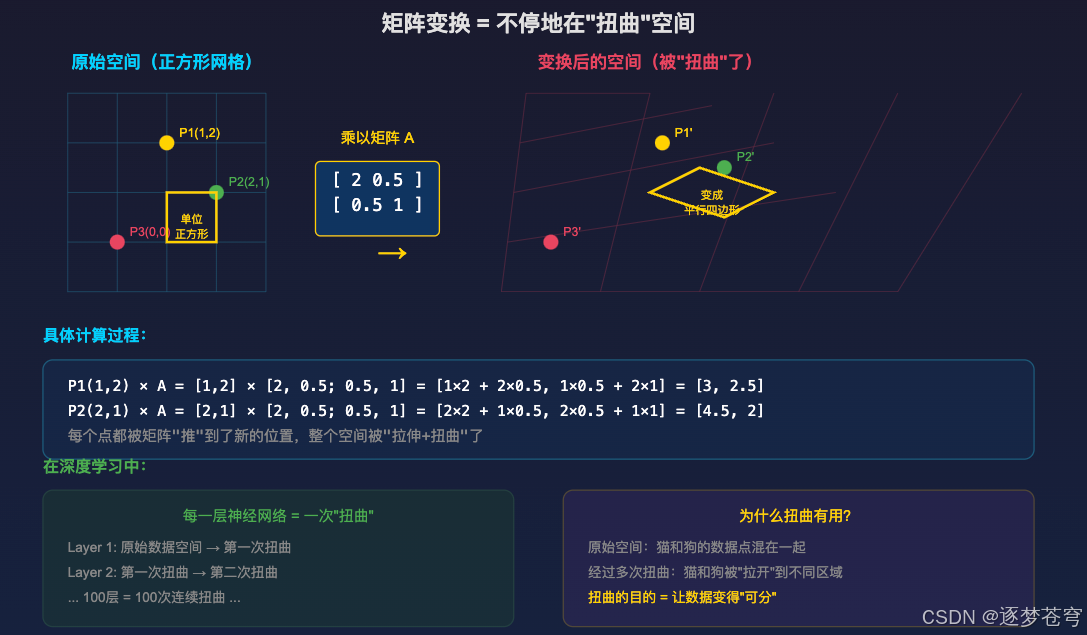
2.3.1 具体理解

想象一张方格纸，上面画着整齐的网格线。当你用一个矩阵去乘这张纸上的每个点：

原本垂直的线可能变斜了（剪切变换）
原本等距的格子可能被拉长或压扁（缩放变换）
整个空间可能被旋转（旋转变换）

神经网络的每一层，本质上就是对数据空间做一次这样的"扭曲"。

2.3.2 为什么扭曲有用？

假设你要分类猫和狗的图片。在原始像素空间里，猫和狗的数据点是混在一起的------它们可能只差几个像素值。

但经过神经网络100层的连续"扭曲"后：

所有"猫"的数据点被挤到了空间的一个角落
所有"狗"的数据点被挤到了另一个角落
中间有一条清晰的"分界线"

深度学习的本质 = 找到一系列"扭曲"（矩阵变换），把原本纠缠在一起的数据，拉扯到可以被简单分开的位置。

2.4 HC（超连接）：打破信息瓶颈

残差连接解决了"能训练"的问题，但它有一个本质瓶颈 -- 所有信息都挤在一条管道里。

2.4.1 信息瓶颈问题

想象大模型在处理一段文本，不同层捕捉到了不同维度的信息：

第 1 层发现了"这句话的主语是'猫'"
第 3 层发现了"语气是疑问句"
第 7 层发现了"涉及因果推理"

这些信息全部要塞进同一条管道 往下传。到了第 50 层，这条管道里的信息是高度压缩、互相覆盖的。模型必须用同一个向量同时表达语法、语义、逻辑等所有信息 -- 带宽不够。

2.4.2 HC 的做法

HC（Hyper-Connections，超连接）把 1 条管道扩成 n n n 条（比如 4 条），不同管道可以分工：

管道 1 专门传语法信息
管道 2 专门传语义信息
管道 3 专门传上下文记忆
管道 4 专门传推理中间状态

层与层之间有一个混合矩阵 H \mathcal{H} H，让管道之间可以交换信息。

HC 的意义：不是让每一层"算得更多"，而是让信息"带得更多"。 计算层（Attention/FFN）没变大，但信息高速公路变宽了。

2.4.3 HC 的致命问题

因为缺乏约束，混合矩阵 H \mathcal{H} H 完全自由学习，会让水压失控。标准 HC 的复合映射增益在 27B 模型上可达 3000 倍，导致大模型训练直接崩溃。

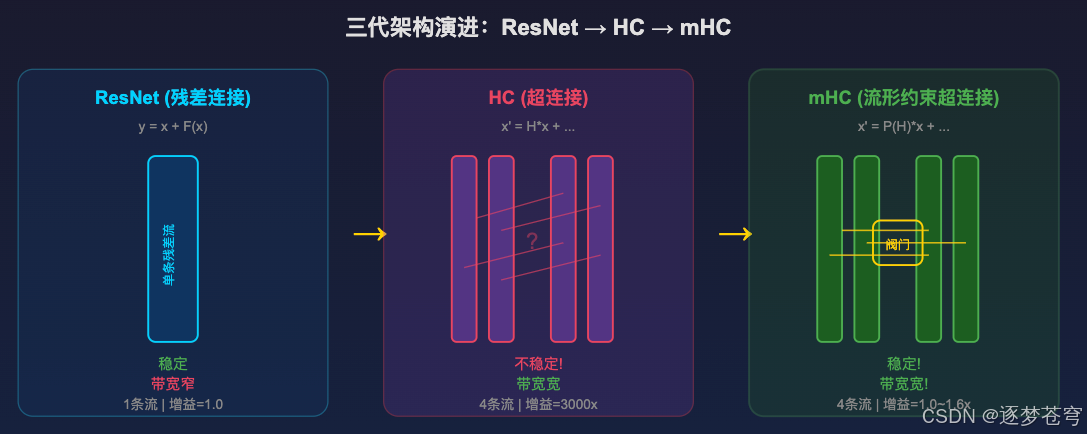
2.5 核心矛盾与 mHC 的诞生

三代架构的递进关系：

架构	能训练深网络？	信息带宽？	训练稳定？
无残差	不能	-	-
ResNet	能	窄（1 条流）	稳定
HC	能	宽（n 条流）	不稳定
mHC	能	宽（n 条流）	稳定

核心矛盾：如何在让模型"脑容量"变大的同时，不让它"精神错乱" -- 这就是 mHC 要解决的问题。

3、核心创新：mHC 流形约束超连接

DeepSeek 的 mHC 做的核心事情是：保留宽车道，但加上了严苛的交通管制（流形约束）。

3.1 核心思想

将混合矩阵强制限制在 Birkhoff 多面体（双随机矩阵的集合）这个"流形"上
强制要求神经网络在混合信息时，流进多少信息，就必须流出多少信息，实现"信息守恒"
用 Sinkhorn-Knopp 算法给混合矩阵加"紧箍咒"，把它变成双随机矩阵

3.2 为什么这么设计

3.2.1 解耦"记忆容量"与"计算成本"

传统模型要增加信息容量，就得把整个模型做宽，计算量暴涨。mHC 的设计巧妙在于：路修得很宽（ n n n 倍残差流），但收费站（Attention/FFN 计算层）没变大。

残差流变宽了，模型能"记住"或"携带"更多的上下文信息
因为计算层只处理压缩后的数据，计算成本几乎没增加（只增加了 6.7%）

3.2.2 解决训练不稳定性

之前的 HC 破坏了恒等映射属性。mHC 通过"流形约束"强行恢复了恒等映射属性。无论网络多深，信号的能量在传播过程中是守恒的。

3.2.3 引入物理与几何的先验

底层哲学: "将物理定律写入神经网络结构"

以前的 AI：通过大量数据暴力喂养，让模型自己去瞎蒙参数

流形约束的 AI：用数学手段强行规定它必须在特定的几何结构上运行

4、关键数学概念

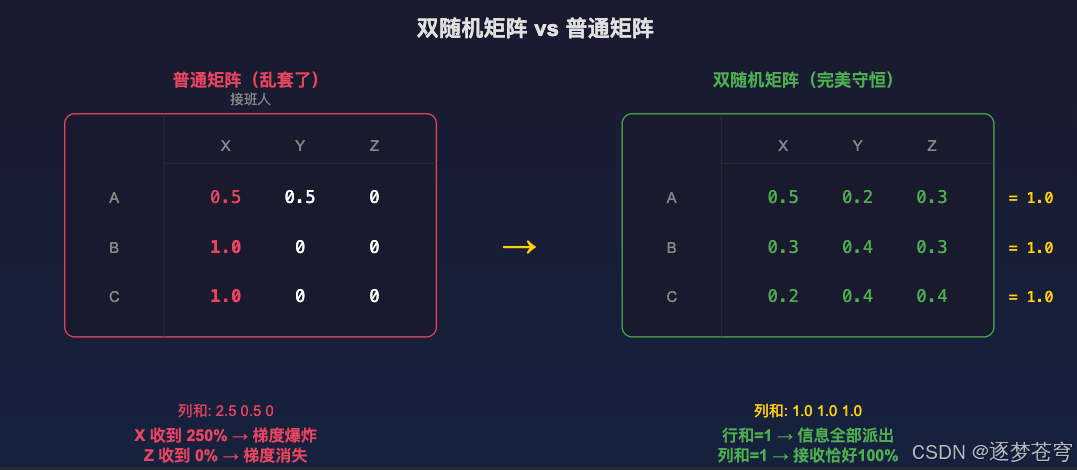
4.1 双随机矩阵：完美的任务分配

我们来看一个**"任务分配"**的场景。

假设有 3 个人（A、B、C） ，要把手里的工作完全移交给 3 个接班人（X、Y、Z）。

4.1.1 普通矩阵（乱套了）

A 把 50% 给 X，50% 给 Y（OK）
B 把 100% 都给 X
C 把 100% 也给 X

结果 : 接班人 X 崩溃了（收到 250% = 梯度爆炸 ）；接班人 Z 没事干（收到 0% = 梯度消失）

4.1.2 双随机矩阵（完美守恒）

DeepSeek 强制要求这个交接单必须同时满足：

规定 1（行和为 1）: 每个人必须把 100% 的活派出去
规定 2（列和为 1）: 每个接班人收到的活加起来恰好是 100%

4.2 核心公式 Eq.6：mHC 的"宪法"

P M r e s ( H l r e s ) : = { H l r e s ∈ R n × n ∣ H l r e s 1 n = 1 n , 1 n ⊤ H l r e s = 1 n ⊤ , H l r e s ⩾ 0 } \mathcal{P}{\mathcal{M}^{\mathrm{res}}}(\mathcal{H}{l}^{\mathrm{res}}) := \left\{\mathcal{H}{l}^{\mathrm{res}} \in \mathbb{R}^{n \times n} \mid \mathcal{H}{l}^{\mathrm{res}} \mathbf{1}{n} = \mathbf{1}{n},\ \mathbf{1}{n}^{\top} \mathcal{H}{l}^{\mathrm{res}} = \mathbf{1}{n}^{\top},\ \mathcal{H}{l}^{\mathrm{res}} \geqslant 0 \right\} PMres(Hlres):={Hlres∈Rn×n∣Hlres1n=1n, 1n⊤Hlres=1n⊤, Hlres⩾0}

三大铁律:

公式	数学含义	人话
H 1 = 1 \mathcal{H} \mathbf{1} = \mathbf{1} H1=1	行和为 1	必须分完，不能私藏
1 ⊤ H = 1 ⊤ \mathbf{1}^{\top} \mathcal{H} = \mathbf{1}^{\top} 1⊤H=1⊤	列和为 1	不能累死人，也不能闲死人
H ⩾ 0 \mathcal{H} \geqslant 0 H⩾0	非负性	不能有"负任务"捣乱

4.3 非负性约束的重要性

如果去掉非负约束（像普通 HC 那样），允许矩阵元素取负值，会引发**"10-9 陷阱"**：

mHC（有约束） : 0.5 + 0.5 = 1 0.5 + 0.5 = 1 0.5+0.5=1，信号平稳
HC（无约束） : 10000 + ( − 9999 ) = 1 10000 + (-9999) = 1 10000+(−9999)=1，虽然结果也是 1，但中间过程涉及巨大的正负数

负值的危害:

梯度爆炸: 权重系数的范数极大，反向传播时梯度疯狂放大
信号对冲: 大数减大数带来巨大浮点精度误差
破坏物理直觉: 负权重会主动破坏其他通道的信息

4.4 什么是凸组合（Convex Combination）

前面提到 mHC 要求的是"凸组合"而非"线性组合"，这个概念很关键。

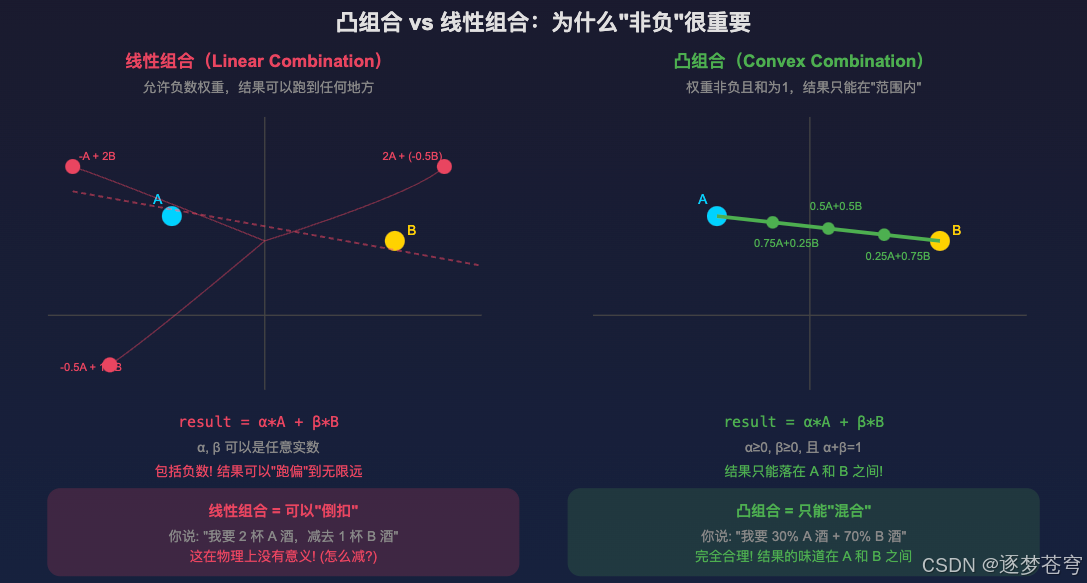
4.4.1 线性组合 vs 凸组合

线性组合 ： r e s u l t = α ⋅ A + β ⋅ B result = \alpha \cdot A + \beta \cdot B result=α⋅A+β⋅B，其中 α , β \alpha, \beta α,β 可以是任意实数（包括负数）。

结果可以跑到"无限远"
比如： 2 A + ( − 1 ) B 2A + (-1)B 2A+(−1)B 意味着"两倍的 A 减去一倍的 B"
问题：物理上没有意义（怎么"减去"一份信息？）

凸组合 ： r e s u l t = α ⋅ A + β ⋅ B result = \alpha \cdot A + \beta \cdot B result=α⋅A+β⋅B，但要求 α ≥ 0 \alpha \geq 0 α≥0, β ≥ 0 \beta \geq 0 β≥0，且 α + β = 1 \alpha + \beta = 1 α+β=1。

结果只能落在 A 和 B 之间
比如： 0.7 A + 0.3 B 0.7A + 0.3B 0.7A+0.3B 意味着"70% 的 A 混合 30% 的 B"
几何上：结果只能在 A、B 连线段上

4.4.2 mHC 为什么选凸组合

mHC 要求混合矩阵是双随机矩阵 （非负 + 行列和为 1），这自然形成了凸组合。

这样做的好处：

信号不会跑飞：混合后的结果始终在"合理范围"内
信息守恒：你混进去多少，就只能拿出来多少
训练稳定：不会出现"10 - 9 = 1"这种数值不稳定的情况

4.5 Softmax：把任意数字变成概率分布

Softmax 是神经网络中最常用的"归一化"操作之一，在这里解释一下它的原理。

4.5.1 Softmax 公式

softmax ( x i ) = e x i ∑ j e x j \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}} softmax(xi)=∑jexjexi

步骤：

对每个输入取指数 e x e^x ex（保证结果为正）
除以所有指数的和（保证结果和为 1）

4.5.2 为什么 Softmax 不够用

Softmax 只保证行和为 1 ，但不管列和。

如果所有老板都想把最好的任务给同一个明星员工，Softmax 完全允许这种情况。结果：明星员工累死，其他员工闲死------这就是信息不均衡。

4.5.3 Sinkhorn 的优势

Sinkhorn 在 Softmax 的基础上，额外强制列和也为 1。这就实现了真正的"信息守恒"：每个来源分配完自己的份额，每个接收者也恰好收到应得的份额。

5、Sinkhorn-Knopp 算法：矩阵平衡术

Sinkhorn-Knopp 算法（1967 年提出）是 mHC 的关键实现手段。

5.1 一句话解释

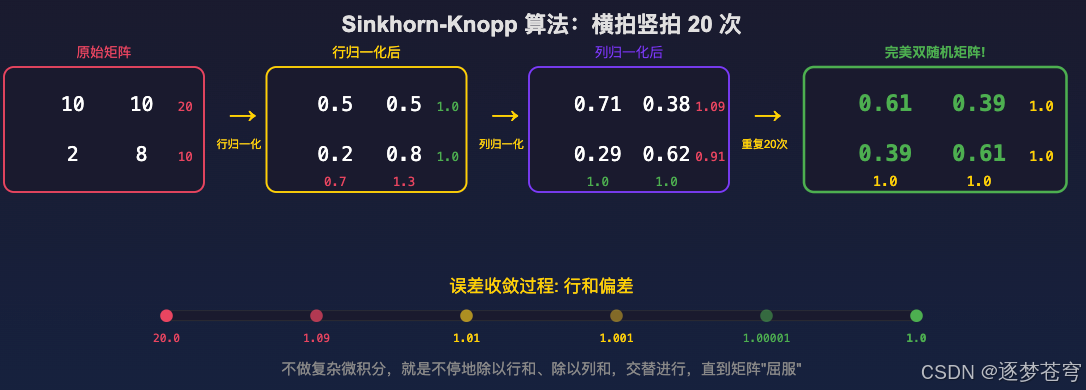
它是一个**"强行平衡器"**。把一个乱七八糟的矩阵，通过不断的"横着捏一下、竖着捏一下"，最终变成行和为 1、列和也为 1 的完美矩阵。

就像揉面团：不停地左右挤、上下挤，最后面团就完美地填满模具。

5.2 手动演算示例

假设有两个老板（A 和 B），要给两个员工（小王和小李）发年终奖。

初始矩阵（乱七八糟）:

	小王	小李	行和
老板 A	10	10	20
老板 B	2	8	10

第一步：行归一化 -> 老板这边平了，但员工这边乱了
第二步：列归一化 -> 员工平了，但老板又歪了（但误差从 20 降到了 1.09）
重复 20 次 -> 误差从 1.09 -> 1.01 -> 1.001 -> ... -> 1.0

5.3 为什么不用 Softmax？

Softmax 的局限 : 只能保证行和为 1 ，但不管列（可能所有老板都把钱给了同一个明星员工）
Sinkhorn 的优势 : 同时锁死行和列，实现真正的"信息守恒"

6、残差连接层的数据流

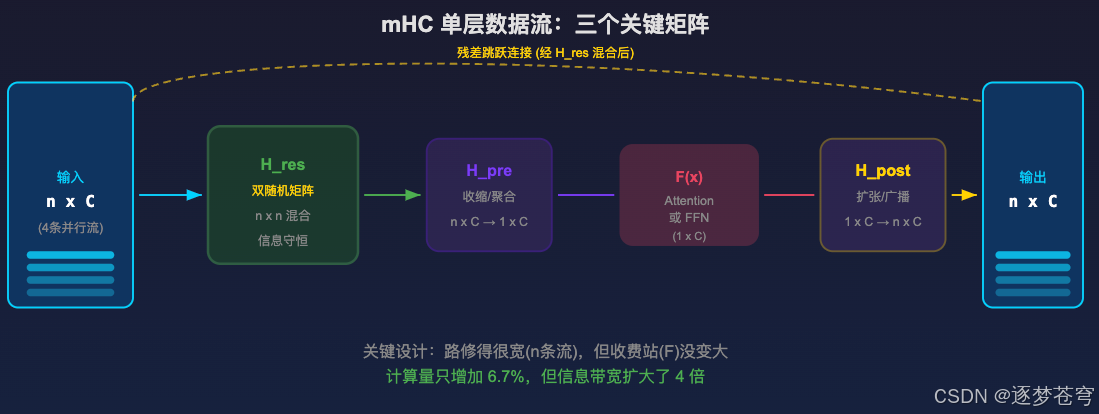
mHC 对传统的"一条线"传输做了扩容。

6.1 数据形式

传入 : 传统残差流是 1 × C 1 \times C 1×C，mHC 扩展为 n × C n \times C n×C （ n = 4 n=4 n=4 条并行流）
传出 : 保持 n × C n \times C n×C 形式，继续传给下一层

6.2 三个关键映射矩阵

矩阵	作用	说明
H r e s H_{res} Hres	残差混合	在 n 个流之间混合，约束为双随机矩阵
H p r e H_{pre} Hpre	收缩/聚合	把 n × C n \times C n×C 压缩成 1 × C 1 \times C 1×C，喂给计算单元
H p o s t H_{post} Hpost	扩张/广播	把 1 × C 1 \times C 1×C 扩张回 n × C n \times C n×C，加回残差流

7、三大工程优化策略

理论很美，但参数变多了 4 倍，怎么不慢？DeepSeek 用了三招解决"富贵病"：

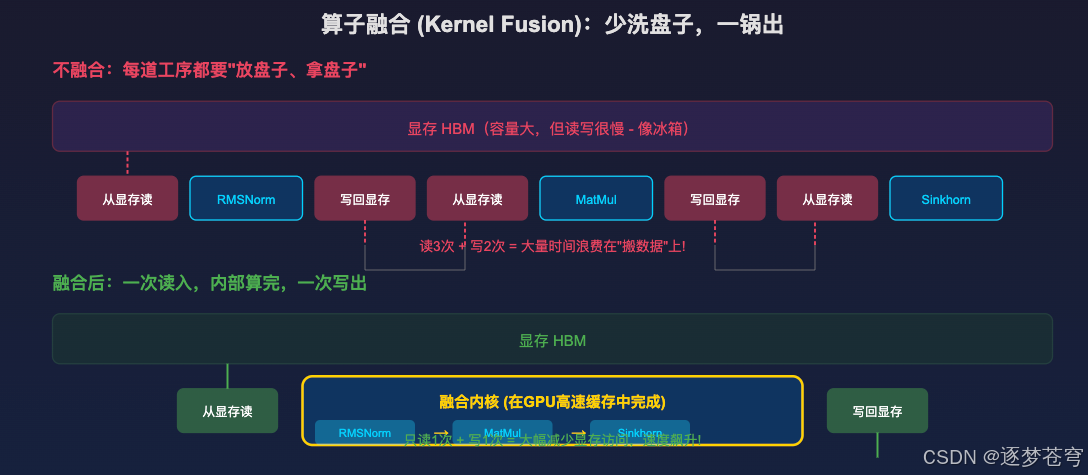
7.1 算子融合 (Kernel Fusion)

核心目的：减少搬运数据的次数

7.1.1 问题背景

GPU 的计算单元（ALU）速度极快，但显存（HBM）读写速度是瓶颈。如果每个小操作都要：

从显存读数据
算一下
写回显存
下一个操作再读出来...

那么大量时间浪费在"搬运数据"上，而不是真正的计算。

7.1.2 解决方案

将 RMSNorm、矩阵乘法、Sinkhorn-Knopp 合并成一个大 Kernel：

数据从显存读入 GPU 高速缓存
在缓存里连续完成所有计算
最后一次性写回显存

类比：就像做菜时"一锅出"------所有配料一次性放进锅里炒完，而不是每放一个配料就端锅去洗一次。

7.2 选择性重计算 (Selective Recomputing)

核心目的：用计算时间换显存空间

7.2.1 问题背景

反向传播需要用到前向传播的中间结果。如果 100 层网络把所有中间结果都存下来，显存会爆炸。

7.2.2 两种极端方案

方案 A（全存）：100 层 = 存 100 份中间结果 -> 显存爆炸
方案 B（全算）：什么都不存，反向传播时从头重算 -> 时间爆炸（计算量翻 100 倍）

7.2.3 mHC 的聪明做法

分类处理：

贵的（存）：Attention 输入、每个 Block 的起点 -> 这些重算代价很高，必须存
便宜的（扔） ： H r e s H_{res} Hres, H p r e H_{pre} Hpre, H p o s t H_{post} Hpost -> 这些矩阵很小，算得很快，现用现算

结果：显存省了，时间只多一点点。

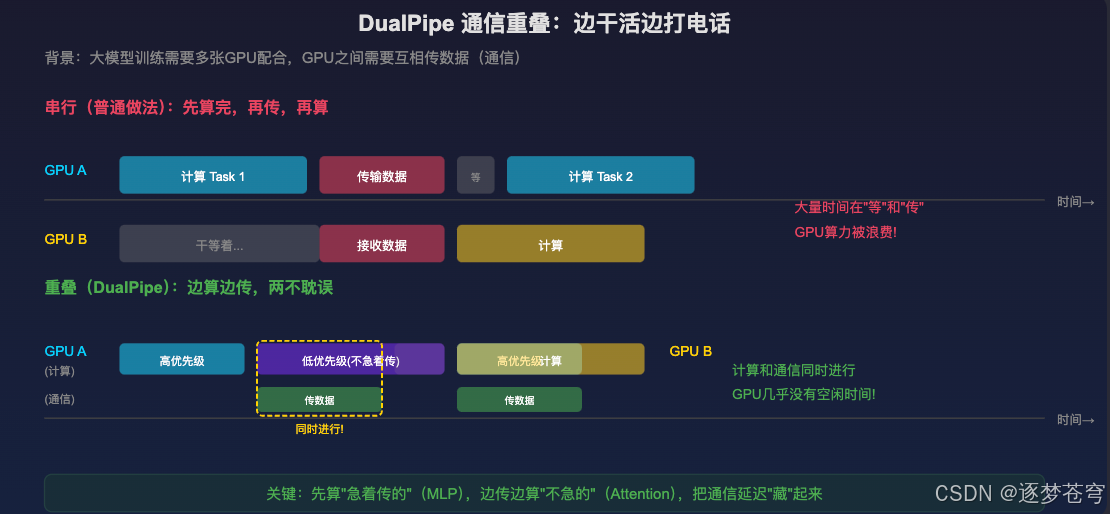
7.3 DualPipe 通信重叠

核心目的：别让 GPU 闲着等快递

7.3.1 问题背景

大模型训练需要多张 GPU 配合，GPU 之间需要互相传数据（通信）。

串行做法 ：先算完 -> 再传 -> 等传完 -> 再算下一步
问题：大量时间在"等"和"传"，GPU 算力被浪费！

7.3.2 DualPipe 的做法

把计算任务分成两类：

高优先级（急着传的）：MLP 部分，计算完要立刻传给下一个 GPU
低优先级（不急着传的）：Attention 部分，可以边算边等

时间安排：

先算高优先级任务，算完立刻开始传输
传输的同时，去算低优先级任务
低优先级算完时，传输也差不多完成了

结果：计算和通信同时进行，GPU 几乎没有空闲时间！

7.3.3 最终效果

模型加宽了 4 倍，训练时间只增加了 6.7%------这就是极致工程优化的威力。

8、三代架构对比

特性	ResNet	HC	mHC
公式	x + F ( x ) x + F(x) x+F(x)	H x + ... \mathcal{H} x + \dots Hx+...	P ( H ) x + ... \mathcal{P}(\mathcal{H}) x + \dots P(H)x+...
混合矩阵	固定单位矩阵	完全自由学习	双随机矩阵
取值范围	0 和 1	( − ∞ , + ∞ ) (-\infty, +\infty) (−∞,+∞)	[ 0 , 1 ] [0, 1] [0,1]
混合方式	不混合	线性组合（允许 10-9=1）	凸组合（只允许 0.5+0.5=1）
复合映射增益	1.0	可达 3000x	1.0 ~ 1.6x
结果	稳定但弱	强但不稳定	既强又稳定

9、深层追问：为什么这些架构创新能让模型学得更好？

很多人直觉上困惑："把结构搞复杂了，凭什么就学得好了？"

答案是：这些变换本身不产生"智能"，它们解决的是信息流通的问题。

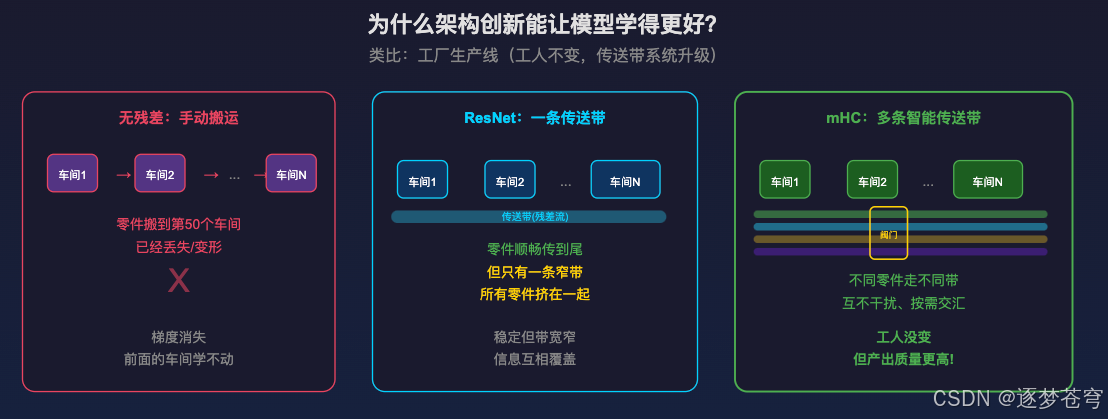
9.1 工厂类比

假设有一个工厂（模型），100 个车间串联（100 层），每个车间里有工人在加工零件（Attention/FFN 做计算）。

车间的工人没变（计算层没变大），变的是车间之间的传送带系统（残差流）。

没有传送带（无残差）：零件搬到第 50 个车间时已经丢了
一条传送带（ResNet）：零件顺畅传到尾，但带子窄，零件挤在一起
多条智能传送带（mHC）：不同零件走不同带，互不干扰

9.2 更丰富的输入信息

传统残差网络中，第 50 层收到的是前 49 层加工后混在一起的一个向量。很多早期层的有用信号已被冲淡。

多流残差让不同类型的信息独立保留。第 50 层从 4 条管道聚合信息，比从 1 条管道提取要丰富得多。

9.3 更有效的梯度回传

多条残差流意味着梯度也有多条回传路径。每一层能收到更准确的梯度信号，参数更新方向更准确。

9.4 约束本身也是一种"知识"

双随机矩阵的约束看似"限制"，实际是在注入先验知识 。就像沿着河床找水源比在沙漠里乱找效率高。约束是指南针，减少了模型需要探索的参数空间。

核心结论：不是"变换更复杂"让模型变好，而是"信息流通更高效"让模型变好。

10、实验结果与核心突破

10.1 实验配置

模型规模：3B、9B 和 27B 参数的 MoE 模型
残差流展开率： n = 4 n = 4 n=4
架构特性：分组查询注意力（GQA）、前置规范化 Transformer

10.2 关键指标

指标	基线 HC	mHC	改进
BBH	48.9%	51.0%	+2.1%
DROP	-	-	+2.3%
训练时间开销	-	+6.7%	极低代价
最大增益幅度	3000x	1.0~1.6x	训练稳定

10.3 核心突破

重新定义"深度"的有效性：只要信息流的组织方式正确，不用增加计算量，光优化信息的"流动管道"就能大幅提升能力
解决"超连接"无法扩展的难题：第一次证明这种架构可以扩展到千亿参数级别且训练稳定
"信息守恒"作为架构定律：将物理守恒定律写进神经网络结构
极致的工程优化：不是纸上谈兵，可直接部署在工业级训练中

11、总结

11.1 关键公式推导脉络

ResNet : y = x + F ( x ) y = x + F(x) y=x+F(x) -- 稳定，但表达力弱
HC : x ′ = H x + ... x' = \mathcal{H} x + \dots x′=Hx+... -- 表达力强，但不稳定
mHC : 将 H \mathcal{H} H 投影到 Birkhoff 多面体上 -- 既稳定又强大
实现: Sinkhorn-Knopp 算法 -- 横拍竖拍 20 次

11.2 一句话概括

mHC 就是给大模型的"神经网络"装上物理阀门。它证明了只要拓扑结构合理，不需要单纯堆参数，也能大幅提升模型能力。这是"几何与物理指导 AI"的胜利。

11.3 后续发展

该方向正在活跃发展中，已有 mHC-lite 等改进版本出现（arXiv: 2601.05732），进一步降低计算开销。

如果这篇文章对你有帮助，欢迎点赞、收藏、关注，你的支持是我持续创作的最大动力！