(以下内容全部出自上述课程)
目录
- 二叉树的遍历
-
- [1. 什么是遍历](#1. 什么是遍历)
- [2. 二叉树的遍历](#2. 二叉树的遍历)
-
- [2.1 二叉树的遍历(手算练习)](#2.1 二叉树的遍历(手算练习))
- [2.2 代码](#2.2 代码)
-
- [2.2.1 先序遍历](#2.2.1 先序遍历)
- [2.2.2 中序遍历](#2.2.2 中序遍历)
- [2.2.3 后序遍历](#2.2.3 后序遍历)
- [2.2.4 先序遍历演示过程](#2.2.4 先序遍历演示过程)
- [3. 求遍历序列](#3. 求遍历序列)
-
- [3.1 先序](#3.1 先序)
- [3.2 中序](#3.2 中序)
- [3.3 后序](#3.3 后序)
- [4. 小结](#4. 小结)
- 二叉树的层序遍历
- 由遍历序列构造二叉树
-
- [1. 引入](#1. 引入)
- [2. 遍历序列](#2. 遍历序列)
-
- [2.1 前序+中序](#2.1 前序+中序)
- [2.2 后序+中序](#2.2 后序+中序)
- [2.3 层序+中序](#2.3 层序+中序)
- [3. 小结](#3. 小结)
- 线索二叉树
-
- [1. 线索二叉树的作用](#1. 线索二叉树的作用)
- [2. 线索二叉树的存储结构](#2. 线索二叉树的存储结构)
-
- [2.1 中序](#2.1 中序)
- [2.2 先序](#2.2 先序)
- [2.3 后序](#2.3 后序)
- [2.4 对比](#2.4 对比)
- [3. 小结](#3. 小结)
- 二叉树线索化
-
- [1. 中序线索化](#1. 中序线索化)
- [2. 先序线索化](#2. 先序线索化)
- [3. 后序线索化](#3. 后序线索化)
- [4. 小结](#4. 小结)
- 在线索二叉树中找前驱后继
-
- [1. 中序](#1. 中序)
- [2. 先序](#2. 先序)
- [3. 后序](#3. 后序)
- [4. 小结](#4. 小结)
二叉树的遍历
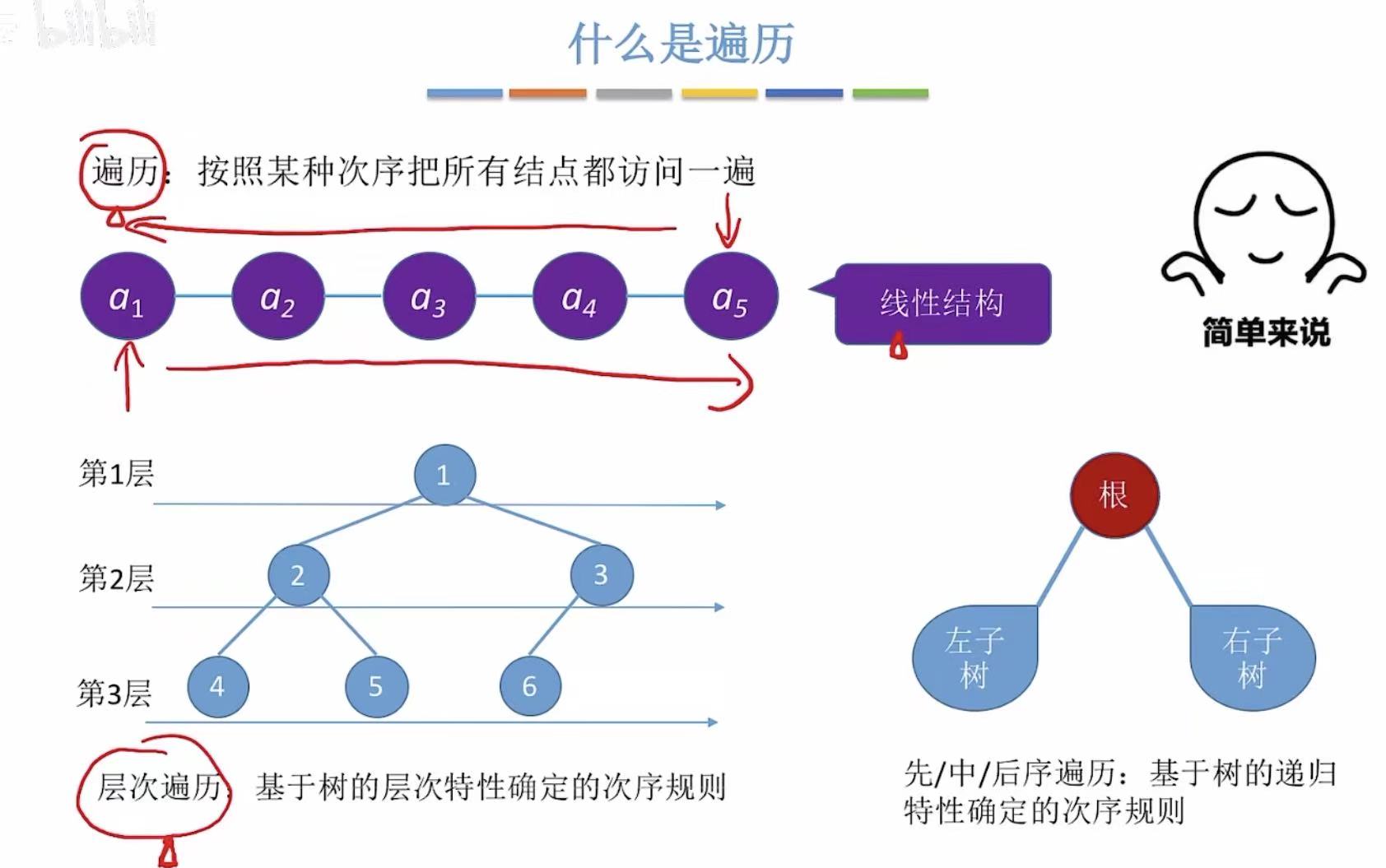
1. 什么是遍历
遍历 :就是把所有结点都访问一遍。
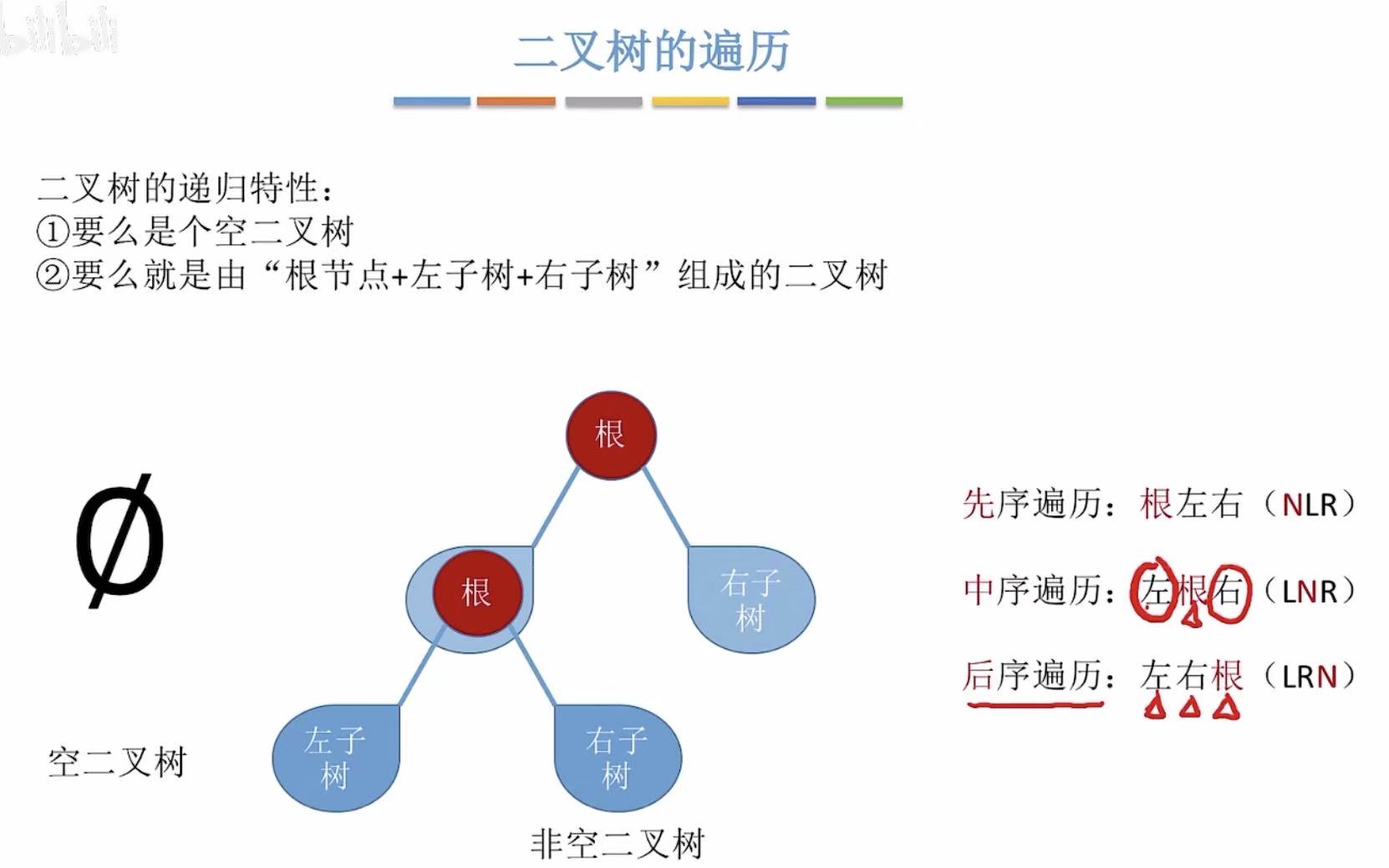
2. 二叉树的遍历
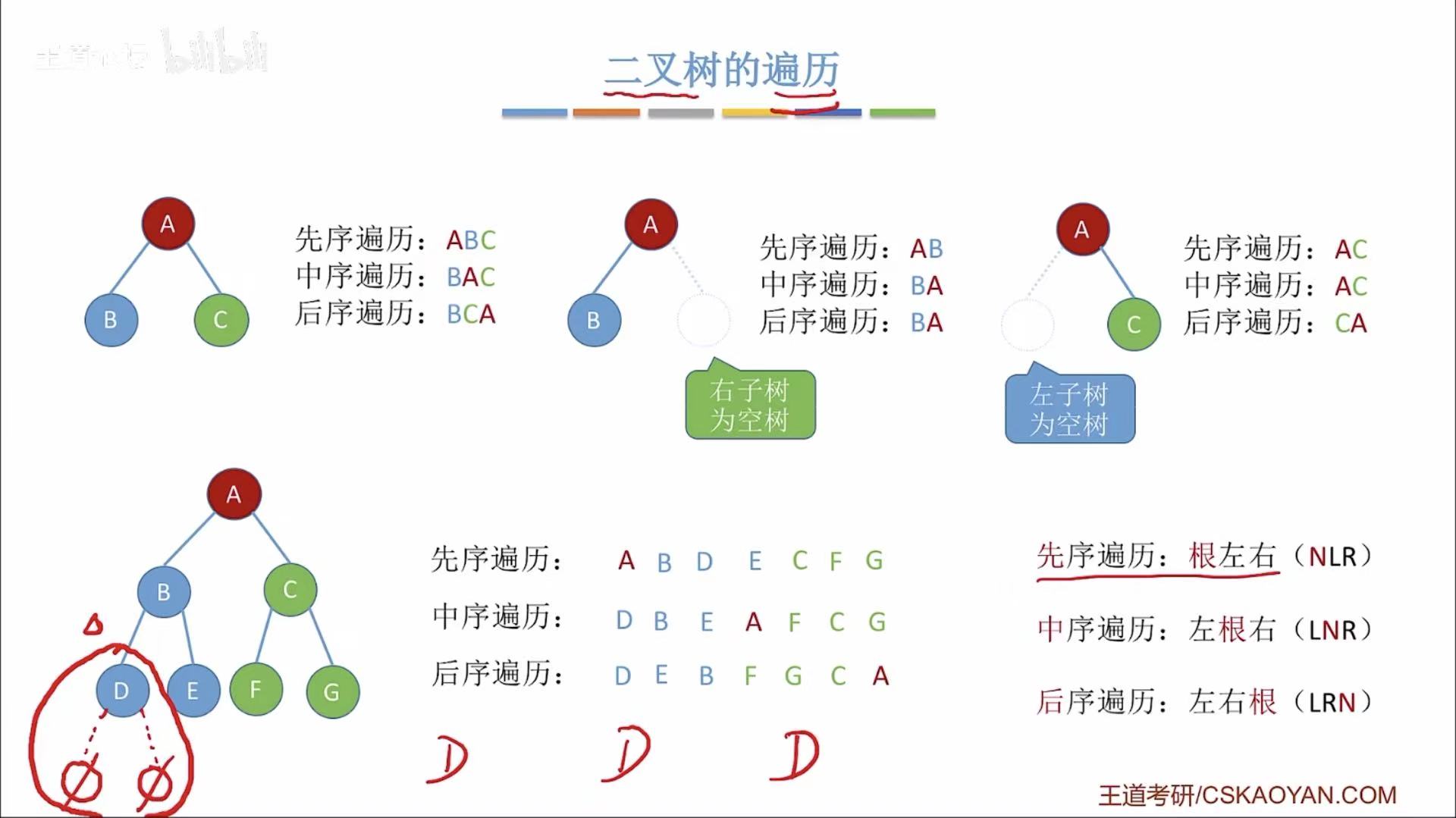
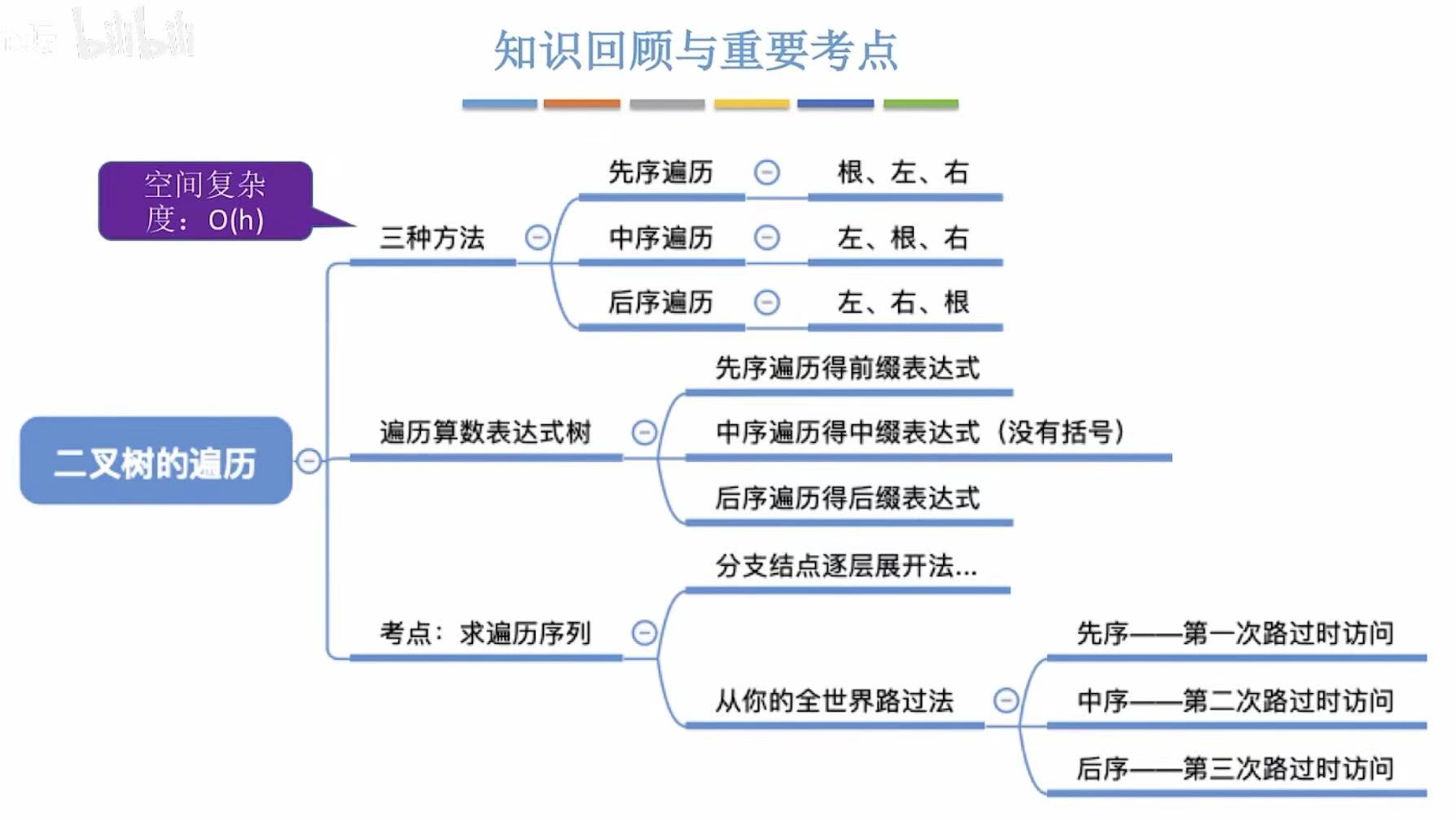
- 先序-先根:根最先被访问。
- 中序-中根:根夹在中间,即第二个被访问。
- 后序-后根 :根最后被访问。
2.1 二叉树的遍历(手算练习)
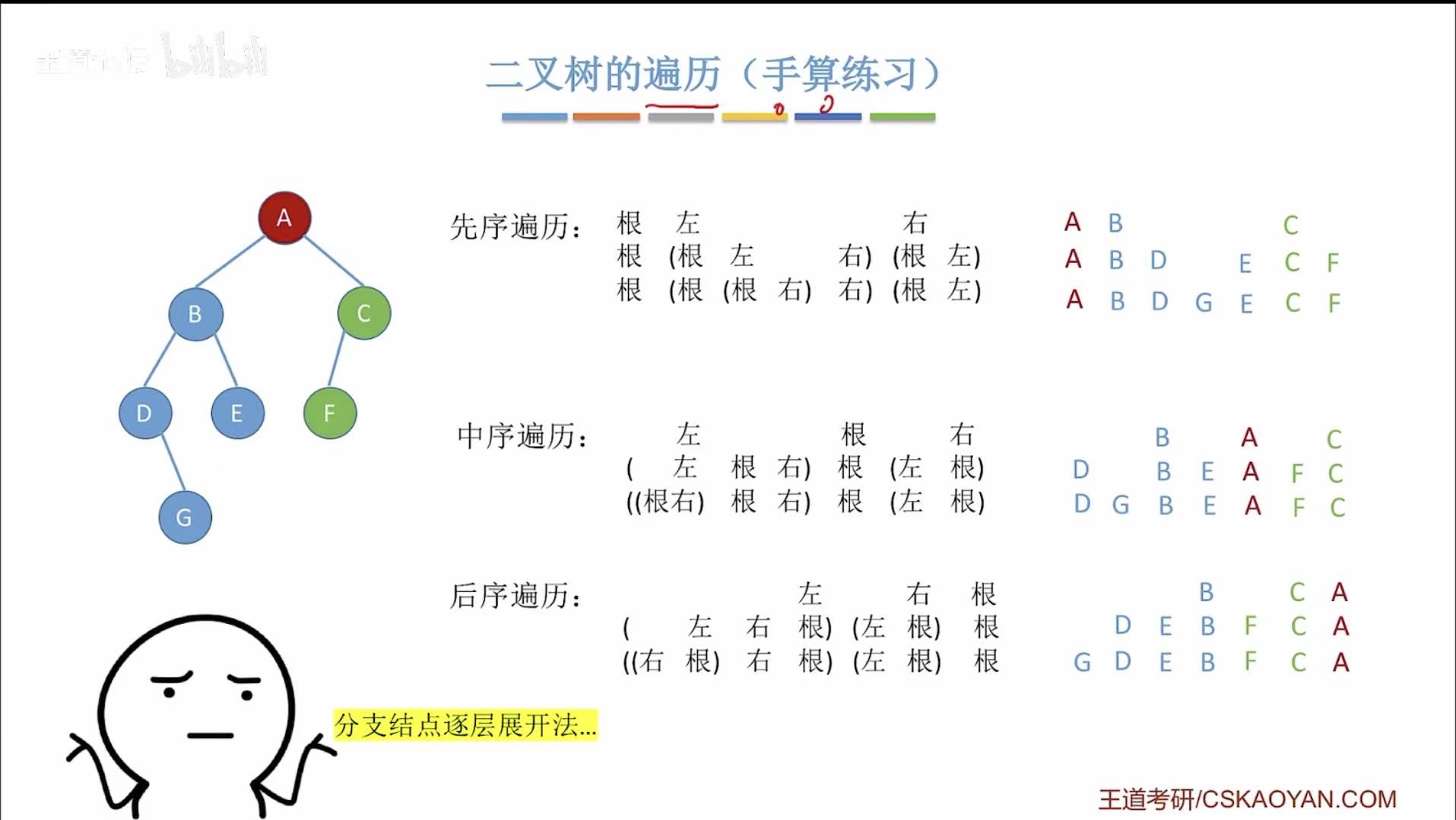
分支结点逐层展开法-先序遍历:
- 第一层+第二层:根左右-->ABC
- 第二层+第三层:根左右-->B:BDE;C:CF
- 第三层+第四层:根左右-->D:DG;
- 最后把每个展开的项代回到原来的位置:A B DG E CF
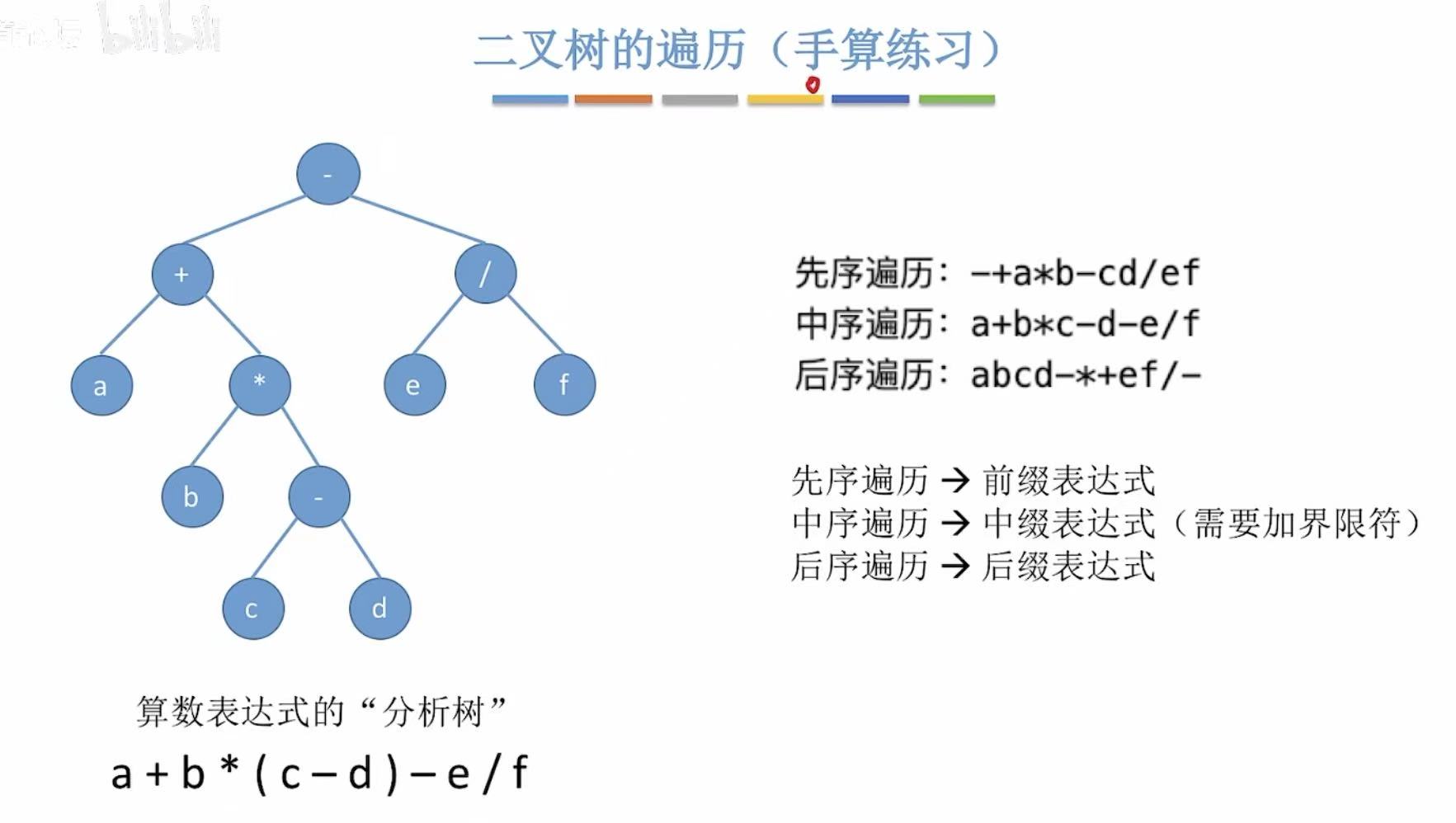
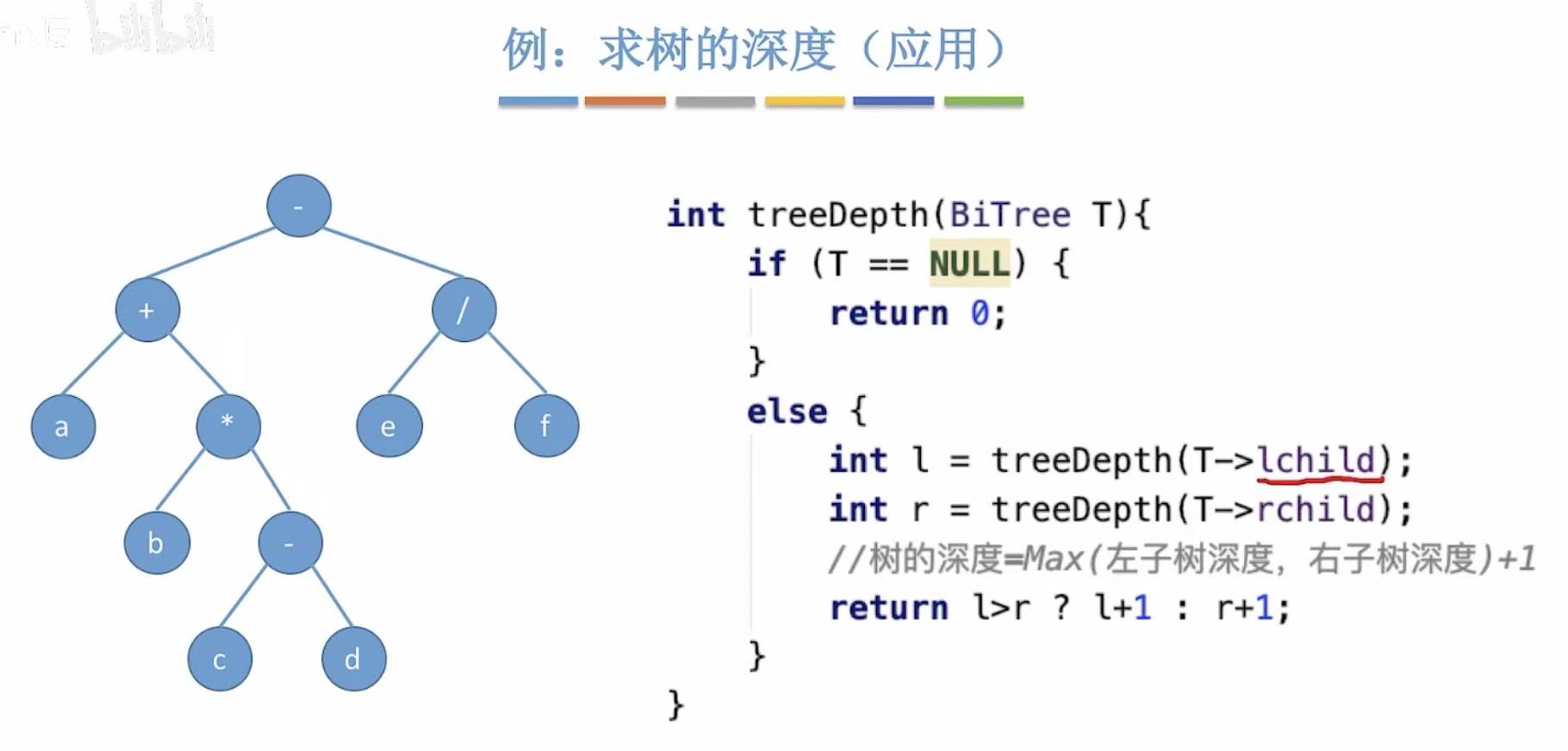
带有运算符号的树就是算数表达式的分析树: - 先序--前缀
- 中序--中缀(需加括号)
- 后序--后缀
2.2 代码
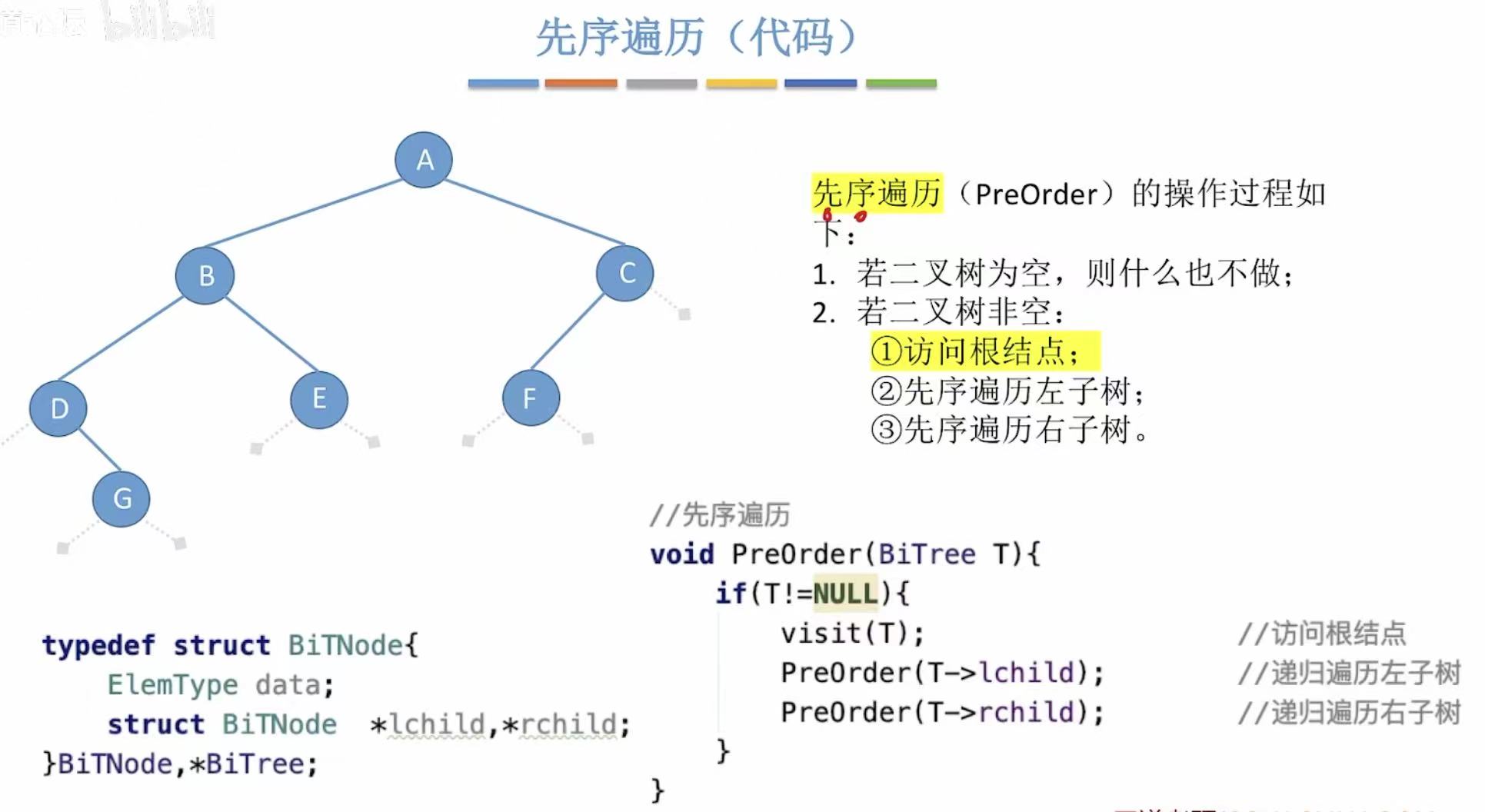
2.2.1 先序遍历
2.2.2 中序遍历
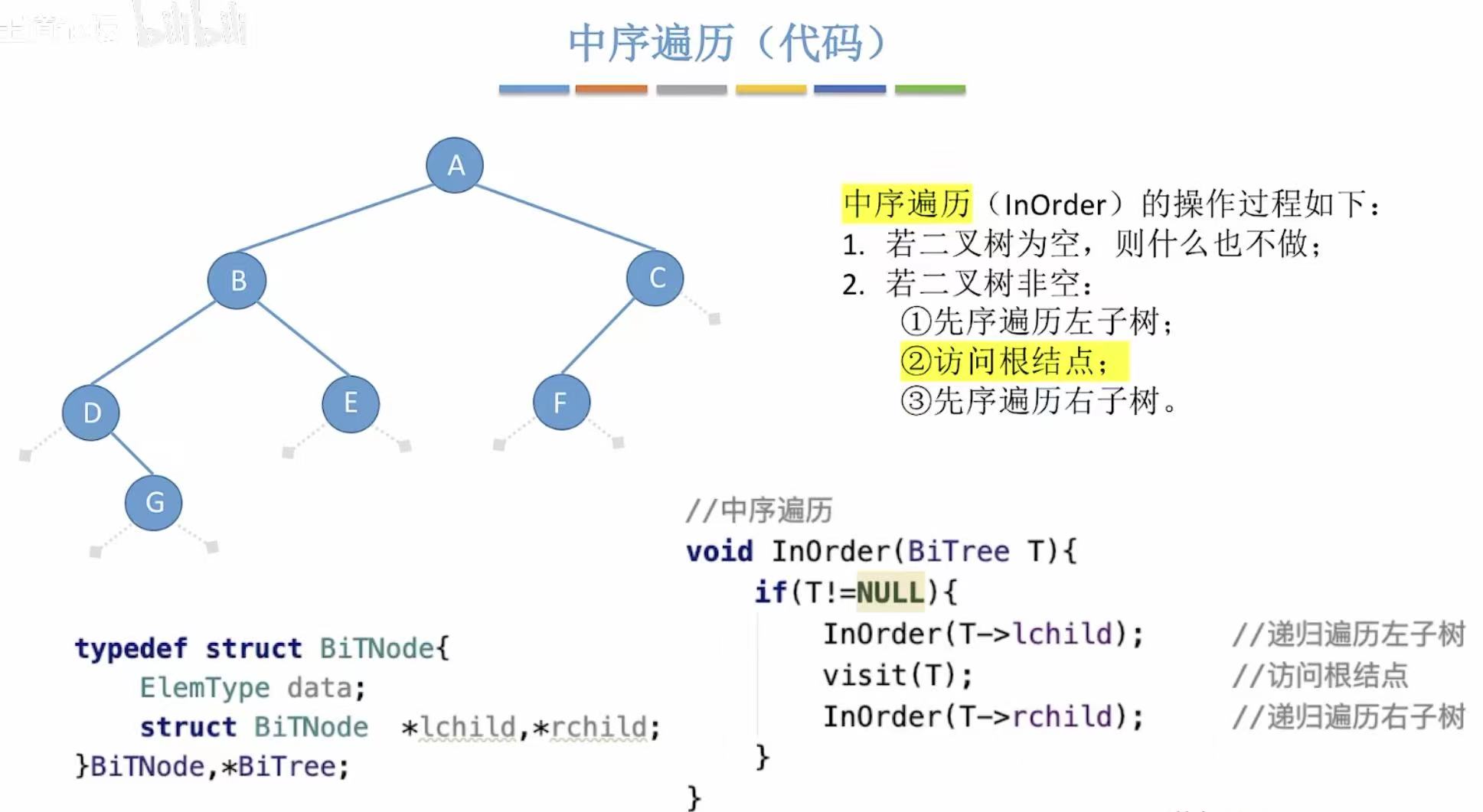
2.2.3 后序遍历
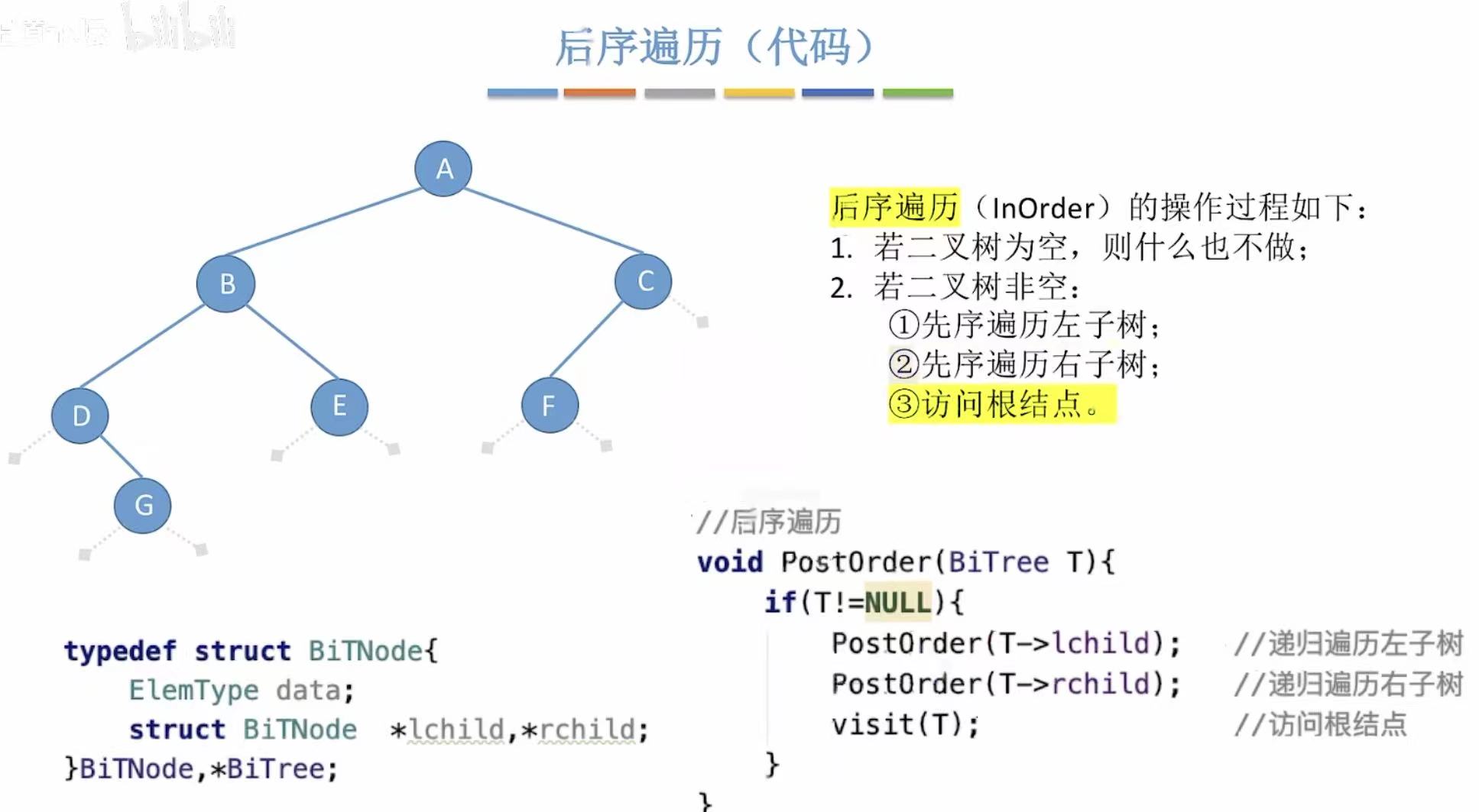
2.2.4 先序遍历演示过程
T-->A-->访问A的左孩子B-->进入递归-->B-->访问B的左孩子D-->D-->访问D的左孩子NULL
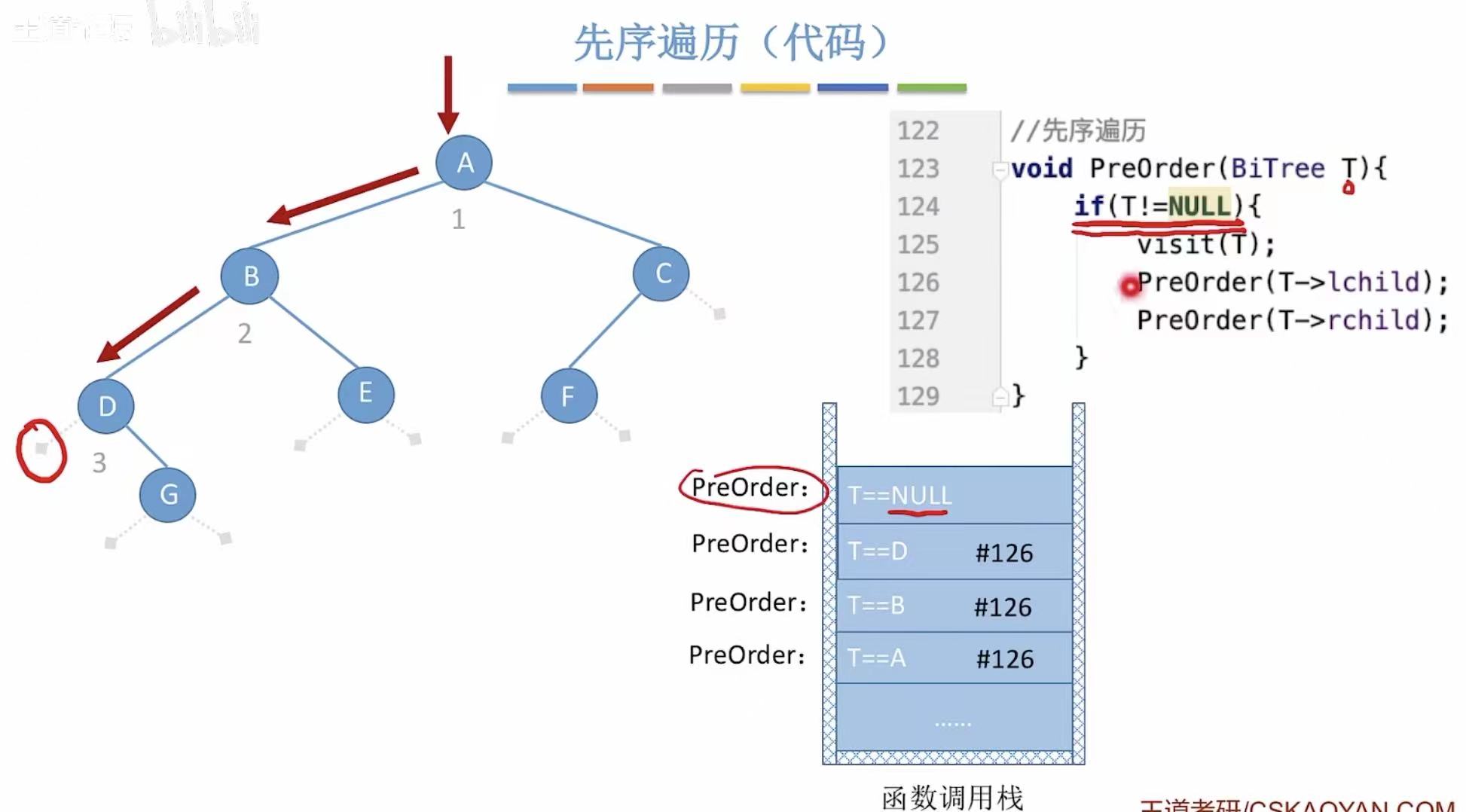
-->访问D的右孩子G-->G-->访问G的左孩子NULL
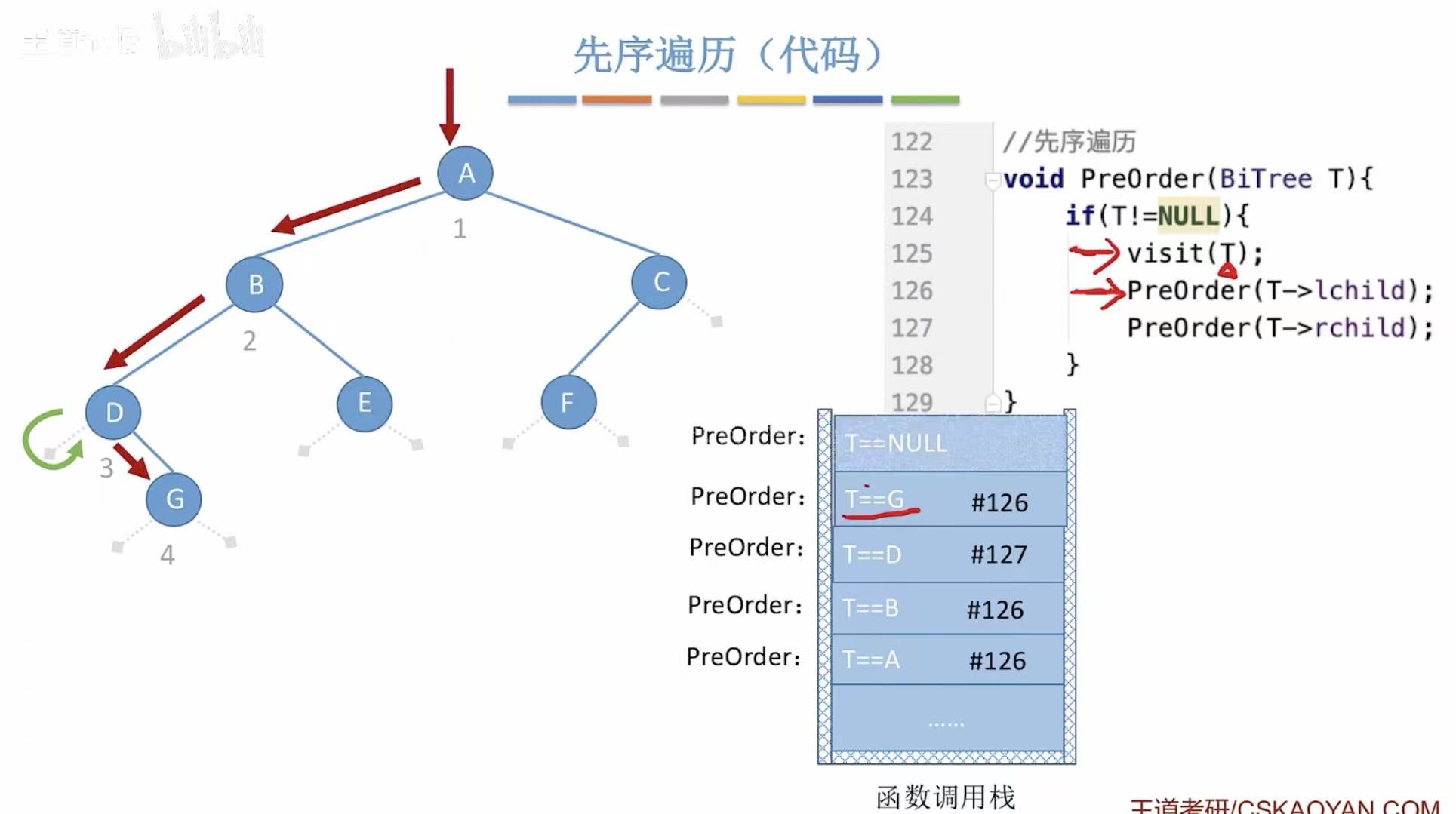
-->访问G的右孩子NULL
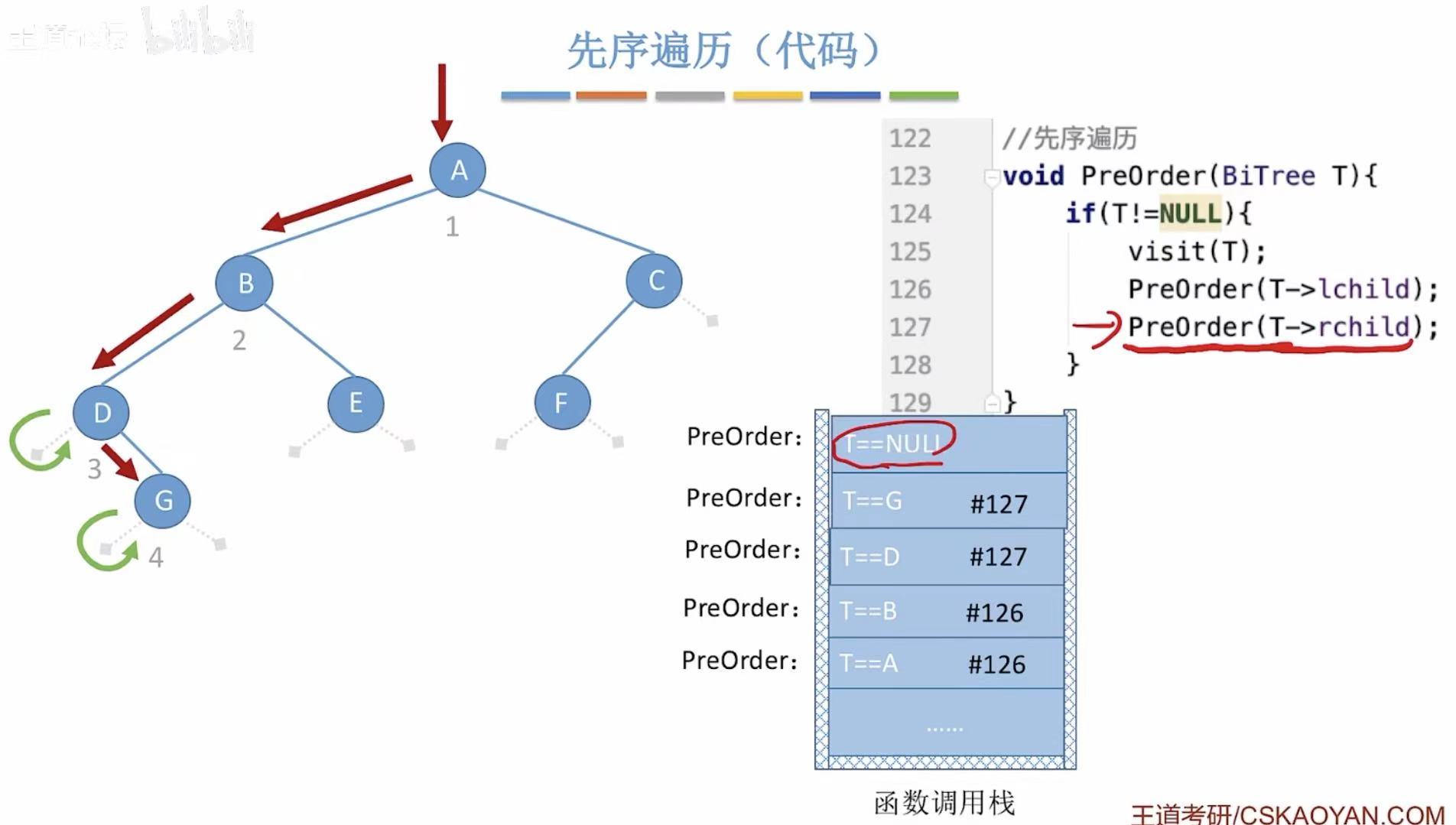
-->返回D-->返回B-->访问B的右孩子E-->E左-->E右-->返回B-->返回A-->...
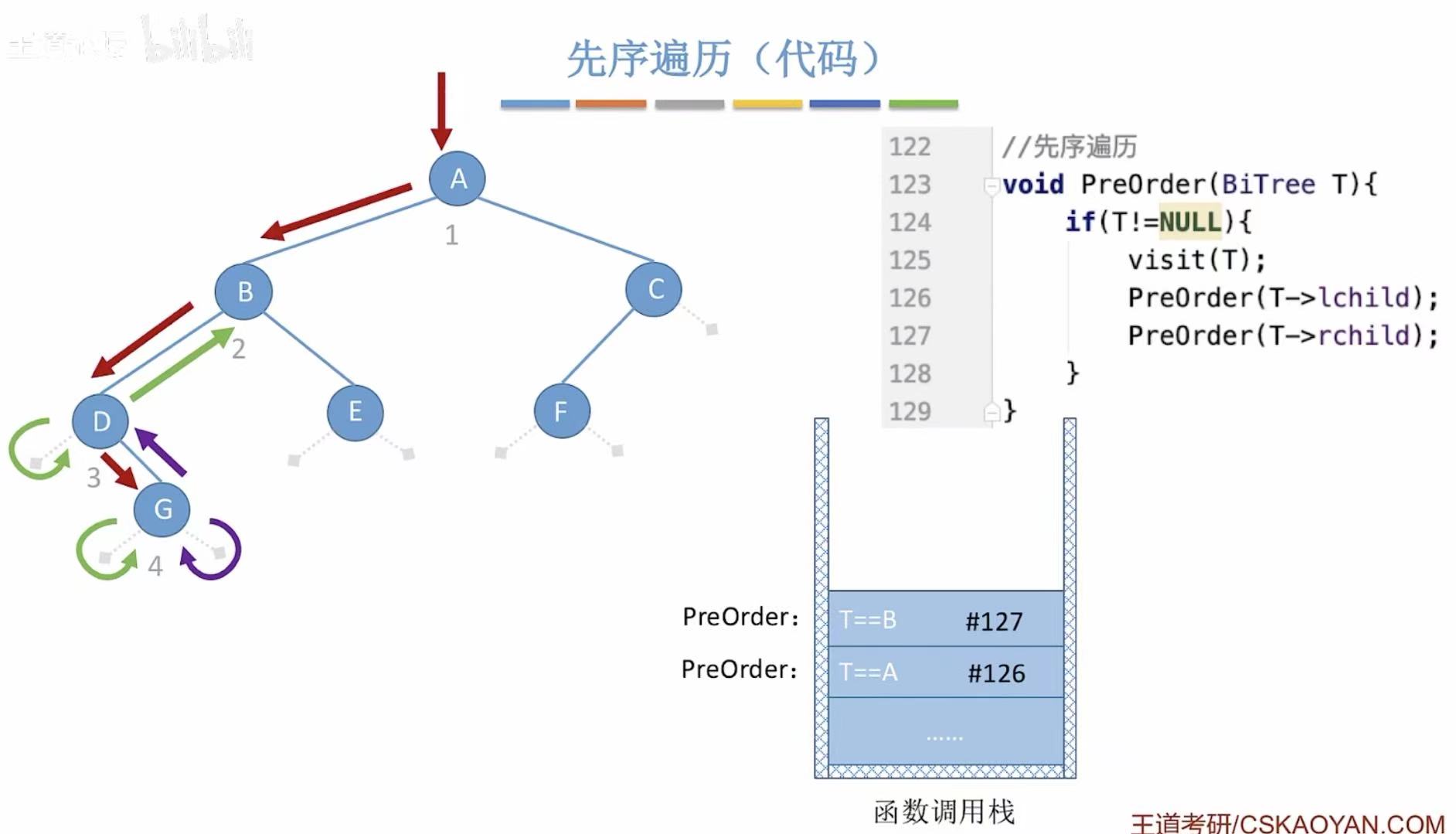
最后全部遍历结束:
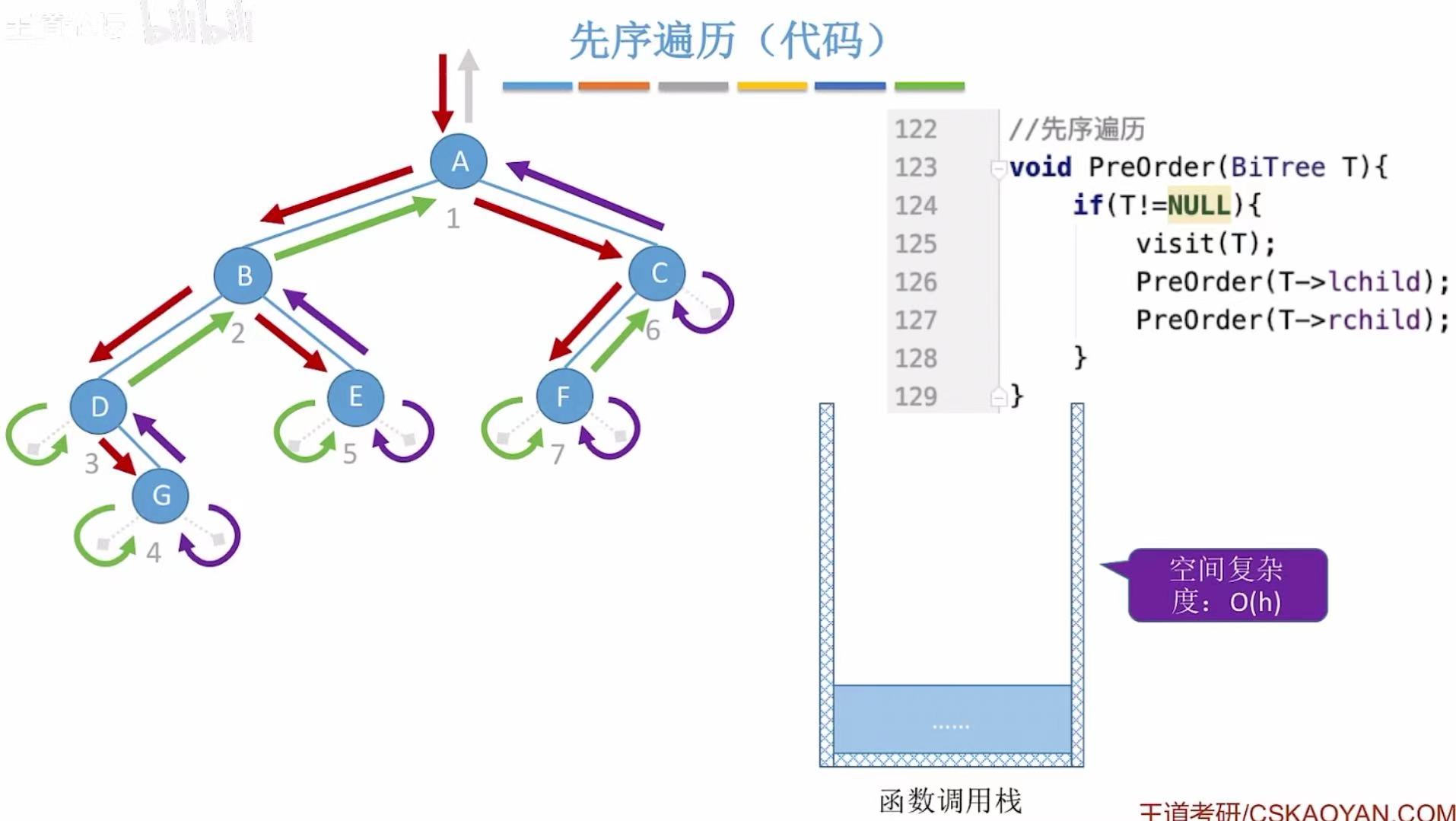
3. 求遍历序列
3.1 先序
先序 :就是第一次路过时访问到的结点。
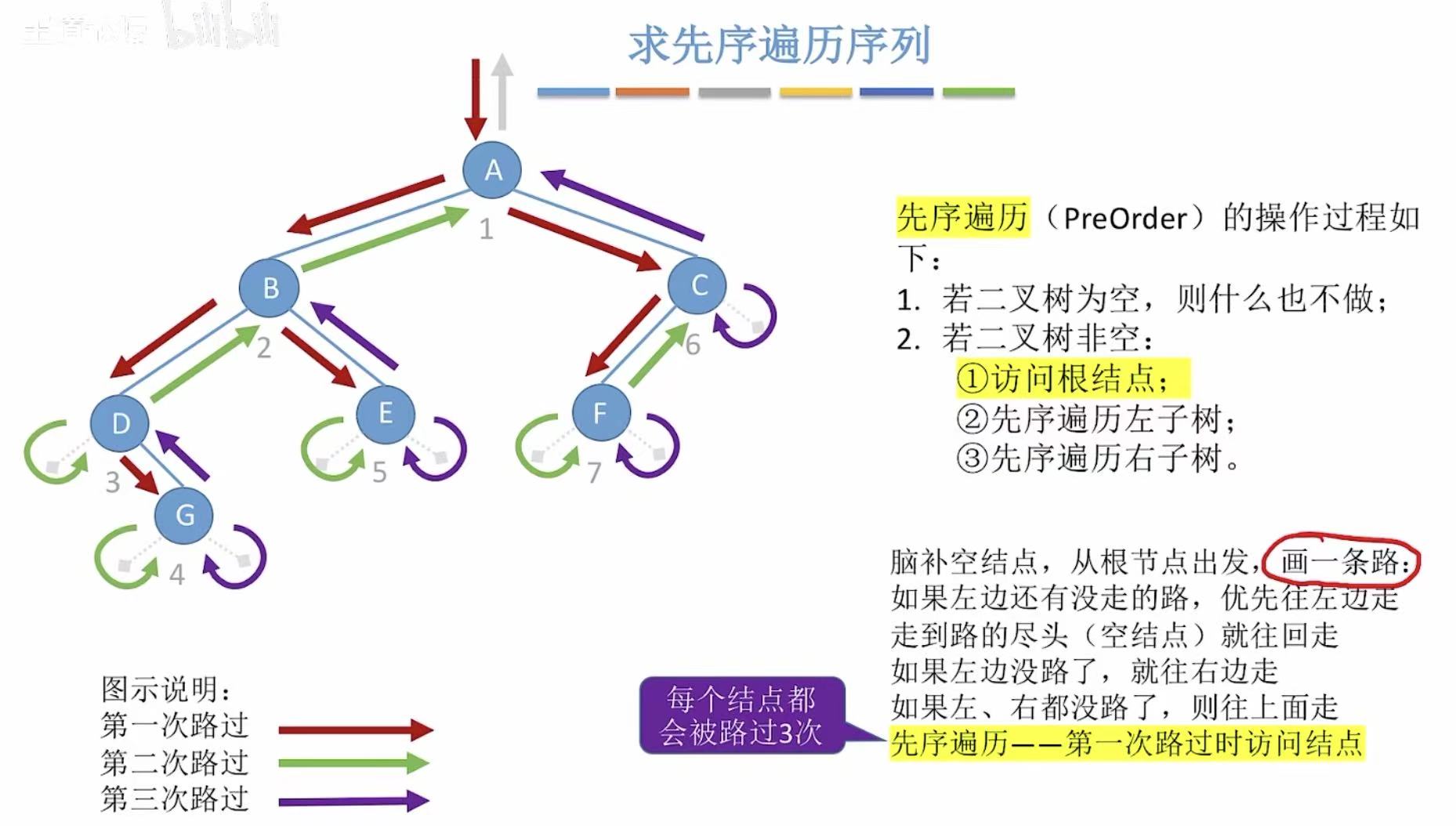
3.2 中序
中序 :就是第二次路过时访问的结点。
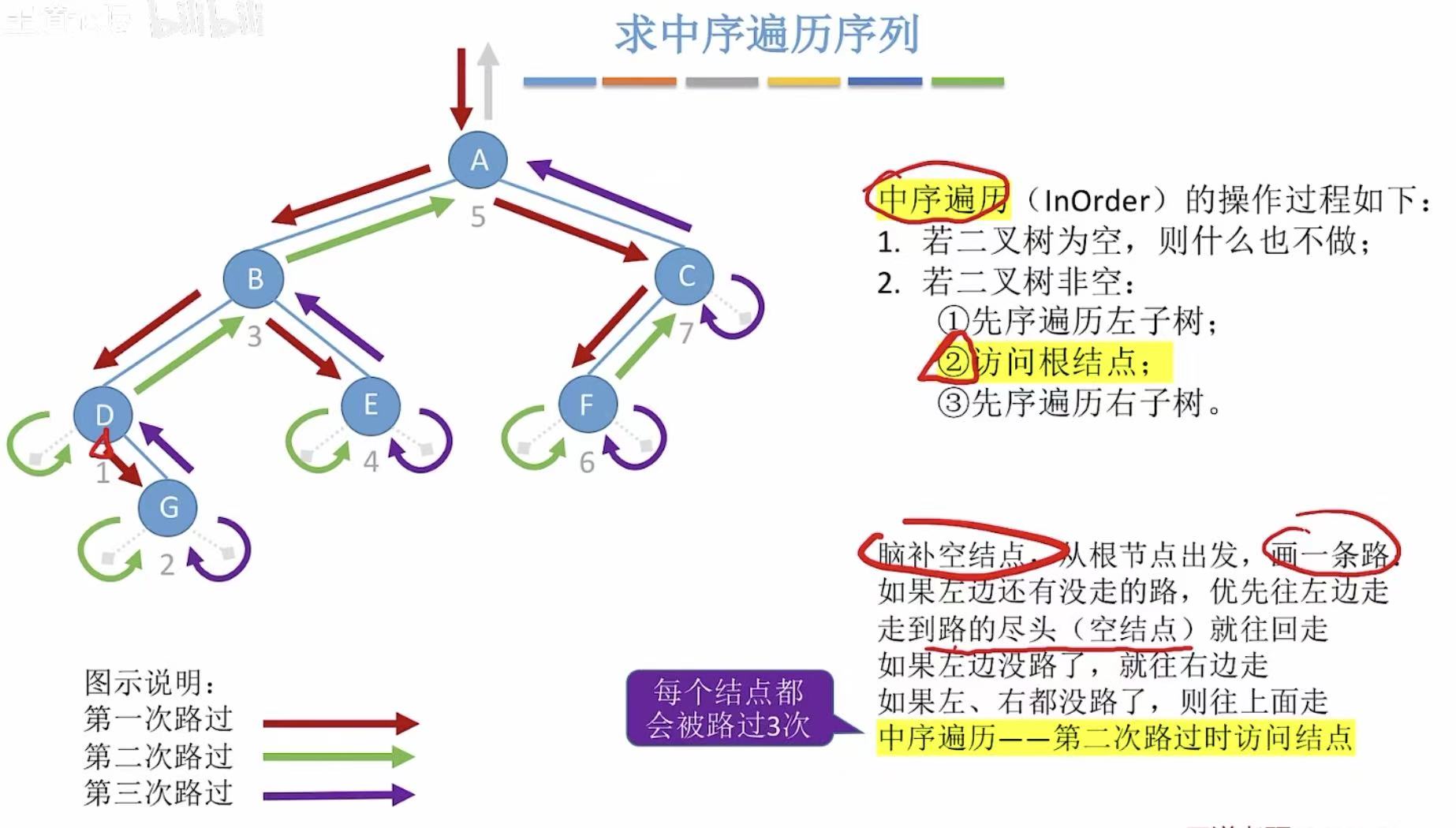
3.3 后序
后序 :就是第三次路过时访问的结点。
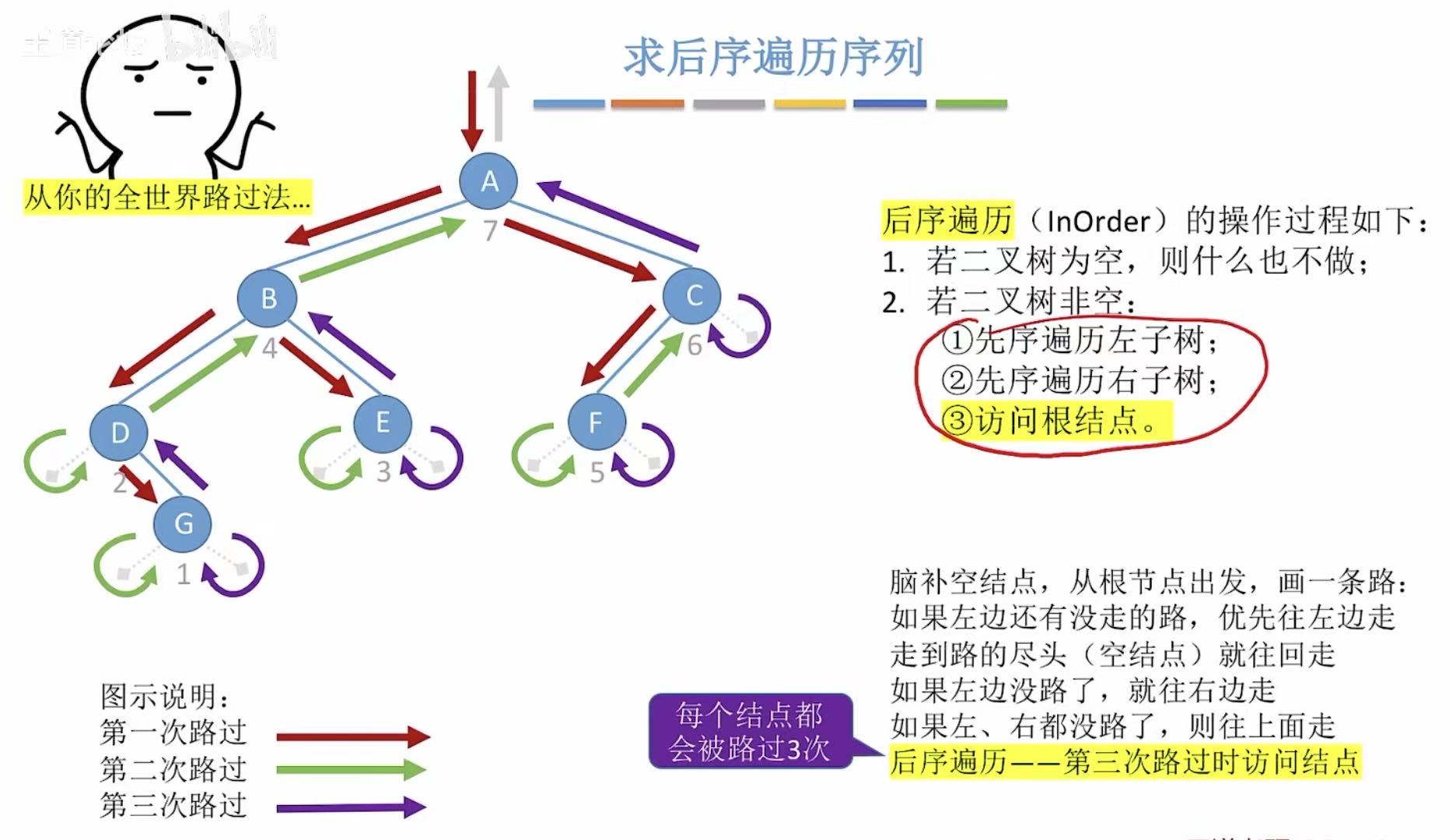
4. 小结
二叉树的层序遍历
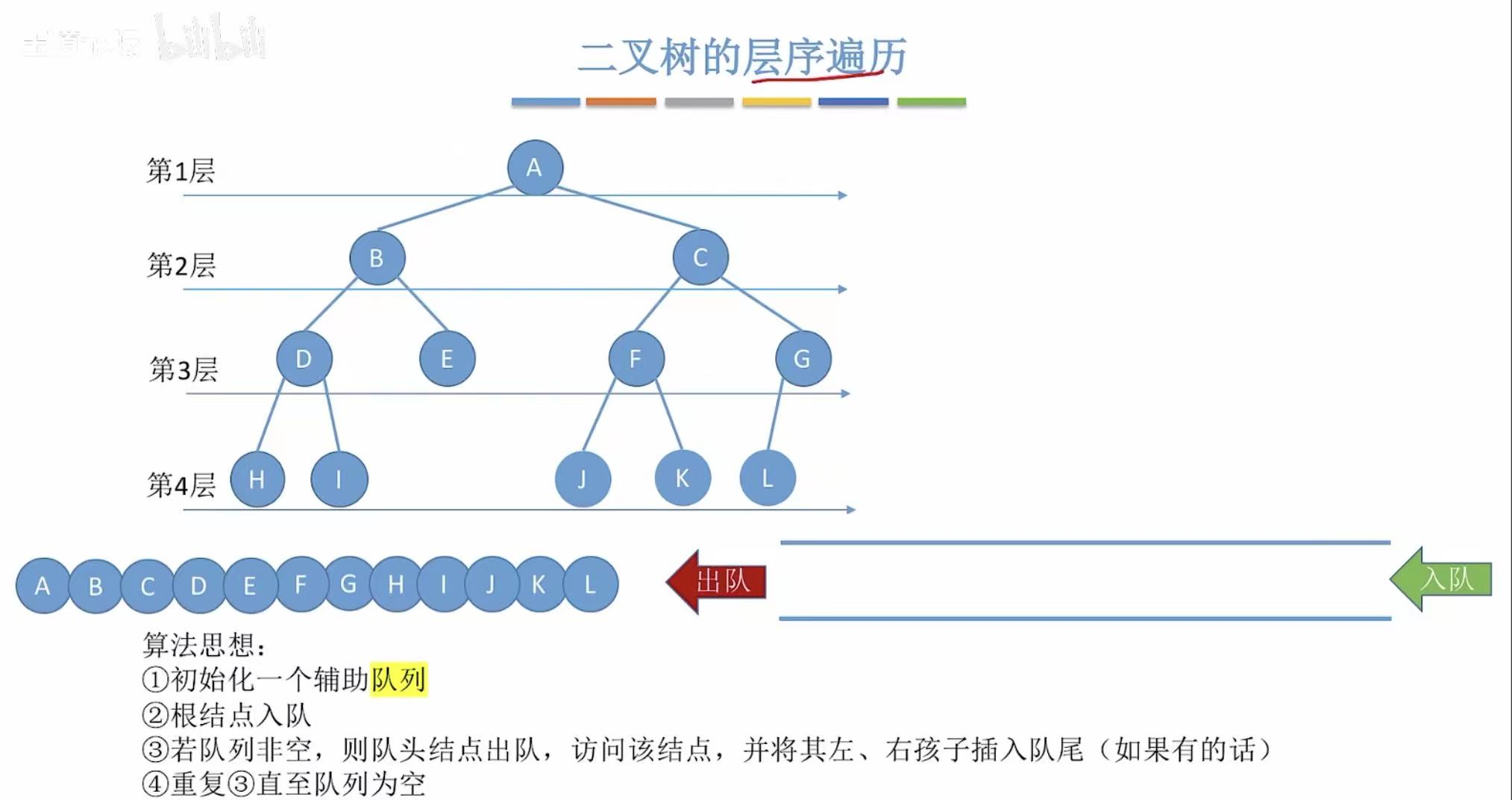


由遍历序列构造二叉树
1. 引入
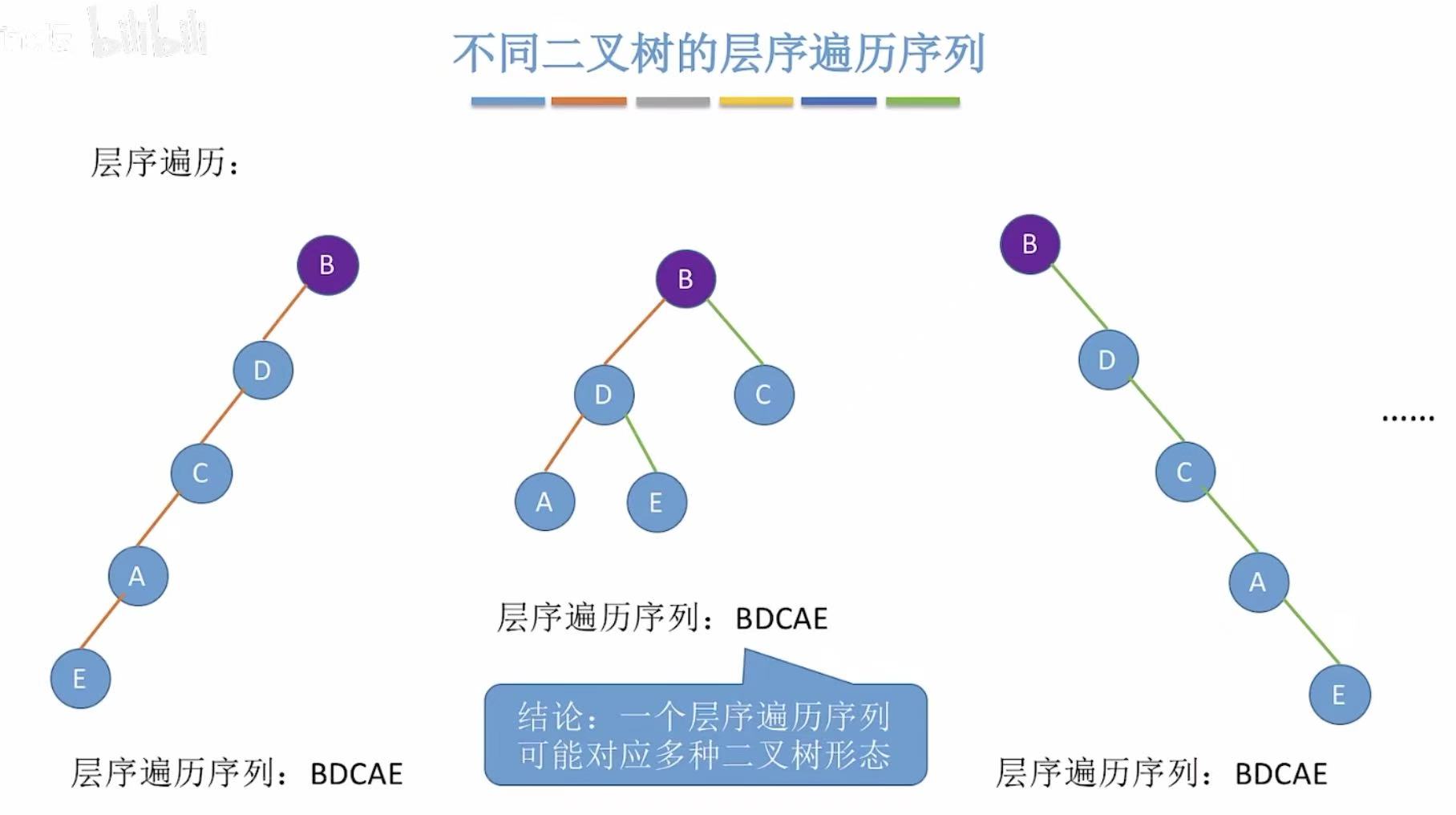
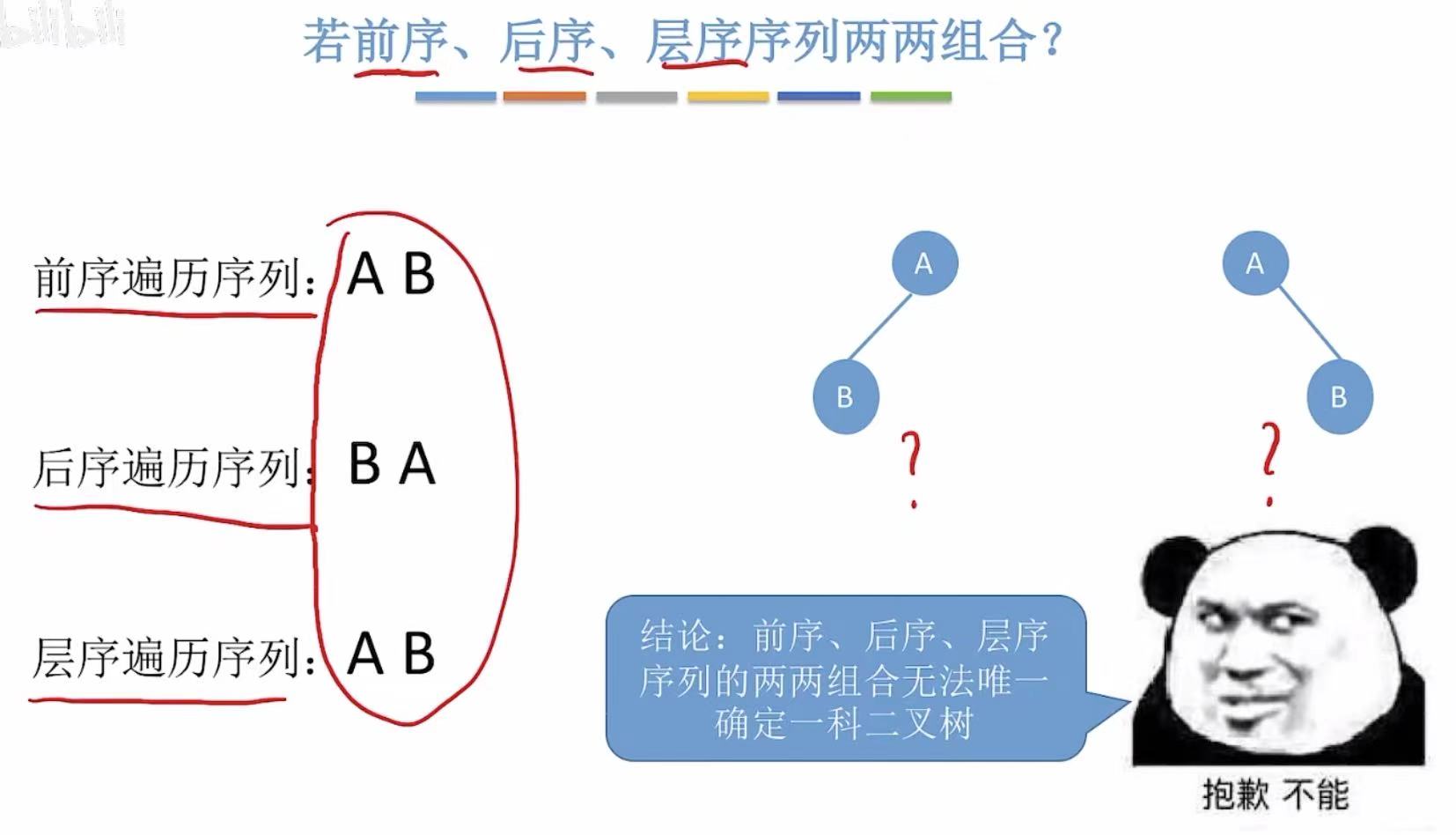
只有一个中序遍历,可以画出很多种不同的二叉树。
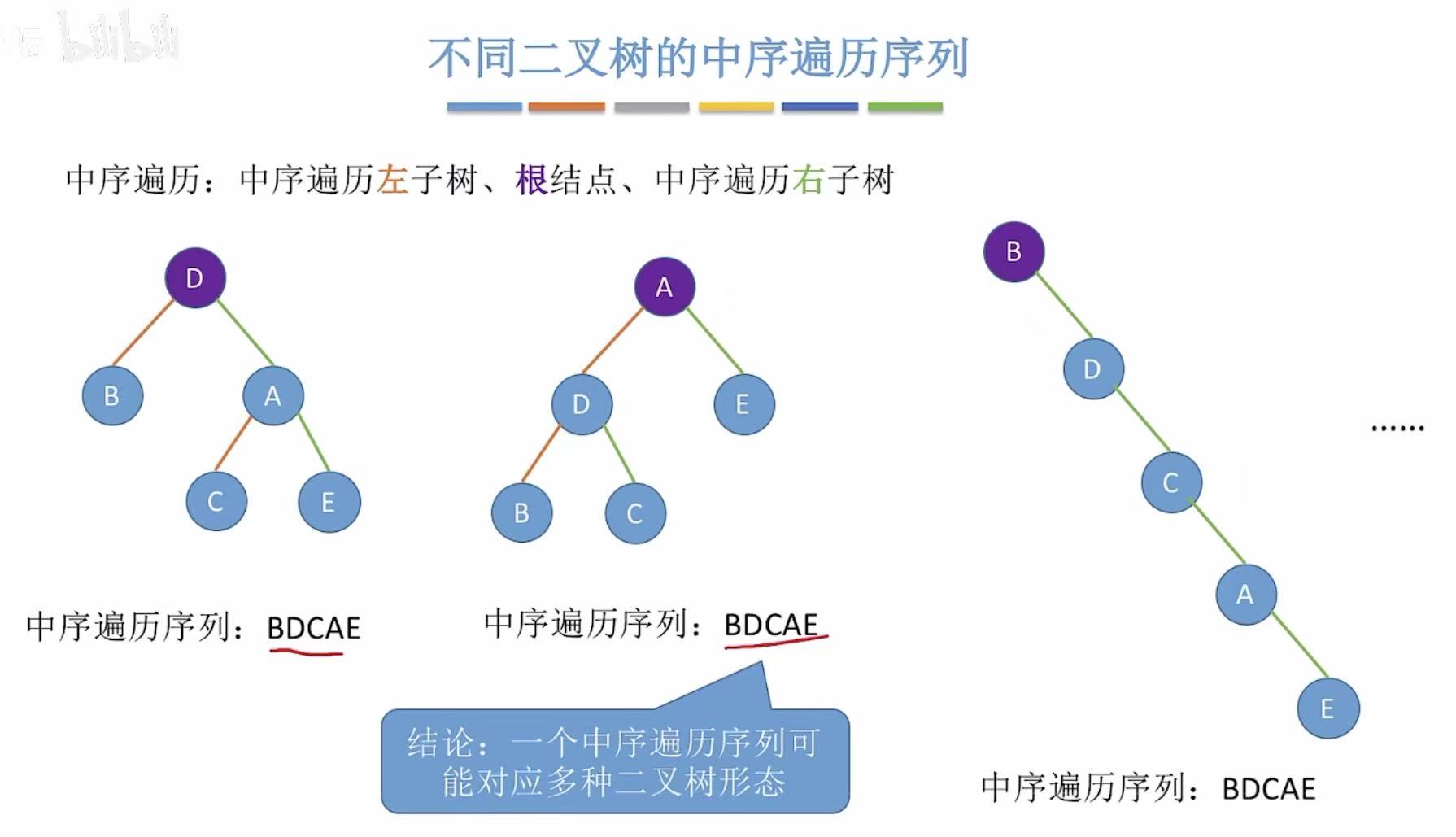
只有一个前序遍历,可以画出很多种不同的二叉树。
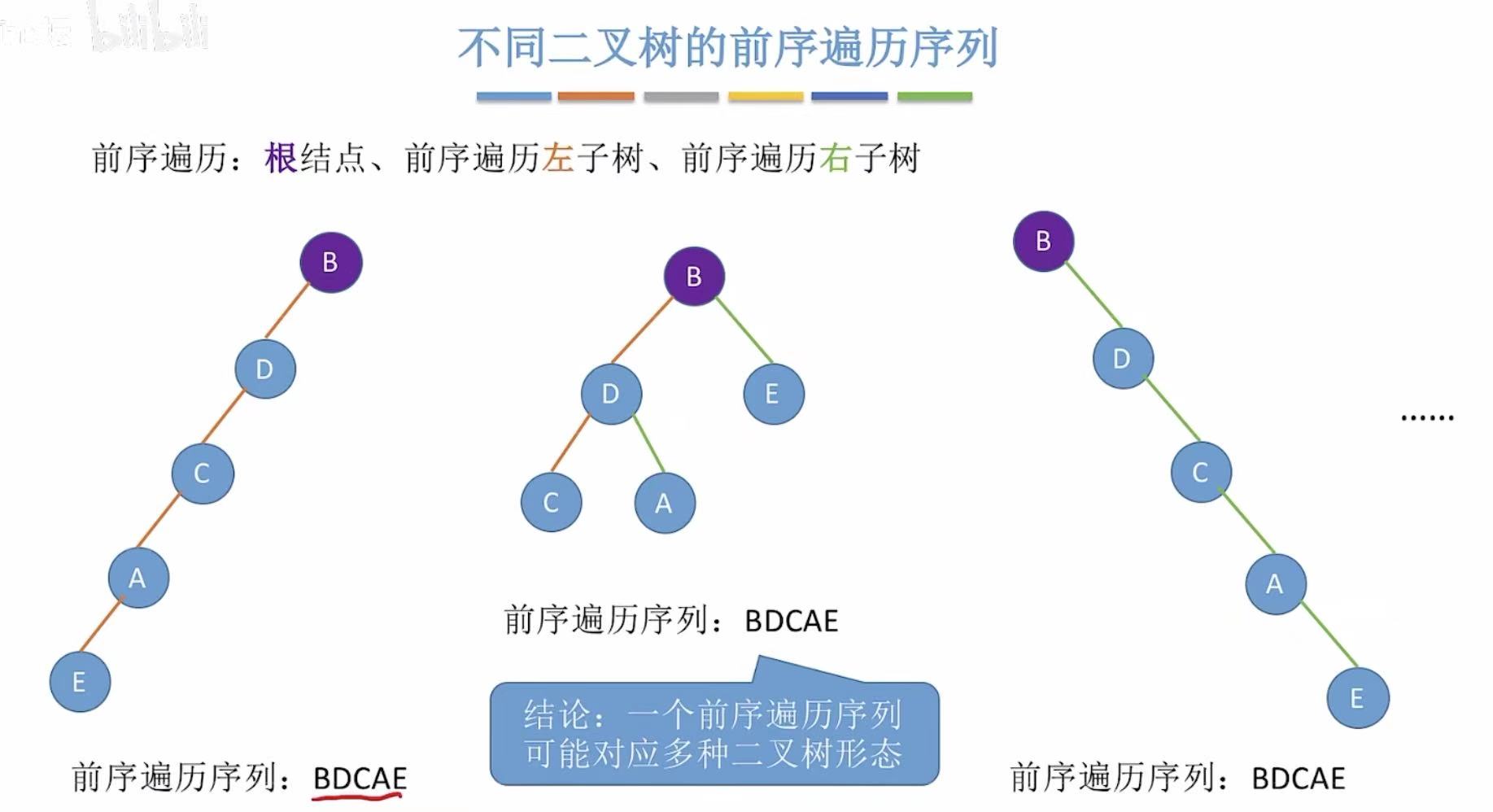
只有一个后序遍历,可以画出很多种不同的二叉树。
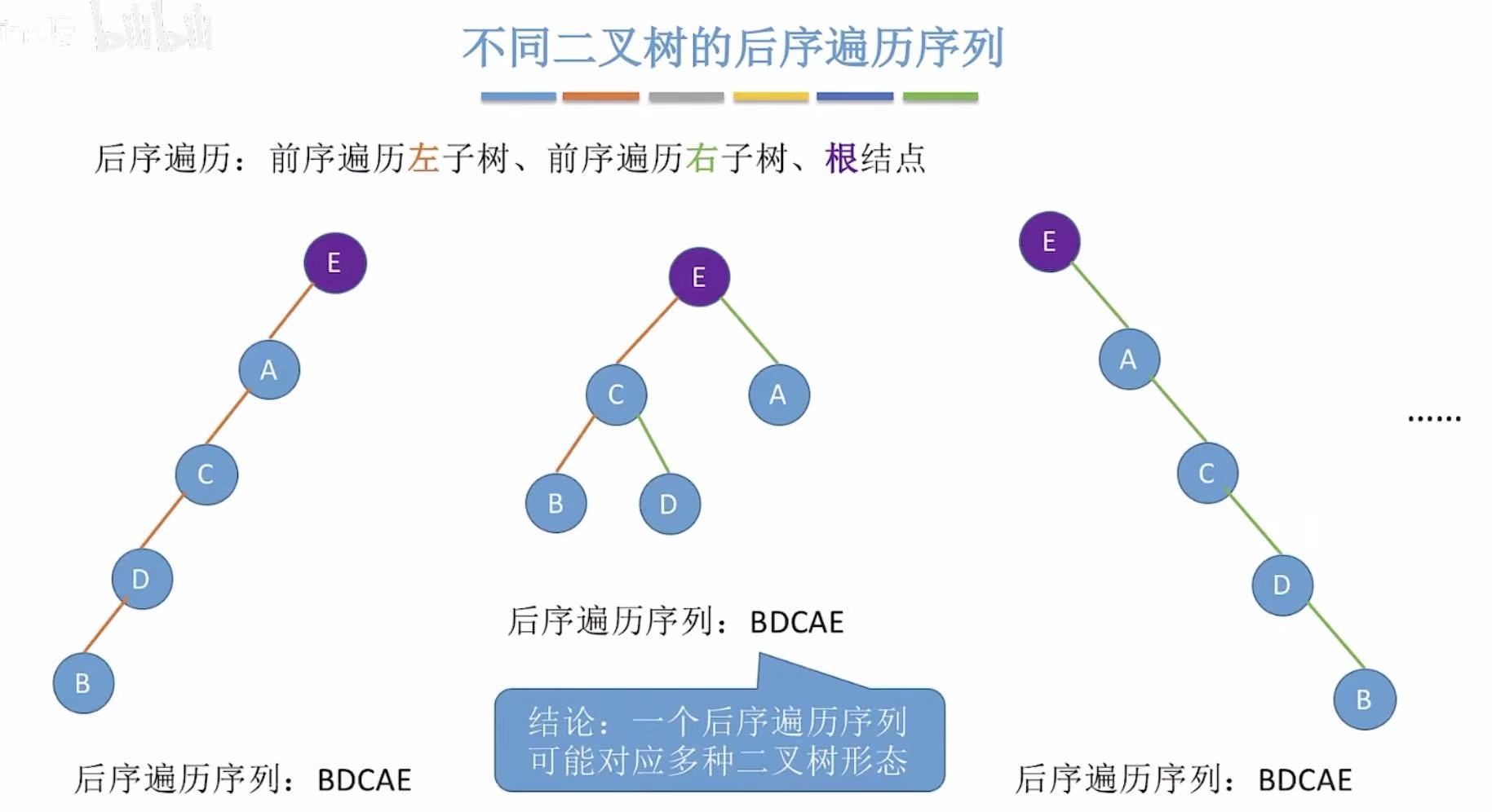
只有一个层序遍历,可以画出很多种不同的二叉树。
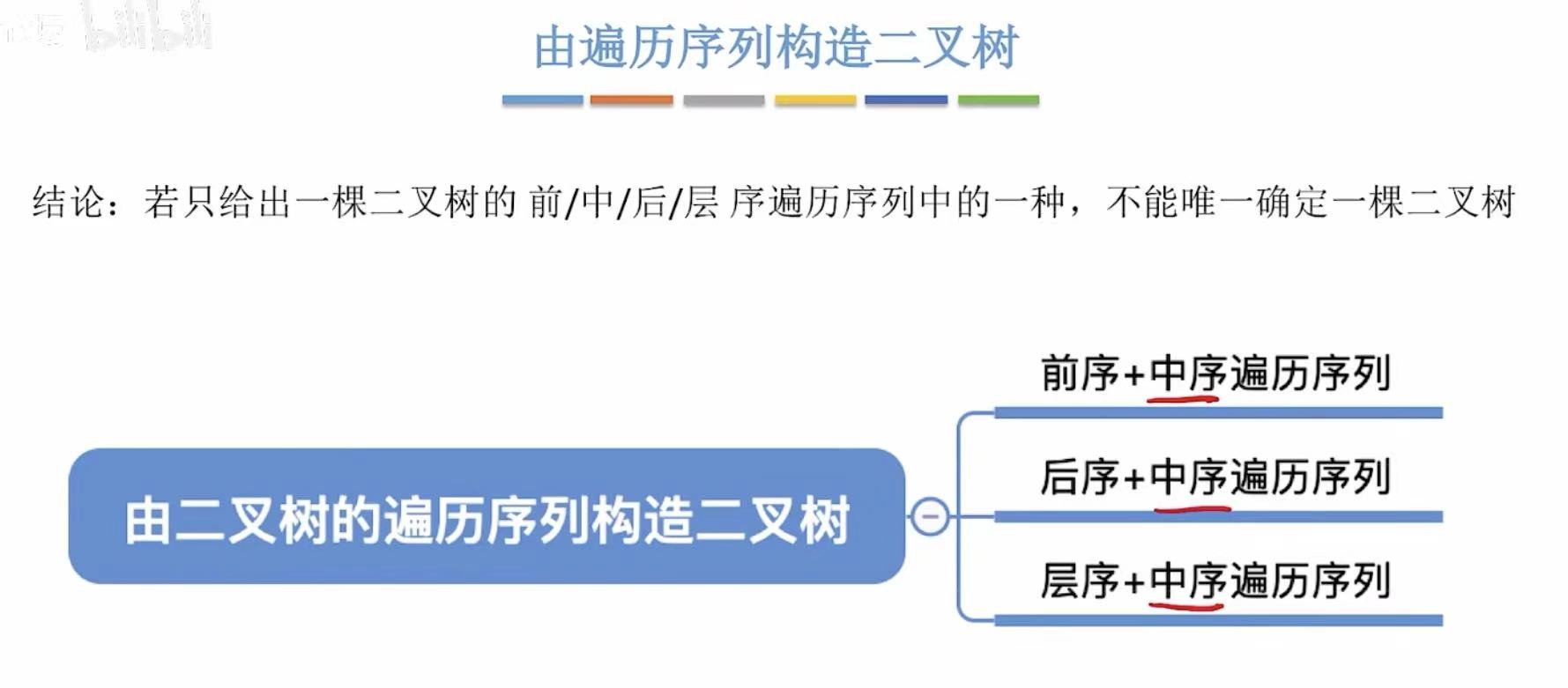
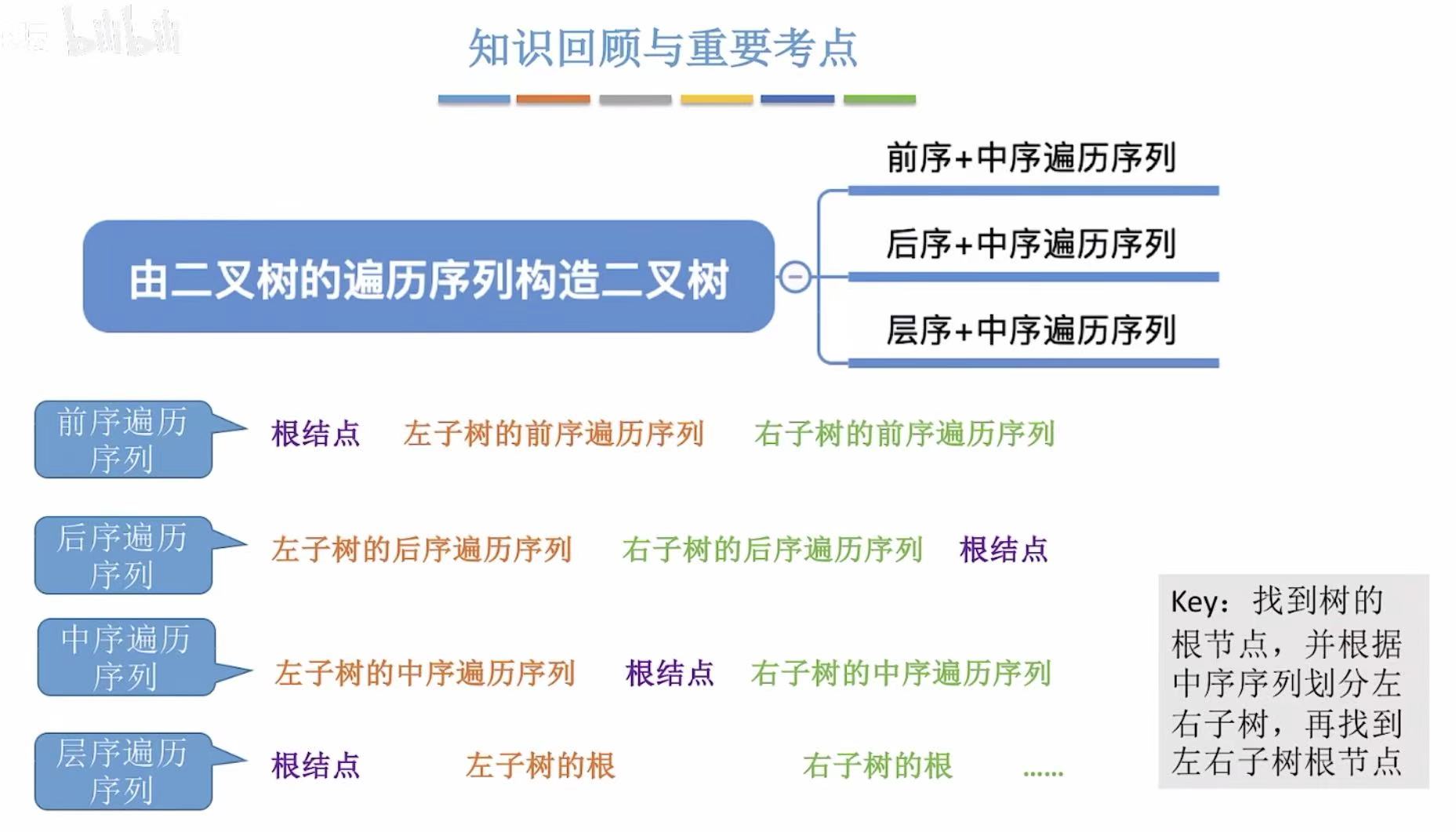
2. 遍历序列
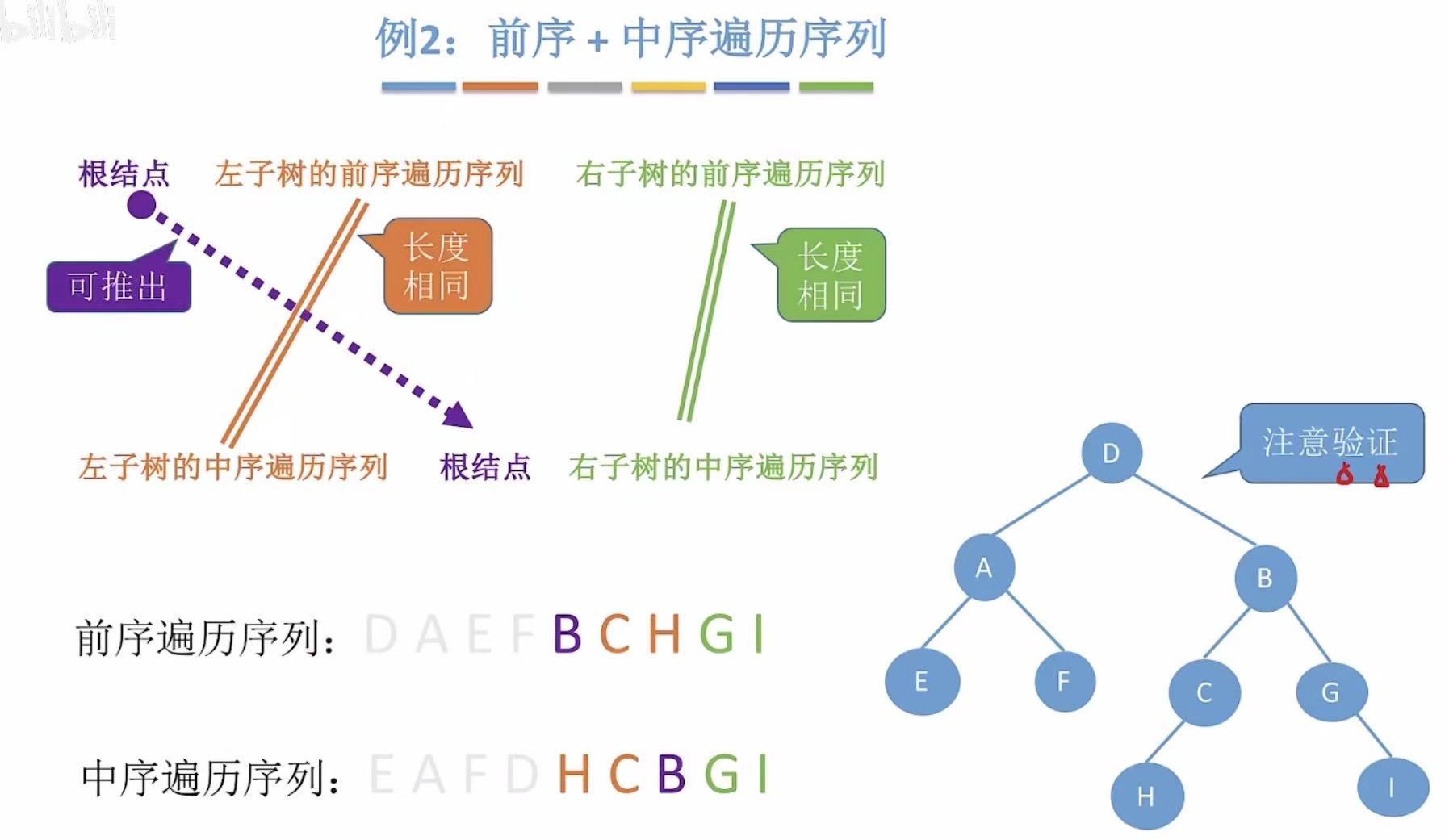
2.1 前序+中序
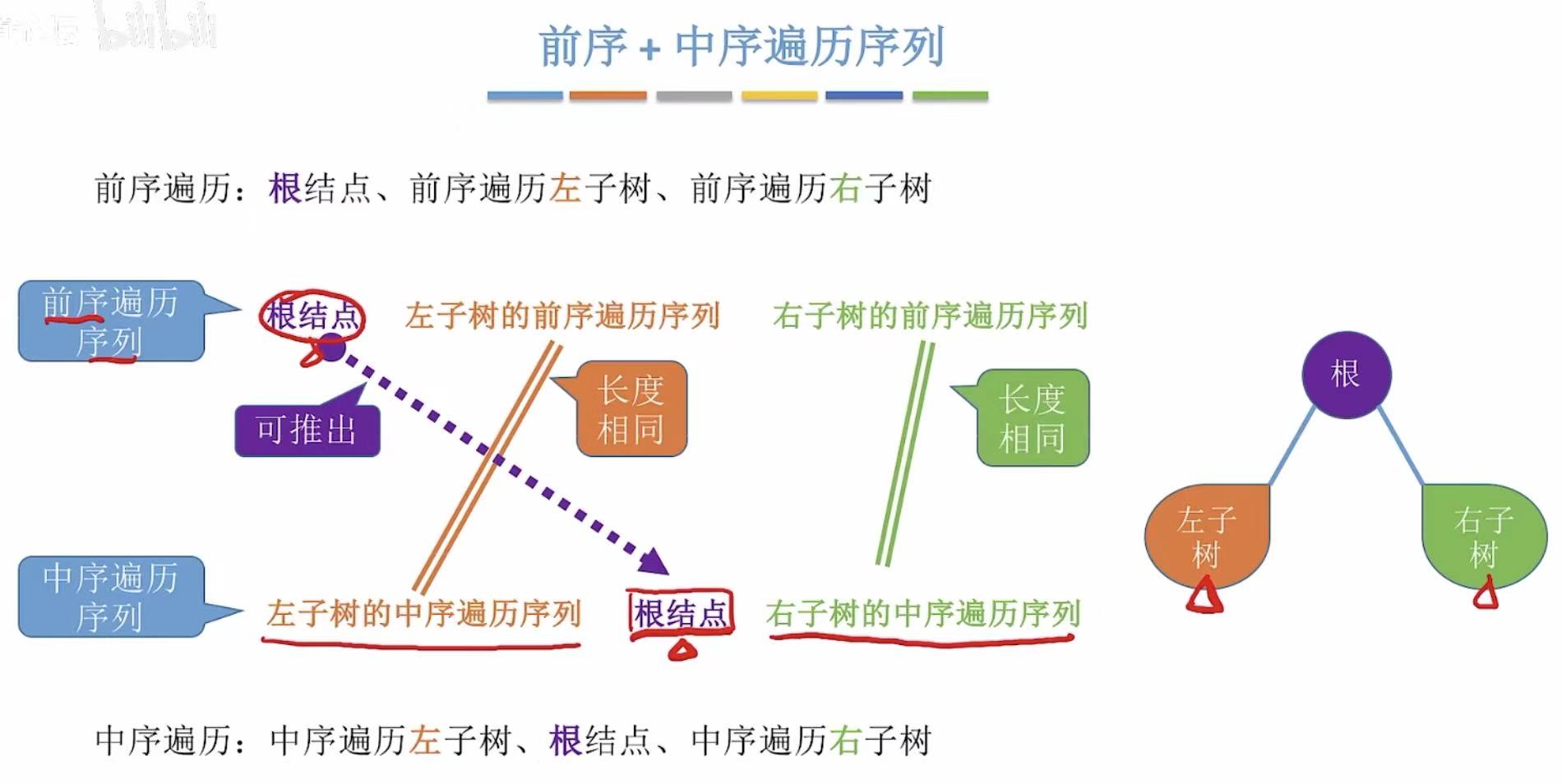
- 前序:根左右-->排在第一个的就是根节点
- 中序:根据前序的根节点,分割出左子树和右子树
- 循环重复上述的两步,就可以画出唯一的一个二叉树。
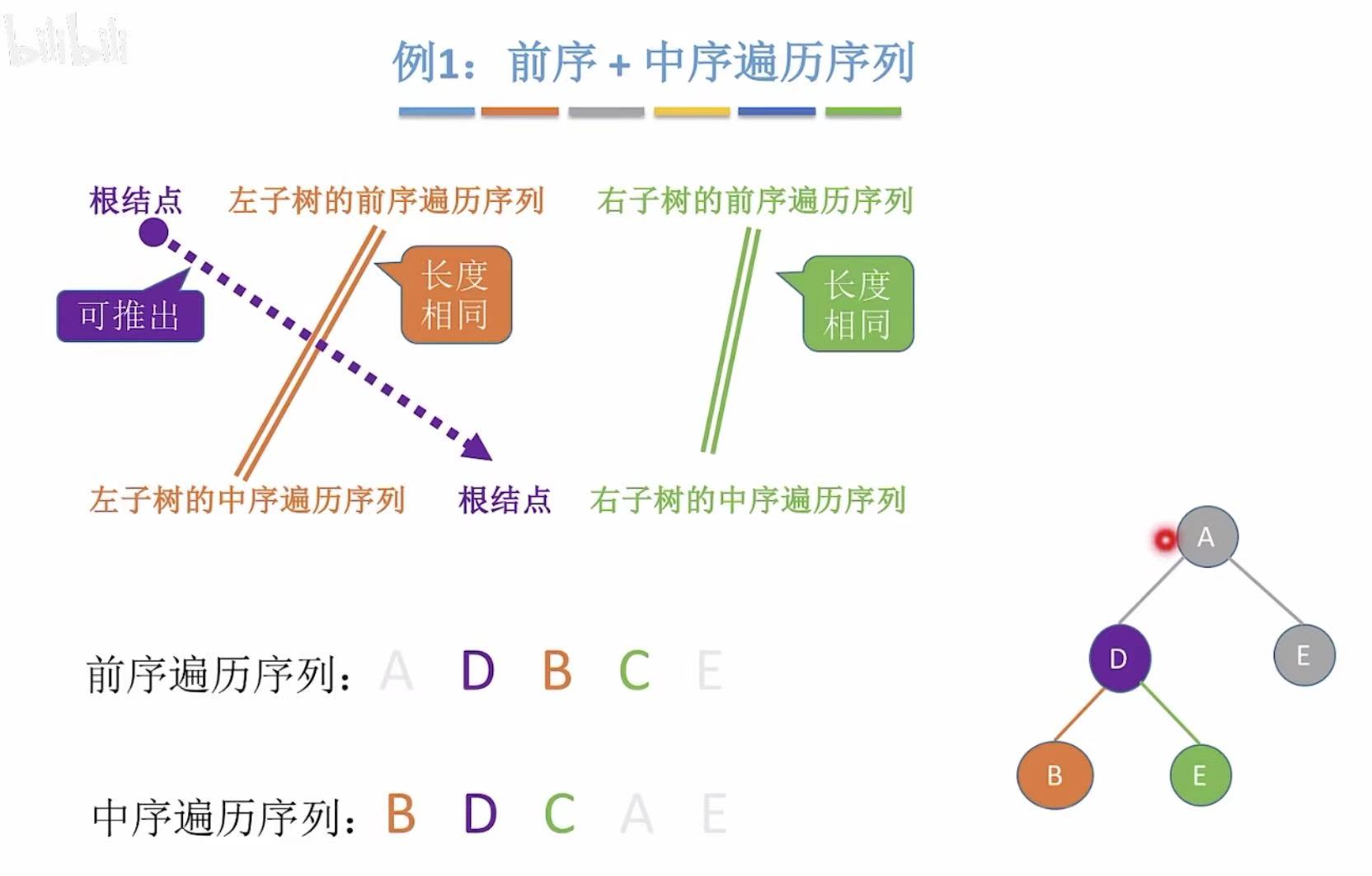
- 前序 :A DBCE-->A是根节点。
- 中序 :BDC A E-->BDC是左子树,E是右子树。
- 前序 :D BC-->D是根节点。
- 中序 :B D C-->B是左子树,C是右子树。
- 前序 :D AEFBCHGI-->D是根节点。
- 中序 :EAF D HCBGI-->EAF是左子树,HCBGI是右子树。
- 前序 :A EF-->A是根节点;B CHGI-->B是根节点。
- 中序 :E A F-->E是左子树,F是右子树;HC B GI-->HC是左子树,GI是右子树。
- 前序 :C H-->C是根节点;G I-->G是根节点。
- 中序 :H C -->H是左子树;G I-->I是右子树。
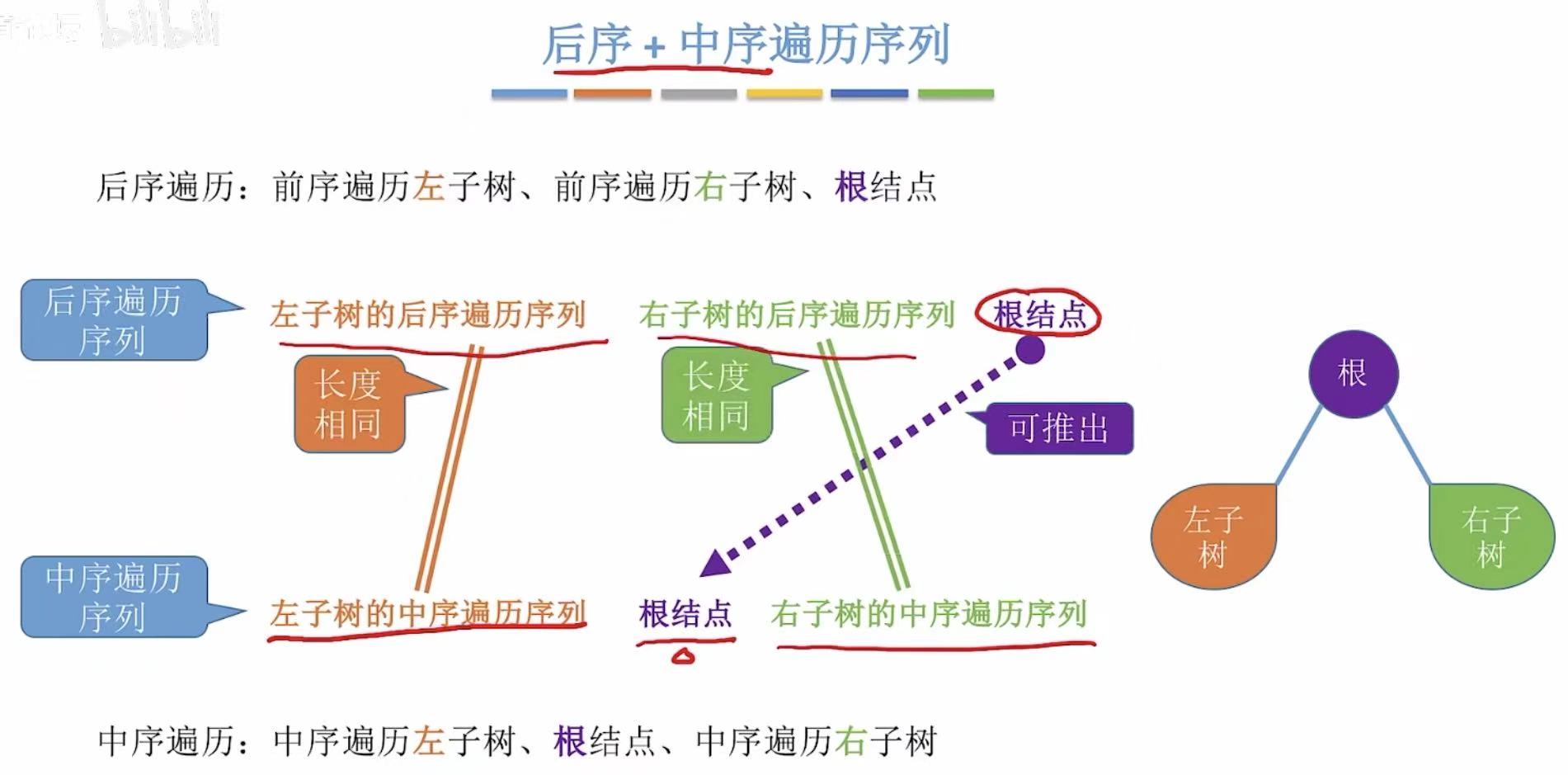
2.2 后序+中序
- 后序:左右根-->排在最后一个的就是根节点
- 中序:根据后序的根节点,分割出左子树和右子树
- 循环重复上述的两步,就可以画出唯一的一个二叉树。
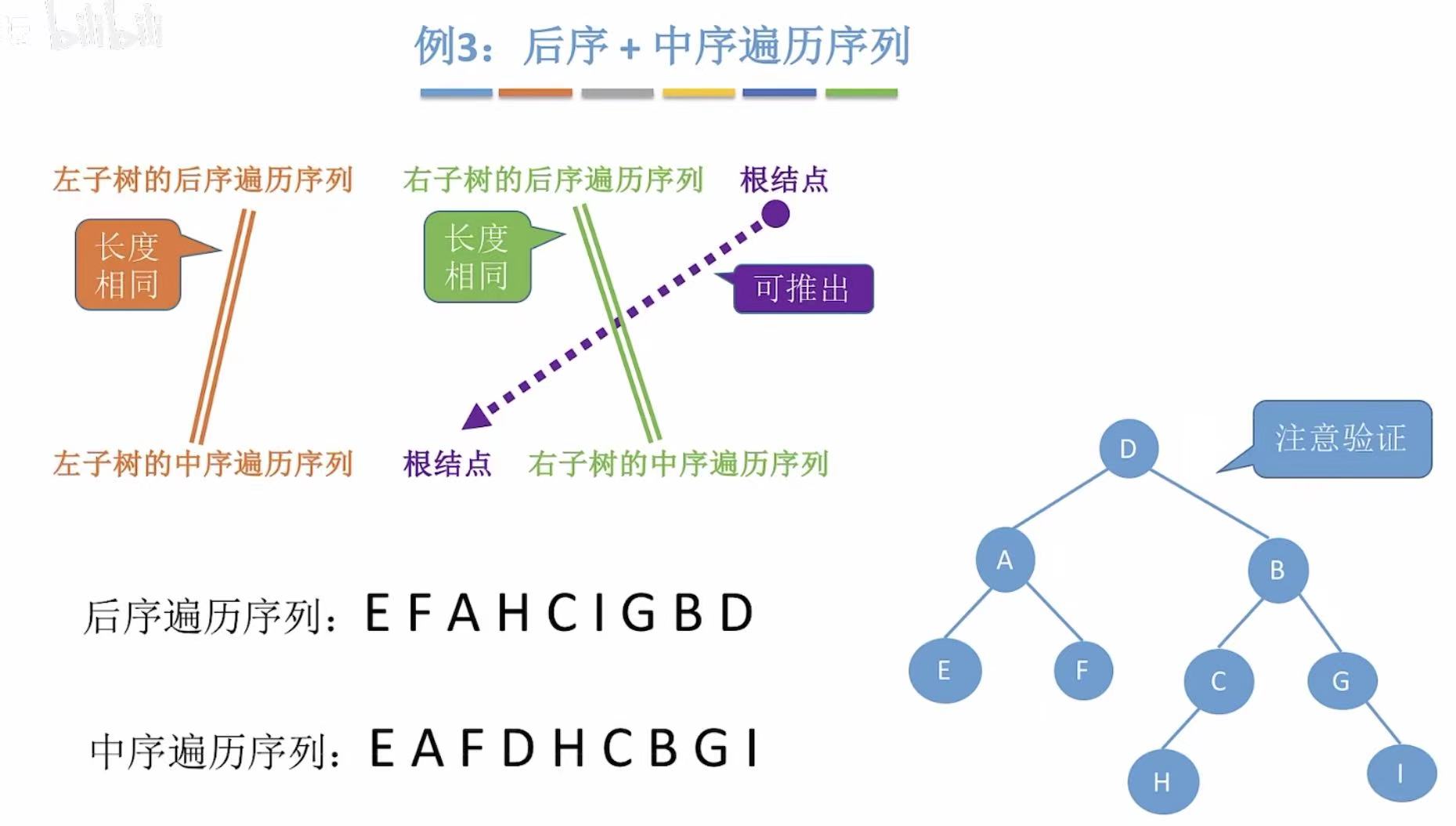
- 后序 :EFAHCIGB D-->D是根节点。
- 中序 :EAF D HCBGI-->EAF是左子树,HCBGI是右子树。
- 后序 :EF A -->A是根节点;HCIG B-->B是根节点。
- 中序 :E A F-->E是左子树,F是右子树;HC B GI-->HC是左子树,GI是右子树。
- 后序 :H C -->C是根节点;I G-->G是根节点。
- 中序 :H C -->H是左子树;G I-->I是右子树。
2.3 层序+中序
- 层序:根左右-->排在第一个的就是根节点
- 中序:根据后序的根节点,分割出左子树的遍历序列和右子树的遍历序列
- 循环重复上述的两步,就可以画出唯一的一个二叉树。
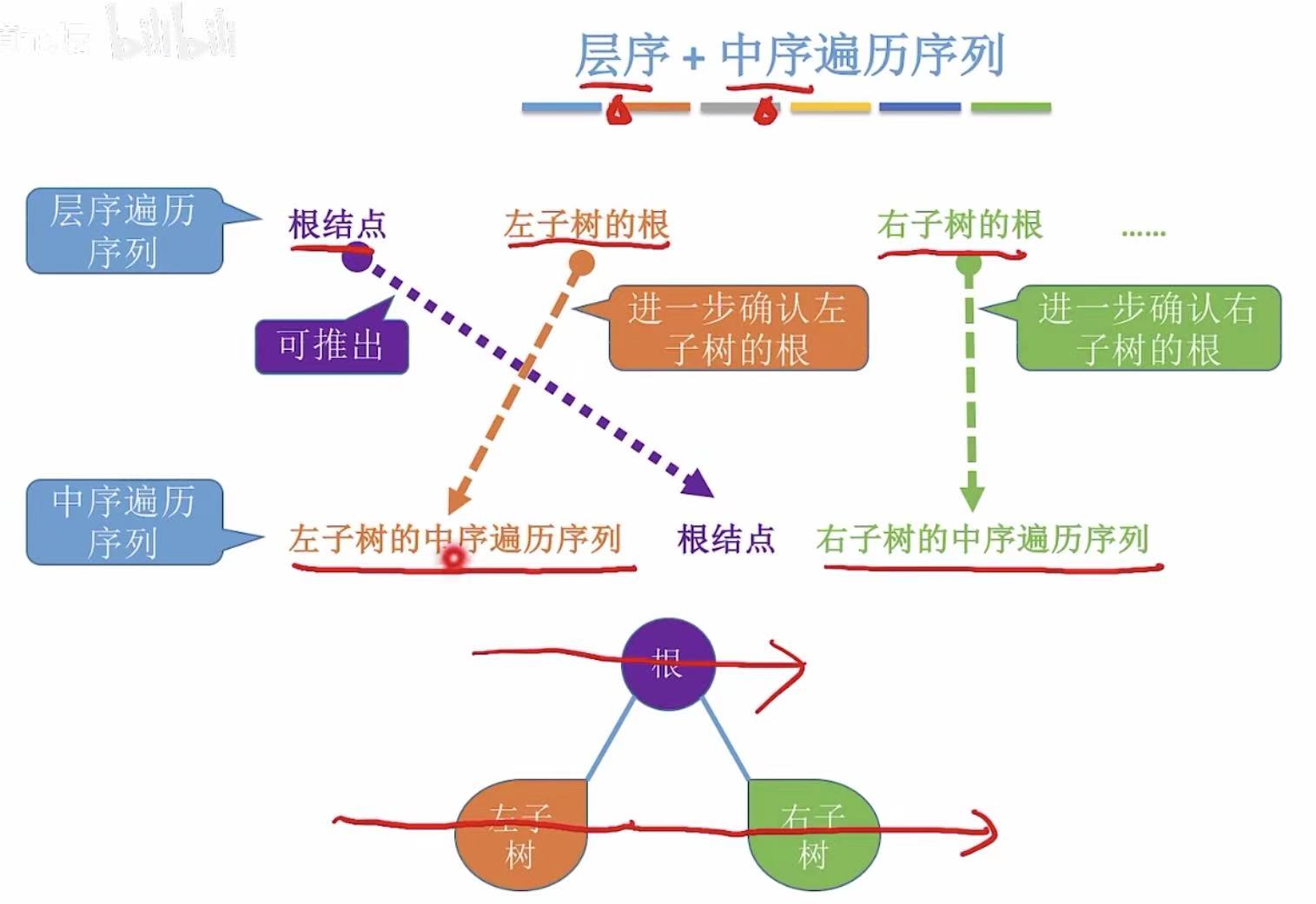
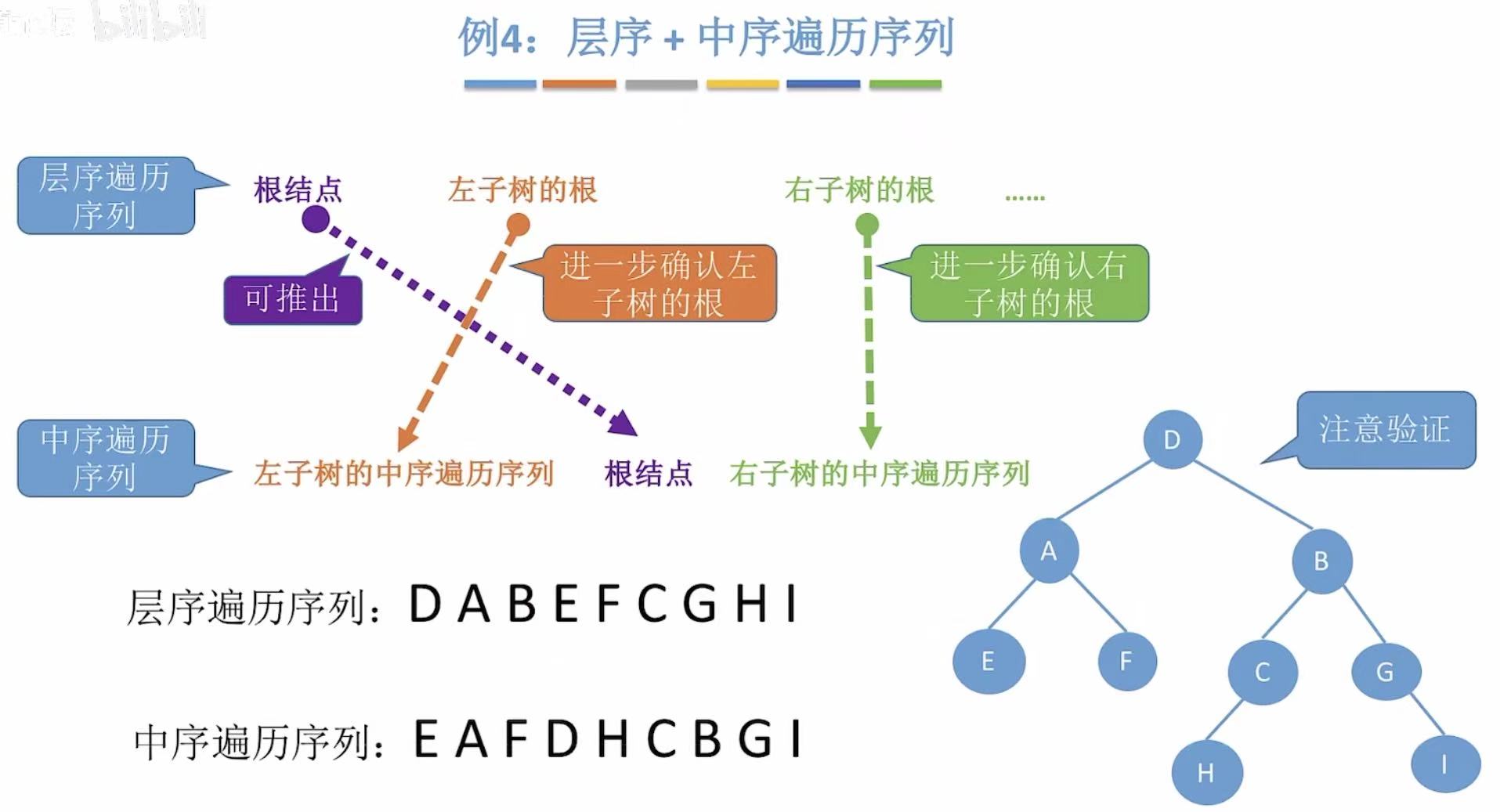
- 层序 :D ABEFCGHI-->D是根节点。
- 中序 :EAF D HCBGI-->EAF是左子树,HCBGI是右子树。
- 层序 :A BEFCGHI-->A是根节点;B EFCGHI-->B是根节点。
- 中序 :E A F-->E是左子树,F是右子树;HC B GI-->HC是左子树,GI是右子树。
- 层序 :C GHI-->C是根节点;G HI-->G是根节点。
- 中序 :H C -->H是左子树;G I-->I是右子树。
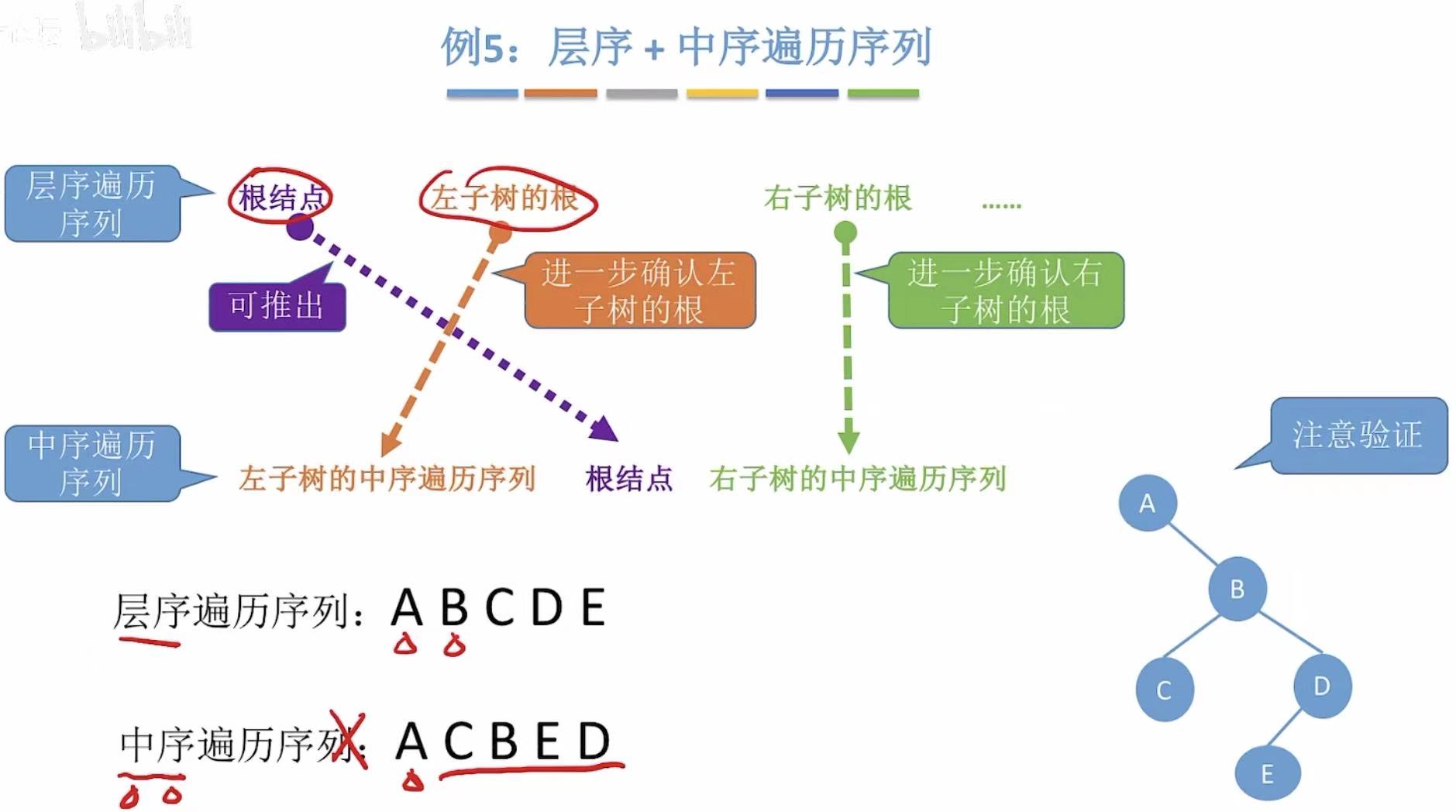
- 层序 :A BCDE-->A是根节点。
- 中序 :A CBED-->A无左子树,CBED是右子树。
- 层序 :B CDE-->B是根节点;
- 中序 :C B ED-->C是左子树,ED是右子树。
- 层序 :D E-->D是根节点;
- 中序 :E D -->E是左子树。
3. 小结
线索二叉树
1. 线索二叉树的作用
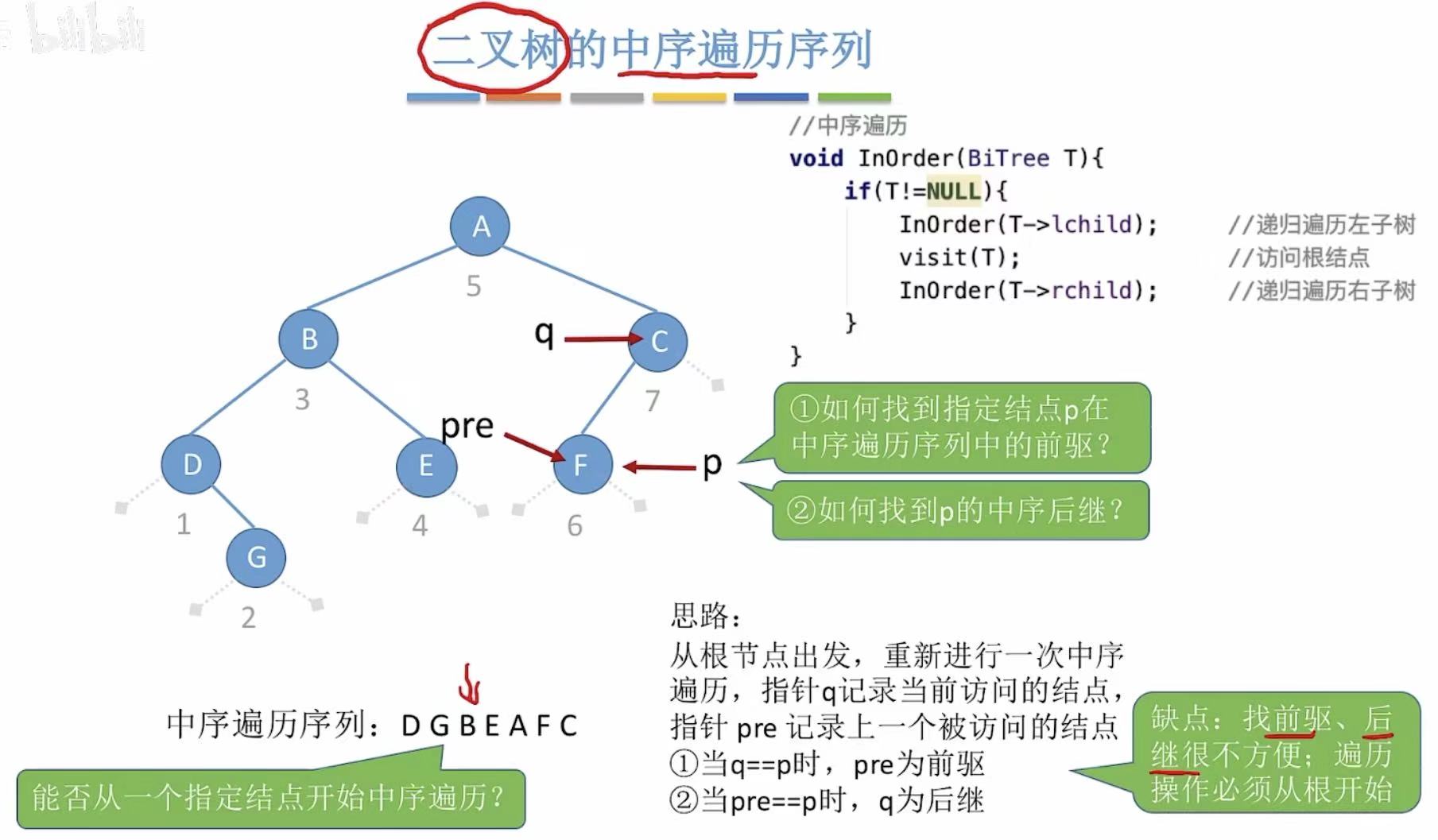
前驱后继 :指的是在中序遍历序列中(也就是最下面的一行英文字母)一个字母的前一个字母是它的前驱,后一个是它的后继。
举个例子 :G的前驱是D,G的后继是B。并且因为是在中序遍历序列中,所以前驱就是先自己一步被访问到的结点。
正常情况下,我们想找这个二叉树某个结点的前驱或者后继,就需要设置两个指针:pre先行一步,q慢它一步。
java
//从放出q开始记录访问顺序,那么pre最开始就有一个空格的时间。
q :DGBEAFC
pre: DGBEAFC
p:当前指针指向的结点那么就可以看到,q=p指向G的时候,pre就是D,也就是p的前驱;反过来pre=p,q就是p的后继。
显然,每次想找其中一个结点的前驱或者后继的时候,就都需要从头遍历一遍,这并不高效,所以就引出了线索二叉树的概念。
没有左孩子或者右孩子的结点,就可以将左右这两个位置指向自己的前驱或者后继,指向的指针就被叫做线索 。
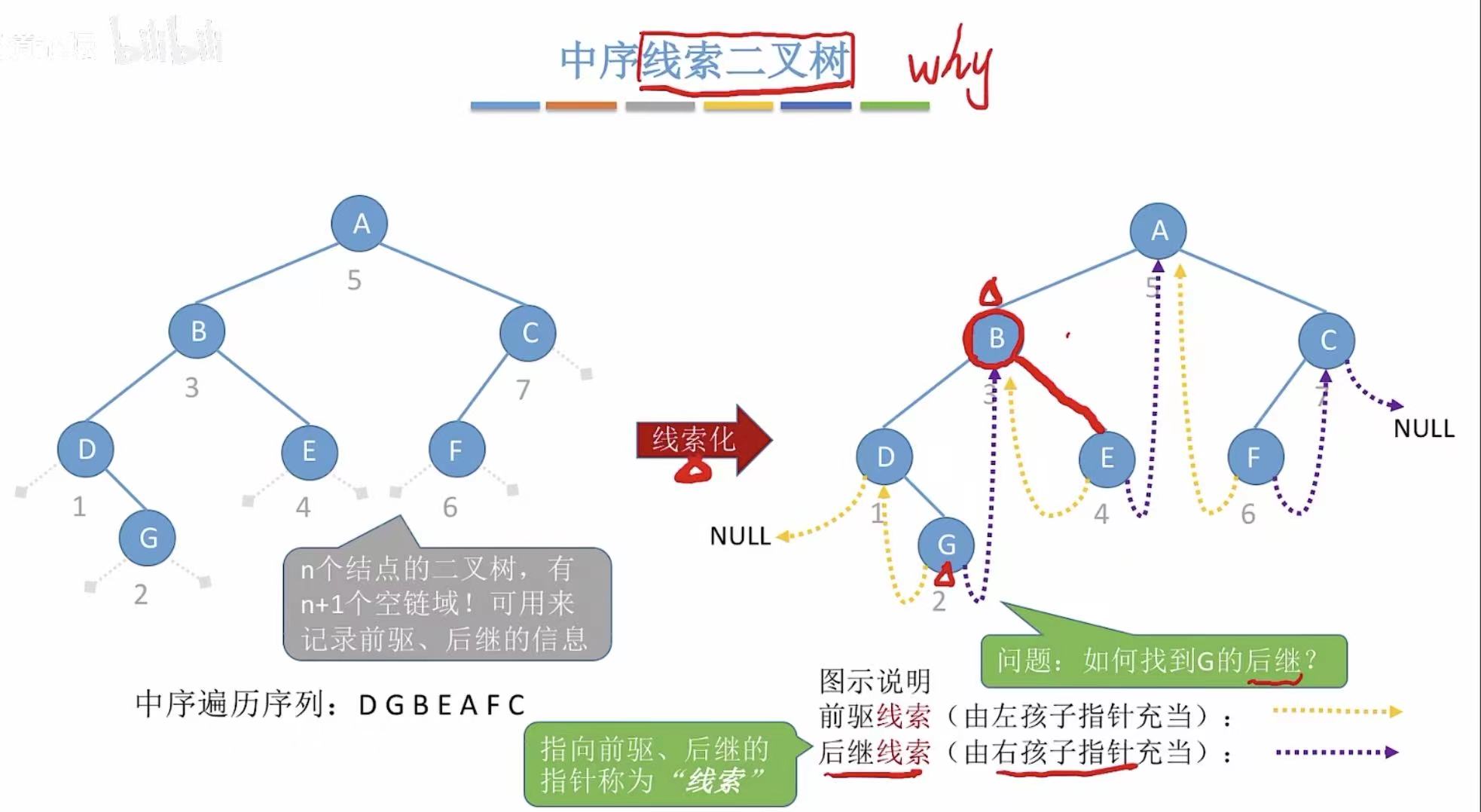
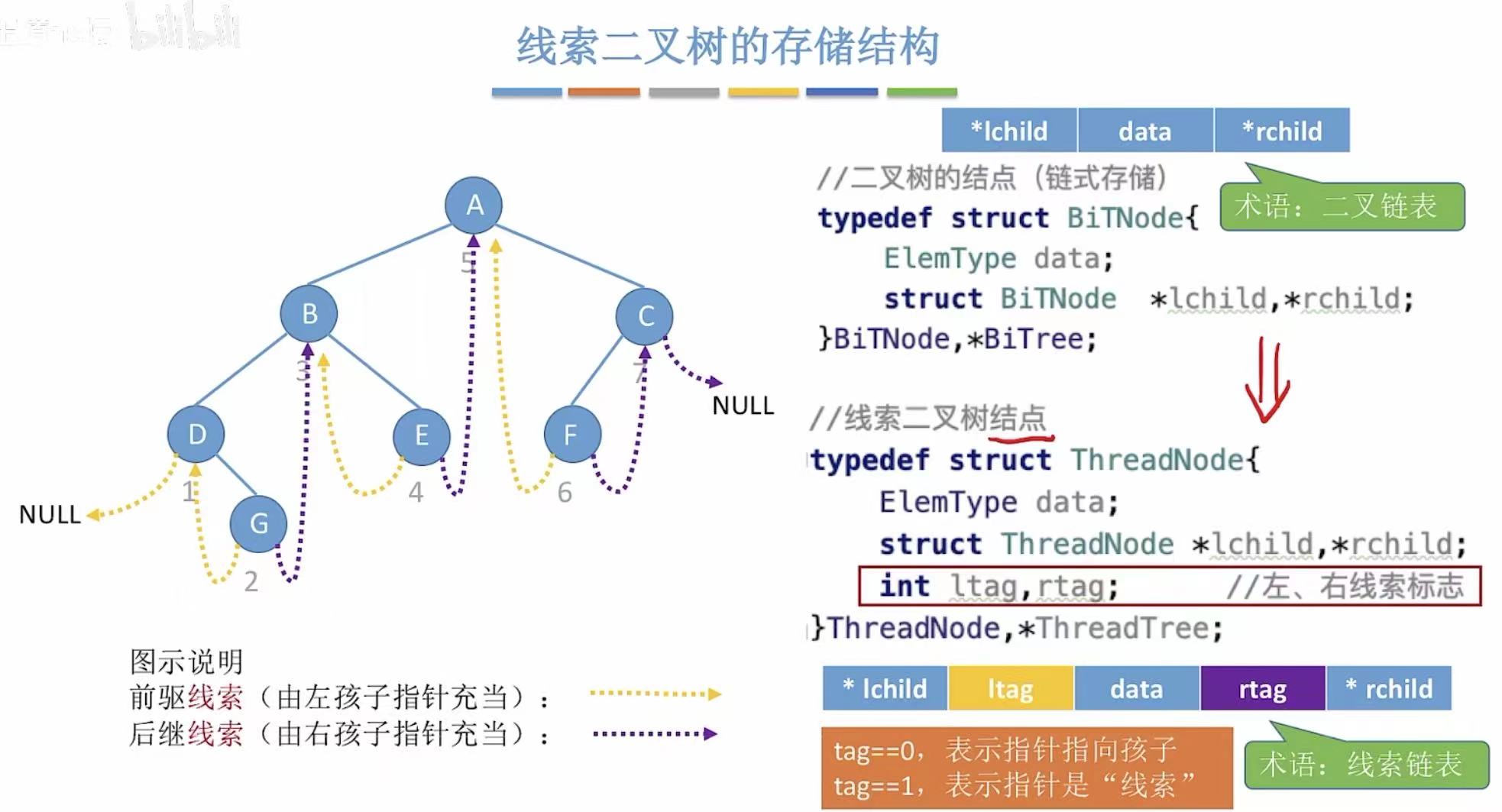
2. 线索二叉树的存储结构
2.1 中序
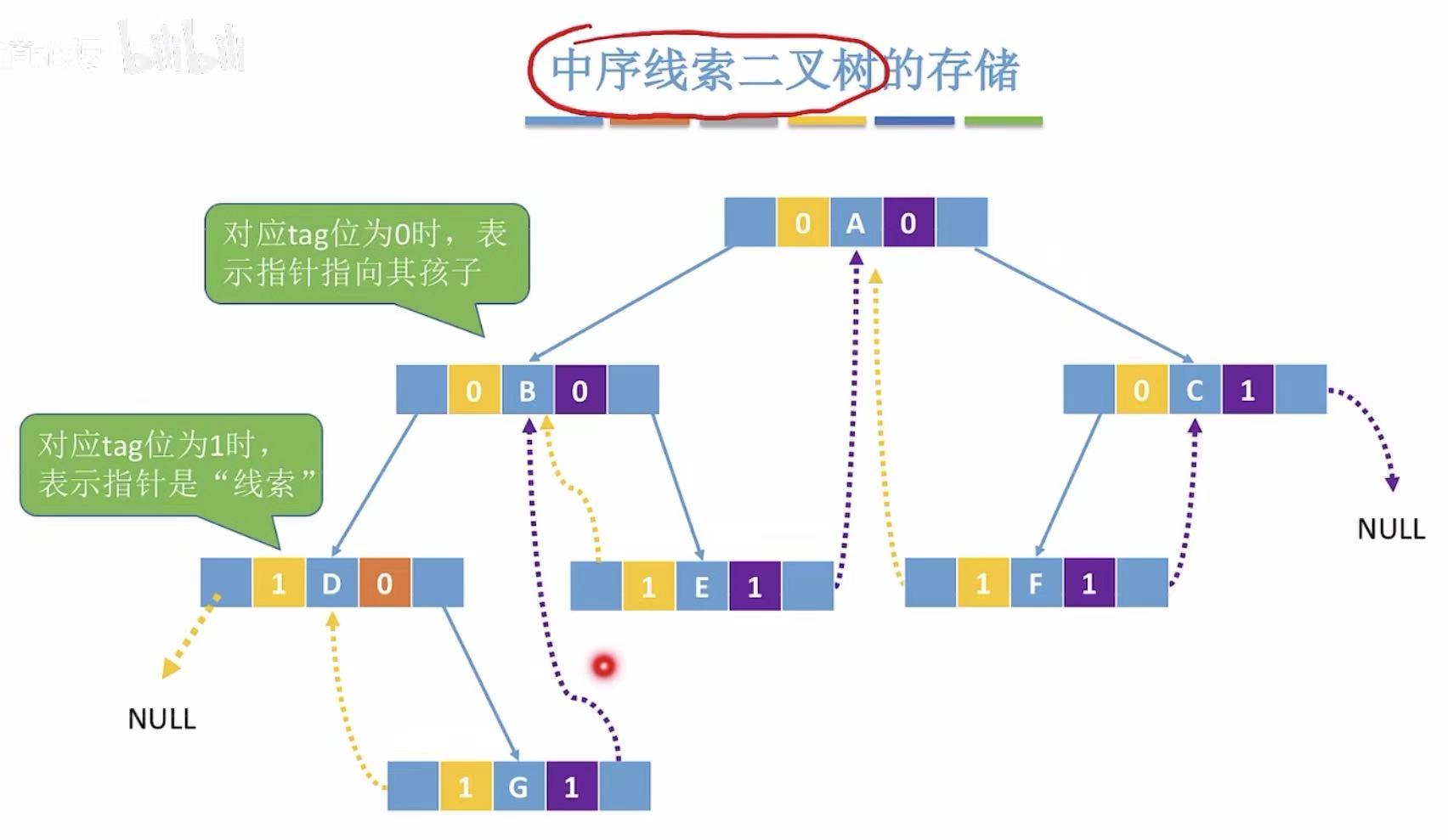
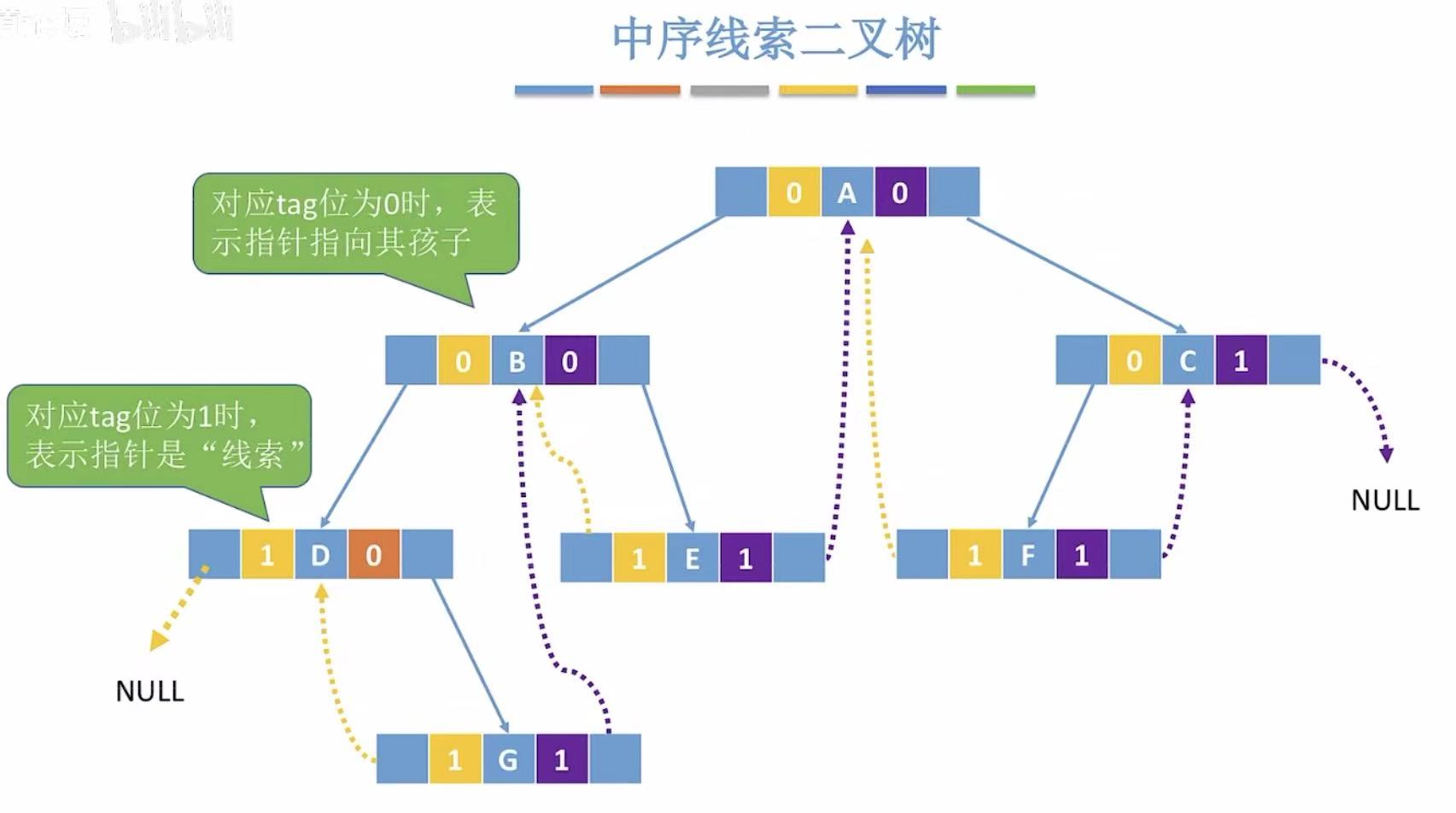
在普通的二叉链表的基础上增加前驱线索和后继线索,就变成了线索链表。
链式存储具体可见:链式存储
DGBEAFC:
- D无前驱,所以黄色指针指向NULL;
- G无左右孩子,所以黄色指针指向前驱D,紫色指针指向后继B;
- 后面以此类推。
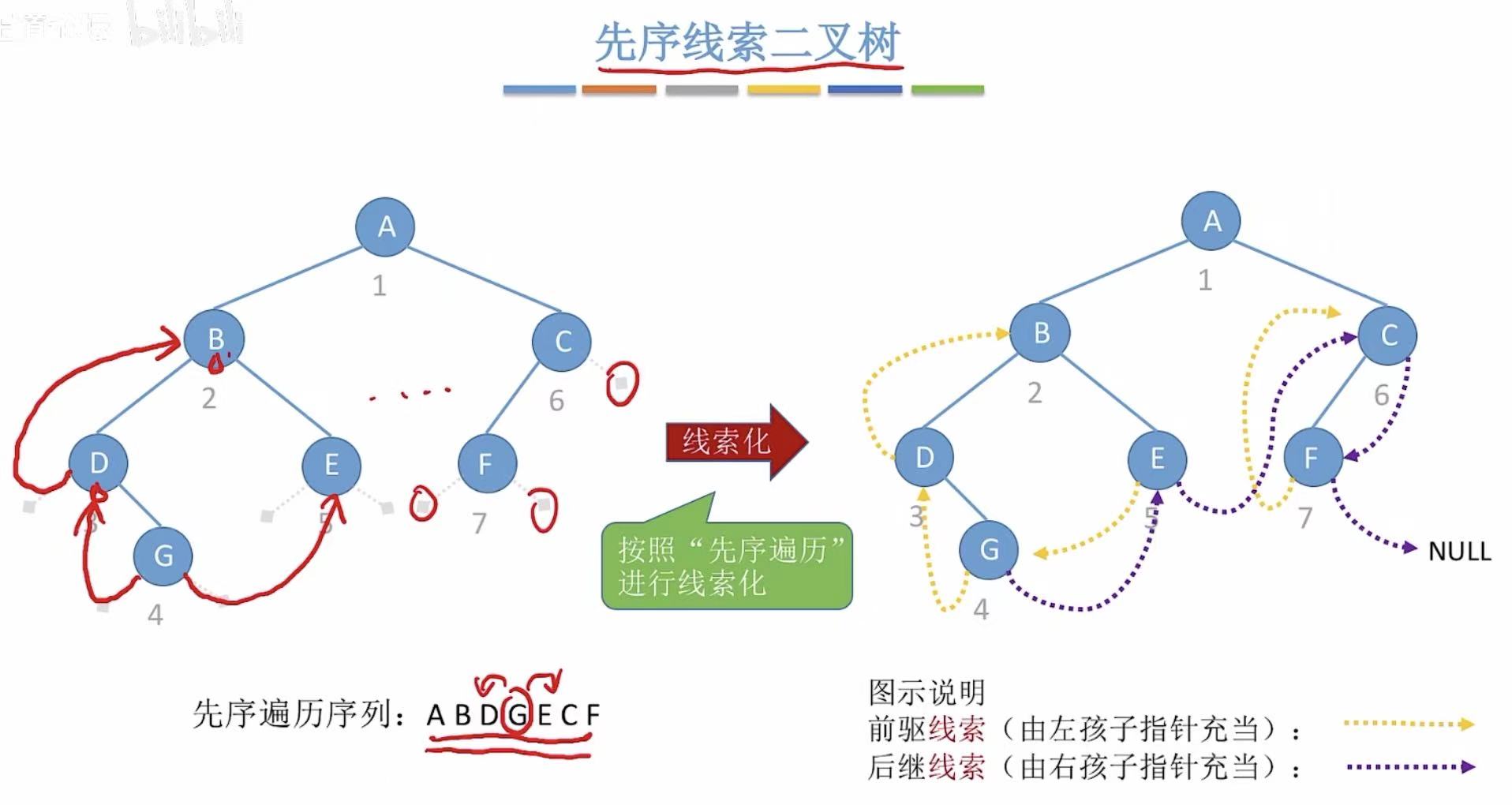
2.2 先序
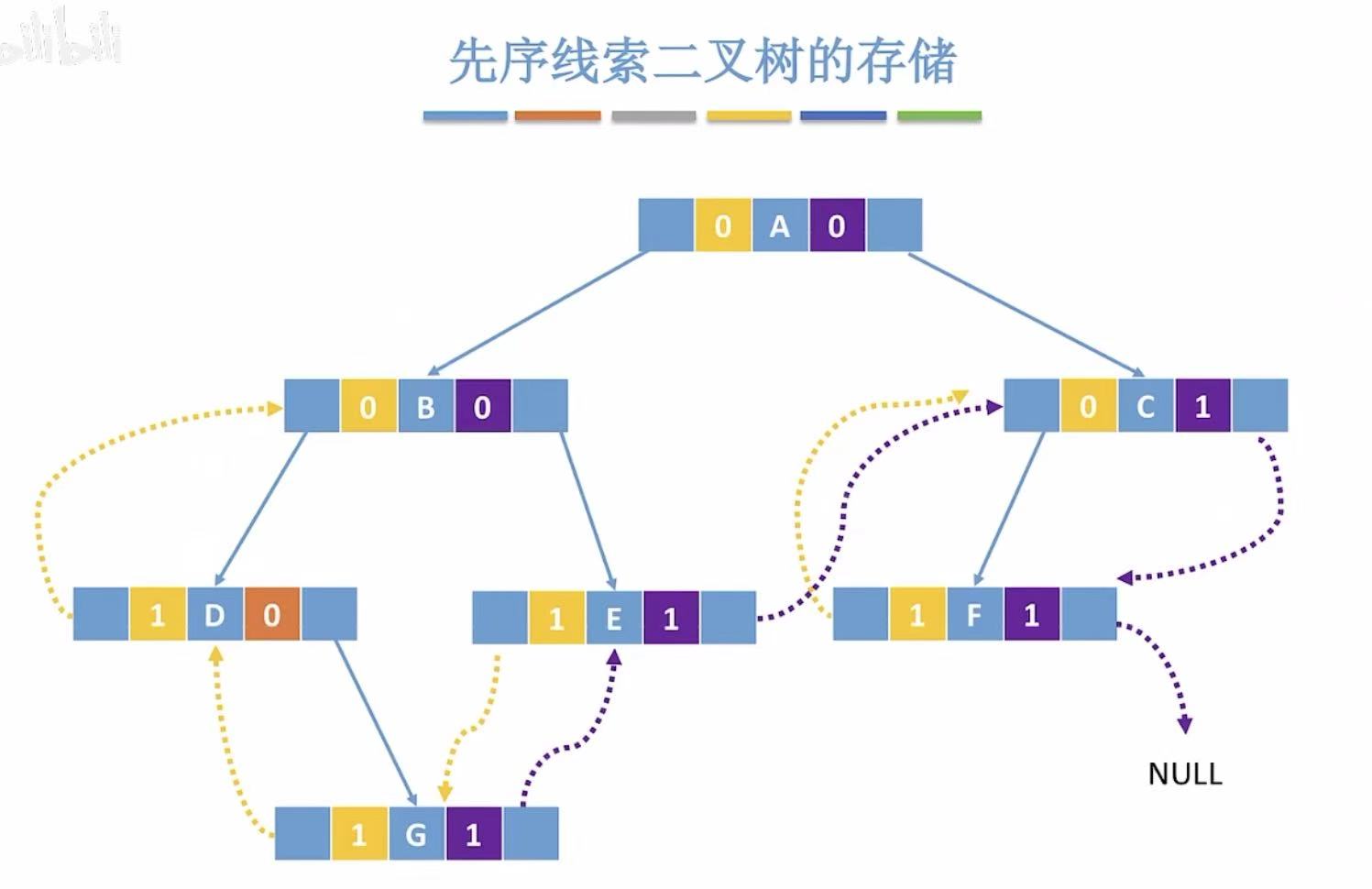
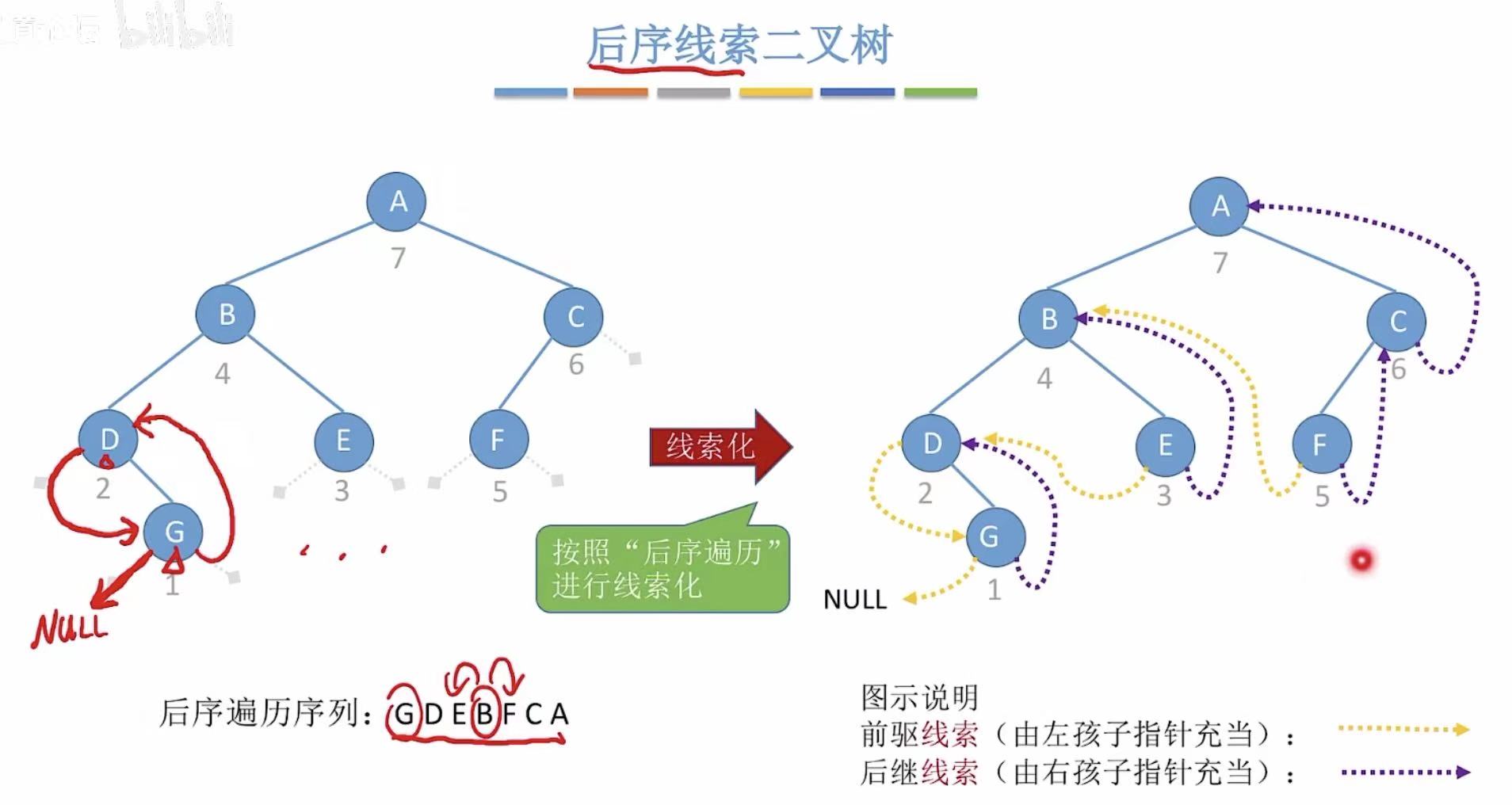
2.3 后序
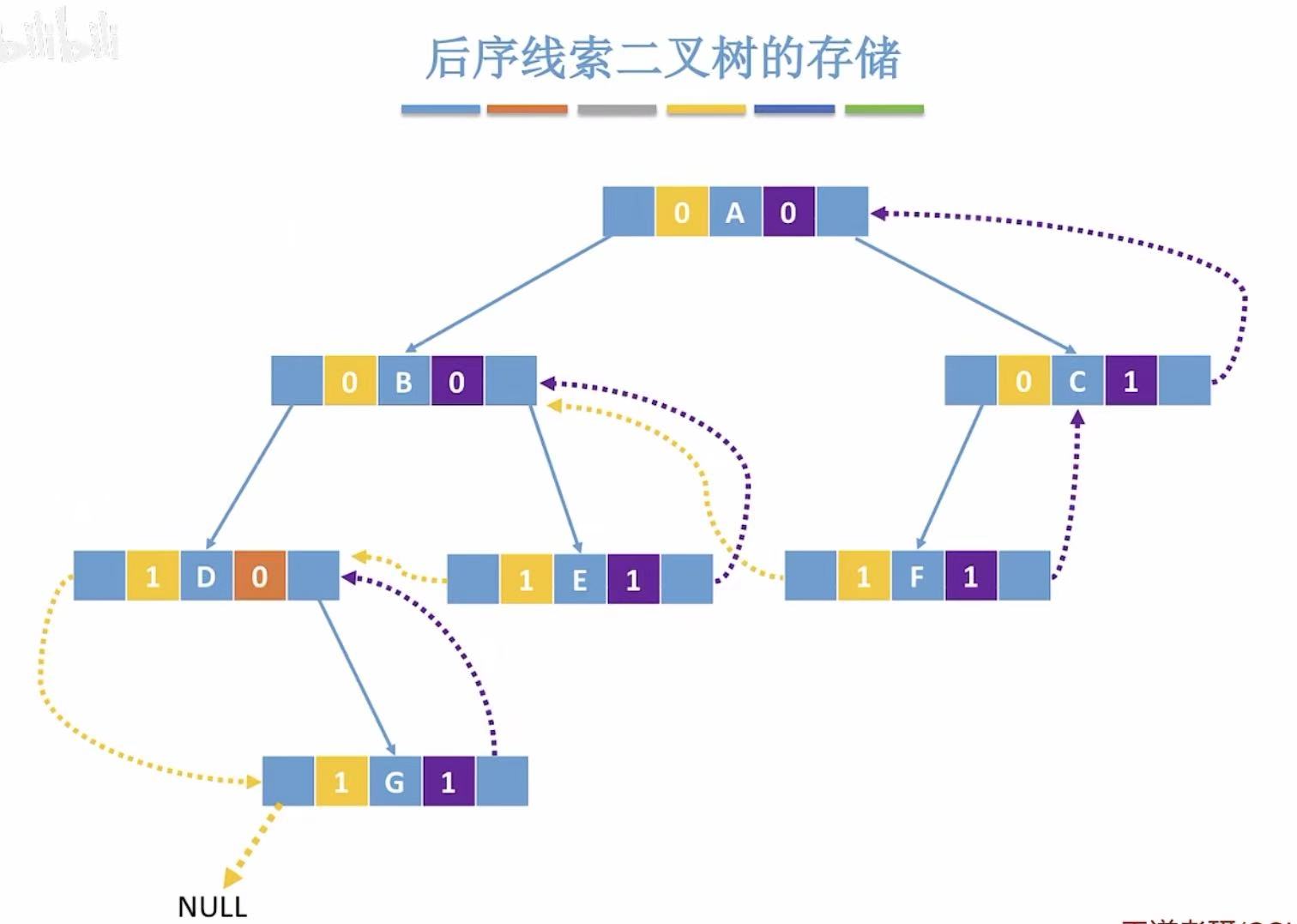
2.4 对比
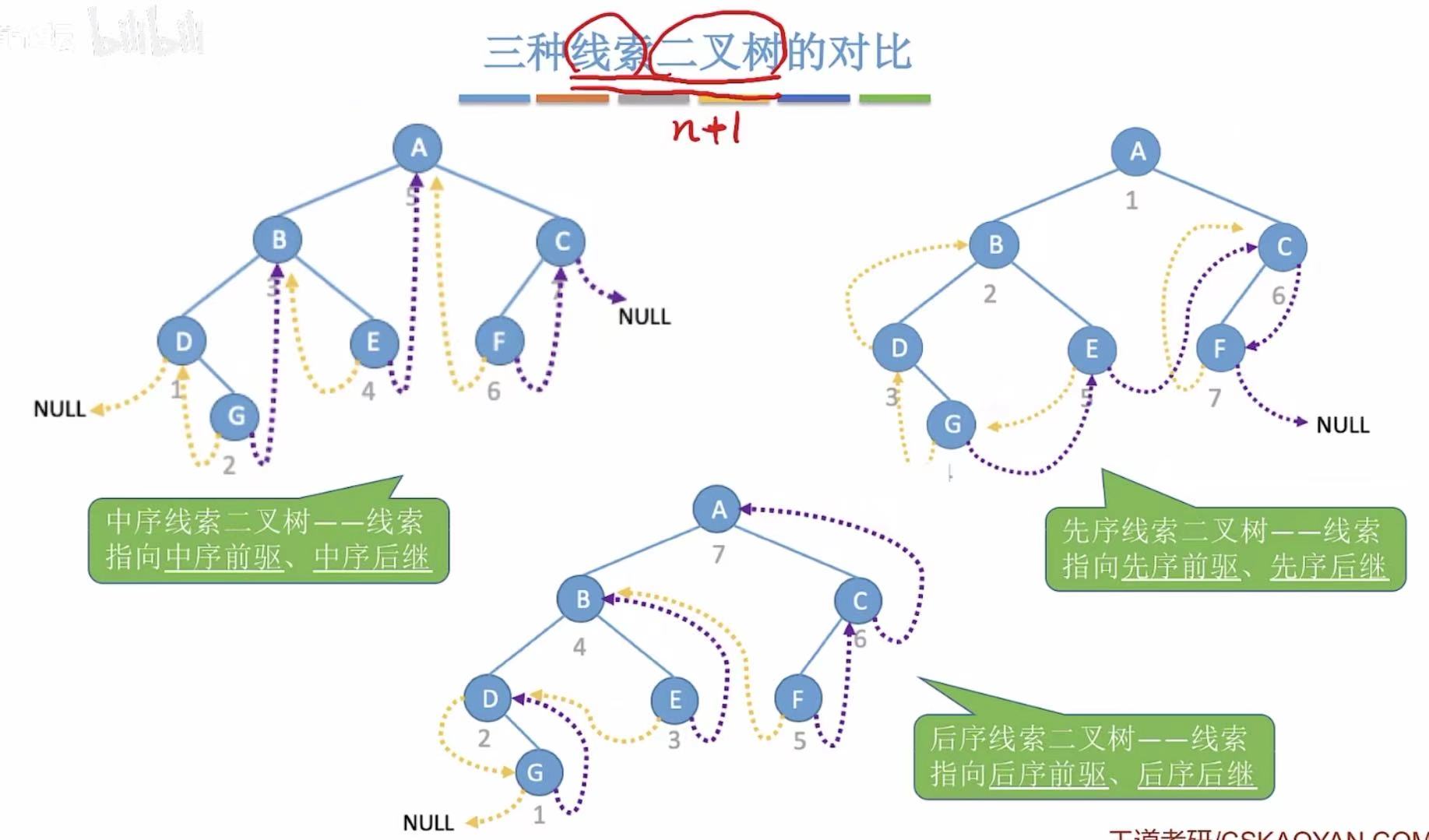
3. 小结
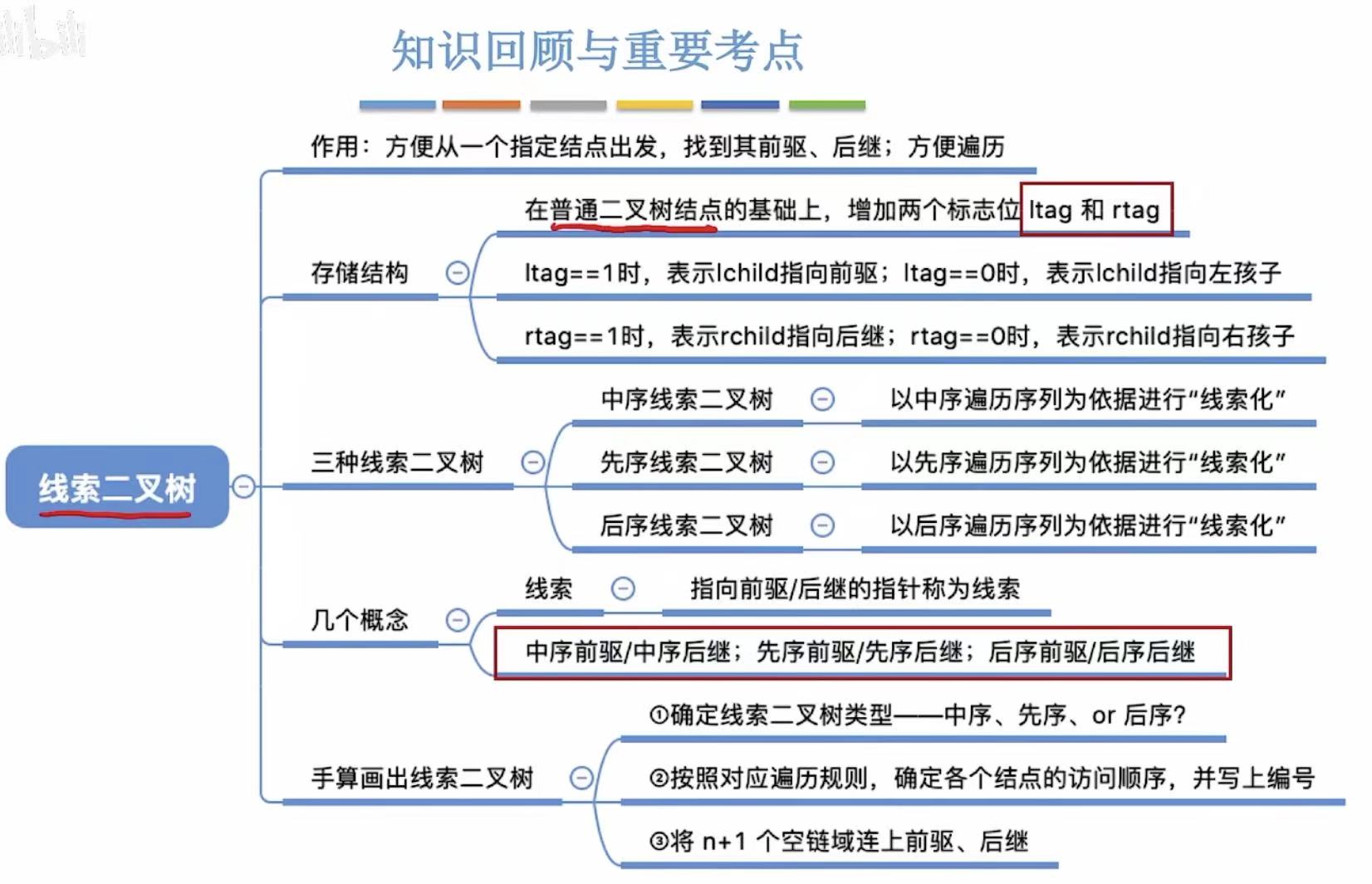
二叉树线索化
用上面最开始提过的方法实现查找前驱是这样了,为了提高代码效率,所以就必须用线索把所有的代码优化一遍。
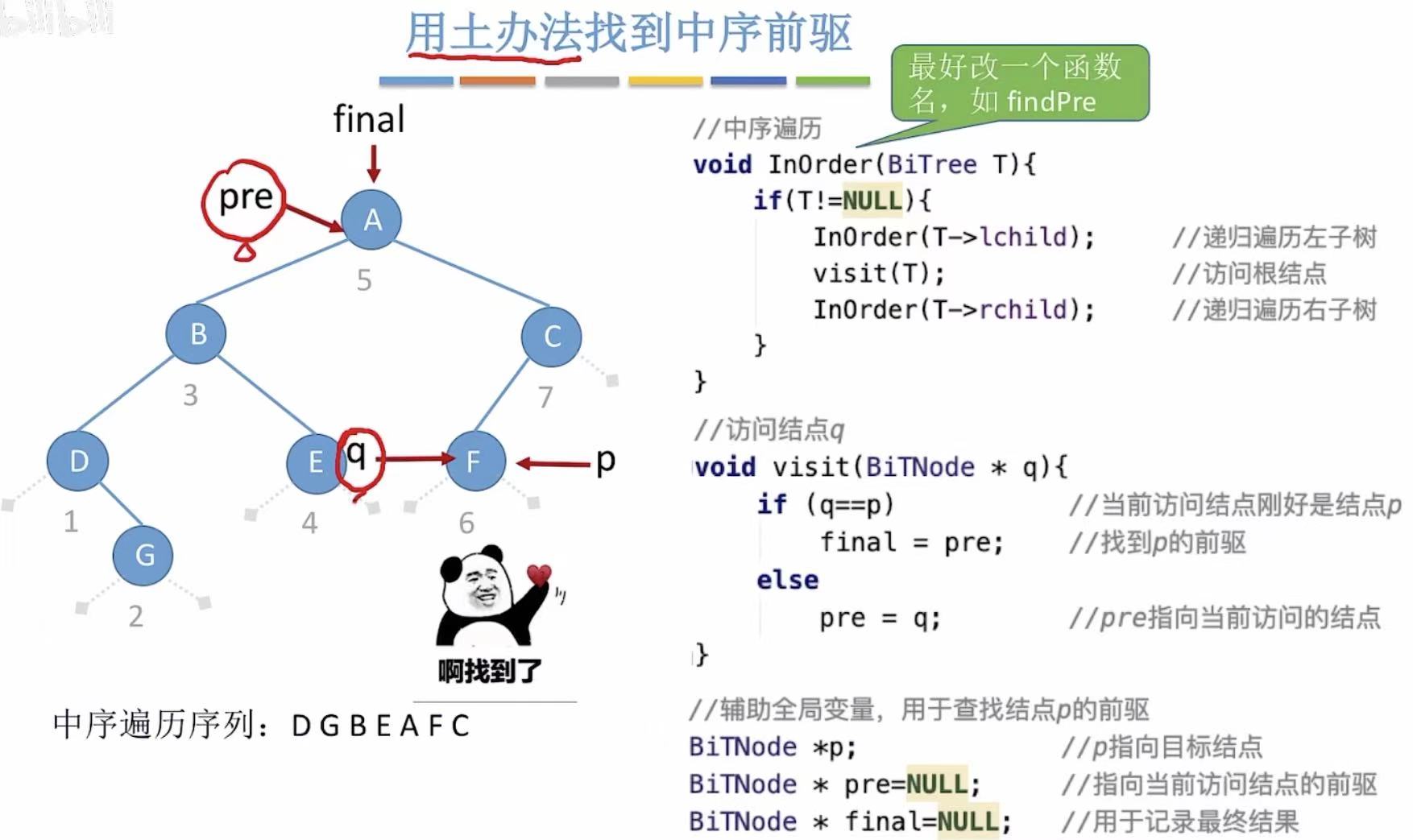
1. 中序线索化
如果指向C,因为C是最后一个被访问的结点,它没有后继,所以给它添加的后继线索就只能指向NULL。
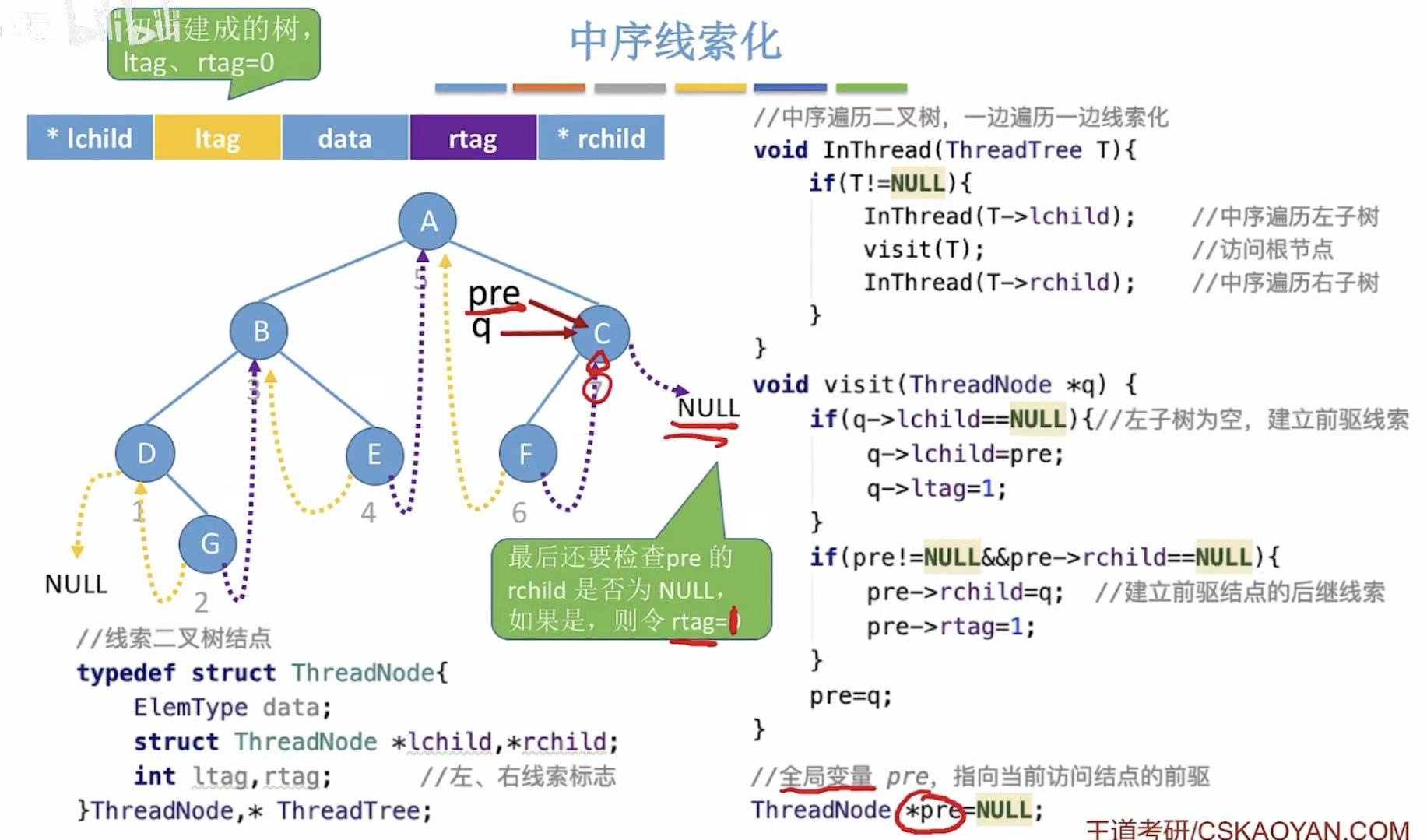
java
// 定义线索二叉树的结点结构
typedef struct ThreadNode {
ElemType data; // 数据域
struct ThreadNode *lchild, *rchild; // 左、右孩子指针
int ltag, rtag; // 线索标志位
// ltag=0 表示 lchild 指向左孩子
// ltag=1 表示 lchild 指向前驱
// rtag=0 表示 rchild 指向右孩子
// rtag=1 表示 rchild 指向后继
} ThreadNode, *ThreadTree;
// 全局变量 pre,用于记录当前访问结点的前驱
ThreadNode *pre = NULL;
// 中序线索化函数:一边中序遍历,一边建立线索
void InThread(ThreadTree T) {
if (T != NULL) { // 如果当前结点不为空
InThread(T->lchild); // 递归线索化左子树
visit(T); // 访问当前结点(建立线索)
InThread(T->rchild); // 递归线索化右子树
}
}
// 辅助函数:在中序遍历时建立前后线索
void visit(ThreadNode *q) {
// 情况1:如果 q 的左孩子为空 → 可以建立前驱线索
if (q->lchild == NULL) {
q->lchild = pre; // 将 q 的左指针指向它的前驱 pre
q->ltag = 1; // 标志为线索(不是孩子)
}
// 情况2:如果 pre 不为空且 pre 的右孩子为空 → 可以建立后继线索
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = q; // 将 pre 的右指针指向 q(即 q 是 pre 的后继)
pre->rtag = 1; // 标志为线索
}
// 更新 pre 为当前结点 q,供下一次使用
pre = q;
}

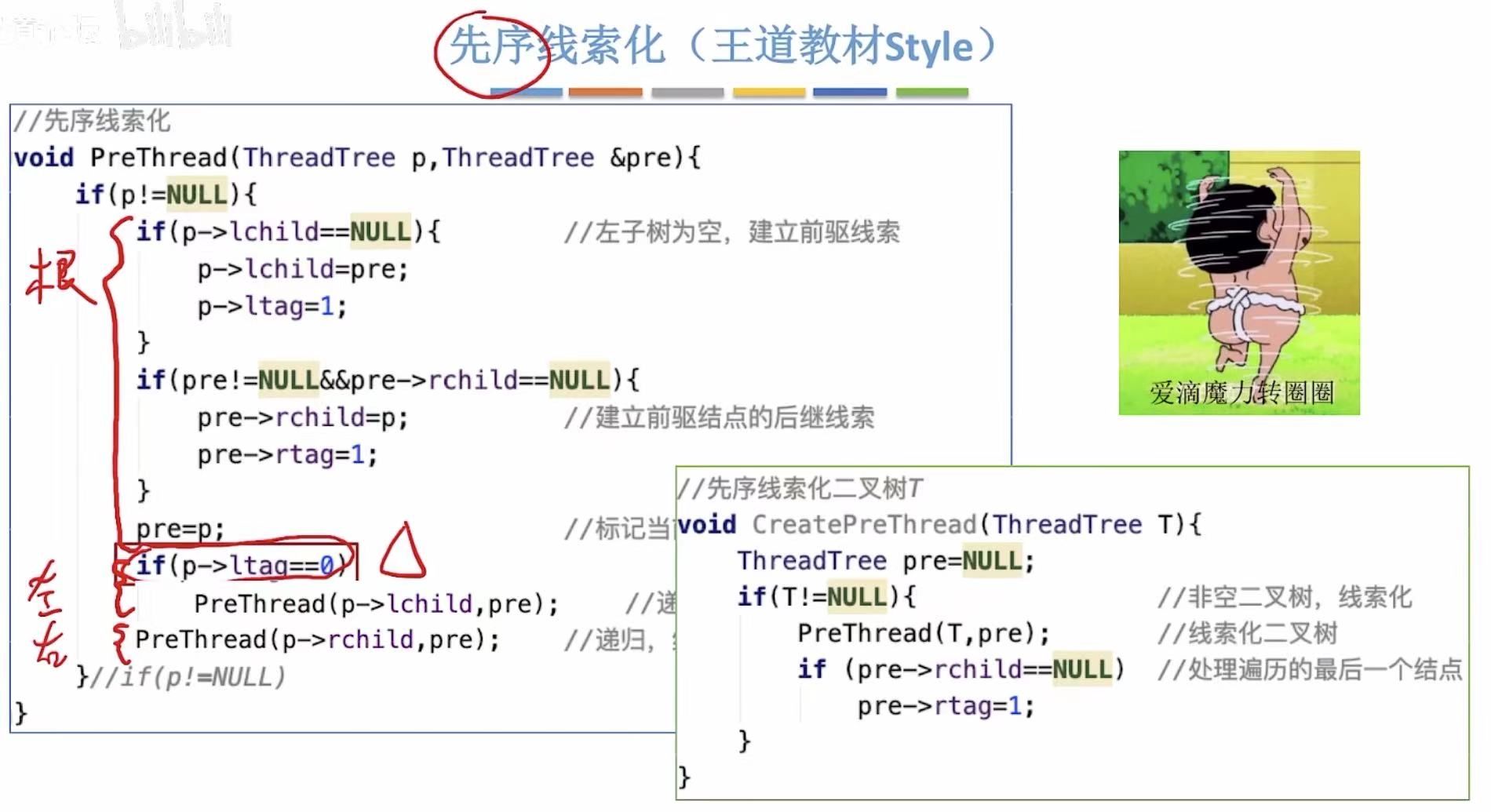
2. 先序线索化
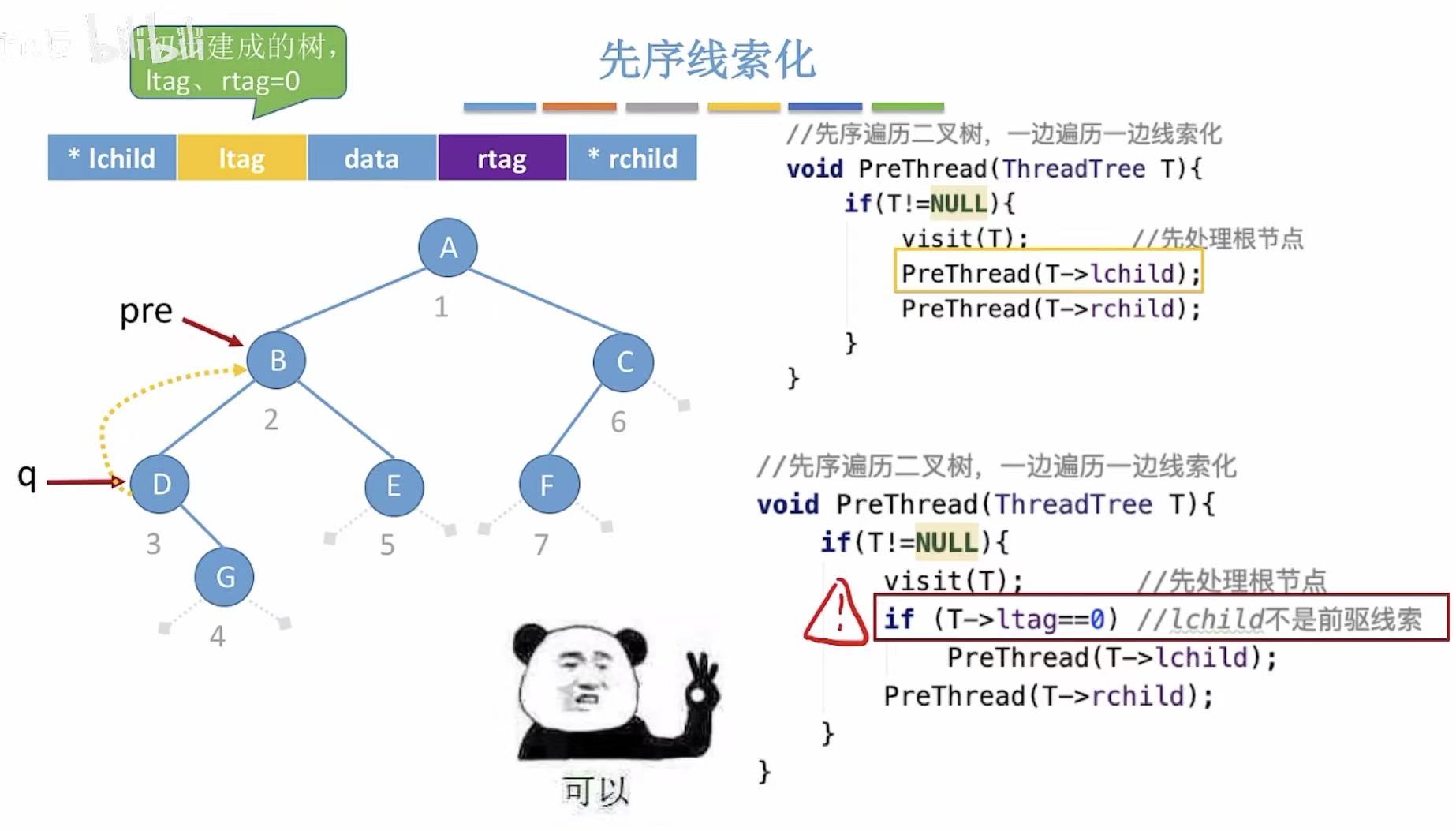
转圈问题:
visit(T):当pre指向B,也就是q指向D且将D结点线索化的时候(D的左侧指针指向B)PreThread(T->lchild):需要继续对D的左孩子进行处理- 这里会误将B认为D的左孩子(因为上一步线索化让这两个结点连在了一起)
- 就会出现D-->B-->D-->B-->...这种无限循环的情况
- 所以进行优化,这里跳到熊猫头表情包的那一张PPT
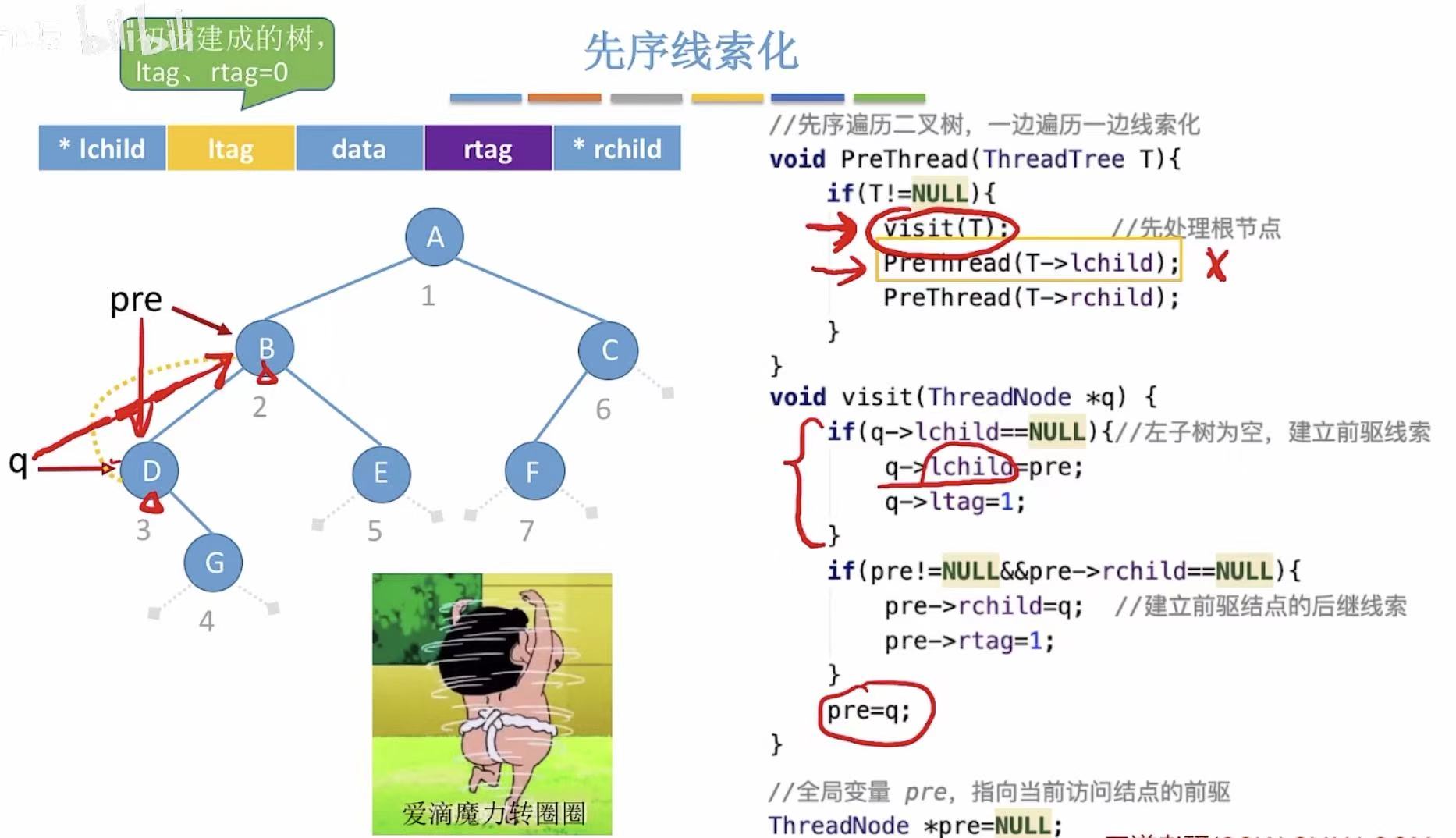
我们需要加上一个判断,只有指向的不是前驱线索的时候,我们才对那个结点进行处理
java
// 定义线索二叉树的结点结构
typedef struct ThreadNode {
ElemType data; // 数据域
struct ThreadNode *lchild, *rchild; // 左、右孩子指针
int ltag, rtag; // 线索标志位
// ltag=0:lchild 指向左孩子
// ltag=1:lchild 指向前驱
// rtag=0:rchild 指向右孩子
// rtag=1:rchild 指向后继
} ThreadNode, *ThreadTree;
// 全局变量 pre,用于记录当前访问结点的前驱
ThreadNode *pre = NULL;
// 主函数:创建并进行先序线索化
void CreatePreThread(ThreadTree T) {
pre = NULL; // 初始化 pre 为 NULL
if (T != NULL) { // 如果树不为空
PreThread(T); // 调用先序线索化函数
}
// 最后处理遍历的最后一个结点(根节点)
if (pre->rchild == NULL) { // 如果最后一个结点的右孩子为空
pre->rtag = 1; // 将其右指针设为线索,指向后继(无后继,但可标记)
}
}
// 先序线索化递归函数
void PreThread(ThreadTree T) {
if (T != NULL) {
visit(T); // 先访问当前结点(处理根节点)
// 只有当左子树不是线索时,才递归处理左子树
if (T->ltag == 0) { // 如果左孩子是真实的孩子(非线索)
PreThread(T->lchild); // 递归处理左子树
}
PreThread(T->rchild); // 处理右子树(无论是否是线索)
}
}
// 辅助函数:在遍历时建立线索
void visit(ThreadNode *q) {
// 情况1:如果 q 的左孩子为空 → 可以建立前驱线索
if (q->lchild == NULL) {
q->lchild = pre; // 将 q 的左指针指向它的前驱 pre
q->ltag = 1; // 标志为线索(不是孩子)
}
// 情况2:如果 pre 不为空且 pre 的右孩子为空 → 可以建立后继线索
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = q; // 将 pre 的右指针指向 q(即 q 是 pre 的后继)
pre->rtag = 1; // 标志为线索
}
// 更新 pre 为当前结点 q,供下一次使用
pre = q;
}
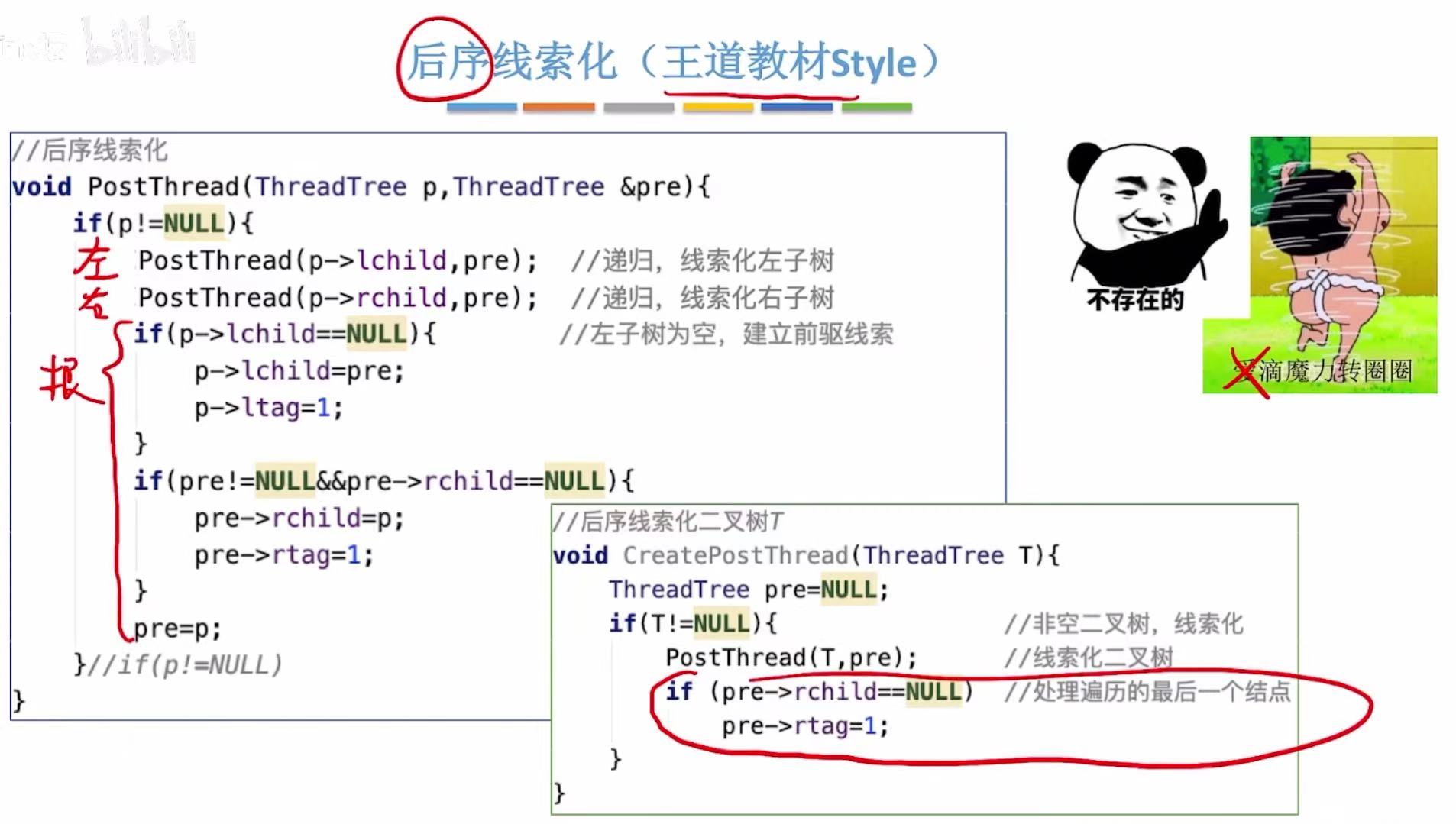
3. 后序线索化
java
// 定义线索二叉树的结点结构
typedef struct ThreadNode {
ElemType data; // 数据域
struct ThreadNode *lchild, *rchild; // 左、右孩子指针
int ltag, rtag; // 线索标志位
// ltag=0:lchild 指向左孩子
// ltag=1:lchild 指向前驱
// rtag=0:rchild 指向右孩子
// rtag=1:rchild 指向后继
} ThreadNode, *ThreadTree;
// 全局变量 pre,用于记录当前访问结点的前驱
ThreadNode *pre = NULL;
// 主函数:创建并进行后序线索化
void CreatePostThread(ThreadTree T) {
pre = NULL; // 初始化 pre 为 NULL
if (T != NULL) { // 如果树不为空
PostThread(T); // 调用后序线索化函数
}
// 最后处理遍历的最后一个结点(根节点)
if (pre->rchild == NULL) { // 如果最后一个结点的右孩子为空
pre->rtag = 1; // 将其右指针设为线索,标记为后继
}
}
// 后序线索化递归函数
void PostThread(ThreadTree T) {
if (T != NULL) {
PostThread(T->lchild); // 递归处理左子树
PostThread(T->rchild); // 递归处理右子树
visit(T); // 访问根节点(最后处理)
}
}
// 辅助函数:在遍历时建立线索
void visit(ThreadNode *q) {
// 情况1:如果 q 的左孩子为空 → 可以建立前驱线索
if (q->lchild == NULL) {
q->lchild = pre; // 将 q 的左指针指向它的前驱 pre
q->ltag = 1; // 标志为线索(不是孩子)
}
// 情况2:如果 pre 不为空且 pre 的右孩子为空 → 可以建立后继线索
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = q; // 将 pre 的右指针指向 q(即 q 是 pre 的后继)
pre->rtag = 1; // 标志为线索
}
// 更新 pre 为当前结点 q,供下一次使用
pre = q;
}
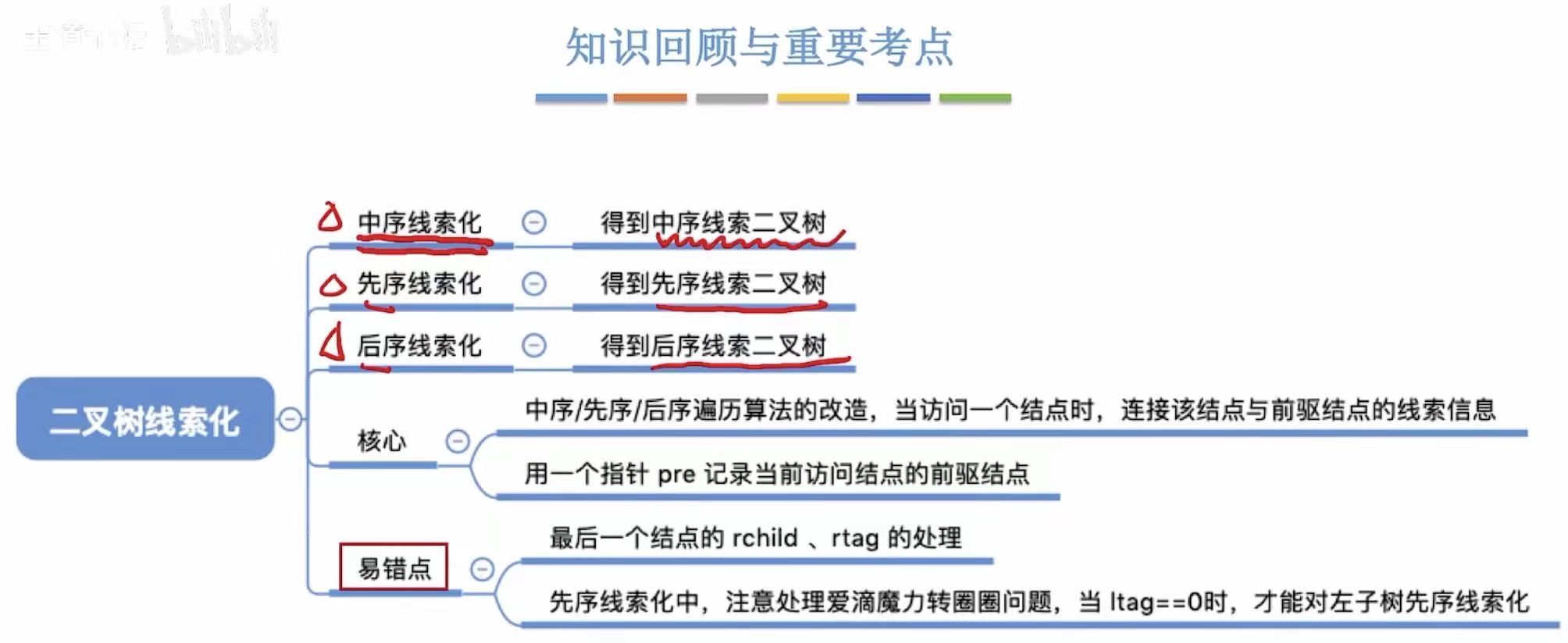
4. 小结
在线索二叉树中找前驱后继
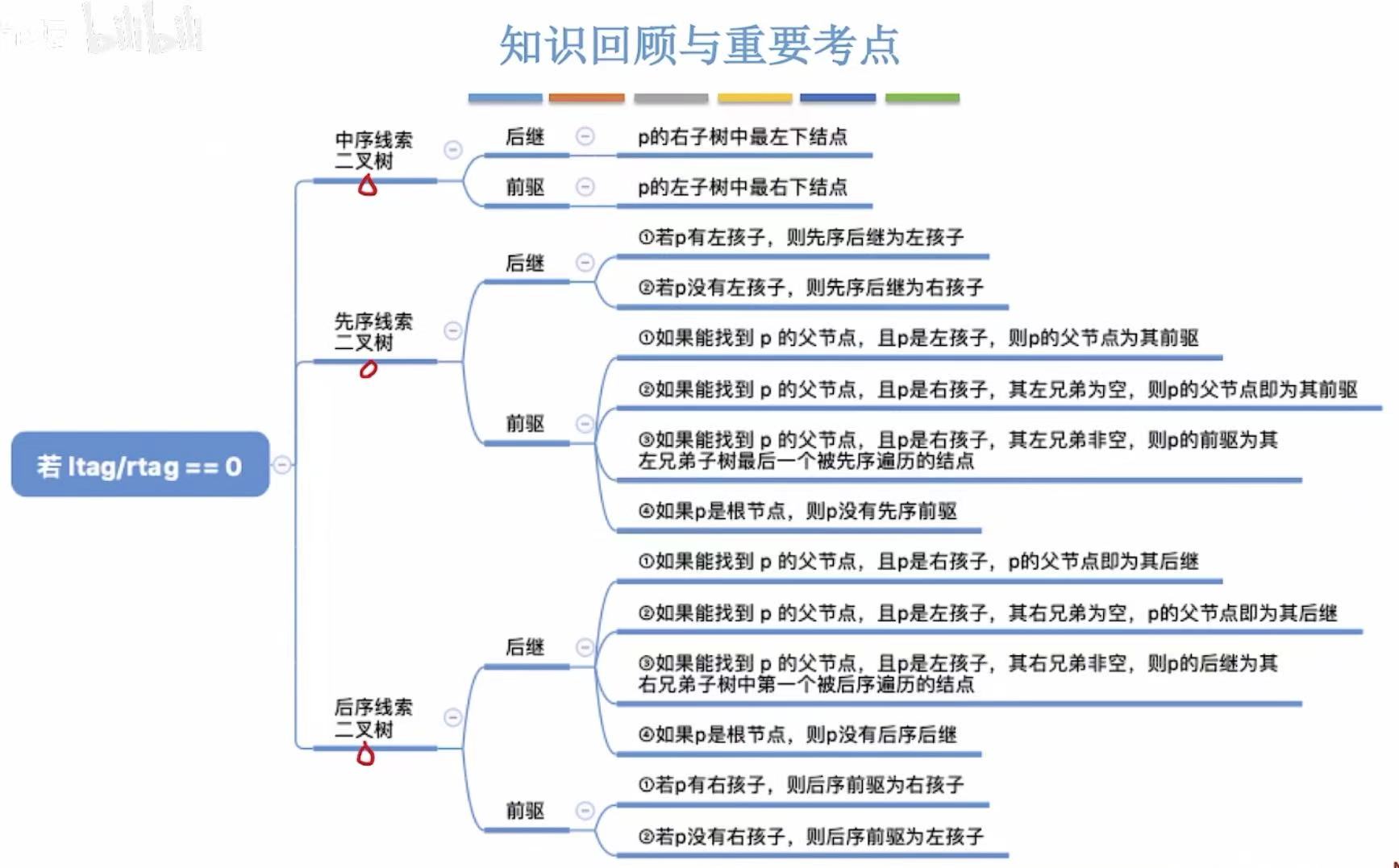
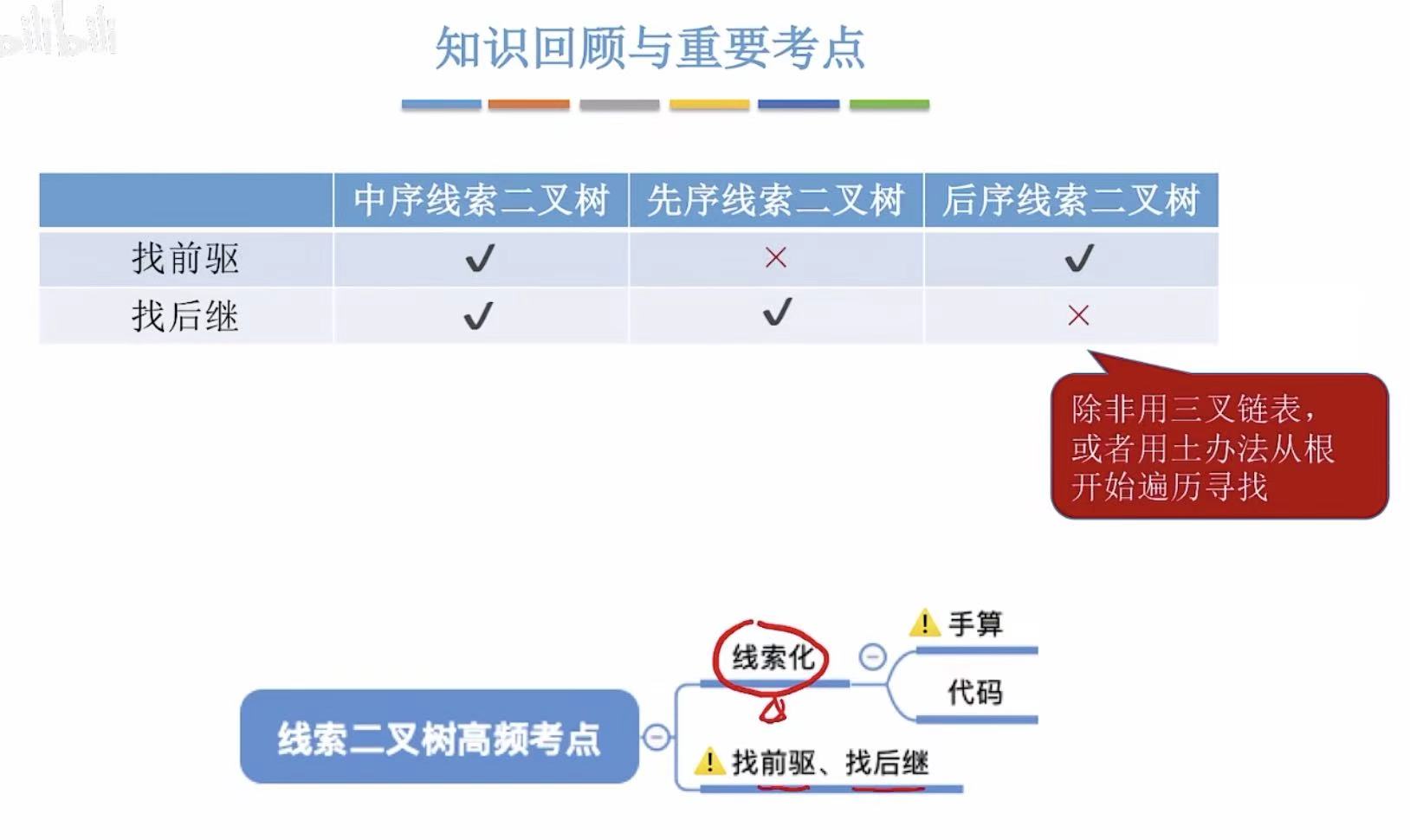
1. 中序
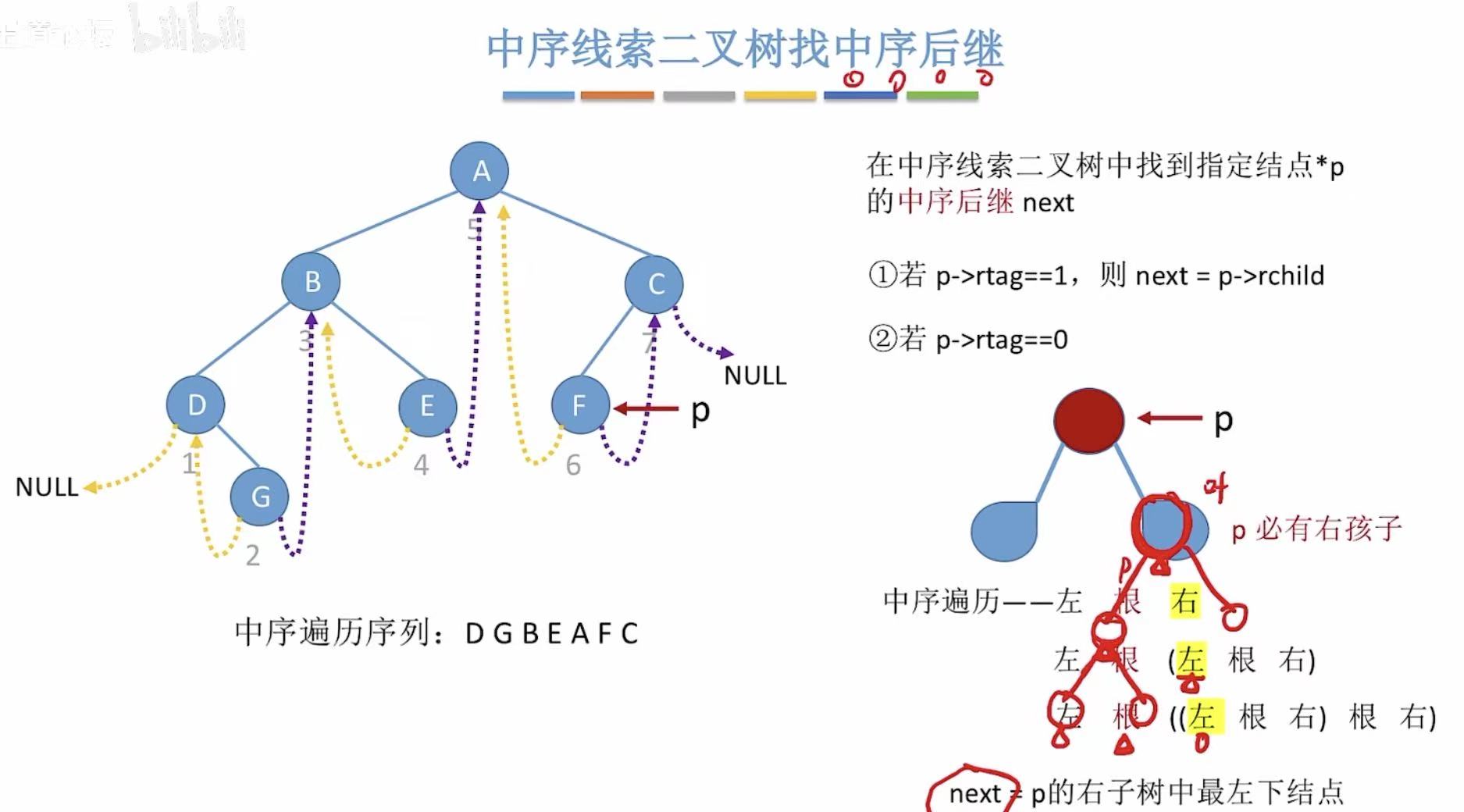
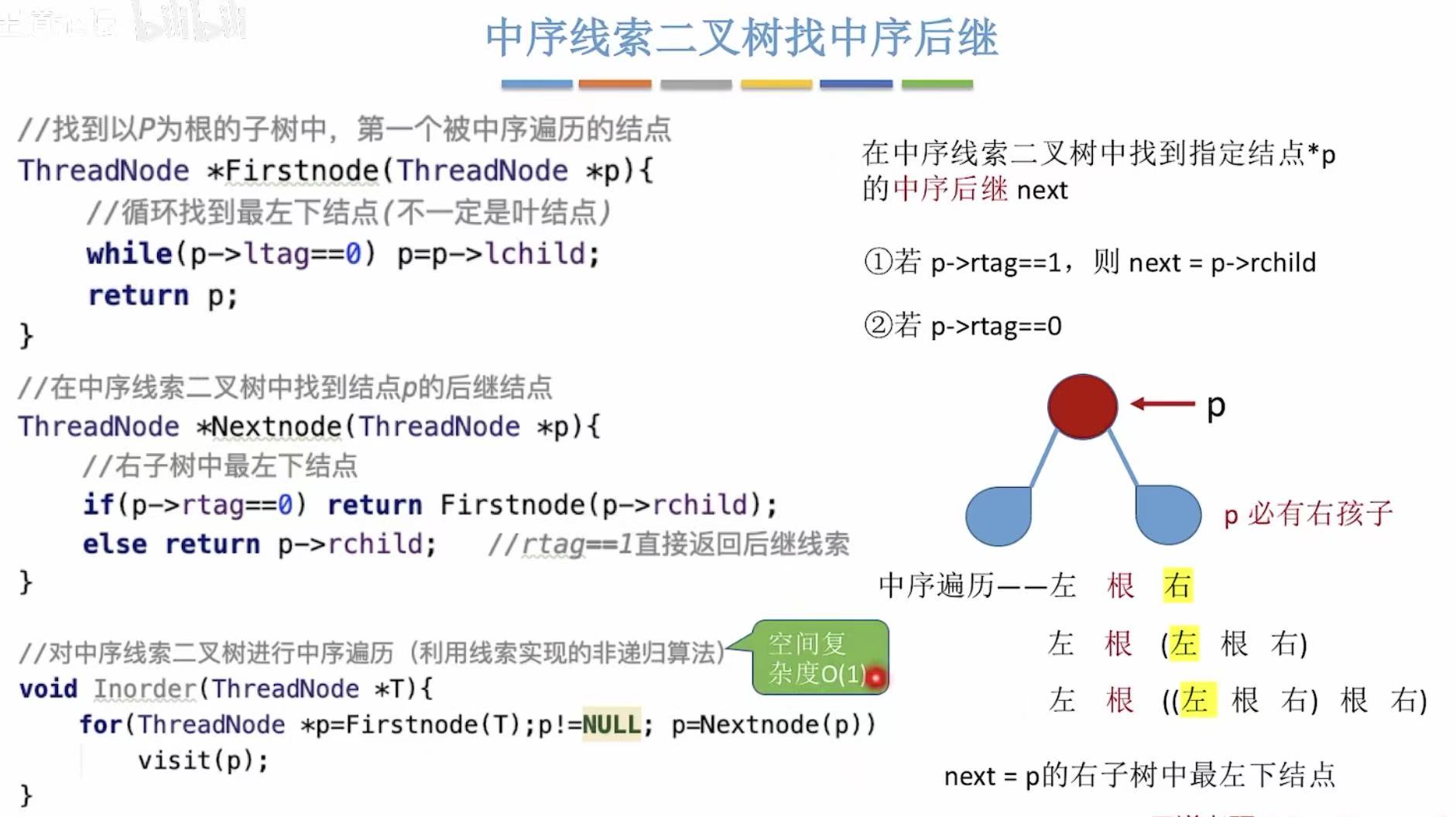
- 有后继线索的可以直接找到后继
- 没有后继线索的,后继是当前结点的右子树中最左下结点
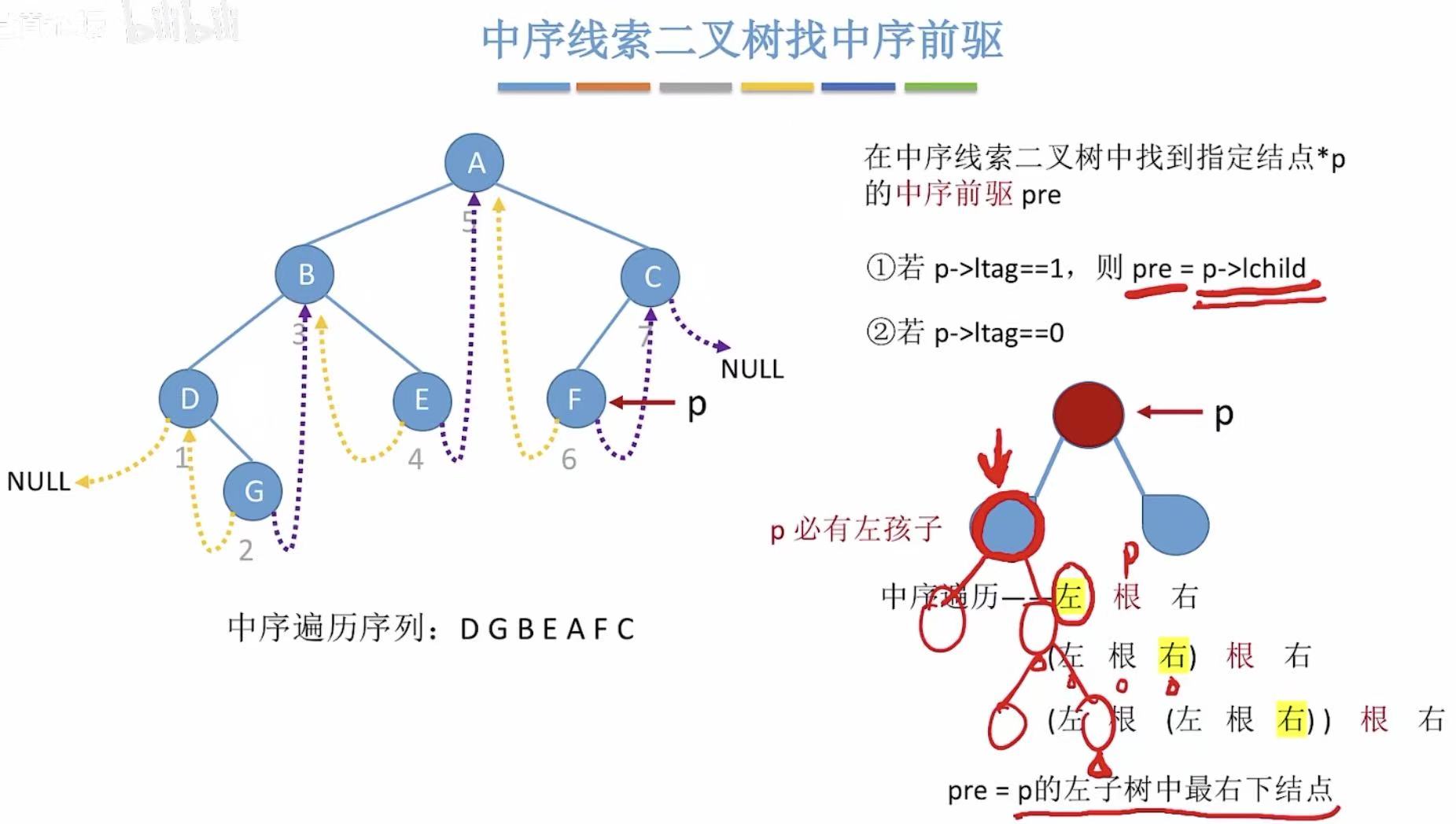
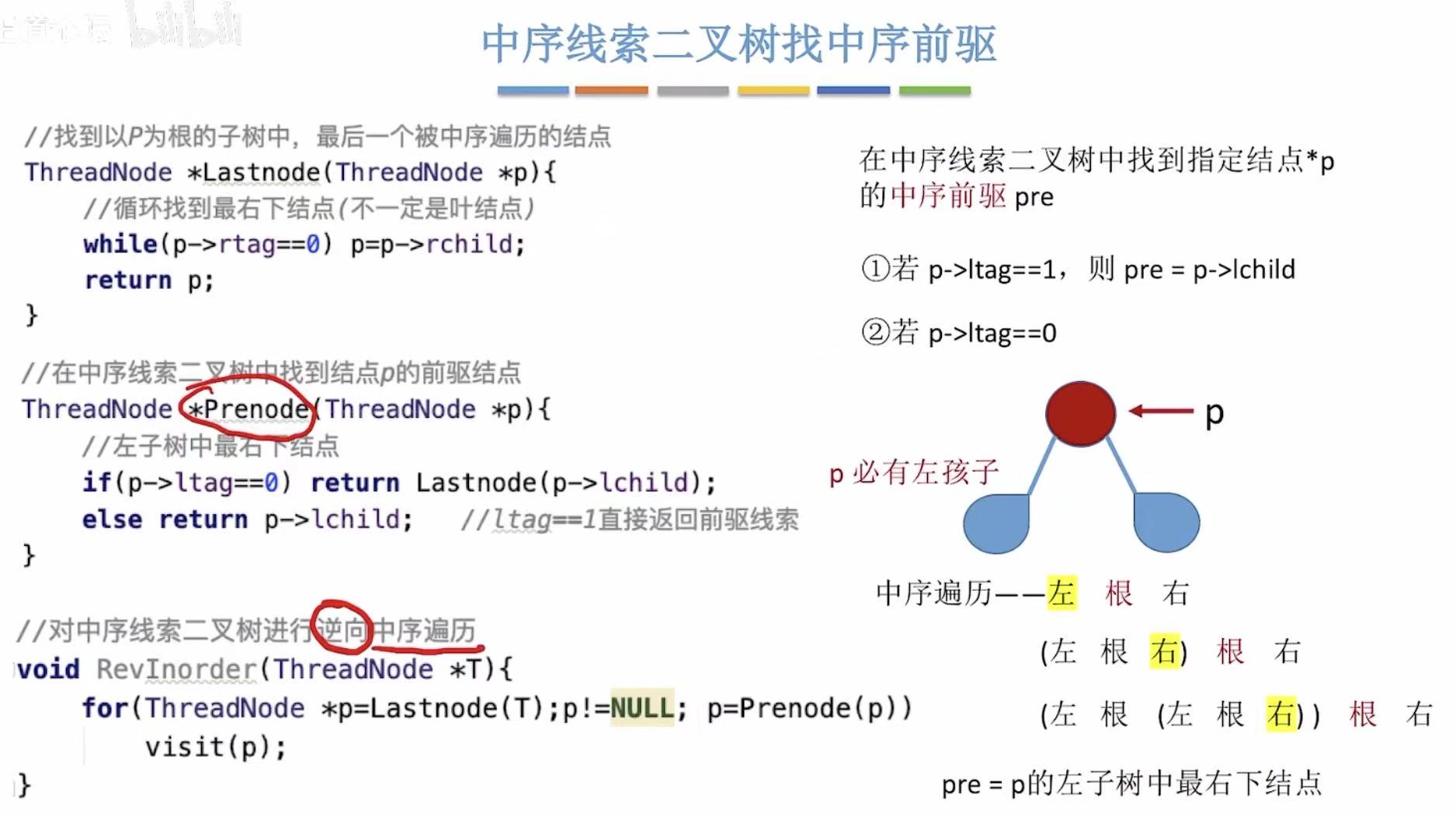
- 有前驱线索的可以直接找到前驱
- 没有前驱线索的,后继是当前结点的左子树中最右下结点
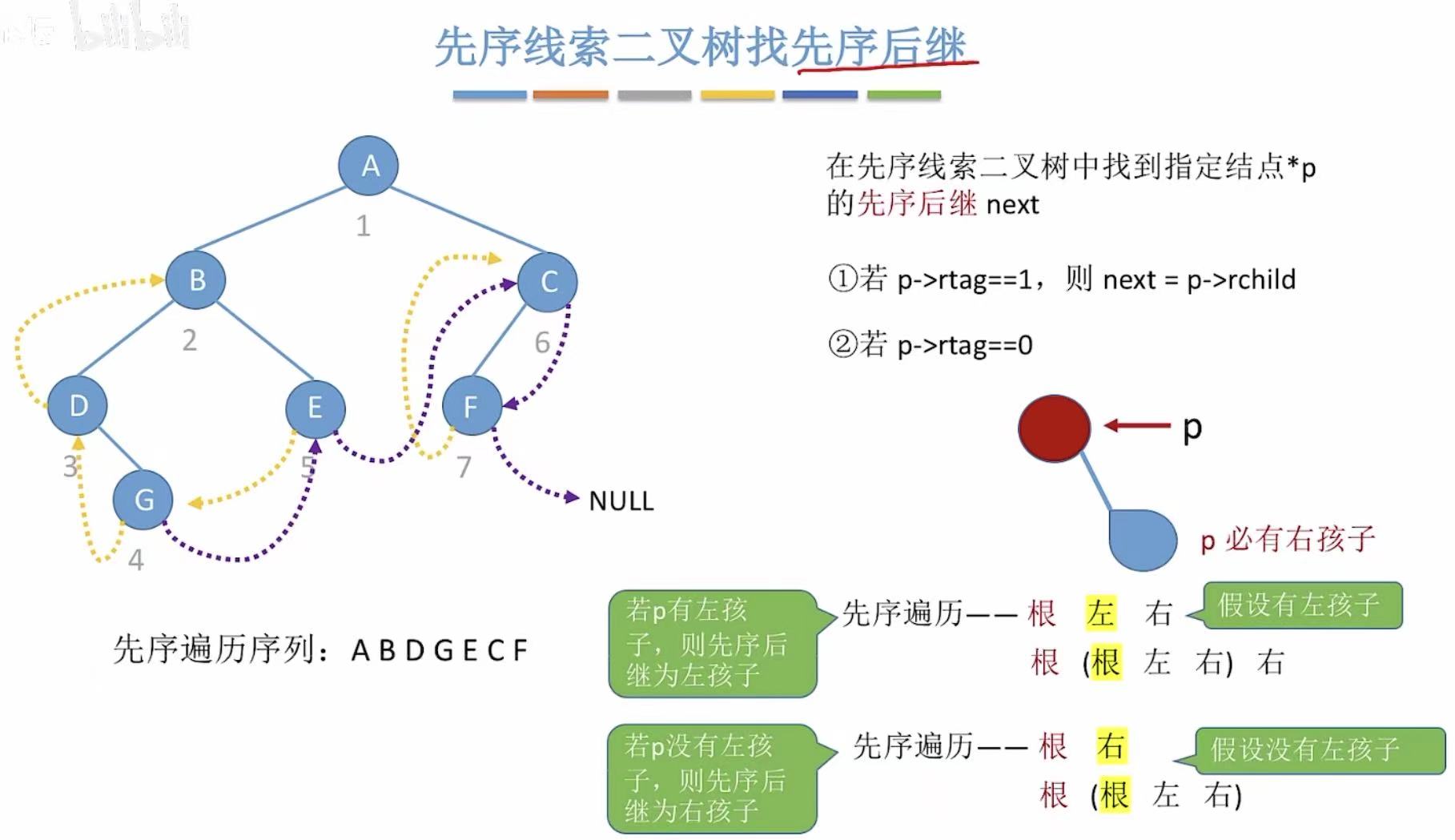
2. 先序
- 有后继线索的可以直接找到后继
- 没有后继线索的,分为两种情况
当前结点有左孩子:后继为左孩子
当前结点没有左孩子:后继为右孩子
- 有前驱线索的可以直接找到前驱
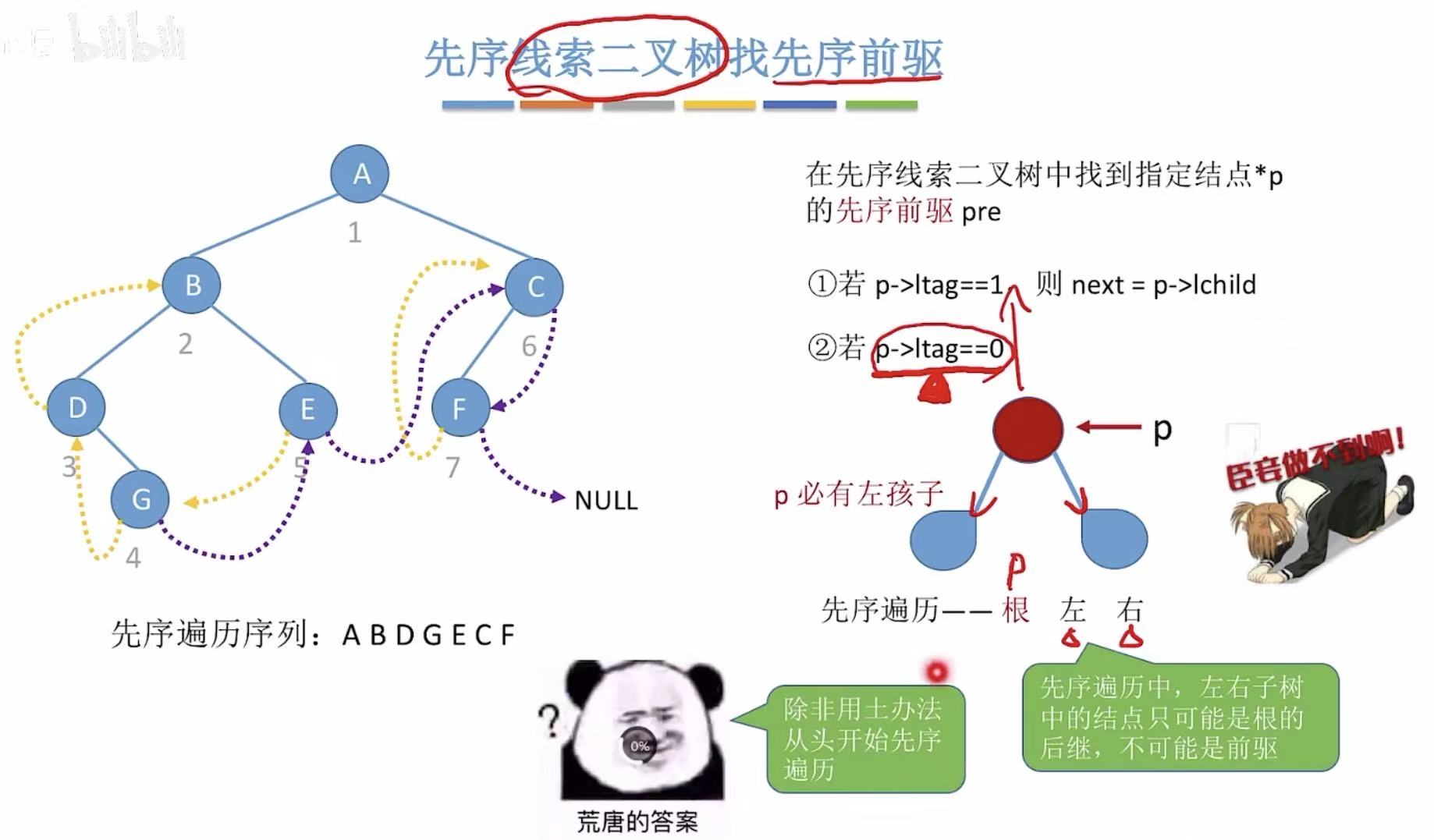
- 没有前驱线索的,分为三种情况:
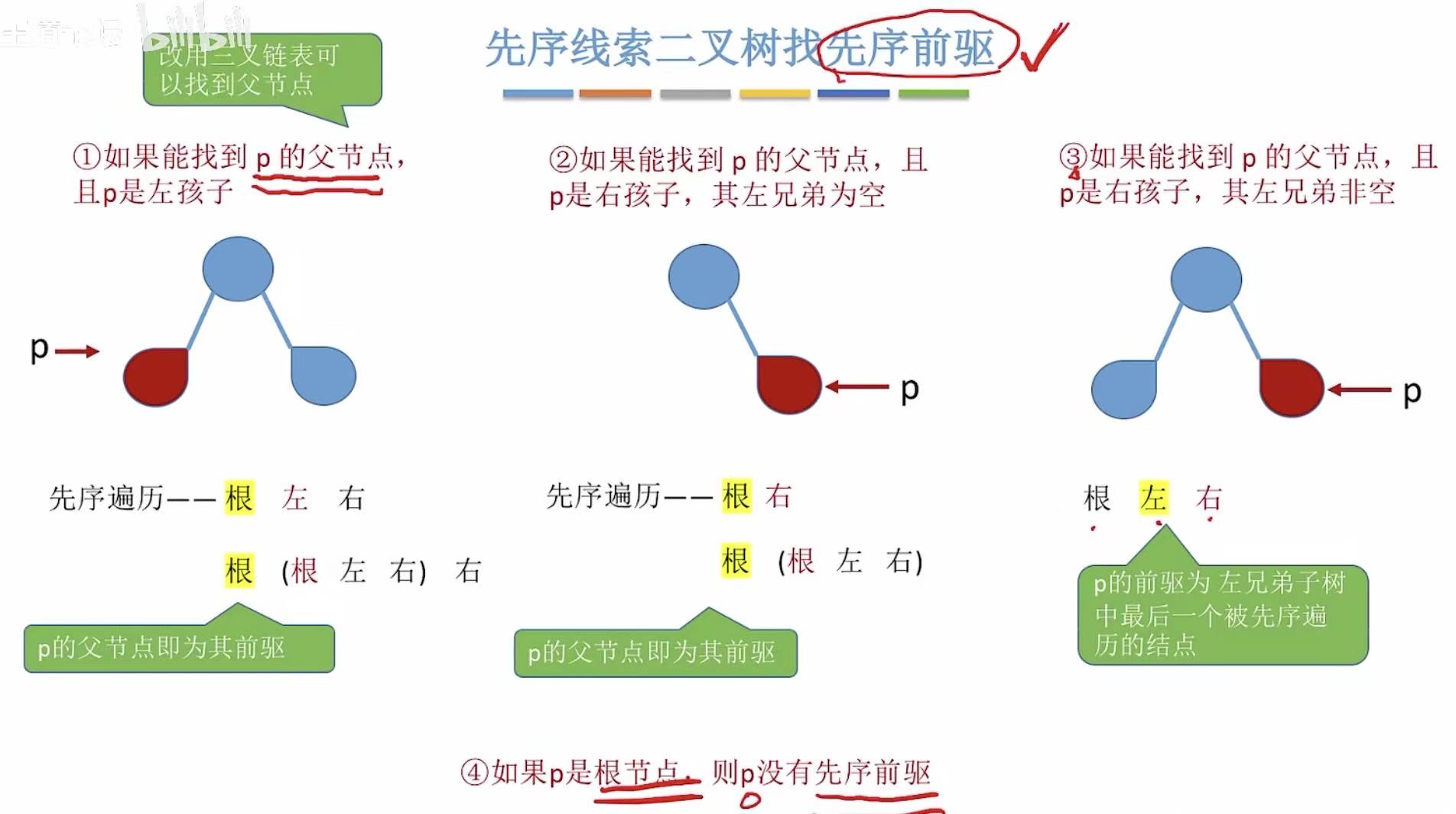
3. 后序
- 有前驱线索的可以直接找到前驱
- 没有前驱线索的,分为两种情况
当前结点有右孩子:后继为右孩子
当前结点没有右孩子:后继为左孩子
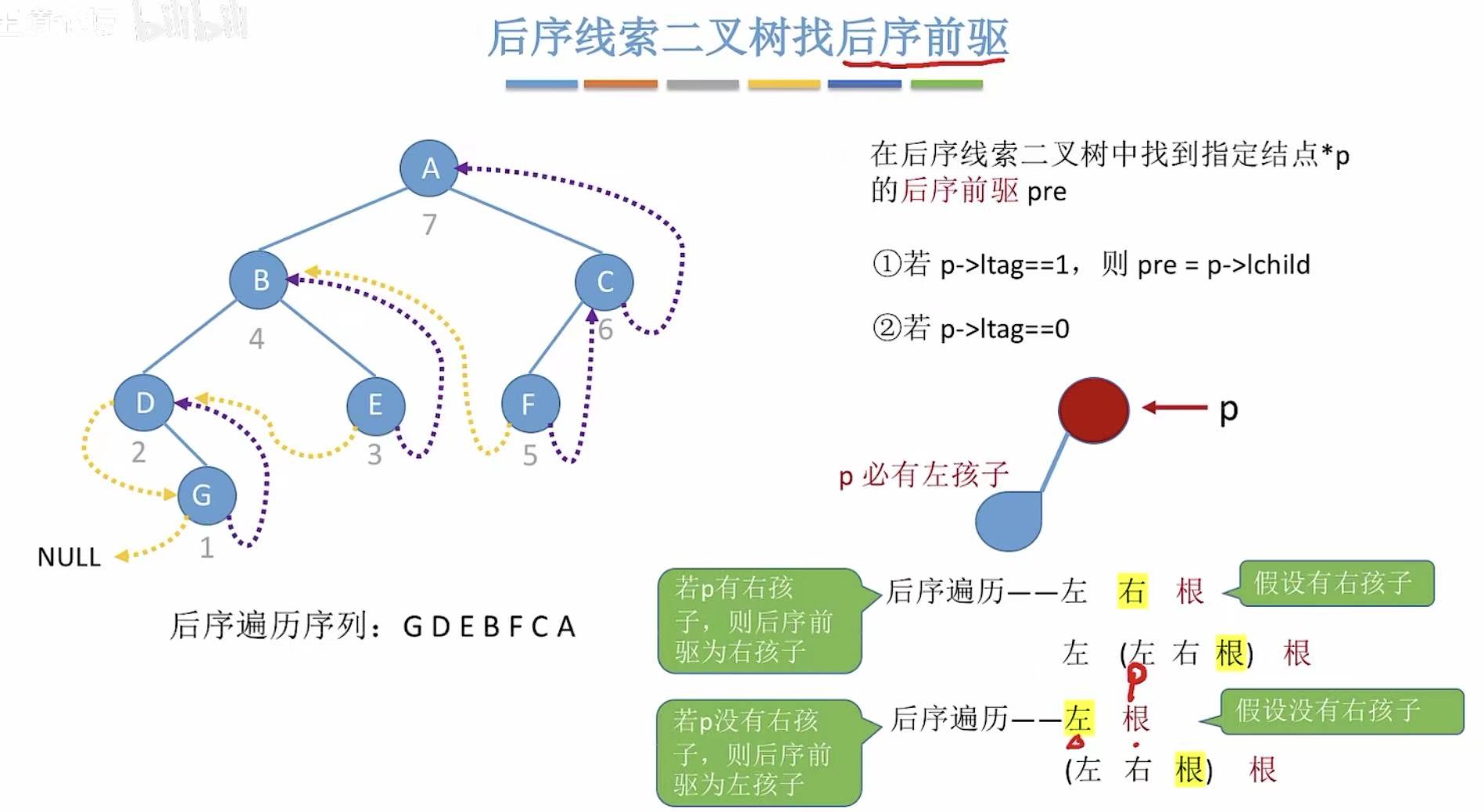
- 有后继线索的可以直接找到后继
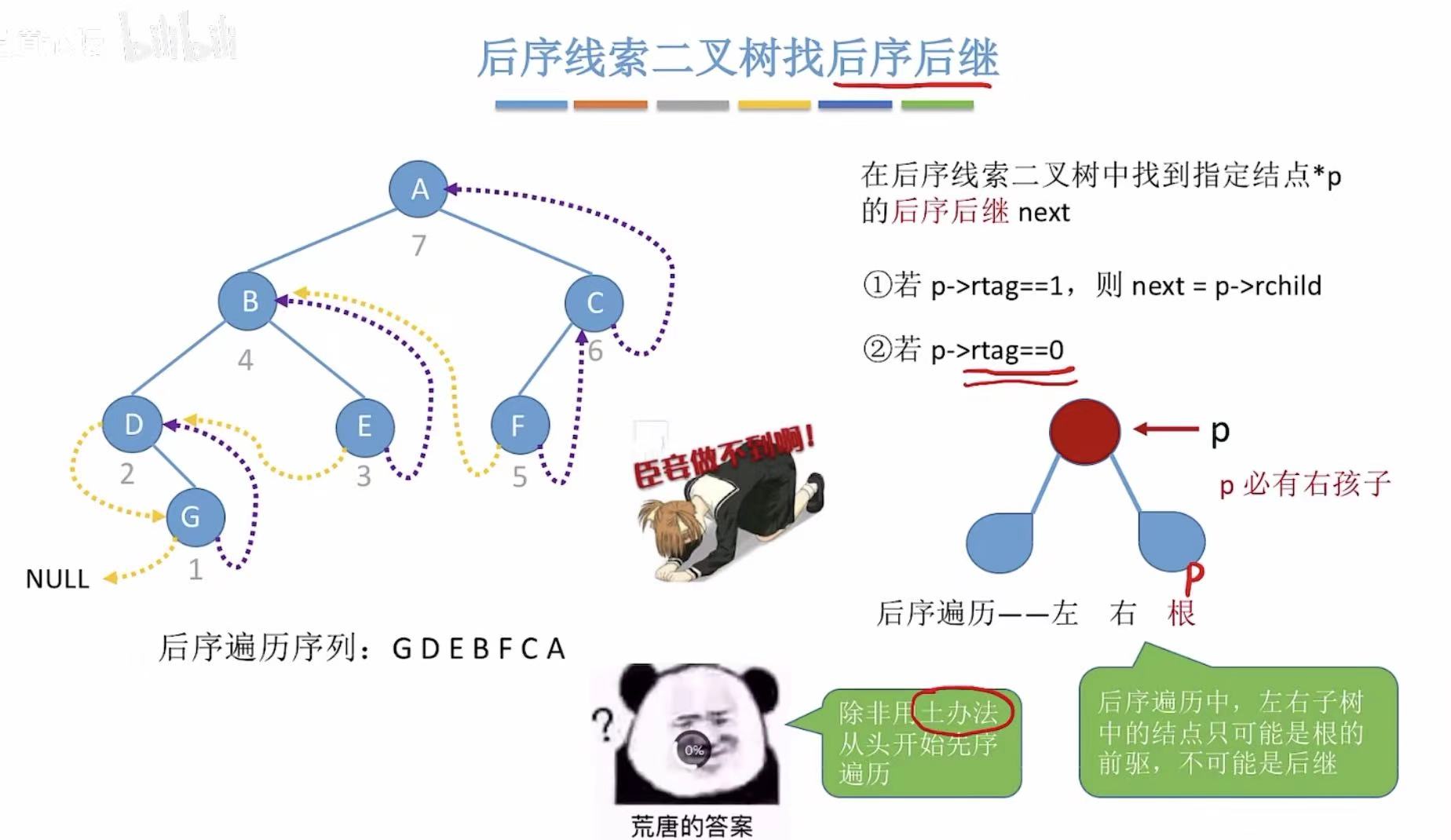
- 没有后继线索的,分为三种情况:
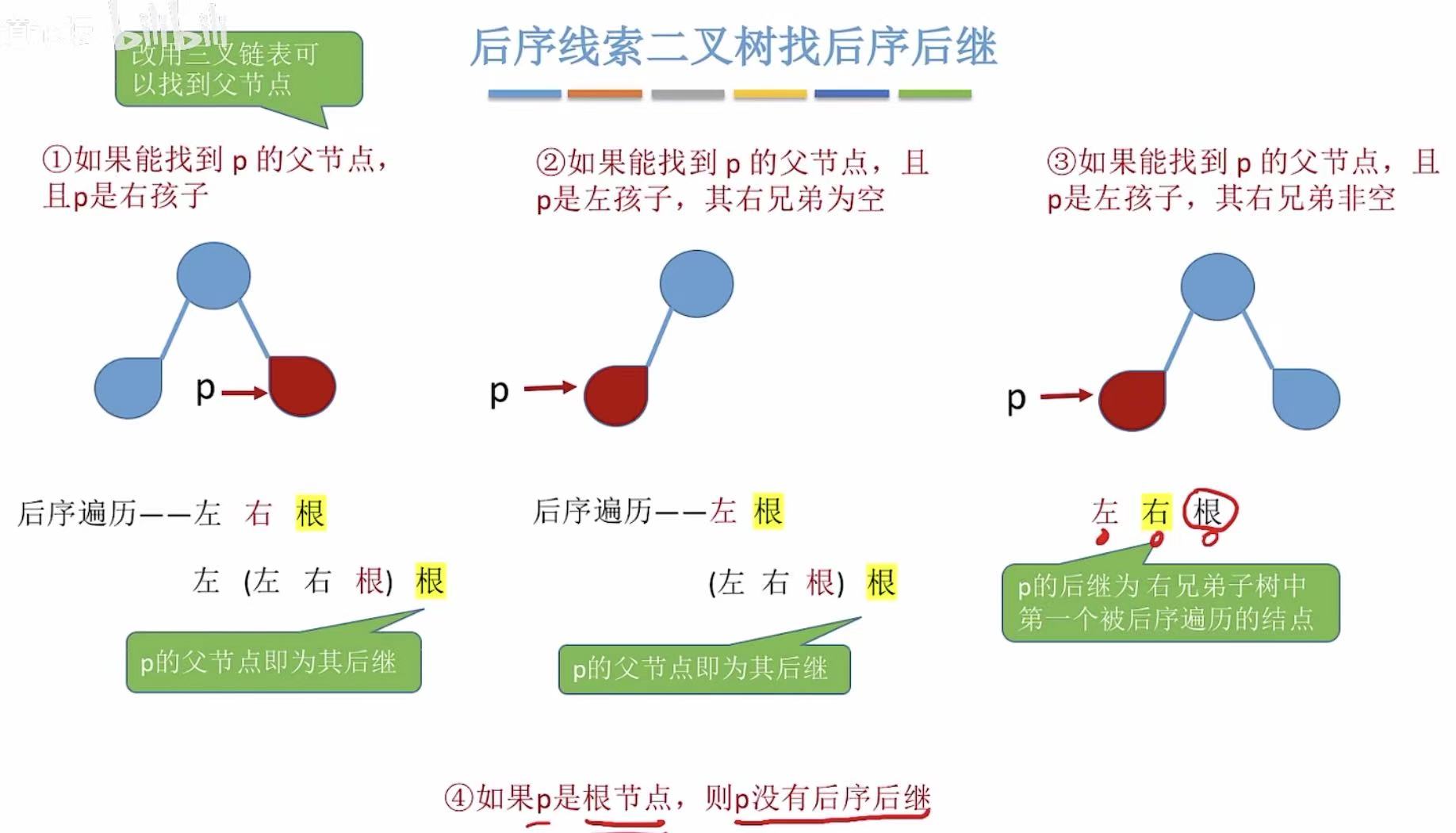
4. 小结