人工智能：深度学习：1.pytorch概述(2)

5. 自动微分

自动微分是 PyTorch 实现深度学习反向传播、求解梯度的核心机制，能自动计算张量运算的梯度（导数），无需手动推导公式，极大简化了模型训练的代码编写。

梯度（导数）

梯度本质就是多元函数的偏导数组成的向量：

• 单变量函数（如 y=x2）只有导数，描述单个变量变化对结果的影响；
• 多变量函数（如 z=x2+y2）对每个变量求偏导数（∂x∂z、∂y∂z），这些偏导数按顺序组合起来，就是函数在该点的梯度。

开启 / 关闭张量梯度计算的方法

在 PyTorch 中，梯度计算的核心是张量的 requires_grad 属性，以下完整说明开启、关闭梯度的方法，以及梯度清零、detach 固定参数的配套用法：

一、开启梯度计算

梯度计算前一般需执行梯度清零（避免梯度累加），仅首次进行梯度运算时无需清零。

1. 定义张量时直接开启 在创建张量的同时，通过 requires_grad=True 参数显式标记该张量需要计算梯度。这种方式是深度学习中最常用的，适合模型权重、待优化参数等需要长期追踪梯度的张量。

2. 已定义张量后动态开启 若张量已创建且默认关闭梯度（requires_grad=False），可通过 tensor.requires_grad_(True) 方法（下划线表示原地修改张量属性）动态开启梯度追踪。这种方式适合临时需要为已有张量开启梯度的场景。

二、关闭梯度计算（三种常用方式）

关闭梯度计算的核心是让张量脱离梯度追踪，适用于验证模型、推理阶段（无需更新参数）、固定部分参数等场景：

1. 动态关闭（原地修改） ：tensor.requires_grad_(False)直接修改原张量的 requires_grad 属性为 False，原地关闭梯度追踪，原张量后续运算不再计算梯度。

2. 脱离计算图（保留原张量） ：tensor.detach()返回一个与原张量共享数值，但脱离梯度追踪的新张量（requires_grad=False），原张量的梯度属性不变；该方式仅固定副本，原张量仍可计算梯度，适合 "参数参与计算但不更新" 的场景。

3. 上下文管理器（临时关闭） ：torch.no_grad()在代码块内临时关闭所有张量的梯度追踪，退出代码块后恢复原有状态，适合推理、验证等无需梯度的场景，不修改张量本身的属性。

示例

import torch

# ========== 1. 开启梯度计算 ==========
# 方法1：定义时开启
x = torch.tensor(2.0, requires_grad=True)
# 方法2：动态开启（先创建无梯度张量，再开启）
y = torch.tensor(3.0)
y.requires_grad_(True)
print("开启梯度后：x.requires_grad =", x.requires_grad)  # 输出：True
print("开启梯度后：y.requires_grad =", y.requires_grad)  # 输出：True

# ========== 2. 梯度清零与多次反向传播 ==========
# 第一次反向传播（首次无需清零）
z1 = x**2 + y**2
z1.backward(retain_graph=True)
print("\n第一次反向传播后：")
print("x.grad =", x.grad.item())  # 输出：4.0
print("y.grad =", y.grad.item())  # 输出：6.0

# 第二次反向传播（不清零，梯度累积）
z2 = x**2 + y**2
z2.backward(retain_graph=True)
print("\n第二次反向传播（不清零）后：")
print("x.grad =", x.grad.item())  # 输出：8.0（4.0+4.0）
print("y.grad =", y.grad.item())  # 输出：12.0（6.0+6.0）

# 梯度清零（多次反向传播必须清零）
x.zero_grad_()
y.zero_grad_()

# 第三次反向传播（清零后）
z3 = x**2 + y**2
z3.backward(retain_graph=True)
print("\n第三次反向传播（清零后）后：")
print("x.grad =", x.grad.item())  # 输出：4.0
print("y.grad =", y.grad.item())  # 输出：6.0

# ========== 3. 关闭梯度计算 ==========
# 方式1：动态关闭（原地修改）
y.requires_grad_(False)
print("\n动态关闭y的梯度后：y.requires_grad =", y.requires_grad)  # 输出：False
z4 = x**2 + y**2
z4.backward(retain_graph=True)
print("动态关闭y后反向传播：y.grad =", y.grad)  # 输出：None（无梯度）

# 恢复y的梯度（重新开启）
y.requires_grad_(True)
x.grad.zero_()  # 清零x梯度

# 方式2：detach() 脱离计算图（固定y，保留原张量梯度）
y_detach = y.detach()
z5 = x**2 + y_detach**2
z5.backward(retain_graph=True)
print("\ndetach()固定y后：")
print("y_detach.requires_grad =", y_detach.requires_grad)  # 输出：False
print("原y.requires_grad =", y.requires_grad)  # 输出：True（原张量不变）
print("x.grad =", x.grad.item())  # 输出：4.0（x仍有梯度）
print("y.grad =", y.grad)  # 输出：None（y无梯度更新）

# 方式3：torch.no_grad() 临时关闭（代码块内无梯度）
x.grad.zero_()
with torch.no_grad():
    z6 = x**2 + y**2
    print("\ntorch.no_grad()内：z6.requires_grad =", z6.requires_grad)  # 输出：False
# 退出上下文后，梯度属性恢复
z7 = x**2 + y**2
z7.backward()
print("退出no_grad后反向传播：x.grad =", x.grad.item())  # 输出：4.0（恢复梯度）

如果想更深的了解计算图的原理及实现，可以参考下面这篇文章。

6.模型相关操作。

6. 模型的操作

一.模型的定义

在 PyTorch 中，自定义神经网络模型的核心方式是继承 torch.nn.Module 类 ，通过重写类的构造函数（__init__）定义网络层，重写 forward 方法定义前向传播逻辑；反向传播则由 Module 类内置的自动微分机制自动生成，无需手动实现。

介绍

• nn.Module 是 PyTorch 中所有神经网络模块的基类，封装了参数管理、设备迁移、梯度计算、模型保存 / 加载等核心功能；
• 构造函数（__init__）：用于初始化网络层（如卷积层、全连接层、激活函数等），将层定义为类的属性，Module 会自动追踪这些层的参数；
• 前向传播（forward）：定义数据从输入到输出的计算流程，是模型的核心逻辑；
• 反向传播：调用 loss.backward() 时，PyTorch 会根据前向传播的计算图自动推导反向传播梯度，无需手动编写。

二. ModuleList 和 Sequential

在 PyTorch 中，nn.ModuleList 和 nn.Sequential 是两种常用的层容器，用于管理神经网络的层结构，简化模型定义；二者核心区别在于是否内置前向传播逻辑、是否强制层的执行顺序。

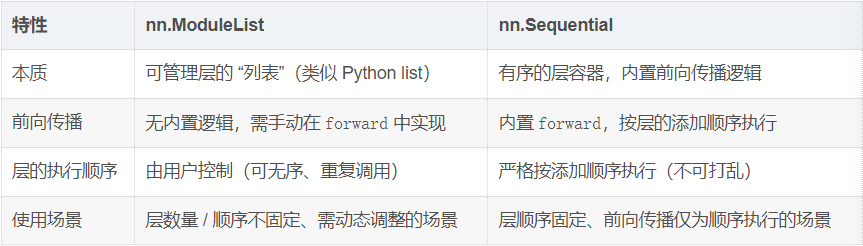
nn.ModuleList 本质是 nn.Module 子类（如层、子模型）的列表，它会被 PyTorch 自动追踪参数，但没有内置的前向传播逻辑 ，需要在 forward 中手动遍历 / 调用层，且层的执行顺序完全由用户决定（可无序）。

nn.Sequential本质是按添加顺序组织的层流水线 ：内置了完整的 forward 前向传播逻辑，无需用户手动编写，传入输入数据后会严格按照层的添加顺序自动执行前向计算，且强制层的执行顺序不可打乱。

示例

import torch
import torch.nn as nn

class ModelWithModuleList(nn.Module):
    def __init__(self):
        super(ModelWithModuleList, self).__init__()
        # 定义ModuleList，存放多个全连接层
        self.layers = nn.ModuleList([
            nn.Linear(10, 20),  # 层0：10→20
            nn.ReLU(),          # 层1：激活函数
            nn.Linear(20, 30)   # 层2：20→30
        ])
        # 可动态添加层（类似list的append）
        self.layers.append(nn.Linear(30, 10))  # 层3：30→10

    def forward(self, x):
        # 手动控制层的执行顺序（可灵活调整，甚至跳过/重复）
        out = self.layers[0](x)  # 先执行层0
        out = self.layers[1](out)  # 再执行层1
        out = self.layers[2](out)  # 再执行层2
        out = self.layers[3](out)  # 最后执行层3
        return out

# 实例化并测试ModuleList模型
model_ml = ModelWithModuleList()
x = torch.randn(2, 10)  # 输入：batch=2，维度=10
output_ml = model_ml(x)
print("ModuleList模型输出形状：", output_ml.shape)
print("ModuleList中的层数量：", len(model_ml.layers))

# ========== 二、nn.Sequential：自带前向传播的"有序容器" ==========
# 方式1：直接传入层（最常用）
model_seq = nn.Sequential(
    nn.Linear(10, 20),
    nn.ReLU(),
    nn.Linear(20, 30),
    nn.Linear(30, 10)
)

# 测试Sequential基础版
output_seq = model_seq(x)
print("\nSequential模型输出形状：", output_seq.shape)
print("Sequential的层结构：\n", model_seq)

# 方式2：带层命名的Sequential
model_seq_named = nn.Sequential(
    nn.ModuleDict({
        "fc1": nn.Linear(10, 20),
        "relu": nn.ReLU(),
        "fc2": nn.Linear(20, 30),
        "fc3": nn.Linear(30, 10)
    })
)

# 按名称访问层并测试
print("\n访问Sequential中的fc1层：", model_seq_named[0]["fc1"])
output_seq_named = model_seq_named(x)
print("带命名的Sequential输出形状：", output_seq_named.shape)

# ========== 三、关键区别演示：顺序 vs 灵活 ==========
class CompareModel(nn.Module):
    def __init__(self):
        super(CompareModel, self).__init__()
        # ModuleList：层存储与执行顺序解耦
        self.ml = nn.ModuleList([
            nn.Linear(10, 20),  # 层0
            nn.Linear(20, 30)   # 层1
        ])
        # Sequential：层存储顺序=执行顺序
        self.seq = nn.Sequential(
            nn.Linear(10, 20),
            nn.Linear(20, 30)
        )

    def forward(self, x):
        # ModuleList：手动逆序执行（演示灵活性）
        out_ml = self.ml[1](self.ml[0](x))  # 正常顺序：0→1
        
        # Sequential：只能按添加顺序执行（无法逆序）
        out_seq = self.seq(x)  # 固定：第一层→第二层
        return out_ml, out_seq

compare_model = CompareModel()
out_ml, out_seq = compare_model(x)
print("\nModuleList输出形状：", out_ml.shape)
print("Sequential输出形状：", out_seq.shape)

# 所有运行结果（注释形式）
"""
ModuleList模型输出形状： torch.Size([2, 10])
ModuleList中的层数量： 4

Sequential模型输出形状： torch.Size([2, 10])
Sequential的层结构：
 Sequential(
  (0): Linear(in_features=10, out_features=20, bias=True)
  (1): ReLU()
  (2): Linear(in_features=20, out_features=30, bias=True)
  (3): Linear(in_features=30, out_features=10, bias=True)
)

访问Sequential中的fc1层： Linear(in_features=10, out_features=20, bias=True)
带命名的Sequential输出形状： torch.Size([2, 10])

ModuleList输出形状： torch.Size([2, 30])
Sequential输出形状： torch.Size([2, 30])
"""

由代码可以看到。 Modulelist需要手动定义列表里面的传播顺序，而sequenttial就是直接按照定义的顺序来进行传播的。

三、模型的保存和加载

在 PyTorch 中，模型保存与加载是模型训练、部署及复用的核心操作，主要分为保存完整模型（结构 + 参数） 和仅保存模型参数两种方式。实际开发中优先选择 "仅保存参数"，因其占用空间更小、兼容性更强；即便保存完整模型，加载时仍需依赖模型类定义，因此 "仅保存参数" 是更主流、更实用的方案。

1.保存和加载整个模型（结构 + 参数）

这种方式会将模型的完整结构、所有可训练参数及相关配置一并保存，加载时可直接获取完整模型对象。

# 保存模型：将模型net保存到save_path指定的路径（格式通常为.pth/.pt）
torch.save(net, save_path)

# 加载模型：从save_path指定的路径加载模型，返回完整模型实例
net = torch.load(save_path)

2 保存和加载模型参数（推荐）

这种方式仅保存模型的可训练参数（通过 state_dict() 方法获取参数字典），不保存模型结构，加载时需先手动定义与原模型一致的结构，再导入参数。

# 保存模型：通过net.state_dict()获取模型参数字典，保存到save_path指定的路径
torch.save(net.state_dict(), save_path)

# 加载模型：先定义与原模型结构一致的模型，再加载参数
net2 = Net()  # 第一步：定义模型结构（必须与保存参数时的模型结构完全一致）
net2.load_state_dict(torch.load(save_path))  # 第二步：加载参数到模型中

7.总结记忆（ Ai生成，仅供参考）

一、核心关键词

PyTorch、张量、动态计算图、自动微分、nn.Module、ModuleList、Sequential、模型保存与加载、哈达玛积、矩阵乘法、广播机制、梯度计算

二、核心记忆点

1. 张量（PyTorch 核心数据结构）

• 本质：高维数组，支持 CPU/GPU 计算 + 自动微分，是深度学习计算的基础；
• 创建方式 ：3 类核心方式（已有数据转换、指定形状创建、固定值创建），注意torch.Tensor(shape)（类构造，随机值）与torch.tensor(data)（函数，需传数据）的区别；
• 关键特性 ：NumPy 互转共享内存（修改同步）；数据类型可通过dtype指定或type()转换，深度学习默认用float32；
• 核心操作 ：
  • 基础属性：shape（形状）、numel()（元素总数）、reshape()（重塑形状）；
  • 运算：按元素运算（加减乘除 /exp，形状需一致或满足广播）、广播机制（自动虚拟扩展张量匹配形状）；
  • 分割：索引切片（视图操作，修改同步原张量）、split()（支持均等 / 不均等分割）；
  • 代数运算：哈达玛积（按元素乘，x*y）≠矩阵乘法（torch.mm/torch.matmul，行 × 列规则）；范数（L1/L2 / 弗罗贝尼乌斯，衡量张量 "模长"）。

2. 自动微分（反向传播核心）

• 核心开关 ：张量requires_grad属性，开启后追踪计算图，支持梯度求解；
• 梯度管理 ：多次反向传播需用zero_grad()清零（避免梯度累加）；关闭梯度有 3 种方式（requires_grad_(False)、detach()、torch.no_grad()）；
• 核心逻辑 ：前向传播构建计算图，backward()自动计算梯度，无需手动推导公式。

3. 模型定义与管理

• 基础规则 ：自定义模型必须继承nn.Module，重写__init__（定义层）和forward（前向传播），反向传播自动生成；
• 层容器区别 ：
  • ModuleList：层的列表，需手动控制执行顺序，灵活度高；
  • Sequential：层的有序流水线，内置前向传播，按添加顺序执行，简洁高效；
• 模型保存加载 ：优先选择 "仅保存参数（state_dict()）"，占用空间小、兼容性强；加载时需先定义相同模型结构，再导入参数。

4. 框架核心优势

PyTorch 采用动态计算图，Python 原生风格，兼顾科研灵活性（易调试）与工业级性能（GPU 加速），是 CV、NLP、大模型训练等领域的主流框架。

三、易混点速记

1. 哈达玛积（x*y）：按元素乘，形状不变；矩阵乘法（torch.mm）：行 × 列，形状由行列数决定；
2. torch.Tensor（大写）：类构造，传形状；torch.tensor（小写）：函数，传数据；
3. ModuleList（手动控顺序）vs Sequential（自动按序执行）；
4. 张量与 NumPy 互转共享内存，修改一方同步影响另一方。