决策树
一种对实例进行分类 的树形结构,通过多层判断区分目标所属类别本质:通过多层判断,从训练数据集中归纳出一组分类规则。
优点:
➤ 计算量小,运算速度快
➤ 易于理解,可清晰查看各属性的重要性
缺点:
➤ 忽略属性间的相关性
➤ 样本类别分布不均匀时,容易影响模型表现


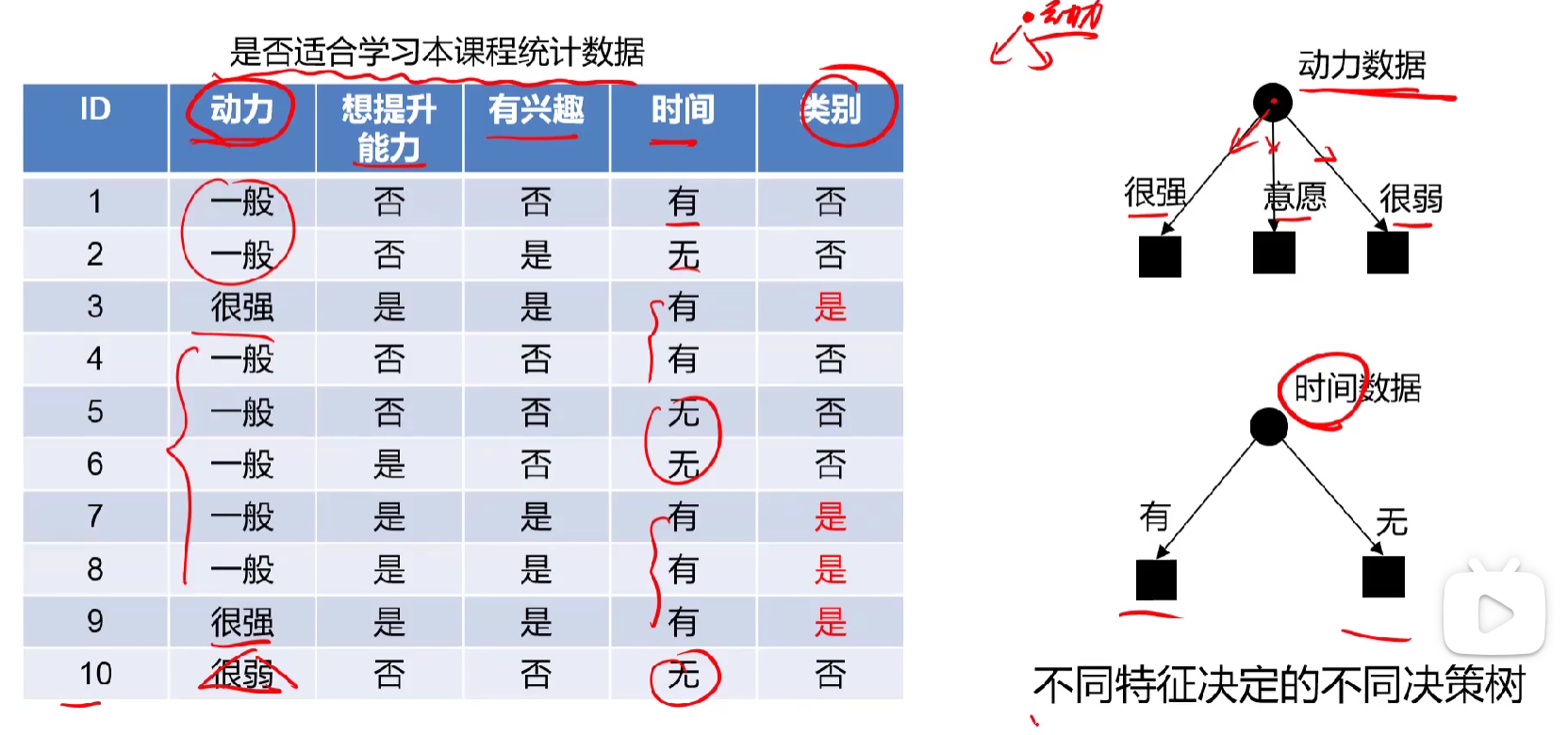
不同特征建立不同的决策树
决策树的构造
ID3利用信息熵原理选择信息增益最大的属性作为分类属性,递归地拓展决策树的分枝,完成决策树的构造
信息熵(entropy)是度量随机变量不确定性 的指标,熵越大,变量的不确定性就越大。


追问1:没太理解信息熵的,举个例子说明


追问2:知道了信息熵,那他对决策树有什么用处呢?




比如说以下是一个判读是否适合学习ai课程的决策树,我们要从哪个特征开始算起呢,这时候就要计算信息熵与信息增益
| ID | 动力 | 想提升能力 | 有兴趣 | 时间 | 类别 |
|---|---|---|---|---|---|
| 1 | 一般 | 否 | 否 | 有 | 否 |
| 2 | 一般 | 否 | 是 | 无 | 否 |
| 3 | 很强 | 是 | 是 | 有 | 是 |
| 4 | 一般 | 否 | 否 | 有 | 否 |
| 5 | 一般 | 否 | 否 | 无 | 否 |
| 6 | 一般 | 是 | 否 | 无 | 否 |
| 7 | 一般 | 是 | 是 | 有 | 是 |
| 8 | 一般 | 是 | 是 | 有 | 是 |
| 9 | 很强 | 是 | 是 | 有 | 是 |
| 10 | 很弱 | 是 | 否 | 无 | 否 |





按照以上步骤分别计算各类特征
| 特征 | 信息增益值 |
|---|---|
| 有兴趣 | 0.6100 |
| 想提升能力 | 0.4200 |
| 时间 | 0.4200 |
| 动力 | 0.3668 |
在本次计算中,"有兴趣" 的信息增益最大(0.6100),因此决策树会优先选择 "有兴趣" 作为根节点的分裂特征。