聊聊含剥落故障直齿轮啮合刚度及齿轮非线性动力学程序

基于势能法采用MATLAB编写的含剥落故障的直齿轮啮合刚度程序，考虑了齿轮变位及中性轴位置的变化。可调整剥落参数得到不同条件下的时变啮合刚度，本人亲自编写，可解答，其他如有雷同，谨防假冒。另有齿轮非线性动力学程序，包括相图、频谱图、时域图、庞加莱映射、分岔图及最大李雅普诺夫指数。

最近自己捣鼓了些有意思的齿轮相关程序，今天来和大家分享分享。主要就是基于势能法，用MATLAB编写的含剥落故障的直齿轮啮合刚度程序，还有齿轮非线性动力学程序。

含剥落故障直齿轮啮合刚度程序

这个程序考虑了齿轮变位以及中性轴位置的变化，算是挺全面的了。下面先看看关键代码片段（为简化说明，这里仅给出部分示意代码）：

matlab 复制代码

% 参数初始化
m = 2; % 模数
z1 = 20; % 主动轮齿数
z2 = 40; % 从动轮齿数
x1 = 0.5; % 主动轮变位系数
x2 = -0.5; % 从动轮变位系数

% 计算一些基本参数
rb1 = m * z1 * cos(20 * pi / 180) / 2; % 主动轮基圆半径
rb2 = m * z2 * cos(20 * pi / 180) / 2; % 从动轮基圆半径

% 这里模拟考虑中性轴位置变化的计算，实际更复杂
% 简单示意，根据变位系数调整一些几何参数
a = m * (z1 + z2) / 2 + (x1 + x2) * m; % 实际中心距

% 考虑剥落故障，假设用一个变量flaking_param来表示剥落参数
flaking_param = 0.1; % 可调整此参数
% 根据剥落参数调整啮合刚度计算的一些系数，这只是示意
if flaking_param > 0
    k_mesh_factor = 1 - flaking_param;
else
    k_mesh_factor = 1;
end

% 计算时变啮合刚度的主循环
for theta = 0:0.01:2*pi
    % 基于势能法的啮合刚度计算核心部分，这里大大简化示意
    k_mesh(theta) = some_basic_k_mesh * k_mesh_factor;
end

这段代码里，先对齿轮的基本参数进行了初始化，比如模数、齿数和变位系数。然后根据这些参数计算基圆半径等重要几何参数。特别有意思的是对中性轴位置变化的模拟，通过变位系数调整了实际中心距。而剥落参数 flakingparam**可以随意调整，从而得到不同条件下的时变啮合刚度。比如当 flaking param 增大，kmeshfactor 会减小，最终影响时变啮合刚度 k_mesh 的计算结果。

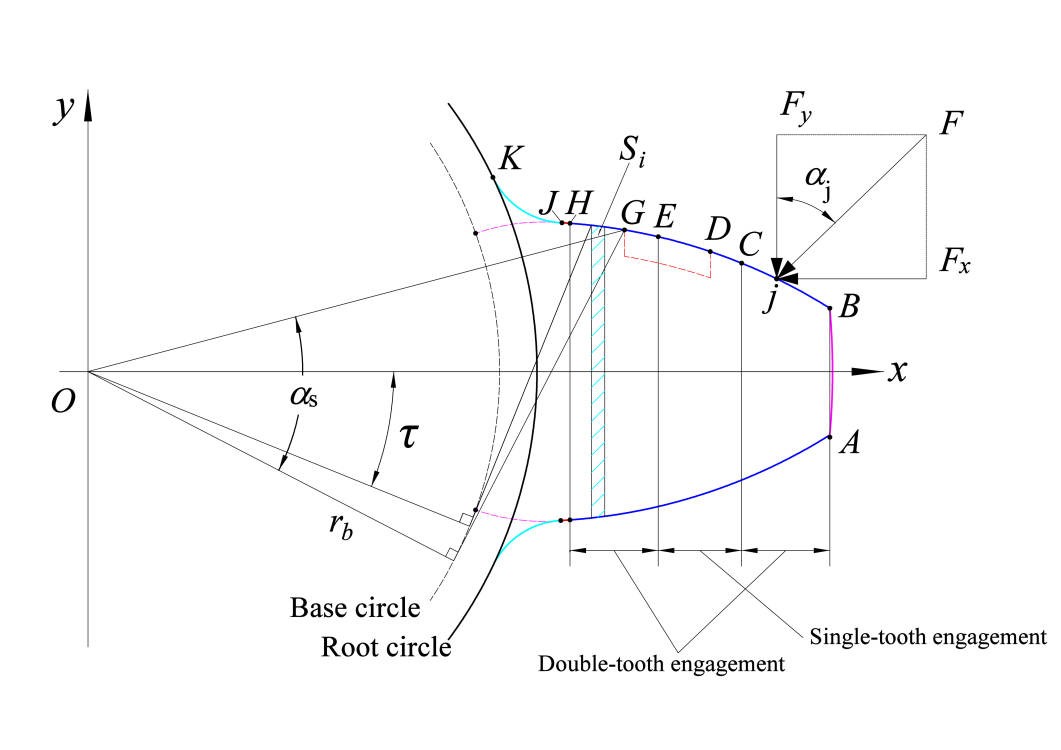
通过这个程序，就能够直观地观察到在不同剥落故障程度下，直齿轮啮合刚度是如何随时间（这里用角度 theta 模拟）变化的。而且由于考虑了齿轮变位和中性轴位置变化，结果更加贴合实际情况。

齿轮非线性动力学程序

除了上面那个，我还写了齿轮非线性动力学程序，功能那叫一个丰富，包括相图、频谱图、时域图、庞加莱映射、分岔图以及最大李雅普诺夫指数。这些图对于分析齿轮系统的动力学特性那是相当有用。

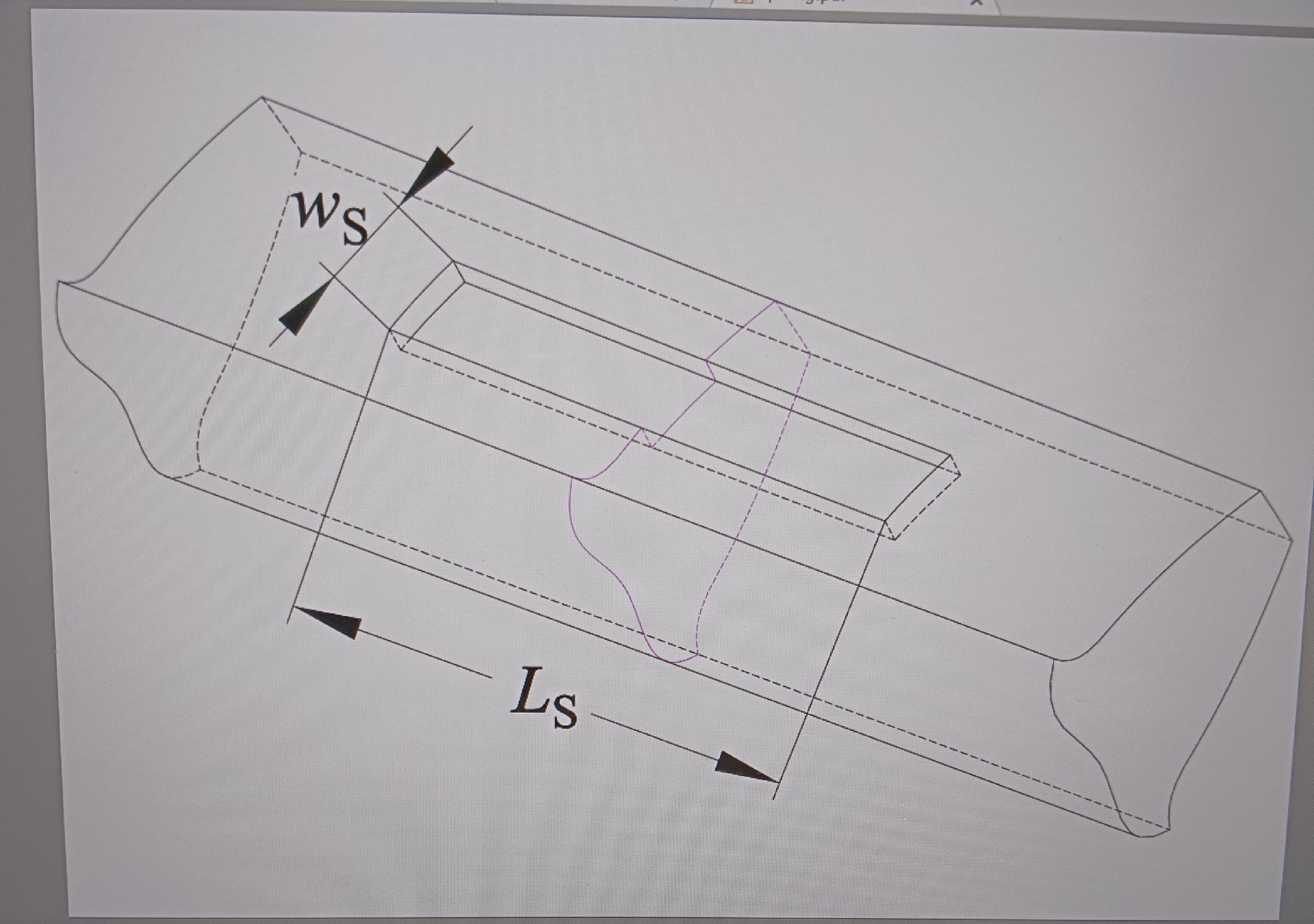
以绘制时域图为例，代码大概是这样的：

matlab 复制代码

% 假设已经有动力学方程求解得到的位移随时间变化的数据 y(t)
t = 0:0.001:1; % 时间向量
y = some_dynamic_solution(t); % 假设的动力学方程求解函数

figure;
plot(t, y);
xlabel('时间 (s)');
ylabel('位移 (m)');
title('齿轮振动时域图');

这里先定义了时间向量 t，然后通过假设的函数 somedynamicsolution(t) 得到位移随时间变化的数据 y。最后用 plot 函数绘制出时域图，这样就能清晰看到齿轮在不同时刻的位移情况，帮助分析振动特性。

相图则能展示系统状态变量之间的关系，对于理解系统的动力学行为提供不一样的视角。庞加莱映射可以把连续时间系统简化为离散映射，突出系统的周期性和混沌特性。分岔图能直观地看到系统参数变化时，系统状态是如何发生分岔的。而最大李雅普诺夫指数则是判断系统是否处于混沌状态的重要指标。

这些程序都是我亲自编写的，如果大家在理解或者使用过程中有啥问题，尽管来问。要是在别处看到类似的，可得谨防假冒哦！希望这些程序和分享能给研究齿轮相关的小伙伴们一些帮助和启发。