【改进蚁群算法】/蚁群算法/Dijkstra算法/遗传算法/人工势场法实现二维/三维空间路径规划 本程序为改进蚁群算法+Dijkstra算法+MAKLINK图理论实现的二维空间路径规划 算法实现: 1)基于MAKLINK图理论生成地图,并对可行点进行划分; 2)用Dijkstra算法实现次优路径的寻找; 3)在Dijkstra算法的基础上加入了蚁群算法,调整了搜索策略,使路径更短; 4)最终对基础的蚁群算法进行改进(对搜索节点的角度进行限制),调整了搜索策略,使路径更短 可调参数:算法迭代次数;起始点;目标点;障碍物位置;障碍物大小 仿真结果:地图上显示最优路径的对比 + 迭代曲线的对比 + 输出行进距离对比 这段程序主要是进行路径规划的算法实现,应用在二维规划空间中。程序的主要思路是使用Dijkstra算法来寻找最短路径。 首先,程序导入障碍物数据和链路端点数据,并在二维规划空间中绘制起点和终点的位置。然后,根据障碍物数据绘制障碍物图形,并绘制自由连接线和中点。 接下来,根据可行路径矩阵绘制所有可行路径。然后使用Dijkstra算法找出最优路径,并在图中标注出最优路径。 接下来,程序使用蚁群算法进行路径规划。首先进行蚁群算法参数的初始化,然后进行迭代搜索。在每次迭代中,蚂蚁根据信息素和启发值选择下一个节点,并更新信息素。最后,程序计算路径长度并更新最优路径。 最后,程序绘制出原始蚁群算法和改进蚁群算法的最短路径,并输出最短路径的长度。 整个程序的结构清晰,逻辑严谨,主要涉及到路径规划、Dijkstra算法和蚁群算法等知识点。通过这段程序的分析,可以了解路径规划算法的实现过程和应用场景。
一、整体架构与核心目标
本代码库围绕二维空间路径规划场景构建,整合了Dijkstra算法、原始蚁群算法及改进蚁群算法,结合MAKLINK图理论实现障碍物环境下的最优路径求解。核心目标是在包含多边形障碍物的200km×200km二维空间中,找到从固定起点S([20,180])到终点T([160,90])的无碰撞最短路径,并通过多算法对比验证路径规划的有效性与优化效果。
【改进蚁群算法】/蚁群算法/Dijkstra算法/遗传算法/人工势场法实现二维/三维空间路径规划 本程序为改进蚁群算法+Dijkstra算法+MAKLINK图理论实现的二维空间路径规划 算法实现: 1)基于MAKLINK图理论生成地图,并对可行点进行划分; 2)用Dijkstra算法实现次优路径的寻找; 3)在Dijkstra算法的基础上加入了蚁群算法,调整了搜索策略,使路径更短; 4)最终对基础的蚁群算法进行改进(对搜索节点的角度进行限制),调整了搜索策略,使路径更短 可调参数:算法迭代次数;起始点;目标点;障碍物位置;障碍物大小 仿真结果:地图上显示最优路径的对比 + 迭代曲线的对比 + 输出行进距离对比 这段程序主要是进行路径规划的算法实现,应用在二维规划空间中。程序的主要思路是使用Dijkstra算法来寻找最短路径。 首先,程序导入障碍物数据和链路端点数据,并在二维规划空间中绘制起点和终点的位置。然后,根据障碍物数据绘制障碍物图形,并绘制自由连接线和中点。 接下来,根据可行路径矩阵绘制所有可行路径。然后使用Dijkstra算法找出最优路径,并在图中标注出最优路径。 接下来,程序使用蚁群算法进行路径规划。首先进行蚁群算法参数的初始化,然后进行迭代搜索。在每次迭代中,蚂蚁根据信息素和启发值选择下一个节点,并更新信息素。最后,程序计算路径长度并更新最优路径。 最后,程序绘制出原始蚁群算法和改进蚁群算法的最短路径,并输出最短路径的长度。 整个程序的结构清晰,逻辑严谨,主要涉及到路径规划、Dijkstra算法和蚁群算法等知识点。通过这段程序的分析,可以了解路径规划算法的实现过程和应用场景。
代码整体采用模块化设计,分为数据加载层、地图构建层、算法计算层与结果可视化层四个核心层级,各模块间通过标准化数据接口(如节点坐标矩阵、可达性矩阵)实现数据交互,确保算法可替换性与扩展性。
二、核心模块功能解析
2.1 数据加载与预处理模块
该模块负责读取与解析路径规划所需的基础数据,为后续算法计算提供标准化输入,核心数据文件及处理逻辑如下:
- 障碍物顶点数据(barrier.txt) :存储4个多边形障碍物的顶点坐标,其中前4个顶点对应第一个障碍物、5-8个顶点对应第二个障碍物、9-12个顶点对应第三个障碍物、13-15个顶点对应第四个障碍物。代码通过
load函数读取数据后,利用fill函数在可视化图层中绘制黑色填充的障碍物图形,明确路径规划的禁忌区域。 - 自由连接线数据(lines.txt):记录MAKLINK图理论生成的20条自由连接线,每条线包含两个端点的编号(对应barrier.txt中的顶点索引)。代码通过循环遍历每条连接线,计算线段中点并存储至数组,同时在可视化图层中以黑色虚线绘制连接线,以星号标记中点并标注序号(v1-v20),形成路径规划的"可行通道"。
- 可达性矩阵数据(matrix.txt):定义22个节点(1个起点、20个连接线中点、1个终点)间的连通关系,矩阵元素为1表示对应两个节点间无碰撞可达,为0则表示不可达。该矩阵是Dijkstra算法与蚁群算法判断路径可行性的核心依据。
2.2 Dijkstra算法路径规划模块(DijkstraPlan.m)
该模块实现经典的Dijkstra算法,用于求解从起点到终点的最短路径,作为后续蚁群算法的初始路径参考,核心功能分为三步:
- 代价矩阵构建 :基于节点坐标(position)与可达性矩阵(sign),计算所有可达节点对的欧氏距离(\\sqrt{(x*i-x* j)\^2+(y*i-y* j)\^2}),不可达节点对的距离设为极大值(10000),形成代价矩阵
cost。 - 最短路径搜索 :初始化起点到各节点的距离数组
dist(起点距离设为0,其余设为极大值)与节点访问标记数组s(起点标记为已访问)。通过循环迭代,每次选择当前未访问节点中距离起点最近的节点,更新该节点的可达节点的距离(若经当前节点的路径更短,则更新距离与前驱节点),直至所有节点处理完成。 - 路径回溯 :通过前驱节点数组
path,从终点反向回溯至起点,生成完整的节点访问序列,为后续蚁群算法提供初始路径框架。
2.3 蚁群算法路径优化模块
该模块包含原始蚁群算法与改进蚁群算法两个版本,均以Dijkstra算法生成的路径为基础,通过模拟蚂蚁觅食的信息素机制进一步优化路径,核心功能与差异如下:
2.3.1 通用核心逻辑
- 参数初始化:设定种群规模(10只蚂蚁)、迭代次数(200次)、信息素计算参数(pheCacuPara=2)、信息素更新参数(pheUpPara=[0.1, 0.0003],分别为信息素挥发系数与初始信息素浓度)、信息素选择阈值(pheThres=0.8)等关键参数,构建启发值矩阵(qfz)与信息素矩阵(phePara/t)。
- 路径搜索机制:蚂蚁在每条连接线上的路径选择采用"阈值+轮盘赌"混合策略:若随机数q≤阈值,选择信息素与启发值乘积最大的节点;若q>阈值,通过轮盘赌算法(基于信息素与启发值的概率分布)选择节点,平衡搜索的贪婪性与随机性。
- 信息素更新:每次迭代后,对找到最短路径的蚂蚁经过的节点进行信息素更新,公式为"当前信息素×(1-挥发系数)+挥发系数×(1/最短路径长度)",强化优质路径的信息素浓度,引导后续蚂蚁向更优路径搜索。
- 路径长度计算:通过循环累加每段路径的欧氏距离,计算每只蚂蚁的路径总长度,记录迭代过程中的最短路径长度(shortestpath)与最优路径坐标(best_path)。
2.3.2 改进蚁群算法优化点
改进蚁群算法在原始版本基础上,通过以下设计提升路径优化效果与搜索效率:
- 动态等分机制:根据每条连接线的实际长度,计算动态等分数量(向上取整),而非原始算法固定的10等分,使短连接线的节点划分更精细、长连接线的节点划分更合理,减少无效搜索。
- 角度启发信息引入:在节点选择过程中,计算当前节点到候选节点的向量与当前节点到终点的向量之间的夹角,将"1/夹角"作为额外启发信息融入信息素计算,引导蚂蚁向更接近终点的方向搜索,降低路径迂回程度。
- 函数模块化 :将轮盘赌选择中的概率累加(sufffun.m)与节点选择(sel.m)功能封装为独立函数,提升代码复用性与可维护性。其中,sufffun.m通过计算累积概率分布实现概率标准化,sel.m通过随机数与累积概率的对比确定选中节点。
2.4 结果可视化与对比模块
该模块通过Matlab的图形绘制功能,直观展示路径规划结果与算法性能对比,核心可视化内容包括:
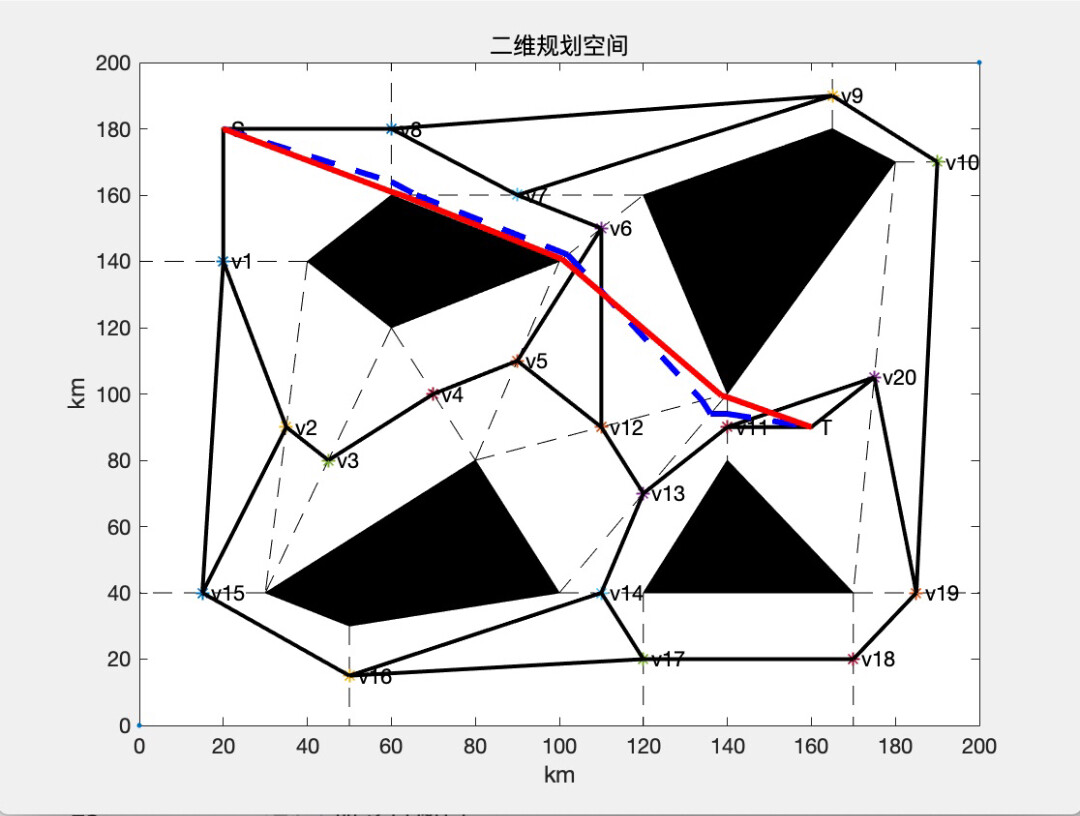
- 地图与可行路径展示:在figure(1)中绘制200km×200km的二维空间、黑色填充的障碍物、黑色虚线的自由连接线、星号标记的中点,以及黑色实线的所有可行路径,同时标注起点S与终点T。
- 算法路径对比:在同一图层中,以黄色虚线绘制Dijkstra算法路径、蓝色虚线绘制原始蚁群算法路径、红色实线绘制改进蚁群算法路径,通过颜色与线型差异直观区分不同算法的路径结果。
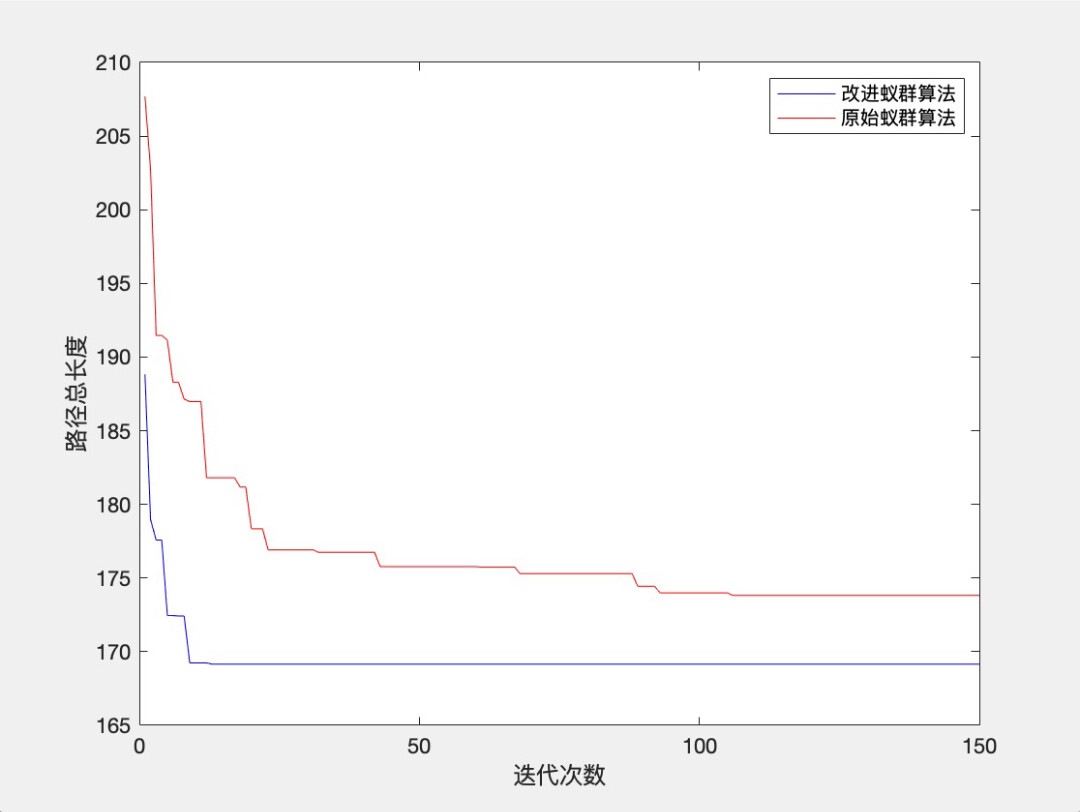
- 迭代性能对比:在figure(2)中绘制迭代次数(1-200)与路径长度的关系曲线,其中蓝色曲线对应改进蚁群算法、红色曲线对应原始蚁群算法,通过曲线的下降趋势与最终收敛值,量化对比两种算法的收敛速度与优化效果。
- 关键数据输出 :通过
disp函数在命令行输出原始蚁群算法与改进蚁群算法的最短路径长度,为算法性能评估提供定量依据。
三、算法工作流程
- 环境初始化 :执行
clc;clear清空工作空间,加载barrier.txt、lines.txt、matrix.txt数据,构建包含障碍物与可行通道的二维地图。 - 初始路径生成:调用DijkstraPlan.m函数,基于可达性矩阵与节点坐标生成起点到终点的初始最短路径,确定路径经过的连接线序列。
- 蚁群算法优化 :
- 原始蚁群算法:基于固定10等分的连接线节点,通过信息素与启发值引导蚂蚁搜索,迭代200次后输出最优路径。
- 改进蚁群算法:基于动态等分的连接线节点,融入角度启发信息,通过模块化函数实现节点选择,迭代200次后输出最优路径。
- 结果展示与对比:绘制地图、可行路径与各算法路径,生成迭代性能曲线,输出最短路径长度,完成算法效果的定性与定量对比。
四、核心应用场景与性能优势
4.1 应用场景
本代码适用于静态障碍物环境下的二维路径规划场景,如无人机低空飞行路径规划、机器人室内导航、无人车园区路径规划等,尤其适合对路径长度与无碰撞性有严格要求的场景。
4.2 性能优势
- 路径可行性保障:基于MAKLINK图理论生成的自由连接线与可达性矩阵,确保所有规划路径均避开障碍物,无碰撞风险。
- 算法互补性强:Dijkstra算法提供稳定的初始路径,避免蚁群算法陷入局部最优;改进蚁群算法通过动态等分与角度启发,在初始路径基础上进一步缩短路径长度,兼顾稳定性与优化效果。
- 可视化程度高:通过多图层、多颜色的图形展示,直观呈现地图环境、可行路径与算法结果,便于算法调试与效果评估。
五、使用注意事项
- 数据文件依赖:代码运行前需确保barrier.txt、lines.txt、matrix.txt三个数据文件与代码文件在同一目录下,且数据格式无误(如matrix.txt需为22×22的矩阵)。
- 参数调整建议:若实际应用场景中障碍物密度、空间范围发生变化,需调整蚁群算法的参数(如种群规模m、迭代次数NC、信息素挥发系数pheUpPara(1)),以适应新场景的路径搜索需求。
- 功能扩展方向:可通过增加障碍物动态变化逻辑(如实时更新barrier.txt数据),扩展为动态环境下的路径规划;通过引入三维节点坐标与高度约束,扩展为三维空间路径规划。