本文参考Kian Sen Ang and I. D. Robertson, "Analysis and design of impedance-transforming planar Marchand baluns, " in IEEE Transactions on Microwave Theory and Techniques, vol. 49, no. 2, pp. 402-406, Feb. 2001, doi: 10.1109/22.903108.
keywords: {Impedance matching;Couplers;Coupling circuits;Diodes;Microstrip;Frequency;Microwave integrated circuits;MMICs;Monolithic integrated circuits;Wideband},同时参考 洁仔爱吃冰淇淋的博客
仅供学习使用
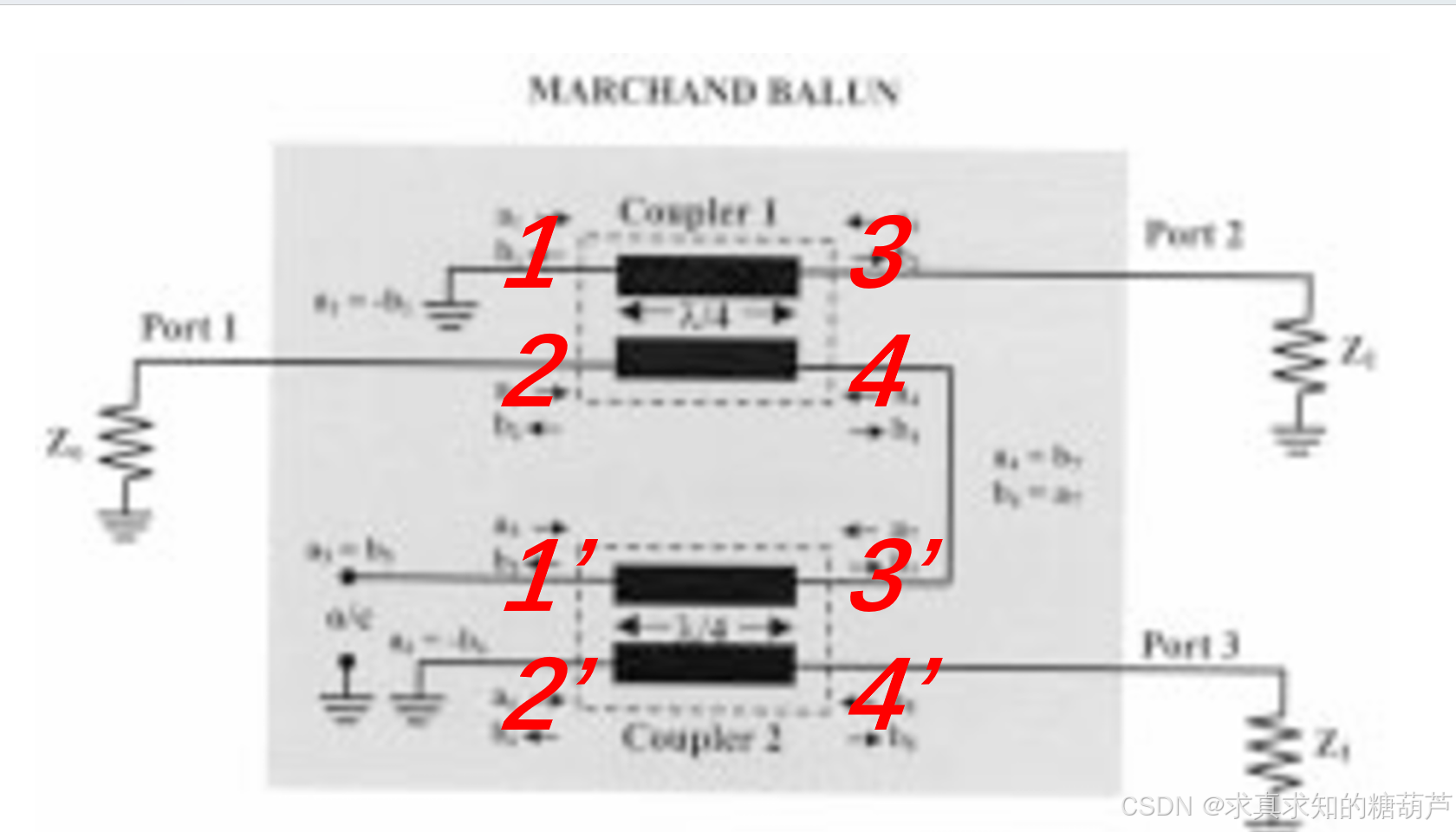
图 1. 作为两个相同耦合器的对称Marchand巴伦框图。
巴伦的框图如图1所示。它为一个源阻抗为 Z o Z_o Zo的非平衡输入提供平衡输出,连接到负载阻抗 Z 1 Z_1 Z1。通常,阻抗 Z 1 Z_1 Z1和 Z o Z_o Zo是不同的。例如,在平衡二极管混频器应用中,平衡信号需要馈入一对二极管,其阻抗可能与50Ω源阻抗不同。因此,除了提供平衡输出外,巴伦还需要在源阻抗和负载阻抗之间执行阻抗变换。
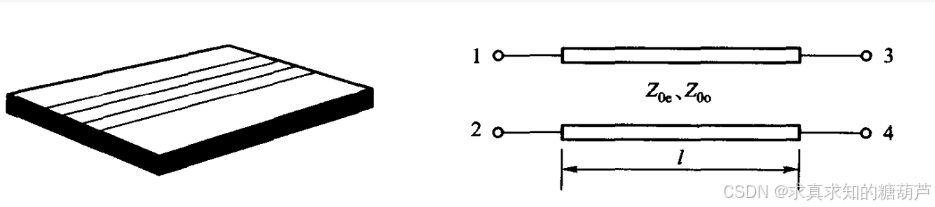
图1.1:端口顺序定义,1输入,2耦合,3直通(这里2和3与常见定向耦合器不同,想按常见定向耦合器定义将结果交换2与3顺序即可),4隔离
如图1所示,平面Marchand巴伦由两个耦合段组成,每个段在工作中心频率处为四分之一波长。对于对称巴伦,巴伦的散射矩阵可以从两个相同耦合器的散射矩阵推导出来。我们首先考虑源阻抗和负载阻抗都等于 Z o Z_o Zo的情况。根据图1中定义的电压波,具有无限方向性和耦合系数 C C C的理想耦合器(端口顺序如图1.1所示)的散射矩阵由下式给出:
S \] c o u p l e r = \[ 0 C − j 1 − C 2 0 C 0 0 − j 1 − C 2 − j 1 − C 2 0 0 C 0 − j 1 − C 2 C 0 \] . ( 1 ) \\begin{align\*}\[S\]_{coupler}=\&\\begin{bmatrix}0\&C\&-j\\sqrt{1-C\^{2}}\&0\\\\ C\&0\&0\&-j\\sqrt{1-C\^{2}}\\\\-j\\sqrt{1-C\^{2}}\&0\&0\&C\\\\ 0\&-j\\sqrt{1-C\^{2}}\&C\&0\\end{bmatrix}.\\end{align\*}\\qquad(1) \[S\]coupler= 0C−j1−C2 0C00−j1−C2 −j1−C2 00C0−j1−C2 C0 .(1) 然后,利用图1中指示的电压波关系(其形式如下)可以获得巴伦的S参数: ### 对于图1中第一段耦合线 由耦合器的散射参数关系,可定义归一化电压波: { b 1 = C a 2 − j 1 − C 2 a 3 b 2 = C a 1 − j 1 − C 2 a 4 b 3 = − j 1 − C 2 a 1 + C a 4 b 4 = − j 1 − C 2 a 2 + C a 3 \\left\\{ \\begin{array}{l} b_{1} = C a_{2} -j\\sqrt{1-C\^{2}}a_{3} \\\\ b_{2} = Ca_{1} -j\\sqrt{1-C\^{2}}a_{4} \\\\ b_{3} = - j\\sqrt{1-C\^{2}}a_{1}+ Ca_{4} \\\\ b_{4} =- j\\sqrt{1-C\^{2}} a_{2} + Ca_{3} \\end{array} \\right. ⎩ ⎨ ⎧b1=Ca2−j1−C2 a3b2=Ca1−j1−C2 a4b3=−j1−C2 a1+Ca4b4=−j1−C2 a2+Ca3 其中 b i b_i bi为反射波 a i a_i ai为入射波 为简化表达式,令: A = C , β = − j 1 − C 2 A =C, \\quad \\beta = -j\\sqrt{1-C\^{2}} A=C,β=−j1−C2 则上式可写为: { b 1 = A a 2 + β a 3 b 2 = A a 1 + β a 4 b 3 = β a 1 + A a 4 b 4 = β a 2 + A a 3 \\left\\{ \\begin{array}{l} b_{1} =A a_{2} + \\beta a_{3} \\\\ b_{2} = A a_{1} + \\beta a_{4} \\\\ b_{3} = \\beta a_{1} + A a_{4} \\\\ b_{4} = \\beta a_{2} +A a_{3} \\end{array} \\right. ⎩ ⎨ ⎧b1=Aa2+βa3b2=Aa1+βa4b3=βa1+Aa4b4=βa2+Aa3 考虑巴伦的连接条件(端口1短路, Γ = Z L − Z 0 Z L + Z 0 = − 1 \\Gamma=\\dfrac{Z_L-Z_0}{Z_L+Z_0}=-1 Γ=ZL+Z0ZL−Z0=−1, b 1 = Γ a 1 b_1=\\Gamma a_1 b1=Γa1): { b 1 = A a 2 + β a 3 = − a 1 b 2 = A a 1 + β a 4 b 3 = β a 1 + A a 4 b 4 = β a 2 + A a 3 \\left\\{ \\begin{array}{l} b_{1} =A a_{2} + \\beta a_{3}=-a_1 \\\\ b_{2} = A a_{1} + \\beta a_{4} \\\\ b_{3} = \\beta a_{1} +A a_{4} \\\\ b_{4} = \\beta a_{2} +A a_{3} \\end{array} \\right. ⎩ ⎨ ⎧b1=Aa2+βa3=−a1b2=Aa1+βa4b3=βa1+Aa4b4=βa2+Aa3 消去 a 1 a_1 a1 { b 2 = − A 2 a 2 − A β a 3 + β a 4 b 3 = − A β a 2 − β 2 a 3 + A a 4 b 4 = β a 2 + A a 3 ( 1.1 ) \\left\\{ \\begin{array}{l} b_{2} = -A\^2 a_{2}-A\\beta a_3 + \\beta a_{4} \\\\ b_{3} =-A\\beta a_{2} -\\beta\^2 a_{3}+Aa_4 \\\\ b_{4} = \\beta a_{2} +A a_{3} \\end{array} \\right.\\quad (1.1) ⎩ ⎨ ⎧b2=−A2a2−Aβa3+βa4b3=−Aβa2−β2a3+Aa4b4=βa2+Aa3(1.1) ### 图1中第二段耦合线 由耦合线方程,带入边界条件,端口 1 ′ 1\^{\\prime} 1′开路,端口 2 ′ 2\^{\\prime} 2′短路: { b 1 ′ = A a 2 ′ + β a 3 ′ = a 1 ′ b 2 ′ = A a 1 ′ + β a 4 ′ = − a 2 ′ b 3 ′ = β a 1 ′ + A a 4 ′ b 4 ′ = β a 2 ′ + A a 3 ′ \\left\\{ \\begin{array}{l} b_{1}\^{\\prime} =A a_{2}\^{\\prime} + \\beta a_{3}\^{\\prime}=a_{1}\^{\\prime}\\\\ b_{2}\^{\\prime} = A a_{1}\^{\\prime} + \\beta a_{4}\^{\\prime}=-a_{2}\^{\\prime} \\\\ b_{3}\^{\\prime} = \\beta a_{1}\^{\\prime} + A a_{4}\^{\\prime} \\\\ b_{4}\^{\\prime} = \\beta a_{2}\^{\\prime} +A a_{3}\^{\\prime} \\end{array} \\right. ⎩ ⎨ ⎧b1′=Aa2′+βa3′=a1′b2′=Aa1′+βa4′=−a2′b3′=βa1′+Aa4′b4′=βa2′+Aa3′ 可解得 a 1 ′ a_1\^{\\prime} a1′ 和 a 2 ′ a_2\^{\\prime} a2′关于 a 3 ′ a_3\^{\\prime} a3′ a 4 ′ a_4\^{\\prime} a4′的表达式 将解代回 b 3 ′ b_3\^{\\prime} b3′ 和 b 4 ′ b_4\^{\\prime} b4′ 的表达式: { b 3 ′ = β a 1 ′ + A a 4 ′ = ( β 2 − β 2 A 2 1 + A 2 ) a 3 ′ + ( A − A β 2 1 + A 2 ) a 4 ′ b 4 ′ = β a 2 ′ + A a 3 ′ = ( A − A β 2 1 + A 2 ) a 3 ′ + ( − β 2 1 + A 2 ) ( 1.2 ) \\left\\{ \\begin{aligned} b_{3}\^{\\prime} = \\beta a_{1}\^{\\prime} + A a_{4}\^{\\prime}=(\\beta\^2-\\dfrac{\\beta\^2A\^2}{1+A\^2})a_3\^{\\prime}+(A-\\dfrac{A\\beta\^2}{1+A\^2})a_4\^{\\prime} \\\\b_{4}\^{\\prime} = \\beta a_{2}\^{\\prime} +A a_{3}\^{\\prime}=(A-\\dfrac{A\\beta\^2}{1+A\^2})a_3\^{\\prime}+(-\\dfrac{\\beta\^2}{1+A\^2}) \\end{aligned} \\right.\\quad (1.2) ⎩ ⎨ ⎧b3′=βa1′+Aa4′=(β2−1+A2β2A2)a3′+(A−1+A2Aβ2)a4′b4′=βa2′+Aa3′=(A−1+A2Aβ2)a3′+(−1+A2β2)(1.2) **结合两者链接关系(第一段线四端口与第二段线三端口连在一起)我们有** { b 4 = a 3 ′ b 3 ′ = a 4 ( 1.3 ) \\left\\{ \\begin{array}{l} b_{4} = a_{3}\^{\\prime}\\\\ b_{3}\^{\\prime} = a_4 \\end{array} \\right.\\quad (1.3) {b4=a3′b3′=a4(1.3) 将 a 4 a_4 a4、 b 4 b_4 b4、 a 3 ′ a_3\^{\\prime} a3′、 b 3 ′ b_3\^{\\prime} b3′ 全部消去后,得到仅关于 a 2 a_2 a2、 a 3 a_3 a3、 a 4 ′ a_4\^{\\prime} a4′ 及对应 b b b 的方程组: { b 2 = ( β 4 − A 2 β 2 1 + A 2 − A 2 ) a 2 + ( A β 3 − A 3 β 3 1 + A 2 − A β ) a 3 + ( A β − A β 3 1 + A 2 ) a 4 ′ b 3 = ( A β 3 − A 3 β 3 1 + A 2 − A β ) a 2 + ( A 2 β 2 − A 4 β 2 1 + A 2 − β 2 ) a 3 + ( A 2 − A 2 β 2 1 + A 2 ) a 4 ′ b 4 ′ = ( A β − A β 3 1 + A 2 ) a 2 + ( A 2 − A 2 β 2 1 + A 2 ) a 3 − ( β 2 1 + A 2 ) a 4 ′ ( 1.4 ) \\left\\{ \\begin{array}{l} \\begin{aligned} b_{2} \&=(\\beta\^4-\\dfrac{A\^2\\beta\^2}{1+A\^2}-A\^2)a_2+(A\\beta\^3-\\dfrac{A\^3\\beta\^3}{1+A\^2}-A\\beta)a_3+(A\\beta-\\dfrac{A\\beta\^3}{1+A\^2})a_4\^\\prime \\end{aligned} \\\\\[15pt\] \\begin{aligned} b_{3} \&= \\left( {A\\beta\^{3}} -\\dfrac{A\^3\\beta\^3}{1+A\^2}- A \\beta \\right) a_{2} + \\left(A\^2\\beta\^{2}- \\frac{A\^{4} \\beta\^{2}}{1+A\^{2}} -\\beta\^{2} \\right) a_{3} + (A\^2-\\frac{A\^2\\beta\^2}{1+A\^2})a_{4}\^{\\prime} \\end{aligned} \\\\\[15pt\] \\begin{aligned} b_{4}\^{\\prime} \&=(A\\beta-\\frac{A\\beta\^3}{1+A\^2})a_{2} +(A\^2-\\frac{A\^2\\beta\^2}{1+A\^2})a_{3} - \\left( \\frac{\\beta\^{2}}{1+A\^{2}} \\right) a_{4}\^{\\prime} \\end{aligned} \\end{array} \\right.\\quad(1.4) ⎩ ⎨ ⎧b2=(β4−1+A2A2β2−A2)a2+(Aβ3−1+A2A3β3−Aβ)a3+(Aβ−1+A2Aβ3)a4′b3=(Aβ3−1+A2A3β3−Aβ)a2+(A2β2−1+A2A4β2−β2)a3+(A2−1+A2A2β2)a4′b4′=(Aβ−1+A2Aβ3)a2+(A2−1+A2A2β2)a3−(1+A2β2)a4′(1.4) A = C , β = − j 1 − C 2 A =C, \\quad \\beta = -j\\sqrt{1-C\^{2}} A=C,β=−j1−C2 将我们一开始的条件带入即可得到下式: \[ S \] balun = \[ 1 − 3 C 2 1 + C 2 j 2 C 1 − C 2 1 + C 2 − j 2 C 1 − C 2 1 + C 2 j 2 C 1 − C 2 1 + C 2 1 − C 2 1 + C 2 2 C 2 1 + C 2 − j 2 C 1 − C 2 1 + C 2 2 C 2 1 + C 2 1 − C 2 1 + C 2 \] . ( 2 ) \[S\]_{\\text{balun}} = \\begin{bmatrix} \\frac{1 - 3C\^2}{1 + C\^2} \& j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \& -j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \\\\ j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \& \\frac{1 - C\^2}{1 + C\^2} \& \\frac{2C\^2}{1 + C\^2} \\\\ -j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \& \\frac{2C\^2}{1 + C\^2} \& \\frac{1 - C\^2}{1 + C\^2} \\end{bmatrix} . \\qquad(2) \[S\]balun= 1+C21−3C2j1+C22C1−C2 −j1+C22C1−C2 j1+C22C1−C2 1+C21−C21+C22C2−j1+C22C1−C2 1+C22C21+C21−C2 .(2)