树形 DP 及树相关杂谈

STY_fish_20122026-02-11 10:09

以下所有以在树上进行为前提。

普通树形 DP

树形 DP 在树上进行， d p x dp_x dpx 表示树上以 x x x 为根的子树的最优状态。

以点为对象的树形 DP

最大独立集

题目：P1352 没有上司的舞会

题意简述

一棵树，每个点有一个价值，不能选择相邻的点，最终能获得的最大价值。

思路

对于每一个人，只有两种情况：去或不去。

那么考虑直接暴搜。 所以 DP 对于每个点的状态只有 0/1。

若 x x x 要去，那么他的所有直接下属都不能去，则有：
d p [ x ] [ 1 ] = ∑ y ∈ c h i l d r e n ( x ) d p [ y ] [ 0 ] dp[x][1]=\sum_{y\in children(x)}dp[y][0] dp[x][1]=y∈children(x)∑dp[y][0]

若 x x x 不去，那么他的下属随便去不去。
d p [ x ] [ 0 ] = ∑ y ∈ c h i l d r e n ( x ) max ⁡ ( d p [ y ] [ 0 ] , d p [ y ] [ 1 ] ) dp[x][0]=\sum_{y\in children(x)}\max(dp[y][0],dp[y][1]) dp[x][0]=y∈children(x)∑max(dp[y][0],dp[y][1])

code

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=6e3+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
int n;
int r[N];
int dp[N][2];
vector<int>a[N];
void dfs(int fa,int x){
	dp[x][1]=r[x];
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		dp[x][1]+=dp[y][0];
		dp[x][0]+=max(dp[y][0],dp[y][1]);
	}
}
signed main(){
	n=read();
	for(int i=1;i<=n;i++)r[i]=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	dfs(1,1);
	print(max(dp[1][1],dp[1][0]));
}

最小支配集

覆盖所有的最小需求量。

题目：P2458 保安站岗

题意简述

一棵树，选择一个点之后可以覆盖其自身和所有与其相邻的点，求使所有点被覆盖最小要选点的数量。

思路

现在一个点有 3 种状态：自己覆盖自己，被父亲覆盖，被儿子覆盖。

d p [ x ] [ 0 ] dp[x][0] dp[x][0]：被儿子盖。
d p [ x ] [ 1 ] dp[x][1] dp[x][1]：被自己盖。
d p [ x ] [ 2 ] dp[x][2] dp[x][2]：被父亲盖。

被自己盖很好想，儿子怎么盖都不影响：
d p [ x ] [ 0 ] = ∑ y ∈ c h i l d r e n ( x ) max ⁡ { d p [ y ] [ 0 ] , d p [ y ] [ 1 ] , d p [ y ] [ 2 ] } dp[x][0]=\sum_{y\in children(x)}\max\{dp[y][0],dp[y][1],dp[y][2]\} dp[x][0]=y∈children(x)∑max{dp[y][0],dp[y][1],dp[y][2]}

被父亲盖也不难想，只是儿子不可能被父亲盖了：
d p [ x ] [ 0 ] = ∑ y ∈ c h i l d r e n ( x ) max ⁡ ( d p [ y ] [ 0 ] , d p [ y ] [ 1 ] ) dp[x][0]=\sum_{y\in children(x)}\max(dp[y][0],dp[y][1]) dp[x][0]=y∈children(x)∑max(dp[y][0],dp[y][1])

至于被儿子盖，只需要有一个儿子被选择就行了，当然是选转换代价更小的。
d p [ x ] [ 1 ] = min ⁡ y ∈ c h i l d r e n ( x ) { d p [ x ] [ 2 ] − min ⁡ ( d p [ y ] [ 0 ] , d p [ y ] [ 1 ] ) + d p [ y ] [ 1 ] } dp[x][1]=\min_{y\in children(x)}\{dp[x][2]-\min(dp[y][0],dp[y][1])+dp[y][1]\} dp[x][1]=y∈children(x)min{dp[x][2]−min(dp[y][0],dp[y][1])+dp[y][1]}

由于 d p [ x ] [ 2 ] dp[x][2] dp[x][2] 值恒不变，可以转化成第一种形式。有：
d p [ x ] [ 1 ] = d p [ x ] [ 2 ] + min ⁡ y ∈ c h i l d r e n ( x ) { − min ⁡ ( d p [ y ] [ 0 ] , d p [ y ] [ 1 ] ) + d p [ y ] [ 1 ] } dp[x][1]=dp[x][2]+\min_{y\in children(x)}\{-\min(dp[y][0],dp[y][1])+dp[y][1]\} dp[x][1]=dp[x][2]+y∈children(x)min{−min(dp[y][0],dp[y][1])+dp[y][1]}

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
#define psp putchar(' ')
#define endl putchar('\n')
using namespace std;
typedef long long ll;
const int N=1e4+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
int n,m,k;
int T;
int dp[N][3];
int r[N];
vector<int>a[N];
//0 waer,1 guoren,2 laoher
void dfs(int fa,int x){
	dp[x][1]=r[x];
	int mn=1e9;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		dp[x][1]+=min({dp[y][0],dp[y][1],dp[y][2]});
		dp[x][2]+=min({dp[y][0],dp[y][1]});
		mn=min(mn,dp[y][1]-min(dp[y][1],dp[y][0]));
	}
	dp[x][0]=dp[x][2]+mn;
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<=n;i++){
		int u=read();
		r[u]=read();
		m=read();
		while(m--){
			int v=read();
			a[u].push_back(v);
			a[v].push_back(u);
		}
	}
	dfs(1,1);
	print(min(dp[1][0],dp[1][1]));
}

变式

题目：P2279 消防局的设立

题意简述

一棵树，选择一个点之后可以覆盖与其距离不超过 2 的点，求使所有点被覆盖最小要选点的数量。

思路

将所有可以覆盖的点拉通了，发现共有 5 层，状态的定义按照每一层。

首先，DP 是在由儿子回溯的过程中进行转移的，所以深度更大的节点被覆盖的优先级更高。

设点 x x x 深度为 d d d， d p [ x ] [ j ] ( 0 ≤ j ≤ 4 ) dp[x][j](0\le j\le 4) dp[x][j](0≤j≤4) 表示深度 d − 2 ∼ d + 2 − j d-2\sim d+2-j d−2∼d+2−j 的点全部被覆盖时的情况。

对于 j = 0 j=0 j=0，此时必定选择了点 x x x，所以情况很好判断：
d p [ x ] [ 0 ] = ∑ y ∈ c h i l d r e n ( x ) min ⁡ ( d p [ y ] [ 0 ... 4 ] ) + 1 dp[x][0]=\sum_{y\in children(x)}\min(dp[y][0\ldots4])+1 dp[x][0]=y∈children(x)∑min(dp[y][0...4])+1

对于 j = 3 j=3 j=3，要求点 x x x 的所有儿子都被覆盖，有：
d p [ x ] [ 3 ] = ∑ y ∈ c h i l d r e n min ⁡ ( d p [ y ] [ 0 ... 2 ] ) dp[x][3]=\sum_{y\in children}\min(dp[y][0\ldots2]) dp[x][3]=y∈children∑min(dp[y][0...2])

对于 j = 4 j=4 j=4，只要求孙子被覆盖，有：
d p [ x ] [ 4 ] = ∑ y ∈ c h i l d r e n ( x ) min ⁡ ( d p [ y ] [ 0 ... 3 ] ) dp[x][4]=\sum_{y\in children(x)}\min(dp[y][0\ldots3]) dp[x][4]=y∈children(x)∑min(dp[y][0...3])

接下来看到 j = 1 j=1 j=1，此时要求儿子中至少一个被选择，按照保安站岗的方法即可。

对于 j = 2 j=2 j=2，此时要保证孙子至少有一个被选择，也就是说，儿子的儿子至少有一个要选择，也就是多一个 d p [ y ] [ 1 ] dp[y][1] dp[y][1]。
code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e3+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
int dep[N];
struct node{
	int x,dep;
	friend bool operator<(node a,node b){
		return a.dep<b.dep;
	}
};
priority_queue<node>q;
int f[N];
void dfs(int fa,int x){
	dep[x]=dep[fa]+1;
	f[x]=fa;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
	}
}
int vis[N];
int ans;
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=2;i<=n;i++){
		int v=read();
		a[i].push_back(v);
		a[v].push_back(i);
	}
	dfs(1,1);
	for(int i=1;i<=n;i++)q.push(node{i,dep[i]});
	while(!q.empty()){
		int x=q.top().x;
		q.pop();
		if(vis[x])continue;
		x=f[f[x]];
		ans++;
		vis[x]=1;
		for(int i=0;i<a[x].size();i++){
			int y=a[x][i];
			vis[y]=1;
			for(int j=0;j<a[y].size();j++){
				int z=a[y][j];
				vis[z]=1;
			}
		}
	}
	print(ans);
}

以边为对象的树形 DP

最小点覆盖

题目：P2016 战略游戏

题意简述

一棵树，选择一个点可以覆盖所有它连接的边，求覆盖所有边的最小选点数。

思路

选择的对象是点，对于点的方案是两种：选/不选。

对于一条边两端的点 x x x 和 y y y，两者至少选一个，可以同时选。

那么有：
d p [ x ] [ 0 ] = ∑ y ∈ c h i l d r e n ( x ) d p [ y ] [ 1 ] d p [ x ] [ 1 ] = ∑ y ∈ c h i l d r e n ( x ) min ⁡ ( d p [ y ] [ 0 ] , d p [ y ] [ 1 ] ) + 1 dp[x][0]=\sum_{y\in children(x)}dp[y][1]\\ dp[x][1]=\sum_{y\in children(x)}\min(dp[y][0],dp[y][1])+1 dp[x][0]=y∈children(x)∑dp[y][1]dp[x][1]=y∈children(x)∑min(dp[y][0],dp[y][1])+1

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define int long long
//#define lc p<<1
//#define rc p<<1|1
//#define lowbit(x) x&-x
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
const int N=1e6+5;
const int M=1e3+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int n,m,k;
int T;
vector<int>a[N];
int dp[N][2];
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		dp[x][0]+=dp[y][1];
		dp[x][1]+=min(dp[y][1],dp[y][0]);
	}
}
int rt;
int f[N];
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<=n;i++)dp[i][1]=1;
	for(int i=1;i<=n;i++){
		int id=read()+1;
		int num=read();
		while(num--){
			int to=read()+1;
			a[id].push_back(to);
			f[to]=1;
		}
	}
	for(int i=1;i<=n;i++)if(!f[i])rt=i;
	dfs(-1,rt);
	print(min(dp[rt][1],dp[rt][0]));
}

最大匹配

题目：被吃了。

题意简述

给你一棵树，求最多的有边直接连接的不重复点对数量。

思路

这次每个点依旧只有两个状态：匹配过/没匹配过。

若这个点不想和儿子匹配，那么儿子的状态就随便了。
d p [ x ] [ 0 ] = ∑ y ∈ c h i l d r e n ( x ) max ⁡ ( d p [ y ] [ 0 ] , d p [ y ] [ 1 ] ) dp[x][0]=\sum_{y\in children(x)}\max(dp[y][0],dp[y][1]) dp[x][0]=y∈children(x)∑max(dp[y][0],dp[y][1])

若当前点需要匹配，则儿子中至少有一个要没匹配过。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=2e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
int dp[N][2];
void dfs(int fa,int x){
	int mx=-1e9;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		dp[x][0]+=max(dp[y][0],dp[y][1]);
		mx=max(mx,dp[y][0]-max(dp[y][0],dp[y][1]));
	}
	dp[x][1]=dp[x][0]+mx+1;
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	dfs(1,1);
	print(max(dp[1][1],dp[1][0]));
}

两个定理

  1. 对于二分图，最小点覆盖数 = = = 最大匹配数。
  2. 对任意图， ∣ 最小点覆盖 ∣ + ∣ 最大独立集 ∣ = ∣ V ∣ |最小点覆盖| + |最大独立集| = |V| ∣最小点覆盖∣+∣最大独立集∣=∣V∣。

对于定理 2，最小点覆盖覆盖了所有的边，所以剩下的点无边相连，自然独立。

树的直径

树的直径：一棵树上最长的链。

相关题目：B4016 树的直径

两次 dfs

策略：贪心。

第一次 dfs：任选一个点 u u u，找到距其最远的的点 x x x。

第二次 dfs：找到距 x x x 最远的点 y y y，路径 x → y x\to y x→y 即为树的直径。

证明（反证）：

若 x → y x\to y x→y 不是直径。

首先，直径一定与 x → y x\to y x→y 相交，因为树是联通的，若不相交则一定有一条链可以将两条链连起来形成更长链，不符合。

如下图：

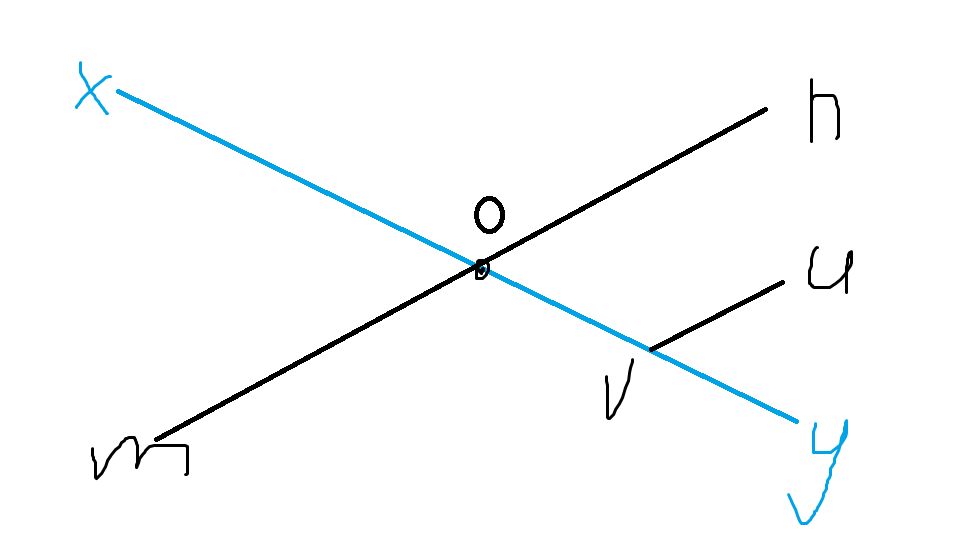
设 m → n m\to n m→n 为直径。

∵ x 为距 u 最远点 \because x\ 为距\ u\ 最远点 ∵x 为距 u 最远点

∴ u → x > u → m , u → x > u → n \therefore \ u\to x>u\to m,u\to x>u\to n ∴ u→x>u→m,u→x>u→n

即 o → x > o → m , o → x > o → n 即\ o\to x>o\to m,o\to x>o\to n 即 o→x>o→m,o→x>o→n

∵ y 为距 x 最远点 \because y\ 为距\ x\ 最远点 ∵y 为距 x 最远点

∴ x → y > x → m , x → y > x → n \therefore \ x\to y>x\to m,x\to y>x\to n ∴ x→y>x→m,x→y>x→n

即 o → y > o → m , o → y > o → n 即\ o\to y>o\to m,o\to y>o\to n 即 o→y>o→m,o→y>o→n

即 x → y > n → m 即\ x\to y>n\to m 即 x→y>n→m

code

cpp 复制代码 
void dfs(int fa,int x){
	dep[x]=dep[fa]+1;
	if(dep[x]>dep[mx])mx=x;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
	}
}
void xfs(int fa,int x,int d){
	ans=max(ans,d);
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs(x,y,d+1);
	}
}

树形 DP

对于一条经过点 x x x 的直径，可以拆分成两部分：以 x x x 为根的子树中向下延伸的最长链和不重合的非严格次长链。

因此，对于每个点求出其第一和第二长链即可。

d 1 x d1_x d1x：点 x x x 向下延伸的最长链。
d 2 x d2_x d2x：点 x x x 向下延伸的次长链。

对于点 x x x 和其孩子 y y y：

  1. 若 d 1 y + 1 > d 1 x d1_y+1>d1_x d1y+1>d1x，则将 d 2 x d2_x d2x 赋值 d 1 x d1_x d1x， d 1 x d1_x d1x 赋值 d 1 y + 1 d1_y+1 d1y+1。
  2. 否则，若 d 1 y > d 2 x d1_y>d2_x d1y>d2x，将 d 2 x d2_x d2x 赋值为 d 1 x d1_x d1x。

code

cpp 复制代码 
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		if(d1[x]<d1[y]+1){
			d2[x]=d1[x];
			d1[x]=d1[y]+1;
		}
		else if(d2[x]<d1[y]+1){
			d2[x]=d1[y]+1;
		}
		ans=max(ans,d1[x]+d2[x]);
	}
}

题目

CF911F Tree Destruction

题目传送门

题意简述

一棵树，每次选择两个点，对答案贡献两点间的距离，之后删去其中一个点，求最大答案以及一种可行方案。

思路

树的直径是树中最长的链，每次与直径上的点求距离明显对答案贡献更大。所以树的直径一直有贡献，需要最晚删除。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
const int N=2e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
int n,m,k;
vector<int>a[N];
int dep1[N];
int dep2[N];
int dep[N];
int pre[N];
int mx1,mx2;
int vis[N];
void fsdw(int fa,int x){
	dep[x]=dep[fa]+1;
	if(dep[x]>dep[mx1])mx1=x;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		fsdw(x,y);
	}
}
void dfs(int fa,int x){
	dep1[x]=dep1[fa]+1;
	pre[x]=fa;
	if(dep1[x]>dep1[mx2])mx2=x;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
	}
}
void xfs(int fa,int x){
	dep2[x]=dep2[fa]+1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs(x,y);
	}
}
int d[N];
struct node{
	int a,b,c;
}f[N];
int cnt;
int ans;
signed main(){
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
		d[u]++,d[v]++;
	}
	fsdw(1,1);
	dfs(mx1,mx1);
	xfs(mx2,mx2);
	int x=mx2;
	vis[x]=1;
	while(x!=mx1){
		x=pre[x];
		vis[x]=1;
	}
	queue<int>q;
	for(int i=1;i<=n;i++)if(d[i]==1)q.push(i);
	while(!q.empty()){
		int x=q.front();
		q.pop();
		if(vis[x])continue;
		if(dep1[x]>dep2[x])f[++cnt]=node{x,mx1,x};
		else f[++cnt]=node{x,mx2,x};
		ans+=max(dep1[x],dep2[x]);
		for(int i=0;i<a[x].size();i++){
			int y=a[x][i];
			if(--d[y]==1)q.push(y);
		}
	}
	x=mx2;
	while(x!=mx1){
		f[++cnt]=node{x,mx1,x};
		ans+=dep1[x];
		x=pre[x];
	}
	print(ans-cnt),endl;
	for(int i=1;i<=cnt;i++)print(f[i].a),psp,print(f[i].b),psp,print(f[i].c),endl;
}

P3304 [SDOI2013] 直径

题目传送门

题意简述

给定一棵树，求有多少条所有直径公用的边。

思路

首先找到其中一条直径 x → y x\to y x→y，接着从点 x x x 向 y y y 走，到达第一个 分叉 u u u 且分叉出的边可以与 x → u x\to u x→u 组成一条直径，此时公共边只可能出现在此时 x → u x\to u x→u 的路径上，原因：

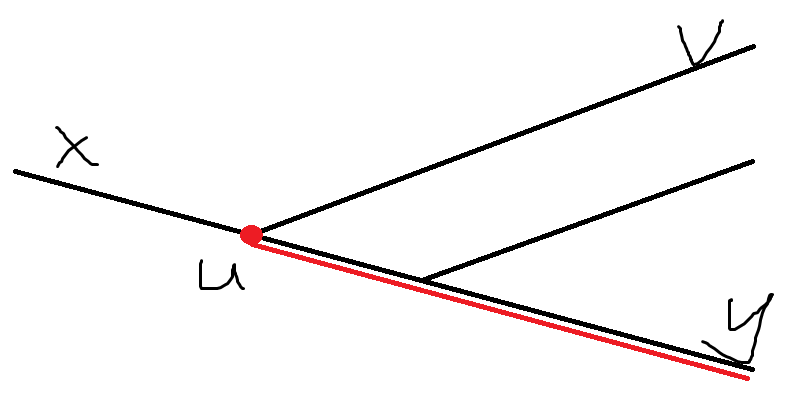
此时 u → y u\to y u→y 的所有边都不会被直径 x → v x\to v x→v 经过。

从点 y y y 开始找同理。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=2e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
int n;
struct node{
	int to,dis;
};
vector<node>a[N];
int d[N],dis[N],isd[N];
int pre[N],son[N];
int vis[N];
int sid[N];
vector<int>zj;
int mx1,mx2;
void dfs(int fa,int x){
	if(d[x]>d[mx1])mx1=x;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		d[y]=d[x]+a[x][i].dis;
		dfs(x,y);
	}
}
void xfs(int fa,int x){
	if(dis[x]>dis[mx2])mx2=x;
	pre[x]=fa;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		dis[y]=dis[x]+a[x][i].dis;
		xfs(x,y);
	}
}
void zfs(int fa,int x){
	son[x]=fa;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		isd[y]=isd[x]+a[x][i].dis;
		zfs(x,y);
	}
}
void Dfs(int u,int fa,int dep,int &mx){
	mx=max(mx,dep);
	for(int i=0;i<a[u].size();i++){
		int v=a[u][i].to;
		if(v==fa||vis[v])continue;
		Dfs(v,u,dep+a[u][i].dis,mx);
	}
}
signed main(){
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read(),w=read();
		a[u].push_back(node{v,w});
		a[v].push_back(node{u,w});
	}
	mx1=1;
	dfs(1,1);
	mx2=mx1;
	dis[mx1]=0;
	xfs(mx1,mx1);
	int L=dis[mx2];
	print(L),endl;
	isd[mx2]=0;
	zfs(mx2,mx2);
	int x=mx2;
	while(x!=mx1){
		zj.push_back(x);
		vis[x]=1;
		x=pre[x];
	}
	zj.push_back(mx1);
	vis[mx1]=1;
	reverse(zj.begin(),zj.end());
	for(int i=0;i<zj.size();i++){
		int u=zj[i];
		int mx=0;
		for(int j=0;j<a[u].size();j++){
			int v=a[u][j].to;
			if(vis[v])continue;
			Dfs(v,u,a[u][j].dis,mx);
		}
		sid[u]=mx;
	}
	int s=mx1;
	for(int i=zj.size()-1;i>=0;i--){
		int u=zj[i];
		if(isd[u]+sid[u]==L){
			s=u;
			break;
		}
	}
	int t=mx2;
	for(int i=0;i<zj.size();i++){
		int u=zj[i];
		if(dis[u]+sid[u]==L){
			t=u;
			break;
		}
	}
	int ids,idt;
	for(int i=0;i<zj.size();i++){
		if(zj[i]==s)ids=i;
		if(zj[i]==t)idt=i;
	}
	print(idt-ids);
}

CF161D Distance in Tree

题目传送门

题意简述

求树上距离为 k k k 的点对数量。

思路

看到 k ≤ 500 k\le 500 k≤500，可以考虑用 d p [ x ] [ j ] dp[x][j] dp[x][j] 表示点 x x x 往下延伸距离为 j j j 的点的数量，转移也很好想。
d p [ x ] [ j ] = ∑ y ∈ c h i l d r e n ( x ) d p [ y ] [ j − 1 ] dp[x][j]=\sum_{y\in children(x)}dp[y][j-1] dp[x][j]=y∈children(x)∑dp[y][j−1]

最终的答案怎么统计？先看一个错误代码：

cpp 复制代码 
for(int i=1;i<=n;i++){
	for(int j=0;j<=k;j++){
		ans+=dp[i][j]*dp[i][k-j];
	}
}

为什么不对？因为这个代码没有保证长度为 j j j 和长度为 k − j k-j k−j 的两条链不重合。

那么怎么保证不重合？全都统计到一堆了，分不出来！

所以问题是"统计到一堆了"，只需要在还没有统计到一堆的时候找答案就行了。在合并之前找答案，这样可以保证链不重合。

有一个细节见代码注释。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=5e4+5;
const int M=505;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
int dp[N][M];
vector<int>a[N];
int ans;
void dfs(int fa,int x){
	dp[x][0]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		for(int j=0;j<k;j++)ans+=dp[x][j]*dp[y][k-1-j];//k-1-j 是因为 u->v 也算长度
		for(int j=1;j<=k;j++)dp[x][j]+=dp[y][j-1];
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read(),k=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	dfs(1,1);
	print(ans);
}

CF1923E Count Paths

题目传送门

题意简述

求一棵树上满足顶点至少为两个，端点颜色相同且中间颜色与端点不同的链的数量。

思路

明显 DP,怎么表示？

发现有两个信息是十分重要的：点编号和链端点颜色。

所以： d p [ x ] [ j ] dp[x][j] dp[x][j] 表示点 x x x 向下延伸的以颜色 j j j 结尾的链的数量。

怎么统计？当点 x x x 的儿子 y y y 没有被合并时， d p [ x ] [ j ] dp[x][j] dp[x][j] 和 d p [ y ] [ j ] dp[y][j] dp[y][j] 明显可以合并出新的链，对答案有贡献。

cpp 复制代码 
ans+=dp[x][color]*cnt;

怎么合并，直接加就行了,但是为了符合要求 3，需要保证颜色不与 c x c_x cx 相同。
d p [ x ] [ j ] = ∑ y ∈ c h i l d r e n ( x ) , j ≠ c x d p [ y ] [ j ] dp[x][j]=\sum_{y\in children(x),j\neq c_x}dp[y][j] dp[x][j]=y∈children(x),j=cx∑dp[y][j]

接着解决时间的问题，我们会发现，合并时有时候 d p [ y ] [ j ] dp[y][j] dp[y][j] 是 0，根本没贡献，这时候就不用合并了，只需要合并有值的。

但是这样还是可以被卡，不妨将合并 x x x 和 y y y 想象成将两堆小球合并成一堆，每次只能移动一个。我们需要的只是合并之后的结果，对于结果在什么位置其实不重要。

现在继续考虑合并小球，明显将数量少的那一堆合并到数量多的那一堆花费的次数更少。

回到题目，明显遍历值较少的加入值较多的更快。

cpp 复制代码 
if(dp[x].size()<dp[y].size())swap(dp[x],dp[y]);

有一种情况对答案也有贡献：只有一条竖着的链。此时也需要统计到答案中，此时其中一端的端点 d p [ x ] [ c [ x ] ] dp[x][c[x]] dp[x][c[x]] 一定要保证是 1，因为这样才能使其他的 d p [ y ] [ c [ x ] ] dp[y][c[x]] dp[y][c[x]] 被正确地统计，但是我们交换的时候会把这玩意换走，然后它就走丢了。

解决方案：自己想，只需要再把 d p [ x ] [ c [ x ] ] dp[x][c[x]] dp[x][c[x]] 换回来就行了。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=2e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
int c[N];
vector<int>a[N];
map<int,int>dp[N];
int ans;
void dfs(int fa,int x){
	dp[x][c[x]]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		if(dp[x].size()<dp[y].size())swap(dp[x],dp[y]),swap(dp[x][c[x]],dp[y][c[x]]);
		for(auto v:dp[y]){
			int color=v.first;
			int cnt=v.second;
			ans+=dp[x][color]*cnt;
			if(color!=c[x])dp[x][color]+=cnt;
		}
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	T=read();
	while(T--){
		n=read();
		for(int i=1;i<=n;i++)c[i]=read(),a[i].clear(),dp[i].clear();
		for(int i=1;i<n;i++){
			int u=read(),v=read();
			a[u].push_back(v);
			a[v].push_back(u);
		}
		ans=0;
		dfs(1,1);
		print(ans),endl;
	}
}

最长同值路径

题目传送门坏了。

题意简述

求一棵树上点权相同的最长链。

思路
真的没什么好说的，数据 1e4 暴力都能过。

我们可以将若干块联通 且颜色相同的部分视为一个独立的树，目标就变成了求这个小树里面的直径。

依旧是树形 DP 求直径的代码，只是需要判断一下颜色。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e4+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
int h[N];
vector<int>a[N];
int d1[N];
int d2[N];
int ans;
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		if(h[x]!=h[y])continue;
		if(d1[y]+1>d1[x]){
			d2[x]=d1[x];
			d1[x]=d1[y]+1;
		}
		else if(d1[y]+1>d2[x]){
			d2[x]=d1[y]+1;
		}
		ans=max(ans,d1[x]+d2[x]);
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<=n;i++)h[i]=read();
	for(int i=1;i<=n;i++){
		if(i*2<=n){
			a[i].push_back(i*2);
			a[i*2].push_back(i);
		}
		if(i*2+1<=n){
			a[i].push_back(i*2+1);
			a[i*2+1].push_back(i);
		}
	}
	dfs(1,1);
	print(ans);
}

Edge Groups

题目传送门

题意简述

求一棵树中将 m m m 条边分成不重复的 m 2 \frac{m}{2} 2m 组的方案数，模 998244353。

思路

考虑一个菊花图，中心为 x x x。

当点 x x x 连接的边数量为奇数时，明显无法完成配对，当为偶数时，可以。

那么方案数？

当有 4 个点时，方案数是 C 4 2 2 = 3 \frac{C_{4}^{2}}{2}=3 2C42=3 种，通过找规律 + + + 暴算可得，当有 2 k 2k 2k 条边时，方案数是 Π i = 1 k C 2 ⋅ i 2 ⋅ i − 2 2 k \frac{\Pi_{i=1}^{k}C_{2\cdot i}^{2\cdot i-2}}{2^k} 2kΠi=1kC2⋅i2⋅i−2，化简得：
S = 2 k ! k ! ⋅ 2 k S=\frac{2k!}{k!\cdot2^k} S=k!⋅2k2k!

回到整棵树上，若点 x x x 的儿子数量为奇数怎么办，把它的父亲拿来凑数就行了，此时要向上传父亲被使用过的标记。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e5+5;
const int mod=998244353;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
int dp[N];
int d[N];
int f[N];
int res=1;
int dfs(int fa,int x){
	int ans=0;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		ans+=dfs(x,y);
	}
	if(ans%2==0){
		res=(res*f[ans])%mod;
		return 1;
	}
	else{
		res=(res*f[ans+1])%mod;
		return 0;
	}
}
int poww(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}	
	return ans;
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	d[0]=1;
	for(int i=1;i<=n;i++)d[i]=d[i-1]*i%mod;
	f[0]=1;
	for(int i=1;i<=n;i++)if(i%2==0)f[i]=d[i]*poww(d[i/2],mod-2)%mod*poww(poww(2,i/2),mod-2)%mod;
	dfs(1,1);
	print(res);
}

P4408 [NOI2003] 逃学的小孩 / 数据生成器

题目传送门

题意简述

树上三个点 A , B , C A,B,C A,B,C，从 A A A 出发，到 B , C B,C B,C 中距离较近的点，再从这个点到剩下的点。求行走的最长距离。

思路

贪心的证明确实能评蓝。

首先，题目看着像个图，实际上就是树。

可以保证，任意两个居住点间有且仅有一条通路。

仅有一条路径，言下之意就是没有环，那么就是树了。

既然是树，那么就很好解决了。

首先，为了使 B → C B\to C B→C 距离更长，两点明显是直径。

接着看到 A A A 点的选择，点 A A A 会先去距离较近的点，那么我们需要求的就是最小距离的最大值。看到这个想到了什么？二分！

直接贪心即可。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=2e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
struct node{
	int to,dis;
};
vector<node>a[N];
int dis1[N];
int dis2[N];
int DIS,mx1,mx2;
void fs(int fa,int x,int dis){
	if(dis>DIS)DIS=dis,mx1=x;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		fs(x,y,dis+a[x][i].dis);
	}
}
void dfs(int fa,int x){
	if(dis1[x]>dis1[mx2])mx2=x;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		dis1[y]=dis1[x]+a[x][i].dis;
		dfs(x,y);
	}
}
void xfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		dis2[y]=dis2[x]+a[x][i].dis;
		xfs(x,y);
	}
}
int ans;
signed main(){
	//ios::sync_with_stdio(0);
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		a[u].push_back(node{v,w});
		a[v].push_back(node{u,w});
	}
	fs(1,1,0);
	dfs(mx1,mx1);
	xfs(mx2,mx2);
	int L=dis1[mx2];
	for(int i=1;i<=n;i++){
		ans=max(ans,min(dis1[i],dis2[i])+L);
	}
	print(ans);
}

树上背包

在一棵树上进行的选一定个数获得最大价值的问题。

题目 ：P2014 [CTSC1997] 选课

题意简述

不想简述了。

O ( N 3 ) O(N^3) O(N3) 解法

d p [ x ] [ i ] [ j ] dp[x][i][j] dp[x][i][j] 表示点 x x x，前 i i i 个儿子，共选了 j j j 个获得的最大价值。

按照优先级从高到低建一棵树，明显：当 x x x 的儿子 y y y 要选时， x x x 也是必选，那么有：

cpp 复制代码 
dp[x][0][1]=s[x];

在合并第 i i i 个儿子 y y y 时，我们可以通过合并前 i − 1 i-1 i−1 个儿子的价值计算。

我们考虑在合并后的点 x x x 的子树中选 l l l 个，那么在子树 y y y 中选择的数量就是 j − l j-l j−l，DP 式子可以推出：

cpp 复制代码 
dp[x][i][j]=max(dp[x][i][j],dp[x][i-1][j-l]+dp[y][cnt][l]);

code

cpp 复制代码 
void dfs(int x){
	sz[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		dfs(y);
		sz[x]+=sz[y];
	}
	dp[x][0][1]=s[x];
	dp[x][0][0]=-1e18;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		int cnt=a[y].size();
		int I=i+1;
		for(int j=0;j<=m;j++){
			dp[x][I][j]=dp[x][I-1][j];
			for(int l=0;l<=min(j,sz[y]);l++){
				dp[x][I][j]=max(dp[x][I][j],dp[x][I-1][j-l]+dp[y][cnt][l]);
			}
		}
	}
}

O ( N M ) O(NM) O(NM) 解法

考虑怎么优化。

首先， j j j 肯定没必要循环到 m m m，最多只有 s z x sz_x szx。

但是这样还是 O ( N 3 ) O(N^3) O(N3) 的。

其实还是有循环被浪费了：在 i = 1 i=1 i=1 这种极端情况下，不可能选到 s z x sz_x szx 个。我们应该有多少点遍历多少。

那么空间呢？看到 i i i 其实没用，把它删了，与普通 01 背包一样的，要倒过来遍历！

code

cpp 复制代码 
void dfs(int x){
	sz[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		dfs(y);
	}
	dp[x][1]=s[x];
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		for(int j=min(sz[x],m);j>=1;j--){
			for(int l=0;l<=min(m-j,sz[y]);l++){
				dp[x][j+l]=max(dp[x][j+l],dp[x][j]+dp[y][l]);
			}
		}
		sz[x]+=sz[y];
	}
}

时间复杂度证明

看 DP 时状态转移的次数，你会发现加入了与 m m m 取更小值后它其实是 O ( N M ) O(NM) O(NM)。

题目

P2015 二叉苹果树

题目传送门

题意简述

一棵树，只能留 Q Q Q 条边，若一条边被删除则其链接的子树全部删除，求最终留下边的最大边权和。

思路

题目给出了保留枝条的数量，其实可以转化到点上。如果只留根节点，其他全砍掉，那么一个苹果都不会保留。所以考虑将边权转移到两端中深度更深的点上。

那这时就不能只保留 Q Q Q 个点了，因为还得保留一个没用但是必要的根节点。

如果要保留点 x x x，那么链 x → r o o t x\to root x→root 都需要保留。

接下来就是模板了。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=105;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
int c[N];
vector<int>a[N];
void add(int x,int y){
	a[x].push_back(y);
	a[y].push_back(x);
}
int sz[N];
int dp[N][N];
int dep[N];
int p[N];
void xfs(int fa,int x){
	dep[x]=dep[fa]+1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs(x,y);
	}
}
void dfs(int fa,int x){
	sz[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
	}
	dp[x][1]=p[x];
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		for(int j=min(m,sz[x]);j>=1;j--){
			for(int l=0;l<=min(m-j,sz[y]);l++){
				dp[x][j+l]=max(dp[x][j+l],dp[x][j]+dp[y][l]);
			}
		}
		sz[x]+=sz[y];
	}
}
int U[N],V[N];
signed main(){
	//ios::sync_with_stdio(0);
	n=read(),m=read()+1;
	for(int i=1;i<n;i++){
		U[i]=read(),V[i]=read();
		add(U[i],V[i]);
		c[i]=read();
	}
	xfs(1,1);
	for(int i=1;i<n;i++){
		int u=U[i],v=V[i];
		if(dep[u]>dep[v])p[u]=c[i];
		else p[v]=c[i];
	}
	dfs(1,1);
	print(dp[1][m]);
}

P1273 有线电视网

题目传送门

题意简述

一棵树，经过边需要代价，到达叶子结点可以获得利益，求在利益为正的前提下可以到达多少叶子结点。

思路

在 DP 的时候，将价值减去当前边的代价，我们最终会得到 d p [ r o o t ] [ 1 ... m ] dp[root][1\ldots m] dp[root][1...m]，第二维即为选的叶子结点数量，价值为正的前提下在第二维找最大值即可。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=5e3+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
int dp[N][N];
struct node{
	int to,dis;
};
vector<node>a[N];
int c[N];
int dfs(int fa,int x){
	dp[x][0]=0;
	dp[x][1]=c[x];
	if(x>n-m)return 1;
	int sz=0;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		int w=a[x][i].dis;
		int s=dfs(x,y);
		for(int j=sz;j>=0;j--){
			for(int l=0;l<=min(m-j,s);l++){
				dp[x][j+l]=max(dp[x][j+l],dp[x][j]+dp[y][l]-w);
			}
		}
		sz+=s;
	}
	return sz;
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read(),m=read();
	for(int i=1;i<=n-m;i++){
		k=read();
		while(k--){
			int v=read(),w=read();
			a[i].push_back(node{v,w});
			a[v].push_back(node{i,w});
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			dp[i][j]=-1e9;
		}
	}
	for(int i=1;i<=n-m;i++)c[i]=-1e9;
	for(int i=n-m+1;i<=n;i++)c[i]=read();
	dfs(1,1);
	int res=0;
	for(int i=1;i<=m;i++){
		if(dp[1][i]>=0)res=i;
	}
	print(res);
}

P3177 [HAOI2015] 树上染色

题目传送门

题意简述

一棵树将 k k k 个点染成黑色，其余染成白色，最终价值为黑色点两两之间距离与白色点两两之间距离的和。

求最大价值。

思路

统计每一条链的长度再累加显然不太合理，最终的价值可以理解成每条边的覆盖次数乘上边权。

考虑点 x x x 和它的儿子 y y y，以 y y y 为根的子树中有 j j j 个黑点，那么其余的地方有 k − j k-j k−j 个黑点，则边 x → y x\to y x→y 被经过的次数为 j ⋅ ( k − j ) j\cdot(k-j) j⋅(k−j)。

按照模版的思想，这道题中每条边的贡献都能计算出，可以转化为背包。

正序遍历在 l l l 为 0 时， d p [ x ] [ j ] dp[x][j] dp[x][j] 会被 d p [ x ] [ j + l ] dp[x][j+l] dp[x][j+l] 先覆盖，后面用的都是错的了。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=2e3+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
struct node{
	int to,dis;
};
vector<node>a[N];
int sz[N];
int dp[N][N];
void dfs(int fa,int x){
	sz[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		dfs(x,y);
		int w=a[x][i].dis;
		for(int j=min(m,sz[x]);j>=0;j--){
			for(int l=min(m-j,sz[y]);l>=0;l--){
				int ex=l*(m-l)*w+(sz[y]-l)*(n-sz[y]-(m-l))*w;
				dp[x][j+l]=max(dp[x][j+l],dp[x][j]+dp[y][l]+ex);
			}
		}
		sz[x]+=sz[y];
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read(),m=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read(),w=read();
		a[u].push_back(node{v,w});
		a[v].push_back(node{u,w});
	}
	dfs(1,1);
	print(dp[1][m]);
}

二次扫描/换根 DP

题目给出一棵树时，不会总是有根树，可能是无根树。这时候可能会出现根选择不同导致最终结果不同的情况。

这个时候需要综合考虑每个点为根的情况，以此求出最优解，但是肯定不是暴力换根，根转移到相邻的点时，并不是所有点的贡献都会改变，或者多数点的变化都是有规律的。

题目

计算机

题目传送门被吃掉了。

题意简述

给定一颗带边权的树，求每个点到距其最远点的距离。

思路

我们发现距其最远点就是直径的两个端点之一，可以直接贪心。

当然也可以 DP。

换根 DP 先随便找一个点找出它的答案，再根据其答案推出其它的点。

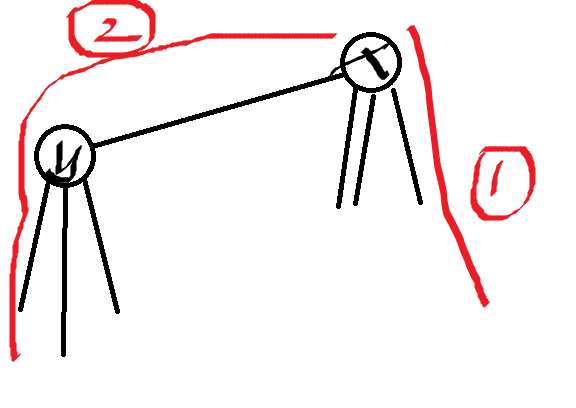
当点 x x x 将根转移给 y y y 时， y y y 的最长路径可能有上图两种情况：经过 y y y/不经过 y y y。

若路径不经过 y y y，那么对于点 y y y 为根的最长路径就是 d 1 x + w ( x , y ) d1_x+w(x,y) d1x+w(x,y)。

若经过呢？明显就不是了。这时候就需要记录次大值，此时 d 1 y = d 2 x + w ( x , y ) d1_y=d2_x+w(x,y) d1y=d2x+w(x,y)

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e4+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
struct node{
	int to,dis;
};
vector<node>a[N];
int d1[N];
int d2[N];
void xfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		int w=a[x][i].dis;
		xfs(x,y);
		int val=d1[y]+w;
		if(val>d1[x])swap(val,d1[x]);
		if(val>d2[x])swap(val,d2[x]);
	}
}
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		if(y==fa)continue;
		int w=a[x][i].dis;
		int val=0;
		if(d1[x]==d1[y]+w)val=d2[x]+w;
		else val=d1[x]+w;
		if(val>d1[y])swap(val,d1[y]);
		if(val>d2[y])swap(val,d2[y]);
		dfs(x,y);
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	while(cin>>n){
		for(int i=1;i<=n;i++)a[i].clear(),d1[i]=d2[i]=0;
		for(int i=2;i<=n;i++){
			int v,w;
			cin>>v>>w;
			a[i].push_back(node{v,w});
			a[v].push_back(node{i,w});
		}
		xfs(1,1);
		dfs(1,1);
		for(int i=1;i<=n;i++){
			cout<<d1[i],endl;
		}
	}
}

P3478 [POI 2008] STA-Station

题目传送门

题意简述

一棵树上求一个点，可以使这个点为根的情况下所有点深度之和最大。

思路

依旧是换根 DP，先随便找一个点求出深度之和，然后画个图瞪眼：

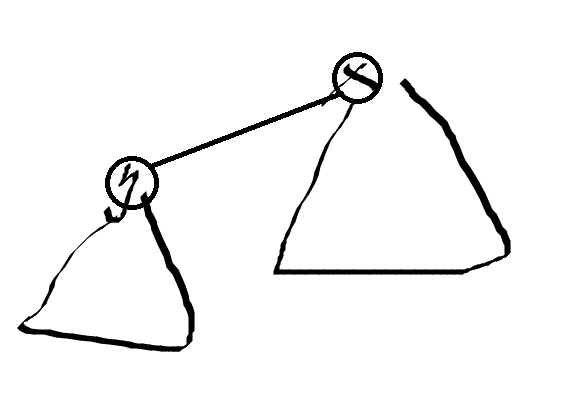
我们发现：当根节点从 x x x 转移到 y y y 时，整颗子树 y y y 向上提，其余点下沉。子树 y y y 上提导致整棵子树所有点深度减一，而下沉则造成所有点深度加一，即：

cpp 复制代码 
dp[y]=dp[x]-sz[y]+(n-sz[y]);

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e6+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
int dep[N];
int sz[N];
int dp[N];
void xfs(int fa,int x){
	dep[x]=dep[fa]+1;
	dp[x]=dep[x];
	sz[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs(x,y);
		dp[x]+=dp[y];
		sz[x]+=sz[y];
	}
}
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dp[y]=dp[x]+(n-sz[y])-(sz[y]);
		dfs(x,y);
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	xfs(1,1);
	dfs(1,1);
	int id=0;
	for(int i=1;i<=n;i++){
		if(dp[i]>dp[id])id=i;
	}
	print(id);
}

::::

CF1187E Tree Painting

题目传送门

题意简述

一棵树，求以合适的点作为根节点时，所有点的子树大小之和的最大值。

思路

依旧瞪眼，依旧老图：

我们会发现：无论是 x , y x,y x,y 中的那一个作为根节点，它们儿子的子树大小始终不变。

我们还发现：我们不用发现就能发现：一个点只能贡献一次。

当以 y y y 为根时，其对答案的贡献为 n n n，既然它贡献了 n n n，它就不能贡献原来的贡献 s z y sz_y szy 了。

看到点 x x x，它本来是贡献 n n n 的，但是现在 n n n 被 y y y 抢了，它就得贡献其它的， 就是 n − s z y n-sz_y n−szy。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=2e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
int sz[N];
int cnt[N];
void xfs(int fa,int x){
	sz[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs(x,y);
		sz[x]+=sz[y];
	}
}
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		cnt[y]=cnt[x]-sz[y]+(n-sz[y]);
		dfs(x,y);
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	xfs(1,1);
	for(int i=1;i<=n;i++)cnt[1]+=sz[i];
	dfs(1,1);
	int ans=0;
	for(int i=1;i<=n;i++)ans=max(ans,cnt[i]);
	print(ans);
}

最小高度树

题目传送门试图传送题目，但失败了。

题意简述

求所有作为根节点可以使树的深度最小的点。

思路

和第一道题一模一样。

以点 x x x 为根时树的深度就是它与距其最远点的距离。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
int d1[N];
int d2[N];
void xfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs(x,y);
		int val=d1[y]+1;
		if(val>d1[x])swap(d1[x],val);
		if(val>d2[x])swap(d2[x],val);
	}
}
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		int val=0;
		if(d1[y]==d1[x]-1)val=d2[x];
		else val=d1[x];
		val++;
		if(val>d1[y])swap(val,d1[y]);
		if(val>d2[y])swap(val,d2[y]);
		dfs(x,y);
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		u++;
		v++;
		a[u].push_back(v);
		a[v].push_back(u);
	}
	xfs(1,1);
	dfs(1,1);
	int mn=1e9;
	for(int i=1;i<=n;i++)mn=min(mn,d1[i]);
	for(int i=1;i<=n;i++)if(d1[i]==mn)print(i-1),psp;
}

P2986 [USACO10MAR] Great Cow Gathering G

题目传送门

题意简述

树上每个点有 c i c_i ci 个人，每条道路有距离 w i w_i wi，找出一个点使所有人到其距离和最小，求最小值。

思路

还是瞪眼，还是老图（这图老好用了）：

我们发现，当这个点从 x x x 转移到 y y y 时， y y y 子树中所有的点到选择点的距离全部减少了 w ( x , y ) w(x,y) w(x,y)，其余点到选择点的距离全都增加了 w ( x , y ) w(x,y) w(x,y)，最后得：

cpp 复制代码 
cnt[y]=cnt[x]-sz[y]*w+(sz[1]-sz[y])*w;

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e5+5;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
int s[N];
struct node{
	int to,dis;
};
vector<node>a[N];
int sz[N];
int cnt[N];
void xfs(int fa,int x){
	sz[x]=s[x];
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		int w=a[x][i].dis;
		if(y==fa)continue;
		xfs(x,y);
		sz[x]+=sz[y];
		cnt[x]+=sz[y]*w;
		cnt[x]+=cnt[y];
	}
}
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i].to;
		int w=a[x][i].dis;
		if(y==fa)continue;
		cnt[y]=cnt[x]-sz[y]*w+(sz[1]-sz[y])*w;
		dfs(x,y);
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<=n;i++)s[i]=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read(),w=read();
		a[u].push_back(node{v,w});
		a[v].push_back(node{u,w});
	}
	xfs(1,1);
	dfs(1,1);
	int mn=1e18;
	for(int i=1;i<=n;i++)mn=min(mn,cnt[i]);
	print(mn);
}

树的同构

树的重心

树的重心为根时，所有子树大小最小

同样的概念：

  1. 作为根节点时使最大深度最小的点
  2. 作为根节点时使所有子树大小不超过 n 2 \frac{n}{2} 2n 的点。

都看到这里了，你应该会用换根 DP 求出树的重心。

树的同构

两棵树，忽略编号，如果有方法通过重新编号使两棵树相同，则称两棵树同构。

下面两棵树是同构的：

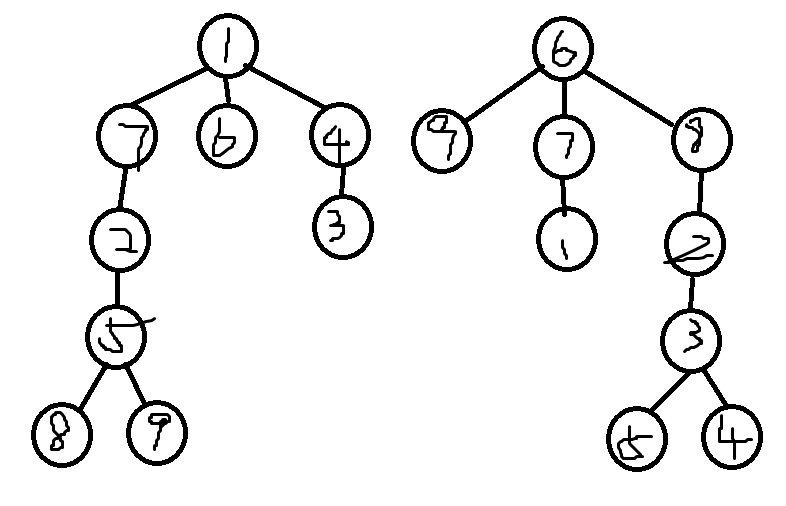
有根树的同构

既然是有根树，明显从根节点开始遍历。

编号对于树是否同构没有影响，需要考虑一种不依赖编号的表示树的方法。

求法 1

题目：树的同构统计

题意简述

一棵树，求其最能选出多少个互不同构的子树。

思路

当搜索一棵树时，用 《 记录，回溯前，用 》 记录。

由于树遍历儿子的顺序不影响其同构，所以合并时还需排序。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e6;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
int lowbit(int x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
string s[N];
void dfs(int fa,int x){
	s[x].push_back('<');
	vector<string>tmp;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfs(x,y);
		tmp.push_back(s[y]);
	}
	sort(tmp.begin(),tmp.end());
	for(int i=0;i<tmp.size();i++){
		s[x]=s[x]+tmp[i];
	}
	s[x].push_back('>');
}
map<string,int>mp;
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	dfs(1,1);
	for(int i=1;i<=n;i++)mp[s[i]]=1;
	print(mp.size());
}

求法 2

题目：树的同构统计 加强版

题意简述

一棵树，求其最能选出多少个互不同构的子树。

思路

求法 1 的缺陷是合并字符串时速度太慢，考虑一种速度较快的合并方法。

哈希可以解决此类问题。

儿子的遍历顺序不影响树的同构，也就是说顺序不作为哈希的对象，哈希的对象是子树的哈希值。
h a s h x = 1 + ∑ y ∈ c h i l d r e n ( x ) h a s h y hash_x=1+\sum_{y\in children(x)}hash_y hashx=1+y∈children(x)∑hashy

但是子树的哈希值为 { 1 , 3 , 3 } \{1,3,3\} {1,3,3} 和子树哈希值为 { 2 , 2 , 3 } \{2,2,3\} {2,2,3} 贡献相同，所以需要再区分：
h a s h x = 1 + ∑ y ∈ c h i l d r e n ( x ) f ( h a s h y ) hash_x=1+\sum_{y\in children(x)}f(hash_y) hashx=1+y∈children(x)∑f(hashy)

函数 f f f 要定义得猎奇一点，最好用位运算：

cpp 复制代码 
typedef unsigned long long ull;
ull lowbit(ull x){
	return x&-x;
}
const ull M=2048995248;
ull f(ull x){
	x^=M;
	x=x*x;
	x^=lowbit(x);
	x^=x<<13;
	x^=x>>7;
	x^=x<<17;
	x^=M;
	x^=lowbit(x*x);
	return x;
}

一个随机数生成器：mt19937_64，用法：

cpp 复制代码 
mt19937_64 rd(time(0));//初始化随机种子
rd()//返回随机数

然后我发现了一个特别强悍的基数：2048995248，这玩意在随机数 mt19937_64 挂掉的时候依旧十分能打。

无根树的同构

题目：Tree Isomorphism

题意简述

判断两棵树是否同构。

求法 1

无根树，那么需要找一个两棵树共有的点作为根。

重心就是个极好的选择，两棵树如果同构，则重心一定在同一位置。

把重心作为根，跑哈希即可。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e5+5;
mt19937_64 rd(time(0));
const int M=2048995248;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
ull lowbit(ull x){
	return x&-x;
}
ull h[N];
ull f(ull x){
	x^=M;
	x=x*x;
	x^=lowbit(x);
	x^=x<<13;
	x^=x>>7;
	x^=x<<17;
	x^=M;
	x^=lowbit(x*x);
	x^=lowbit(M);
	x^=(x*4*lowbit(x)+lowbit(x));
	return x;
}
int n,m,k;
int T;
vector<int>a[N];
vector<int>b[N];
int ans;
int da[N];
int sza[N];
int db[N];
int szb[N];
void za(int fa,int x){
	sza[x]=1;
	int mxy=0;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		za(x,y);
		sza[x]+=sza[y];
		mxy=max(mxy,sza[y]);
	}
	int mx=max(mxy,n-sza[x]);
	ans=min(ans,mx);
	da[x]=mx;
}
void zb(int fa,int x){
	szb[x]=1;
	int mxy=0;
	for(int i=0;i<b[x].size();i++){
		int y=b[x][i];
		if(y==fa)continue;
		zb(x,y);
		szb[x]+=szb[y];
		mxy=max(mxy,szb[y]);
	}
	int mx=max(mxy,n-szb[x]);
	ans=min(ans,mx);
	db[x]=mx;
}
void dfsa(int fa,int x){
	h[x]=1;
	if(!x)return;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		dfsa(x,y);
		h[x]=(h[x]+f(h[y]));
	}
}
void dfsb(int fa,int x){
	h[x]=1;
	if(!x)return;
	for(int i=0;i<b[x].size();i++){
		int y=b[x][i];
		if(y==fa)continue;
		dfsb(x,y);
		h[x]=(h[x]+f(h[y]));
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	T=read();
	while(T--){
		n=read();
		for(int i=1;i<=n;i++)a[i].clear(),b[i].clear();
		for(int i=1;i<n;i++){
			int u=read(),v=read();
			a[u].push_back(v);
			a[v].push_back(u);
		}
		for(int i=1;i<n;i++){
			int u=read(),v=read();
			b[u].push_back(v);
			b[v].push_back(u);
		}
		ans=1e9;
		za(1,1);
		pair<int,int>A,B;
		for(int i=1;i<=n;i++){
			if(da[i]==ans){
				if(A.first)A.second=i;
				else A.first=i;
			}
		}
		ans=1e9;
		zb(1,1);
		for(int i=1;i<=n;i++){
			if(db[i]==ans){
				if(B.first)B.second=i;
				else B.first=i;
			}
		}
		pair<ull,ull>ansa,ansb;
		dfsa(A.first,A.first);
		ansa.first=h[A.first];
		dfsa(A.second,A.second);
		ansa.second=h[A.second];
		dfsb(B.first,B.first);
		ansb.first=h[B.first];
		dfsb(B.second,B.second);
		ansb.second=h[B.second];
		if(ansa.first>ansa.second)swap(ansa.second,ansa.first);
		if(ansb.first>ansb.second)swap(ansb.second,ansb.first);
		if(ansa.first==ansb.first&&ansa.second==ansb.second)putstr("YES\n");
		else putstr("NO\n");
	}
}

求法 2

既然没有根，把所有点作为根的结果全都求出来就行了。

考虑换根 DP，还是老图：

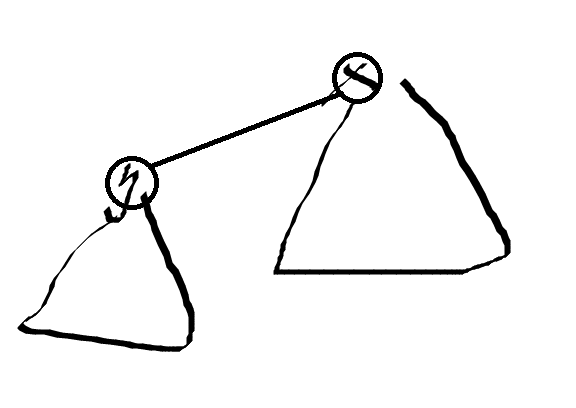
我们发现，当 x x x 为根时， h a s h x hash_x hashx 的值是 x x x 底下那一坨加上 f ( h a s h y ) f(hash_y) f(hashy)，所以 x x x 下面那一坨就可以求出来：
h a s h o t h e r = h a s h x − f ( h a s h y ) hash_{other}=hash_x-f(hash_y) hashother=hashx−f(hashy)

那么当 y y y 为根时， h a s h y hash_y hashy 的值也就可以求出来：
h a s h y = h a s h y + f ( h a s h o t h e r ) hash_y=hash_y+f(hash_{other}) hashy=hashy+f(hashother)

展开得：
h a s h y = h a s h y + f ( h a s h x − f ( h a s h y ) ) hash_y=hash_y+f(hash_x-f(hash_y)) hashy=hashy+f(hashx−f(hashy))

还是瞪眼法，式子有点麻烦，无非多瞪一会，再念一点神秘小咒语而已。

求出了 n n n 个点的哈希值，自然也就可以比较两棵树是否同构了。

code

cpp 复制代码 
#include<bits/stdc++.h>
#define int long long
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e6+5;
mt19937_64 rd(time(0));
const ull M=2048995248;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
ull lowbit(ull x){
	return x&-x;
}
int n,m,k;//expect
int T;
vector<int>a[N];
vector<int>b[N];
ull h1[N];
ull h2[N];
ull f(ull x){
	x^=M;
	x=x*x;
	x^=lowbit(x);
	x^=x<<13;
	x^=x>>7;
	x^=x<<17;
	x^=M;
	x^=lowbit(x*x);
	x^=lowbit(M);
	x^=(x*4*lowbit(x)+lowbit(x));
	return x;
}
void xfs1(int fa,int x){
	h1[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs1(x,y);
		h1[x]=(h1[x]+f(h1[y]));
	}
}
void xfs2(int fa,int x){
	h2[x]=1;
	for(int i=0;i<b[x].size();i++){
		int y=b[x][i];
		if(y==fa)continue;
		xfs2(x,y);
		h2[x]=(h2[x]+f(h2[y]));
	}
}
void dfs1(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		h1[y]=h1[y]+f(h1[x]-f(h1[y]));
		dfs1(x,y);
	}
}
void dfs2(int fa,int x){
	for(int i=0;i<b[x].size();i++){
		int y=b[x][i];
		if(y==fa)continue;
		h2[y]=h2[y]+f(h2[x]-f(h2[y]));
		dfs2(x,y);
	}
}
signed main(){
	//ios::sync_with_stdio(0);
	T=read();
	while(T--){
		n=read();
		for(int i=1;i<=n;i++)a[i].clear(),b[i].clear();
		for(int i=1;i<n;i++){
			int u=read(),v=read();
			a[u].push_back(v);
			a[v].push_back(u);
		}
		xfs1(1,1);
		for(int i=1;i<n;i++){
			int u=read(),v=read();
			b[u].push_back(v);
			b[v].push_back(u);
		}
		xfs2(1,1);
		dfs1(1,1);
		dfs2(1,1);
		sort(h1+1,h1+1+n);
		sort(h2+1,h2+1+n);
		bool flag=1;
		for(int i=1;i<=n;i++){
			if(h1[i]!=h2[i]){
				flag=0;
				break;
			}
		}
		if(flag)putstr("YES\n");
		else putstr("NO\n");
	}	
}

题目

P4323 [JSOI2016] 独特的树叶

题目传送门

题意简述

两棵树 A , B A,B A,B， B B B 由 A A A 添加一个点 u u u 得到，求出编号最小的可能的点 u u u。

思路

先对两棵树求哈希（换根）。

显而易见，若删除点 u u u，两棵树同构，所以当 u u u 为根时，除了点 u u u 以外所有点的哈希值都能与树 A A A 对应。

添加的点 u u u 显然是个叶子节点，所以当以 u u u 为根时，它一定只有一个儿子 v v v，按照哈希的式子，有:
d p u = f ( d p v ) + 1 dp_u=f(dp_v)+1 dpu=f(dpv)+1

由于删除点 u u u 可以使两棵树同构，所以 d p v dp_v dpv 的值一定可以与点 A A A 中某个点为根时的哈希值对应，可以看做是半已知的。

那么 f ( d p v ) + 1 f(dp_v)+1 f(dpv)+1 也是半已知的。只要有点能与其中一个 f ( d p v ) + 1 f(dp_v)+1 f(dpv)+1 对应，那么这个点就是增加的点。

code

cpp 复制代码 
#include<bits/stdc++.h>
//#define lc p<<1
//#define rc p<<1|1
#define endl putchar('\n')
#define psp putchar(' ')
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=1e5+5;
const ull M=2048995248;
int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x<10){putchar(x+'0');return;}
	print(x/10);
	putchar(x%10+'0');
}
void putstr(string s){
	for(int i=0;i<s.size();i++)putchar(s[i]);
}
ull lowbit(ull x){
	return x&-x;
}
int n,m,k;
int T;
vector<int>a[N];
ull h[N];
ull f(ull x){
	x^=M;
	x^=lowbit((x<<4)+M);
	x*=lowbit(x);
	x=x*x*x;
	x^=x<<13;
	x^=x>>7;
	x^=x<<17;
	x^=lowbit(x*x);
	x^=M;
	x^=lowbit(M*x-48);
	return x;
}
void xfs(int fa,int x){
	h[x]=1;
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		xfs(x,y);
		h[x]+=f(h[y]);
	}
}
void dfs(int fa,int x){
	for(int i=0;i<a[x].size();i++){
		int y=a[x][i];
		if(y==fa)continue;
		h[y]=h[y]+f(h[x]-f(h[y]));
		dfs(x,y);
	}
}
map<ull,int>mp;
signed main(){
	//ios::sync_with_stdio(0);
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	xfs(1,1);
	dfs(1,1);
	for(int i=1;i<=n;i++)mp[f(h[i])+1]=1,a[i].clear();
	for(int i=1;i<=n;i++){
		int u=read(),v=read();
		a[u].push_back(v);
		a[v].push_back(u);
	}
	xfs(1,1);
	dfs(1,1);
	for(int i=1;i<=n+1;i++){
		if(mp[h[i]]){
			print(i);
			return 0;
		}
	}
}
相关推荐
寻寻觅觅☆6 小时前
东华OJ-基础题-106-大整数相加（C++）
开发语言·c++·算法
偷吃的耗子7 小时前
【CNN算法理解】：三、AlexNet 训练模块(附代码)
深度学习·算法·cnn
化学在逃硬闯CS7 小时前
Leetcode1382. 将二叉搜索树变平衡
数据结构·算法
ceclar1238 小时前
C++使用format
开发语言·c++·算法
Gofarlic_OMS8 小时前
科学计算领域MATLAB许可证管理工具对比推荐
运维·开发语言·算法·matlab·自动化
夏鹏今天学习了吗8 小时前
【LeetCode热题100（100/100）】数据流的中位数
算法·leetcode·职场和发展
忙什么果9 小时前
上位机、下位机、FPGA、算法放在哪层合适？
算法·fpga开发
董董灿是个攻城狮9 小时前
AI 视觉连载4：YUV 的图像表示
算法
ArturiaZ10 小时前
【day24】
c++·算法·图论
大江东去浪淘尽千古风流人物10 小时前
【SLAM】Hydra-Foundations 层次化空间感知：机器人如何像人类一样理解3D环境
深度学习·算法·3d·机器人·概率论·slam
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03openclaw配置教程（linux+局域网ollama）04UV安装并设置国内源05Linux下V2Ray安装配置指南06openclaw使用nginx反代部署过程 与disconnected (1008): pairing required解决07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08【Linux操作系统12】Git版本控制与GDB调试：从入门到实践09Vue-skills的中文文档10OpenClaw Chrome扩展使用教程 - 浏览器中继控制