《LeetCode 顺序刷题》1 -10

1、[简单] 两数之和

数组 哈希表

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

C++

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hash;
        for (int i = 0; i < nums.size(); ++i) {
            int gap = target - nums[i];
            if (hash.count(gap)) {
                return {hash[gap], i};
            } else {
                hash[nums[i]] = i;
            }
        }
        return {-1, -1};
    }
};

Java

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
        for (int i = 0; i < nums.length; ++i) {
            if (hash.containsKey(target - nums[i])) {
                return new int[] { hash.get(target - nums[i]), i };
            }
            hash.put(nums[i], i);
        }
        return new int[0];
    }
}

Python

解题思路

1. 滑动窗口 ：使用两个指针 left 和 right 来表示窗口的左右边界。right 指针用于扩展窗口，left 指针用于收缩窗口。
2. 哈希表：使用一个哈希表（或数组）来记录窗口中每个字符的出现次数。
3. 窗口扩展 ：移动 right 指针，将字符加入窗口，并更新哈希表。
4. 窗口收缩 ：如果发现某个字符在哈希表中的值大于 1（即重复），则移动 left 指针，缩小窗口，并更新哈希表。
5. 更新结果：在每次窗口扩展后，计算当前窗口的长度，并更新最大长度。

复杂度分析

• 时间复杂度 ：O(n)，其中 n 是字符串的长度。每个字符只会被遍历一次。
• 空间复杂度 ：O(min(m, n))，其中 m 是字符集的大小。哈希表最多存储 m 个字符。

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        n = len(nums)
        for i in range(n):
            for j in range(i+1, n):
                if nums[i] + nums[j] == target:
                    return [i, j]

        return []

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        hashtable = dict();
        for i, num in enumerate(nums):
            if target - num in hashtable:
                return [hashtable[target - num], i]
            hashtable[nums[i]] = i;
        return []

2、[中等] 两数相加

链表 数学

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

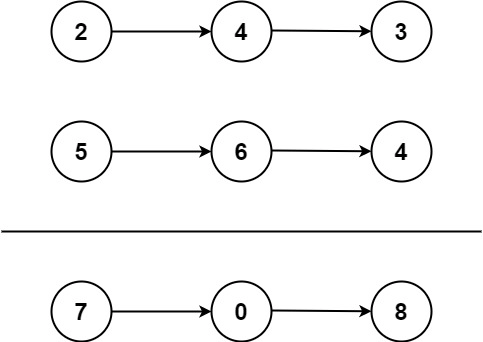
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

C++

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        if (!l1) {
            return l2;
        }
        if (!l2) {
            return l1;
        }
        ListNode head, *cur = &head, *cur1 = l1, *cur2 = l2;
        int add = 0;
        while (cur1 || cur2 || add) {
            if (cur1) {
                add += cur1->val;
                cur1 = cur1->next;
            }
            if (cur2) {
                add += cur2->val;
                cur2 = cur2->next;
            }
            cur->next = new ListNode(add % 10);
            cur = cur->next;
            add /= 10;
        }
        return head.next;
    }
};

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        // 如果其中一个链表为空，直接返回另一个链表
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }
        // 创建一个虚拟头节点，用于简化链表操作
        ListNode head = new ListNode(0);
        ListNode cur = head, cur1 = l1, cur2 = l2;
        int carry = 0; // 进位值
        // 遍历两个链表，直到所有节点都处理完且没有进位
        while (cur1 != null || cur2 != null || carry != 0) {
            // 如果当前节点不为空，将其值加到进位中
            if (cur1 != null) {
                carry += cur1.val;
                cur1 = cur1.next;
            }
            if (cur2 != null) {
                carry += cur2.val;
                cur2 = cur2.next;
            }
            // 创建新节点，存储当前位的值
            cur.next = new ListNode(carry % 10);
            cur = cur.next;
            // 更新进位
            carry /= 10;
        }
        // 返回结果链表的头节点
        return head.next;
    }
}

Python

class Solution(object):
    def addTwoNumbers(self, l1, l2):
        """
        :type l1: Optional[ListNode]
        :type l2: Optional[ListNode]
        :rtype: Optional[ListNode]
        """
        cur = dummy = ListNode()        # 哨兵节点
        carry = 0   # 进位
        while l1 or l2 or carry:        # 有一个不是空节点，或者还有进位，就继续迭代
            if l1:
                carry += l1.val         # 节点值和进位加在一起
                l1 = l1.next            # 下一个节点
            if l2:
                carry += l2.val
                l2 = l2.next
            cur.next = ListNode(carry % 10) # 每个节点保存一个数位
            carry //= 10                    # 新的进位
            cur = cur.next                  # 下一个节点
        return dummy.next                   # 哨兵节点的下一个节点就是头节点

3、[中等] 无重复字符的最长字串

哈希表 字符串 滑动窗口

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
  请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

C++

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int hash[128] = {0}; // 使用数组来模拟哈希表
        int left = 0, right = 0, n = s.size();
        int ret = 0;

        while (right < n) {
            hash[s[right]]++; // 进入窗口
            while (hash[s[right]] > 1) {
                hash[s[left++]]--;
            }
            right++;
            ret = max(ret, right - left);
        }

        return ret;
    }
};

Java

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 使用数组来模拟哈希表，记录字符的出现次数
        int[] hash = new int[128];
        int left = 0, right = 0, n = s.length();
        int maxLength = 0;

        while (right < n) {
            // 将当前字符加入窗口
            hash[s.charAt(right)]++;
            // 如果当前字符重复，移动左指针缩小窗口
            while (hash[s.charAt(right)] > 1) {
                hash[s.charAt(left++)]--;
            }
            // 更新最大长度
            right++;
            maxLength = Math.max(maxLength, right - left);
        }

        return maxLength;
    }
}

Python

解题思路

1. 滑动窗口 ：使用两个指针 left 和 right 来表示窗口的左右边界。right 指针用于扩展窗口，left 指针用于收缩窗口。
2. 哈希表：使用一个哈希表（或数组）来记录窗口中每个字符的出现次数。
3. 窗口扩展 ：移动 right 指针，将字符加入窗口，并更新哈希表。
4. 窗口收缩 ：如果发现某个字符在哈希表中的值大于 1（即重复），则移动 left 指针，缩小窗口，并更新哈希表。
5. 更新结果：在每次窗口扩展后，计算当前窗口的长度，并更新最大长度。

复杂度分析

• 时间复杂度 ：O(n)，其中 n 是字符串的长度。每个字符只会被遍历一次。
• 空间复杂度 ：O(min(m, n))，其中 m 是字符集的大小。哈希表最多存储 m 个字符。

class Solution(object):
    def lengthOfLongestSubstring(self, s):
        # 使用哈希表记录字符出现的次数
        hash_map = {}
        left = 0        # 窗口左边界
        max_len = 0     # 最长字串的长度

        for right in range(len(s)):
            # 如果字符已经存在于哈希表中，移动左边界
            if s[right] in hash_map:
                left = max(left, hash_map[s[right]] + 1)
            # 更新字符的最新位置
            hash_map[s[right]] = right
            # 更新最大长度
            max_len = max(max_len, right - left + 1)
        
        return max_len

4、[困难] 寻找两个正序数组的中位数

二分查找

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

C++

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size();
        int m = nums2.size();
        vector<int> v;
        v.resize(n + m);
        int i = 0, j = 0, k = 0;
        while (j < n && k < m) {
            if (nums1[j] < nums2[k]) {
                v[i++] = nums1[j++];
            } else {
                v[i++] = nums2[k++];
            }
        }
        while (j < n) {
            v[i++] = nums1[j++];
        }
        while (k < m) {
            v[i++] = nums2[k++];
        }
        int mid = (n + m) / 2;
        if ((n + m) % 2 == 1) {
            return v[mid];
        } else {
            return (v[mid] + v[mid - 1]) / 2.0;
        }
    }
};

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int totalLength = nums1.size() + nums2.size();
        if (totalLength % 2 == 1) {
            return getKthElement(nums1, nums2, (totalLength + 1) / 2);
        } else {
            return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
        }
    }

    int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
        int m = nums1.size();
        int n = nums2.size();
        int index1 = 0, index2 = 0;

        while (true) {
            if (index1 == m) {
                return nums2[index2 + k - 1];
            }
            if (index2 == n) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return min(nums1[index1], nums2[index2]);
            }

            int newIndex1 = min(index1 + k / 2 - 1, m - 1);
            int newIndex2 = min(index2 + k / 2 - 1, n - 1);
            int pivot1 = nums1[newIndex1];
            int pivot2 = nums2[newIndex2];

            if (pivot1 <= pivot2) {
                k -= newIndex1 - index1 + 1;
                index1 = newIndex1 + 1;
            } else {
                k -= newIndex2 - index2 + 1;
                index2 = newIndex2 + 1;
            }
        }
    }
};

Java

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        int[] merged = new int[n + m]; // 合并后的数组
        int i = 0, j = 0, k = 0;
        // 合并两个有序数组
        while (j < n && k < m) {
            if (nums1[j] < nums2[k]) {
                merged[i++] = nums1[j++];
            } else {
                merged[i++] = nums2[k++];
            }
        }
        // 如果 nums1 还有剩余元素
        while (j < n) {
            merged[i++] = nums1[j++];
        }
        // 如果 nums2 还有剩余元素
        while (k < m) {
            merged[i++] = nums2[k++];
        }
        // 计算中位数
        int mid = (n + m) / 2;
        if ((n + m) % 2 == 1) {
            return merged[mid]; // 奇数长度，直接返回中间元素
        } else {
            return (merged[mid] + merged[mid - 1]) / 2.0; // 偶数长度，返回中间两个元素的平均值
        }
    }
}

Python

解题思路

1. 合并数组 ：直接合并两个有序数组，然后找到中位数。这种方法的时间复杂度为 O(m + n)，不符合题目要求。
2. 二分查找 ：利用有序数组的性质，通过二分查找的方式找到中位数，时间复杂度为 O(log(m + n))。

二分查找的思路

• 将问题转化为在两个有序数组中寻找第 k 小的数。
• 每次比较两个数组中第 k/2 小的数，排除较小的那一部分。
• 递归或迭代地缩小范围，直到找到第 k 小的数。

复杂度分析

• 时间复杂度 ：O(log(m + n))，每次递归或迭代都会将问题规模减半。
• 空间复杂度 ：O(1)，只使用了常数级别的额外空间。

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        def findKth(nums1, nums2, k):
            # 确保 nums1 是较短的数组
            if len(nums1) > len(nums2):
                nums1, nums2 = nums2, nums1
            # 如果 nums1 为空, 直接返回 nums2 的第 k 小的数
            if not nums1:
                return nums2[k - 1]
            # 如果 k == 1，返回两个数组的最小值
            if k == 1:
                return min(nums1[0], nums2[0])
            # 取 nums1 和 nums2 的第 k//2 个数
            i = min(len(nums1), k // 2)
            j = min(len(nums2), k // 2)
            # 比较 nums1[i-1] 和 nums2[j-1], 排除较小的那一部分
            if nums1[i - 1] < nums2[j - 1]:
                return findKth(nums1[i:], nums2, k - i)
            else:
                return findKth(nums1, nums2[j:], k - j)

        m, n = len(nums1), len(nums2)
        total = m + n
        # 如果总长度为奇数, 返回第 (total + 1) // 2 小的数
        if total % 2 == 1:
            return findKth(nums1, nums2, (total + 1) // 2)
        # 如果总长度为偶数, 返回第 total // 2 和第 total // 2 + 1 小的数的平均值
        else:
            return (findKth(nums1, nums2, total // 2) + findKth(nums1, nums2, total // 2 + 1)) / 2

5、[中等] 最长回文子串

动态规划

给你一个字符串 s，找到 s 中最长的 回文 子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

C++

动态规划

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if (n < 2) {
            return s;
        }

        vector<vector<bool>> dp(n, vector(n, false));
        int len = 1, begin = 0;

        for (int j = 0; j < n; ++j) {
            for (int i = 0; i <= j; ++i) {
                if (s[i] == s[j]) {
                    dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
                }
                if (dp[i][j] && j - i + 1 > len) {
                    len = j - i + 1, begin = i;
                }
            }
        }

        return s.substr(begin, len);
    }
};

中心扩展

class Solution {
public:
    string longestPalindrome(string s) {
        // 中心扩展算法
        int begin = 0, len = 0, n = s.size();
        for (int i = 0; i < n; ++i) // 一次枚举所有的中点
        {
            // 先做一次奇数长度的扩展
            int left = i, right = i;
            while (left >= 0 && right < n && s[left] == s[right]) {
                --left;
                ++right;
            }
            if (right - left - 1 > len) {
                begin = left + 1;
                len = right - left - 1;
            }

            // 偶数长度的扩展
            left = i, right = i + 1;
            while (left >= 0 && right < n && s[left] == s[right]) {
                --left;
                ++right;
            }
            if (right - left - 1 > len) {
                begin = left + 1;
                len = right - left - 1;
            }
        }

        return s.substr(begin, len);
    }
};

Java

1. 动态规划 ：使用动态规划来解决这个问题。定义 dp[i][j] 表示字符串 s[i..j] 是否是回文子串。
2. 初始化 ：所有长度为 1 的子串都是回文子串，即 dp[i][i] = true。
3. 状态转移 ：
   • 如果 s[i] == s[j]，且 s[i+1..j-1] 是回文子串，则 s[i..j] 也是回文子串。
   • 如果 j - i < 3，即子串长度为 2 或 3，直接判断 s[i] == s[j] 即可。
4. 更新最长回文子串：在填充动态规划表的过程中，记录最长回文子串的长度和起始位置。
5. 返回结果：根据记录的起始位置和长度，返回最长回文子串。

class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        if (n < 2) {
            return s; // 如果字符串长度小于 2，直接返回
        }

        // 动态规划，dp[i][j] 表示 s[i..j] 是否是回文子串
        boolean[][] dp = new boolean[n][n];
        int maxLen = 1; // 最长回文子串的长度
        int begin = 0; // 最长回文子串的起始位置

        // 初始化：所有长度为 1 的字串都是回文子串
        for (int i = 0; i < n; ++i) {
            dp[i][i] = true;
        }

        // 动态规划填充表
        for (int j = 1; j < n; ++j) {
            for (int i = 0; i < j; ++i) {
                if (s.charAt(i) == s.charAt(j)) {
                    // 如果 s[i] == s[j]，且 s[i+1..j-1] 是回文子串, 则 s[i..j] 也是回文子串
                    if (j - i < 3) {
                        dp[i][j] = true; // 长度小于等于 3 时，直接为 true
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }
                // 更新最长回文子串的信息
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }

        // 返回最长回文子串
        return s.substring(begin, begin + maxLen);
    }
}

Python

解题思路

1. 动态规划 ：
   • 定义 dp[i][j] 表示字符串从索引 i 到 j 的子串是否是回文。
   • 如果 s[i] == s[j]，则 dp[i][j] 的值取决于 dp[i + 1][j - 1]。
   • 如果 j - i < 2（即子串长度为 1 或 2），则直接判断 s[i] == s[j]。
   • 在遍历过程中，记录最长的回文子串的起始位置和长度。
2. 中心扩展法 ：
   • 遍历字符串，以每个字符为中心向左右扩展，找到最长的回文子串。
   • 需要考虑奇数长度和偶数长度的情况。

这里我们使用 动态规划 的方法来实现。

复杂度分析

• 时间复杂度 ：O(n^2)，其中 n 是字符串的长度。需要填充一个 n x n 的动态规划表。
• 空间复杂度 ：O(n^2)，用于存储动态规划表。

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        if n < 2:       # 如果字符串长度小于 2, 直接返回
            return s

        # 初始化动态规划表
        dp = [[False] * n for _ in range(n)]
        max_len = 1     # 最长回文子串的长度
        start = 0       # 最长回文子串的起始位置

        # 所有长度为 1 的子串都是回文
        for i in range(n):
            dp[i][i] = True

        # 遍历所有可能的子串长度
        for length in range(2, n + 1):
            for i in range(n):
                j = i + length - 1      # 子串的结束位置
                if j >= n:              # 如果结束位置超出范围, 跳出循环
                    break
                # 判断子串是否是回文
                if s[i] == s[j]:
                    if length == 2:     # 长度为 2 的子串
                        dp[i][j] = True
                    else:               # 长度大于 2 的子串
                        dp[i][j] = dp[i + 1][j - 1]
                # 更新最长回文子串的信息
                if dp[i][j] and length > max_len:
                    max_len = length
                    start = i

        # 返回最长回文子串
        return s[start:start + max_len]

6、[中等] Z 字形变换

字符串 数学

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。

请你实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows);

示例 1：

输入：s = "PAYPALISHIRING", numRows = 3
输出："PAHNAPLSIIGYIR"

示例 2：

输入：s = "PAYPALISHIRING", numRows = 4
输出："PINALSIGYAHRPI"
解释：
P     I    N
A   L S  I G
Y A   H R
P     I

示例 3：

输入：s = "A", numRows = 1
输出："A"

C++

class Solution {
public:
    string convert(string s, int numRows) {
        if (numRows == 1) {
            return s;
        }
        string ret;
        int d = 2 * numRows - 2;
        int n = s.size();

        // 1. 先处理第一行
        for (int i = 0; i < n; i += d) {
            ret += s[i];
        }

        // 2. 处理中间行
        for (int k = 1; k < numRows - 1; k++) {
            for (int i = k, j = d - k; i < n || j < n; i += d, j += d) {
                if (i < n) {
                    ret += s[i];
                }
                if (j < n) {
                    ret += s[j];
                }
            }
        }

        // 3. 处理最后一行
        for (int i = numRows - 1; i < n; i += d) {
            ret += s[i];
        }

        return ret;
    }
};

Python

解题思路

1. 模拟 Z 字形排列 ：
   • 创建一个包含 numRows 个字符串的列表，用于存储每一行的字符。
   • 使用一个变量 current_row 表示当前字符应该放在哪一行。
   • 使用一个变量 direction 表示当前是向下移动还是向上移动。
   • 遍历字符串，将字符添加到对应的行中，并根据方向更新 current_row。
2. 逐行读取字符 ：
   • 将每一行的字符按顺序拼接起来，得到最终结果。

复杂度分析

• 时间复杂度 ：O(n)，其中 n 是字符串的长度。每个字符只会被处理一次。
• 空间复杂度 ：O(n)，用于存储每一行的字符。

class Solution:
    def convert(self, s: str, numRows: int) -> str:
        if numRows == 1 or numRows >= len(s):   # 特殊情况处理
            return s

        # 初始化每一行的字符串
        rows = [""] * numRows
        current_row = 0                         # 当前行
        direction = -1                          # 移动方向: 1 表示向下, -1 表示向上

        for char in s:
            rows[current_row] += char           # 将字符添加到当前行
            if current_row == 0 or current_row == numRows - 1:      # 改变方向
                direction *= -1
            current_row += direction            # 更新当前行

        # 将所有行的字符串拼接起来
        return "".join(rows)

7、[中等] 整数反转

数学

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

输入：x = 123
输出：321

示例 2：

输入：x = -123
输出：-321

示例 3：

输入：x = 120
输出：21

示例 4：

输入：x = 0
输出：0

C++

class Solution {
public:
    int reverse(int x) {
        int ret = 0;
        while (x != 0) {
            if (ret < INT_MIN / 10 || ret > INT_MAX / 10) {
                return 0;
            }
            int digit = x % 10;
            x /= 10;
            ret = ret * 10 + digit;
        }
        return ret;
    }
};

Java

class Solution {
    public int reverse(int x) {
        int reversed = 0;
        while (x != 0) {
            // 检查是否溢出
            if (reversed < Integer.MIN_VALUE / 10 || reversed > Integer.MAX_VALUE / 10) {
                return 0;
            }
            int digit = x % 10; // 获取最后一位数字
            x /= 10; // 去掉最后一位数字
            reversed = reversed * 10 + digit; // 将数字添加到反转结果中
        }
        return reversed;
    }
}

Python

class Solution:
    def reverse(self, x: int) -> int:
        INT_MIN, INT_MAX = -(2**31), 2**31 - 1  # 32 位有符号整数的范围
        ret = 0
        # 初始化结果变量

        while x != 0:
            # 检查是否超出范围
            # INT_MIN 也是一个负数，不能写成 rev < INT_MIN // 10
            if ret < INT_MIN // 10 + 1 or ret > INT_MAX // 10:
                return 0
            digit = x % 10 if x > 0 else -(-x % 10)  # 处理负数
            x = x // 10 if x > 0 else -(-x // 10)  # 处理负数
            ret = ret * 10 + digit  # 更新结果

        return ret

8、[中等] 字符串转换整数

字符串

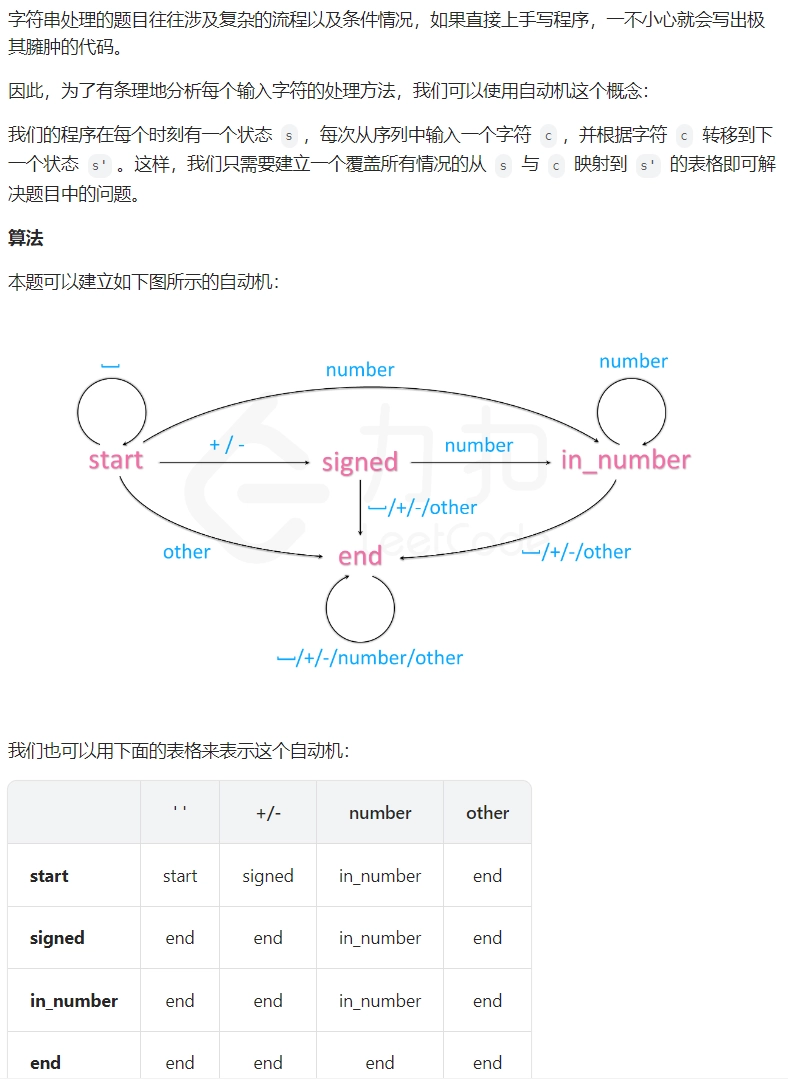
class Automaton {
private:
    unordered_map<string, vector<string>> table = {
        {"start", {"start", "signed", "in_number", "end"}},
        {"signed", {"end", "end", "in_number", "end"}},
        {"in_number", {"end", "end", "in_number", "end"}},
        {"end", {"end", "end", "end", "end"}}};

    int get_col(char c) {
        if (isspace(c)) {
            return 0;
        }
        if (c == '+' || c == '-') {
            return 1;
        }
        if (isdigit(c)) {
            return 2;
        }
        return 3;
    }

public:
    string state = "start";
    int sign = 1;
    long long ret = 0;

    void get(char c) {
        state = table[state][get_col(c)];
        if (state == "in_number") {
            ret = ret * 10 + c - '0';
            ret = sign == 1 ? min(ret, (long long)INT_MAX) : min(ret, -(long long)INT_MIN);
        } else if (state == "signed") {
            sign = c == '+' ? 1 : -1;
        }
    }
};

class Solution {
public:
    int myAtoi(string s) {
        Automaton automaton;
        for (char c : s) {
            automaton.get(c);
        }
        return automaton.sign * automaton.ret;
    }
};

9、[简单] 回文数

数学

class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0) {
            return false;
        }

        long long ret = 0;
        int tmp = x;
        while (tmp) {
            ret = ret * 10 + tmp % 10;
            tmp /= 10;
        }

        return ret == x;
    }
};

class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0 || x % 10 == 0 && x != 0) {
            return false;
        }

        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }
        return x == revertedNumber || x == revertedNumber / 10;
    }
};

10、[困难] 正则表达式

字符串 动态规划

class Solution {
public:
    bool isMatch(string s, string p) {
        s = " " + s;
        p = " " + p;
        int m = s.size();
        int n = p.size();
        vector<vector<bool>> dp(m, vector(n, false));
        dp[0][0] = true;
        for (int j = 2; j <= n; j += 2) {
            if (p[j] == '*') {
                dp[0][j] = true;
            } else {
                break;
            }
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (p[j] == '*') {
                    dp[i][j] = dp[i][j - 2] || (p[j - 1] == '.' || p[j - 1] == s[i]) && dp[i - 1][j];
                } else {
                    dp[i][j] = (p[j] == s[i] || p[j] == '.') && dp[i - 1][j - 1];
                }
            }
        }
        return dp[m - 1][n - 1];
    }
};