2026牛客寒假算法赛（一）

题目难度分析：

L Need Zero 675 ~ 730 数论, 数学, 枚举, 贪心, gcd与exgcd

C Array Covering 820 ~ 943 贪心

E Block Game 825 ~ 935 模拟, 贪心, 构造、Ad-hoc

K Constructive 1091 ~ 1198 数学, 构造, 分类讨论、不变量分析

B Card Game 1299 ~ 1556 贪心, 组合数学, 排序

A A+B Problem 1375 ~ 1429 动态规划, 组合数学, 概率期望, 模运算, 快速幂, 枚举

H Blackboard 1764 ~ 1877 动态规划, 位运算, 双指针/滑动窗口, 前缀和：

G Digital Folding 1901 ~ 2145 贪心, 数位DP, 构造、数学, 枚举, 同余, Ad-hoc

I AND vs MEX 1958 ~ 2070 位运算, 数学, 分类讨论, 构造、贪心

D Sequence Coloring 2220 ~ 2340 二分答案, 贪心, RMQ, ST表, 倍增

F Permutation Counting 2493 ~ 2579 并查集, 线段树, 贪心, 组合数学, 离线处理、构造

J MST Problem 2538 ~ 2637 生成树, 贪心, 并查集, 排序, 线段树、Boruvka算法, 等价转换

L Need Zero

一、题目概述

题目描述

小笨拿到一个正整数 n，现在他希望 n 的个位数是0，为此他必须执行下述操作恰好一次：

选择一个正整数x（),并执行 n = n * x

你的任务是找到最小的合法解 x

输入描述:
复制代码
        输入一个正整数 n（），表示小苯拿到的数字。
输出描述:
复制代码
        输出一个正整数，表示最小的合法解 x（可以证明在题目的限定范围内一定有解）。

二、思路：

目标：让n变为10的倍数。

（1）暴力做法，从1遍历到10，一定找得到答案x，见代码1。

（2）n本身有4种可能，10的倍数，2的倍数，5的倍数，都不是。分别对应x为：1，5，2，10

三、参考代码O(1)

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    if(n % 10 == 0) cout << 1;
    else if(n % 2 == 0) cout << 5;
    else if(n % 5 == 0) cout << 2;
    else cout << 10;
    return 0;
}

C Array Covering

一、题目概述

题目描述

给定长度为n的数组，其中第i的数的值为

小笨希望数组中所有数字的总和尽可能大，为此它可以做任意次如下操作：

选择一对下标l，r（），接着将（l，r）开区间内所有的数都变成区间端点出处较大者。

你的任务是求出数组总和的最大值

输入描述:

每个测试文件均包含多组测试数据。第一行输入一个整数 T（）代表数据组数，每组测试数据描述如下：

第一行输入一个正整数 n（），表示数组 a 的长度。

第二行输入 n 个正整数（），表示最初时所有数字的值。

输出描述:

对于每一组测试数据，新起一行输出一个正整数，表示在可以进行任意次操作的情况下，所有数字之和的最大值。

二、思路：

目标：找到最大的数组之和。

因为可以任意次操作，很容易想到可以使所有的数都变成边缘最大值，除了a[1]和a[n]。

三、参考代码 O(n)

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int a[N];
void solve(){
    long long n;
    cin >> n;
    int maxn = 0;
    for(int i = 1; i <= n; i ++){
        cin >> a[i];
        maxn = max(maxn, a[i]);
    }
    if(n == 1) cout << a[1] << endl;
    else cout << a[1] + a[n] + maxn * (n - 2) << endl;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T --){
        solve();
    }
    return 0;
}

E Block Game

一、题目概述

题目描述

小笨正在玩方块小游戏，游戏中有一排 n 个方块，每个方块都有一个数字，此外，他还有一个写着数字k的万能方块，游戏过程如下：

小笨可以任意次如下操作：

将万能方块从方块序列的最左侧插入，同时第 n 个方块被挤出这一行，成为新的万能方块。

你的任务是计算出，按照最优方式经过若干次操作后，从左往右数第一个 方块上的数字加上最终的万能方块上的数字的总和的最大值。

输入描述:

每个测试文件均包含多组测试数据。第一行输入一个整数 T（）代表数据组数，每组测试数据描述如下：

第一行输入两个整数 n,k（，），表示方块个数、初始的万能方块上的数字。

第二行输入n 个整数，表示从左往右数第 iii 个方块上写的数字。

输出描述:

对于每一组测试数据，新起一行输出一个整数，表示最终：从左往右数第一个方块上的数字 + 万能方块上的数字之和（即）的最大值。

二、思路：

目标：找的最大值。

注意到，这种形式有一些像队列，队首插入，队尾弹出。所以每相邻的两个数都可能成为k + a[1]，所以我们只需要找到相邻两个数最大即可。

三、参考代码 O(n)

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int a[N];
void solve(){
    int n, k;
    cin >> n >> k;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    int maxn = -1e7;
    for(int i = 2; i <= n; i ++){
        maxn = max(maxn, a[i] + a[i - 1]);
    }
    maxn = max(maxn, a[n] + k);
    maxn = max(maxn, a[1] + k);
    cout << maxn << endl;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T --){
        solve();
    }
    return 0;
}

K Constructive

略，过于简单

B Card Game

一、题目概述

题目描述

小苯正在和小红玩卡牌游戏。游戏中有张牌，每张牌上都有一个数字，所有牌的数字恰好构成了一个长度为的++排列++ 。

游戏最初时，张卡牌被恰好平均分成了两组 n 张牌，并分别发给了两人，小苯第 i 张牌上的数字是，而小红第 i 张牌上的数字是，具体的游戏过程如下：

如果两人之中有一人已经没有牌了，则游戏结束。

比较两人当前手牌中的最前一张，对应数字大的那一方得一分并将该张牌从自己手牌移除；另一方不得分，手牌也不变。随后进入下一轮。

而现在小苯希望自己的得分尽可能多，为此他在游戏开始前可以任意地 重新排列自己的牌，以得到更高的游戏分数。

现在你的任务则是求出，有多少种重新排列（选择不进行重排也是一种方案）的方式，能使得小苯得到他能得到的最高分。由于答案可能很大，请将答案对 998 244 353 取模后输出。

输入描述:

每个测试文件均包含多组测试数据。第一行输入一个整数 T（）代表数据组数，每组测试数据描述如下：

第一行输入一个正整数 n（），表示两人的卡牌数量。

第二行输入 n 个正整数，表示小苯的卡牌上的数字。

第三行输入 n 个正整数 )，表示小红的卡牌上的数字。

（保证 a 数组和 b 数组共同构成一个长度为的排列。）

输出描述:

对于每一组测试数据，新起一行输出一个整数，表示小苯重新排列自己卡牌，使得他能得到的最高分的方案数对 998 244 353 取模后的值。

二、思路：

目标：使小笨（a）的得分最多，即尽可能多的打大于b的牌，得一分，但舍牌。

误区：不同于田忌赛马，因为小的那张牌只是丢一分，但不会被删除。所以没必要让比b较大的a比掉它。

因为我们知道，只要a都大于，所有的a都可以得分，所以我们的思路是让a降序排序，看看能到。但其实我们无需关注i是几，因为只需a的得分最大即可，b不管。

方法统计，我们知道，大于的一定要排在小于它的之前，这样才能都得分，如果有比它小的，就提前被消耗掉了，比它大的a也跑不掉了。所以，大于bmin之前的a可以任意排序，小于bmin的也可以任意排序，因为也不可能跑掉了。

设x为a大于的数量，y为小于它的数量，根据排列组合公式，有

即

三、参考代码 O(n)

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
const int MOD = 998244353;
int a[N];
void solve(){
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];  //输入a的值
    int minn = 1e9;
    for(int i = 1; i <= n; i ++){
        int x; //只需要记录b的min即可，不管b得分
        cin >> x;
        if(x < minn) minn = x;
    }
    int x = 0, y = 0;
    //x:a大于bmin的数量，a的得分。
    //y：bmin大于a的数量，此次得分已为极限
    for(int i = n; i >= 1; i --){
        if(a[i] > minn) x ++;
        else y ++;
    }
    int ans = 1;
    //x的全排列
    for(int i = 1; i <= x; i ++){
        ans = ans * i % MOD;
    }
    //y的全排列
    for(int i = 1; i <= y; i ++){
        ans = ans * i % MOD;
    }
    cout << ans << endl;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T --){
        solve();
    }
    return 0;
}

A A+B Problem

略，不想做

H Blackboard

一、题目概述

题目描述

小红在黑板上写了一个计算式，具体来讲是 n 个数字，其中间由 n−1 个加号（'+ '）连接组成：。

现在小苯想去擦去黑板上的一些 '+' 运算符，但他擦得很不干净，只擦去了加号中的横线（'-'），剩下的部分就是一个竖线（'|'）了。巧合的是，| 恰好也是一个运算符：按位或 or 。

小苯想知道，有多少种不同的擦黑板方式，能使得按照新算式进行计算，结果和擦黑板前的算式计算结果相同，请你帮他算一算。注意，不擦黑板也是一种方案。由于答案可能很大，请将答案对 998 244 353 取模后输出。

【注】

特别的，在本题中我们认为 or 运算符的优先级大于加法运算 '+' 。

两种擦黑板方式不同当且仅当存在至少一个运算符位置，其在其中一个方式中为 '+'，而在另一个方式中为 '|'（即按位或 or）。

输入描述:

每个测试文件均包含多组测试数据。第一行输入一个整数 T（）代表数据组数，每组测试数据描述如下：

第一行输入一个整数 n（），表示黑板上的数字个数。

第二行输入 n 个整数，表示黑板上的数字。

输出描述:

对于每一组测试数据，新起一行输出一个整数，表示不同的擦黑板方案个数对 998 244 353 取模后的答案。

二、思路：

目标：找出方案数。

我们先要明确一个目标，就是把'+'改成'|'后，它的值不变，即，当时，我们就有了三种选择，或或，如何统计一共有多少种选择呢？可以参考区间划分dp问题。

三、参考代码 O(n)

cpp 复制代码

#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
using namespace std;
using ll = long long;
int t;
int MOD = 998244353;

void solve(){
    int n; cin >> n;
    int lst = 0;
    vector<int> a(n + 1);
    vector<int> pre(n + 1);
    for(int i = 1;i <= n;i++){
        cin >> a[i];
        //pre[i] 存储的是 i 左边最近的一个非0元素的下标
        pre[i] = lst;// lst 记录上一个非0的位置
        if(a[i] > 0) lst = i;
    }
    vector<int> dp(n + 2);
    vector<int> s(n + 2);//前缀和数组
    dp[1] = 1,s[1] = 1;
    for(int i = 1;i <= n;i++){
        int j = i;//该区间向前找
        int val = 0;
        while(j > 0 && (val & a[j]) == 0){ //还没找到头 且 当前区间的val & 下一位还等于0
            val |= a[j];
            j = pre[j];//直接跳到上一个非0数，忽略中间的0
        }
        // 合法的上一刀位置范围是 [j+1, i]
        // 对应的 dp 值之和就是 s[i] - s[j]
        dp[i + 1] = (s[i] - s[j] + MOD) % MOD;
        s[i + 1] = (s[i] + dp[i + 1]) % MOD;
    }
    cout << dp[n + 1] << endl;
}

int main(){
    ios::sync_with_stdio(false),cin.tie(nullptr);
    cout.tie(0);
    cin >> t;
    while(t--){
        solve();
    }
    return 0;
}

G Digital Folding

一、题目概述

题目描述

小苯发现了一种特殊的数字运算，称为"数字折叠"。对于一个正整数 x，定义其 "折叠数" 为：

将 x 的十进制数位翻转并去除前导 0 ，x 的值更改为翻转后得到的新数。

例如，123操作后会变为 321，而 120 会变为 21。

现在小苯拿到了一个区间 [l,r]，他想知道如果将区间中所有的整数 i（）的折叠数都求出，那么其中的最大值是多少。你的任务就是求出这个最大值。

输入描述:

每个测试文件均包含多组测试数据。第一行输入一个整数 T（）代表数据组数，每组测试数据描述如下：

在一行上输入两个整数 l, r（），表示询问的区间。

输出描述:

对于每一组测试数据，新起一行输出一个整数，表示区间中所有数的 "折叠数" 的最大值。

二、思路：

目标：找到[l, r]区间内的数中，翻转后最大的那个。

首先要使数最大，有两点：1，位数最大；2，高位尽可能大->9

基于这两点，首先构造出的数一定和r位数相同（除了r为1000等），然后尽可能这个数位数大，高位数尽可能大。

Step 1：

使l和r位数相同，l位数不够，补前导0

Step 2：

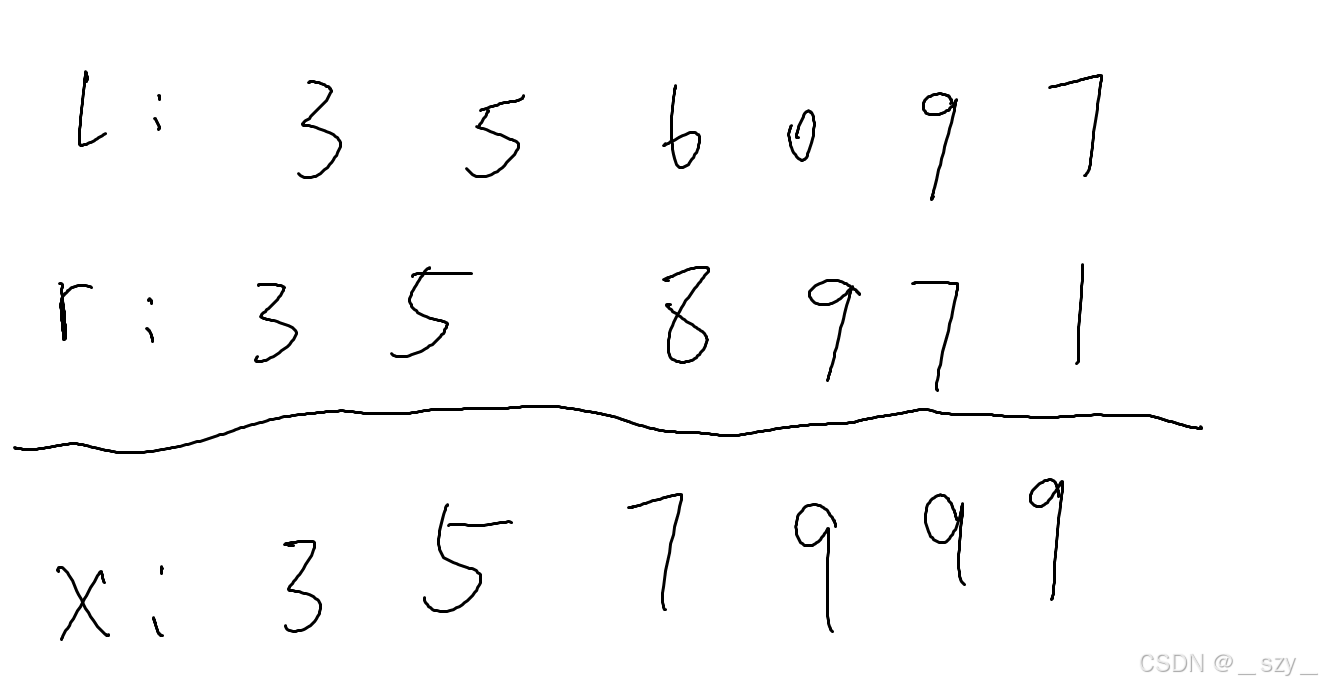
我们发现一个规律，构造的数，高位一定取l与r的交集，下一位为r对应位数的数小1，这样后面都能补9，同时翻转的数最大，除非本来后面就都是9，则不用，eg：

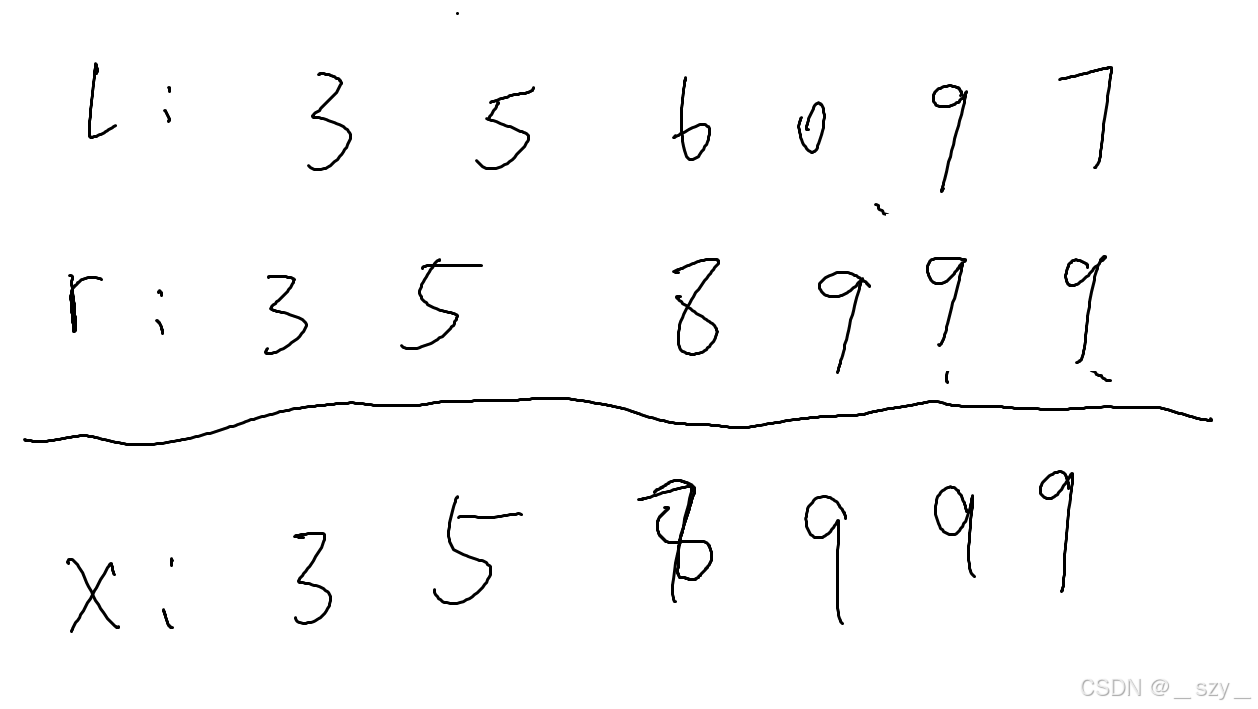
基于规律，不妨数字直接用字符串表示

三、参考代码 O(n)

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;

//反转折叠数
long long reverse_number(long long x) 
{
    long long res = 0;
    while (x > 0) 
    {
        res = res * 10 + (x % 10);
        x /= 10;
    }
    return res;
}

long long solve(long long l, long long r) 
{
    //初始化答案为r的折叠数
    long long ans = reverse_number(r);
    
    // 找到最接近r且低位全是9的数
    for (long long p = 10; p <= r; p *= 10) 
    {
        long long candidate = r - (r % p) - 1;
        if (candidate >= l)
        {
            ans = max(ans, reverse_number(candidate));
        }
    }
    
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    int t;
    cin >> t;
    
    while (t--) 
    {
        long long l, r;
        cin >> l >> r;
        cout << solve(l, r) << '\n';
    }
    
    return 0;
}