【Day28】55.跳跃游戏 45.跳跃游戏II

文章目录

• 55.跳跃游戏
• 题目：
• 思路：
• • [示例1：nums = [2,3,1,1,4]](#示例1：nums = [2,3,1,1,4])
  • [示例2：nums = [3,2,1,0,4]](#示例2：nums = [3,2,1,0,4])
• 代码实现（Go）：
• 45.跳跃游戏II
• 题目：
• 思路：
• • 示例：
• 代码实现（Go）：

55.跳跃游戏

题目：

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]

输出：true

解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]

输出：false

解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

提示：

1 <= nums.length <= 10^4

0 <= nums[i] <= 10^5

---

思路：

1. 初始化 ：定义一个变量 max_reach，表示当前能跳到的最远下标，初始值为 0（一开始站在第一个位置）。
2. 遍历数组 ：从第一个下标开始，逐个检查每个位置：
   • 如果当前下标 i 已经超过了 max_reach，说明这个位置根本到不了，直接返回 false；
   • 否则，更新 max_reach：max_reach = max(max_reach, i + nums[i])（当前位置能跳的最远位置 = 之前的最远位置 vs 当前位置i + 该位置能跳的最大长度）；
   • 如果 max_reach 已经 >= 数组最后一个下标，说明能到终点，直接返回 true。
3. 遍历结束 ：如果遍历完都没提前返回，说明到不了终点，返回 false。

在位置 i，能跳的最大长度是 nums [i]，

但也可以跳 1、2...nums [i]-1 步（不是必须跳满）。
只要max_reach能覆盖某个位置，这个位置之前的所有位置都能到达。

---

示例1：nums = [2,3,1,1,4]

• 初始 max_reach = 0
• i=0：i<=max_reach（0<=0），更新 max_reach = max(0, 0+2)=2 → 能到下标2
• i=1：i<=max_reach（1<=2），更新 max_reach = max(2,1+3)=4 → 4已经是最后一个下标（数组长度5，最后下标4），直接返回true

示例2：nums = [3,2,1,0,4]

• 初始 max_reach = 0
• i=0：更新 max_reach = max(0,0+3)=3
• i=1：i<=3，更新 max_reach = max(3,1+2)=3
• i=2：i<=3，更新 max_reach = max(3,2+1)=3
• i=3：i<=3，更新 max_reach = max(3,3+0)=3
• i=4：i=4 > max_reach=3 → 直接返回false

---

代码实现（Go）：

package main

import "fmt"

func canJump(nums []int) bool {
	n := len(nums)
	maxReach := 0 // 记录当前能到达的最远下标

	for i := 0; i < n; i++ {
		// 当前下标超过最远可达位置，直接返回false
		if i > maxReach {
			return false
		}

		// 更新最远可达位置
		curReach := i + nums[i] // 当前位置i + 该位置能跳的最大长度
		if curReach > maxReach {
			maxReach = curReach
		}

		// 提前终止：已能到达最后一个下标
		if maxReach >= n-1 {
			return true
		}
	}
	return false
}

func main() {
	var n int
	fmt.Scan(&n)

	nums := make([]int, n)
	for i := 0; i < n; i++ {
		fmt.Scan(&nums[i])
	}

	if canJump(nums) {
		fmt.Println("true")
	} else {
		fmt.Println("false")
	}
}

或者：

func main() {
	var num int
	var nums []int
	// 循环读取所有输入的整数（直到输入结束）
	for {
		_, err := fmt.Scan(&num)
		if err != nil {
			break
		}
		nums = append(nums, num)
	}
	// 输出结果
	fmt.Println(canJump(nums))
}

---

45.跳跃游戏II

题目：

给定一个长度为 n 的 0 索引整数数组 nums。初始位置在下标 0。

每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在索引 i 处，你可以跳转到任意 (i + j) 处：

• 0 <= j <= nums[i] 且
• i + j < n

返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。

示例 1:

输入: nums = [2,3,1,1,4]

输出: 2

解释: 跳到最后一个位置的最小跳跃数是 2。

从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]

输出: 2

提示:

1 <= nums.length <= 10^4

0 <= nums[i] <= 1000

题目保证可以到达 n - 1

---

思路：

通过「贪心」的策略进行正向查找，每次在当前能到达的范围内，选择能跳到最远位置的点，这样能保证跳跃次数最少。

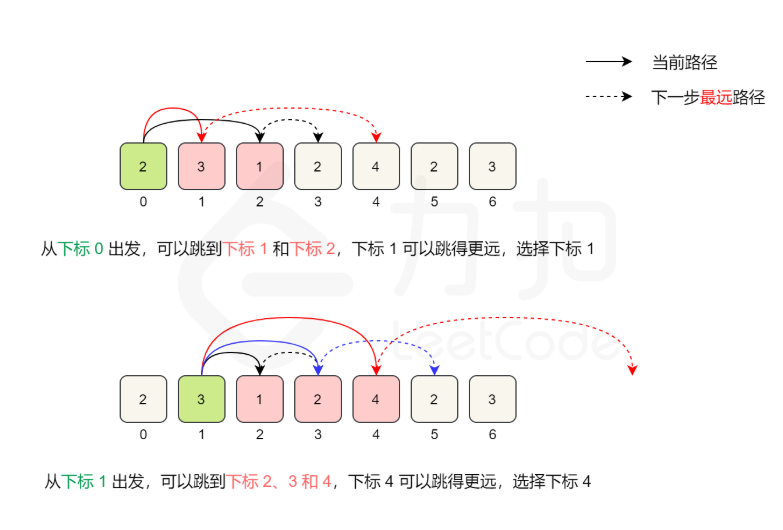
例如，对于数组 [2,3,1,2,4,2,3]，

初始位置是下标 0，从下标 0 出发，最远可到达下标 2。

下标 0 可到达的位置中，下标 1 的值是 3，从下标 1 出发可以达到更远的位置，因此第一步到达下标 1。

从下标 1 出发，最远可到达下标 4。

下标 1 可到达的位置中，下标 4 的值是 4 ，

从下标 4 出发可以达到更远的位置，因此第二步到达下标 4。

---

1. 定义三个关键变量：
   • steps：记录跳跃的次数
   • curEnd：当前跳跃能到达的最远边界
   • maxPosition：在遍历过程中，能到达的全局最远位置
2. 遍历数组（不遍历最后一个元素，因为到达最后一个元素就完成了，最后不需要再跳跃到其他位置）：
   • 每次更新maxPosition为 max(maxPosition, i + nums[i])
   • 当遍历到curEnd时，说明需要进行一次跳跃：
     • steps加1
     • 将curEnd更新为当前的maxPosition
3. 当curEnd超过或等于最后一个元素的下标时，提前终止。

在遍历数组时，不访问最后一个元素 ，因为在访问最后一个元素之前，边界一定大于等于最后一个位置，否则就无法跳到最后一个位置了。

---

示例：

nums = [3, 7]（数组长度n=2，终点下标是1）

初始值：

• steps = 0（跳跃次数初始为0）
• currentEnd = 0（当前跳的边界初始是下标0）
• maxPosition = 0（全局最远位置初始是0）
• 遍历范围：i 只需要遍历到 n-2 = 0（也就是只遍历i=0这一个位置）

第一步：进入循环，i=0

1. 计算 i + nums[i]：0 + 3 = 3，这个值比当前的maxPosition（0）大，所以把maxPosition更新为3；
2. 检查 i == currentEnd：i=0，currentEnd=0，条件成立，进入这个判断块：
   • 第一步：steps++ → steps 从0变成1（这代表我们确定要跳一次）；
   • 第二步：currentEnd = maxPosition → currentEnd 从0更新为3（下一跳的边界变成3）；
   • 第三步：检查 currentEnd >= n-1：currentEnd=3，n-1=1，3≥1成立，触发break，直接跳出循环；

第二步：循环终止，返回结果

最终steps的值是1，也就是从下标0跳到下标1只需要1次跳跃（哪怕nums[0]=3，能跳3步，也只需要跳1步就到终点）。

---

代码实现（Go）：

package main

import "fmt"

func jump(nums []int) int {
	n := len(nums)

	steps := 0       // 跳跃次数
	curEnd := 0      // 当前跳跃的最远边界
	maxPosition := 0 // 全局能到达的最远位置

	// 遍历到倒数第二个元素即可
	for i := 0; i < n-1; i++ {
		// 更新全局最远位置，当前位置i + 该位置能跳的最大长度
		if i+nums[i] > maxPosition {
			maxPosition = i + nums[i]
		}
		// 到达当前边界，必须跳一次
		if i == curEnd {
			steps++
			curEnd = maxPosition // 把下一跳的边界更新为当前能到的最远位置
			// 提前终止：如果新边界已经能到终点，不用继续遍历了
			if curEnd >= n-1 {
				break
			}
		}
	}
	return steps
}

func main() {
	var n int
	fmt.Scan(&n)
	nums := make([]int, n)

	for i := 0; i < n; i++ {
		fmt.Scan(&nums[i])
	}
	fmt.Println(jump(nums))
}

---