一、为什么要对示教数据进行时间对齐
在机器人示教学习的过程中,往往需要采集多条示教数据,但是采集得到的数据有个问题,就是不同数据的时间长度可能不一样。比如我们示教一个拿水杯倒水的过程,分为三个阶段,阶段一是放置杯子,阶段二是拿起水壶倒水,第三个阶段是把水壶放下。我们肯定不能保证每一次示教都是用了3秒来放置杯子,有可能第二次示教的时候比较慢用了5秒才把杯子放好。这就存在时间不对齐的情况。但我们基本能保证所有示教数据都是包含了三个阶段的。现在我们就要用时间对齐的方式,把所有的示教数据每个阶段用的时间都对齐。
举个例子
可以看到黑色的线条是第一条示教数据,和蓝色的第二条示教数据是没有对齐的,很明显的两个波峰没有对齐,也就是第二条示教过程速度太快了,明显比第一条数据超前了。如果数据不对齐直接进行示教学习是不行的,数据不一致学到的结果是错误的。
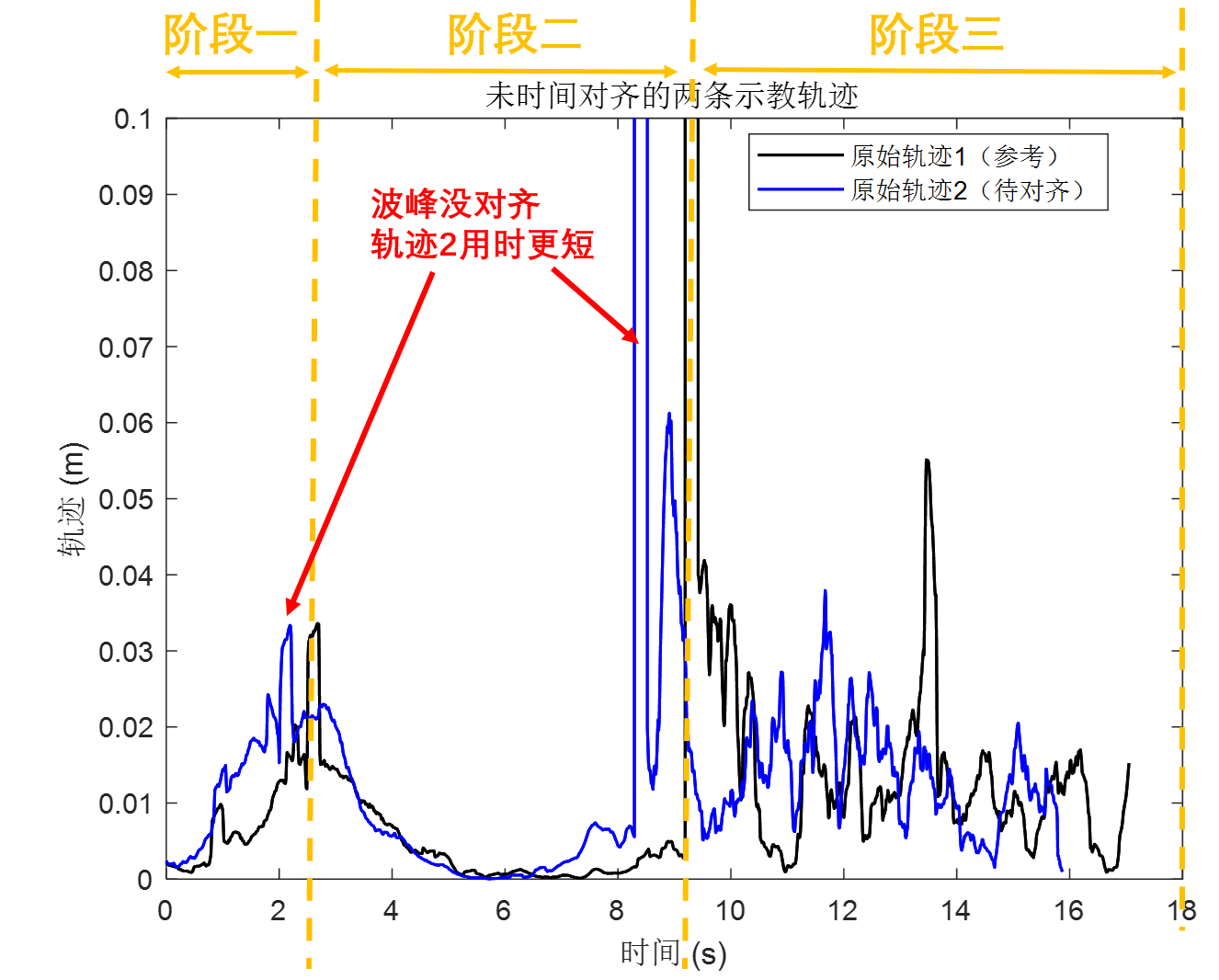
图1 未时间对齐的两条轨迹
可以看到图2是使用了时间对齐算法之后的两条轨迹,两个波峰基本对齐了。在这里由于轨迹1(黑色)的时间更长,所以我们把轨迹1当做参考轨迹,放缩轨迹2(蓝色),得到放缩后的轨迹2(红色),这样时间对齐了之后就可以进行后面的示教学习了。
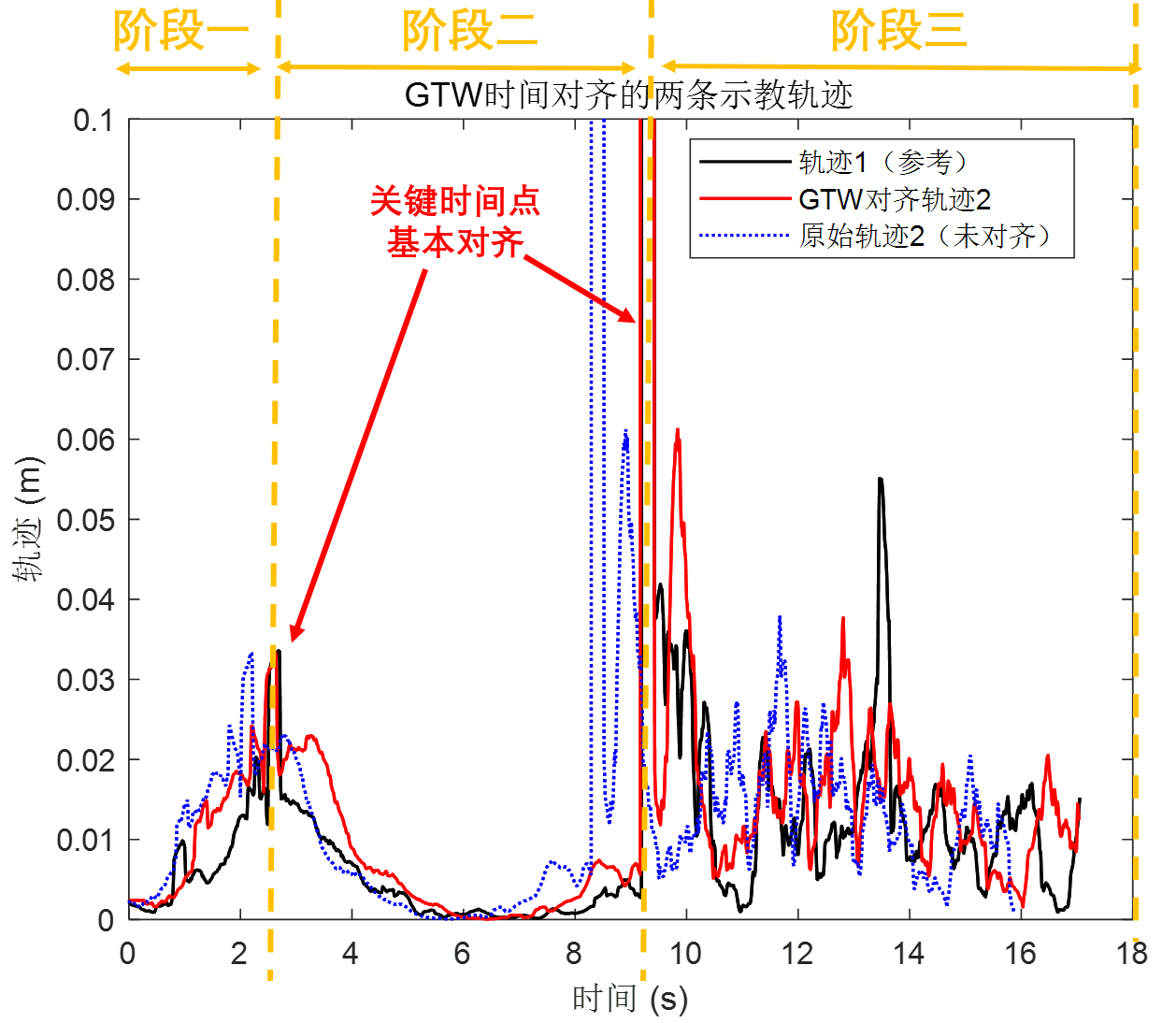
图2 GTW时间对齐的两条轨迹
二、时间对齐算法DTW & GTW
比较常见的时间对齐算法就是DTW(动态时间规整,D ynamic T ime W arping)和GTW(广义时间规整,G eneralized T ime Warping)。
2.1 DTW
(1)核心目标: 对齐两条一维时间序列,即使它们在时间轴上有非线性伸缩(如速度快慢不一)。
(2)关键原理:
-
单一维度比对: 计算两个序列点之间的距离矩阵(通常是欧氏距离)。
-
路径搜索: 在距离矩阵中,寻找一条从起点到终点的累积代价最小的路径。这条路径定义了如何"扭曲"一条序列的时间轴以匹配另一条。
-
约束: 路径搜索通常受单调性、连续性和边界条件约束。
(3)优点:
-
概念直观,算法经典且成熟。
-
对于对齐一维信号(如语音波形、单变量传感器数据)非常有效。
-
计算相对简单,有大量优化和变种算法(如FastDTW)。
(4)局限性:
-
主要为一维设计 :对于多维时间序列(如空间坐标
(x, y, z)、多通道EEG信号),标准做法是计算各维度的DTW然后求和或平均,但这忽略了维度间的相关性。 -
仅扭曲时间 :它只对时间轴进行非线性伸缩,无法处理空间上的变换。例如,如果两个运动轨迹除了速度不同,方向还略有旋转或缩放,DTW无法纠正这些。
(5)比喻: DTW就像让两个人以不同的速度朗读同一句话,算法负责找到他们每个音节之间的对应关系。
2.2 GTW
(1) 核心目标: 对齐两条多维 时间序列,不仅允许时间轴的非线性伸缩,还允许序列在特征空间 (即各个维度构成的空间)中进行一个线性变换(如旋转、缩放、平移)。
(2) 关键原理:
-
联合优化: GTW同时优化两个东西:
-
时间扭曲路径:类似于DTW,决定时间点之间的对应关系。
-
空间变换矩阵 :一个线性变换矩阵 W,用于将一条序列的特征空间映射到另一条序列的特征空间,以最小化对齐后的距离。
-
-
数学模型: 目标函数通常是:
最小化 ||序列A - W * 序列B(时间扭曲后)||^2,同时满足时间路径的约束。
(3) 优点:
-
处理多维数据:天然适用于对齐轨迹、姿态序列、多变量信号等。
-
同时校正时空差异:不仅能处理速度变化(时间扭曲),还能补偿坐标系偏移、方向旋转、尺度缩放等空间差异。例如,对齐不同人、不同视角下做的同一个手势。
-
更强大的表达能力:对于复杂的数据对齐问题,GTW通常能获得比DTW更优、更物理意义合理的对齐结果。
(4) 局限性:
-
计算更复杂:联合优化时间路径和空间变换是一个更困难的问题,通常需要迭代算法(如坐标下降法:交替优化W和时间路径),计算成本远高于DTW。
-
参数更多:需要选择或设计空间变换的形式(如仿射变换、刚性变换等)。
-
可能过拟合:如果变换过于灵活或数据噪声大,可能学到没有意义的对齐。
(5) 比喻: GTW就像让两个人在不同地点、面对不同方向、以不同速度画同一个图形。算法不仅要找出笔画顺序的对应(时间扭曲),还要纠正位置和方向的差异(空间变换),才能判断他们画的是否是同一个东西。
| 特性 | DTW | GTW |
|---|---|---|
| 核心能力 | 时间轴的非线性对齐 | 时间轴非线性对齐 + 特征空间线性变换 |
| 数据维度 | 主要为一维,多维需独立处理 | 原生支持多维时间序列 |
| 对齐对象 | 两条"曲线" | 两条"轨迹"或"点云序列" |
| 处理的变化 | 时间伸缩、局部加速/减速 | 时间伸缩 + 空间旋转/平移/缩放 |
| 计算复杂度 | 相对较低 (O(nm)) | 较高,需要迭代优化 |
| 典型应用 | 语音识别、一维传感器信号匹配 | 动作识别(不同人、不同视角)、轨迹对齐、多变量生物信号分析 |
三、进一步详细介绍DTW原理算法
1. 问题形式化
1.1 轨迹表示
设有两条示教轨迹,通过不同的演示得到,其时间长度不一致:
参考轨迹 R(已标准化):
其中 表示第
个时间点的状态向量,包含位置、姿态等信息。
查询轨迹 (待对齐):
其中,通常
。
1.2 对齐目标
寻找一个时间扭曲函数 ,使得:
-
两条轨迹在扭曲后的时间轴上尽可能相似
-
满足时间序列的基本约束(单调性、连续性)
-
最小化累积对齐误差
2. DTW核心算法:动态规划求解
2.1 局部距离度量
首先定义轨迹点之间的局部距离。常用欧氏距离:
对于多特征融合,可采用加权距离:
其中为第
个特征的权重。
构建一个的累积距离矩阵
,其中:
-
-
对于
-
对于
-
主矩阵元素通过动态规划计算
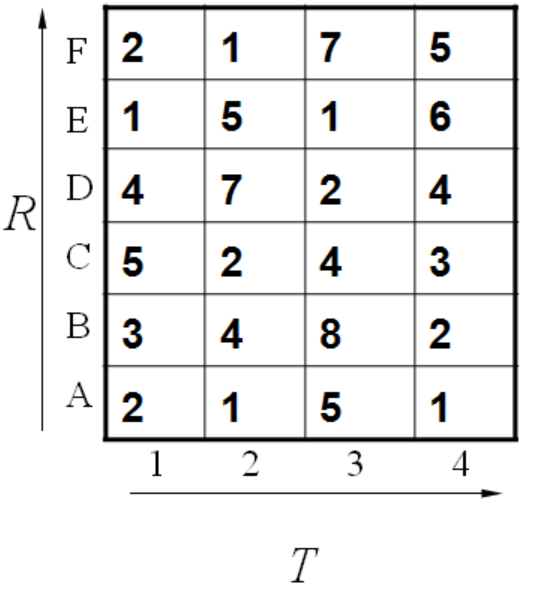
上面的表格其实就是比较形象化的矩阵D,其实就是把两条示教数据之间每个点之间的距离列成这样一个表格。
目的是什么呢?
目的就是把原来的问题:"寻找一个时间扭曲函数
,使得扭曲后两条轨迹具有最小化累积对齐误差"转换成了下面的问题:"寻找一条从左下角到右上角的最短路径"
有点化代数为几何的思想,这就有点像我们熟悉的路径最优算法
2.3 动态规划递推公式
对于和
:
其中项为移动惩罚,标准DTW中通常取
。
这个递推公式比较好理解,其实就是每个网格到起点的最短距离
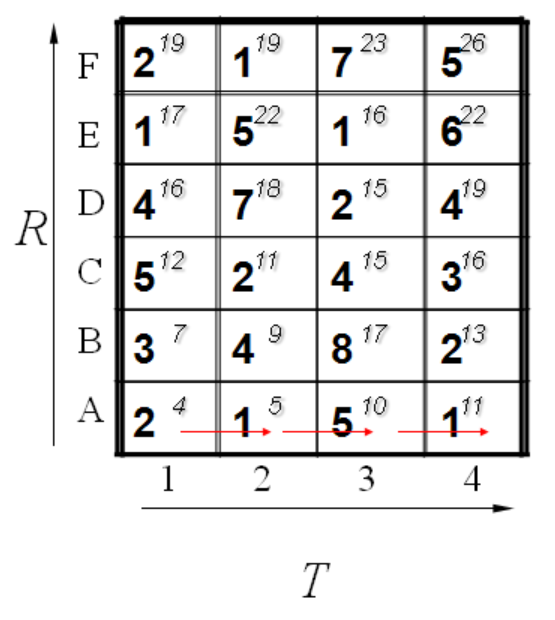
这怎么得来的呢?比如说g(1,1)=4, 当然前提都假设是g(0,0)=0,就是说g(1,1)=g(0,0)+2d(1,1)=0+2*2=4.
g(2,2)=9是一样的道理。首先如果从g(1,2)来算的话是g(2,2)=g(1,2)+d(2,2)=5+4=9,因为是竖着上去的。
如果从g(2,1)来算的话是g(2,2)=g(2,1)+d(2,2)=7+4=11,因为是横着往右走的。
如果从g(1,1)来算的话,g(2,2)=g(1,1)+2*d(2,2)=4+2*4=12.因为是斜着过去的。
综上所述,取最小值为9. 所有g(2,2)=9.
当然在这之前要计算出g(1,1),g(2,1),g(1,2).因此计算g(I,j)也是有一定顺序的。
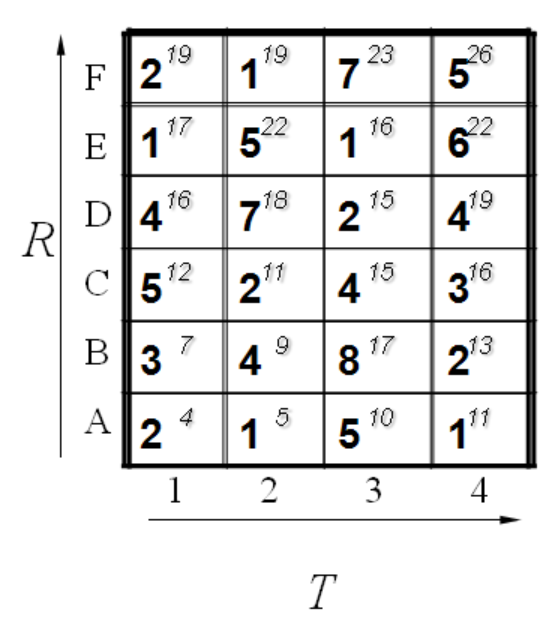
其基本顺序可以体现在如下:
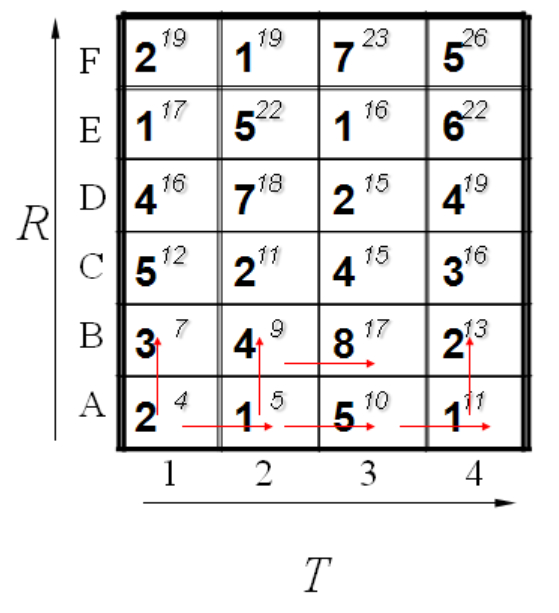
计算了第一排,其中每一个红色的箭头表示最小值来源的那个方向。当计算了第二排后的结果如下:
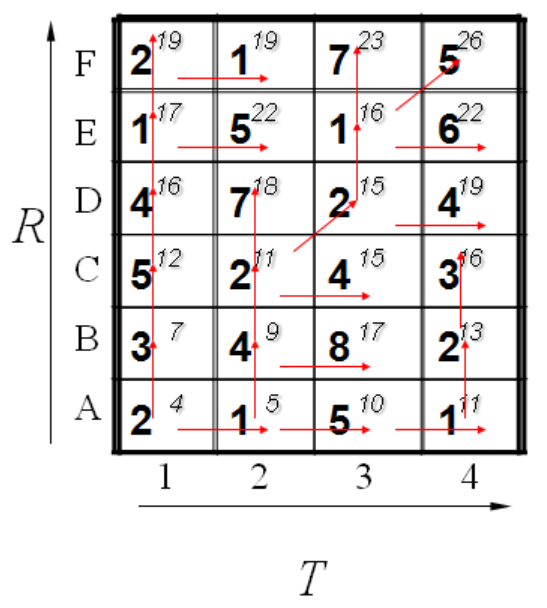
最后都算完了的结果如下:
到此为止,我们已经得到了答案,即2个模板直接的距离为26。
2.4 回溯求取最优路径
从终点开始,反向回溯到起点
:
1. 回溯条件 :对于当前位置,选择上一位置:
其中former集合为 。
2. 路径记录 :将 加入路径序列
。
3. 迭代回溯 :设置,重复直到
。
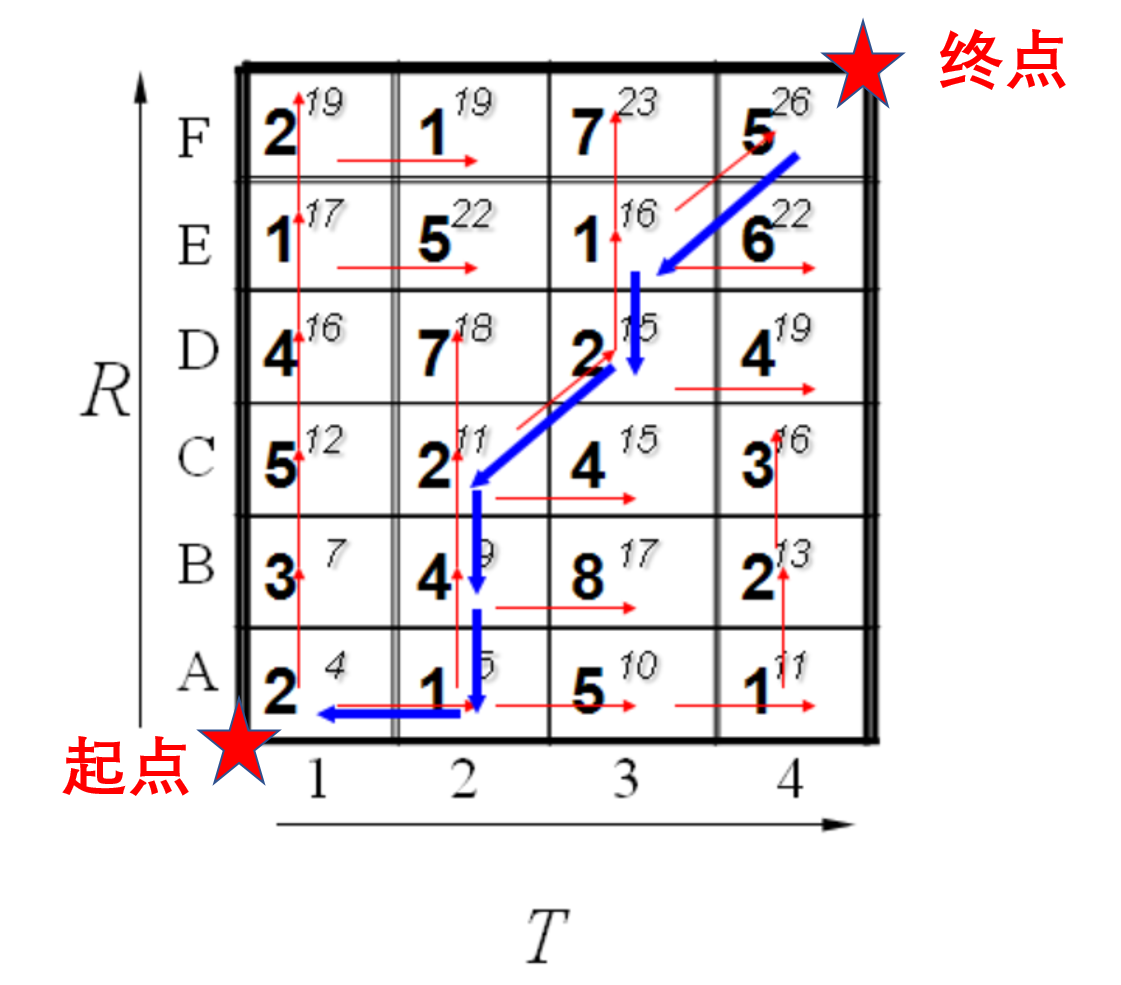
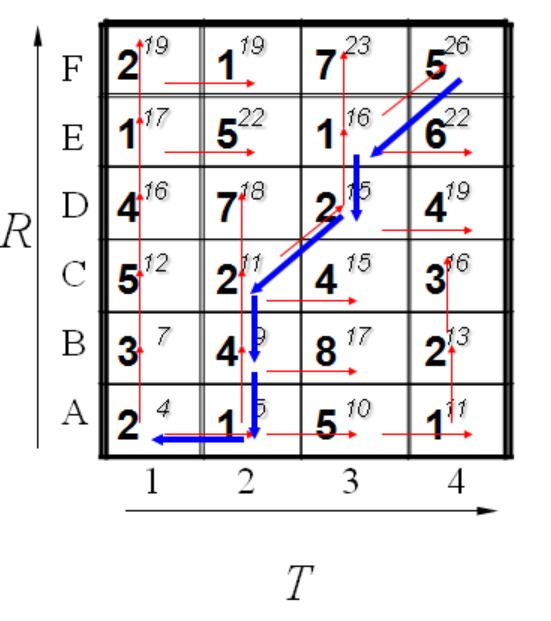
我们可以通过回溯找到最短距离的路径,通过箭头方向反推回去。如下所示
这样就得到的最优的路径。当然这个最优的路径再转换回序列中,就是最优对齐路径。比如这里得到的最优对齐路径为P={(1,1),(2,1),(2,2),(2,3),(3,4),(3,5),(4,6)}
2.5 最优对齐路径
得到最优对齐路径:
其中:
-
-
-
对于所有
:
且
(单调性约束)
-
路径长度
满足:
这里的最优对齐路径,在轨迹上,其实就是第一个轨迹的
点和第二个轨迹的
点是对应的,就比如我们最开头举的例子,如果轨迹1的波峰点是
,那么就应该和轨迹2的波峰点
对应,在最优对齐轨迹里面就有
这里为了方便理解,再放一个图,下面的图中虚线连接的地方就表示两条轨迹的这两个点是分别对应的,这样算出来的这两条轨迹的距离是最小的。等我们对齐的时候,虚线其实就类似于橡皮筋,会把这两条轨迹相互拉靠近,让他们尽可能的对齐,当然对齐并不表示然他们完全一致,时间对齐是不会改变他们原来的几何特性的。
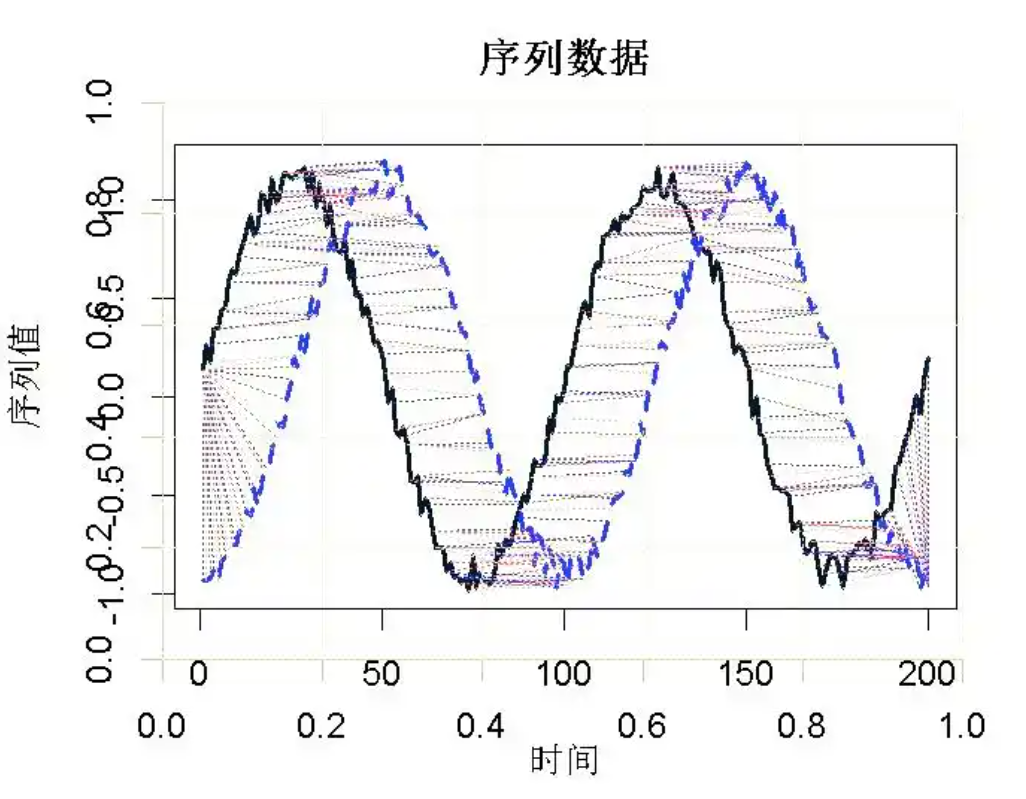
图3 最优对齐轨迹
3. 从DTW路径到时间对齐
我们前面找到了最优对齐路径,接下来就是通过插值让这两条轨迹真正的对齐。
3.1 路径分析
DTW路径 建立了离散的对应关系:
-
参考轨迹的第
个点对应查询轨迹的第
个点
-
但两条轨迹的长度不同(
)
-
路径可能不是一一对应(一个点可能对应多个点)
3.2 时间映射函数构建
目标:构建连续时间映射函数 ,使得:
对于所有 。
3.2.1 参数化表示
将路径点归一化到单位区间:
得到点集:
3.2.2 插值函数选择
选择适当的插值函数 ,满足:
-
单调性 :
(时间不能倒流)
-
边界条件 :
,
-
插值条件 :
常用方法:
a) 分段线性插值 :
对于:
b) 单调三次样条(PCHIP) :
构建分段三次多项式 在
上:
满足:
-
,
-
,
-
导数
通过保证单调性的方法计算
c) 时间规整基函数 :
使用基函数展开:
其中 为基函数(如多项式、B样条),系数
通过最小二乘求解:
其中第二项为正则化项,控制平滑度。
3.3 轨迹重采样
3.3.1 参考时间轴
参考轨迹的时间轴(归一化):
3.3.2 查询轨迹时间映射
对每个参考时间点,计算对应的查询时间:
3.3.3 查询轨迹插值
对于查询轨迹的每个维度 ,构建插值函数
:
其中,
是查询轨迹第
个点在第
维的值。
3.3.4 对齐后查询轨迹
对齐后的查询轨迹 长度为
:
其中。
4. 算法总结
4.1 DTW对齐完整流程
-
输入:
-
参考轨迹
-
查询轨迹
-
-
距离计算:
-
动态规划:
边界:
,
,
-
路径回溯:
其中
-
时间映射构建:
-
归一化:
,
-
构建插值函数
-
-
轨迹重采样:
-
对每个
:
-
插值:
-
-
输出:
-
对齐后的查询轨迹
-
时间映射函数
-
4.2 数学性质
定理1(最优性) :
DTW算法找到的路径在所有满足单调性和连续性的路径中,使累积距离
最小。
证明 :
由动态规划的最优子结构性质,表示从
到
的最小累积距离。递推公式保证了局部最优选择导致全局最优。
定理2(复杂度) :
标准DTW算法的时间复杂度为,空间复杂度为
。
定理3(时间映射性质) :
若采用单调插值方法(如PCHIP),时间映射函数 ττ 满足:
-
单调性:
对于
-
边界条件:
,
-
连续性:
四、DTW实现代码
Matlab
%% 清除工作区
clear all; close all; clc;
%% 1. 创建模拟轨迹数据
fprintf('=== 创建模拟轨迹数据 ===\n');
% 轨迹1(参考轨迹):正弦波 + 噪声
N = 100; % 轨迹1长度
t1 = linspace(0, 2*pi, N);
x1 = sin(t1) + 0.1*randn(1, N);
y1 = 0.5*cos(t1) + 0.1*randn(1, N);
z1 = 0.3*sin(2*t1) + 0.1*randn(1, N);
% 轨迹2(查询轨迹):拉伸的正弦波 + 噪声
M = 150; % 轨迹2长度(不同长度)
t2 = linspace(0, 3*pi, M); % 时间轴不同
% 添加非线性时间扭曲
t2_warped = t2 + 0.5*sin(0.5*t2); % 非线性时间扭曲
x2 = sin(t2_warped) + 0.1*randn(1, M);
y2 = 0.5*cos(t2_warped) + 0.1*randn(1, M);
z2 = 0.3*sin(2*t2_warped) + 0.1*randn(1, M);
% 创建轨迹数据结构
traj1.pos = [x1; y1; z1]; % 3×N
traj2.pos = [x2; y2; z2]; % 3×M
traj1.time = linspace(0, 10, N); % 10秒
traj2.time = linspace(0, 15, M); % 15秒(不同时长)
fprintf('轨迹1长度: %d, 时间: 0-%.1f秒\n', N, traj1.time(end));
fprintf('轨迹2长度: %d, 时间: 0-%.1f秒\n', M, traj2.time(end));
%% 2. 可视化原始轨迹
figure('Position', [100, 100, 1200, 400]);
% 子图1:3D轨迹
subplot(1, 3, 1);
plot3(x1, y1, z1, 'b-', 'LineWidth', 2); hold on;
plot3(x2, y2, z2, 'r-', 'LineWidth', 1.5);
scatter3(x1(1), y1(1), z1(1), 50, 'b', 'filled');
scatter3(x1(end), y1(end), z1(end), 50, 'b', '^', 'filled');
scatter3(x2(1), y2(1), z2(1), 50, 'r', 'filled');
scatter3(x2(end), y2(end), z2(end), 50, 'r', '^', 'filled');
xlabel('X'); ylabel('Y'); zlabel('Z');
title('原始3D轨迹');
legend('轨迹1(参考)', '轨迹2(查询)', '起点', '终点', 'Location', 'best');
grid on; view(45, 30);
% 子图2:位置分量随时间变化
subplot(1, 3, 2);
plot(traj1.time, x1, 'b-', 'LineWidth', 2); hold on;
plot(traj2.time, x2, 'r-', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('X位置');
title('X分量随时间变化');
legend('轨迹1', '轨迹2');
grid on;
subplot(1, 3, 3);
plot(traj1.time, y1, 'b-', 'LineWidth', 2); hold on;
plot(traj2.time, y2, 'r-', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('Y位置');
title('Y分量随时间变化');
legend('轨迹1', '轨迹2');
grid on;
%% 3. 自定义DTW函数实现
function [dist, D, path] = my_dtw(seq1, seq2)
% 自定义DTW实现
% seq1: 参考序列 (d×N 或 1×N)
% seq2: 查询序列 (d×M 或 1×M)
% dist: DTW距离
% D: 累积距离矩阵
% path: 对齐路径
% 确保是行向量或列向量(对于一维序列)
if size(seq1, 1) > 1 && size(seq1, 2) == 1
seq1 = seq1';
end
if size(seq2, 1) > 1 && size(seq2, 2) == 1
seq2 = seq2';
end
% 获取序列长度
N = size(seq1, 2);
M = size(seq2, 2);
% 初始化累积距离矩阵
D = inf(N+1, M+1);
D(1, 1) = 0;
% 计算局部距离矩阵
local_dist = zeros(N, M);
for i = 1:N
for j = 1:M
% 欧氏距离
local_dist(i, j) = norm(seq1(:, i) - seq2(:, j));
end
end
% 动态规划计算累积距离
for i = 1:N
for j = 1:M
cost = local_dist(i, j);
D(i+1, j+1) = cost + min([D(i, j+1), D(i+1, j), D(i, j)]);
end
end
% 最终距离
dist = D(N+1, M+1);
% 回溯求路径
i = N;
j = M;
path = [];
while i > 0 && j > 0
path = [[i; j], path];
if i == 1
j = j - 1;
elseif j == 1
i = i - 1;
else
% 找到最小累积距离的方向
[~, idx] = min([D(i, j+1), D(i+1, j), D(i, j)]);
switch idx
case 1 % 向上
i = i - 1;
case 2 % 向左
j = j - 1;
case 3 % 对角线
i = i - 1;
j = j - 1;
end
end
end
end
%% 4. 使用自定义DTW对齐轨迹
fprintf('\n=== 使用自定义DTW对齐轨迹 ===\n');
% 计算DTW
tic;
[dtw_dist, D_matrix, dtw_path] = my_dtw(traj1.pos, traj2.pos);
dtw_time = toc;
fprintf('自定义DTW结果:\n');
fprintf(' DTW距离: %.4f\n', dtw_dist);
fprintf(' 计算时间: %.4f秒\n', dtw_time);
fprintf(' 路径长度: %d\n', size(dtw_path, 2));
% 存储路径
ix = dtw_path(1, :); % 参考轨迹索引
iy = dtw_path(2, :); % 查询轨迹索引
%% 修复DTW代码 - 解决矩阵维度问题
fprintf('\n=== 使用MATLAB内置DTW函数 ===\n');
% 如果MATLAB有信号处理工具箱,可以使用内置dtw
if exist('dtw', 'file') == 2
tic;
% 方法1:分别对每个维度计算DTW,然后取平均路径
fprintf(' 方法:分别对每个维度计算DTW\n');
% 初始化路径存储
all_ix = cell(3, 1);
all_iy = cell(3, 1);
all_dist = zeros(3, 1);
for dim = 1:3
% 提取单个维度数据(转换为行向量)
x1_dim = traj1.pos(dim, :);
x2_dim = traj2.pos(dim, :);
% 计算该维度的DTW
[all_dist(dim), all_ix{dim}, all_iy{dim}] = dtw(x1_dim, x2_dim);
end
% 取平均路径(简单方法:取第一个维度的路径)
matlab_ix = all_ix{1};
matlab_iy = all_iy{1};
matlab_dist = mean(all_dist);
matlab_time = toc;
fprintf('MATLAB内置DTW结果:\n');
fprintf(' DTW距离: %.4f\n', matlab_dist);
fprintf(' 计算时间: %.4f秒\n', matlab_time);
fprintf(' 路径长度: %d\n', length(matlab_ix));
% ==================== 方法2:使用向量化方法 ====================
% 或者我们可以创建一个更稳健的方法
fprintf('\n 方法2:向量化DTW方法\n');
% 将3D数据展平为1D向量
% 方法:连接所有维度的数据
x1_flat = traj1.pos(:)'; % 展平为行向量
x2_flat = traj2.pos(:)';
% 由于长度不同,需要处理
% 我们可以通过重复采样使长度匹配
min_len = min(length(x1_flat), length(x2_flat));
x1_flat_resized = resample(x1_flat, min_len, length(x1_flat));
x2_flat_resized = resample(x2_flat, min_len, length(x2_flat));
% 计算DTW
try
[flat_dist, flat_ix, flat_iy] = dtw(x1_flat_resized, x2_flat_resized);
fprintf(' 向量化DTW距离: %.4f\n', flat_dist);
catch
fprintf(' 向量化DTW失败\n');
end
else
fprintf('MATLAB信号处理工具箱未安装,跳过内置DTW\n');
matlab_ix = ix;
matlab_iy = iy;
end
%% 6. 构建时间映射函数
fprintf('\n=== 构建时间映射函数 ===\n');
% 使用自定义DTW路径
% 归一化索引到[0,1]
ref_indices_norm = (ix - 1) / (N - 1);
query_indices_norm = (iy - 1) / (M - 1);
% 确保唯一且单调
[ref_indices_norm_unique, unique_idx] = unique(ref_indices_norm, 'stable');
query_indices_norm_unique = query_indices_norm(unique_idx);
% 创建时间映射函数
time_map_func = @(t) interp1(ref_indices_norm_unique, ...
query_indices_norm_unique, ...
t, 'pchip', 'extrap');
% 测试时间映射函数
test_points = linspace(0, 1, 5);
test_mapped = time_map_func(test_points);
fprintf('时间映射测试:\n');
fprintf(' 参考时间点: %s\n', mat2str(test_points, 2));
fprintf(' 映射到查询: %s\n', mat2str(test_mapped, 2));
%% 7. 对齐查询轨迹到参考时间轴
fprintf('\n=== 对齐查询轨迹到参考时间轴 ===\n');
% 参考轨迹的归一化时间轴
ref_time_norm = linspace(0, 1, N);
% 计算查询轨迹对应的归一化时间
query_time_mapped_norm = time_map_func(ref_time_norm);
query_time_mapped_norm = max(0, min(1, query_time_mapped_norm));
% 转换为实际时间
query_time_mapped = query_time_mapped_norm * (traj2.time(end) - traj2.time(1)) + traj2.time(1);
% 对齐查询轨迹的所有维度
traj2_aligned.pos = zeros(3, N);
for dim = 1:3
traj2_aligned.pos(dim, :) = interp1(traj2.time, traj2.pos(dim, :), ...
query_time_mapped, 'pchip', 'extrap');
end
% 对齐后的时间轴(使用参考轨迹的时间轴)
traj2_aligned.time = traj1.time;
fprintf('对齐完成:\n');
fprintf(' 原始查询轨迹长度: %d\n', M);
fprintf(' 对齐后查询轨迹长度: %d\n', N);
%% 8. 可视化DTW对齐过程
figure('Position', [100, 100, 1200, 800]);
% 子图1:累积距离矩阵和DTW路径
subplot(2, 3, 1);
imagesc(D_matrix(2:end, 2:end)); % 去掉第一行第一列(无穷大)
hold on;
plot(ix, iy, 'w-', 'LineWidth', 1.5);
colorbar;
xlabel('查询轨迹索引');
ylabel('参考轨迹索引');
title('累积距离矩阵和DTW路径');
axis tight;
% 子图2:DTW路径
subplot(2, 3, 2);
plot(ix, iy, 'b-', 'LineWidth', 1.5);
hold on;
plot([1, N], [1, M], 'r--', 'LineWidth', 1);
xlabel('参考轨迹索引');
ylabel('查询轨迹索引');
title('DTW对齐路径');
legend('DTW路径', '对角线', 'Location', 'best');
grid on;
axis equal;
xlim([1, N]);
ylim([1, M]);
% 子图3:时间映射函数
subplot(2, 3, 3);
plot(ref_indices_norm_unique, query_indices_norm_unique, 'b.', 'MarkerSize', 10);
hold on;
plot(ref_time_norm, query_time_mapped_norm, 'r-', 'LineWidth', 1.5);
plot([0, 1], [0, 1], 'k--', 'LineWidth', 1);
xlabel('参考时间(归一化)');
ylabel('查询时间(归一化)');
title('时间映射函数');
legend('DTW对应点', '插值函数', '无扭曲', 'Location', 'best');
grid on;
% 子图4:原始轨迹X分量对比
subplot(2, 3, 4);
plot(traj1.time, traj1.pos(1, :), 'b-', 'LineWidth', 2); hold on;
plot(traj2.time, traj2.pos(1, :), 'r-', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('X位置');
title('原始轨迹X分量');
legend('轨迹1', '轨迹2');
grid on;
% 子图5:对齐后轨迹X分量对比
subplot(2, 3, 5);
plot(traj1.time, traj1.pos(1, :), 'b-', 'LineWidth', 2); hold on;
plot(traj2_aligned.time, traj2_aligned.pos(1, :), 'r-', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('X位置');
title('对齐后轨迹X分量');
legend('轨迹1', '轨迹2(对齐后)');
grid on;
% 子图6:对齐误差
subplot(2, 3, 6);
alignment_error = sqrt(sum((traj1.pos - traj2_aligned.pos).^2, 1));
plot(traj1.time, alignment_error, 'k-', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('对齐误差');
title('逐点对齐误差');
grid on;
fprintf('平均对齐误差: %.4f\n', mean(alignment_error));
%% 9. 可视化3D对齐结果
figure('Position', [100, 100, 800, 600]);
% 原始轨迹
subplot(2, 2, 1);
plot3(traj1.pos(1,:), traj1.pos(2,:), traj1.pos(3,:), 'b-', 'LineWidth', 2);
hold on;
plot3(traj2.pos(1,:), traj2.pos(2,:), traj2.pos(3,:), 'r-', 'LineWidth', 1.5);
xlabel('X'); ylabel('Y'); zlabel('Z');
title('原始3D轨迹');
legend('轨迹1', '轨迹2', 'Location', 'best');
grid on; view(45, 30);
% 对齐后轨迹
subplot(2, 2, 2);
plot3(traj1.pos(1,:), traj1.pos(2,:), traj1.pos(3,:), 'b-', 'LineWidth', 2);
hold on;
plot3(traj2_aligned.pos(1,:), traj2_aligned.pos(2,:), traj2_aligned.pos(3,:), 'r-', 'LineWidth', 1.5);
xlabel('X'); ylabel('Y'); zlabel('Z');
title('对齐后3D轨迹');
legend('轨迹1', '轨迹2(对齐后)', 'Location', 'best');
grid on; view(45, 30);
% DTW对应点连接
subplot(2, 2, 3);
plot3(traj1.pos(1,:), traj1.pos(2,:), traj1.pos(3,:), 'b-', 'LineWidth', 2);
hold on;
plot3(traj2.pos(1,:), traj2.pos(2,:), traj2.pos(3,:), 'r-', 'LineWidth', 1.5);
% 绘制一些对应点连接线
n_connections = min(20, length(ix));
connection_indices = round(linspace(1, length(ix), n_connections));
for k = connection_indices
i = ix(k);
j = iy(k);
plot3([traj1.pos(1,i), traj2.pos(1,j)], ...
[traj1.pos(2,i), traj2.pos(2,j)], ...
[traj1.pos(3,i), traj2.pos(3,j)], ...
'g-', 'LineWidth', 0.5);
end
xlabel('X'); ylabel('Y'); zlabel('Z');
title('DTW对应点连接');
legend('轨迹1', '轨迹2', 'DTW对应', 'Location', 'best');
grid on; view(45, 30);
% 对齐误差热图
subplot(2, 2, 4);
imagesc(alignment_error);
colorbar;
xlabel('时间点索引');
ylabel('维度');
title('对齐误差热图');
%% 10. 扩展:能量曲线对齐示例
fprintf('\n=== 能量曲线对齐示例 ===\n');
% 创建模拟能量曲线(基于位置数据的动能)
traj1.energy = sum(traj1.pos.^2, 1); % 简化的"动能"
traj2.energy = sum(traj2.pos.^2, 1);
% 对能量曲线进行DTW对齐
[energy_dist, ~, energy_path] = my_dtw(traj1.energy, traj2.energy);
% 使用能量DTW路径对齐位置数据
energy_ix = energy_path(1, :);
energy_iy = energy_path(2, :);
% 构建能量对齐的时间映射
energy_ref_norm = (energy_ix - 1) / (N - 1);
energy_query_norm = (energy_iy - 1) / (M - 1);
[energy_ref_unique, energy_unique_idx] = unique(energy_ref_norm, 'stable');
energy_query_unique = energy_query_norm(energy_unique_idx);
energy_time_map_func = @(t) interp1(energy_ref_unique, ...
energy_query_unique, ...
t, 'pchip', 'extrap');
% 对齐能量曲线
energy_query_time_mapped_norm = energy_time_map_func(ref_time_norm);
energy_query_time_mapped_norm = max(0, min(1, energy_query_time_mapped_norm));
energy_query_time_mapped = energy_query_time_mapped_norm * ...
(traj2.time(end) - traj2.time(1)) + traj2.time(1);
traj2_energy_aligned.energy = interp1(traj2.time, traj2.energy, ...
energy_query_time_mapped, 'pchip', 'extrap');
% 可视化能量对齐
figure('Position', [100, 100, 1000, 400]);
subplot(1, 2, 1);
plot(traj1.time, traj1.energy, 'b-', 'LineWidth', 2); hold on;
plot(traj2.time, traj2.energy, 'r-', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('能量');
title('原始能量曲线');
legend('轨迹1能量', '轨迹2能量');
grid on;
subplot(1, 2, 2);
plot(traj1.time, traj1.energy, 'b-', 'LineWidth', 2); hold on;
plot(traj1.time, traj2_energy_aligned.energy, 'r-', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('能量');
title('对齐后能量曲线');
legend('轨迹1能量', '轨迹2能量(对齐后)');
grid on;
fprintf('能量曲线DTW距离: %.4f\n', energy_dist);
%% 12. 总结输出
fprintf('\n=== 总结 ===\n');
fprintf('1. 成功创建了长度为%d和%d的两条轨迹\n', N, M);
fprintf('2. 实现了自定义DTW算法\n');
fprintf('3. 通过DTW找到了最优对齐路径\n');
fprintf('4. 构建了时间映射函数\n');
fprintf('5. 将查询轨迹对齐到参考轨迹的时间轴\n');
fprintf('6. 可视化展示了对齐过程和结果\n');
fprintf('7. 扩展了能量曲线对齐示例\n');
if exist('dtw', 'file') == 2
fprintf('8. 对比了自定义DTW和MATLAB内置DTW的效果\n');
end
fprintf('\n示例完成!\n');
这里篇幅太长了,关于GTW在下一个文章里介绍吧