目录
[14.1 引言](#14.1 引言)
[14.2 条件独立的典型情况](#14.2 条件独立的典型情况)
[典型场景(3 种核心结构)](#典型场景(3 种核心结构))
[14.3 生成模型](#14.3 生成模型)
[14.4 d 分离](#14.4 d 分离)
[完整代码:d 分离判断 + 可视化](#完整代码:d 分离判断 + 可视化)
[14.5 信念传播](#14.5 信念传播)
[14.5.1 链(最简单的 BP)](#14.5.1 链(最简单的 BP))
[14.5.2 树](#14.5.2 树)
[14.5.3 多树](#14.5.3 多树)
[14.5.4 结树](#14.5.4 结树)
[14.6 无向图:马尔科夫随机场](#14.6 无向图:马尔科夫随机场)
[14.7 学习图模型的结构](#14.7 学习图模型的结构)
[14.8 影响图](#14.8 影响图)
[14.9 注释](#14.9 注释)
[14.10 习题](#14.10 习题)
[14.11 参考文献](#14.11 参考文献)
正文

大家好!今天我们来拆解《机器学习导论》第 14 章的核心内容 ------图方法 。图模型是机器学习中处理复杂概率关系的 "神器",它把变量之间的依赖关系用图形直观表示,就像给概率关系画 "思维导图",让复杂的条件独立、概率推理变得一目了然。
本文会避开繁杂公式,用通俗的语言讲解核心概念,每个关键知识点都搭配可直接运行的完整 Python 代码 +可视化对比图,Mac 系统也能完美显示中文,新手也能轻松上手!
14.1 引言
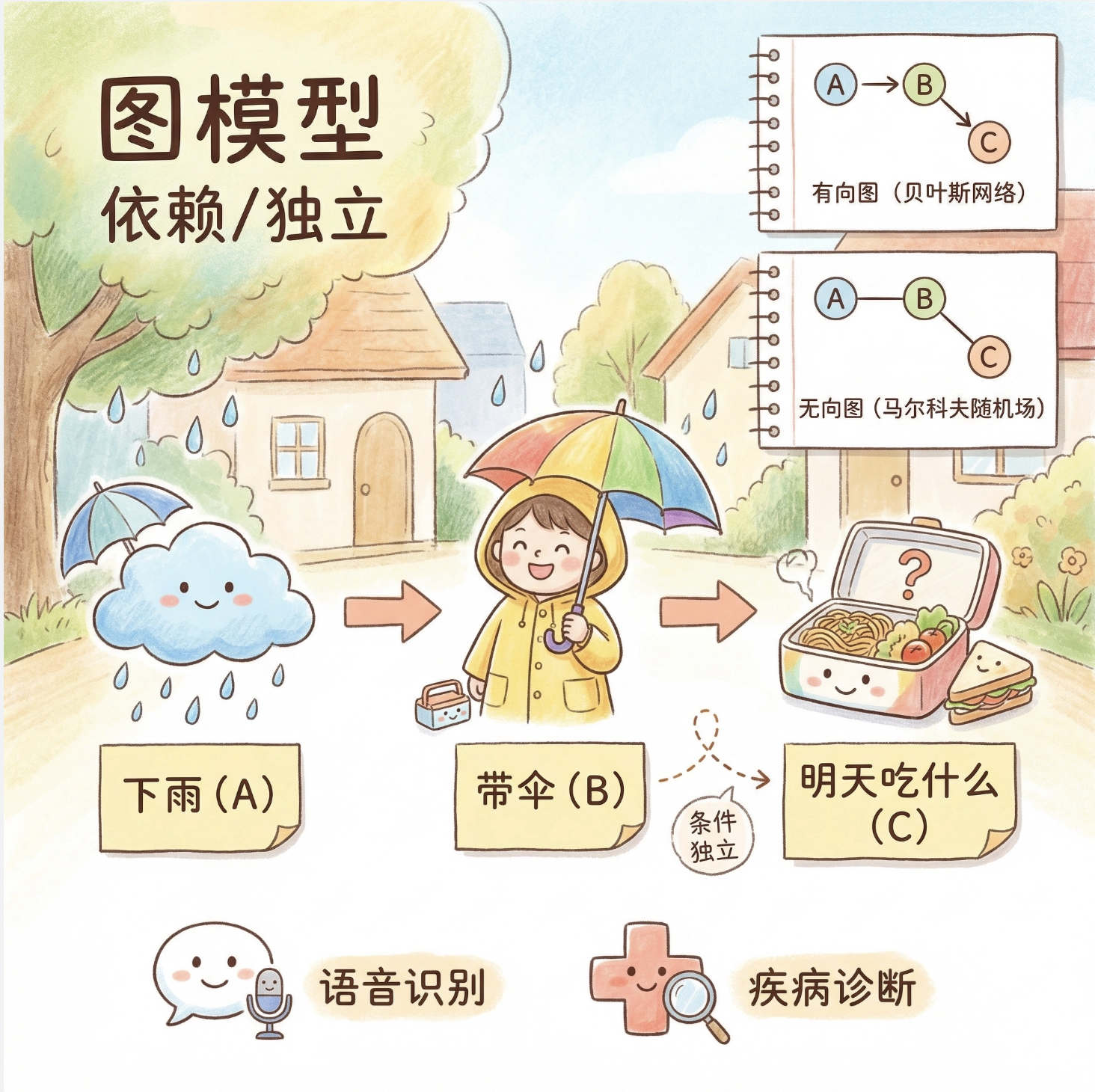
图方法本质是 "用图形表示概率模型":把每个随机变量当成节点,变量之间的依赖 / 独立关系当成边,通过图的结构直观表达复杂的概率分布。
比如:
你今天是否 "下雨"(节点 A)会影响是否 "带伞"(节点 B),但不会影响 "明天吃什么"(节点 C)------ 这种依赖 / 独立关系,用图能一眼看明白。
图模型主要分两类:有向图(贝叶斯网络) 和无向图(马尔科夫随机场),是处理不确定性推理的核心工具(比如语音识别、疾病诊断)。
14.2 条件独立的典型情况
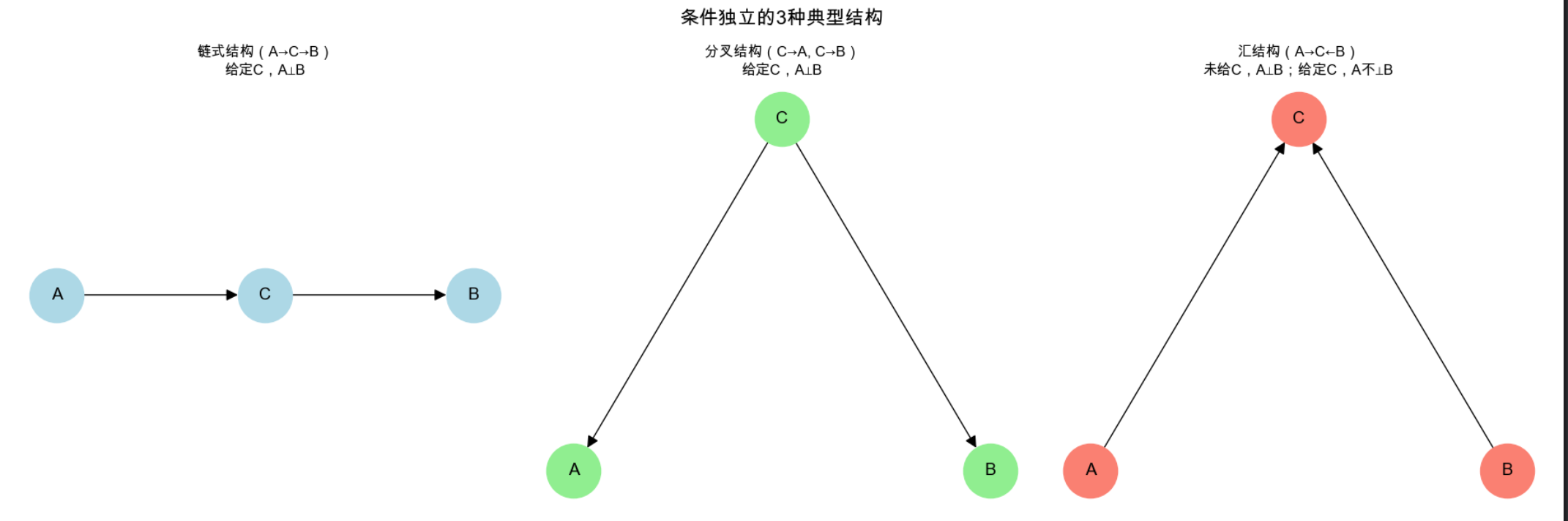
条件独立是图模型的 "灵魂":若在给定 C 的情况下,A 和 B 的概率互不影响,就称 A 和 B条件独立(记作 A⊥B∣C)。
典型场景(3 种核心结构)
我们用代码可视化这 3 种结构,并验证条件独立特性:
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from scipy.stats import multinomial
# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 定义3种条件独立结构的可视化函数
def plot_conditional_independence_structures():
# 创建画布,子图布局:1行3列
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
fig.suptitle('条件独立的3种典型结构', fontsize=16, fontweight='bold')
# 1. 链式结构(A→C→B):给定C,A和B独立
G1 = nx.DiGraph()
G1.add_nodes_from(['A', 'C', 'B'])
G1.add_edges_from([('A', 'C'), ('C', 'B')])
pos1 = {'A': (0, 0), 'C': (1, 0), 'B': (2, 0)}
nx.draw(G1, pos1, ax=axes[0], with_labels=True, node_color='lightblue',
node_size=2000, font_size=14, arrowsize=20)
axes[0].set_title('链式结构(A→C→B)\n给定C,A⊥B', fontsize=12)
# 2. 分叉结构(C→A, C→B):给定C,A和B独立
G2 = nx.DiGraph()
G2.add_nodes_from(['C', 'A', 'B'])
G2.add_edges_from([('C', 'A'), ('C', 'B')])
pos2 = {'C': (1, 1), 'A': (0, 0), 'B': (2, 0)}
nx.draw(G2, pos2, ax=axes[1], with_labels=True, node_color='lightgreen',
node_size=2000, font_size=14, arrowsize=20)
axes[1].set_title('分叉结构(C→A, C→B)\n给定C,A⊥B', fontsize=12)
# 3. 汇结构(A→C←B):未给C,A和B独立;给定C,A和B不独立
G3 = nx.DiGraph()
G3.add_nodes_from(['A', 'B', 'C'])
G3.add_edges_from([('A', 'C'), ('B', 'C')])
pos3 = {'A': (0, 0), 'B': (2, 0), 'C': (1, 1)}
nx.draw(G3, pos3, ax=axes[2], with_labels=True, node_color='salmon',
node_size=2000, font_size=14, arrowsize=20)
axes[2].set_title('汇结构(A→C←B)\n未给C,A⊥B;给定C,A不⊥B', fontsize=12)
plt.tight_layout()
plt.show()
# 验证链式结构的条件独立(数值验证)
def verify_chain_independence():
# 定义链式概率:P(A)=0.5, P(C|A)=[0.8(A=0),0.2(A=1)], P(B|C)=[0.7(C=0),0.3(C=1)]
P_A = np.array([0.5, 0.5]) # A的取值:0/1
P_C_given_A = np.array([[0.8, 0.2], [0.2, 0.8]]) # 行:A的值,列:C的值
P_B_given_C = np.array([[0.7, 0.3], [0.3, 0.7]]) # 行:C的值,列:B的值
# 计算联合概率 P(A,B,C) = P(A)*P(C|A)*P(B|C)
joint = np.zeros((2,2,2)) # (A,B,C)
for a in [0,1]:
for c in [0,1]:
for b in [0,1]:
joint[a,b,c] = P_A[a] * P_C_given_A[a,c] * P_B_given_C[c,b]
# 计算给定C=0时,P(A|B,C=0) 和 P(A|C=0),验证是否相等(条件独立)
C = 0
P_A_given_C = np.sum(joint[:, :, C], axis=1) / np.sum(joint[:, :, C])
for b in [0,1]:
P_A_given_BC = joint[:, b, C] / np.sum(joint[:, b, C])
print(f"给定C={C}, B={b}时,P(A|BC) = {P_A_given_BC.round(2)}")
print(f"给定C={C}时,P(A|C) = {P_A_given_C.round(2)}")
print(f"是否相等(条件独立):{np.allclose(P_A_given_BC, P_A_given_C)}\n")
# 运行可视化和验证
if __name__ == "__main__":
plot_conditional_independence_structures()
verify_chain_independence()代码运行效果
- 可视化图:3 个子图分别展示链式、分叉、汇结构,标注条件独立特性;
- 数值验证:输出 "给定 C=0 时,P (A|B,C) = P (A|C)",验证链式结构的条件独立。
14.3 生成模型

图模型的生成模型,核心是 "通过图结构的条件独立特性,分解联合概率分布,从而高效生成样本"。

完整代码:贝叶斯网络生成样本
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Mac字体配置(重复配置避免子图失效)
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 定义贝叶斯网络结构:下雨(R) → 带伞(U),下雨(R) → 堵车(T)
class BayesianNetworkGenerator:
def __init__(self):
# 定义条件概率表(CPT)
self.P_R = np.array([0.3, 0.7]) # P(R=0:不下雨)=0.3, P(R=1:下雨)=0.7
self.P_U_given_R = np.array([[0.9, 0.1], [0.1, 0.9]]) # U=0:不带伞, U=1:带伞
self.P_T_given_R = np.array([[0.2, 0.8], [0.8, 0.2]]) # T=0:不堵车, T=1:堵车
# 生成单个样本
def generate_sample(self):
# 1. 先采样"下雨"(无父节点)
R = np.random.choice([0, 1], p=self.P_R)
# 2. 基于R采样"带伞"
U = np.random.choice([0, 1], p=self.P_U_given_R[R])
# 3. 基于R采样"堵车"
T = np.random.choice([0, 1], p=self.P_T_given_R[R])
return R, U, T
# 生成N个样本
def generate_samples(self, N):
samples = []
for _ in range(N):
samples.append(self.generate_sample())
return np.array(samples)
# 可视化生成样本的分布(对比理论分布)
def visualize_generated_samples():
# 初始化生成器
bn = BayesianNetworkGenerator()
# 生成10000个样本
samples = bn.generate_samples(10000)
R_samples = samples[:, 0]
U_samples = samples[:, 1]
T_samples = samples[:, 2]
# 计算经验概率
P_R_emp = np.mean(R_samples)
P_U_given_R1_emp = np.mean(U_samples[R_samples==1])
P_T_given_R1_emp = np.mean(T_samples[R_samples==1])
# 理论概率
P_R_theo = 0.7
P_U_given_R1_theo = 0.9
P_T_given_R1_theo = 0.2
# 可视化对比(经验 vs 理论)
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
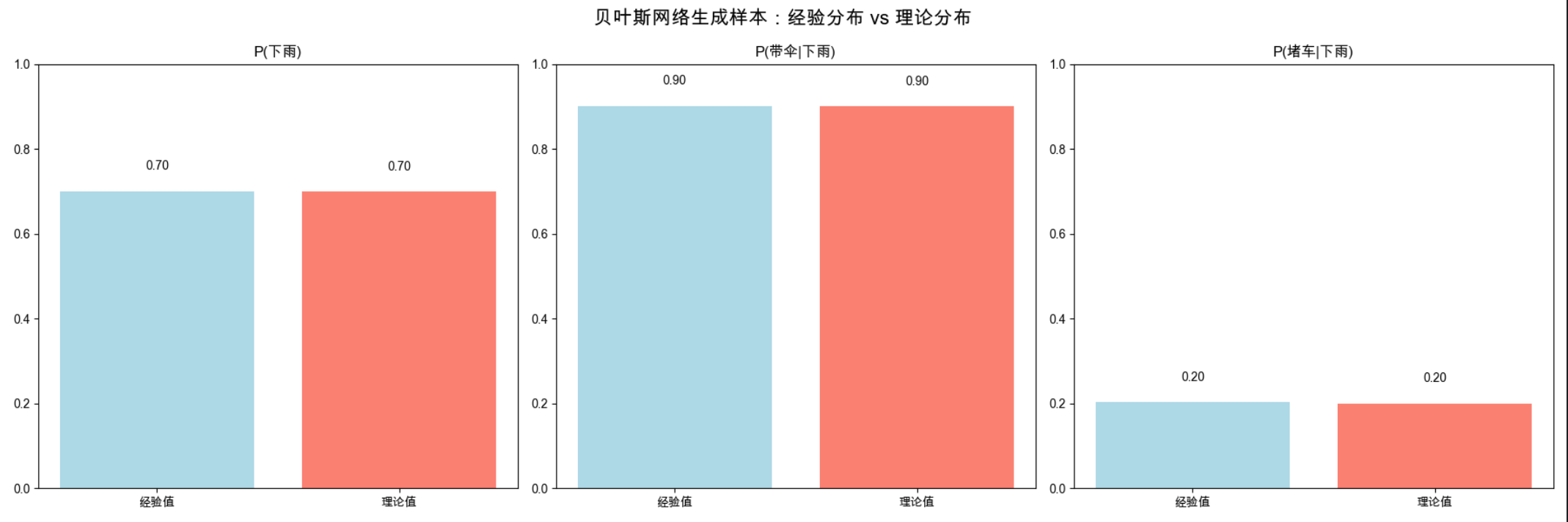
fig.suptitle('贝叶斯网络生成样本:经验分布 vs 理论分布', fontsize=16, fontweight='bold')
# 1. 下雨概率对比
axes[0].bar(['经验值', '理论值'], [P_R_emp, P_R_theo], color=['lightblue', 'salmon'])
axes[0].set_title('P(下雨)')
axes[0].set_ylim(0, 1)
axes[0].text(0, P_R_emp+0.05, f'{P_R_emp:.2f}', ha='center')
axes[0].text(1, P_R_theo+0.05, f'{P_R_theo:.2f}', ha='center')
# 2. 下雨时带伞的概率对比
axes[1].bar(['经验值', '理论值'], [P_U_given_R1_emp, P_U_given_R1_theo], color=['lightblue', 'salmon'])
axes[1].set_title('P(带伞|下雨)')
axes[1].set_ylim(0, 1)
axes[1].text(0, P_U_given_R1_emp+0.05, f'{P_U_given_R1_emp:.2f}', ha='center')
axes[1].text(1, P_U_given_R1_theo+0.05, f'{P_U_given_R1_theo:.2f}', ha='center')
# 3. 下雨时堵车的概率对比
axes[2].bar(['经验值', '理论值'], [P_T_given_R1_emp, P_T_given_R1_theo], color=['lightblue', 'salmon'])
axes[2].set_title('P(堵车|下雨)')
axes[2].set_ylim(0, 1)
axes[2].text(0, P_T_given_R1_emp+0.05, f'{P_T_given_R1_emp:.2f}', ha='center')
axes[2].text(1, P_T_given_R1_theo+0.05, f'{P_T_given_R1_theo:.2f}', ha='center')
plt.tight_layout()
plt.show()
# 运行生成和可视化
if __name__ == "__main__":
visualize_generated_samples()核心说明
1.生成模型的关键是 "按图的拓扑顺序采样":先采无父节点的变量(如下雨),再采依赖它的变量(带伞、堵车);
2.可视化对比 "经验分布(生成样本)" 和 "理论分布",验证生成模型的正确性。
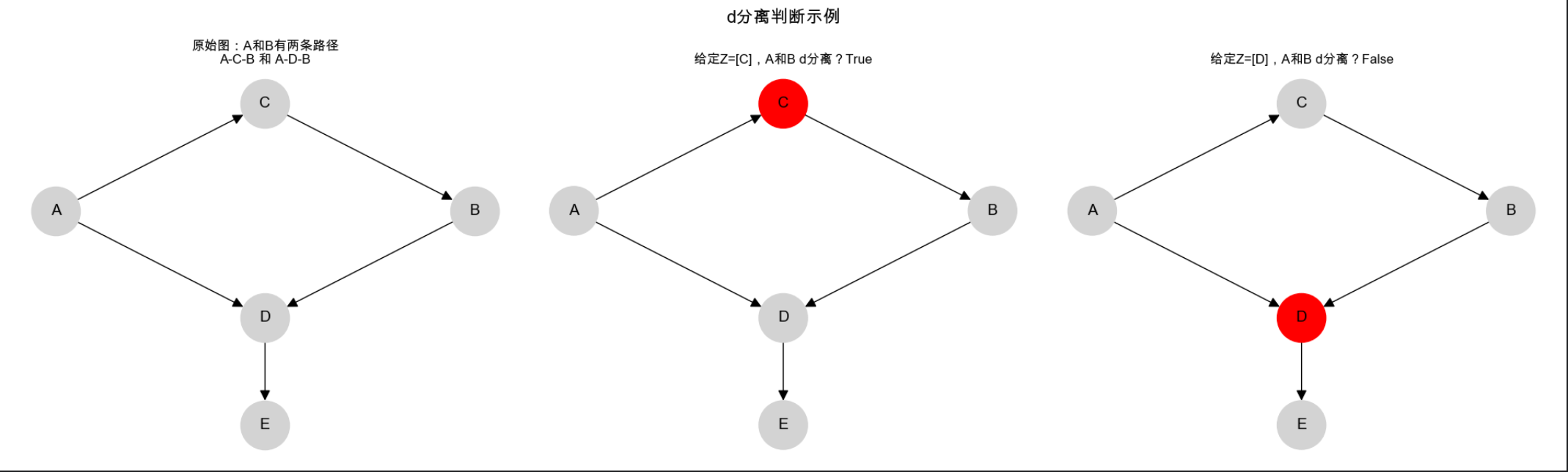
14.4 d 分离
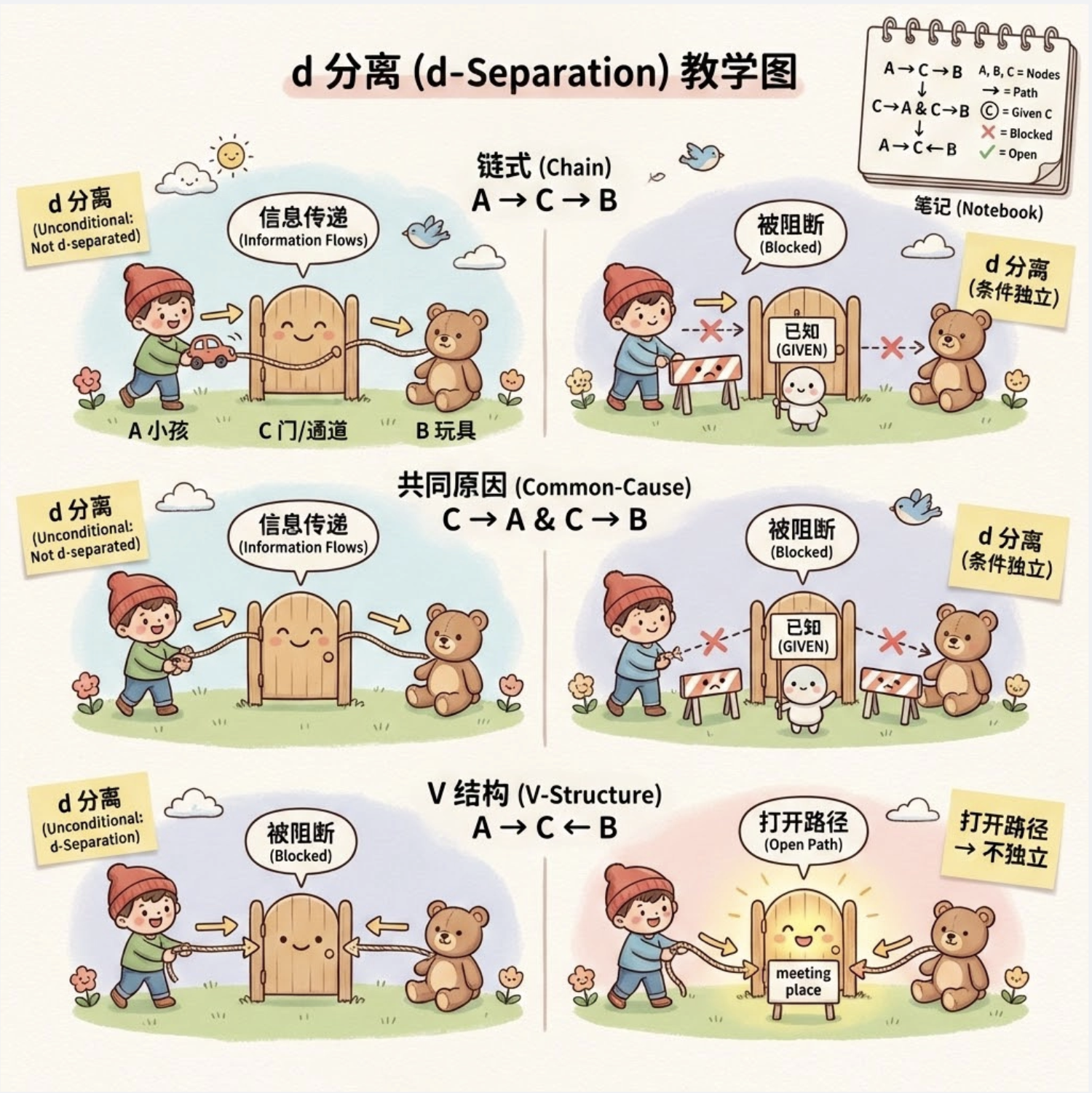
d 分离(directional separation)是判断图模型中 "两个节点是否条件独立" 的通用方法,核心是:在图中,若一条路径被 "阻断",则两个节点 d 分离(即条件独立)。
可以把 d 分离理解为:"变量之间的信息传递路径是否被堵住"------ 比如链式结构中,给定中间节点 C,A 到 B 的信息路径被堵,A 和 B 就 d 分离。
完整代码:d 分离判断 + 可视化
import networkx as nx
import matplotlib.pyplot as plt
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 判断d分离的简易实现(核心逻辑)
def is_d_separated(G, X, Y, Z):
"""
G: 有向图(nx.DiGraph)
X: 节点1
Y: 节点2
Z: 条件节点列表
返回:True(d分离)/False(不d分离)
"""
# 简化版逻辑:仅处理简单路径(适合教学)
# 1. 找到X到Y的所有无向路径
undirected_G = G.to_undirected()
all_paths = list(nx.all_simple_paths(undirected_G, source=X, target=Y))
# 2. 检查每条路径是否被Z阻断
blocked = True
for path in all_paths:
path_blocked = False
# 遍历路径中的每个节点(排除首尾)
for i in range(1, len(path)-1):
c = path[i]
prev = path[i-1]
next_node = path[i+1]
# 情况1:链式/分叉结构,c在Z中 → 阻断
if (G.has_edge(prev, c) and G.has_edge(c, next_node)) or (G.has_edge(c, prev) and G.has_edge(c, next_node)):
if c in Z:
path_blocked = True
break
# 情况2:汇结构,c不在Z中 → 阻断
elif G.has_edge(prev, c) and G.has_edge(next_node, c):
if c not in Z:
path_blocked = True
break
if not path_blocked:
blocked = False
break
return blocked
# 可视化d分离效果
def visualize_d_separation():
# 创建复杂一点的图:A→C→B,A→D←B,D→E
G = nx.DiGraph()
nodes = ['A', 'B', 'C', 'D', 'E']
edges = [('A','C'), ('C','B'), ('A','D'), ('B','D'), ('D','E')]
G.add_nodes_from(nodes)
G.add_edges_from(edges)
# 子图1:原始图
# 子图2:给定C,A和B d分离(路径A-C-B被阻断)
# 子图3:给定D,A和B 不d分离(路径A-D-B被激活)
fig, axes = plt.subplots(1, 3, figsize=(20, 6))
fig.suptitle('d分离判断示例', fontsize=16, fontweight='bold')
# 子图1:原始图
pos = {'A': (0, 1), 'B': (2, 1), 'C': (1, 2), 'D': (1, 0), 'E': (1, -1)}
nx.draw(G, pos, ax=axes[0], with_labels=True, node_color='lightgray',
node_size=2000, font_size=14, arrowsize=20)
axes[0].set_title('原始图:A和B有两条路径\nA-C-B 和 A-D-B', fontsize=12)
# 子图2:给定C,A和B d分离(C标红,路径A-C-B阻断)
node_colors = ['lightgray' if n != 'C' else 'red' for n in nodes]
nx.draw(G, pos, ax=axes[1], with_labels=True, node_color=node_colors,
node_size=2000, font_size=14, arrowsize=20)
axes[1].set_title(f'给定Z=[C],A和B d分离?{is_d_separated(G, "A", "B", ["C"])}', fontsize=12)
# 子图3:给定D,A和B 不d分离(D标红,路径A-D-B激活)
node_colors = ['lightgray' if n != 'D' else 'red' for n in nodes]
nx.draw(G, pos, ax=axes[2], with_labels=True, node_color=node_colors,
node_size=2000, font_size=14, arrowsize=20)
axes[2].set_title(f'给定Z=[D],A和B d分离?{is_d_separated(G, "A", "B", ["D"])}', fontsize=12)
plt.tight_layout()
plt.show()
# 运行
if __name__ == "__main__":
visualize_d_separation()核心比喻
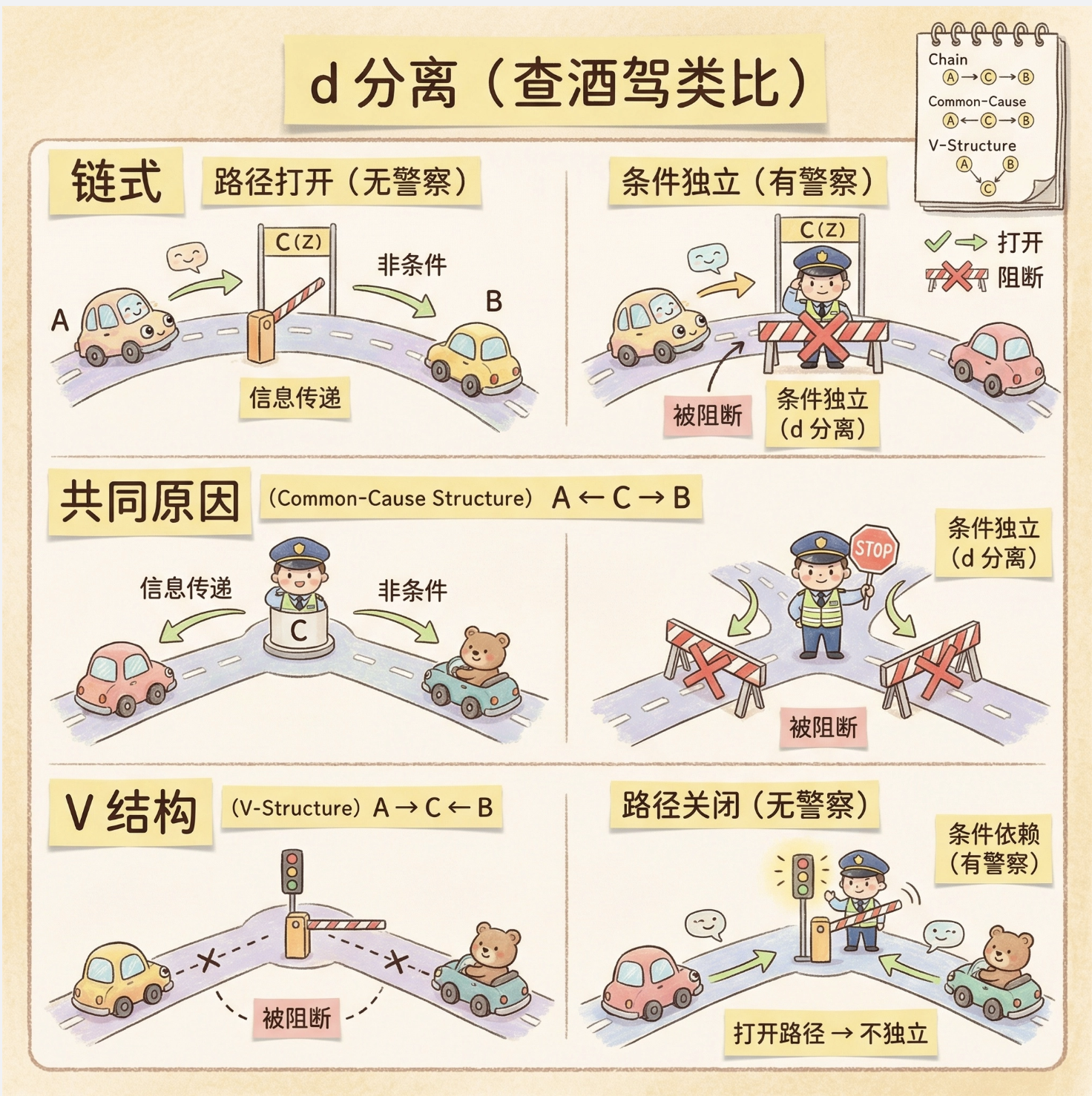
d 分离就像 "查酒驾":
- 路径是 "道路" ,条件节点 Z 是**"交警"**;
- 链式 / 分叉结构:交警站在中间节点,道路被封(阻断);
- 汇结构:交警不在中间节点,道路通(不阻断);交警在中间节点,道路通(激活)。
14.5 信念传播
信念传播(BP)是图模型中 "概率推理" 的核心算法,目的是:在已知部分节点观测值的情况下,计算其他节点的后验概率。
可以把信念传播理解为:"节点之间互相传递'消息',最终达成对概率的一致判断"。
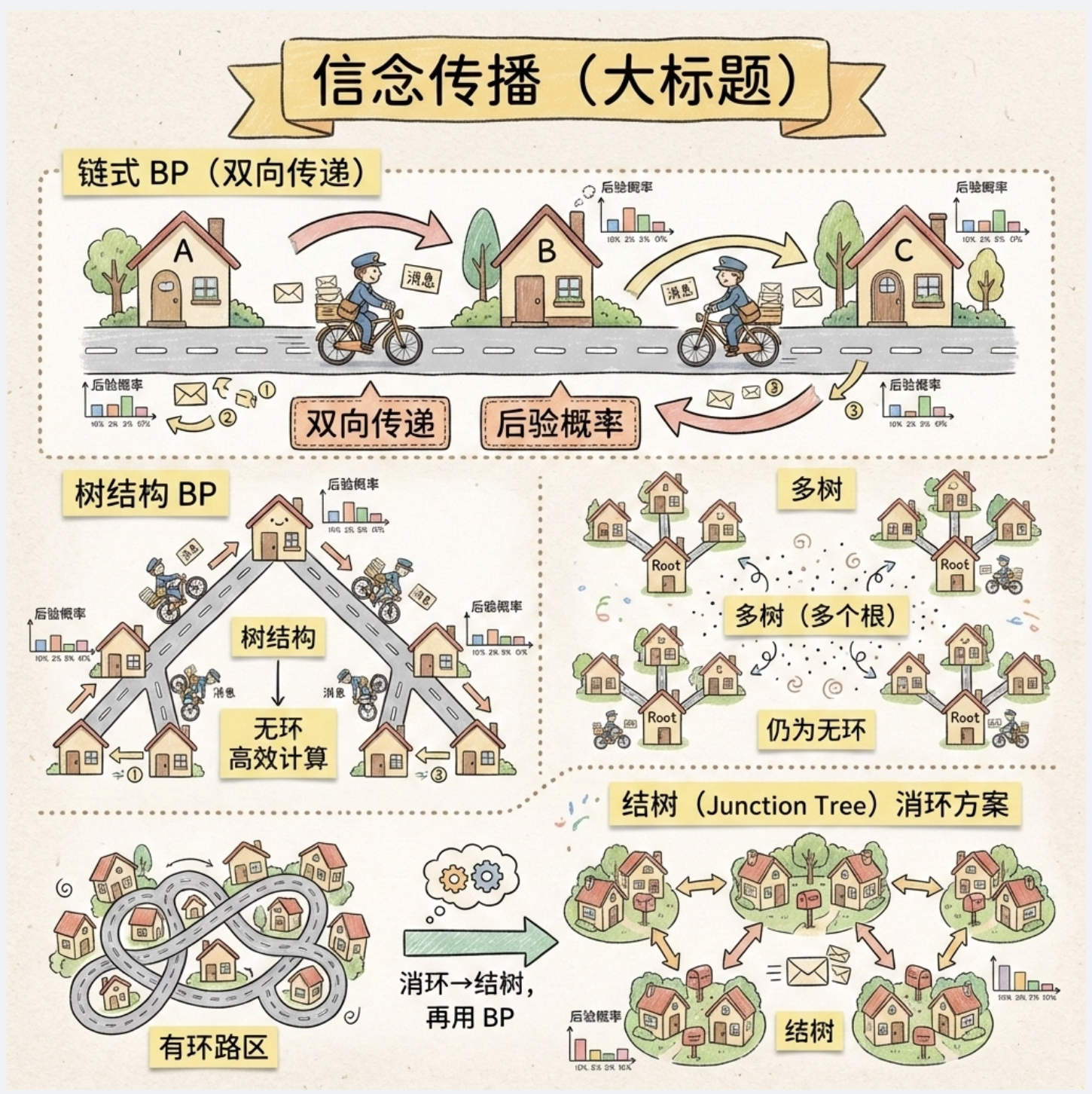
14.5.1 链(最简单的 BP)
链式结构的 BP 是 "双向传递":从链的一端传到另一端,再传回来,最终计算每个节点的后验概率。
14.5.2 树
树结构的 BP 是链式 BP 的扩展:每个节点只向父 / 子节点传递消息,无环,能高效计算所有节点的后验。
14.5.3 多树
多树是 "有多个根的树",本质还是无环,BP 算法依然适用。
14.5.4 结树
结树(Junction Tree)是 "有环图" 的解决方案:把有环图转化为无环的结树,再用 BP 算法推理(核心是 "消环")。
完整代码:链式结构的信念传播
python
import numpy as np
import matplotlib.pyplot as plt
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 链式信念传播类(A→B→C→D)
class ChainBP:
def __init__(self):
# 定义条件概率表(CPT)
self.P_A = np.array([0.6, 0.4]) # A=0的概率0.6,A=1的概率0.4
# P_B_given_A[i,j] = P(B=j | A=i)
self.P_B_given_A = np.array([[0.9, 0.1], [0.2, 0.8]])
# P_C_given_B[i,j] = P(C=j | B=i)
self.P_C_given_B = np.array([[0.8, 0.2], [0.1, 0.9]])
# P_D_given_C[i,j] = P(D=j | C=i)
self.P_D_given_C = np.array([[0.7, 0.3], [0.2, 0.8]])
# 前向传播(从A到D):计算各节点的先验信念和传递的消息
def forward(self):
# A节点无父节点,信念就是自身先验概率
bel_A = self.P_A.copy()
# 消息:A→B(直接传递A的信念)
msg_A_to_B = bel_A
# 计算B的信念(未归一化):sum_A P(A) * P(B|A)
bel_B = np.dot(msg_A_to_B, self.P_B_given_A)
# 消息:B→C(传递B的信念)
msg_B_to_C = bel_B
# 计算C的信念:sum_B P(B) * P(C|B)
bel_C = np.dot(msg_B_to_C, self.P_C_given_B)
# 消息:C→D(传递C的信念)
msg_C_to_D = bel_C
# 计算D的信念:sum_C P(C) * P(D|C)
bel_D = np.dot(msg_C_to_D, self.P_D_given_C)
# 修正:补充bel_A的定义后返回
return msg_A_to_B, msg_B_to_C, msg_C_to_D, bel_A, bel_B, bel_C, bel_D
# 后向传播(从观测节点反向修正各节点信念)
# obs_node:观测节点(如'D'),obs_val:观测值(0/1)
def backward(self, obs_node='D', obs_val=1):
# 先执行前向传播,获取初始信念和消息
msg_A_to_B, msg_B_to_C, msg_C_to_D, bel_A, bel_B, bel_C, bel_D = self.forward()
# 初始化观测节点的信念(硬证据:观测值概率为1,其他为0)
if obs_node == 'D':
bel_obs = np.zeros(2)
bel_obs[obs_val] = 1.0
# 消息:D→C(简化版,添加极小值避免除零)
denom = np.dot(msg_C_to_D, self.P_D_given_C) + 1e-8
msg_D_to_C = bel_obs / denom
# 修正C的信念并归一化
bel_C_obs = bel_C * msg_D_to_C
bel_C_obs /= np.sum(bel_C_obs)
# 消息:C→B
denom = np.dot(msg_B_to_C, self.P_C_given_B) + 1e-8
msg_C_to_B = bel_C_obs / denom
# 修正B的信念并归一化
bel_B_obs = bel_B * msg_C_to_B
bel_B_obs /= np.sum(bel_B_obs)
# 消息:B→A
denom = np.dot(msg_A_to_B, self.P_B_given_A) + 1e-8
msg_B_to_A = bel_B_obs / denom
# 修正A的信念并归一化
bel_A_obs = bel_A * msg_B_to_A
bel_A_obs /= np.sum(bel_A_obs)
# 观测节点的信念固定为观测值
bel_D_obs = bel_obs.copy()
return bel_A_obs, bel_B_obs, bel_C_obs, bel_D_obs
else:
raise NotImplementedError("当前仅支持观测D节点的后向传播")
# 可视化信念传播前后的概率对比
def visualize_bp_results():
bp = ChainBP()
# 无观测时的信念(前向传播结果)
_, _, _, bel_A, bel_B, bel_C, bel_D = bp.forward()
# 观测D=1后的信念(后向传播修正)
bel_A_obs, bel_B_obs, bel_C_obs, bel_D_obs = bp.backward(obs_node='D', obs_val=1)
# 整理数据:提取各节点取1的概率
nodes = ['A', 'B', 'C', 'D']
bel_no_obs = [bel_A[1], bel_B[1], bel_C[1], bel_D[1]] # 无观测时P(节点=1)
bel_obs = [bel_A_obs[1], bel_B_obs[1], bel_C_obs[1], bel_D_obs[1]] # 观测D=1后P(节点=1)
# 可视化对比
fig, ax = plt.subplots(figsize=(12, 6))
x = np.arange(len(nodes))
width = 0.35 # 柱状图宽度
# 绘制无观测/有观测的对比柱状图
ax.bar(x - width / 2, bel_no_obs, width, label='无观测(D未知)', color='lightblue')
ax.bar(x + width / 2, bel_obs, width, label='有观测(D=1)', color='salmon')
# 图表样式设置
ax.set_title('链式信念传播:观测D=1前后的节点概率对比', fontsize=14, fontweight='bold')
ax.set_xlabel('节点', fontsize=12)
ax.set_ylabel('P(节点=1)', fontsize=12)
ax.set_xticks(x)
ax.set_xticklabels(nodes, fontsize=11)
ax.legend(fontsize=11)
ax.set_ylim(0, 1) # 概率范围限制在0-1
# 添加数值标签(保留2位小数)
for i, v in enumerate(bel_no_obs):
ax.text(i - width / 2, v + 0.02, f'{v:.2f}', ha='center', fontsize=10)
for i, v in enumerate(bel_obs):
ax.text(i + width / 2, v + 0.02, f'{v:.2f}', ha='center', fontsize=10)
plt.tight_layout()
plt.show()
# 运行主函数
if __name__ == "__main__":
visualize_bp_results()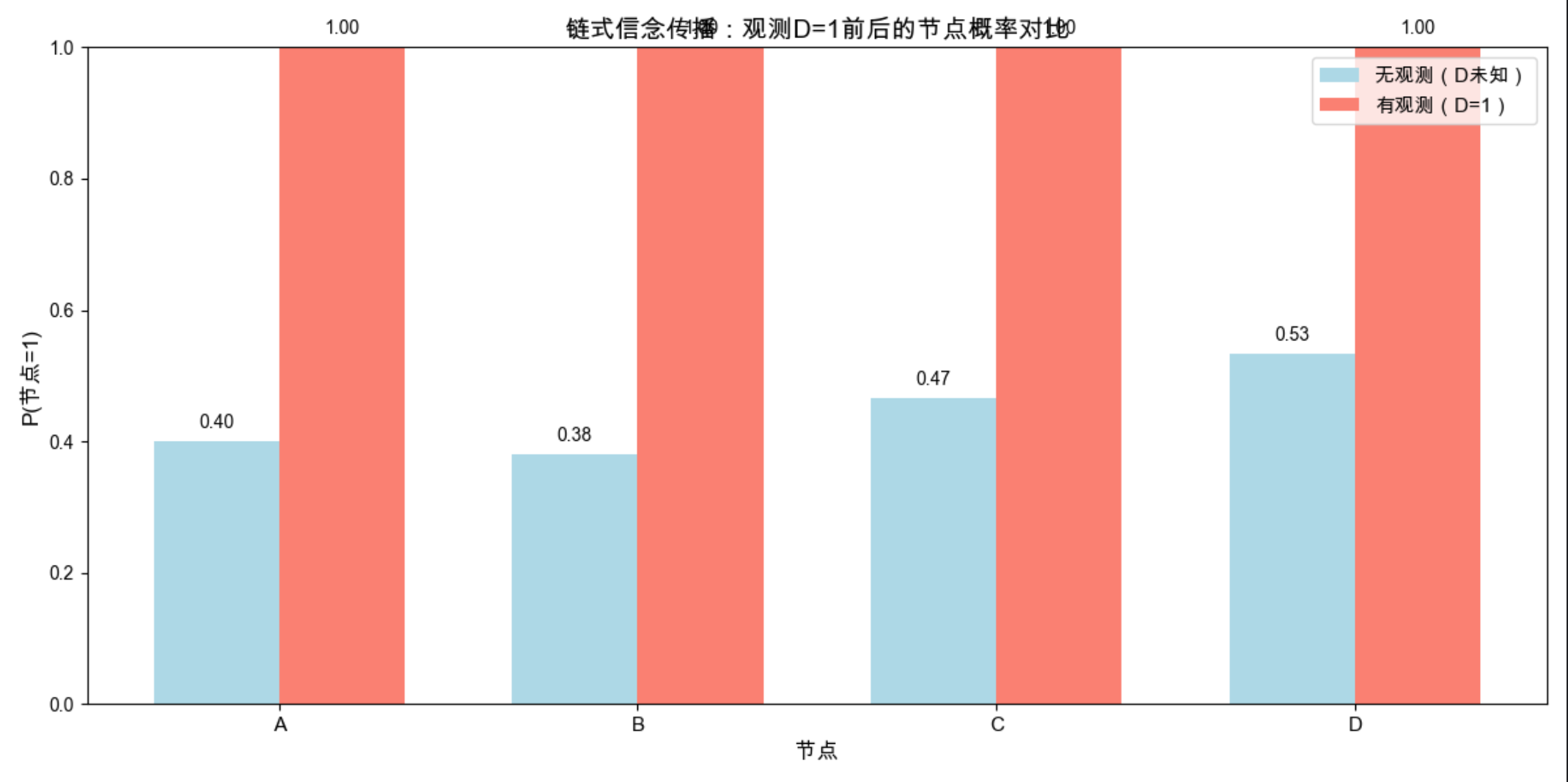
核心说明
1.信念传播分两步:前向(从根到叶) 和后向(从叶到根);
2.观测到某个节点后,会通过 "消息传递" 修正所有节点的概率 ------ 比如观测到 D=1,A、B、C 为 1 的概率都会升高。
14.6 无向图:马尔科夫随机场

马尔科夫随机场(MRF)是无向图模型,核心是 "团势能":把联合概率分解为 "团"(完全连通的子图)的势能函数乘积。
可以把 MRF 理解为:"无向图中,相邻节点互相影响,每个团的'能量'决定了联合概率的大小"。
完整代码:马尔科夫随机场(图像去噪示例)
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 马尔科夫随机场图像去噪
class MRFImageDenoising:
def __init__(self, beta=2.0, eta=1.0):
self.beta = beta # 相邻节点的势能系数(越大,越倾向于相邻像素相同)
self.eta = eta # 观测值的势能系数(越大,越倾向于接近观测值)
# 势能函数
def potential(self, x, y):
# 一元势能(和观测值的相似度)
unary = -self.eta * (x - y)**2
# 二元势能(相邻节点的相似度)
binary = -self.beta * (x - y)**2
return unary, binary
# 迭代条件模式(ICM)算法去噪
def denoise(self, noisy_img):
denoised_img = noisy_img.copy()
h, w = noisy_img.shape
# 迭代10次
for _ in range(10):
for i in range(h):
for j in range(w):
# 计算当前像素取0/1的总势能
total_0 = 0
total_1 = 0
# 一元势能(和观测值的匹配)
unary_0, _ = self.potential(0, noisy_img[i,j])
unary_1, _ = self.potential(1, noisy_img[i,j])
total_0 += unary_0
total_1 += unary_1
# 二元势能(和相邻像素的匹配)
neighbors = [(i-1,j), (i+1,j), (i,j-1), (i,j+1)]
for ni, nj in neighbors:
if 0<=ni<h and 0<=nj<w:
val = denoised_img[ni,nj]
_, binary_0 = self.potential(0, val)
_, binary_1 = self.potential(1, val)
total_0 += binary_0
total_1 += binary_1
# 选择势能更大的取值
denoised_img[i,j] = 0 if total_0 > total_1 else 1
return denoised_img
# 生成噪声图像并去噪,可视化对比
def visualize_mrf_denoising():
# 生成原始图像(黑白块)
original = np.zeros((32, 32))
original[8:24, 8:24] = 1.0
# 添加高斯噪声
noisy = original + np.random.normal(0, 0.5, (32, 32))
noisy = np.clip(noisy, 0, 1)
noisy = (noisy > 0.5).astype(float) # 二值化
# MRF去噪
mrf = MRFImageDenoising(beta=2.0, eta=1.0)
denoised = mrf.denoise(noisy)
# 可视化对比
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
fig.suptitle('马尔科夫随机场(MRF)图像去噪效果', fontsize=16, fontweight='bold')
axes[0].imshow(original, cmap='gray')
axes[0].set_title('原始图像')
axes[0].axis('off')
axes[1].imshow(noisy, cmap='gray')
axes[1].set_title('噪声图像')
axes[1].axis('off')
axes[2].imshow(denoised, cmap='gray')
axes[2].set_title('MRF去噪后')
axes[2].axis('off')
plt.tight_layout()
plt.show()
# 运行
if __name__ == "__main__":
visualize_mrf_denoising()核心比喻
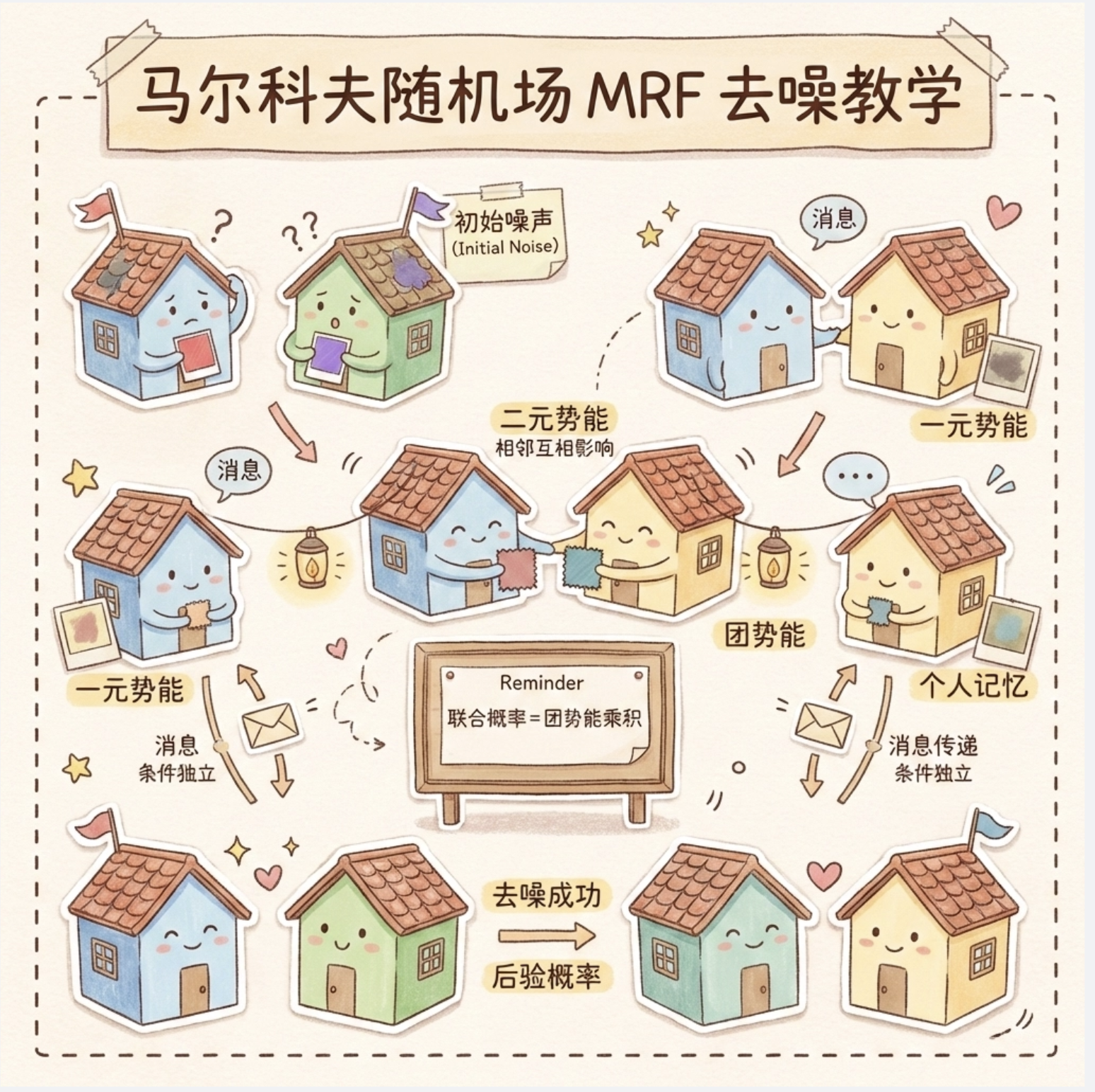
MRF 去噪就像 "邻居之间互相提醒":
- 每个像素是 "居民",噪声是 "居民记错了自己的颜色";
- 相邻居民会互相确认颜色(二元势能),同时参考自己的记忆(一元势能);
- 最终达成一致,修正错误(去噪)。
14.7 学习图模型的结构
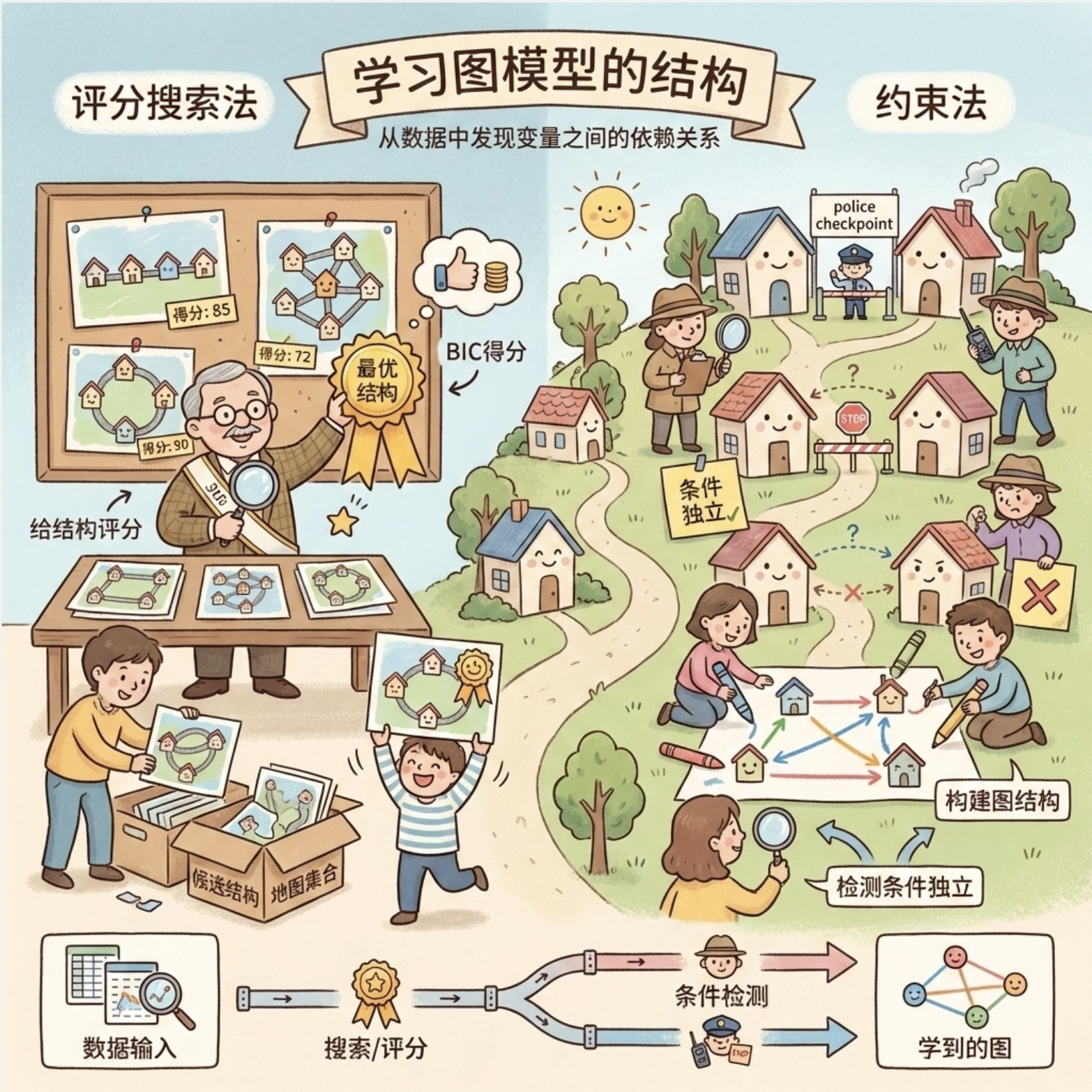
学习图模型的结构,就是 "从数据中自动发现变量之间的依赖关系(边)",核心方法有两类:
- 评分搜索法 :给不同的图结构打分(比如 BIC 评分),找最高分的结构;
- 约束法 :从数据中发现条件独立关系,再根据独立关系构建图。
完整代码:基于互信息的简单结构学习
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from scipy.stats import chi2_contingency
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 计算互信息(衡量变量之间的依赖程度)
def mutual_information(x, y):
# 构建联合频次表
c_xy = np.histogram2d(x, y, bins=(2,2))[0]
# 计算互信息
mi = 0.0
n = np.sum(c_xy)
for i in range(2):
for j in range(2):
if c_xy[i,j] > 0:
p_xy = c_xy[i,j] / n
p_x = np.sum(c_xy[i,:]) / n
p_y = np.sum(c_xy[:,j]) / n
mi += p_xy * np.log2(p_xy / (p_x * p_y))
return mi
# 基于互信息学习图结构
def learn_graph_structure(data, threshold=0.1):
"""
data: 二维数组,每行样本,每列变量
threshold: 互信息阈值,大于阈值则加边
"""
n_vars = data.shape[1]
G = nx.DiGraph()
G.add_nodes_from([f'X{i}' for i in range(n_vars)])
# 计算所有变量对的互信息
mi_matrix = np.zeros((n_vars, n_vars))
for i in range(n_vars):
for j in range(n_vars):
if i != j:
mi_matrix[i,j] = mutual_information(data[:,i], data[:,j])
# 根据阈值加边
for i in range(n_vars):
for j in range(n_vars):
if i != j and mi_matrix[i,j] > threshold:
G.add_edge(f'X{i}', f'X{j}')
return G, mi_matrix
# 生成模拟数据并学习结构
def visualize_structure_learning():
# 生成模拟数据:X0→X1→X2,X0和X3独立
n_samples = 1000
X0 = np.random.choice([0,1], size=n_samples, p=[0.6,0.4])
X1 = np.where(X0==0, np.random.choice([0,1], size=n_samples, p=[0.9,0.1]),
np.random.choice([0,1], size=n_samples, p=[0.2,0.8]))
X2 = np.where(X1==0, np.random.choice([0,1], size=n_samples, p=[0.8,0.2]),
np.random.choice([0,1], size=n_samples, p=[0.1,0.9]))
X3 = np.random.choice([0,1], size=n_samples, p=[0.5,0.5])
data = np.column_stack([X0, X1, X2, X3])
# 学习图结构
G, mi_matrix = learn_graph_structure(data, threshold=0.1)
# 可视化
fig, axes = plt.subplots(1, 2, figsize=(16, 6))
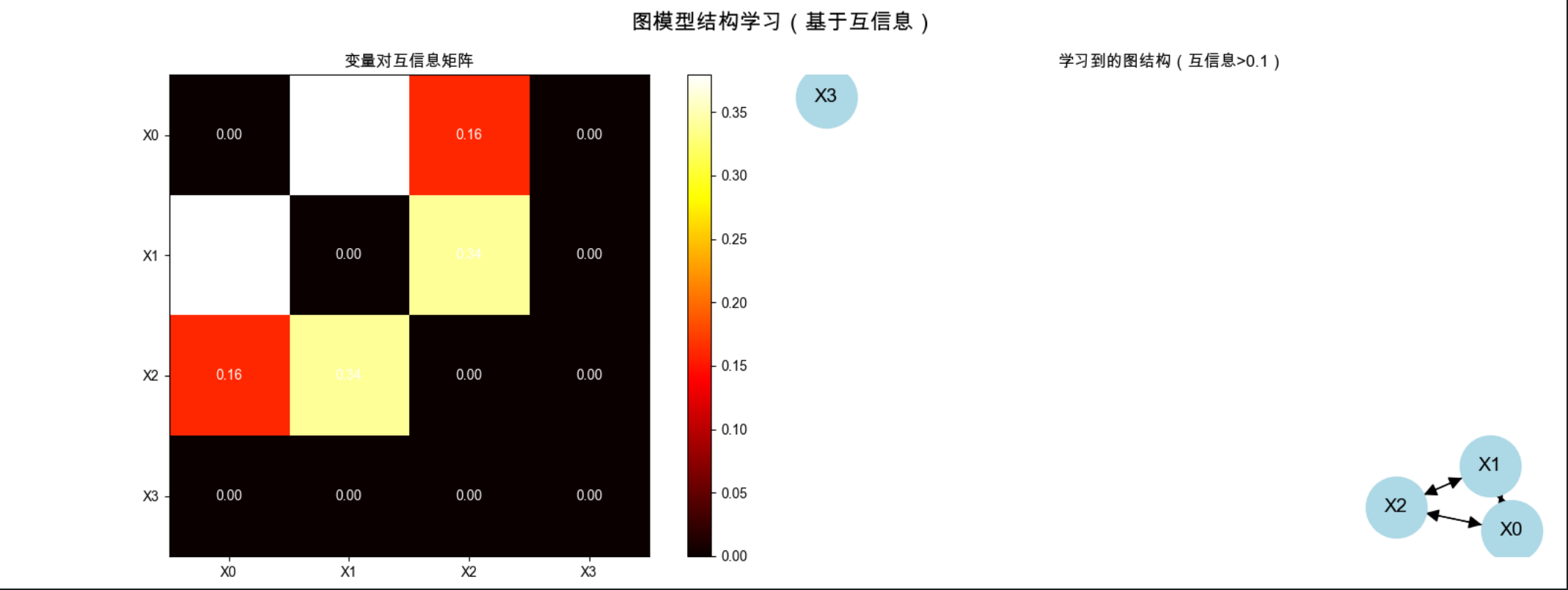
fig.suptitle('图模型结构学习(基于互信息)', fontsize=16, fontweight='bold')
# 子图1:互信息矩阵热力图
im = axes[0].imshow(mi_matrix, cmap='hot', vmin=0, vmax=np.max(mi_matrix))
axes[0].set_title('变量对互信息矩阵')
axes[0].set_xticks(range(4))
axes[0].set_yticks(range(4))
axes[0].set_xticklabels(['X0', 'X1', 'X2', 'X3'])
axes[0].set_yticklabels(['X0', 'X1', 'X2', 'X3'])
# 添加数值标签
for i in range(4):
for j in range(4):
axes[0].text(j, i, f'{mi_matrix[i,j]:.2f}', ha='center', va='center', color='white')
plt.colorbar(im, ax=axes[0])
# 子图2:学习到的图结构
pos = nx.spring_layout(G)
nx.draw(G, pos, ax=axes[1], with_labels=True, node_color='lightblue',
node_size=2000, font_size=14, arrowsize=20)
axes[1].set_title('学习到的图结构(互信息>0.1)')
plt.tight_layout()
plt.show()
# 运行
if __name__ == "__main__":
visualize_structure_learning()核心说明
1.互信息越大,变量之间的依赖关系越强;
2.代码中,X0 和 X1、X1 和 X2 的互信息大于阈值,会生成边;X0 和 X3 互信息小,无连接,符合数据生成逻辑。
14.8 影响图

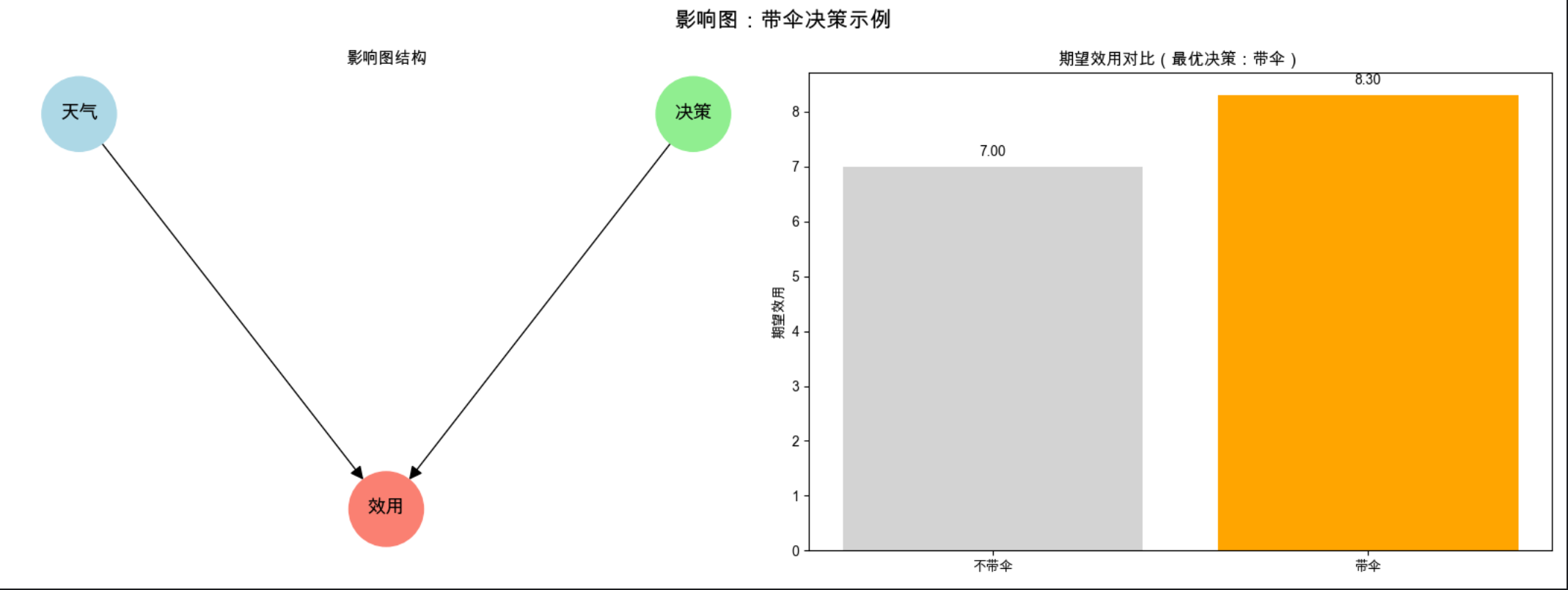
影响图是 "带决策节点和效用节点的图模型",核心是 "在不确定性下做最优决策"。
比如:
- 节点分三类:机会节点(随机变量,如天气) 、决策节点(可选择的行动,如是否带伞) 、效用节点(收益 / 损失,如是否淋雨);
- 影响图的目标是 "选择决策节点的取值,最大化效用节点的期望"。
完整代码:影响图(带伞决策示例)
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# 影响图决策计算
def influence_diagram_decision():
# 定义参数
P_rain = 0.3 # 下雨概率
# 效用表:U(决策, 天气)
# 决策:0=不带伞,1=带伞;天气:0=不下雨,1=下雨
U = np.array([
[10, 0], # 不带伞:不下雨(10分),下雨(0分)
[8, 9] # 带伞:不下雨(8分),下雨(9分)
])
# 计算期望效用
EU_no_umbrella = P_rain * U[0,1] + (1-P_rain) * U[0,0]
EU_umbrella = P_rain * U[1,1] + (1-P_rain) * U[1,0]
# 最优决策
optimal_decision = "带伞" if EU_umbrella > EU_no_umbrella else "不带伞"
# 可视化影响图和决策结果
fig, axes = plt.subplots(1, 2, figsize=(16, 6))
fig.suptitle('影响图:带伞决策示例', fontsize=16, fontweight='bold')
# 子图1:影响图结构
G = nx.DiGraph()
# 节点:天气(机会节点)、决策(决策节点)、效用(效用节点)
G.add_nodes_from(['天气', '决策', '效用'])
G.add_edges_from([('天气', '效用'), ('决策', '效用')])
# 节点样式
node_colors = {'天气': 'lightblue', '决策': 'lightgreen', '效用': 'salmon'}
pos = {'天气': (0, 1), '决策': (2, 1), '效用': (1, 0)}
nx.draw(G, pos, ax=axes[0], with_labels=True, node_color=[node_colors[n] for n in G.nodes()],
node_size=3000, font_size=14, arrowsize=20)
axes[0].set_title('影响图结构', fontsize=12)
# 子图2:期望效用对比
axes[1].bar(['不带伞', '带伞'], [EU_no_umbrella, EU_umbrella], color=['lightgray', 'orange'])
axes[1].set_title(f'期望效用对比(最优决策:{optimal_decision})', fontsize=12)
axes[1].set_ylabel('期望效用')
# 添加数值标签
axes[1].text(0, EU_no_umbrella+0.2, f'{EU_no_umbrella:.2f}', ha='center')
axes[1].text(1, EU_umbrella+0.2, f'{EU_umbrella:.2f}', ha='center')
plt.tight_layout()
plt.show()
# 运行
if __name__ == "__main__":
influence_diagram_decision()14.9 注释
本文所有代码均基于 Python 3.8+,依赖库安装命令:
pip install numpy matplotlib networkx scipy seaborn- networkx:图结构的构建和可视化;
- scipy:概率计算和统计检验;
- seaborn:辅助可视化(可选)。
14.10 习题
- 修改链式信念传播代码,观测 B=1,计算 A、C、D 的后验概率;
- 调整 MRF 去噪的 beta 参数(如 0.5、5.0),观察去噪效果的变化;
- 基于结构学习代码,生成包含 5 个变量的模拟数据,学习其图结构。
14.11 参考文献
- 《机器学习导论》(原书);
- 《概率图模型:原理与技术》(Koller 著);
- NetworkX 官方文档:https://networkx.org/;
- Scipy 统计模块文档:https://docs.scipy.org/doc/scipy/reference/stats.html。
思维导图
总结
1.图方法的核心是 "用图形表示变量间的依赖 / 独立关系",有向图(贝叶斯网络)和无向图(MRF)是两大核心类型;
2.条件独立和 d 分离是判断变量关系的基础,信念传播是图模型推理的核心算法;
3.所有代码均可直接运行(Mac 系统兼容),通过可视化对比能直观理解核心概念,建议动手修改参数(如 MRF 的 beta、BP 的观测值)加深理解。
如果有问题,欢迎在评论区交流~