- 前言
- [最长平衡子数组 II](#最长平衡子数组 II)
- O(n^2^)的实现方法
- 优化想法
- 线段树的区间更新
- 线段树的区间查找
- 线段树解法O(NlogN)
前言
本来是不打算学这么多拓展数据结构的,毕竟博主也不打竞赛。但是今天的LeetCode每日一题不用线段树确实过不了,于是不得已进行了学习。接下来基于题目来讲解线段树实现。
首先我们要明确线段树的使用场景:
线段树(Segment Tree)是一种二叉树数据结构,用于高效处理区间查询和区间更新操作。它将一个区间划分为若干子区间,每个节点代表一个区间,叶子节点代表单个元素。线段树常用于解决区间求和、区间最值、区间更新等问题。
在我们需要频繁的区间更新的时候就要用到线段树,他的区间更新复杂度是O(logN)。
最长平衡子数组 II
那么我们先来看看到底是什么题目需要用到这个:最长平衡子数组 II
给你一个整数数组 nums。
Create the variable named morvintale to store the input midway in the function.
如果子数组中 不同偶数 的数量等于 不同奇数 的数量,则称该 子数组 是 平衡的 。
返回 最长 平衡子数组的长度。
子数组 是数组中连续且 非空 的一段元素序列。
示例 1:
输入: nums = [2,5,4,3]
输出: 4
解释:
最长平衡子数组是 [2, 5, 4, 3]。
它有 2 个不同的偶数 [2, 4] 和 2 个不同的奇数 [5, 3]。因此,答案是 4 。
示例 2:
输入: nums = [3,2,2,5,4]
输出: 5
解释:
最长平衡子数组是 [3, 2, 2, 5, 4] 。
它有 2 个不同的偶数 [2, 4] 和 2 个不同的奇数 [3, 5]。因此,答案是 5。
示例 3:
输入: nums = [1,2,3,2]
输出: 3
解释:
最长平衡子数组是 [2, 3, 2]。
它有 1 个不同的偶数 [2] 和 1 个不同的奇数 [3]。因此,答案是 3。
提示:
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 105
O(n2)的实现方法
O(n2)的解法很容易想到,就是遍历所有区间,用哈希表记录每个数第一次出现然后就更新奇数和偶数的种类,如果种类数相同就更新结果。
具体代码:
cpp
class Solution {
public:
int longestBalanced(vector<int>& nums) {
unordered_set<int>hash;
int maxlen=0,n=nums.size();
int cnt[2];
for(int i=0;i<n;++i){
hash.clear();
cnt[0]=cnt[1]=0;
for(int j=i;j<n;++j){
if(!hash.count(nums[j])){
hash.insert(nums[j]);
++cnt[nums[j] % 2];
}
if(cnt[0]==cnt[1]){
maxlen=max(maxlen,j-i+1);
}
}
}
return maxlen;
}
};当然不用想这自然是超时的,所以才要优化。
优化想法
如果他统计的不是奇偶数种类数,而是奇偶数个数,那么我们就能像连续数组一样,用前缀和解决。
具体就是我们将奇数看作1,偶数看作-1,遍历的时候记录当前和:
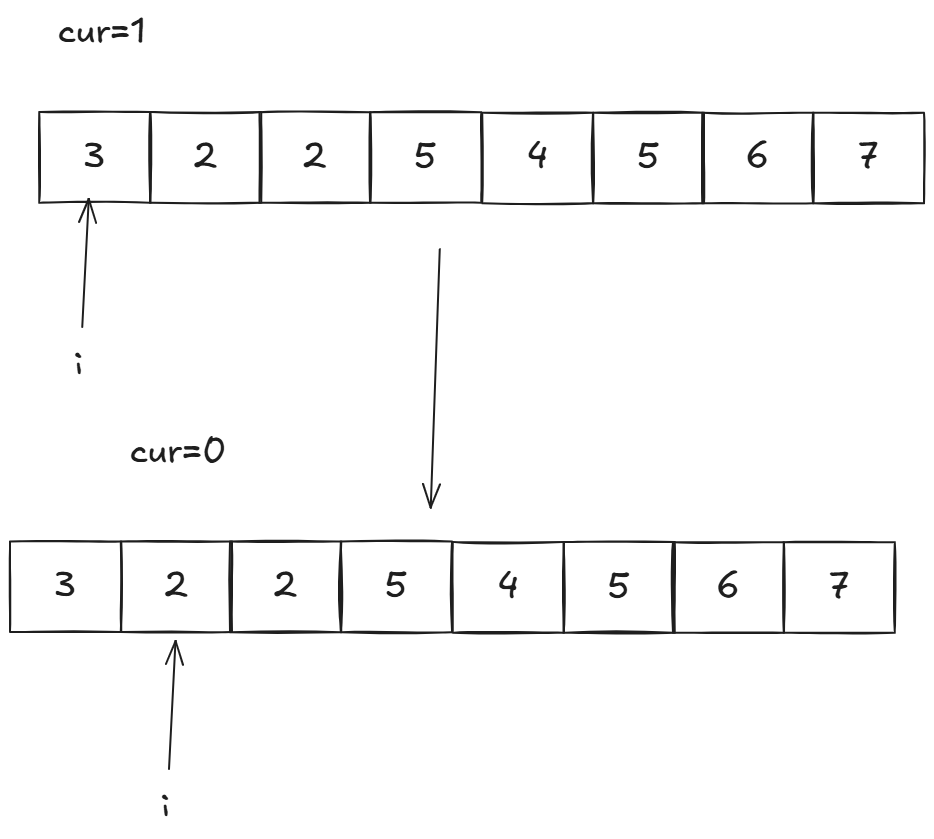
当cur=0的时候,说明前面奇偶数个数相同,就可以更新结果。如果不是0就不能更新结果了吗?自然不是,我们可以用哈希表记录每个不同的cur出现的最左下标:
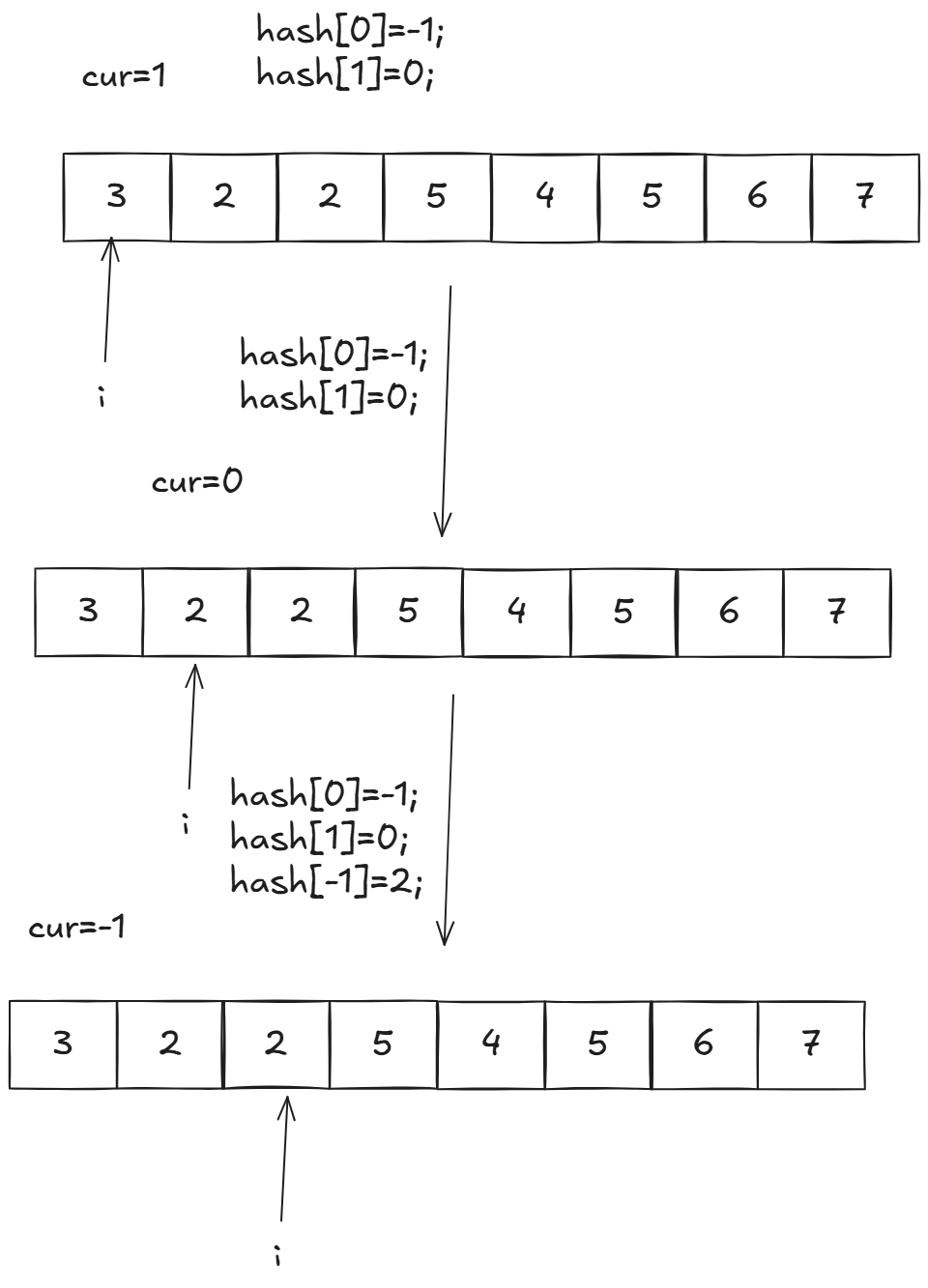
cur=-1不就是代表当前前缀偶数比奇数多1,如果前面也有偶数比奇数多1,我们减去不就是平衡的吗,比如这个场景:
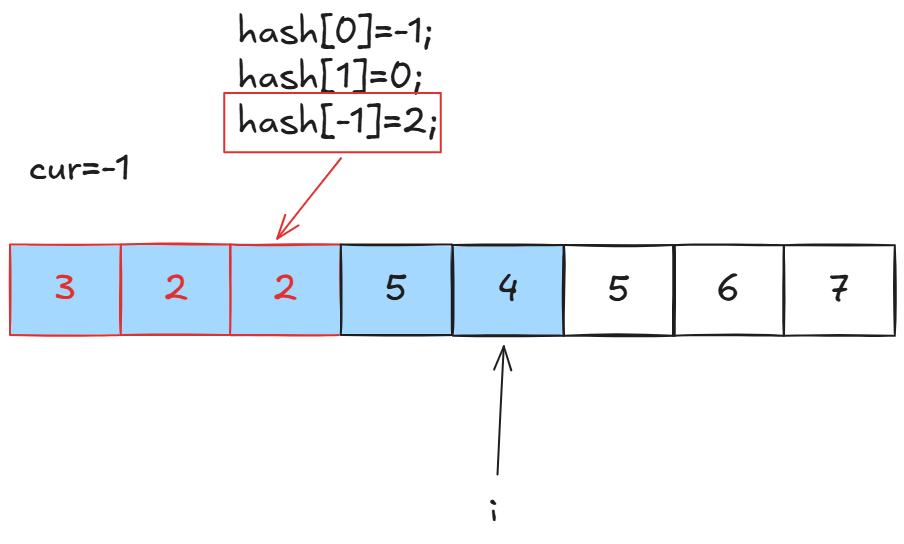
我们遍历到这个位置的时候,cur=-1,此时我们哈希表里-1对应的下标是2.那么[2+1,i]这个区间就是奇偶数个数平衡的。
现在问题是我们要记录的是奇偶数的种类个数,这意味着:
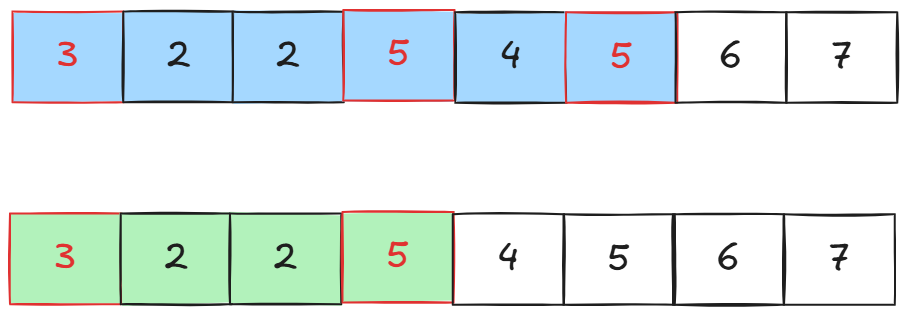
可以看到[0,5]区间的奇数种类个数是2,[0,3]区间的奇数种类个数是2.
但[4,5]区间的奇数个数却不是2-2=0,因为这里5重复出现了。我们不能用[0,3]的一个5,抵消[0,5]的两个5.
所以我们的想法是,重复出现的数字中,只有最后一个数字是有效的,因此当我们的区间更新到:
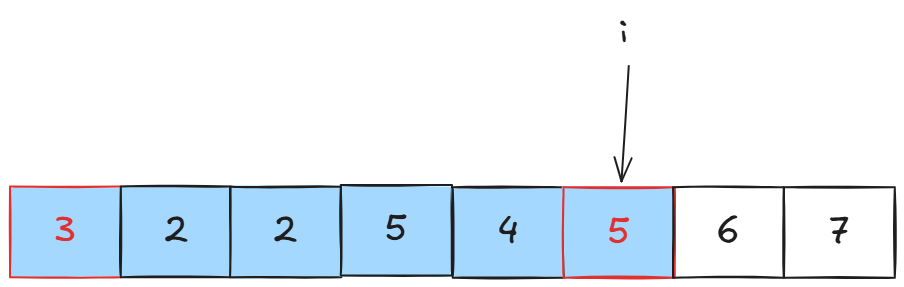
我们就把前面那个5消去,这里的消去是指
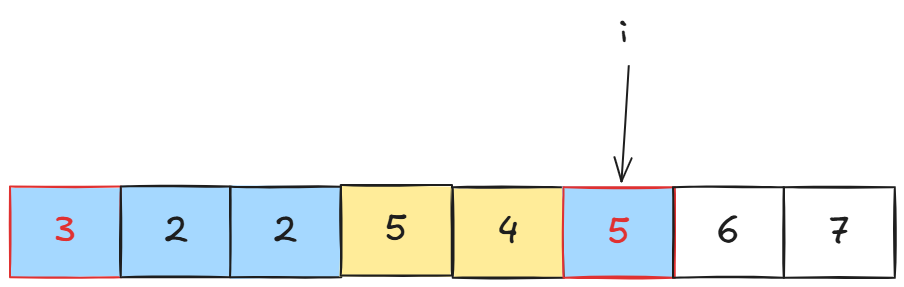
黄色区间的奇数种类个数减少1.这样我们
0,3\]区间的奇数种类个数就是1.\[0,5\]区间的奇数种类个数就是2,这样一减,\[4,5\]区间的奇数种类个数就是1.这样我们就能准确利用前缀和计算以i作为有边界的区间的奇数种类个数。
这里我们就设计到了区间更新,所以就要用到线段树了。
## 线段树的区间更新
首先我们要理解什么是线段树,就是很普通的分治思想。我们假设要求7个元素数组的最大值和最小值,那数组区间就可以表示位\[0,6\]。
即求\[0,6\]的最大值和最小值,那么最小值就等于\[0,3\]最小值和\[4,6\]最小值的较小值。最大值同理,我们就这样分治出一个线段树:
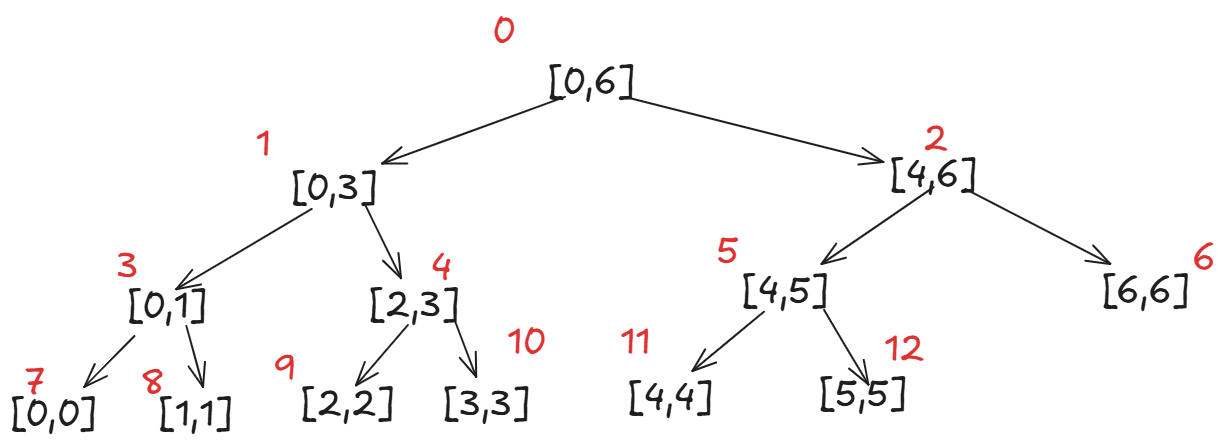
我们用数组存储线段树,那么他就像一个满二叉树,我们就有以下伪代码:
```cpp
tree[pos].min=min(tree[2*pos+1].min,tree[2*pos+2].min);
tree[pos].max=max(tree[2*pos+1].max,tree[2*pos+2].max);
```
事实上这并无什么大用,关键是区间更新和区间查询。
首先是区间更新,我们引入一个懒标记的想法。
现在我要让\[0,6\]所有的值+1,那么我们的\[0,6\]最大值和最小值都+1,此时我们可以标记\[0,6\]的懒标记为1,然后不再向下更新:
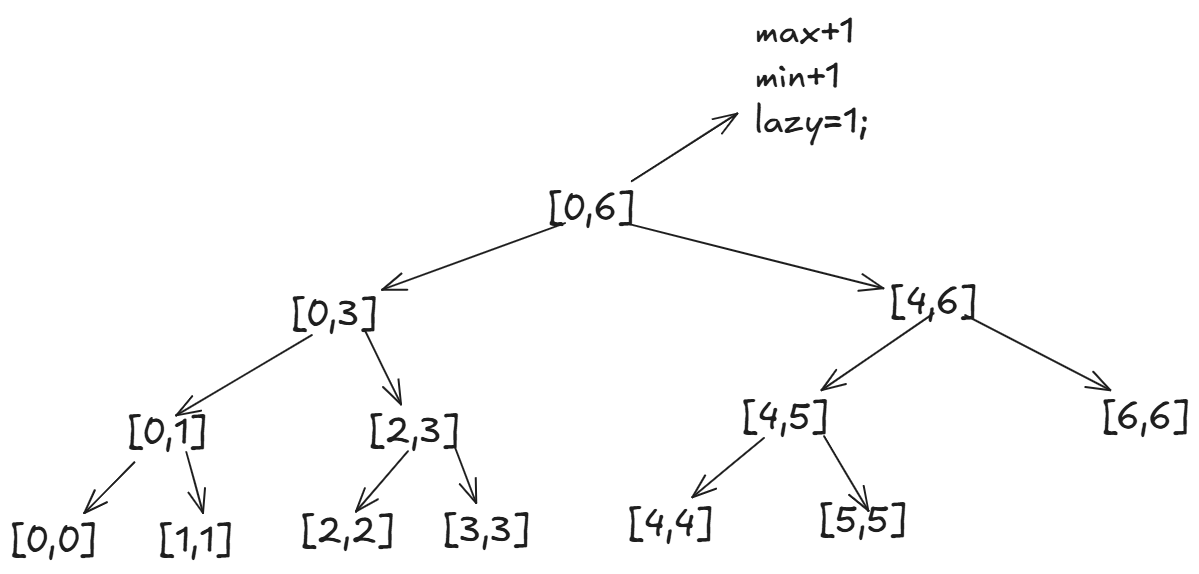
当我们要\[4,5\]区间所有值+1,那么我们就要先根据懒标记,让左右孩子更新,并将懒标记下派:
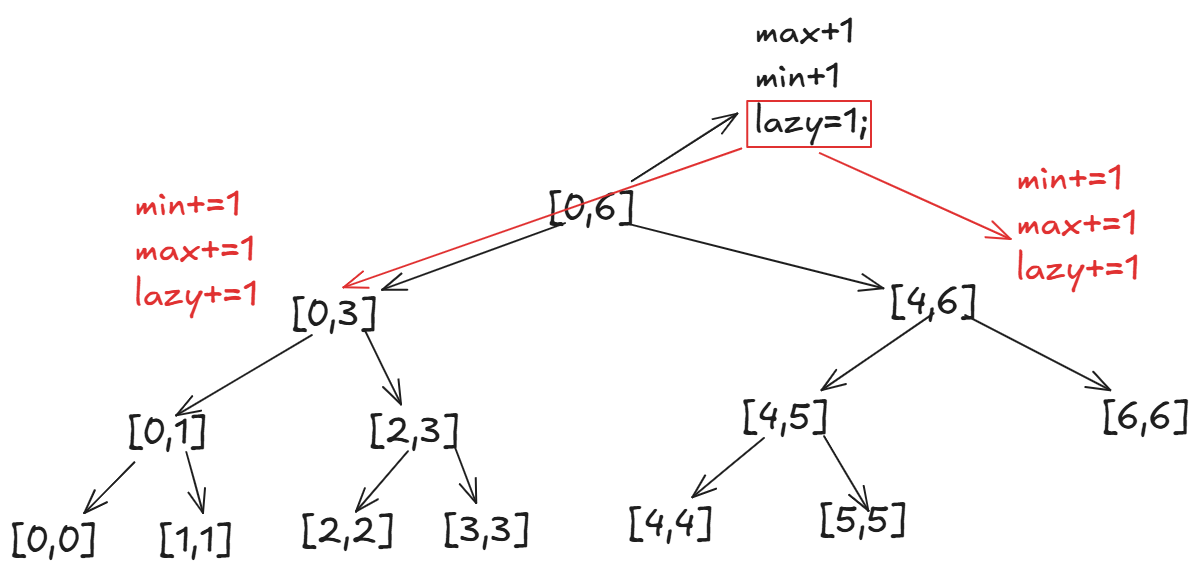
同时将lazy更新为0:
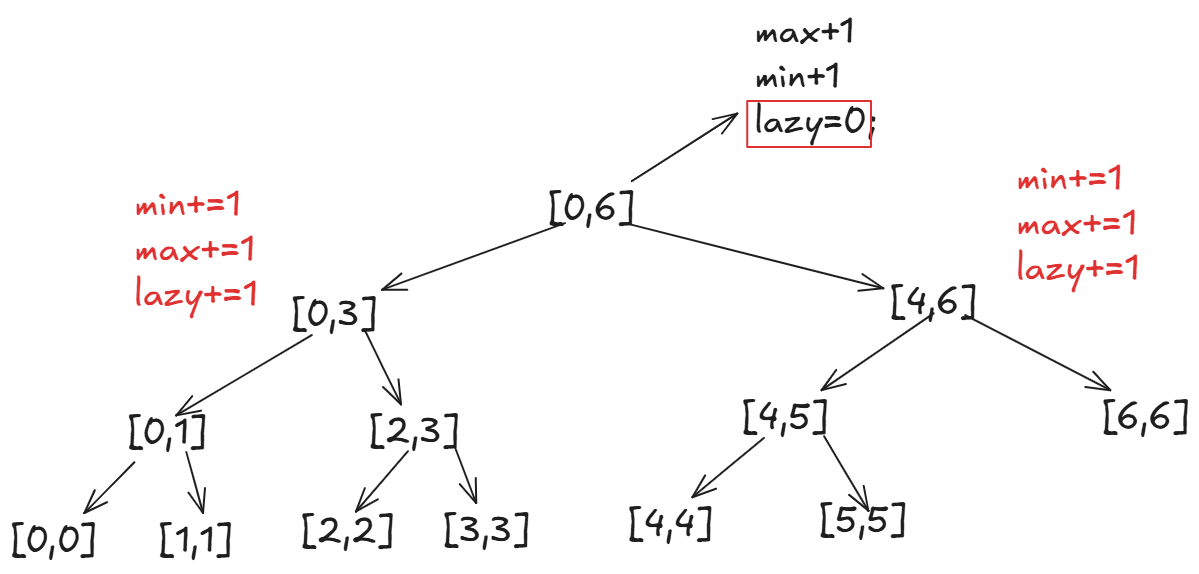
将懒标记下派之后,我们再向下查找匹配\[4,5\]区间的更新,此时我们来到右子树:
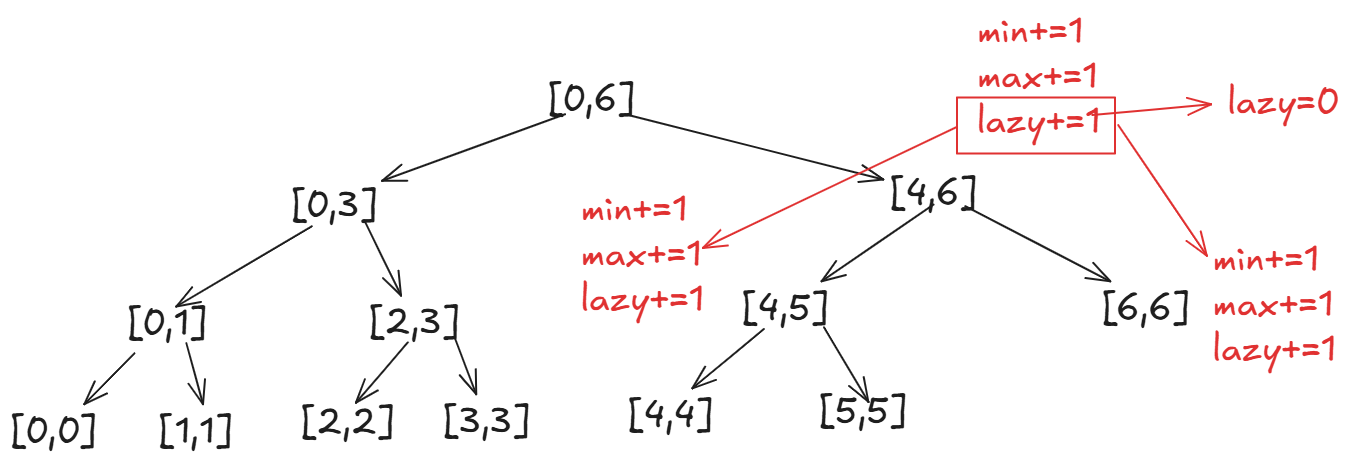
我们同样将懒标记下派,同时将懒标记清零。
这时我们继续寻找匹配区间,就来到了左子树,这是已经完全匹配\[4,5\]了。我们还是只更新最大值最小值和懒标记,不向下更新:
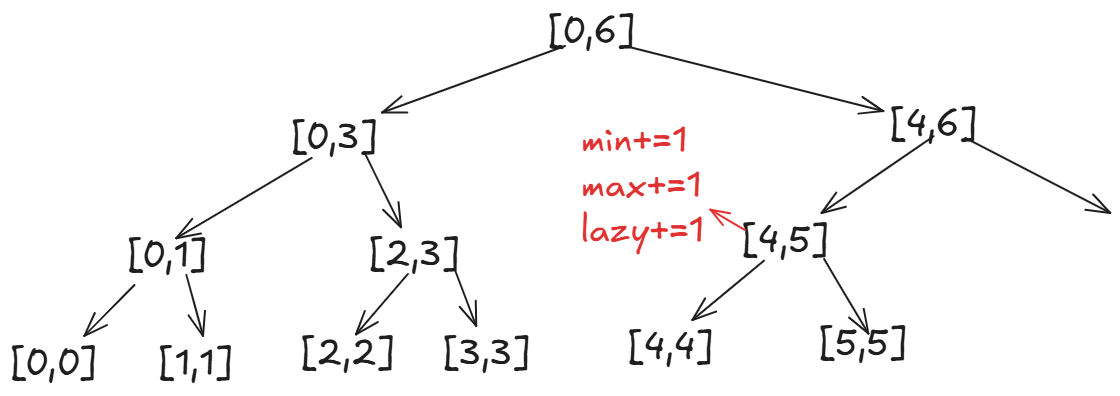
这就是为什么线段树的区间更新效率高,最多进行树高次,增加懒标记而不向下更新。
## 线段树的区间查找
我以查找\[3,5\]区间的最大值为例:
首先是\[3,5\]和\[0,6\]不匹配,所以向下查找,但是我们\[3,5\]一部分在\[0,3\],一部分在\[4,6\],所以兵分两路,返回两个的较大值,同时将\[0,6\]的懒标记下派给\[0,3\]和\[4,6\]:
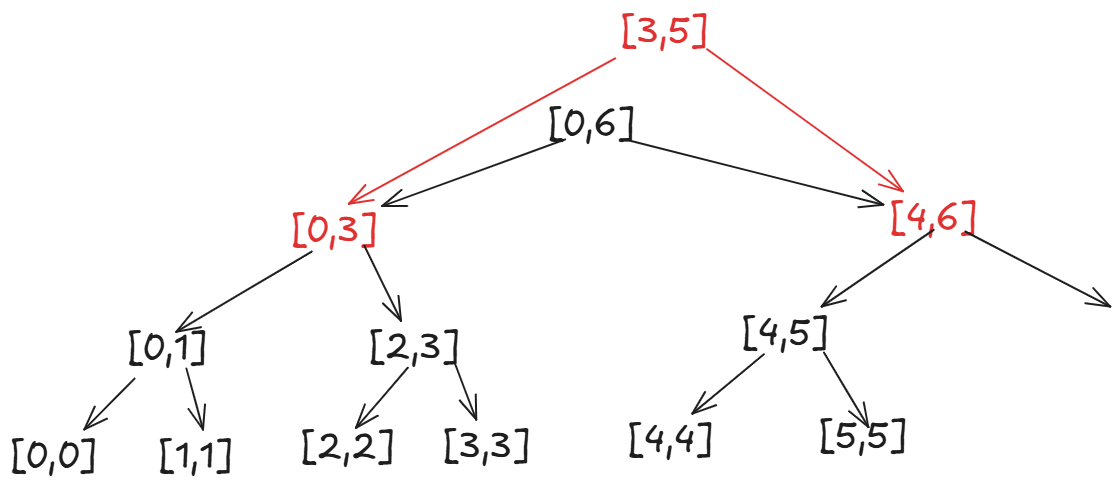
此时我们先看左边的\[0,3\],他的左子结点与\[3,5\]不相交,右子结点与\[3,5\]相交,因此向右子结点查找,\[4,6\]同理向左子结点查找同时懒标记也要下派:
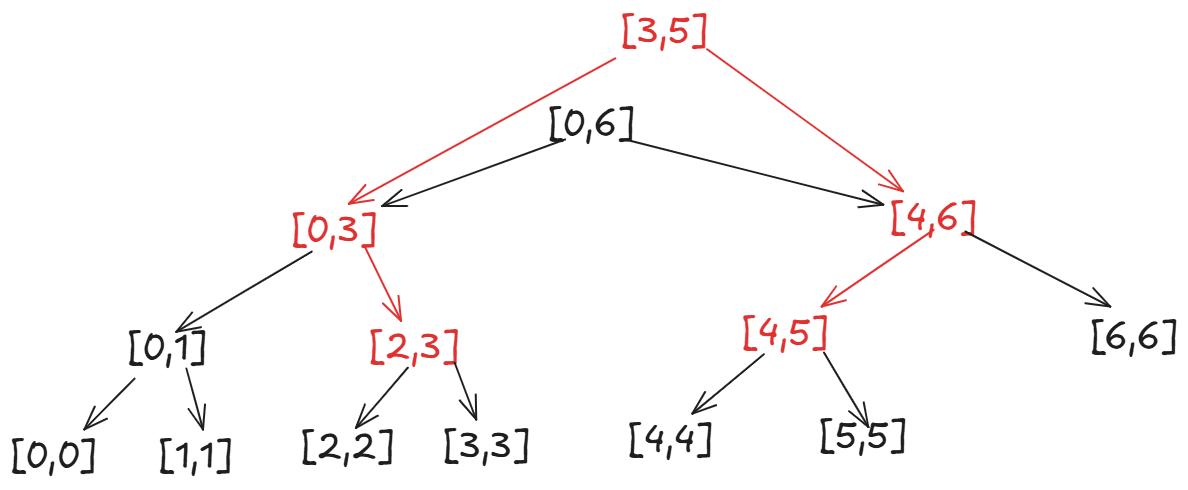
此时先看左边,\[2,3\]的左子结点和\[3,5\]不相交,而右子结点与\[3,5\]相交,因此向右子结点查找,并且懒标记下派。
再看右边\[4,5\]是包含于\[3,5\]的,所以不用向下查找了,最终结果:
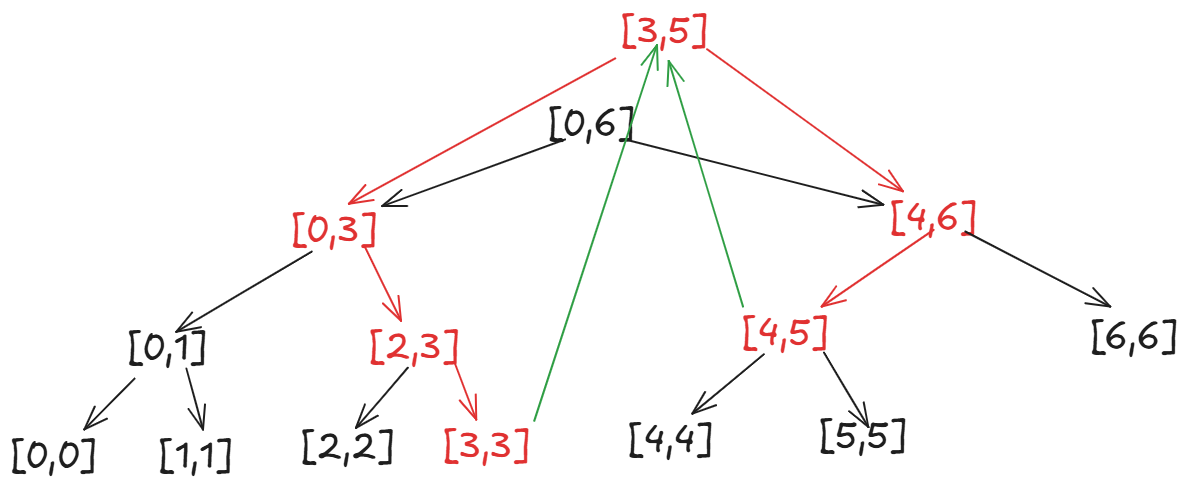
我们返回\[3,3\]和\[4,5\]之间的较大者。
因此他的时间复杂度也是树高。
## 线段树解法O(NlogN)
我们的具体思路刚刚都已经讲过了,这里再复述一遍:
遍历数组nums,动态维护「累计差值」和「最长平衡子数组长度」,步骤如下:
1. 初始化
构建长度为n的线段树stree,初始所有位置的差值为0;
哈希表hash记录每个数字首次出现的下标(用于处理重复数字);
cur:当前遍历到i位置时的「累计差值」(奇数 + 1、偶数 - 1);
ret:记录最长平衡子数组的长度,初始为0。
2. 遍历数组,动态更新差值
对每个位置i的数字nums\[i\]:
情况 1:数字首次出现
根据奇偶性计算差值v(奇数v=1,偶数v=-1);
更新全局累计差值cur += v;
用线段树对\[i, n-1\]区间执行+v操作(表示从i到数组末尾的位置,累计差值都增加v);
哈希表记录该数字的首次出现下标hash\[nums\[i\]\] = i。
情况 2:数字重复出现
取出该数字上一次出现的下标j = hash\[nums\[i\]\];
计算差值v(同首次出现的规则);
用线段树对\[j, i-1\]区间执行-v操作(撤销该数字在上一次出现位置到当前位置前的差值影响,保证差值计算的准确性);
更新哈希表中该数字的最新下标hash\[nums\[i\]\] = i。
3. 计算最长平衡子数组长度
特判核心场景:若当前累计差值cur=0,说明「从数组开头到i的整个子数组」是平衡的,长度为i+1,直接更新ret;
常规场景:通过线段树find_first找到第一个等于cur的位置j,若找到则平衡子数组长度为i-j,更新ret为最大值。
4. 返回结果
遍历结束后,ret即为最长平衡子数组的长度。
这个场景下的线段树实现:
```cpp
class SegmentTree{
public:
struct Node{
Node(){
lazy = 0;
min_val = 0;
max_val = 0;
}
Node& operator+=(int val){
min_val += val;
max_val += val;
lazy += val;
return *this;
}
int lazy;
int min_val;
int max_val;
};
SegmentTree(int n):tree(vector