初识简单 堆

概念

是一种特殊的数据结构，它可以被视为一棵完全二叉树的数组表示

按完全二叉树的顺序存储方式存储 在一 个一维数组中

堆 实际就是在完全二叉树的基础上进行了一些调整

性质

堆中某个节点的值总是不大于或不小于其父节点的值；

堆总是一棵完全二叉树。

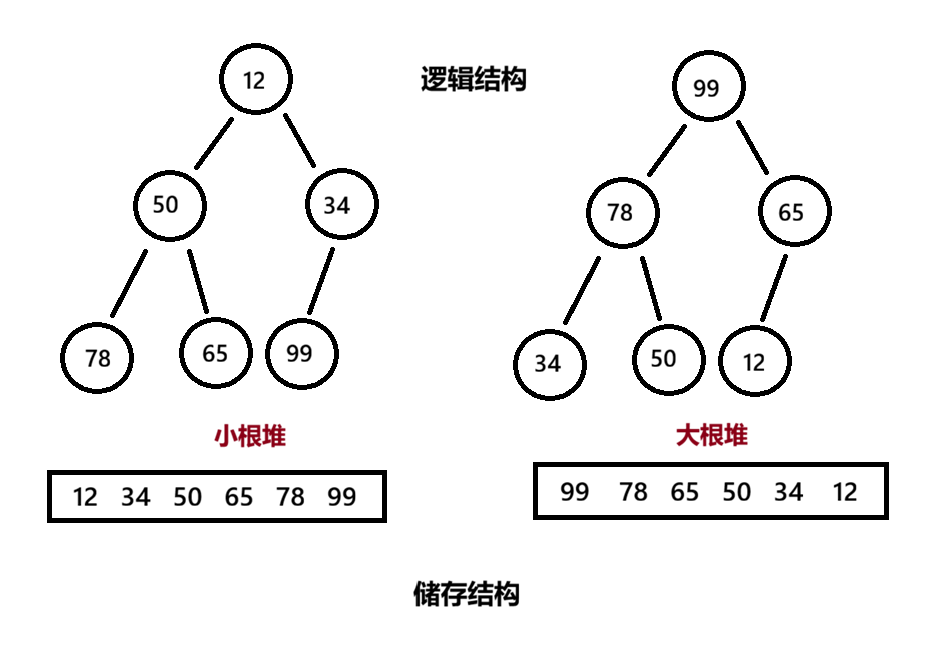
此外 堆的构建对于非完全二叉树，则不适合使用顺序方式进行存储，存入在数组中必须要存储空节 点，就会导致空间利用率比较低。

构建

构建堆分为向下调整 和 向上调整

向下调整

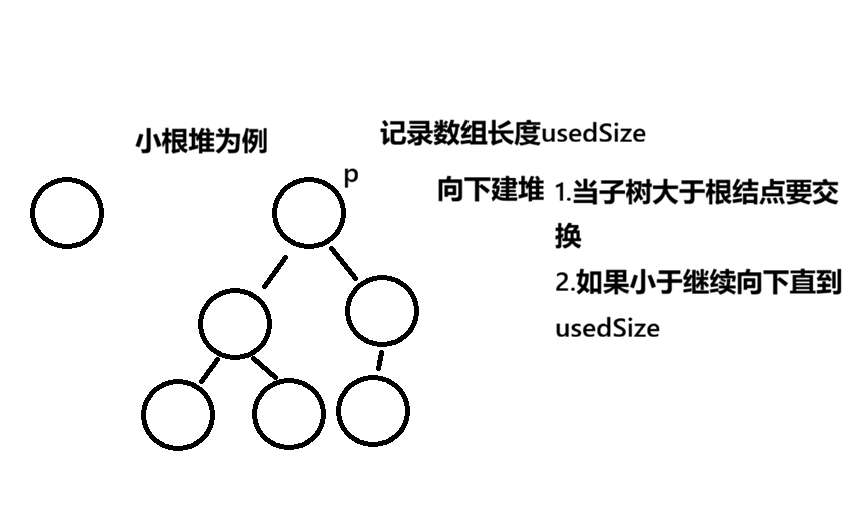
public void createHeap(){ 
    for(int parent = (usedSize - 1 -1)/ 2 ; parent > 0;parent--){                    呃  siftDown(parent,usedSize);   
} 
}
private void siftDown(int parent, int usedSize) {
   int child = 2 * parent - 1;
   while (child < usedSize){
      if (child + 1 < usedSize && elem[child] < elem[child+1]) {
                child++;
      }
      if (elem[child] > elem[child+1]) {
         swap(elem,child,parent);
      }
   }
}

向上调整（时间复杂度相对向下调整高）

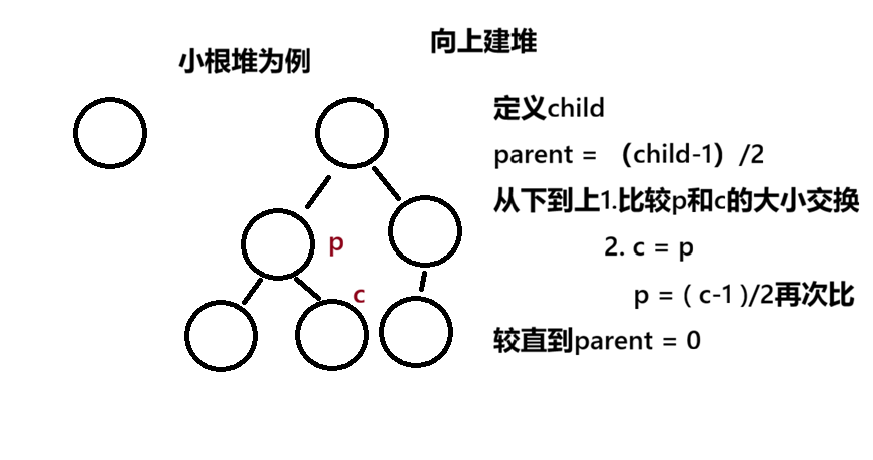
private  void siftUp(int child){
 int parent = (child -1) / 2;
 while(parent >= 0 ){
    if(elem[parent] < elem [child]){
       swap(elem,child,parent);
       child = parent;
       parent = (child-1) / 2;
    }
    else{
       break;
    }
 }
}

时间复杂度

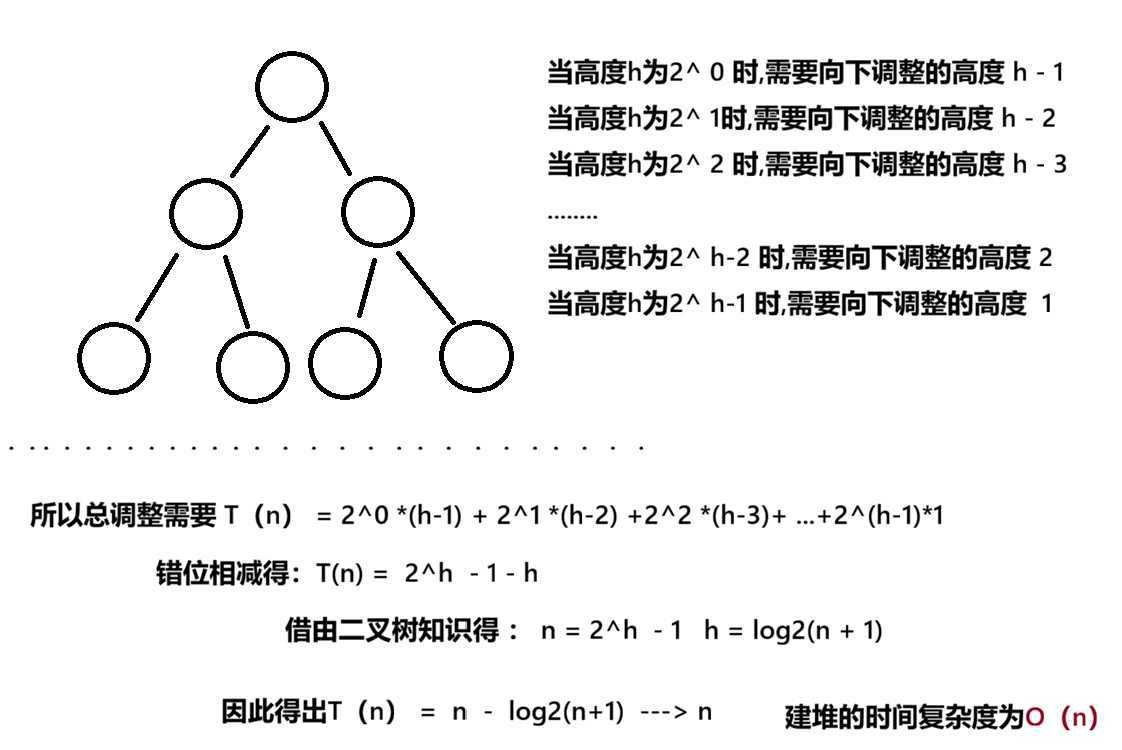
堆的插入与删除

在完成堆的插入与删除时要考虑当数组为满 和为空的情况

public boolean isFull(){
   return  this.usedSize == elem.length;
}
public boolean isEmpty() {
   return usedSize == 0;
}

offer

//已满 扩容数组

if(isFull()){
   elem = Arrays.copyOf(elem,2*elem.length);
}
//拿到值 usedSize向后移动一步
elem[usedSize] =val;
usedSize++;

poll

//删除 从栈顶元素删除

if(isEmpty()){
   return  -1;
}
int val = elem[0];
swap(elem,0,usedSize - 1 );
siftDown(0,usedSize -1 );
usedSize--;
return  val;

PriorityQueue 优先级队列

PriorityQueue底层使用了堆这种数据结构

Java集合框架中提供了PriorityQueue 和PriorityBlockingQueue 两种类型的优先级队列PriorityQueue 是线程 不安全的

PriorityBlockingQueue 是线程 安全的

因此堆中的方法都是适用于PriorityQueue

boolean offer (E e) E peek () E poll () int size () void clear () boolean isEmpty()

堆的应用

用堆作为底层结构封装 优先级队列

堆排序

建堆

升序：建大堆

降序：建小堆

堆删除思想来进行排序

heapsort

public void heapsort() {
   int end = usedSize - 1;
   while (end > 0) {
      swap(elem, 0, end);
      siftDown(0, end);
      end--;
   }
}

Top-k

最小K ： 建立大根堆

最大K ： 建立小根堆

这里提供两种方法解决

1.整体法

public int\[\] smallestK(int\[\] arr, int k) {

PriorityQueue<Integer> priorityqueue = new PriorityQueue<>();

for(int i = 0; i < arr.length; i++){

priorityqueue.offer(arri);

}

int \[\] ret =new int k; for(int i = 0 ; i < k ; i ++){

reti = priorityqueue.poll();

}

return ret;

}

2.分部法

 public int[] smallestK(int[] arr, int k) {
        PriorityQueue<Integer> priorityqueue = new PriorityQueue<>();
      for(int  i = 0; i < arr.length; i++){
        priorityqueue.offer(arr[i]);
      }
      //n-k
      for(int i = k;  i < arr.length ; i++ ){
        int peekVal = priorityqueue.peek();
        if(arr[i] < peekVal){
            priorityqueue.poll();
            priorityqueue.offer(arr[i]);
        }
      }
        int[] ret  = new int [k];
        for(int j = 0 ;j < k ; j++){
            ret[j] =  priorityqueue.poll();
        }
        return ret;
     
    }