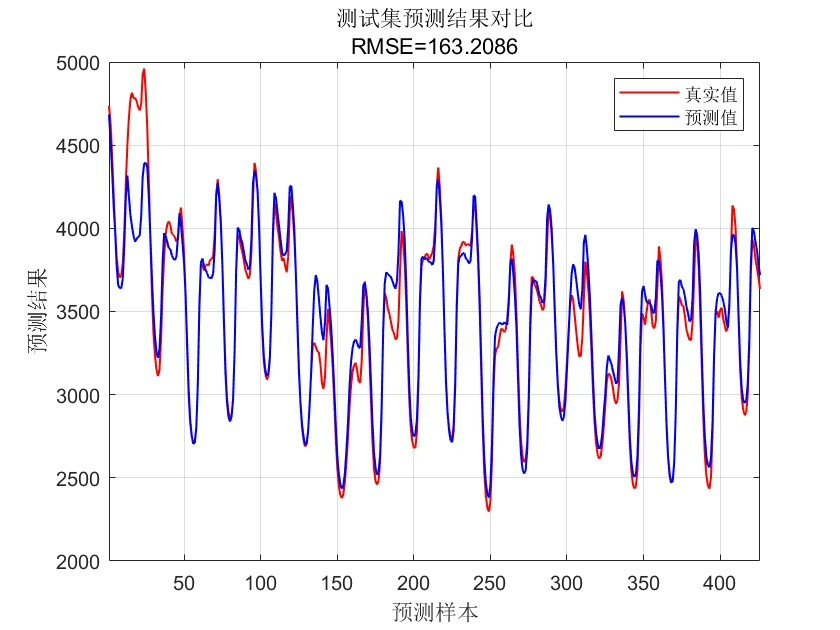
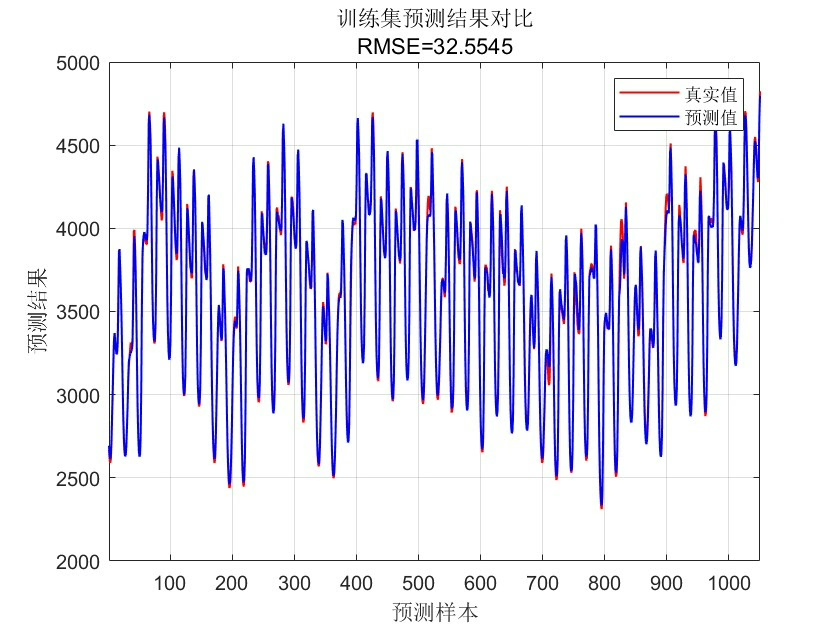
基于粒子群优化支持向量机(PSO-SVM)的多变量时间序列预测 PSO-SVM多变量时间序列 ...

基于粒子群优化支持向量机(PSO-SVM)的多变量时间序列预测 PSO-SVM多变量时间序列 matlab代码注：暂无Matlab版本要求 -- 推荐 2018B 版本及以上注：采用 Libsvm 工具箱（无需安装，可直接运行），仅支持 Windows 64位系统

多变量时间序列预测这玩意儿在工业场景里特别常见，比如电网负荷预测或者化工过程监控。传统SVM调参能把人逼疯，这时候试试粒子群优化（PSO）捆绑SVM的组合拳就很有意思。今天咱们用Matlab搞个能直接运行的demo，顺便拆解几个代码里容易翻车的坑点。

先看数据预处理部分。假设我们有个三变量的传感器数据集，时间戳和三个特征列排得整整齐齐：

matlab 复制代码

data = csvread('sensor_data.csv');  % 三列特征+最后一列目标值
X = data(:,1:3); y = data(:,4);
[n_samples, n_features] = size(X);

这里有个骚操作------时间滑窗构建。把连续5个时间点的特征堆叠成输入向量，预测第6个时刻的目标值：

matlab 复制代码

lag = 5;
X_new = zeros(n_samples-lag, lag*n_features);
for i = 1:n_samples-lag
    X_new(i,:) = reshape(X(i:i+lag-1,:),1,[]);
end
y_new = y(lag+1:end);  % 目标序列对齐

归一化处理千万别偷懒，否则SVM会被量纲玩坏。注意训练集和测试集要分开处理，防止数据穿越：

matlab 复制代码

% 数据集拆分
train_ratio = 0.8;
split_idx = floor(length(y_new)*train_ratio);
X_train = X_new(1:split_idx,:);
X_test = X_new(split_idx+1:end,:);
y_train = y_new(1:split_idx);
y_test = y_new(split_idx+1:end);

% 归一化
[X_train, ps_x] = mapminmax(X_train', 0, 1);
X_train = X_train';
X_test = mapminmax('apply', X_test', ps_x)';
[y_train, ps_y] = mapminmax(y_train', 0, 1);
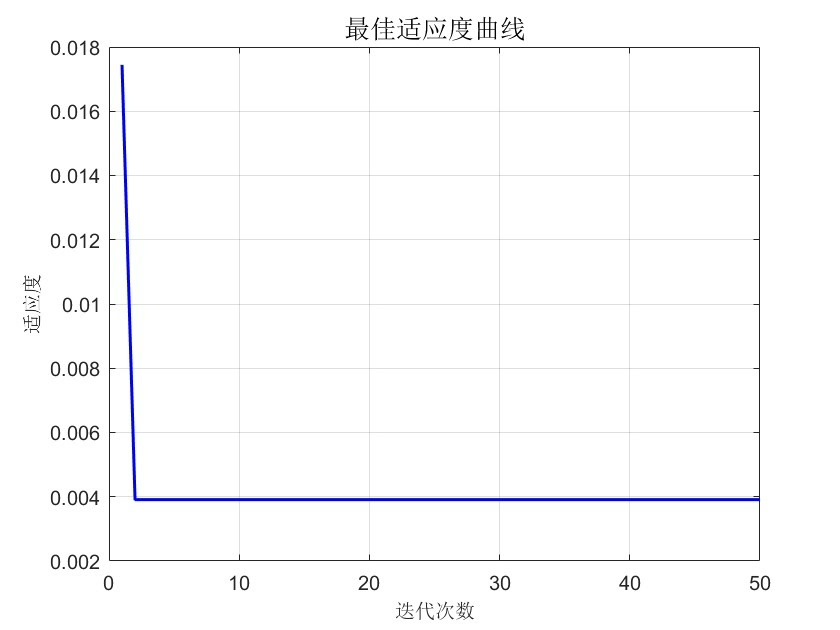
y_train = y_train';

PSO优化环节是重头戏。这里设置20个粒子迭代50次，搜索SVM的C和gamma参数：

matlab 复制代码

% 参数搜索范围
param_range = [0.1, 100;    % C的范围
               0.01, 10];   % gamma的范围 

% PSO配置
options = psooptimset('PopulationSize',20, 'Generations',50,...
                     'Display','iter', 'PlotFcns',@psoplotbestf);

适应度函数设计是灵魂所在，用5折交叉验证的均方误差作为评估标准：

matlab 复制代码

function fitness = svm_fitness(params)
    C = params(1);
    g = params(2);
    cmd = ['-s 3 -t 2 -c ', num2str(C), ' -g ', num2str(g), ' -p 0.1'];
    mse = svm_cv(y_train, X_train, cmd, 5); % 自定义交叉验证函数
    fitness = mse;  % 找最小误差
end

跑完PSO拿到最优参数后，训练最终模型：

matlab 复制代码

[best_params, ~] = pso(@svm_fitness, 2, [], [], [], [],...
                      param_range(:,1), param_range(:,2), [], options);

% 最佳参数注入
cmd = ['-s 3 -t 2 -c ', num2str(best_params(1)), ...
       ' -g ', num2str(best_params(2)), ' -p 0.1'];
model = svmtrain(y_train, X_train, cmd);

预测阶段要注意反归一化才能得到真实量纲的结果：

matlab 复制代码

y_train_pred = svmpredict(y_train, X_train, model);
y_test_pred = svmpredict(y_test, X_test, model);

% 反归一化
y_train_real = mapminmax('reverse', y_train_pred', ps_y)';
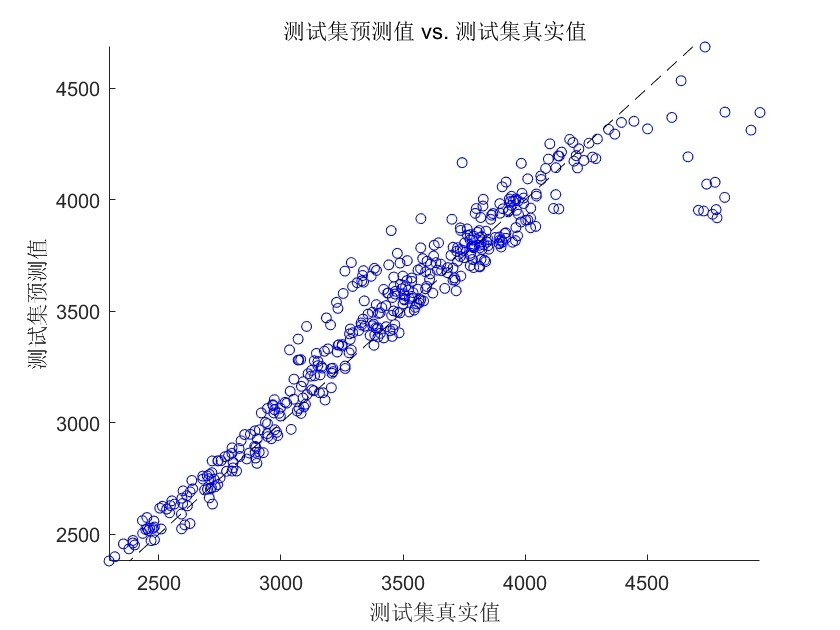
y_test_real = mapminmax('reverse', y_test_pred', ps_y)';

最后用动态误差曲线展示效果更直观：

matlab 复制代码

figure('Color',[1 1 1])
subplot(2,1,1)
plot(y_test_real,'r-o','LineWidth',1.5)
hold on
plot(y_test,'b--s','LineWidth',1)
legend('预测值','真实值')
title('测试集预测效果')

subplot(2,1,2)
abs_err = abs(y_test_real - y_test);
plot(abs_err,'k-*')
title('绝对误差波动')

几个实战经验：1）Libsvm的Windows依赖问题可能导致闪退，建议在脚本开头添加版本校验；2）粒子群容易早熟，可以尝试动态惯性权重改进；3）多变量时序的滞后阶数选择比参数优化更重要，建议先用互信息法确定lag值。这个框架换成股票预测或者设备寿命预估也完全hold得住，改改数据输入就能复用。