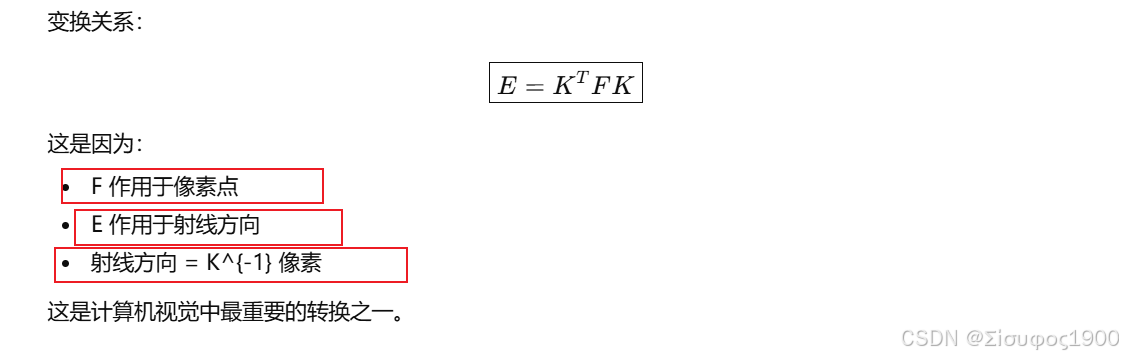
一、为什么需要从 F 得到 E?
若两台相机的内参矩阵分别是
-
K1:左相机
-
K2:右相机
则基础矩阵与本质矩阵关系为:
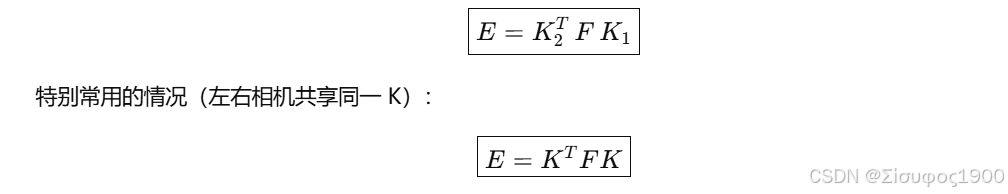
-
F(基础矩阵) 工作在 像素坐标系(image coordinates)
-
E(本质矩阵) 工作在 归一化相机坐标系(camera normalized coordinates)
两者的区别是:
像素坐标需要使用内参矩阵 K 才能转成真实的几何光线方向。
| 符号 | 含义 | 维度 |
|---|---|---|
| (F) | 基础矩阵(像素坐标下 epipolar 几何) | 3×3 |
| (E) | 本质矩阵(相机归一化坐标系下 epipolar 几何) | 3×3 |
| (K) | 相机内参矩阵 | 3×3 |
| (x, x') | 像素坐标(齐次) | 3×1 |
| (\tilde{x}, \tilde{x}') | 归一化坐标(投影到相机坐标系) | 3×1 |
二、核心思想:像素坐标与归一化坐标的关系
像素坐标:

三、E = [T]× R 为什么必须在归一化空间?
通过几何可以得:
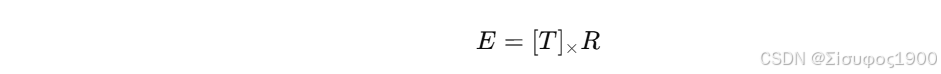
这个公式成立的前提是:
-
x1,x 必须表示为 3D 相机坐标系下的方向向量
-
而不是像素坐标
像素坐标要转换:

E = Kᵀ F K 的更几何化推导(直观图)
cpp
像素点 x1 --K^{-1}--> 归一化点 x̂1 --极几何--> x̂2 --K--> 像素点 x2极线约束在两个世界中都应该成立:
cpp
pixel: x2ᵀ F x1 = 0
normalized: x̂2ᵀ E x̂1 = 0因为
cpp
像素坐标 = K * 归一化坐标四、MATLAB 数值验证
下面的代码会:
-
随机生成 R、T
-
构造真实的本质矩阵 Etrue = [T]×R
-
假设内参 K
-
计算 F = K^{-T} Etrue K^{-1}
-
再恢复 Eest = Kᵀ F K
-
验证 Eest 是否等于 Etrue(在尺度内)
cpp
%% 随机生成 R
[U,~,V] = svd(randn(3,3));
R = U*V';
if det(R)<0, R(:,3) = -R(:,3); end
%% 随机平移 T
T = randn(3,1);
T = T / norm(T);
%============================================================
%% 叉乘矩阵
Tx = [0 -T(3) T(2);
T(3) 0 -T(1);
-T(2) T(1) 0];
%% 真实本质矩阵
E_true = Tx * R;
%============================================================
%% 相机内参 自己设置的
K = [1000 0 320;
0 1000 240;
0 0 1];
%============================================================
%% 根据 E_true 构造 F
F = inv(K)' * E_true * inv(K);
%% 再根据 F 恢复 E
E_est = K' * F * K;
%% 归一化以比较
E_true = E_true / norm(E_true);
E_est = E_est / norm(E_est);
disp('真实 E :');
disp(E_true);
disp('恢复 E = K'' F K :');
disp(E_est);
disp('误差 = ');
disp(E_est - E_true);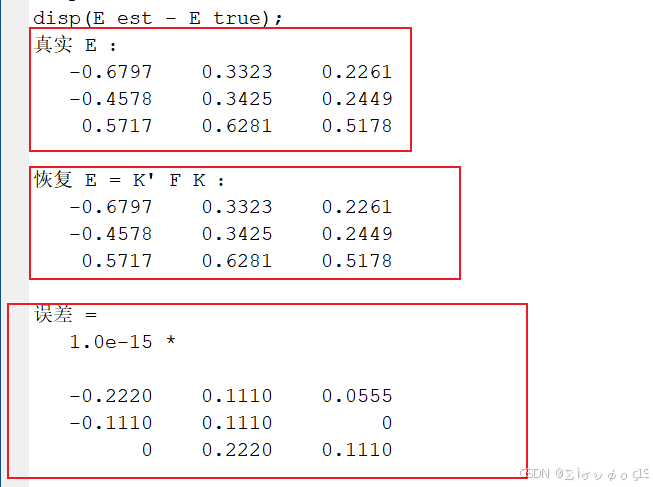
五、总结
| 矩阵 | 坐标系 | 几何意义 |
|---|---|---|
| F | 像素坐标 | 两幅图像的极线关系 |
| E | 归一化相机坐标 | 相机相对姿态(R、T)的真正规律 |