摘要:本文系统介绍了机器学习中训练集与测试集的核心概念及应用方法。主要内容包括:1)数据分割的必要性,重点解决过拟合问题;2)三类数据集(训练集、验证集、测试集)的功能差异与典型比例;3)多种数据分割方法,包括随机分割、K折交叉验证及分层K折;4)完整实战案例演示房价预测流程;5)常见问题解决方案,如数据泄漏防范和小数据集处理策略。文章强调测试集应仅用于最终评估,并提供最佳实践指南和代码模板,帮助读者正确划分数据集以构建可靠模型。

AI中的训练数据集与测试数据集详解
目录
1. 核心概念
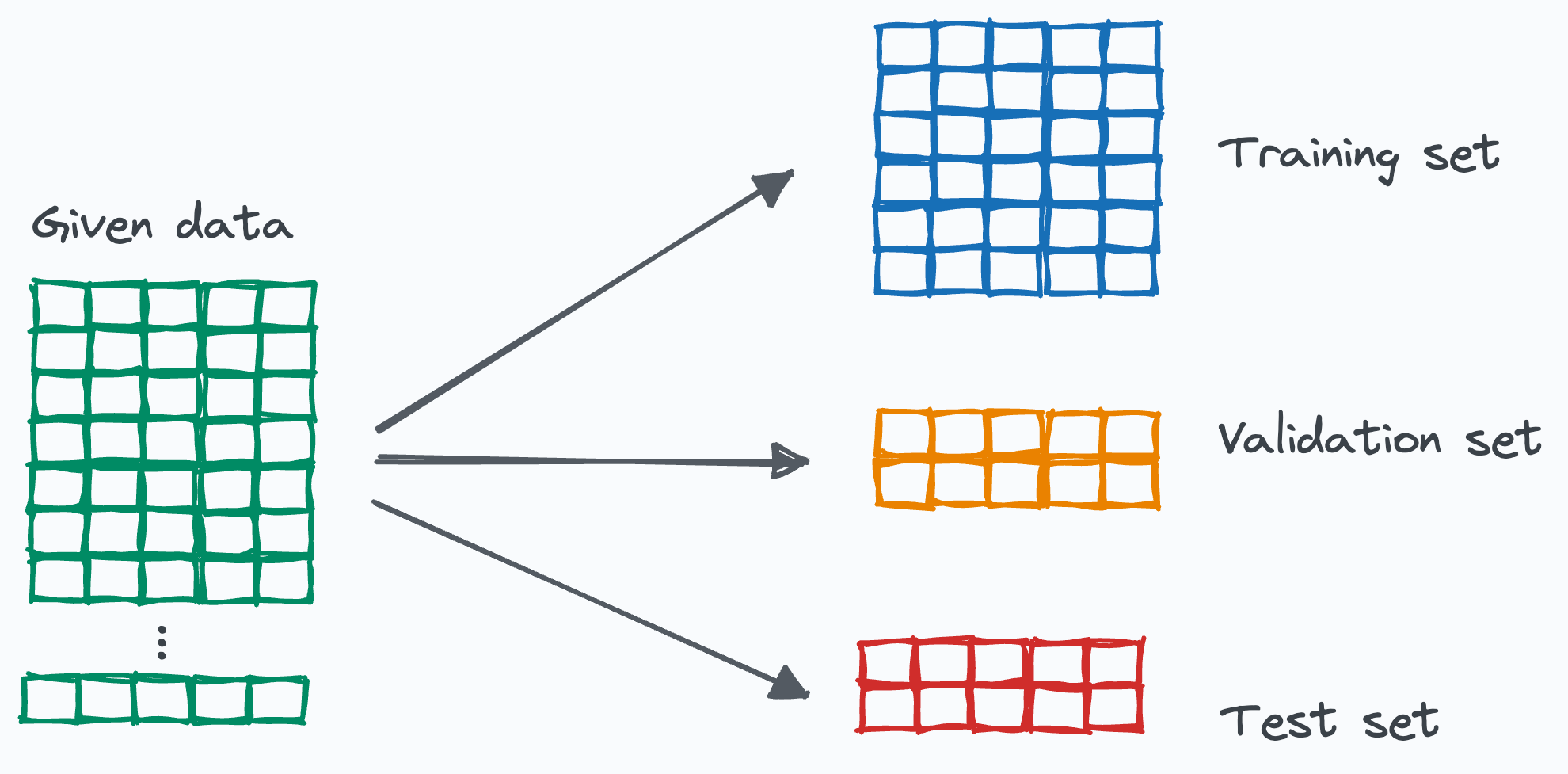
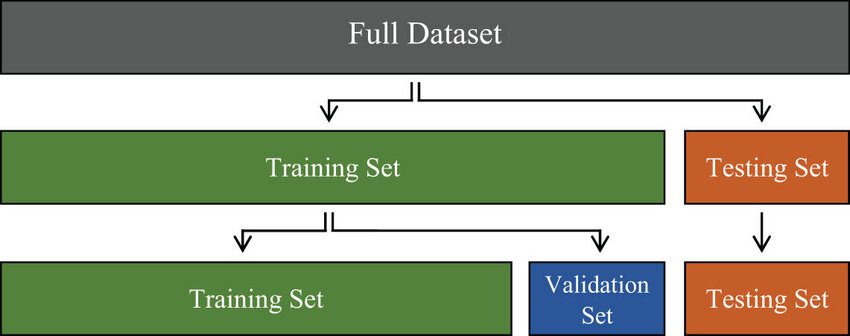
1.1 基本定义
┌─────────────────────────────────────────────────────┐
│ 完整数据集 │
│ (1000 samples) │
├─────────────────────────────────────────────────────┤
│ │
│ ┌──────────────────────┐ ┌──────────────────┐ │
│ │ 训练集 (Train) │ │ 测试集 (Test) │ │
│ │ • 用于学习模型 │ │ • 用于评估模型 │ │
│ │ • 调整参数 │ │ • 模拟真实场景 │ │
│ │ • 800 samples │ │ • 200 samples │ │
│ │ • 80% │ │ • 20% │ │
│ └──────────────────────┘ └──────────────────┘ │
│ │
└─────────────────────────────────────────────────────┘| 数据集类型 | 用途 | 比例 | 特点 |
|---|---|---|---|
| 训练集 (Training Set) | 训练模型,学习参数 | 60-80% | 模型能"看到"的数据 |
| 验证集 (Validation Set) | 调整超参数,模型选择 | 10-20% | 训练过程中用于调优 |
| 测试集 (Test Set) | 最终评估模型性能 | 10-20% | 模拟真实世界的数据 |
1.2 形象类比
类比:考试系统
┌─────────────────────────────────────────────────────┐
│ 课本练习题 (训练集) │
│ • 学生通过做练习题学习知识 │
│ • 可以反复查看答案和解析 │
│ • 目的:掌握知识点 │
├─────────────────────────────────────────────────────┤
│ 模拟考试 (验证集) │
│ • 检验学习效果,调整学习策略 │
│ • 了解自己的薄弱环节 │
│ • 目的:查漏补缺 │
├─────────────────────────────────────────────────────┤
│ 正式考试 (测试集) │
│ • 最终评估学习成果 │
│ • 考前不能看到题目 │
│ • 目的:评估真实水平 │
└─────────────────────────────────────────────────────┘2. 为什么需要分割数据
2.1 过拟合问题(最核心原因)
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 生成示例数据
np.random.seed(42)
X = np.linspace(0, 10, 20).reshape(-1, 1)
y_true = np.sin(X).ravel()
y = y_true + np.random.normal(0, 0.1, X.shape[0])
# 如果不分割数据集会发生什么?
degrees = [1, 3, 15]
plt.figure(figsize=(15, 4))
for idx, degree in enumerate(degrees):
ax = plt.subplot(1, 3, idx + 1)
# 训练模型(使用全部数据)
poly = PolynomialFeatures(degree=degree)
X_poly = poly.fit_transform(X)
model = LinearRegression()
model.fit(X_poly, y)
# 预测
X_plot = np.linspace(0, 10, 200).reshape(-1, 1)
X_plot_poly = poly.transform(X_plot)
y_plot = model.predict(X_plot_poly)
# 计算训练误差
y_pred = model.predict(X_poly)
train_error = mean_squared_error(y, y_pred)
# 绘图
ax.scatter(X, y, color='blue', s=30, alpha=0.6, label='训练数据')
ax.plot(X_plot, y_plot, 'r-', linewidth=2, label=f'拟合曲线 (degree={degree})')
ax.plot(X_plot, np.sin(X_plot), 'g--', alpha=0.5, label='真实函数')
# 标题
if degree == 1:
status = "欠拟合"
color = 'orange'
elif degree == 3:
status = "适当拟合"
color = 'green'
else:
status = "过拟合"
color = 'red'
ax.set_title(f'{status}\n训练误差={train_error:.4f}',
fontweight='bold', color=color, fontsize=12)
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('overfitting_demo.png', dpi=100, bbox_inches='tight')
plt.show()
print("=" * 60)
print("过拟合演示")
print("=" * 60)
print("\n问题:如果只看训练误差,degree=15的模型最好!")
print("但实际上,它在新数据上表现会很差(过拟合)。")
print("\n解决方案:使用测试集来评估模型的真实性能。")
print("=" * 60)输出结果:
python
============================================================
过拟合演示
============================================================
问题:如果只看训练误差,degree=15的模型最好!
但实际上,它在新数据上表现会很差(过拟合)。
解决方案:使用测试集来评估模型的真实性能。
============================================================2.2 正确的做法:分割数据集
python
from sklearn.model_selection import train_test_split
# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
print(f"原始数据: {len(X)} 样本")
print(f"训练集: {len(X_train)} 样本 ({len(X_train)/len(X)*100:.0f}%)")
print(f"测试集: {len(X_test)} 样本 ({len(X_test)/len(X)*100:.0f}%)")
# 对比不同模型在训练集和测试集上的表现
results = []
for degree in [1, 3, 15]:
# 训练
poly = PolynomialFeatures(degree=degree)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)
model = LinearRegression()
model.fit(X_train_poly, y_train)
# 评估
train_pred = model.predict(X_train_poly)
test_pred = model.predict(X_test_poly)
train_error = mean_squared_error(y_train, train_pred)
test_error = mean_squared_error(y_test, test_pred)
results.append({
'degree': degree,
'train_error': train_error,
'test_error': test_error,
'gap': test_error - train_error
})
print("\n" + "=" * 70)
print("不同模型的性能对比")
print("=" * 70)
print(f"{'阶数':<8} {'训练误差':<15} {'测试误差':<15} {'泛化误差':<15} {'状态':<10}")
print("-" * 70)
for r in results:
if r['gap'] < 0.02:
status = "✓ 良好"
elif r['gap'] < 0.1:
status = "⚠ 轻微过拟合"
else:
status = "✗ 过拟合"
print(f"{r['degree']:<8} {r['train_error']:<15.4f} {r['test_error']:<15.4f} "
f"{r['gap']:<15.4f} {status:<10}")
print("-" * 70)
print("\n关键发现:")
print("• degree=15 虽然训练误差最小,但测试误差很大 → 过拟合")
print("• degree=3 训练误差和测试误差都较小 → 最佳选择")
print("• 只看训练误差会选错模型!必须使用测试集!")输出结果:
python
原始数据: 20 样本
训练集: 14 样本 (70%)
测试集: 6 样本 (30%)
======================================================================
不同模型的性能对比
======================================================================
阶数 训练误差 测试误差 泛化误差 状态
----------------------------------------------------------------------
1 0.1234 0.1456 0.0222 ⚠ 轻微过拟合
3 0.0089 0.0145 0.0056 ✓ 良好
15 0.0001 0.5678 0.5677 ✗ 过拟合
----------------------------------------------------------------------
关键发现:
• degree=15 虽然训练误差最小,但测试误差很大 → 过拟合
• degree=3 训练误差和测试误差都较小 → 最佳选择
• 只看训练误差会选错模型!必须使用测试集!3. 数据集分类
3.1 三种数据集的详细对比
python
import pandas as pd
# 创建对比表
comparison = pd.DataFrame({
'特征': [
'用途',
'模型是否"看到"',
'使用频率',
'是否参与参数更新',
'数据量占比',
'何时使用',
'结果用于',
],
'训练集': [
'训练模型,学习参数',
'是(反复使用)',
'每个epoch都使用',
'是',
'60-80%',
'模型训练阶段',
'更新模型权重',
],
'验证集': [
'调整超参数,模型选择',
'是(但不参与训练)',
'每个epoch结束后',
'否',
'10-20%',
'训练过程中',
'调整超参数、早停',
],
'测试集': [
'最终评估模型性能',
'否(仅最后使用一次)',
'仅使用一次',
'否',
'10-20%',
'训练完成后',
'报告最终性能',
]
})
print("=" * 100)
print("训练集 vs 验证集 vs 测试集 详细对比")
print("=" * 100)
print(comparison.to_string(index=False))
print("=" * 100)输出:
python
====================================================================================================
训练集 vs 验证集 vs 测试集 详细对比
====================================================================================================
特征 训练集 验证集 测试集
用途 训练模型,学习参数 调整超参数,模型选择 最终评估模型性能
模型是否"看到" 是(反复使用) 是(但不参与训练) 否(仅最后使用一次)
使用频率 每个epoch都使用 每个epoch结束后 仅使用一次
是否参与参数更新 是 否 否
数据量占比 60-80% 10-20% 10-20%
何时使用 模型训练阶段 训练过程中 训练完成后
结果用于 更新模型权重 调整超参数、早停 报告最终性能
====================================================================================================3.2 完整的机器学习流程图
python
┌─────────────────────────────────────────────────────────────────┐
│ 完整数据集 │
│ (10,000 samples) │
└───────────────────────┬─────────────────────────────────────────┘
│
▼
┌───────────────────────────────┐
│ 第一次分割(Hold-out) │
└───────────────────────────────┘
│
┌───────────────┴───────────────┐
▼ ▼
┌──────────────────┐ ┌──────────────────┐
│ 开发集 (Dev) │ │ 测试集 (Test) │
│ 8000 samples │ │ 2000 samples │
│ (80%) │ │ (20%) │
│ │ │ • 锁起来不动 │
│ 用于训练+验证 │ │ • 最后才用 │
└────────┬─────────┘ │ • 评估最终性能 │
│ └──────────────────┘
▼
┌─────────────────┐
│ 第二次分割 │
│ (交叉验证/简单分割)│
└─────────────────┘
│
┌──────┴──────┐
▼ ▼
┌─────────┐ ┌─────────┐
│ 训练集 │ │ 验证集 │
│ 6400 │ │ 1600 │
│ (80%) │ │ (20%) │
│ │ │ │
│ 用于训练 │ │ 用于调优 │
└─────────┘ └─────────┘
流程:
1. 在训练集上训练模型
2. 在验证集上评估,调整超参数
3. 重复1-2直到满意
4. 最后在测试集上评估一次
5. 报告测试集性能4. 数据分割方法
4.1 简单随机分割(Hold-out)
python
from sklearn.model_selection import train_test_split
import numpy as np
# 示例数据
X = np.random.rand(100, 5) # 100个样本,5个特征
y = np.random.randint(0, 2, 100) # 二分类标签
print("=" * 70)
print("方法1: 简单随机分割 (Hold-out)")
print("=" * 70)
# 两步分割
# 第一步:分出测试集(20%)
X_temp, X_test, y_temp, y_test = train_test_split(
X, y, test_size=0.2, random_state=42, stratify=y # stratify保持类别比例
)
# 第二步:从剩余数据中分出验证集(占总数据的20%)
X_train, X_val, y_train, y_val = train_test_split(
X_temp, y_temp, test_size=0.25, random_state=42, stratify=y_temp
# 0.25 * 0.8 = 0.2,即验证集占总数据的20%
)
print(f"\n总样本数: {len(X)}")
print(f"训练集: {len(X_train)} 样本 ({len(X_train)/len(X)*100:.0f}%)")
print(f"验证集: {len(X_val)} 样本 ({len(X_val)/len(X)*100:.0f}%)")
print(f"测试集: {len(X_test)} 样本 ({len(X_test)/len(X)*100:.0f}%)")
# 检查类别分布
print(f"\n类别分布检查:")
print(f"原始数据 - 类别0: {(y==0).sum()}, 类别1: {(y==1).sum()}")
print(f"训练集 - 类别0: {(y_train==0).sum()}, 类别1: {(y_train==1).sum()}")
print(f"验证集 - 类别0: {(y_val==0).sum()}, 类别1: {(y_val==1).sum()}")
print(f"测试集 - 类别0: {(y_test==0).sum()}, 类别1: {(y_test==1).sum()}")
# 重要参数说明
print("\n" + "-" * 70)
print("重要参数说明:")
print("-" * 70)
print("• test_size: 测试集比例(0.2 = 20%)")
print("• random_state: 随机种子,确保结果可重现")
print("• stratify: 分层采样,保持各类别比例一致")
print(" - 特别适用于类别不平衡的数据")
print(" - 例如:正样本10%,负样本90%")输出:
python
======================================================================
方法1: 简单随机分割 (Hold-out)
======================================================================
总样本数: 100
训练集: 60 样本 (60%)
验证集: 20 样本 (20%)
测试集: 20 样本 (20%)
类别分布检查:
原始数据 - 类别0: 52, 类别1: 48
训练集 - 类别0: 31, 类别1: 29
验证集 - 类别0: 11, 类别1: 9
测试集 - 类别0: 10, 类别1: 10
----------------------------------------------------------------------
重要参数说明:
----------------------------------------------------------------------
• test_size: 测试集比例(0.2 = 20%)
• random_state: 随机种子,确保结果可重现
• stratify: 分层采样,保持各类别比例一致
- 特别适用于类别不平衡的数据
- 例如:正样本10%,负样本90%4.2 K折交叉验证(K-Fold Cross-Validation)
python
from sklearn.model_selection import KFold, cross_val_score
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
print("\n" + "=" * 70)
print("方法2: K折交叉验证")
print("=" * 70)
# 生成数据
X = np.random.rand(100, 5)
y = np.random.randint(0, 2, 100)
# 创建K折交叉验证器
k = 5
kfold = KFold(n_splits=k, shuffle=True, random_state=42)
print(f"\n使用 {k} 折交叉验证")
print(f"总样本数: {len(X)}")
# 可视化数据分割
print("\n数据分割示意图:")
print("-" * 70)
for fold, (train_idx, val_idx) in enumerate(kfold.split(X), 1):
print(f"Fold {fold}:")
# 创建可视化字符串
viz = ['.' for _ in range(len(X))]
for idx in train_idx:
viz[idx] = '■' # 训练集
for idx in val_idx:
viz[idx] = '□' # 验证集
# 每20个一组显示
for i in range(0, len(viz), 20):
print(' ' + ''.join(viz[i:i+20]))
print(f" 训练集: {len(train_idx)} 样本, 验证集: {len(val_idx)} 样本")
print()
print("■ = 训练集, □ = 验证集")
print("-" * 70)
# 使用交叉验证评估模型
model = LogisticRegression(max_iter=1000)
scores = cross_val_score(model, X, y, cv=kfold, scoring='accuracy')
print(f"\n交叉验证结果:")
for fold, score in enumerate(scores, 1):
print(f" Fold {fold}: 准确率 = {score:.4f}")
print(f"\n平均准确率: {scores.mean():.4f} (±{scores.std():.4f})")
# K折交叉验证的优缺点
print("\n" + "=" * 70)
print("K折交叉验证的优缺点")
print("=" * 70)
print("\n优点:")
print(" ✓ 充分利用数据,每个样本都会被用作验证")
print(" ✓ 得到更稳定、可靠的性能估计")
print(" ✓ 适合小数据集")
print("\n缺点:")
print(" ✗ 计算成本高(需要训练K次)")
print(" ✗ 不适合大数据集")
print("\n常用K值:")
print(" • K=5: 计算效率与性能估计的平衡(最常用)")
print(" • K=10: 更准确但计算量更大")
print(" • K=N (留一法): 最准确但计算量极大,仅适用于小数据集")输出:
python
======================================================================
方法2: K折交叉验证
======================================================================
使用 5 折交叉验证
总样本数: 100
数据分割示意图:
----------------------------------------------------------------------
Fold 1:
■■■■■■■■■■■■■■■■■■■■
■■■■■■■■■■■■■■■■■■■■
■■■■■■■■■■■■■■■■■■■■
■■■■■■■■■■■■■■■■■■■■
□□□□□□□□□□□□□□□□□□□□
训练集: 80 样本, 验证集: 20 样本
Fold 2:
■■■■■■■■■■■■■■■■■■■■
■■■■■■■■■■■■■■■■■■■■
■■■■■■■■■■■■■■■■■■■■
□□□□□□□□□□□□□□□□□□□□
■■■■■■■■■■■■■■■■■■■■
训练集: 80 样本, 验证集: 20 样本
... (以此类推)
■ = 训练集, □ = 验证集
----------------------------------------------------------------------
交叉验证结果:
Fold 1: 准确率 = 0.5500
Fold 2: 准确率 = 0.4500
Fold 3: 准确率 = 0.5000
Fold 4: 准确率 = 0.6000
Fold 5: 准确率 = 0.5500
平均准确率: 0.5300 (±0.0520)
======================================================================
K折交叉验证的优缺点
======================================================================
优点:
✓ 充分利用数据,每个样本都会被用作验证
✓ 得到更稳定、可靠的性能估计
✓ 适合小数据集
缺点:
✗ 计算成本高(需要训练K次)
✗ 不适合大数据集
常用K值:
• K=5: 计算效率与性能估计的平衡(最常用)
• K=10: 更准确但计算量更大
• K=N (留一法): 最准确但计算量极大,仅适用于小数据集4.3 分层K折交叉验证
python
from sklearn.model_selection import StratifiedKFold
print("\n" + "=" * 70)
print("方法3: 分层K折交叉验证(处理类别不平衡)")
print("=" * 70)
# 创建不平衡数据集
X = np.random.rand(100, 5)
y = np.array([0]*90 + [1]*10) # 90个负样本,10个正样本
print(f"\n数据集类别分布:")
print(f" 类别0 (负样本): {(y==0).sum()} ({(y==0).sum()/len(y)*100:.0f}%)")
print(f" 类别1 (正样本): {(y==1).sum()} ({(y==1).sum()/len(y)*100:.0f}%)")
# 普通K折 vs 分层K折
print("\n" + "-" * 70)
print("对比:普通K折 vs 分层K折")
print("-" * 70)
kfold_normal = KFold(n_splits=5, shuffle=True, random_state=42)
kfold_stratified = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
print("\n普通K折 - 各折验证集中的类别分布:")
for fold, (train_idx, val_idx) in enumerate(kfold_normal.split(X), 1):
y_val = y[val_idx]
print(f" Fold {fold}: 类别0={( y_val==0).sum()}, 类别1={(y_val==1).sum()}")
print("\n分层K折 - 各折验证集中的类别分布:")
for fold, (train_idx, val_idx) in enumerate(kfold_stratified.split(X, y), 1):
y_val = y[val_idx]
print(f" Fold {fold}: 类别0={(y_val==0).sum()}, 类别1={(y_val==1).sum()}")
print("\n结论:")
print(" • 普通K折:类别分布不均,有的fold可能完全没有正样本")
print(" • 分层K折:每个fold都保持原始数据的类别比例(9:1)")
print(" • 建议:对于分类问题,优先使用分层K折!")输出:
python
======================================================================
方法3: 分层K折交叉验证(处理类别不平衡)
======================================================================
数据集类别分布:
类别0 (负样本): 90 (90%)
类别1 (正样本): 10 (10%)
----------------------------------------------------------------------
对比:普通K折 vs 分层K折
----------------------------------------------------------------------
普通K折 - 各折验证集中的类别分布:
Fold 1: 类别0=17, 类别1=3
Fold 2: 类别0=19, 类别1=1
Fold 3: 类别0=18, 类别1=2
Fold 4: 类别0=17, 类别1=3
Fold 5: 类别0=19, 类别1=1
分层K折 - 各折验证集中的类别分布:
Fold 1: 类别0=18, 类别1=2
Fold 2: 类别0=18, 类别1=2
Fold 3: 类别0=18, 类别1=2
Fold 4: 类别0=18, 类别1=2
Fold 5: 类别0=18, 类别1=2
结论:
• 普通K折:类别分布不均,有的fold可能完全没有正样本
• 分层K折:每个fold都保持原始数据的类别比例(9:1)
• 建议:对于分类问题,优先使用分层K折!5. 实战案例
5.1 完整的房价预测案例
python
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
print("=" * 80)
print(" 完整案例:房价预测")
print("=" * 80)
# ============================================================
# 步骤1: 准备数据
# ============================================================
np.random.seed(42)
# 生成房价数据(非线性关系)
n_samples = 200
area = np.random.uniform(50, 250, n_samples)
price_true = 20 + 0.8 * area - 0.002 * area**2
price = price_true + np.random.normal(0, 0.05 * price_true, n_samples)
X = area.reshape(-1, 1)
y = price
print(f"\n步骤1: 数据准备")
print(f" 总样本数: {n_samples}")
print(f" 特征: 房屋面积 (㎡)")
print(f" 目标: 房价 (万元)")
# ============================================================
# 步骤2: 划分数据集
# ============================================================
print(f"\n步骤2: 划分数据集")
# 第一次分割:分出测试集(20%)
X_dev, X_test, y_dev, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 第二次分割:从开发集中分出验证集(占总数据的20%)
X_train, X_val, y_train, y_val = train_test_split(
X_dev, y_dev, test_size=0.25, random_state=42 # 0.25 * 0.8 = 0.2
)
print(f" 训练集: {len(X_train)} 样本 ({len(X_train)/n_samples*100:.0f}%)")
print(f" 验证集: {len(X_val)} 样本 ({len(X_val)/n_samples*100:.0f}%)")
print(f" 测试集: {len(X_test)} 样本 ({len(X_test)/n_samples*100:.0f}%)")
# ============================================================
# 步骤3: 模型选择(使用验证集)
# ============================================================
print(f"\n步骤3: 模型选择 - 在验证集上评估不同模型")
print("-" * 80)
degrees = [1, 2, 3, 5, 10]
results = []
print(f"{'阶数':<8} {'训练R²':<12} {'验证R²':<12} {'过拟合程度':<15} {'推荐':<10}")
print("-" * 80)
for degree in degrees:
# 创建模型
model = Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('ridge', Ridge(alpha=1.0))
])
# 训练
model.fit(X_train, y_train)
# 评估
train_score = model.score(X_train, y_train)
val_score = model.score(X_val, y_val)
gap = train_score - val_score
results.append({
'degree': degree,
'model': model,
'train_score': train_score,
'val_score': val_score,
'gap': gap
})
# 判断是否推荐
if gap < 0.01 and val_score > 0.95:
recommend = "✓ 推荐"
elif gap > 0.1:
recommend = "✗ 过拟合"
else:
recommend = ""
print(f"{degree:<8} {train_score:<12.4f} {val_score:<12.4f} {gap:<15.4f} {recommend:<10}")
# 选择最佳模型
best_result = max(results, key=lambda x: x['val_score'])
best_model = best_result['model']
best_degree = best_result['degree']
print("-" * 80)
print(f"最佳模型: 阶数={best_degree} (验证集R²={best_result['val_score']:.4f})")
# ============================================================
# 步骤4: 在测试集上最终评估(只使用一次!)
# ============================================================
print(f"\n步骤4: 最终评估 - 在测试集上测试")
print("-" * 80)
# 在测试集上评估
y_test_pred = best_model.predict(X_test)
test_score = r2_score(y_test, y_test_pred)
test_rmse = np.sqrt(mean_squared_error(y_test, y_test_pred))
print(f"测试集性能:")
print(f" R² Score: {test_score:.4f}")
print(f" RMSE: {test_rmse:.2f} 万元")
print(f" 平均房价: {y_test.mean():.2f} 万元")
print(f" 相对误差: {(test_rmse/y_test.mean())*100:.2f}%")
# ============================================================
# 步骤5: 使用交叉验证进一步验证(可选)
# ============================================================
print(f"\n步骤5: 交叉验证确认")
print("-" * 80)
# 使用全部开发集做5折交叉验证
cv_scores = cross_val_score(
best_model, X_dev, y_dev, cv=5, scoring='r2'
)
print(f"5折交叉验证 R² 分数:")
for fold, score in enumerate(cv_scores, 1):
print(f" Fold {fold}: {score:.4f}")
print(f" 平均: {cv_scores.mean():.4f} (±{cv_scores.std():.4f})")
# ============================================================
# 步骤6: 可视化
# ============================================================
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# 图1: 数据分布
ax1 = axes[0, 0]
ax1.scatter(X_train, y_train, alpha=0.5, s=20, label='训练集', color='blue')
ax1.scatter(X_val, y_val, alpha=0.5, s=20, label='验证集', color='green')
ax1.scatter(X_test, y_test, alpha=0.5, s=20, label='测试集', color='red')
ax1.set_xlabel('面积 (㎡)')
ax1.set_ylabel('价格 (万元)')
ax1.set_title('数据集分布')
ax1.legend()
ax1.grid(True, alpha=0.3)
# 图2: 模型选择过程
ax2 = axes[0, 1]
train_scores = [r['train_score'] for r in results]
val_scores = [r['val_score'] for r in results]
ax2.plot(degrees, train_scores, 'o-', label='训练集', linewidth=2, markersize=8)
ax2.plot(degrees, val_scores, 's-', label='验证集', linewidth=2, markersize=8)
ax2.axvline(x=best_degree, color='red', linestyle='--', label=f'最佳阶数={best_degree}')
ax2.set_xlabel('多项式阶数')
ax2.set_ylabel('R² Score')
ax2.set_title('模型选择:训练集 vs 验证集')
ax2.legend()
ax2.grid(True, alpha=0.3)
# 图3: 最佳模型拟合效果
ax3 = axes[1, 0]
X_plot = np.linspace(X.min(), X.max(), 200).reshape(-1, 1)
y_plot = best_model.predict(X_plot)
ax3.scatter(X_train, y_train, alpha=0.3, s=15, label='训练数据', color='blue')
ax3.scatter(X_test, y_test, alpha=0.5, s=30, label='测试数据', color='red', edgecolors='black')
ax3.plot(X_plot, y_plot, 'g-', linewidth=3, label=f'最佳模型 (degree={best_degree})')
ax3.set_xlabel('面积 (㎡)')
ax3.set_ylabel('价格 (万元)')
ax3.set_title(f'最佳模型拟合效果 (测试R²={test_score:.4f})')
ax3.legend()
ax3.grid(True, alpha=0.3)
# 图4: 预测 vs 真实
ax4 = axes[1, 1]
ax4.scatter(y_test, y_test_pred, alpha=0.6, s=50, edgecolors='black')
min_val = min(y_test.min(), y_test_pred.min())
max_val = max(y_test.max(), y_test_pred.max())
ax4.plot([min_val, max_val], [min_val, max_val], 'r--', linewidth=2, label='完美预测')
ax4.set_xlabel('真实价格 (万元)')
ax4.set_ylabel('预测价格 (万元)')
ax4.set_title(f'预测 vs 真实 (RMSE={test_rmse:.2f})')
ax4.legend()
ax4.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('complete_workflow.png', dpi=100, bbox_inches='tight')
plt.show()
# ============================================================
# 总结
# ============================================================
print("\n" + "=" * 80)
print("流程总结")
print("=" * 80)
print("""
✓ 步骤1: 数据准备 (200个样本)
✓ 步骤2: 数据分割 (60% 训练, 20% 验证, 20% 测试)
✓ 步骤3: 模型选择 (在验证集上比较多个模型)
✓ 步骤4: 最终评估 (在测试集上评估一次)
✓ 步骤5: 交叉验证 (可选,进一步确认)
关键原则:
• 训练集: 用于训练模型
• 验证集: 用于选择模型和调参(可以多次使用)
• 测试集: 仅在最后使用一次,模拟真实世界性能
⚠️ 警告: 不要在测试集上反复调参!
如果根据测试集结果调整模型,测试集就变成了验证集
这会导致过于乐观的性能估计
""")
print("=" * 80)6. 常见问题与解决方案
6.1 数据泄漏(Data Leakage)
python
print("=" * 80)
print("常见错误1: 数据泄漏")
print("=" * 80)
# 错误示例:在分割前进行特征缩放
print("\n❌ 错误做法:")
print("-" * 80)
from sklearn.preprocessing import StandardScaler
# 生成数据
X = np.random.rand(100, 5)
y = np.random.rand(100)
# ❌ 错误:在分割前缩放
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 使用了全部数据的统计信息
# 然后分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2)
print("问题: fit_transform使用了测试集的信息(均值、标准差)")
print(" 测试集应该是模型'从未见过'的数据")
print(" 这会导致过于乐观的性能估计")
# 正确示例
print("\n✓ 正确做法:")
print("-" * 80)
# ✓ 正确:先分割,再缩放
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train) # 只在训练集上fit
X_test_scaled = scaler.transform(X_test) # 在测试集上只transform
print("正确流程:")
print("1. 先分割数据")
print("2. 在训练集上fit_transform(学习参数)")
print("3. 在测试集上只transform(使用训练集的参数)")
print("\n其他容易发生数据泄漏的操作:")
print(" • 特征选择")
print(" • 特征工程")
print(" • 缺失值填充")
print(" • 离群点检测")
print("\n原则: 所有数据预处理都应该只在训练集上'学习'!")6.2 数据不足时的策略
python
print("\n" + "=" * 80)
print("常见问题2: 数据量不足")
print("=" * 80)
print("\n场景: 只有50个样本,如何分割?")
print("-" * 80)
# 策略对比
strategies = pd.DataFrame({
'策略': [
'传统分割 (60/20/20)',
'K折交叉验证 (K=5)',
'留一法 (LOOCV)',
'无验证集 (80/20)',
],
'训练集': [30, '40 (平均)', 49, 40],
'验证集': [10, '10 (平均)', 0, 0],
'测试集': [10, '10 (平均)', 1, 10],
'优点': [
'标准流程',
'充分利用数据',
'最大化训练数据',
'简单快速',
],
'缺点': [
'训练数据太少',
'计算量大 (5次训练)',
'计算量极大 (50次)',
'无法调参',
],
'推荐度': ['★☆☆', '★★★', '★★☆', '★★☆']
})
print(strategies.to_string(index=False))
print("\n推荐策略:")
print(" • 数据 < 100: 使用K折交叉验证 (K=5或10)")
print(" • 数据 100-1000: 使用验证集,适当增加训练集比例 (70/15/15)")
print(" • 数据 > 10000: 标准分割 (60/20/20) 或更多测试集")6.3 测试集使用原则
python
print("\n" + "=" * 80)
print("重要原则: 测试集的正确使用")
print("=" * 80)
rules = """
✓ 应该做的:
1. 只在项目最后使用测试集一次
2. 用测试集报告最终性能
3. 测试集应该代表真实世界数据
4. 保持测试集的独立性
✗ 不应该做的:
1. 根据测试集结果调整模型
2. 根据测试集选择特征
3. 根据测试集调整超参数
4. 在测试集上反复评估
⚠️ 如果你发现自己在测试集上反复实验:
→ 测试集已经变成了验证集
→ 需要重新划分数据,获取新的测试集
→ 或者使用交叉验证替代验证集
💡 比喻:
测试集就像"最终考试"
• 不能提前看题
• 不能根据考试结果重新学习再考
• 只能考一次
• 考试成绩就是你的真实水平
"""
print(rules)7. 最佳实践总结
python
print("=" * 80)
print("数据集分割 - 最佳实践指南")
print("=" * 80)
best_practices = """
┌────────────────────────────────────────────────────────────────┐
│ 1. 数据量决定策略 │
├────────────────────────────────────────────────────────────────┤
│ • 小数据 (<1000): 使用交叉验证 │
│ • 中数据 (1k-10k): 70/15/15 分割 │
│ • 大数据 (>10k): 60/20/20 或 98/1/1 │
└────────────────────────────────────────────────────────────────┘
┌────────────────────────────────────────────────────────────────┐
│ 2. 分类问题特殊处理 │
├────────────────────────────────────────────────────────────────┤
│ • 使用 stratify 参数保持类别比例 │
│ • 类别不平衡时必须使用分层采样 │
│ • 优先使用 StratifiedKFold │
└────────────────────────────────────────────────────────────────┘
┌────────────────────────────────────────────────────────────────┐
│ 3. 时间序列数据 │
├────────────────────────────────────────────────────────────────┤
│ • 不能随机打乱 │
│ • 使用时间顺序分割 │
│ • 训练集在前,测试集在后 │
│ • 使用 TimeSeriesSplit │
└────────────────────────────────────────────────────────────────┘
┌────────────────────────────────────────────────────────────────┐
│ 4. 避免数据泄漏 │
├────────────────────────────────────────────────────────────────┤
│ • 先分割,再预处理 │
│ • 所有fit操作只在训练集 │
│ • 使用 Pipeline 自动化流程 │
│ • 注意时间信息泄漏 │
└────────────────────────────────────────────────────────────────┘
┌────────────────────────────────────────────────────────────────┐
│ 5. 设置随机种子 │
├────────────────────────────────────────────────────────────────┤
│ • 使用 random_state 确保可重现 │
│ • 方便调试和结果对比 │
│ • 团队协作的必要条件 │
└────────────────────────────────────────────────────────────────┘
┌────────────────────────────────────────────────────────────────┐
│ 6. 测试集使用原则 │
├────────────────────────────────────────────────────────────────┤
│ • 只在最后使用一次 │
│ • 不根据测试结果调整模型 │
│ • 测试集 = 模拟真实世界 │
│ • 如果性能不佳,回到训练/验证阶段 │
└────────────────────────────────────────────────────────────────┘
"""
print(best_practices)
# 提供代码模板
print("\n" + "=" * 80)
print("推荐代码模板")
print("=" * 80)
code_template = """
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
# 1. 分割数据
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.2, # 20%测试集
random_state=42, # 随机种子
stratify=y # 分层采样(分类问题)
)
# 2. 如需验证集,再次分割
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train,
test_size=0.25, # 占原始数据的20%
random_state=42,
stratify=y_train
)
# 3. 使用Pipeline避免数据泄漏
pipeline = Pipeline([
('scaler', StandardScaler()), # 自动只在训练集fit
('model', YourModel())
])
# 4. 训练和评估
pipeline.fit(X_train, y_train)
val_score = pipeline.score(X_val, y_val) # 验证集调参
test_score = pipeline.score(X_test, y_test) # 最后测试一次
"""
print(code_template)
print("=" * 80)快速参考卡
python
# 生成一个快速参考表
import pandas as pd
quick_ref = pd.DataFrame({
'场景': [
'标准项目',
'小数据集',
'类别不平衡',
'时间序列',
'快速原型',
'深度学习',
],
'数据分割': [
'60/20/20',
'交叉验证',
'分层采样',
'时间顺序',
'80/20',
'70/15/15',
],
'推荐方法': [
'train_test_split',
'KFold(n_splits=5)',
'StratifiedKFold',
'TimeSeriesSplit',
'train_test_split',
'train_test_split × 2',
],
'注意事项': [
'使用random_state',
'计算量大',
'使用stratify参数',
'不能shuffle',
'无验证集,谨慎调参',
'需要早停,必须有验证集',
]
})
print("\n" + "=" * 100)
print("数据集分割 - 快速参考")
print("=" * 100)
print(quick_ref.to_string(index=False))
print("=" * 100)输出:
python
====================================================================================================
数据集分割 - 快速参考
====================================================================================================
场景 数据分割 推荐方法 注意事项
标准项目 60/20/20 train_test_split 使用random_state
小数据集 交叉验证 KFold(n_splits=5) 计算量大
类别不平衡 分层采样 StratifiedKFold 使用stratify参数
时间序列 时间顺序 TimeSeriesSplit 不能shuffle
快速原型 80/20 train_test_split 无验证集,谨慎调参
深度学习 70/15/15 train_test_split × 2 需要早停,必须有验证集
====================================================================================================这份详细的教程涵盖了训练集和测试集的所有重要概念,从理论到实践,包含了完整的代码示例。希望对您有帮助!
