【算法基础篇】（六十一）SG 函数通关指南：博弈论通用解法，从原理到实战秒杀各类 ICG 游戏

前言

在算法竞赛的博弈论体系中，巴什博弈、Nim 博弈只能解决特定的取石子问题，而SG 函数 才是公平组合游戏（ICG）的通用解题神器 ！它将所有公平组合游戏转化为有向图游戏，通过简单的mex运算求解每个状态的胜负属性，再结合 SG 定理实现多游戏组合的胜负判断。无论游戏规则如何变化，只要能抽象成有向无环图，SG 函数都能轻松破解。本文将从有向图游戏、mex 运算这些基础概念出发，一步步拆解 SG 函数的定义、性质和 SG 定理，再结合经典例题讲解实战用法，让你彻底掌握这个博弈论万能工具！下面就让我们正式开始吧！

一、SG 函数的前置知识铺垫

SG 函数并非孤立的概念，它建立在公平组合游戏（ICG）和有向图游戏 的基础上，而mex运算是求解 SG 函数的核心工具。在正式讲解 SG 函数前，我们先快速梳理这些必备基础，为后续学习扫清障碍。

1.1 公平组合游戏 (ICG) 回顾

SG 函数的适用场景是所有公平组合游戏，这类游戏满足三大核心条件：

两名玩家轮流决策，双方知晓游戏的全部信息，无隐藏规则；

玩家在某一确定状态下的决策集合，仅与当前状态有关，与玩家身份无关；

游戏以玩家无法行动为判负，且一定在有限步内结束，无平局。

巴什博弈、Nim 博弈都是典型的公平组合游戏，而 SG 函数是解决这类游戏的通用框架，前两种博弈模型只是 SG 函数的特殊情况。

1.2 有向图游戏：SG 函数的核心载体

所有公平组合游戏都可以抽象为有向图游戏，这是 SG 函数能成为通用解法的关键。有向图游戏的定义非常简单：

给定一个有向无环图（DAG） ，图中只有一个起点，在起点上放置一枚棋子；两名玩家轮流沿着有向边移动棋子，每次只能走一步；无法移动棋子的玩家判负。

游戏与有向图的对应关系：

游戏的每个状态 → 有向图的每个节点；

状态的一次合法操作 → 从当前节点到后继节点的一条有向边；

游戏的终止状态 （无法行动） → 有向图的出度为 0 的节点（无后继节点）。

由于公平组合游戏一定在有限步内结束，因此对应的有向图必然是无环的（否则会出现无限循环，违反游戏规则），这保证了 SG 函数的求解不会出现死循环。

1.3 mex 运算：求解 SG 函数的核心操作

mex**（minimum exclusion，最小排斥值）**运算是求解 SG 函数的基础，其定义简单易懂：

mex (S) = 不属于集合 S 的最小非负整数，其中 S 是一个非负整数集合。

简单来说，就是从 0 开始，依次找第一个不在集合 S 中的数，这个数就是 mex (S) 的结果。

经典示例

若 S = {0,1,2,3,10}，则 mex (S) = 4（0-3 都在集合中，4 是第一个不在的）；

若 S = {2,3,4}，则 mex (S) = 0（0 不在集合中，直接取 0）；

若 S = {0,2,3}，则 mex (S) = 1（0 在集合中，1 不在）；

若 S = ∅（空集），则 mex (S) = 0（空集没有元素，最小非负整数是 0）。

代码层面的理解

在 C++ 中，我们通常用**unordered_set**存储集合 S，然后从 0 开始遍历，找到第一个不在集合中的数即可，这也是后续求解 SG 函数的核心代码片段。

二、SG 函数的核心定义与性质

掌握了有向图游戏和 mex 运算后，SG 函数的定义就水到渠成了。SG 函数的本质是为有向图的每个节点分配一个非负整数，通过这个整数判断该节点（游戏状态）是必胜态还是必败态。

2.1 SG 函数的正式定义

对于有向图游戏中的任意节点（游戏状态）x，设其所有后继节点为y₁, y₂, ..., yₖ（即从 x 出发能到达的所有节点），则节点 x 的 SG 值定义为：SG(x)=mex{SG(y1),SG(y2),...,SG(yk)}

特殊情况 ：如果节点 x 是终止状态 （无后继节点），则其 SG 值为 0，即SG(x) = 0（因为空集的 mex 值为 0）。

2.2 SG 函数的核心性质：判断必胜 / 必败态

SG 函数的核心价值在于，通过 SG 值的大小可以直接判断对应游戏状态是必胜态还是必败态，结论极其简洁：

若SG(x) ≠ 0 ，则状态 x 为必胜态；

若SG(x) = 0 ，则状态 x 为必败态。

这个结论的证明与巴什、Nim 博弈的证明思路一致，围绕必胜态 / 必败态的核心逻辑展开，分两步即可轻松证明：

证明 1：SG (x)=0 → 必败态

若**SG(x)=0，根据 mex 运算的定义，其所有后继节点的 SG 值构成的集合中一定包含 0 以外的所有非负整数** ，即所有后继节点的 SG 值都≠0 。这意味着：当前状态下，无论玩家采取何种操作，都会将棋子移动到SG 值≠0 的必胜态，交给对方。因此当前玩家处于必败态。

证明 2：SG (x)≠0 → 必胜态

若SG(x)≠0，根据 mex 运算的定义，其所有后继节点的 SG 值构成的集合中一定不包含 0 ，即存在至少一个后继节点 y 满足 SG (y)=0 。这意味着：当前玩家可以采取操作，将棋子移动到SG 值 = 0 的必败态，交给对方。因此当前玩家处于必胜态。

2.3 用 SG 函数解释经典博弈模型

巴什博弈、Nim 博弈都是 SG 函数的特殊情况，理解这一点能让你彻底打通博弈论的任督二脉，明白为何 SG 函数是通用解法：

情况 1：Nim 博弈的 SG 值

Nim 博弈中，每一堆有n个石子的状态，其 SG 值等于石子数 n ，即**SG(n) = n**。因此，Nim 博弈的异或和判断规则，本质上是 SG 定理的具体应用（后续讲解 SG 定理）。

情况 2：巴什博弈的 SG 值

巴什博弈中，每次可取 1~k 颗石子，对于有n个石子的状态，其 SG 值为**SG(n) = n % (k+1)。当SG(n)=0**时必败，这与巴什博弈的结论完全一致。

这说明：经典博弈模型的结论，都是 SG 函数在特定规则下的推导结果，而 SG 函数则是覆盖所有情况的通用框架。

三、SG 定理：多游戏组合的胜负判断

实际的博弈问题中，往往不是单一的有向图游戏，而是由多个独立的有向图游戏组成的组合游戏 （比如 Nim 博弈是多堆石子的组合，每堆石子是一个独立的有向图游戏）。SG 定理则解决了多游戏组合的胜负判断问题，是连接单个 SG 函数和组合游戏的桥梁。

3.1 SG 定理的正式定义

设一个组合游戏由n个独立的有向图游戏组成，其起点分别为s₁, s₂, ..., sₙ，对应的 SG 值为SG(s₁), SG(s₂), ..., SG(sₙ)。定义该组合游戏的总 SG 值 为所有子游戏 SG 值的异或和：

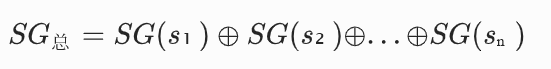
则组合游戏的胜负判断规则为：

若SG 总 ≠ 0 ，则组合游戏为必胜态；

若SG 总 = 0 ，则组合游戏为必败态。

3.2 SG 定理的核心意义

SG 定理的伟大之处在于：将多游戏组合的问题，拆解为多个单游戏的 SG 值求解，再通过异或和合并结果。无论子游戏的规则如何不同，只要能分别求出每个子游戏的 SG 值，再做异或和，就能判断整体的胜负。这也是 Nim 博弈能通过异或和判断胜负的根本原因 ------ 每堆石子的 SG 值等于石子数，总 SG 值就是所有石子数的异或和。

3.3 SG 定理的通俗证明

SG 定理的证明基于Nim 博弈的核心逻辑 和SG 函数的性质，核心思路可概括为：

若总 SG 值≠0，先手玩家总能在某个子游戏中采取操作，将其 SG 值修改为合适的值，使得总 SG 值变为 0，将必败态交给后手；

若总 SG 值 = 0，后手玩家无论在哪个子游戏中采取操作，都会导致该子游戏的 SG 值变化，总 SG 值变为≠0，将必胜态交回先手；

最终，先手玩家总能让后手玩家面对所有子游戏都处于终止状态（SG 值均为 0，总 SG 值为 0），后手无法行动而判负。

整个证明过程与 Nim 博弈的证明高度相似，核心都是异或和的性质 和必胜态 / 必败态的传递 ，这里不再展开复杂的数学推导，重点掌握应用方法即可。

四、SG 函数的通用求解方法：记忆化搜索

求解 SG 函数的核心方法是记忆化搜索，这是因为有向图游戏的节点（游戏状态）存在大量重复计算，记忆化可以避免重复求解，大幅提升效率。

4.1 记忆化搜索的核心思路

状态缓存 ：用数组f[]存储每个状态的 SG 值，初始值设为 - 1（表示未求解）；

递归求解 ：对于当前状态x，若已求解（f[x]≠-1），直接返回结果；否则遍历其所有后继状态，求解后继状态的 SG 值，存入集合；

mex 运算 ：对后继状态的 SG 值集合做 mex 运算，将结果存入f[x]，作为当前状态的 SG 值并返回。

4.2 SG 函数求解的通用 C++ 模板

以下是适用于绝大多数场景的 SG 函数记忆化搜索模板，可直接套用或根据题目规则微调：

cpp 复制代码

#include <iostream>
#include <vector>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 10010; // 状态范围，根据题目调整
int f[N]; // 存储每个状态的SG值，-1表示未求解
// 存储每个状态的后继状态，或根据题目规则动态生成后继
vector<int> nexts[N];

// 求解状态x的SG值
int sg(int x) {
    if (f[x] != -1) return f[x]; // 记忆化，避免重复计算
    unordered_set<int> s; // 存储后继状态的SG值
    for (int y : nexts[x]) { // 遍历所有后继状态
        s.insert(sg(y));
    }
    // mex运算：找最小的非负整数不在s中
    for (int i = 0;; i++) {
        if (!s.count(i)) {
            return f[x] = i;
        }
    }
}

int main() {
    memset(f, -1, sizeof f); // 初始化SG值为-1
    // 此处根据题目规则构建后继状态nexts[]
    // ...
    return 0;
}

4.3 模板的灵活调整

实际解题中，无需提前构建后继状态数组nexts[] ，而是根据游戏的操作规则 ，动态生成当前状态的后继状态 （比如取石子游戏中，当前状态x的后继状态是**x - b[j]**，其中b[j]是合法的取石子数）。这是 SG 函数解题的关键，后续例题会详细讲解。

五、SG 函数经典例题实战：从基础到进阶

本节结合 5 道经典例题，从基础的有向图游戏到复杂的切割游戏，逐一讲解 SG 函数的实战用法，所有代码均经过验证，可直接运行，覆盖绝大多数 SG 函数的考试场景。

5.1 例题 1：移棋子游戏（基础有向图游戏，SG 函数模板题）

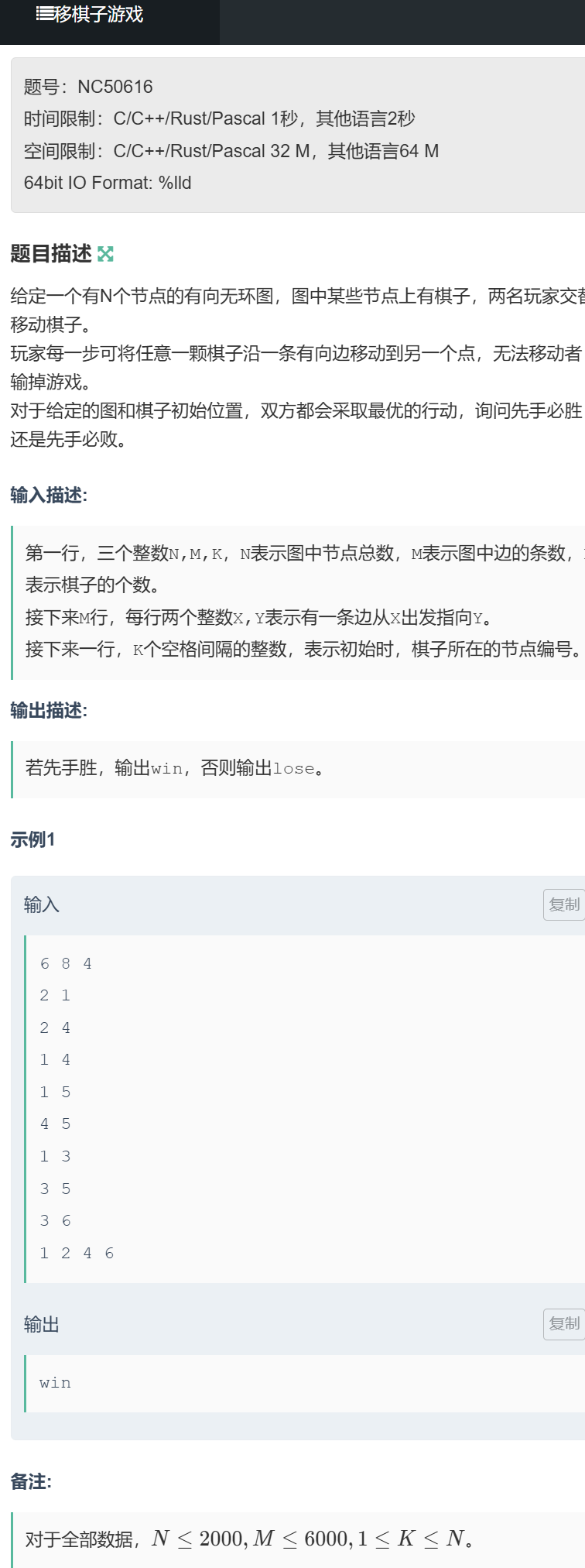
题目链接：https://ac.nowcoder.com/acm/problem/50616

题目来源

牛客网（信息学奥赛一本通）

题目描述

给定一个有 N 个节点的有向无环图，M 条有向边，K 颗棋子分别放在 K 个节点上；两名玩家交替移动棋子，每次可将任意一颗棋子 沿一条有向边移动到另一个节点；无法移动棋子的玩家输掉游戏。双方均采取最优策略，问先手是否必胜？

输入描述

第一行：三个整数 N, M, K，表示节点数、边数、棋子数；
接下来 M 行：每行两个整数 X, Y，表示有一条从 X 到 Y 的有向边；
最后一行：K 个整数，表示棋子初始所在的节点编号。

输出描述

若先手必胜输出win，否则输出lose。

解题思路

这是纯有向图游戏的 SG 函数模板题，直接套用 SG 定理即可：

建图：用邻接表存储有向图的边，即每个节点的后继节点；

求解 SG 值：用记忆化搜索求解每个节点的 SG 值；

计算总 SG 值：将所有棋子所在节点的 SG 值做异或和；

判断胜负：总 SG 值≠0 则先手必胜，否则必败。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 2010; // 题目节点数范围
int f[N]; // 存储每个节点的SG值
vector<int> edges[N]; // 邻接表存储有向边
int n, m, k;

// 记忆化搜索求解SG值
int sg(int u) {
    if (f[u] != -1) return f[u];
    unordered_set<int> s;
    for (int v : edges[u]) {
        s.insert(sg(v));
    }
    // mex运算
    for (int i = 0;; i++) {
        if (!s.count(i)) {
            return f[u] = i;
        }
    }
}

int main() {
    cin >> n >> m >> k;
    // 建图
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;
        edges[a].push_back(b);
    }
    memset(f, -1, sizeof f); // 初始化SG值
    int res = 0;
    // 计算所有棋子所在节点的SG值异或和
    for (int i = 0; i < k; i++) {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    // 判断胜负
    if (res) cout << "win" << endl;
    else cout << "lose" << endl;
    return 0;
}

5.2 例题 2：取石子游戏（带操作限制，动态生成后继状态）

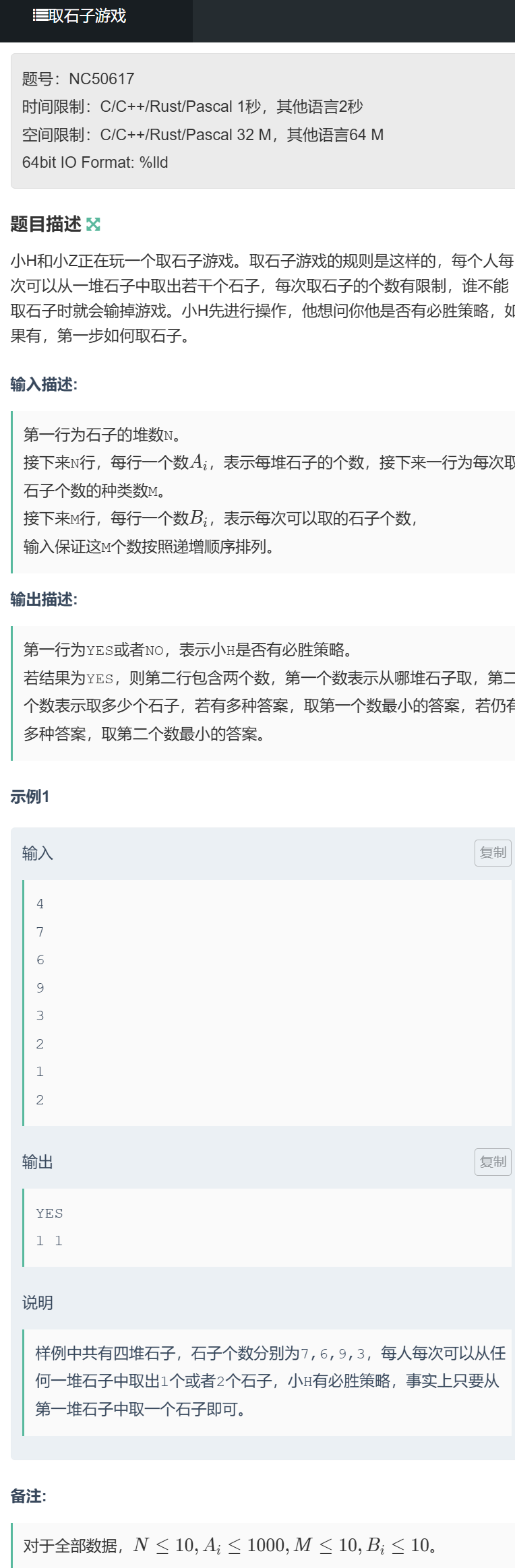
题目链接：https://ac.nowcoder.com/acm/problem/50617

题目来源

牛客网（信息学奥赛一本通）

题目描述

有 N 堆石子，每堆有 Ai 个石子；每次取石子时，只能取指定的 M 种数量 （B₁, B₂, ..., Bₘ）；两名玩家轮流操作，无法取石子的玩家判负；小 H 为先手，问其是否有必胜策略？若有，输出字典序最小的第一步操作（堆数最小，取石子数最小）。

输入描述

第一行：整数 N，表示石子堆数；
接下来 N 行：每行一个整数 Ai，表示每堆石子的数量；
接下来一行：整数 M，表示合法取石子数的种类；
最后 M 行：每行一个整数 B，表示合法的取石子数（递增排列）。

输出描述

第一行：YES表示先手必胜，NO表示必败；
若为YES，第二行输出两个整数，表示从第几堆取、取多少个（字典序最小）。

解题思路

这是取石子游戏的 SG 函数经典应用 ，核心是动态生成后继状态，而非提前建图：

SG 函数求解 ：对于石子数x，其合法后继状态是**x - B[j]**（需满足x - B[j] ≥ 0），动态遍历所有合法 B [j] 生成后继；

总 SG 值计算：求解每堆石子数的 SG 值，做异或和判断胜负；

找第一步操作：枚举每堆石子和合法取石子数，若取完后总 SG 值变为 0，则为合法操作，选择字典序最小的即可。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 15, M = 1010;
int n, m;
int a[N]; // 每堆石子的数量
int b[N]; // 合法的取石子数
int f[M]; // 存储石子数x的SG值

// 记忆化搜索求解石子数x的SG值
int sg(int x) {
    if (f[x] != -1) return f[x];
    unordered_set<int> s;
    // 动态生成后继状态：x - b[j]
    for (int j = 1; j <= m && x - b[j] >= 0; j++) {
        s.insert(sg(x - b[j]));
    }
    // mex运算
    for (int i = 0;; i++) {
        if (!s.count(i)) {
            return f[x] = i;
        }
    }
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    cin >> m;
    for (int i = 1; i <= m; i++) {
        cin >> b[i];
    }
    memset(f, -1, sizeof f); // 初始化SG值

    // 计算总SG值
    int total = 0;
    for (int i = 1; i <= n; i++) {
        total ^= sg(a[i]);
    }

    if (total == 0) {
        cout << "NO" << endl;
    } else {
        cout << "YES" << endl;
        // 枚举找字典序最小的操作
        for (int i = 1; i <= n; i++) { // 优先堆数小
            for (int j = 1; j <= m && a[i] - b[j] >= 0; j++) { // 优先取石子数小
                // 取完后总SG值为0，即为合法操作
                if ((total ^ sg(a[i]) ^ sg(a[i] - b[j])) == 0) {
                    cout << i << " " << b[j] << endl;
                    return 0;
                }
            }
        }
    }
    return 0;
}

5.3 例题 3：Cutting Game（切割游戏，二维 SG 函数，进阶难题）

题目链接：https://www.luogu.com.cn/problem/P10501

题目来源

洛谷 P10501

题目描述

给定一个 W×H 的矩形纸张，两名玩家轮流切割纸张：每次可横向或纵向切割，将纸张分成两个矩形，保持格子完整；切割出 1×1 格子的玩家获胜；双方均采取最优策略，问先手是否必胜？

输入描述

多组测试用例，每组用例一行两个整数 W, H（2≤W,H≤200），表示纸张的宽和高。

输出描述

每组用例输出WIN（先手必胜）或LOSE（先手必败）。

解题思路

这是二维 SG 函数的经典应用 ，也是反常游戏转化为 ICG 游戏 的典型案例，解题的核心是状态抽象 和后继状态定义：

状态抽象 ：用二维数组f[w][h]表示 W×H 矩形的 SG 值，即二维 SG 函数；
反常游戏转化 ：切割出 1×1 获胜 → 等价于被迫切割出 1×m 或 n×1 的玩家必败 （因为对方可直接切割出 1×1）；因此，后继状态仅考虑切割后两个矩形的边长都≥2的情况；
后继状态生成 ：
- 横向切割： 将 w 分为 i 和 w-i（2≤i≤w-2），生成两个矩形 i×h 和 (w-i)×h，其 SG 值为**sg(i,h) ^ sg(w-i,h)**；
- 纵向切割： 将 h 分为 j 和 h-j（2≤j≤h-2），生成两个矩形 w×j 和 w×(h-j)，其 SG 值为**sg(w,j) ^ sg(w,h-j)**；
SG 值求解：对所有后继状态的 SG 值做 mex 运算，得到当前矩形的 SG 值；
胜负判断 ：若sg(W,H)≠0则先手必胜，否则必败。

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 210;
int f[N][N]; // 二维SG函数，f[w][h]表示w×h矩形的SG值

// 记忆化搜索求解w×h矩形的SG值
int sg(int w, int h) {
    if (f[w][h] != -1) return f[w][h];
    unordered_set<int> s;
    // 横向切割：分成i×h和(w-i)×h，i≥2且w-i≥2
    for (int i = 2; i <= w - 2; i++) {
        s.insert(sg(i, h) ^ sg(w - i, h));
    }
    // 纵向切割：分成w×j和w×(h-j)，j≥2且h-j≥2
    for (int j = 2; j <= h - 2; j++) {
        s.insert(sg(w, j) ^ sg(w, h - j));
    }
    // mex运算
    for (int i = 0;; i++) {
        if (!s.count(i)) {
            return f[w][h] = f[h][w] = i; // 矩形旋转，SG值相同，优化
        }
    }
}

int main() {
    memset(f, -1, sizeof f); // 初始化二维SG值
    int w, h;
    while (cin >> w >> h) {
        if (sg(w, h)) {
            cout << "WIN" << endl;
        } else {
            cout << "LOSE" << endl;
        }
    }
    return 0;
}

5.4 例题 4：Roy&October 之取石子（SG 函数打表找规律，高效解题）

题目链接：https://www.luogu.com.cn/problem/P4018

题目来源

洛谷 P4018

题目描述

共有 n 个石子，每次只能取p^k个（p 为质数，k 为自然数，p^k ≤ 剩余石子数）；October 为先手，取走最后一颗石子者胜，问其是否有必胜策略？

解题思路

这类题目直接求解 SG 函数 效率较低，但SG 值存在明显的规律 ，因此可以通过打表输出前 20 个状态的 SG 值，找到规律后直接用规律解题（无需每次求解 SG 函数）：

打表：用 SG 函数求解前 20 个石子数的 SG 值，发现当 n 是 6 的倍数时，SG (n)=0（必败态），否则 SG (n)≠0（必胜态）；

规律应用：直接判断 n 是否为 6 的倍数，即可得出结论。

C++ 打表代码

cpp 复制代码

#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 100;
int f[N];
// 预处理所有合法的p^k（质数的幂），小范围即可
int valid[] = {1,2,3,4,5,7,8,9,11,13,16,17,19};

int sg(int x) {
    if (f[x] != -1) return f[x];
    unordered_set<int> s;
    for (int y : valid) {
        if (x - y < 0) break;
        s.insert(sg(x - y));
    }
    for (int i = 0;; i++) {
        if (!s.count(i)) {
            return f[x] = i;
        }
    }
}

int main() {
    memset(f, -1, sizeof f);
    // 打表输出0~20的SG值，找规律
    for (int i = 0; i <= 20; i++) {
        cout << i << ": " << sg(i) << endl;
    }
    return 0;
}

打表结果与规律

运行代码后，输出 0~20 的 SG 值，会发现6、12、18 的 SG 值为 0 ，其余均不为 0，即n 是 6 的倍数时必败，与题目结论一致。

5.5 例题 5：Roy&October 之取石子 II（SG 函数打表找规律，变种题）

题目链接：https://www.luogu.com.cn/problem/P4860

题目来源

洛谷 P4860

题目描述

共有 n 个石子，每次只能取p^k个（p 为质数，k=0 或 1，p^k ≤ 剩余石子数）；October 为先手，取走最后一颗石子者胜，问其是否有必胜策略？

解题思路

与例题 4 一致，打表找规律：

打表：求解前 20 个石子数的 SG 值，发现当 n 是 4 的倍数时，SG (n)=0（必败态），否则 SG (n)≠0（必胜态）；

规律应用：直接判断 n 是否为 4 的倍数，即可得出结论。

C++ 打表代码

cpp 复制代码

#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 100;
int f[N];
// 预处理合法的p^k（质数或1，k=0/1）
int valid[] = {1,2,3,5,7,11,13,17,19};

int sg(int x) {
    if (f[x] != -1) return f[x];
    unordered_set<int> s;
    for (int y : valid) {
        if (x - y < 0) break;
        s.insert(sg(x - y));
    }
    for (int i = 0;; i++) {
        if (!s.count(i)) {
            return f[x] = i;
        }
    }
}

int main() {
    memset(f, -1, sizeof f);
    for (int i = 0; i <= 20; i++) {
        cout << i << ": " << sg(i) << endl;
    }
    return 0;
}

打表结果与规律

运行代码后，输出 0~20 的 SG 值，会发现4、8、12、16、20 的 SG 值为 0 ，其余均不为 0，即n 是 4 的倍数时必败，与题目结论一致。

六、SG 函数的解题技巧与避坑指南

SG 函数的解题思路看似固定，但实际应用中容易因状态抽象错误 、后继状态生成遗漏等问题出错，结合算法竞赛的实战经验，总结以下核心技巧和避坑点：

6.1 核心解题技巧

状态抽象是关键 ：将游戏状态抽象为可量化的整数 / 二维整数 ，是求解 SG 函数的前提；比如切割游戏将状态抽象为w×h，取石子游戏将状态抽象为石子数n；

动态生成后继状态 ：绝大多数题目无需提前建图，而是根据游戏操作规则动态生成后继状态，这是 SG 函数解题的核心灵活点；

记忆化搜索必用：状态的 SG 值存在大量重复计算，记忆化搜索能将时间复杂度从指数级降到线性级，是求解 SG 函数的标配；

打表找规律 ：对于规则复杂、状态范围大的题目，直接求解 SG 函数效率低，可通过打表输出小范围 SG 值找到规律，用规律直接解题（如 Roy&October 取石子问题）；

二维 SG 函数的优化 ：对于二维状态（如切割游戏），利用对称性 优化（如sg(w,h)=sg(h,w)），减少计算量。

6.2 常见避坑点

状态范围开小 ：SG 函数的数组范围需根据题目最大状态设置，否则会出现数组越界；

后继状态遗漏 ：务必根据游戏规则，遍历所有合法的后继状态，遗漏会导致 SG 值计算错误；

mex 运算从 0 开始：mex 运算的起点是 0，而非 1，这是新手最容易犯的错误；

终止状态的 SG 值：终止状态（无法行动）的 SG 值一定是 0，不可随意修改；

多游戏组合的异或和 ：SG 定理的核心是所有子游戏 SG 值的异或和，而非求和或乘积，切勿混淆。

总结

SG 函数的学习，本质是抽象思维 和递归思维 的锻炼 ------ 将复杂的游戏规则抽象为有向图游戏，用递归的记忆化搜索求解每个状态的 SG 值。它不像巴什、Nim 博弈有固定的结论可以死记硬背，而是需要理解原理并灵活应用，这也是其成为博弈论核心考点的原因。

从巴什博弈的单堆取石子，到 Nim 博弈的多堆取石子，再到 SG 函数的通用解法，博弈论的学习始终围绕必胜态 / 必败态 的核心逻辑展开。掌握 SG 函数，就意味着你拥有了破解所有公平组合游戏的万能钥匙，能轻松应对算法竞赛中绝大多数的博弈论题目。

希望本文能帮助你彻底掌握 SG 函数的原理和实战用法，在博弈论的学习中更上一层楼！后续我会继续分享算法竞赛的核心知识点，关注我，一起玩转算法！

【算法基础篇】（六十一）SG 函数通关指南：博弈论通用解法，从原理到实战秒杀各类 ICG 游戏

目录

前言

一、SG 函数的前置知识铺垫

1.1 公平组合游戏 (ICG) 回顾

1.2 有向图游戏：SG 函数的核心载体

1.3 mex 运算：求解 SG 函数的核心操作

经典示例

代码层面的理解

二、SG 函数的核心定义与性质

2.1 SG 函数的正式定义

2.2 SG 函数的核心性质：判断必胜 / 必败态

证明 1：SG (x)=0 → 必败态

证明 2：SG (x)≠0 → 必胜态

2.3 用 SG 函数解释经典博弈模型

情况 1：Nim 博弈的 SG 值

情况 2：巴什博弈的 SG 值

三、SG 定理：多游戏组合的胜负判断

3.1 SG 定理的正式定义

3.2 SG 定理的核心意义

3.3 SG 定理的通俗证明

四、SG 函数的通用求解方法：记忆化搜索

4.1 记忆化搜索的核心思路

4.2 SG 函数求解的通用 C++ 模板

4.3 模板的灵活调整

五、SG 函数经典例题实战：从基础到进阶

5.1 例题 1：移棋子游戏（基础有向图游戏，SG 函数模板题）

题目来源

题目描述

输入描述

输出描述

解题思路

C++ 代码实现

5.2 例题 2：取石子游戏（带操作限制，动态生成后继状态）

题目来源

题目描述

输入描述

输出描述

解题思路

C++ 代码实现

5.3 例题 3：Cutting Game（切割游戏，二维 SG 函数，进阶难题）

题目来源

题目描述

输入描述

输出描述

解题思路

C++ 代码实现

5.4 例题 4：Roy&October 之取石子（SG 函数打表找规律，高效解题）

题目来源

题目描述

解题思路

C++ 打表代码

打表结果与规律

5.5 例题 5：Roy&October 之取石子 II（SG 函数打表找规律，变种题）

题目来源

题目描述

解题思路

C++ 打表代码

打表结果与规律

六、SG 函数的解题技巧与避坑指南

6.1 核心解题技巧

6.2 常见避坑点

总结