Leetcode 118 从中序与后序遍历序列构造二叉树 | 二叉树的最大深度

1 题目

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

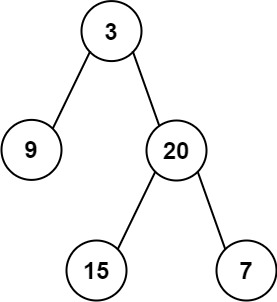
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

2 代码实现

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    unordered_map<int,int> inorder_map;
    TreeNode* build(vector<int>& postorder ,int post_start ,int post_end ,int in_start){
        if (post_start> post_end){
            return nullptr;
        }
        int root_val = postorder[post_end];
        TreeNode* root = new TreeNode(root_val);

        int root_idx_in = inorder_map[root_val];
        int left_subtree_size = root_idx_in - in_start;

        root -> left = build(postorder , post_start ,post_start + left_subtree_size - 1 , in_start);
        root -> right = build(postorder ,post_start + left_subtree_size ,post_end - 1 ,root_idx_in +1 );
        return root ;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int n = inorder.size();
        for (int i = 0 ; i < n ; ++i){
            inorder_map[inorder[i]] = i ;
        }
        return build(postorder , 0 , n -1 , 0 );
    }
};

js

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
var buildTree = function(inorder, postorder) {
    const inorderMap = new Map();
    const n = inorder.length;
    for (let i = 0 ; i < n ; i++){
        inorderMap.set(inorder[i] , i);
    }
    const build = (postStart , postEnd , inStart) => {
        if (postStart > postEnd){
            return null ;
        }
        const rootVal = postorder[postEnd];
        const root = new TreeNode(rootVal);

        const rootIdx = inorderMap.get (rootVal);
        const leftSubtreeSize = rootIdx - inStart ;

        root.left = build (postStart ,postStart + leftSubtreeSize - 1 , inStart);
        root.right = build(postStart + leftSubtreeSize , postEnd - 1 , rootIdx + 1 );
        return root ;
    }
    return build (0 , n- 1 ,0);
};

思考

这个是数据结构的题目，我知道怎么做，中序是左根右，后序是左右根，不知道怎么说，这该如何是好，不知道从哪里写，我只会手写做题...

题解

你现在想解决的是从中序和后序遍历序列构造二叉树的问题，知道中序是左根右、后序是左右根的遍历规则，但不知道怎么把这个手写解题的思路转化成 C++ 代码，我来一步步帮你实现。

解题思路

核心思路是利用遍历序列的特性递归构建：

1. 后序遍历的最后一个元素是当前子树的根节点；
2. 在中序遍历中找到根节点的位置，左边是左子树的中序序列，右边是右子树的中序序列；
3. 根据中序中左 / 右子树的节点数量，拆分后序序列（后序中前 N 个是左子树，中间 M 个是右子树，最后 1 个是根）；
4. 递归构建左子树和右子树，挂载到根节点上。

为了提高查找根节点在中序中位置的效率，我们可以先用哈希表存储中序序列的 "值 - 索引" 映射。

C++ 完整代码实现

#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;

// 定义二叉树节点结构
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
private:
    // 哈希表存储中序序列的 值->索引，避免每次查找根节点都遍历
    unordered_map<int, int> inorder_map;

    /**
     * 递归构建二叉树
     * @param postorder 后序遍历数组
     * @param post_start 后序序列当前子树的起始索引
     * @param post_end 后序序列当前子树的结束索引
     * @param in_start 中序序列当前子树的起始索引
     * @return 当前子树的根节点
     */
    TreeNode* build(vector<int>& postorder, int post_start, int post_end, int in_start) {
        // 递归终止条件：起始索引 > 结束索引，说明当前子树无节点
        if (post_start > post_end) {
            return nullptr;
        }

        // 1. 后序序列的最后一个元素是当前子树的根节点
        int root_val = postorder[post_end];
        TreeNode* root = new TreeNode(root_val);

        // 2. 找到根节点在中序序列中的索引
        int root_idx_in = inorder_map[root_val];
        // 计算左子树的节点数量（中序中根左边的节点数）
        int left_subtree_size = root_idx_in - in_start;

        // 3. 递归构建左子树
        // 后序中左子树范围：[post_start, post_start + left_subtree_size - 1]
        // 中序中左子树范围：[in_start, root_idx_in - 1]
        root->left = build(postorder, post_start, post_start + left_subtree_size - 1, in_start);

        // 4. 递归构建右子树
        // 后序中右子树范围：[post_start + left_subtree_size, post_end - 1]
        // 中序中右子树范围：[root_idx_in + 1, 末尾]
        root->right = build(postorder, post_start + left_subtree_size, post_end - 1, root_idx_in + 1);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        // 初始化哈希表
        int n = inorder.size();
        for (int i = 0; i < n; ++i) {
            inorder_map[inorder[i]] = i;
        }
        // 调用递归函数，初始范围是整个后序序列和中序序列的起始位置
        return build(postorder, 0, n - 1, 0);
    }
};

// 辅助函数：层序遍历打印二叉树（验证结果）
void printTree(TreeNode* root) {
    if (!root) {
        cout << "[]" << endl;
        return;
    }
    vector<TreeNode*> queue;
    queue.push_back(root);
    vector<string> res;
    while (!queue.empty()) {
        TreeNode* node = queue.front();
        queue.erase(queue.begin());
        if (node) {
            res.push_back(to_string(node->val));
            queue.push_back(node->left);
            queue.push_back(node->right);
        } else {
            res.push_back("null");
        }
    }
    // 去掉末尾多余的null
    while (!res.empty() && res.back() == "null") {
        res.pop_back();
    }
    cout << "[";
    for (int i = 0; i < res.size(); ++i) {
        if (i > 0) cout << ",";
        cout << res[i];
    }
    cout << "]" << endl;
}

// 测试用例
int main() {
    Solution s;
    // 示例1
    vector<int> inorder1 = {9,3,15,20,7};
    vector<int> postorder1 = {9,15,7,20,3};
    TreeNode* root1 = s.buildTree(inorder1, postorder1);
    printTree(root1); // 输出：[3,9,20,null,null,15,7]

    // 示例2
    vector<int> inorder2 = {-1};
    vector<int> postorder2 = {-1};
    TreeNode* root2 = s.buildTree(inorder2, postorder2);
    printTree(root2); // 输出：[-1]

    return 0;
}

代码关键部分解释

1. 哈希表初始化 ：inorder_map 存储中序序列每个值对应的索引，把查找根节点位置的时间复杂度从 O (n) 降到 O (1)；
2. 递归函数 build ：
   • 参数 post_start/post_end 限定当前子树在后序序列的范围，in_start 限定当前子树在中序序列的起始位置；
   • 先取后序末尾元素作为根节点，再拆分出左 / 右子树的范围，递归构建；
3. 递归终止条件 ：当 post_start > post_end 时，说明当前子树没有节点，返回nullptr；
4. 辅助打印函数：层序遍历打印二叉树，方便验证结果是否符合预期。

总结

1. 核心逻辑：后序找根，中序分左右，递归构建子树；
2. 优化技巧：用哈希表存储中序索引，避免重复遍历，提升效率；
3. 递归边界：注意后序 / 中序序列的索引范围，避免越界（比如左子树节点数为 0 时，直接返回 null）。

这段代码可以直接编译运行，输入示例中的测试用例就能得到对应的二叉树结构，你可以结合手写解题的思路，对照代码里的索引拆分逻辑，理解如何把 "找根 - 分左右 - 递归" 的思路转化为代码。

3 题目

104. 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

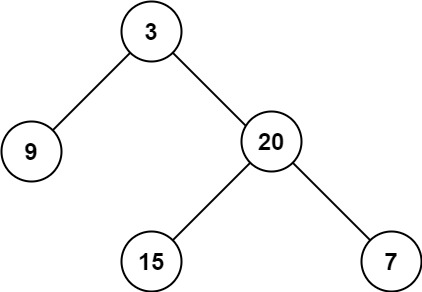
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

4 代码实现

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int left = maxDepth(root -> left );
        int right = maxDepth(root -> right );
        int res = max(left , right) + 1;
        return res ;

    }
};

js

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if (root == null){
        return 0 ;
    }
    let left = maxDepth(root.left);
    let right = maxDepth(root.right);
    let res = left > right ? left : right;
    return res + 1 ;
};

思考

dfs，递归，其实我都不知道自己这样写是不是对的。

自己写的不知道哪里错了

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int depth = 1 ;
        maxDepth(root -> left );
        maxDepth(root -> right );
        if (root -> left || root -> right){
            depth ++ ;
        }
        return depth;

    }
};

核心提醒 1：递归的返回值被 "浪费" 了

你写了 maxDepth(root -> left) 和 maxDepth(root -> right)，但这两个递归调用会返回左 / 右子树的深度 ------ 你却完全没接收这个返回值，相当于白递归了，根本没用到左右子树的真实深度。

举个例子：示例 1 中根节点 3 的左子树（9）深度是 1，右子树（20）深度是 2，但你的代码没拿到这两个数，自然没法选最大的那个。

核心提醒 2：深度计算逻辑错误

你用 if (root -> left || root -> right) { depth ++; } 来加深度，这个逻辑只判断 "有没有子节点"，但没考虑：

• 比如节点 20 有两个子节点（15、7），它的深度应该是 "1（自己） + 子树最大深度 1"=2，但你的逻辑只会无脑 + 1，没法处理 "子树本身还有多层" 的情况；
• 比如叶子节点（9、15、7），没有子节点，depth 应该保持 1，但你的逻辑也不会错；但非叶子节点的深度计算会完全偏离。

管好你自己！

终于通过了~之前虽然提交过但是居然直接调cpp的库哈哈哈...当时不求甚解也丝毫不懂递归。

递归写二叉树，每一个节点只需要管好它自己：

1. 我不问左边到底有多深、右边到底有多深
2. 我不帮左边算、不帮右边算
3. 我只做一件事：把左边的结果、右边的结果拿过来 → 选个大的 +1 → 还给上层

「管好你自己」就是：

• 别越界：不去管子树怎么算
• 别偷懒：把自己该加的 1 加上
• 别乱改：只处理当前这一层的逻辑
• 别瞎操心：递归会把下面的结果乖乖给你

只处理当前节点，剩下的交给递归。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int left = maxDepth(root -> left );
        int right = maxDepth(root -> right );
        int res = max(left , right) + 1;
        return res ;

    }
};

5 小结

总是不求甚解，一看都是做过的或者类似的题目，但是自己纯手写一遍也还是不会，需要好好总结和反思，还有lc抓紧白天写，不要拖拖拉拉！