【LeetCode】119. 杨辉三角 II

熬了夜的程序员2026-02-13 11:36

119. 杨辉三角 II

题目描述

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

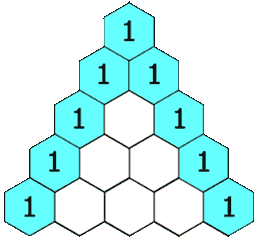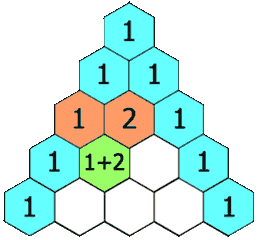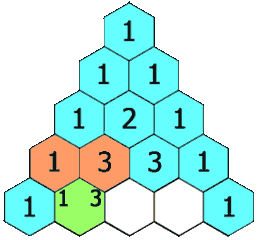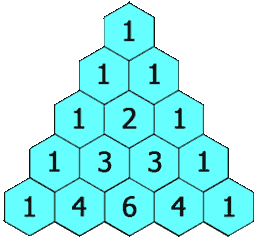
在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1：

输入 : rowIndex = 3

输出 : [1,3,3,1]

示例 2:

输入 : rowIndex = 0

输出 : [1]

示例 3:

输入 : rowIndex = 1

输出 : [1,1]

提示:

  • 0 <= rowIndex <= 33

进阶：

你可以优化你的算法到 O(rowIndex) 空间复杂度吗？

问题深度分析

这是118题的变种 ，核心区别在于只需要返回第 rowIndex 行，而不需要生成所有行。这为空间优化提供了更大的空间，可以使用 O(k) 空间（k为行索引）来生成第k行。

问题本质

返回杨辉三角的第 rowIndex 行，其中：

  • 第0行 ：[1]
  • 第i行 ：有 i+1 个元素
  • 第i行第j个元素 ：等于第 i-1 行第 j-1 个元素和第 j 个元素之和
  • 边界 ：首尾元素都是 1

核心思想

空间优化：

  1. 滚动数组：只保存当前行，从上一行计算
  2. 从后往前更新：避免覆盖未使用的值
  3. 组合数公式 ：直接计算 C(rowIndex, k)
  4. 对称性：只计算一半，另一半对称复制

关键难点

  1. 空间优化：如何用O(k)空间生成第k行
  2. 从后往前更新：避免覆盖上一行的值
  3. 组合数计算：直接计算组合数，避免存储所有行
  4. 索引处理：注意数组索引从0开始

算法对比

方法 时间复杂度 空间复杂度 特点
方法一：动态规划（二维数组） O(n²) O(n²) 生成所有行，空间浪费
方法二：滚动数组（从前往后） O(n²) O(n) 需要两个数组
方法三：滚动数组（从后往前） O(n²) O(n) 只需一个数组，最优
方法四：组合数公式 O(n) O(n) 直接计算，最快

说明：

  • n：行索引 rowIndex

算法流程图

主算法流程

渲染错误: Mermaid 渲染失败: Parse error on line 15: ... F --> F1[初始化prev = [1]] F1 --> F2[遍 -----------------------^ Expecting 'SQE', 'DOUBLECIRCLEEND', 'PE', '-)', 'STADIUMEND', 'SUBROUTINEEND', 'PIPE', 'CYLINDEREND', 'DIAMOND_STOP', 'TAGEND', 'TRAPEND', 'INVTRAPEND', 'UNICODE_TEXT', 'TEXT', 'TAGSTART', got 'SQS'

方法三：从后往前更新详细流程

渲染错误: Mermaid 渲染失败: Parse error on line 2: ...x=3] --> B[初始化row = [1]] B --> C[i = -----------------------^ Expecting 'SQE', 'DOUBLECIRCLEEND', 'PE', '-)', 'STADIUMEND', 'SUBROUTINEEND', 'PIPE', 'CYLINDEREND', 'DIAMOND_STOP', 'TAGEND', 'TRAPEND', 'INVTRAPEND', 'UNICODE_TEXT', 'TEXT', 'TAGSTART', got 'SQS'

从后往前更新的优势示意图

渲染错误: Mermaid 渲染失败: Parse error on line 3: ...）" A1[row = [1,1,1,1]] --> A2[更新 ----------------------^ Expecting 'SQE', 'DOUBLECIRCLEEND', 'PE', '-)', 'STADIUMEND', 'SUBROUTINEEND', 'PIPE', 'CYLINDEREND', 'DIAMOND_STOP', 'TAGEND', 'TRAPEND', 'INVTRAPEND', 'UNICODE_TEXT', 'TEXT', 'TAGSTART', got 'SQS'

复杂度分析

时间复杂度

  1. 方法一（二维DP）：O(n²)

    • 需要生成所有 n+1 行
    • 总元素数：1 + 2 + ... + (n+1) = O(n²)

  2. 方法二（滚动数组从前往后）：O(n²)

    • 需要生成所有行
    • 每行需要 O(n) 时间

  3. 方法三（滚动数组从后往前）：O(n²)

    • 需要生成所有行
    • 每行需要 O(n) 时间

  4. 方法四（组合数公式）：O(n)

    • 只需要计算 n+1 个组合数
    • 每个组合数需要 O(1) 时间（利用递推）

空间复杂度

  1. 方法一（二维DP）：O(n²)

    • 存储所有 n+1 行

  2. 方法二（滚动数组从前往后）：O(n)

    • 需要两个数组：prev 和 curr

  3. 方法三（滚动数组从后往前）：O(n)

    • 只需要一个数组：row
    • 最优空间复杂度

  4. 方法四（组合数公式）：O(n)

    • 存储结果数组

关键优化技巧

技巧一：从后往前更新（关键优化）

核心思想：从后往前更新数组，避免覆盖未使用的值。

go 复制代码 
// 方法三：滚动数组（从后往前）
func getRow3(rowIndex int) []int {
    row := []int{1}
    
    for i := 1; i <= rowIndex; i++ {
        // 在末尾添加1
        row = append(row, 1)
        
        // 从后往前更新，避免覆盖
        for j := i - 1; j >= 1; j-- {
            row[j] = row[j] + row[j-1]
        }
    }
    
    return row
}

优势：

  • 只需要一个数组
  • 从后往前更新，不会覆盖未使用的值
  • 空间复杂度 O(n)

为什么从后往前？

  • 如果从前往后：row[j] = row[j] + row[j-1] 会覆盖 row[j]，导致后续计算错误
  • 如果从后往前：先更新后面的值，前面的值还未被修改，保证正确性

技巧二：组合数公式（最快）

核心思想 ：直接计算组合数 C(rowIndex, k)，利用递推关系优化。

go 复制代码 
// 方法四：组合数公式
func getRow4(rowIndex int) []int {
    row := make([]int, rowIndex+1)
    row[0] = 1
    
    // 利用递推关系：C(n, k) = C(n, k-1) * (n-k+1) / k
    for j := 1; j <= rowIndex; j++ {
        row[j] = row[j-1] * (rowIndex - j + 1) / j
    }
    
    return row
}

优势：

  • 时间复杂度 O(n)
  • 空间复杂度 O(n)
  • 不需要生成前面的行

递推关系：

  • C(n, k) = C(n, k-1) * (n-k+1) / k
  • 从 C(n, 0) = 1 开始，逐步计算

技巧三：滚动数组（从前往后）

核心思想：使用两个数组，从上一行计算当前行。

go 复制代码 
// 方法二：滚动数组（从前往后）
func getRow2(rowIndex int) []int {
    prev := []int{1}
    
    for i := 1; i <= rowIndex; i++ {
        curr := make([]int, i+1)
        curr[0] = 1
        curr[i] = 1
        
        for j := 1; j < i; j++ {
            curr[j] = prev[j-1] + prev[j]
        }
        
        prev = curr
    }
    
    return prev
}

优势：

  • 逻辑清晰
  • 空间复杂度 O(n)
  • 需要两个数组

技巧四：二维DP（不推荐）

核心思想：生成所有行，返回第rowIndex行。

go 复制代码 
// 方法一：二维DP（不推荐）
func getRow1(rowIndex int) []int {
    triangle := make([][]int, rowIndex+1)
    
    for i := 0; i <= rowIndex; i++ {
        row := make([]int, i+1)
        row[0] = 1
        row[i] = 1
        
        for j := 1; j < i; j++ {
            row[j] = triangle[i-1][j-1] + triangle[i-1][j]
        }
        
        triangle[i] = row
    }
    
    return triangle[rowIndex]
}

优势：

  • 思路直观
  • 但空间浪费，不推荐

边界情况处理

1. rowIndex = 0

go 复制代码 
if rowIndex == 0 {
    return []int{1}
}

2. rowIndex = 1

go 复制代码 
// 直接返回 [1, 1]
return []int{1, 1}

3. 数组索引边界

go 复制代码 
// 确保不越界
for j := i - 1; j >= 1; j-- {  // j从i-1开始，到1结束
    row[j] = row[j] + row[j-1]
}

4. 组合数计算溢出

go 复制代码 
// 使用long类型或逐步计算
row[j] = row[j-1] * (rowIndex - j + 1) / j

测试用例设计

基础测试

  1. rowIndex = 0

    • 输入：0
    • 输出：[1]

  2. rowIndex = 1

    • 输入：1
    • 输出：[1,1]

  3. rowIndex = 2

    • 输入：2
    • 输出：[1,2,1]

标准测试

  1. rowIndex = 3

    • 输入：3
    • 输出：[1,3,3,1]

  2. rowIndex = 4

    • 输入：4
    • 输出：[1,4,6,4,1]

  3. rowIndex = 5

    • 输入：5
    • 输出：[1,5,10,10,5,1]

边界测试

  1. rowIndex = 33（最大值）

    • 测试最大输入
    • 验证性能和正确性

  2. 对称性验证

    • 验证 row[j] == row[rowIndex-j]
    • 验证每行是否关于中心对称

常见错误与陷阱

错误一：从前往后更新导致覆盖

错误代码：

go 复制代码 
row := []int{1, 1, 1, 1}
for j := 1; j < 3; j++ {
    row[j] = row[j] + row[j-1]  // 错误：会覆盖row[j]
}
// row = [1, 2, 3, 1] 错误！

正确做法：

go 复制代码 
row := []int{1, 1, 1, 1}
for j := 2; j >= 1; j-- {  // 从后往前
    row[j] = row[j] + row[j-1]
}
// row = [1, 3, 3, 1] 正确！

错误二：忘记添加末尾的1

错误代码：

go 复制代码 
row := []int{1}
for i := 1; i <= rowIndex; i++ {
    // 忘记添加1
    for j := i - 1; j >= 1; j-- {
        row[j] = row[j] + row[j-1]
    }
}

正确做法：

go 复制代码 
row := []int{1}
for i := 1; i <= rowIndex; i++ {
    row = append(row, 1)  // 先添加1
    for j := i - 1; j >= 1; j-- {
        row[j] = row[j] + row[j-1]
    }
}

错误三：组合数计算溢出

错误代码：

go 复制代码 
func combination(n, k int) int {
    numerator := factorial(n)
    denominator := factorial(k) * factorial(n-k)
    return numerator / denominator  // 可能溢出
}

正确做法：

go 复制代码 
// 利用递推关系，逐步计算
row[j] = row[j-1] * (rowIndex - j + 1) / j

错误四：索引越界

错误代码：

go 复制代码 
for j := 0; j < i; j++ {
    row[j] = row[j] + row[j-1]  // j=0时，j-1=-1越界
}

正确做法：

go 复制代码 
for j := i - 1; j >= 1; j-- {  // j从i-1开始，到1结束
    row[j] = row[j] + row[j-1]
}

实战技巧总结

1. 从后往前更新的重要性

  • 避免覆盖：从后往前更新，不会覆盖未使用的值
  • 空间优化：只需要一个数组
  • 关键技巧：这是O(n)空间的关键

2. 组合数递推关系

  • 公式 ：C(n, k) = C(n, k-1) * (n-k+1) / k
  • 优势：O(n)时间复杂度
  • 应用：直接计算，无需生成前面的行

3. 空间优化思路

  • 滚动数组：只保存当前行
  • 从后往前：避免覆盖
  • 组合数公式：直接计算

4. 与118题的区别

  • 118题：生成所有行，空间O(n²)
  • 119题：只生成第k行，空间可以优化到O(k)

进阶扩展

扩展一：查询特定位置

  • 给定 (i, j)，返回 triangle[i][j]
  • 可以直接计算 C(i, j)

扩展二：大数支持

  • 使用大整数类型
  • 处理溢出情况

扩展三：打印第k行

  • 格式化输出
  • 居中对齐显示

扩展四：批量查询

  • 给定多个 rowIndex，批量返回
  • 可以预计算或缓存

应用场景

1. 组合数学

  • 场景 ：计算组合数 C(n, k)
  • 优势：快速计算特定行的组合数

2. 概率论

  • 场景：二项分布计算
  • 优势：快速获取二项系数

3. 算法优化

  • 场景：动态规划中的组合数计算
  • 优势：O(n)空间复杂度

4. 数学计算

  • 场景：需要特定行的杨辉三角
  • 优势：不需要生成所有行

相关题目

  • 118. 杨辉三角：生成所有行
  • 120. 三角形最小路径和：动态规划变种
  • 组合数问题：利用组合数公式

总结

本题是118题的优化版本 ，核心在于空间优化。通过四种不同的方法，我们展示了：

  1. 二维DP方法：直观但空间浪费
  2. 滚动数组从前往后：需要两个数组
  3. 滚动数组从后往前：最优解，只需一个数组
  4. 组合数公式方法：最快，O(n)时间

关键要点：

  • 从后往前更新：这是O(n)空间的关键技巧
  • 组合数递推 ：C(n, k) = C(n, k-1) * (n-k+1) / k
  • 空间优化：只需要一个数组，从后往前更新
  • 时间复杂度：可以优化到O(n)

掌握本题有助于理解空间优化技巧 和组合数计算 ，特别是从后往前更新这一重要技巧，在动态规划问题中经常使用。

完整题解代码

go 复制代码 
package main

import (
	"fmt"
)

// =========================== 方法一：动态规划（二维数组，不推荐） ===========================
// 时间复杂度：O(n²)，空间复杂度：O(n²)
func getRow1(rowIndex int) []int {
	triangle := make([][]int, rowIndex+1)

	for i := 0; i <= rowIndex; i++ {
		row := make([]int, i+1)
		row[0] = 1
		row[i] = 1

		for j := 1; j < i; j++ {
			row[j] = triangle[i-1][j-1] + triangle[i-1][j]
		}

		triangle[i] = row
	}

	return triangle[rowIndex]
}

// =========================== 方法二：滚动数组（从前往后） ===========================
// 时间复杂度：O(n²)，空间复杂度：O(n)
func getRow2(rowIndex int) []int {
	prev := []int{1}

	for i := 1; i <= rowIndex; i++ {
		curr := make([]int, i+1)
		curr[0] = 1
		curr[i] = 1

		for j := 1; j < i; j++ {
			curr[j] = prev[j-1] + prev[j]
		}

		prev = curr
	}

	return prev
}

// =========================== 方法三：滚动数组（从后往前，最优解） ===========================
// 时间复杂度：O(n²)，空间复杂度：O(n)
func getRow3(rowIndex int) []int {
	row := []int{1}

	for i := 1; i <= rowIndex; i++ {
		// 在末尾添加1
		row = append(row, 1)

		// 从后往前更新，避免覆盖未使用的值
		for j := i - 1; j >= 1; j-- {
			row[j] = row[j] + row[j-1]
		}
	}

	return row
}

// =========================== 方法四：组合数公式（最快） ===========================
// 时间复杂度：O(n)，空间复杂度：O(n)
func getRow4(rowIndex int) []int {
	row := make([]int, rowIndex+1)
	row[0] = 1

	// 利用递推关系：C(n, k) = C(n, k-1) * (n-k+1) / k
	for j := 1; j <= rowIndex; j++ {
		row[j] = row[j-1] * (rowIndex - j + 1) / j
	}

	return row
}

// =========================== 工具函数：比较切片 ===========================
func equal(a, b []int) bool {
	if len(a) != len(b) {
		return false
	}
	for i := range a {
		if a[i] != b[i] {
			return false
		}
	}
	return true
}

// =========================== 测试 ===========================
func main() {
	fmt.Println("=== LeetCode 119: 杨辉三角 II ===\n")

	testCases := []struct {
		name     string
		rowIndex int
		expected []int
	}{
		{
			name:     "rowIndex = 0",
			rowIndex: 0,
			expected: []int{1},
		},
		{
			name:     "rowIndex = 1",
			rowIndex: 1,
			expected: []int{1, 1},
		},
		{
			name:     "rowIndex = 2",
			rowIndex: 2,
			expected: []int{1, 2, 1},
		},
		{
			name:     "rowIndex = 3",
			rowIndex: 3,
			expected: []int{1, 3, 3, 1},
		},
		{
			name:     "rowIndex = 4",
			rowIndex: 4,
			expected: []int{1, 4, 6, 4, 1},
		},
		{
			name:     "rowIndex = 5",
			rowIndex: 5,
			expected: []int{1, 5, 10, 10, 5, 1},
		},
		{
			name:     "rowIndex = 6",
			rowIndex: 6,
			expected: []int{1, 6, 15, 20, 15, 6, 1},
		},
		{
			name:     "rowIndex = 10",
			rowIndex: 10,
			expected: []int{1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1},
		},
	}

	methods := []struct {
		name string
		fn   func(int) []int
	}{
		{"方法一：动态规划（二维数组）", getRow1},
		{"方法二：滚动数组（从前往后）", getRow2},
		{"方法三：滚动数组（从后往前）", getRow3},
		{"方法四：组合数公式", getRow4},
	}

	allPassed := true
	for _, method := range methods {
		fmt.Printf("--- %s ---\n", method.name)
		passed := 0
		for i, tc := range testCases {
			result := method.fn(tc.rowIndex)

			if equal(result, tc.expected) {
				fmt.Printf("  Test %d: ✓ PASSED\n", i+1)
				passed++
			} else {
				fmt.Printf("  Test %d: ✗ FAILED\n", i+1)
				fmt.Printf("    输入: rowIndex = %d\n", tc.rowIndex)
				fmt.Printf("    期望: %v\n", tc.expected)
				fmt.Printf("    得到: %v\n", result)
				allPassed = false
			}
		}
		fmt.Printf("通过率: %d/%d\n\n", passed, len(testCases))
	}

	if allPassed {
		fmt.Println("🎉 所有测试通过！")
	} else {
		fmt.Println("❌ 部分测试失败")
	}
}
相关推荐
sali-tec2 小时前
C# 基于OpenCv的视觉工作流-章24-SURF特征点
图像处理·人工智能·opencv·算法·计算机视觉
hillstream32 小时前
从这次xAI重组说开去--用类比的思维来理解
人工智能·算法·xai·elon.mask
菜鸡儿齐2 小时前
leetcode-最长连续序列
数据结构·算法·leetcode
寻寻觅觅☆2 小时前
东华OJ-基础题-120-顺序的分数（C++）
开发语言·c++·算法
Tisfy2 小时前
LeetCode 3713.最长的平衡子串 I：计数（模拟）
算法·leetcode·题解·模拟
月疯2 小时前
陀螺仪和加速度计（模拟状态，计算运动状态）
算法
Σίσυφος19002 小时前
双目立体视觉 数学推导（从 F → E → R,T）
算法
Hcoco_me2 小时前
目标追踪概述、分类
人工智能·深度学习·算法·机器学习·分类·数据挖掘·自动驾驶
熬了夜的程序员2 小时前
【LeetCode】117. 填充每个节点的下一个右侧节点指针 II
java·算法·leetcode
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03243 行 microGPT：把“训练 + 推理”拆到骨头里04openclaw配置教程（linux+局域网ollama）05UV安装并设置国内源06Zsh/Bash Conda设置延迟启动，启动速度优化07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08openclaw 配置飞书 报错 应用未建立长连接09MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法10Palantir官方深度解析本体 Ontology系统及知识图谱、大模型：企业自主决策的核心AI引擎