本文参考Kian Sen Ang and I. D. Robertson, "Analysis and design of impedance-transforming planar Marchand baluns, " in IEEE Transactions on Microwave Theory and Techniques, vol. 49, no. 2, pp. 402-406, Feb. 2001, doi: 10.1109/22.903108.
keywords: {Impedance matching;Couplers;Coupling circuits;Diodes;Microstrip;Frequency;Microwave integrated circuits;MMICs;Monolithic integrated circuits;Wideband},详细推导一下下公式,并且指出其中的可能的作者笔误,并提出一些疑问,希望大佬们来答疑解惑一下,仅供学习使用
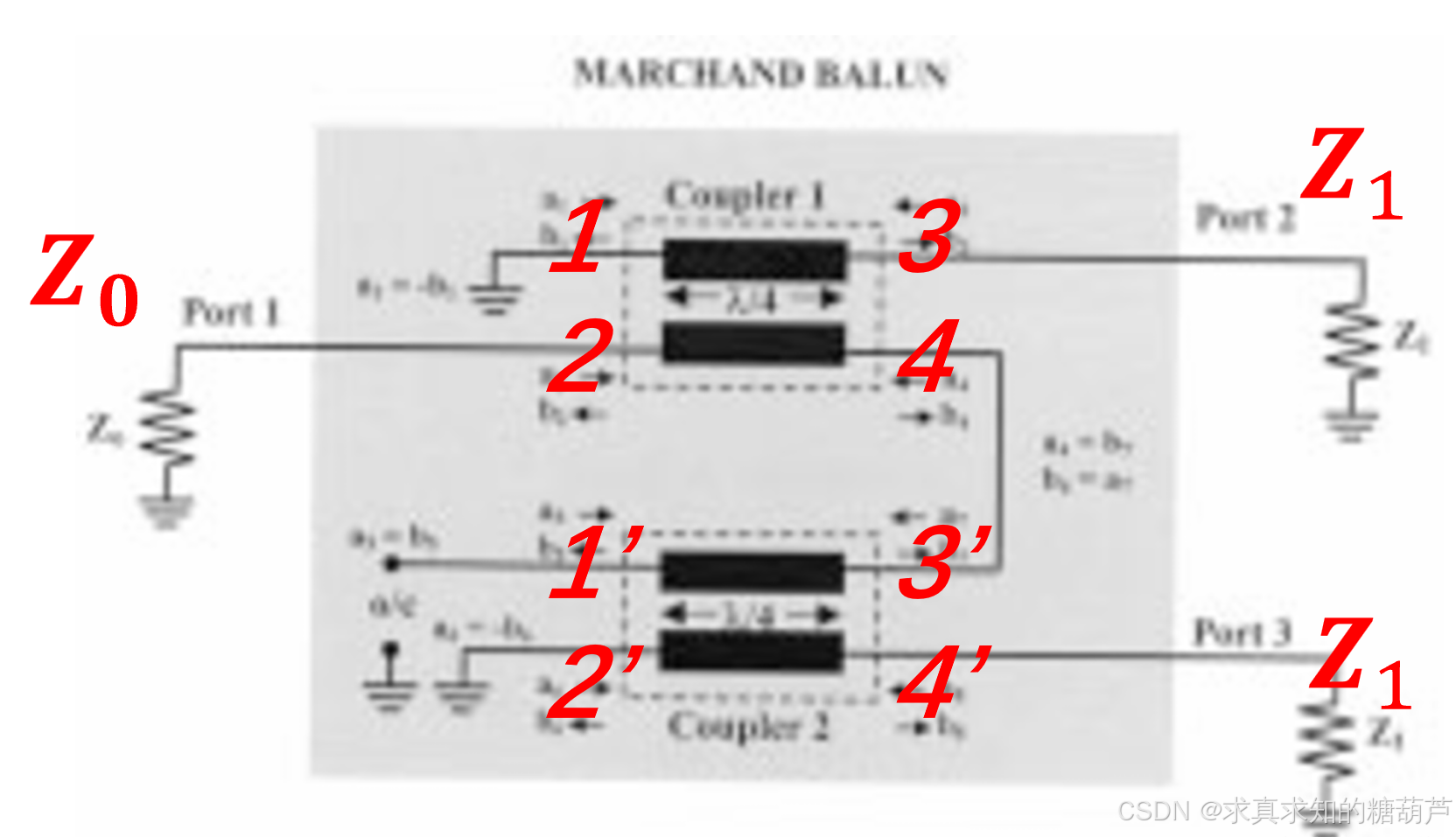
图 1. 作为两个相同耦合器的对称Marchand巴伦框图。
二、分析
巴伦的框图如图1所示。它为一个源阻抗为ZoZ_oZo的非平衡输入提供平衡输出,连接到负载阻抗Z1Z_1Z1。通常,阻抗Z1Z_1Z1和ZoZ_oZo是不同的。例如,在平衡二极管混频器应用中,平衡信号需要馈入一对二极管,其阻抗可能与50Ω源阻抗不同。因此,除了提供平衡输出外,巴伦还需要在源阻抗和负载阻抗之间执行阻抗变换。
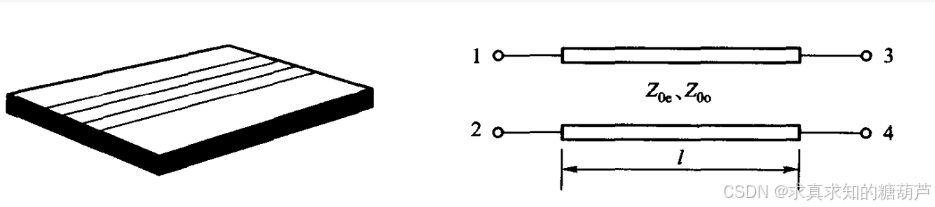
图1.1:端口顺序定义,1输入,2耦合,3直通(这里2和3与常见定向耦合器不同,想按常见定向耦合器定义将结果交换2与3顺序即可),4隔离
接上集对称均匀耦合线,终端参考阻抗均为Z0Z_0Z0的巴伦的S参数:
S\]balun=\[1−3C21+C2j2C1−C21+C2−j2C1−C21+C2j2C1−C21+C21−C21+C22C21+C2−j2C1−C21+C22C21+C21−C21+C2\].(2) \[S\]_{\\text{balun}} = \\begin{bmatrix} \\frac{1 - 3C\^2}{1 + C\^2} \& j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \& -j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \\\\ j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \& \\frac{1 - C\^2}{1 + C\^2} \& \\frac{2C\^2}{1 + C\^2} \\\\ -j \\frac{2C \\sqrt{1 - C\^2}}{1 + C\^2} \& \\frac{2C\^2}{1 + C\^2} \& \\frac{1 - C\^2}{1 + C\^2} \\end{bmatrix} . \\qquad(2) \[S\]balun= 1+C21−3C2j1+C22C1−C2 −j1+C22C1−C2 j1+C22C1−C2 1+C21−C21+C22C2−j1+C22C1−C2 1+C22C21+C21−C2 .(2) 当如图1所示,**巴伦的负载阻抗从ZoZ_oZo变为Z1Z_1Z1时,巴伦的S矩阵必须从\[S\]balun\[S\]_{\\text{balun}}\[S\]balun修改为\[S\]balun′\[S\]_{\\text{balun}}\^{\\prime}\[S\]balun′。**两个矩阵之间的关系由以下矩阵方程给出:**(其中+表示共轭转置,假设参考阻抗均为实数,\[I\]\[I\]\[I\]表示单位矩阵)** \[S\]balun′=\[A\]−1(\[S\]balun−\[Γ\]+)(\[I\]−\[Γ\]\[S\]balun)−1\[A\]+(3) \[S\]_{\\text{balun}}\^{\\prime} = \[A\]\^{-1} \\left( \[S\]_{\\text{balun}} - \[\\Gamma\]\^{+} \\right) (\[I\] - \[\\Gamma\]\[S\]_{\\text{balun}})\^{-1}\[A\]\^{+} \\qquad(3) \[S\]balun′=\[A\]−1(\[S\]balun−\[Γ\]+)(\[I\]−\[Γ\]\[S\]balun)−1\[A\]+(3) *** ** * ** *** ## 1 推导转换矩阵 ### 1.1 归一化电压波的定义 设网络有NNN个端口。对于端口iii,当参考阻抗为ZiZ_iZi(假设实数,分母阻抗实部也可写为ZiZ_iZi)时,定义归一化入射波aia_iai和反射波bib_ibi: ai=Vi+ZiIi2Zi,bi=Vi−ZiIi2Zi a_i = \\frac{V_i + Z_i I_i}{2\\sqrt{Z_i}}, \\quad b_i = \\frac{V_i - Z_i I_i}{2\\sqrt{Z_i}} ai=2Zi Vi+ZiIi,bi=2Zi Vi−ZiIi 其中ViV_iVi和IiI_iIi是端口的电压和电流(电流方向为流入网络)。类似地,当参考阻抗变为Zi′Z_i'Zi′(假设实数)时,定义: ai′=Vi+Zi′Ii2Zi′,bi′=Vi−Zi′Ii2Zi′ a_i' = \\frac{V_i + Z_i' I_i}{2\\sqrt{Z_i'}}, \\quad b_i' = \\frac{V_i - Z_i' I_i}{2\\sqrt{Z_i'}} ai′=2Zi′ Vi+Zi′Ii,bi′=2Zi′ Vi−Zi′Ii ### 1.2 新旧波之间的变换关系 由电压和电流的表达式相等: Zi(ai+bi)=Zi′(ai′+bi′),1Zi(ai−bi)=1Zi′(ai′−bi′) \\sqrt{Z_i}(a_i + b_i) = \\sqrt{Z_i'}(a_i' + b_i'), \\quad \\frac{1}{\\sqrt{Z_i}}(a_i - b_i) = \\frac{1}{\\sqrt{Z_i'}}(a_i' - b_i') Zi (ai+bi)=Zi′ (ai′+bi′),Zi 1(ai−bi)=Zi′ 1(ai′−bi′) 解得: ai=1Ai(ai′+Γibi′),bi=1Ai(Γiai′+bi′) a_i = \\frac{1}{A_i}(a_i' + \\Gamma_i b_i'), \\quad b_i = \\frac{1}{A_i}(\\Gamma_i a_i' + b_i') ai=Ai1(ai′+Γibi′),bi=Ai1(Γiai′+bi′) 其中: Γi=Zi′−ZiZi′+Zi,Ai=2ZiZi′Zi′+Zi \\Gamma_i = \\frac{Z_i' - Z_i}{Z_i' + Z_i}, \\quad A_i = \\frac{2\\sqrt{Z_i Z_i'}}{Z_i' + Z_i} Γi=Zi′+ZiZi′−Zi,Ai=Zi′+Zi2ZiZi′ 对于所有端口,写成向量和矩阵形式: a=\[A\]−1(a′+\[Γ\]b′),b=\[A\]−1(\[Γ\]a′+b′)(A) \\mathbf{a} = \[A\]\^{-1} (\\mathbf{a}' + \[\\Gamma\] \\mathbf{b}'), \\quad \\mathbf{b} = \[A\]\^{-1} (\[\\Gamma\] \\mathbf{a}' + \\mathbf{b}') \\quad(A)a=\[A\]−1(a′+\[Γ\]b′),b=\[A\]−1(\[Γ\]a′+b′)(A) 这里\[A\]\[A\]\[A\]和\[Γ\]\[\\Gamma\]\[Γ\]是N×NN \\times NN×N对角矩阵,其对角线元素分别为AiA_iAi和Γi\\Gamma_iΓi。 ### 1.3 网络关系与新的散射矩阵 原始散射矩阵\[S\]\[S\]\[S\]满足: b=\[S\]a \\mathbf{b} = \[S\] \\mathbf{a} b=\[S\]a 新的散射矩阵\[S\]′\[S\]'\[S\]′满足: b′=\[S\]′a′ \\mathbf{b}' = \[S\]' \\mathbf{a}' b′=\[S\]′a′ 将步骤1.2的我们求得的a,b\\mathbf{a},\\mathbf{b}a,b即(A)式代入b=\[S\]a\\mathbf{b} = \[S\] \\mathbf{a}b=\[S\]a: \[A\]−1(\[Γ\]a′+b′)=\[S\]\[A\]−1(a′+\[Γ\]b′) \[A\]\^{-1} (\[\\Gamma\] \\mathbf{a}' + \\mathbf{b}') = \[S\] \[A\]\^{-1} (\\mathbf{a}' + \[\\Gamma\] \\mathbf{b}') \[A\]−1(\[Γ\]a′+b′)=\[S\]\[A\]−1(a′+\[Γ\]b′) 两边左乘\[A\]\[A\]\[A\]: \[Γ\]a′+b′=\[A\]\[S\]\[A\]−1(a′+\[Γ\]b′) \[\\Gamma\] \\mathbf{a}' + \\mathbf{b}' = \[A\]\[S\]\[A\]\^{-1} (\\mathbf{a}' + \[\\Gamma\] \\mathbf{b}') \[Γ\]a′+b′=\[A\]\[S\]\[A\]−1(a′+\[Γ\]b′) 整理出b′\\mathbf{b}'b′项: b′−\[A\]\[S\]\[A\]−1\[Γ\]b′=\[A\]\[S\]\[A\]−1a′−\[Γ\]a′ \\mathbf{b}' - \[A\]\[S\]\[A\]\^{-1} \[\\Gamma\] \\mathbf{b}' = \[A\]\[S\]\[A\]\^{-1} \\mathbf{a}' - \[\\Gamma\] \\mathbf{a}' b′−\[A\]\[S\]\[A\]−1\[Γ\]b′=\[A\]\[S\]\[A\]−1a′−\[Γ\]a′ 即: (\[I\]−\[A\]\[S\]\[A\]−1\[Γ\])b′=(\[A\]\[S\]\[A\]−1−\[Γ\])a′ \\left( \[I\] - \[A\]\[S\]\[A\]\^{-1} \[\\Gamma\] \\right) \\mathbf{b}' = \\left( \[A\]\[S\]\[A\]\^{-1} - \[\\Gamma\] \\right) \\mathbf{a}' (\[I\]−\[A\]\[S\]\[A\]−1\[Γ\])b′=(\[A\]\[S\]\[A\]−1−\[Γ\])a′ 因此: b′=(\[I\]−\[A\]\[S\]\[A\]−1\[Γ\])−1(\[A\]\[S\]\[A\]−1−\[Γ\])a′ \\mathbf{b}' = \\left( \[I\] - \[A\]\[S\]\[A\]\^{-1} \[\\Gamma\] \\right)\^{-1} \\left( \[A\]\[S\]\[A\]\^{-1} - \[\\Gamma\] \\right) \\mathbf{a}' b′=(\[I\]−\[A\]\[S\]\[A\]−1\[Γ\])−1(\[A\]\[S\]\[A\]−1−\[Γ\])a′ 所以新的散射矩阵为: \[S\]′=(\[I\]−\[A\]\[S\]\[A\]−1\[Γ\])−1(\[A\]\[S\]\[A\]−1−\[Γ\])(\*) \[S\]' = \\left( \[I\] - \[A\]\[S\]\[A\]\^{-1} \[\\Gamma\] \\right)\^{-1} \\left( \[A\]\[S\]\[A\]\^{-1} - \[\\Gamma\] \\right) \\tag{\*} \[S\]′=(\[I\]−\[A\]\[S\]\[A\]−1\[Γ\])−1(\[A\]\[S\]\[A\]−1−\[Γ\])(\*) ### 1.4 疑问论文中给出的公式形式如下,不清楚由来希望大佬们解惑 \[S\]balun′=\[A\]−1(\[S\]balun−\[Γ\]+)(\[I\]−\[Γ\]\[S\]balun)−1\[A\]+(3) \[S\]_{\\text{balun}}' = \[A\]\^{-1} \\left( \[S\]_{\\text{balun}} - \[\\Gamma\]\^{+} \\right) \\left( \[I\] - \[\\Gamma\]\[S\]_{\\text{balun}} \\right)\^{-1} \[A\]\^{+} \\quad(3)\[S\]balun′=\[A\]−1(\[S\]balun−\[Γ\]+)(\[I\]−\[Γ\]\[S\]balun)−1\[A\]+(3) **有一些参考文献**  参考文献:**J. C. Tippet and R. A. Speciale, "A Rigorous Technique for Measuring the Scattering Matrix of a Multiport Device with a 2-Port Network Analyzer," in IEEE Transactions on Microwave Theory and Techniques, vol. 30, no. 5, pp. 661-666, May 1982, doi: 10.1109/TMTT.1982.1131118. keywords: {Reflection;Testing;Performance evaluation;Measurement techniques;Performance analysis;Impedance measurement;Scattering parameters;Microwave measurements;Microwave devices},** **微波工程4.3节广义散射矩阵中也给出**   *** ** * ** *** 其中\[I\]\[I\]\[I\]是单位矩阵,而\[Γ\]\[\\Gamma\]\[Γ\]和\[A\]\[A\]\[A\]由下式给出**论文中公式(4)的\[A\]\[A\]\[A\]矩阵第一个元素应为1(对应端口1无阻抗变换,这样才能保证在Z1=Z0Z_1=Z_0Z1=Z0时矩阵退化为\[S\]balun\[S\]_{\\text{balun}}\[S\]balun。** \[Γ\]=\[0000Z1−ZoZ1+Zo000Z1−ZoZ1+Zo\]\[A\]=\[00002Z1ZoZ1+Zo0002Z1ZoZ1+Zo\](4有问题) \[\\Gamma\] = \\left\[ \\begin{array}{ccc} 0 \& 0 \& 0 \\\\ 0 \& \\dfrac{Z_1 - Z_o}{Z_1 + Z_o} \& 0 \\\\ 0 \& 0 \& \\dfrac{Z_1 - Z_o}{Z_1 + Z_o} \\end{array} \\right\] \[A\] = \\left\[ \\begin{array}{ccc} 0 \& 0 \& 0 \\\\ 0 \& \\dfrac{2\\sqrt{Z_1 Z_o}}{Z_1 + Z_o} \& 0 \\\\ 0 \& 0 \& \\dfrac{2\\sqrt{Z_1 Z_o}}{Z_1 + Z_o} \\end{array} \\right\]\\quad(4有问题) \[Γ\]= 0000Z1+ZoZ1−Zo000Z1+ZoZ1−Zo \[A\]= 0000Z1+Zo2Z1Zo 000Z1+Zo2Z1Zo (4有问题) \[Γ\]=diag(0, Z1−ZoZ1+Zo, Z1−ZoZ1+Zo),\[A\]=diag(1, 2Z1ZoZ1+Zo, 2Z1ZoZ1+Zo)(4修改后) \[\\Gamma\] = \\operatorname{diag}\\left(0,\\ \\frac{Z_1 - Z_o}{Z_1 + Z_o},\\ \\frac{Z_1 - Z_o}{Z_1 + Z_o}\\right), \\quad \[A\] = \\operatorname{diag}\\left(1,\\ \\frac{2\\sqrt{Z_1 Z_o}}{Z_1 + Z_o},\\ \\frac{2\\sqrt{Z_1 Z_o}}{Z_1 + Z_o}\\right) \\quad(4修改后)\[Γ\]=diag(0, Z1+ZoZ1−Zo, Z1+ZoZ1−Zo),\[A\]=diag(1, Z1+Zo2Z1Zo , Z1+Zo2Z1Zo )(4修改后) 由于ZoZ_oZo和Z1Z_1Z1为实数,\[A\]\[A\]\[A\]和\[Γ\]\[\\Gamma\]\[Γ\]为实对角矩阵,故\[A\]+=\[A\]\[A\]\^+ = \[A\]\[A\]+=\[A\],\[Γ\]+=\[Γ\]\[\\Gamma\]\^+ = \[\\Gamma\]\[Γ\]+=\[Γ\],公式简化为上述实数形式。代入已知的\[S\]balun\[S\]_{\\text{balun}}\[S\]balun(公式(2)),即可推导出阻抗变换后的散射矩阵(公式(5))。 ## 2.计算转换后矩阵 S参数重新归一化理论用于将端口参考阻抗从全为ZoZ_oZo转换为端口1为ZoZ_oZo、端口2和3为Z1Z_1Z1。: ### 2.1 定义矩阵 原始巴伦S矩阵(所有端口参考阻抗为ZoZ_oZo): \[S\]balun=\[1−3C21+C2j2C1−C21+C2−j2C1−C21+C2j2C1−C21+C21−C21+C22C21+C2−j2C1−C21+C22C21+C21−C21+C2\] \[S\]_{\\text{balun}} = \\begin{bmatrix} \\frac{1-3C\^2}{1+C\^2} \& j\\frac{2C\\sqrt{1-C\^2}}{1+C\^2} \& -j\\frac{2C\\sqrt{1-C\^2}}{1+C\^2} \\\\ j\\frac{2C\\sqrt{1-C\^2}}{1+C\^2} \& \\frac{1-C\^2}{1+C\^2} \& \\frac{2C\^2}{1+C\^2} \\\\ -j\\frac{2C\\sqrt{1-C\^2}}{1+C\^2} \& \\frac{2C\^2}{1+C\^2} \& \\frac{1-C\^2}{1+C\^2} \\end{bmatrix} \[S\]balun= 1+C21−3C2j1+C22C1−C2 −j1+C22C1−C2 j1+C22C1−C2 1+C21−C21+C22C2−j1+C22C1−C2 1+C22C21+C21−C2 记: **S11=1−3C21+C2,S12=S21=jD,S13=S31=−jD,S22=S33=E,S23=S32=FS_{11} = \\frac{1-3C\^2}{1+C\^2},\\quad S_{12}=S_{21}=jD,\\quad S_{13}=S_{31}=-jD,\\quad S_{22}=S_{33}=E,\\quad S_{23}=S_{32}=FS11=1+C21−3C2,S12=S21=jD,S13=S31=−jD,S22=S33=E,S23=S32=F 其中D=2C1−C21+C2D=\\frac{2C\\sqrt{1-C\^2}}{1+C\^2}D=1+C22C1−C2 ,E=1−C21+C2E=\\frac{1-C\^2}{1+C\^2}E=1+C21−C2,F=2C21+C2F=\\frac{2C\^2}{1+C\^2}F=1+C22C2,且满足E+F=1E+F=1E+F=1,S112+2D2=1S_{11}\^2+2D\^2=1S112+2D2=1。 阻抗变换参数: γ=Z1−ZoZ1+Zo,α=2Z1ZoZ1+Zo,n=Z1Zo\\gamma = \\frac{Z_1-Z_o}{Z_1+Z_o},\\quad \\alpha = \\frac{2\\sqrt{Z_1Z_o}}{Z_1+Z_o},\\quad n=\\frac{Z_1}{Z_o}γ=Z1+ZoZ1−Zo,α=Z1+Zo2Z1Zo ,n=ZoZ1 则γ=n−1n+1\\gamma=\\frac{n-1}{n+1}γ=n+1n−1,α=2nn+1\\alpha=\\frac{2\\sqrt{n}}{n+1}α=n+12n 。 对角矩阵: \[Γ\]=\[0000γ000γ\],\[A\]=\[1000α000α\],\[I\]=\[100010001\]\[\\Gamma\] = \\begin{bmatrix} 0 \& 0 \& 0 \\\\ 0 \& \\gamma \& 0 \\\\ 0 \& 0 \& \\gamma \\end{bmatrix},\\quad \[A\] = \\begin{bmatrix} 1 \& 0 \& 0 \\\\ 0 \& \\alpha \& 0 \\\\ 0 \& 0 \& \\alpha \\end{bmatrix},\\quad \[I\] = \\begin{bmatrix} 1 \& 0 \& 0 \\\\ 0 \& 1 \& 0 \\\\ 0 \& 0 \& 1 \\end{bmatrix}\[Γ\]= 0000γ000γ ,\[A\]= 1000α000α ,\[I\]= 100010001** ### 2.2 计算中间矩阵 #### (1) \[S\]balun−\[Γ\]\[S\]_{\\text{balun}} - \[\\Gamma\]\[S\]balun−\[Γ
S\]balun−\[Γ\]=\[S11S12S13S21S22−γS23S31S32S33−γ\] \[S\]_{\\text{balun}} - \[\\Gamma\] = \\begin{bmatrix} S_{11} \& S_{12} \& S_{13} \\\\ S_{21} \& S_{22}-\\gamma \& S_{23} \\\\ S_{31} \& S_{32} \& S_{33}-\\gamma \\end{bmatrix} \[S\]balun−\[Γ\]= S11S21S31S12S22−γS32S13S23S33−γ #### (2) \[Γ\]\[S\]balun\[\\Gamma\]\[S\]_{\\text{balun}}\[Γ\]\[S\]balun \[Γ\]\[S\]balun=\[000γS21γS22γS23γS31γS32γS33\] \[\\Gamma\]\[S\]_{\\text{balun}} = \\begin{bmatrix} 0 \& 0 \& 0 \\\\ \\gamma S_{21} \& \\gamma S_{22} \& \\gamma S_{23} \\\\ \\gamma S_{31} \& \\gamma S_{32} \& \\gamma S_{33} \\end{bmatrix} \[Γ\]\[S\]balun= 0γS21γS310γS22γS320γS23γS33 #### (3) \[I\]−\[Γ\]\[S\]balun\[I\] - \[\\Gamma\]\[S\]_{\\text{balun}}\[I\]−\[Γ\]\[S\]balun M=\[I\]−\[Γ\]\[S\]balun=\[100−γS211−γS22−γS23−γS31−γS321−γS33\] M = \[I\] - \[\\Gamma\]\[S\]_{\\text{balun}} = \\begin{bmatrix} 1 \& 0 \& 0 \\\\ -\\gamma S_{21} \& 1-\\gamma S_{22} \& -\\gamma S_{23} \\\\ -\\gamma S_{31} \& -\\gamma S_{32} \& 1-\\gamma S_{33} \\end{bmatrix} M=\[I\]−\[Γ\]\[S\]balun= 1−γS21−γS3101−γS22−γS320−γS231−γS33 利用对称性S31=−S21S_{31}=-S_{21}S31=−S21,S32=S23S_{32}=S_{23}S32=S23,S33=S22S_{33}=S_{22}S33=S22,令a=1−γS22a=1-\\gamma S_{22}a=1−γS22,b=−γS23b=-\\gamma S_{23}b=−γS23,则: M=\[100−γS21abγS21ba\] M = \\begin{bmatrix} 1 \& 0 \& 0 \\\\ -\\gamma S_{21} \& a \& b \\\\ \\gamma S_{21} \& b \& a \\end{bmatrix} M= 1−γS21γS210ab0ba ### 2.3 求M−1M\^{-1}M−1 利用分块矩阵求逆公式,得到: M−1=\[100kaa2−b2−ba2−b2−k−ba2−b2aa2−b2\] M\^{-1} = \\begin{bmatrix} 1 \& 0 \& 0 \\\\ k \& \\frac{a}{a\^2-b\^2} \& -\\frac{b}{a\^2-b\^2} \\\\ -k \& -\\frac{b}{a\^2-b\^2} \& \\frac{a}{a\^2-b\^2} \\end{bmatrix} M−1= 1k−k0a2−b2a−a2−b2b0−a2−b2ba2−b2a 其中k=γS21(a+b)a2−b2k = \\frac{\\gamma S_{21}(a+b)}{a\^2-b\^2}k=a2−b2γS21(a+b),且a+b=1−γa+b=1-\\gammaa+b=1−γ,a−b=1−γS11a-b=1-\\gamma S_{11}a−b=1−γS11,a2−b2=(1−γ)(1−γS11)a\^2-b\^2=(1-\\gamma)(1-\\gamma S_{11})a2−b2=(1−γ)(1−γS11)。 ### 2.4 计算P=(\[S\]balun−\[Γ\])M−1P = (\[S\]_{\\text{balun}} - \[\\Gamma\]) M\^{-1}P=(\[S\]balun−\[Γ\])M−1 通过矩阵乘法,并利用**上述蓝色恒等式**简化,得到: P11=S11−γ1−γS11,P12=S121−γS11=jD1−γS11,P13=−jD1−γS11,P21=jD(1−γ2)α(1−γS11),P22=E(1−γ)1−γS11,P23=F(1+γ)1−γS11,P31=−P21,P32=P23,P33=P22. \\begin{aligned} P_{11} \&= \\frac{S_{11}-\\gamma}{1-\\gamma S_{11}}, \\\\ P_{12} \&= \\frac{S_{12}}{1-\\gamma S_{11}} = \\frac{jD}{1-\\gamma S_{11}}, \\\\ P_{13} \&= -\\frac{jD}{1-\\gamma S_{11}}, \\\\ P_{21} \&= \\frac{jD(1-\\gamma\^2)}{\\alpha(1-\\gamma S_{11})}, \\\\ P_{22} \&= \\frac{E(1-\\gamma)}{1-\\gamma S_{11}}, \\\\ P_{23} \&= \\frac{F(1+\\gamma)}{1-\\gamma S_{11}}, \\\\ P_{31} \&= -P_{21}, \\\\ P_{32} \&= P_{23}, \\\\ P_{33} \&= P_{22}. \\end{aligned} P11P12P13P21P22P23P31P32P33=1−γS11S11−γ,=1−γS11S12=1−γS11jD,=−1−γS11jD,=α(1−γS11)jD(1−γ2),=1−γS11E(1−γ),=1−γS11F(1+γ),=−P21,=P23,=P22. ### 2.5 计算\[S\]balun′=\[A\]−1P\[A\]\[S\]_{\\text{balun}}' = \[A\]\^{-1} P \[A\]\[S\]balun′=\[A\]−1P\[A
左乘[A]−1=diag(1,1/α,1/α)[A]^{-1} = \operatorname{diag}(1,1/\alpha,1/\alpha)[A]−1=diag(1,1/α,1/α),右乘[A]=diag(1,α,α)[A] = \operatorname{diag}(1,\alpha,\alpha)[A]=diag(1,α,α),得到最终S参数:
S11′=P11=S11−γ1−γS11,S12′=αP12=αjD1−γS11,S13′=αP13=−αjD1−γS11,S21′=P21α=jD(1−γ2)α2(1−γS11)=αjD1−γS11(因 1−γ2=α2),S22′=P22=E(1−γ)1−γS11,S23′=P23=F(1+γ)1−γS11,S31′=P31α=−αjD1−γS11,S32′=P32=F(1+γ)1−γS11,S33′=P33=E(1−γ)1−γS11. \begin{aligned} S_{11}' &= P_{11} = \frac{S_{11}-\gamma}{1-\gamma S_{11}}, \\ S_{12}' &= \alpha P_{12} = \frac{\alpha jD}{1-\gamma S_{11}}, \\ S_{13}' &= \alpha P_{13} = -\frac{\alpha jD}{1-\gamma S_{11}}, \\ S_{21}' &= \frac{P_{21}}{\alpha} = \frac{jD(1-\gamma^2)}{\alpha^2(1-\gamma S_{11})} = \frac{\alpha jD}{1-\gamma S_{11}} \quad (\text{因 } 1-\gamma^2=\alpha^2), \\ S_{22}' &= P_{22} = \frac{E(1-\gamma)}{1-\gamma S_{11}}, \\ S_{23}' &= P_{23} = \frac{F(1+\gamma)}{1-\gamma S_{11}}, \\ S_{31}' &= \frac{P_{31}}{\alpha} = -\frac{\alpha jD}{1-\gamma S_{11}}, \\ S_{32}' &= P_{32} = \frac{F(1+\gamma)}{1-\gamma S_{11}}, \\ S_{33}' &= P_{33} = \frac{E(1-\gamma)}{1-\gamma S_{11}}. \end{aligned} S11′S12′S13′S21′S22′S23′S31′S32′S33′=P11=1−γS11S11−γ,=αP12=1−γS11αjD,=αP13=−1−γS11αjD,=αP21=α2(1−γS11)jD(1−γ2)=1−γS11αjD(因 1−γ2=α2),=P22=1−γS11E(1−γ),=P23=1−γS11F(1+γ),=αP31=−1−γS11αjD,=P32=1−γS11F(1+γ),=P33=1−γS11E(1−γ).
2.6 代入具体表达式
将S11S_{11}S11、DDD、EEE、FFF、γ\gammaγ、α\alphaα用CCC和n=Z1/Zon=Z_1/Z_on=Z1/Zo表示,并计算公共分母:
1−γS11=2[1+(2n−1)C2](n+1)(1+C2) 1-\gamma S_{11} = \frac{2[1+(2n-1)C^2]}{(n+1)(1+C^2)} 1−γS11=(n+1)(1+C2)2[1+(2n−1)C2]
代入化简后得到公式(5):
S\]balun′=\[1−C2(2n+1)1+C2(2n−1)j2C1−C2n1+C2(2n−1)−j2C1−C2n1+C2(2n−1)j2C1−C2n1+C2(2n−1)1−C21+C2(2n−1)2C2n1+C2(2n−1)−j2C1−C2n1+C2(2n−1)2C2n1+C2(2n−1)1−C21+C2(2n−1)\] \[S\]_{\\text{balun}}' = \\begin{bmatrix} \\frac{1-C\^2(2n+1)}{1+C\^2(2n-1)} \& j\\frac{2C\\sqrt{1-C\^2}\\sqrt{n}}{1+C\^2(2n-1)} \& -j\\frac{2C\\sqrt{1-C\^2}\\sqrt{n}}{1+C\^2(2n-1)} \\\\ j\\frac{2C\\sqrt{1-C\^2}\\sqrt{n}}{1+C\^2(2n-1)} \& \\frac{1-C\^2}{1+C\^2(2n-1)} \& \\frac{2C\^2 n}{1+C\^2(2n-1)} \\\\ -j\\frac{2C\\sqrt{1-C\^2}\\sqrt{n}}{1+C\^2(2n-1)} \& \\frac{2C\^2 n}{1+C\^2(2n-1)} \& \\frac{1-C\^2}{1+C\^2(2n-1)} \\end{bmatrix} \[S\]balun′= 1+C2(2n−1)1−C2(2n+1)j1+C2(2n−1)2C1−C2 n −j1+C2(2n−1)2C1−C2 n j1+C2(2n−1)2C1−C2 n 1+C2(2n−1)1−C21+C2(2n−1)2C2n−j1+C2(2n−1)2C1−C2 n 1+C2(2n−1)2C2n1+C2(2n−1)1−C2 **带入n即可得到论文公式(5),但其中S23′S_{23}'S23′和S32′S_{32}'S32′含有虚数单位jjj,带入Z1=Z0Z_1=Z_0Z1=Z0条件后无法化简到2式。跟我们推导的不一样,不过(8)式结果相同** 原文中公式如下。 \[S\]balun′=\[1−C2(2Z1Zo+1)1+C2(2Z1Zo−1)j2C1−C2Z1Zo1+C2(2Z1Zo−1)−j2C1−C2Z1Zo1+C2(2Z1Zo−1)j2C1−C2Z1Zo1+C2(2Z1Zo−1)1−C21+C2(2Z1Zo−1)j2C2(Z1Zo)1+C2(2Z1Zo−1)−j2C1−C2Z1Zo1+C2(2Z1Zo−1)j2C(Z1Zo)1+C2(2Z1Zo−1)1−C21+C2(2Z1Zo−1)\](5) \[S\]_{\\text{balun}}\^{\\prime}=\\begin{bmatrix}\\frac{1-C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}+1\\right)}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&-j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\\\\\\\\ j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&\\frac{1-C\^{2}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&j\\frac{2C\^{2}\\left(\\sqrt{\\frac{Z_{1}}{Z_{o}}}\\right)}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\\\\\\\\-j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&j\\frac{2C\\left(\\frac{Z_{1}}{Z_{o}}\\right)}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&\\frac{1-C\^{2}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\\end{bmatrix} \\qquad(5) \[S\]balun′= 1+C2(Zo2Z1−1)1−C2(Zo2Z1+1)j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 −j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 1+C2(Zo2Z1−1)1−C2j1+C2(Zo2Z1−1)2C(ZoZ1)−j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 j1+C2(Zo2Z1−1)2C2(ZoZ1 )1+C2(Zo2Z1−1)1−C2 (5) \[S\]balun′=\[1−C2(2Z1Zo+1)1+C2(2Z1Zo−1)j2C1−C2Z1Zo1+C2(2Z1Zo−1)−j2C1−C2Z1Zo1+C2(2Z1Zo−1)j2C1−C2Z1Zo1+C2(2Z1Zo−1)1−C21+C2(2Z1Zo−1)2C2(Z1Zo)1+C2(2Z1Zo−1)−j2C1−C2Z1Zo1+C2(2Z1Zo−1)2C2(Z1Zo)1+C2(2Z1Zo−1)1−C21+C2(2Z1Zo−1)\](5修改后) \[S\]_{\\text{balun}}\^{\\prime}=\\begin{bmatrix}\\frac{1-C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}+1\\right)}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&-j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\\\\\\\\ j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&\\frac{1-C\^{2}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&\\frac{2C\^2\\left(\\frac{Z_{1}}{Z_{o}}\\right)}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\\\\\\\\-j\\frac{2C\\sqrt{1-C\^{2}}\\sqrt{\\frac{Z_{1}}{Z_{o}}}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&\\frac{2C\^2\\left(\\frac{Z_{1}}{Z_{o}}\\right)}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\&\\frac{1-C\^{2}}{1+C\^{2}\\left(\\frac{2Z_{1}}{Z_{o}}-1\\right)}\\end{bmatrix} \\qquad(5修改后) \[S\]balun′= 1+C2(Zo2Z1−1)1−C2(Zo2Z1+1)j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 −j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 1+C2(Zo2Z1−1)1−C21+C2(Zo2Z1−1)2C2(ZoZ1)−j1+C2(Zo2Z1−1)2C1−C2 ZoZ1 1+C2(Zo2Z1−1)2C2(ZoZ1)1+C2(Zo2Z1−1)1−C2 (5修改后) (5)式表明,**无论耦合系数和端口阻抗如何,使用相同的耦合段会导致巴伦输出具有相等的幅度和相反的相位。为了实现到每个端口的最佳功率传输**-3 dB,我们要求: ∣Sb,21′∣=∣Sb,31′∣=12.(6) \|S_{b,21}\^{\\prime}\|=\|S_{b,31}\^{\\prime}\|=\\frac{1}{\\sqrt{2}}.\\quad{(6)} ∣Sb,21′∣=∣Sb,31′∣=2 1.(6) **根据(5)式和(6)式,获得最佳巴伦性能所需的耦合系数为:** C=12Z1Zo+1.(7) C=\\frac{1}{\\sqrt{\\frac{2Z_{1}}{Z_{o}}+1}}.\\quad{(7)} C=Zo2Z1+1 1.(7) 有趣的是,当所有端口都端接相同阻抗(例如50Ω),即阻抗变换比为1时,所需的耦合系数是-4.8 dB,而不是-3 dB。根据(5)式,使用通常假设的-3 dB耦合器\[6\]将导致中心频率处的插入损耗和输出隔离为-3.5 dB,输入和输出回波损耗为-9.5 dB。当满足(7)式时,(5)式给出的巴伦S矩阵简化为: \[S\]balun=\[0j2−j2j21212−j21212\].(8) \[S\]_{\\text{balun}}=\\begin{bmatrix}0\&\\frac{j}{\\sqrt{2}}\&-\\frac{j}{\\sqrt{2}}\\\\\\frac{j}{\\sqrt{2}}\&\\frac{1}{2}\&\\frac{1}{2}\\\\-\\frac{j}{\\sqrt{2}}\&\\frac{1}{2}\&\\frac{1}{2}\\end{bmatrix}.\\quad{(8)} \[S\]balun= 02 j−2 j2 j2121−2 j2121 .(8) 这是一个无耗巴伦可达到的最佳S矩阵。它在输入端匹配,传输系数为-3 dB且相位相反。