📈 OFDM-IM 容量增强仿真平台
GIM + MM + IQ 三大容量扩展技术,突破传统索引调制比特率极限




📌 为什么选择本仿真平台?
| 痛点 | 本平台解决方案 |
|---|---|
| 📚 固定激活数限制索引空间 | ✅ GIM 广义索引:可变激活数,索引空间扩大 2-4 倍 |
| 🔧 调制阶数浪费额外比特 | ✅ MM 多模调制:每个激活子载波携带模式选择比特 |
| 📊 I/Q 资源耦合利用 | ✅ IQ 独立索引:实部虚部分别索引,并行双倍效率 |
| ⚡ 容量提升难以量化 | ✅ 内置 容量分析对比工具,直观展示各技术增益 |
| 📡 检测算法对应难 | ✅ 每种技术配套 专用解调器,算法一一对应 |
🎯 核心价值
|---|
| |
🔬 学术研究价值
- 三大容量扩展技术完整实现
- 索引空间理论上界研究
- 频谱效率 vs 复杂度权衡分析
- 不同场景最优技术选择
💼 工程应用价值
- 高频谱效率需求场景首选
- 灵活的参数配置空间
- 结构化的技术对比框架
- 完整的收发链路验证
⚡ 技术亮点
🌊 三大容量增强技术对比
text
┌─────────────────────────────────────────────────────────────────┐
│ 容量增强技术对比 │
├──────────────┬──────────────┬──────────────┬──────────────────┤
│ 基础 IM │ GIM │ MM │ IQ │
├──────────────┼──────────────┼──────────────┼──────────────────┤
│ 固定 k 个 │ k ∈ [k1,k2] │ 每个子载波 │ I/Q 独立索引 │
│ 激活子载波 │ 可变激活数 │ 独立选模式 │ 并行处理 │
├──────────────┼──────────────┼──────────────┼──────────────────┤
│ C(n,k) │ Σ C(n,ki) │ k × Nm 模式 │ 2 × C(n,k) │
│ 索引数 │ 索引空间大 │ 比特倍增 │ 双倍索引 │
└──────────────┴──────────────┴──────────────┴──────────────────┘📊 容量对比 (n=4, k=2, M=4)
| 技术 | 索引比特 p1 | 数据比特 p2 | 总比特/子块 | vs 基础 IM |
|---|---|---|---|---|
| 基础 IM | 2 | 4 | 6 | 基准 |
| GIM (k∈[1,4]) | 4 | ~5 | 9 | +50% |
| MM (4模式) | 2 | 8 | 10 | +67% |
| IQ | 4 | 4 | 8 | +33% |
💡 MM 最强容量:通过模式选择比特,每个激活子载波额外携带 log₂(Nm) 比特。
🖥️ 运行环境
最低要求
| 项目 | 要求 |
|---|---|
| MATLAB版本 | R2021b 或更高 |
| 必需工具箱 | Communications Toolbox |
| 基础依赖 | P1 基础包 |
| 内存 | 4 GB+ |
快速验证
matlab
>> cd packages/P3_容量增强包
>> setup_path
>> generate_plots_enhanced🧠 算法原理
GIM 广义索引调制
核心思想:允许激活子载波数量可变,融合多种 C(n,k) 组合。
索引空间:
∣SGIM∣=∑k=kminkmaxC(n,k) |\mathcal{S}{GIM}| = \sum{k=k_{min}}^{k_{max}} C(n,k) ∣SGIM∣=k=kmin∑kmaxC(n,k)
索引比特:
p1,GIM=⌊log2∣SGIM∣⌋ p_{1,GIM} = \lfloor \log_2 |\mathcal{S}_{GIM}| \rfloor p1,GIM=⌊log2∣SGIM∣⌋
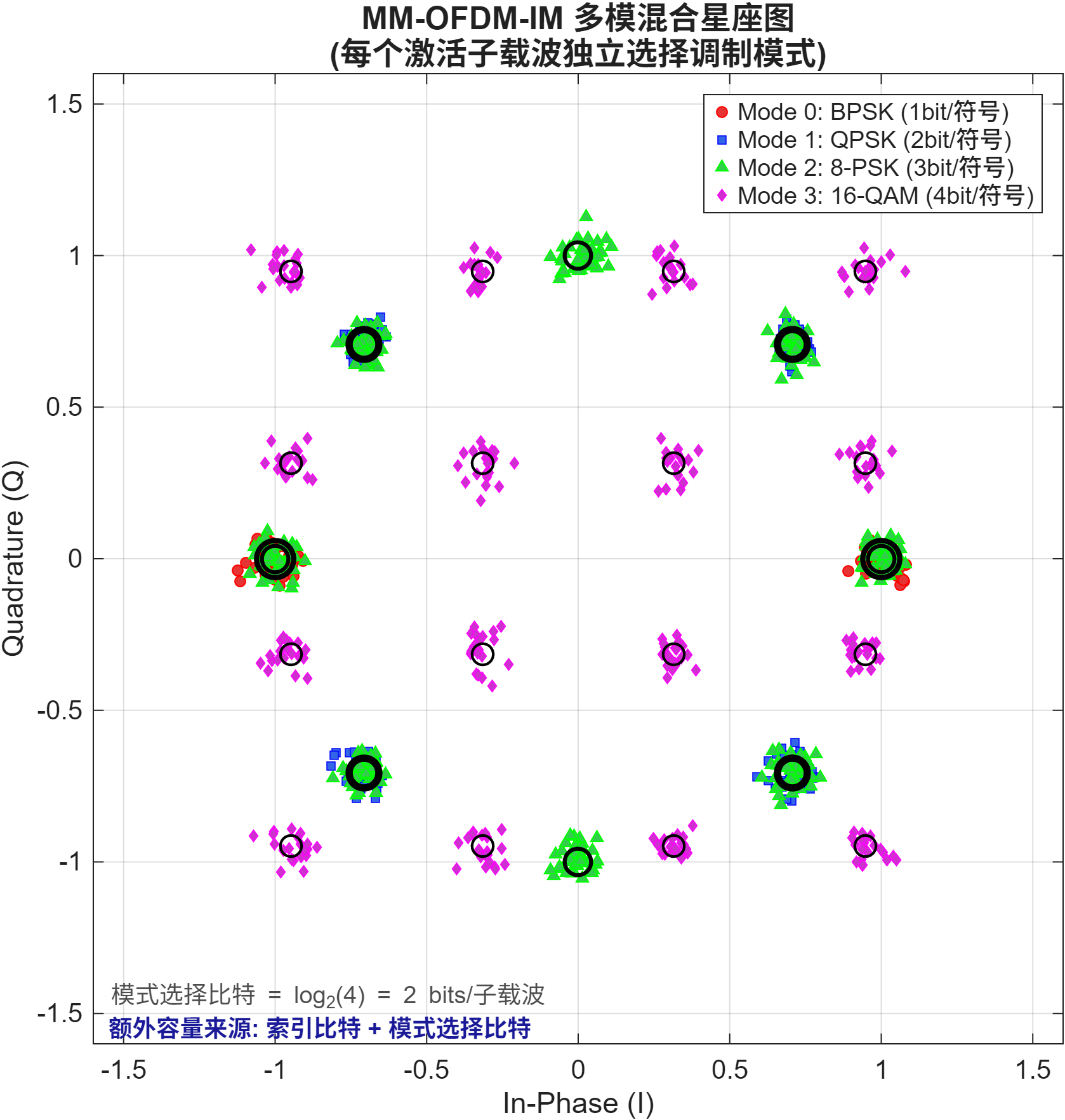
MM 多模索引调制
核心思想:每个激活子载波独立选择调制模式。
总比特数:
pMM=p1+k⋅(log2Nm+mˉ) p_{MM} = p_1 + k \cdot (\log_2 N_m + \bar{m}) pMM=p1+k⋅(log2Nm+mˉ)
其中 mˉ\bar{m}mˉ 为各模式的平均数据比特。
IQ 独立索引调制
核心思想:I 和 Q 分量使用独立的激活模式。
索引比特:
p1,IQ=2×⌊log2C(n,k)⌋ p_{1,IQ} = 2 \times \lfloor \log_2 C(n,k) \rfloor p1,IQ=2×⌊log2C(n,k)⌋
📁 项目结构
text
P3_容量增强包/
├── 📂 gim/ # GIM 广义索引
│ ├── gim_modulator.m # 🚀 GIM 调制器
│ ├── gim_demodulator.m # GIM 解调器
│ └── gim_table.m # 可变激活索引表
│
├── 📂 mm/ # MM 多模调制
│ ├── mm_modulator.m # 🚀 MM 调制器
│ └── mm_demodulator.m # MM 解调器
│
├── 📂 iq/ # IQ 独立索引
│ ├── iq_modulator.m # 🚀 IQ 调制器
│ └── iq_demodulator.m # IQ 解调器
│
├── 📂 core/ # 继承 P1 核心模块
├── 📂 config/ # 配置 (扩展 GIM/MM/IQ 参数)
│
├── 📂 docs/ # 文档
│ ├── 算法文档.md # 📘 三技术原理推导
│ ├── 代码文档.md # 📒 接口说明
│ └── 项目文档.md # 📗 本文档
│
├── generate_plots.m # 📊 容量对比曲线
└── generate_plots_enhanced.m # 📊 MM 多模星座图代码统计:
- 📄 25+ 个核心 MATLAB 文件
- 📝 2500+ 行精炼代码
- 💬 100% 中文详细注释
🎬 仿真演示
一键运行
matlab
>> cd packages/P3_容量增强包
>> setup_path
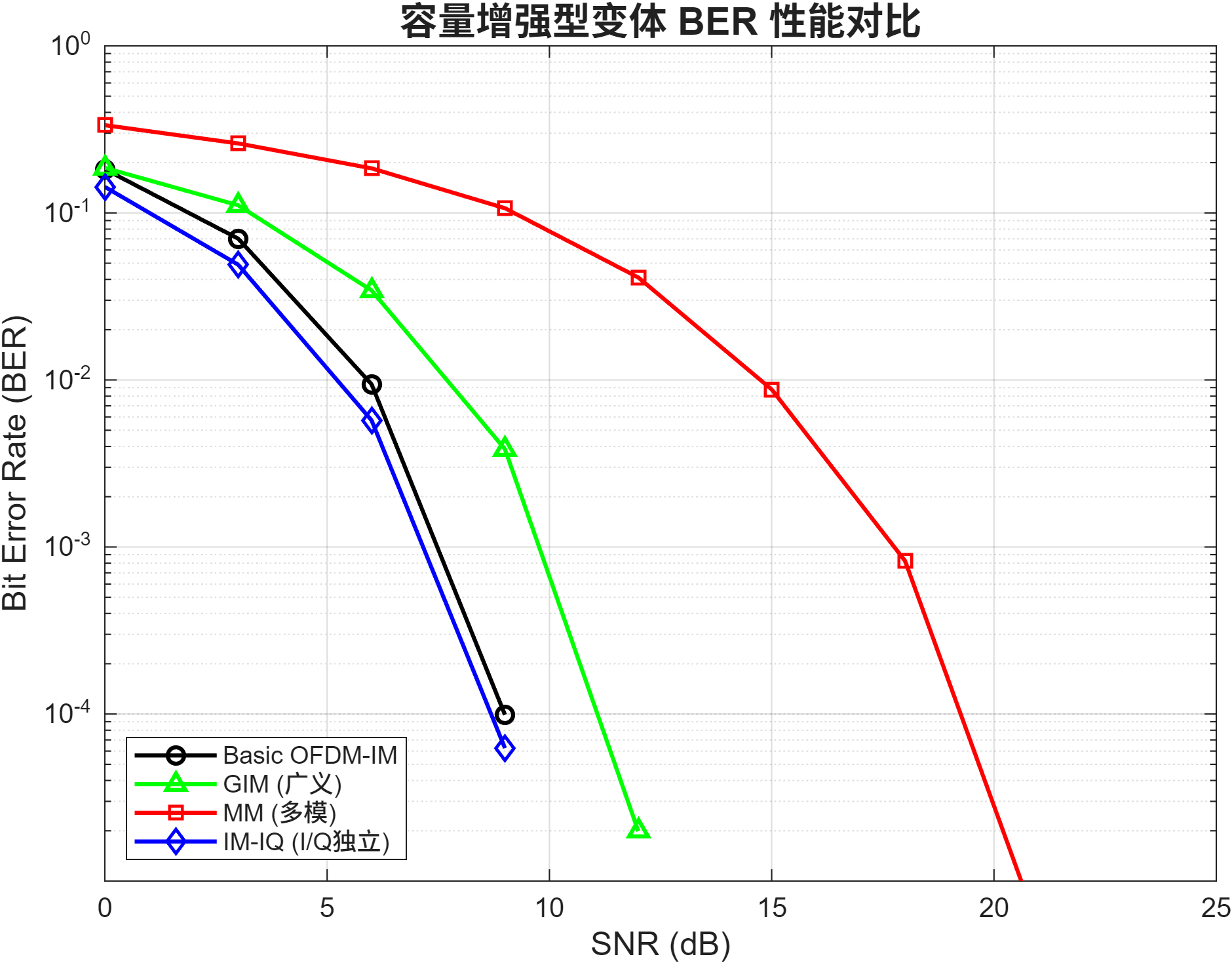
>> generate_ber_plots % 三技术 BER 对比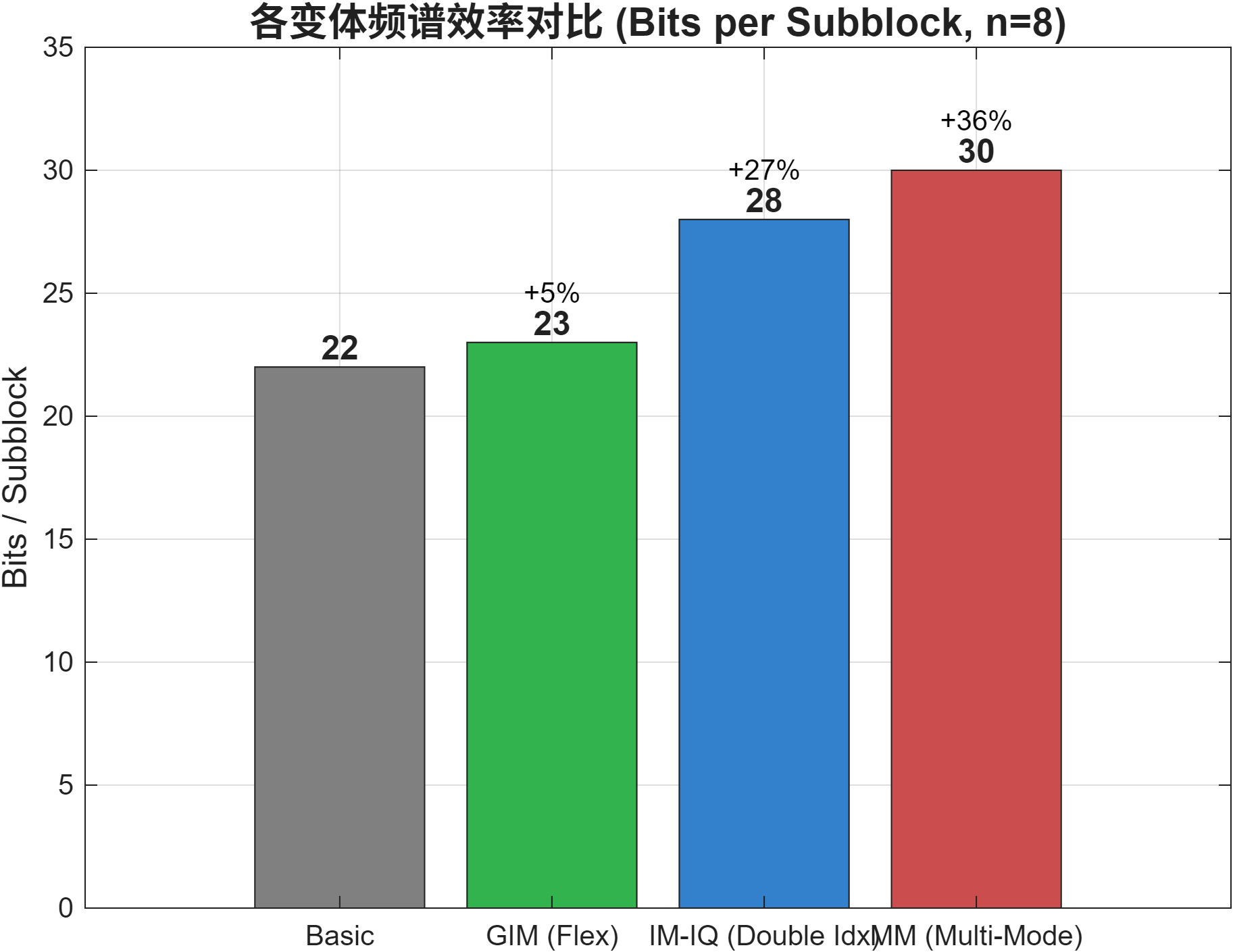
📦 您将获得
| 内容 | 说明 |
|---|---|
| 📁 完整源码 | GIM + MM + IQ 三技术完整实现 |
| 📖 原理文档 | 索引空间扩展数学推导 |
| 🚀 容量提升 | 最高 67% 频谱效率增益 |
| 📊 对比工具 | 一键生成三技术性能对比 |
| 🔧 灵活配置 | 可变 k 范围、模式数、调制阶数 |
| 📡 可视化 | 多模星座图、容量对比曲线 |
🛒 获取方式
本文代码仅为核心片段,完整版工程已整理好。 关注公众号 【3GPP仿真实验室】进行获取。
📚 参考文献
- M. Wen et al. (2017): "Generalized Index Modulation Aided OFDM." IEEE Trans. Wireless Commun., vol. 16, no. 3.
- B. Zheng et al. (2019): "Multiple-Mode OFDM with Index Modulation." IEEE Trans. Signal Process., vol. 67, no. 9.
- E. Başar et al. (2017): "OFDM with Index Modulation Using In-Phase and Quadrature Indices." IEEE Trans. Veh. Technol., vol. 66, no. 5.