基础算法：高精度

喜欢吃燃面2026-02-13 13:20

目录

哈喽，编程搭子们！😜 又到了沉浸式敲代码的快乐时间～把生活调成「代码模式」，带着满满的热爱钻进编程的奇妙世界------今天也要敲出超酷的代码，冲鸭！🚀

✨ 我的博客主页：喜欢吃燃面
📚 我的专栏（持续更新ing）：
《C语言》 |
《C语言之数据结构》 |
《C++》 |
《Linux学习笔记》

💖 超感谢你点开这篇博客！真心希望这些内容能帮到正在打怪升级的你～如果有任何想法、疑问，或者想交流学习心得，都欢迎留言/私信，咱们一起在编程路上互相陪伴、共同进步呀！

一.概念

当数据的值特别大，各种类型都存不下的时候，此时就要用高精度算法来计算加减乘除：

  • 先用字符串读入这个数，然后用数组逆序存储该数的每一位；
  • 利用数组，模拟加减乘除运算的过程。

高精度算法本质上还是模拟算法，用代码模拟小学列竖式计算加减乘除的过程。

二.高精度加法

1.题目

高精度加法

2.解题思路（模拟竖式计算）

2.1 核心思想

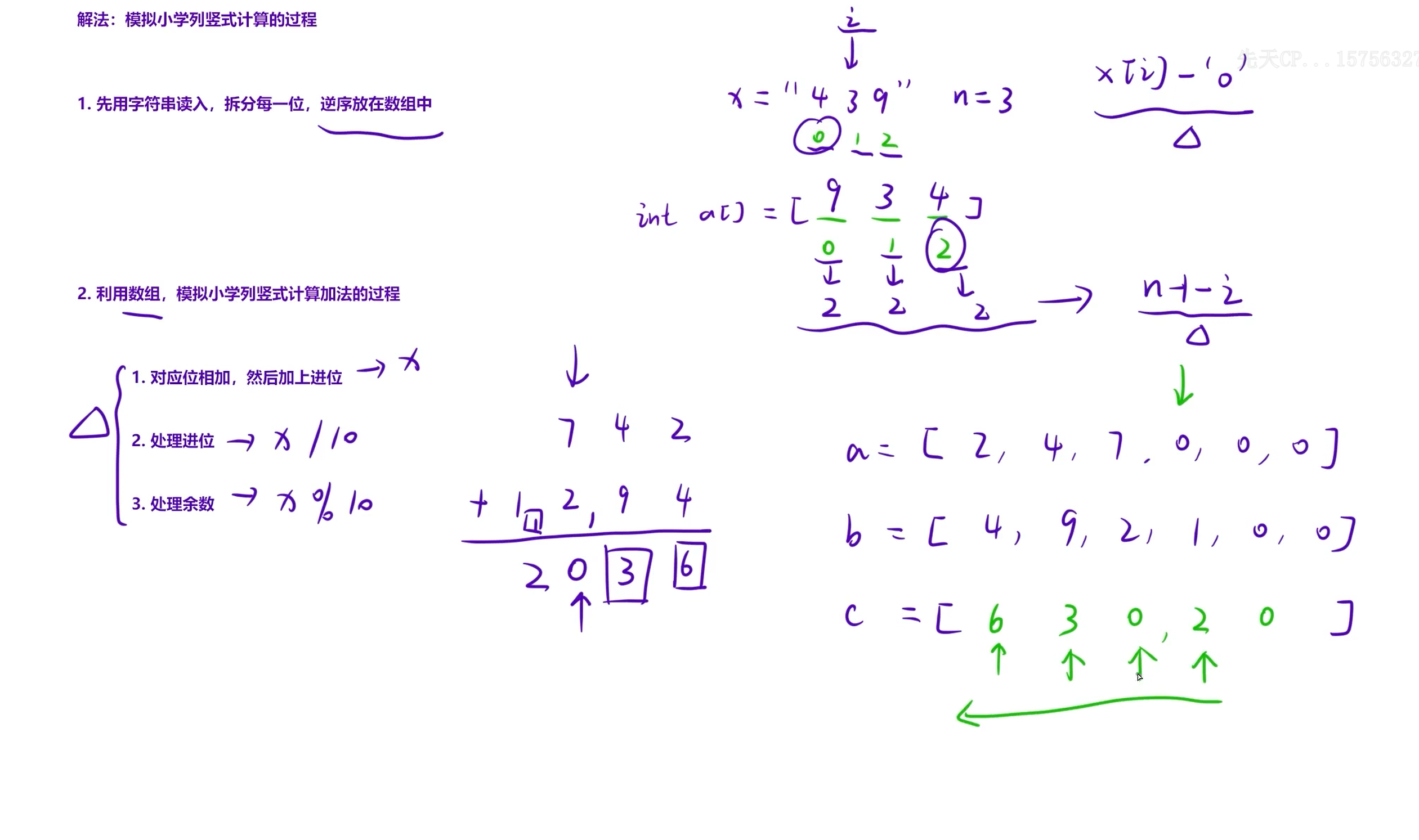
用数组模拟小学竖式加法的过程，解决C++中普通整型无法存储的超大整数运算问题。

2. 2 步骤拆解

① 输入与格式转换

  • 用字符串 s1、s2 读入两个超大整数。
  • 将字符串逐位逆序存入数组 a1、a2，低位在前 （个位在数组下标1，十位在下标2，以此类推），方便从低位到高位逐位计算。
    • 例如：字符串 "439" → 数组 a1 = [0, 9, 3, 4, ...]（下标0未使用，下标1存个位9，下标2存十位3，下标3存百位4）。

② 逐位相加与进位处理

  • 初始化进位为0，从下标1开始遍历两个数组：
    1. 对应位相加：ret[i] = a1[i] + a2[i] + 上一位的进位。
    2. 计算新的进位：ret[i+1] = ret[i] / 10。
    3. 保留当前位结果：ret[i] = ret[i] % 10。
  • 遍历结束后，若最高位仍有进位（ret[i] != 0），则结果长度为 i，否则为 i-1。

③ 结果输出

  • 数组 ret 中存储的结果是低位在前的，因此需要从后往前（从高位到低位）倒序输出，得到最终的和。

2.3 代码对应逻辑

代码部分 对应思路
a1[n1 - i] = s1[i] - '0' 将字符串逆序存入数组，实现低位在前
ret[i] += a1[i] + a2[i] 对应位相加并加上进位
ret[i + 1] = ret[i] / 10 计算并传递进位到下一位
ret[i] %= 10 保留当前位的个位作为结果
for (int k = cnt; k >= 1; k--) 倒序输出数组，得到正确的数字顺序

2.4 关键细节

  • 数组初始化 ：全局数组 a1、a2、ret 会被自动初始化为0，因此超出输入长度的位会自动补0，无需额外处理。
  • 边界处理 ：循环条件 i <= n1 || i <= n2 确保两个数的所有位都被处理，即使位数不同也能正确对齐。
  • 最终进位 ：如果最高位相加后仍有进位，需要将其作为新的最高位，因此结果长度 cnt 需要根据 ret[i] 是否为0来判断。

3.参考代码

cpp 复制代码 
#include<iostream>
#include<string>
using namespace std;

const int N = 1e5 + 10;  // 适配超长数字的数组最大长度
int a1[N], a2[N], ret[N];// a1/a2:存储两个数的各位(低位在前)，ret:存储加法结果
int cnt, n1, n2;         // cnt:加法结果有效长度，n1/n2:两个数的位数
string s1, s2;           // 存储输入的超大数字字符串

// 高精度加法核心：低位对齐逐位相加，处理进位
void addBigInt() {
    int i = 1;
    // 逐位相加（超出长度的位因全局数组初始为0，自动补0）
    while (i <= n1 || i <= n2) {
        ret[i] += a1[i] + a2[i];  // 累加当前位数值 + 上一位进位
        ret[i + 1] = ret[i] / 10; // 计算当前位的进位（传递到下一位）
        ret[i] %= 10;             // 保留当前位的最终结果（取余）
        i++;
    }
    // 处理最终进位：有进位则结果长度+1，否则取当前最大位
    cnt = ret[i] ? i : i - 1;
}

// 测试函数：输入处理、格式转换、执行加法、输出结果
void test(void (*func)()) {
    cin >> s1 >> s2;
    n1 = s1.size(), n2 = s2.size();

    // 字符串转数组（低位在前，适配逐位计算）
    for (int i = 0; i < n1; i++) a1[n1 - i] = s1[i] - '0';
    for (int i = 0; i < n2; i++) a2[n2 - i] = s2[i] - '0';
   
    func(); // 执行高精度加法

    // 倒序输出结果（ret低位在前，需从高位到低位打印）
    for (int k = cnt; k >= 1; k--) cout << ret[k];
    cout << endl;
}

int main() {
    test(addBigInt); // 调用测试函数执行高精度加法
    return 0;
}

三.高精度减法

1.题目

高精度减法

2.解题思路（模拟竖式借位)

2.1 核心思想

用数组模拟小学竖式减法的过程，解决超大整数（超出 long long 范围）的减法问题。关键是先判断大小，保证用大数减小数，再处理借位和前导零。

2.2 步骤拆解

① 输入与大小判断

  • 用字符串 s1、s2 读入两个超大整数。
  • 先判断 s1 和 s2 的大小：
    • 若长度不同，短的数更小；
    • 若长度相同，按字典序比较，字典序小的数更小。
  • 如果 s1 < s2，交换两者并输出负号，保证后续用大数减小数，避免处理负数借位。

② 字符串转数组（低位在前）

  • 将字符串逆序存入数组 a1、a2，个位在数组下标1，十位在下标2，以此类推 ，方便从低位到高位逐位借位计算。
    • 例如：字符串 "439" → 数组 a1 = [0, 9, 3, 4, ...]（下标0未使用）。

③ 逐位相减与借位处理

  • 从下标1开始遍历两个数组：
    1. 如果 a1[i] < a2[i]，说明当前位不够减，需要向高位借位：
      • a1[i] += 10（本位补10）
      • a1[i+1] -= 1（高位减1，完成借位）
    2. 计算当前位结果：ret[i] = a1[i] - a2[i]。
  • 遍历结束后，从后往前跳过结果数组 ret 中的前导零，确定有效长度 cnt。

④ 结果输出

  • 数组 ret 中存储的结果是低位在前的，因此需要从后往前（从高位到低位）倒序输出，得到最终的差。
  • 如果之前交换过 s1 和 s2，输出时前面要加上负号。

2.3 代码对应逻辑

代码部分 对应思路
cmp 函数 比较两个大数字符串的大小，决定是否需要交换和输出负号
a1[n1 - i] = s1[i] - '0' 将字符串逆序存入数组，实现低位在前
a1[i] < a2[i] 时借位 模拟竖式减法中"本位不够减，向高位借1当10"的操作
while (i > 1 && ret[i] == 0) i-- 跳过结果数组中的前导零，确定有效输出长度
for (int k = cnt; k >= 1; k--) 倒序输出数组，得到正确的数字顺序

2.4 关键细节

  • 大小判断：必须先保证用大数减小数，否则借位逻辑会出错，无法得到正确结果。
  • 借位传递：借位操作会影响高位，需要在逐位计算时实时更新数组值。
  • 前导零处理 ：结果数组中可能存在高位零，输出前必须跳过，避免输出如 00123 这样的无效格式。
  • 边界情况 ：当两数相等时，直接输出 0，无需进入减法逻辑。

3.参考代码

cpp 复制代码 
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;

const int N = 1e5 + 10;  // 数组最大长度，适配超长数字
int a1[N], a2[N], ret[N];// a1/a2存两个数的各位(低位在前)，ret存减法结果
int cnt, n1, n2;         // cnt:结果有效长度 n1/n2:两个数的位数
string s1, s2;           // 存储输入的超大数字字符串

// 数组初始化函数：清空指定数组的指定长度区间（预留声明）


// 比较函数：s1 < s2 返回true，否则false
bool cmp(const string& s1, const string& s2)
{
    if (s1.size() != s2.size()) return s1.size() < s2.size(); // 长度不同，短的更小
    return s1 < s2; // 长度相同，字典序小的更小
}

// 高精度减法核心：a1 - a2 (保证a1 >= a2)，结果存入ret
void subBigInt()
{
    int i = 1;
    // 逐位相减，覆盖两个数的所有有效位
    while (i <= n1 || i <= n2)
    {
        if (a1[i] < a2[i]) // 当前位数值不足，需向高位借位
        {
            a1[i] += 10;    // 本位补10
            a1[i + 1]--;    // 高位减1，完成借位操作
        }
        ret[i] = a1[i] - a2[i]; // 计算当前位减法结果
        i++;
    }
    // 跳过结果前导零，确定有效长度
    while (i > 1 && ret[i] == 0) i--;
    cnt = i; // 最终结果的有效位数
}

// 测试函数：处理输入、格式转换、调用减法、输出结果
void test(void (*func)()) {
    cin >> s1 >> s2; // 输入两个超大数字字符串

    if (s1 == s2) { // 两数相等，减法结果直接为0
        cout << 0;
        return;
    }

    // 保证a1存大数、a2存小数：若s1 < s2则交换，输出负号
    if (cmp(s1, s2)) { 
        swap(s1, s2);   // 交换后s1为大数，s2为小数
        cout<<"-";
    }
    n1 = s1.size(), n2 = s2.size(); // 更新交换后的数字位数

    // 字符串转数组（低位在前）：字符串高位对应数组高位，低位对应数组低位
    for (int i = 0; i < n1; i++) a1[n1 - i] = s1[i] - '0';
    for (int i = 0; i < n2; i++) a2[n2 - i] = s2[i] - '0';
    
    func(); // 执行高精度减法核心逻辑

    // 倒序输出结果（ret低位在前，需从高位到低位打印）
    for (int k = cnt; k >= 1; k--) cout << ret[k];
}

int main() {
    test(subBigInt); // 调用测试函数执行高精度减法
    return 0;
}

四.高精度乘法

1.题目

高精度乘法

2.解题思路（模拟竖式逐位相乘）

2.1 核心思想

核心思想

用数组模拟小学竖式乘法的过程，解决超大整数（超出 long long 范围）的乘法问题。核心是逐位相乘、累加进位、去除前导零。

2. 2 步骤拆解

① 特殊情况处理

  • 如果输入的两个数中有一个是 "0"，直接输出 0，无需进入后续计算。

② 字符串转数组（低位在前）

  • 将字符串逆序存入数组 a1、a2，个位在数组下标1，十位在下标2，以此类推 ，方便从低位到高位逐位计算。
    • 例如：字符串 "123" → 数组 a1 = [0, 3, 2, 1, ...]（下标0未使用）。

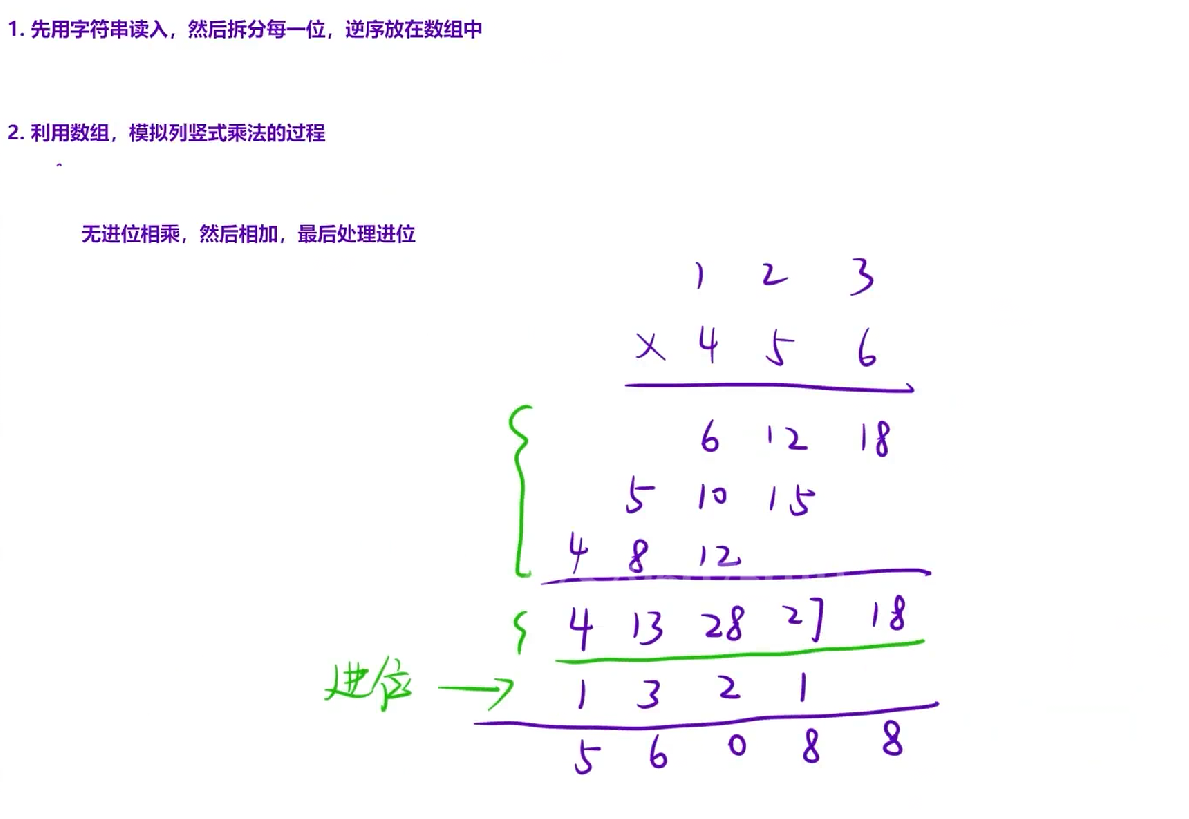
③ 逐位相乘与累加

  • 遍历第一个数的每一位 a1[j]，再遍历第二个数的每一位 a2[k]：
    • 第 j 位和第 k 位相乘的结果，会累加到结果数组的第 j + k - 1 位（即 ret[i]，其中 i 从 j 开始递增）。
    • 这一步只做无进位的累加，不处理进位。

④ 统一处理进位

  • 遍历结果数组 ret，从低位到高位：
    • 如果 ret[i] >= 10，则将 ret[i] / 10 进位到下一位 ret[i+1]，并将 ret[i] %= 10 保留个位。
    • 这一步确保每一位的数值都在 0-9 之间。

⑤ 去除前导零并输出

  • 从结果数组的最大可能长度（n1 + n2）向前遍历，找到第一个非零位，确定有效长度 cnt。
  • 倒序输出结果数组（从高位到低位），得到最终的乘积。

2.3 代码对应逻辑

代码部分 对应思路
`s1 == "0"
a1[n1 - i] = s1[i] - '0' 将字符串逆序存入数组，实现低位在前
ret[i] += a1[j] * a2[k] 逐位相乘并累加到结果数组的对应位置
ret[i + 1] += ret[i] / 10 处理进位，将高位值传递到下一位
while (i > 1 && !ret[i]) i-- 跳过结果数组中的前导零，确定有效输出长度
for (int k = cnt; k >= 1; k--) 倒序输出数组，得到正确的数字顺序

2.4 关键细节

  • 数组初始化：在计算前清空数组，避免随机值干扰结果。
  • 结果长度 ：两个长度为 n1 和 n2 的数相乘，结果最大长度为 n1 + n2。
  • 前导零处理 ：结果数组中可能存在高位零，输出前必须跳过，避免输出如 00123 这样的无效格式。
  • 逐位累加：先完成所有位的相乘累加，再统一处理进位，比边乘边进位更清晰高效。

3.参考代码

cpp 复制代码 
#include<iostream>
#include<string>
using namespace std;

const int N = 1e5 + 10;  // 数组最大长度，适配超长数字存储
int a1[N], a2[N], ret[N];// a1/a2:存储两个数的各位(低位在前)，ret:存储乘法结果
int cnt, n1, n2;         // cnt:结果有效长度，n1/n2:两个数的位数
string s1, s2;           // 存储输入的两个超长数字字符串

// 高精度乘法核心函数：实现大数乘法与进位处理
void mulBigInt()
{
    // 1. 逐位相乘，累加到结果对应位置
    int i = 1;
    for (int j = 1; j <= n1; j++)  // 遍历第一个数的每一位
    {
        i = j;  // 结果起始位置：第j位乘第k位，结果落在j+k-1位（等价i从j开始递增）
        for (int k = 1; k <= n2; k++)  // 遍历第二个数的每一位
        {
            ret[i] += a1[j] * a2[k];  //累加无进位的乘积到对应位置
            i++;
        }
    }
   
    // 2. 处理每一位的进位（两数相乘最大位数为n1+n2）
    for (i = 1; i <= n1 + n2; i++)
    {
        if (ret[i] >= 10)  // 当前位值≥10，需要进位
        {
            ret[i + 1] += ret[i] / 10;  // 进位值加到下一位
            ret[i] %= 10;               // 保留当前位的个位
        }
    }
    
    // 3. 确定结果的有效长度（跳过末尾的0）
    while (i > 1 && !ret[i]) i--;  // 从最大位数往前找第一个非0位
    cnt = i;  // 最终有效长度
}

// 测试函数：处理输入、格式转换、调用乘法、输出结果
// func: 指向高精度乘法核心函数的指针
void test(void (*func)()) {
    cin >> s1 >> s2;
    // 特殊情况：任一数为0，结果直接为0
    if (s1 == "0" || s2 == "0")
    {
        cout << 0;
        return;
    }
    
    // 初始化数组（避免随机值干扰）
    for (int i = 0; i < N; i++) a1[i] = a2[i] = ret[i] = 0;
    
    // 获取两个数的位数
    n1 = s1.size(), n2 = s2.size();
    
    // 字符串转数组（低位在前，下标从1开始）
    for (int i = 0; i < n1; i++) a1[n1 - i] = s1[i] - '0';
    for (int i = 0; i < n2; i++) a2[n2 - i] = s2[i] - '0';

    func();  // 执行高精度乘法

    // 倒序输出结果（ret低位在前，需从高位到低位打印）
    for (int k = cnt; k >= 1; k--) cout << ret[k];
    cout << endl;
}

int main()
{
    test(mulBigInt);  // 调用测试函数执行乘法
    return 0;
}

五.高精度除法

1.题目

高精度除法

2.解题思路（模拟竖式试商）

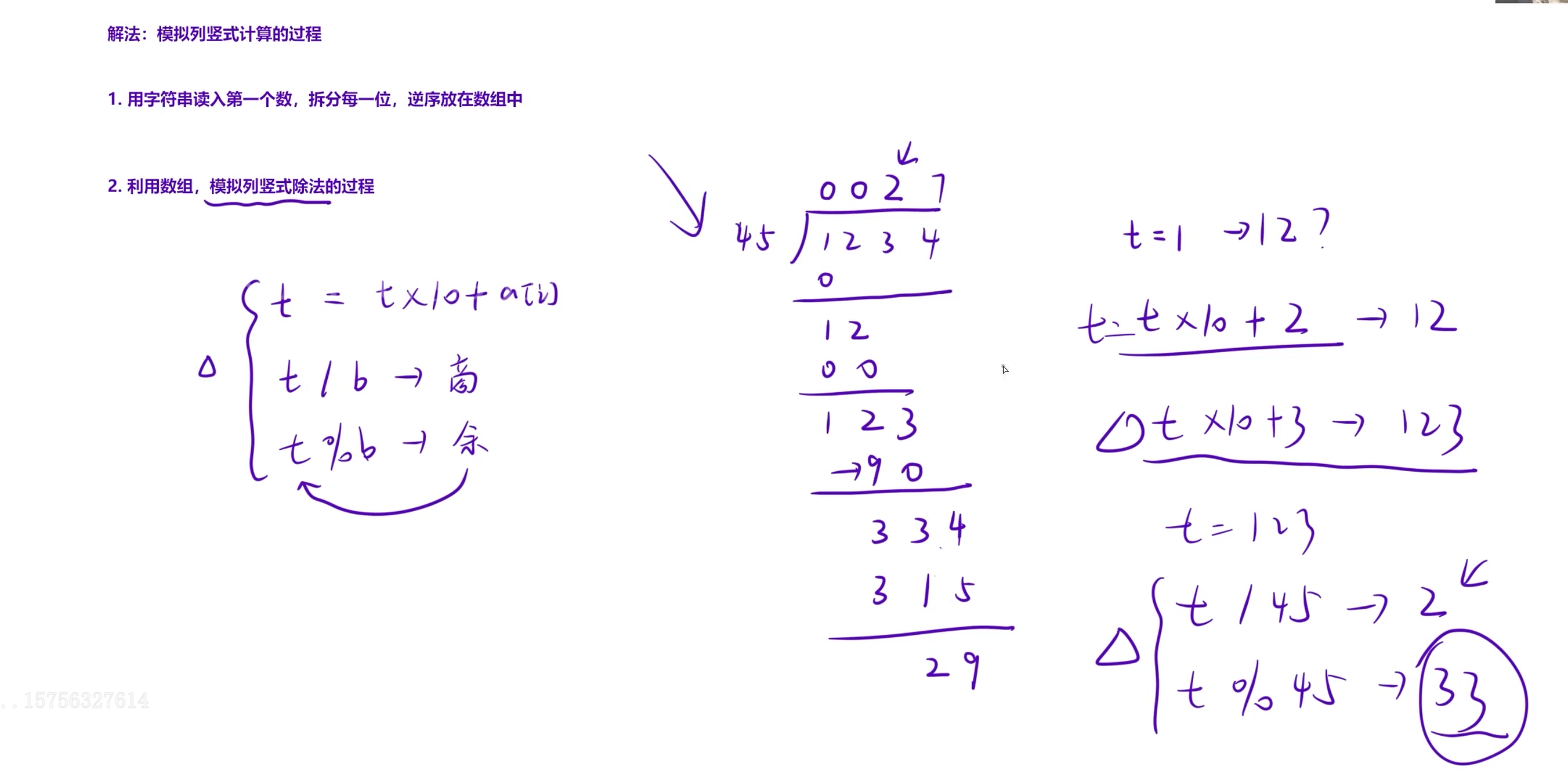
2.1 核心思想

这道题的特点是：被除数是高精度大数（可达 (10^{5000})），除数是低精度整数( 10^9)。我们可以模拟小学竖式除法的"逐位试商"过程，用数组存储大数，用普通整数做除法运算，避免复杂的高精度除法。

2.2 步骤拆解

① 输入与格式转换

  • 用字符串 s 读入被除数，将其逐位逆序存入数组 a，低位在前 （个位在数组下标1，十位在下标2，以此类推），方便从高位到低位逐位试商。
    • 例如：字符串 "1234" → 数组 a = [0, 4, 3, 2, 1, ...]（下标0未使用，下标1存个位4，下标4存千位1）。

② 逐位试商与余数更新

  • 初始化余数 t = 0，从被除数的最高位（数组下标 la）开始，逐位处理：
    1. 用当前余数 t 拼接下一位数字：t = t * 10 + a[i]，形成新的被除数片段。
    2. 计算当前位的商：ret[i] = t / b。
    3. 更新余数：t = t % b，用于下一位的拼接。
  • 这一步完全模拟了竖式除法中"落下一位，再试商"的过程。

③ 去除前导零并输出

  • 从商数组 ret 的最高位开始，跳过所有前导零，确定有效长度 cnt。
  • 如果 cnt 为0，说明被除数小于除数，商为0；否则从高位到低位倒序输出商数组。

2.3 代码对应逻辑

代码部分 对应思路
a[la - i] = s[i] - '0' 将字符串逆序存入数组，实现低位在前
t = t * 10 + a[i] 模拟竖式中"落下一位"，拼接出新的被除数片段
ret[i] = t / b 计算当前位的商值
t %= b 更新余数，用于下一位拼接
while (cnt && !ret[cnt]) cnt-- 跳过商数组中的前导零，确定有效输出长度
while (cnt) cout << ret[cnt--] 从高位到低位打印商，得到正确的数字顺序

2.4 关键细节

  • 数据类型 ：使用 long long 存储中间余数 t，防止 t * 10 + a[i] 时溢出。
  • 边界处理：当被除数为0或小于除数时，商为0，需要单独处理，避免输出空串。
  • 前导零 ：商数组中可能存在高位零，输出前必须跳过，避免输出如 00123 这样的无效格式。
  • 方向 ：与加减乘不同，除法是从高位到低位逐位计算，因此数组虽然低位在前，但遍历顺序是从后往前。

3.参考代码

cpp 复制代码 
![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/d512247cad9a4f00b6957a69dbd86742.png)
#include<iostream>
#include<string>
using namespace std;

const int N = 1e5 + 10;  // 数组最大长度，适配超长数字存储
int a[N], b, ret[N];     // a:被除数(低位在前)，b:低精度除数，ret:商(低位在前)
int cnt, la;             // cnt:商的有效长度，la:被除数的位数
string s;                // 存储输入的被除数字符串
typedef long long LL;    // 防止中间计算溢出


// 高精度除以低精度核心（逐位试商法）
void divBigInt()
{
    LL t = 0;            // 存储当前计算的余数
    // 从被除数最高位到最低位逐位计算
    for (int i = la; i; i--)
    {
        t = t * 10 + a[i]; // 余数拼接当前位，形成新的被除数片段
        ret[i] = t / b;    // 计算当前位的商值
        t %= b;            // 更新余数（保留除后剩余值）
    }
    // 跳过商的前导零，确定有效长度
    while (cnt && !ret[cnt]) cnt--;
}

// 测试函数：输入处理、格式转换、执行除法、输出结果
void test(void (*func)()) {
    cin >> s >> b;       // 输入：被除数(字符串) 除数(整数)
    la = s.size();       // 获取被除数的位数
    cnt = la;            // 初始化商的长度为被除数长度
    // 字符串转数组（低位在前，适配逐位计算）
    for (int i = 0; i < la; i++) a[la - i] = s[i] - '0';

    func(); // 执行高精度除法

    // 输出商（处理商为0的边界情况）
    if (!cnt)  // cnt为0表示商是0（被除数<除数）
    {
        cout << 0;
        return;
    }
    // 从高位到低位打印商（ret低位在前）
    while (cnt) cout << ret[cnt--];
    cout << endl;
}

int main()
{
    test(divBigInt); // 调用测试函数执行高精度除法
    return 0;
}
相关推荐
3GPP仿真实验室1 小时前
【Matlab源码】6G候选波形：OFDM-IM 增强仿真平台 GIM、MM、IQ
开发语言·网络·matlab
xuxie991 小时前
【无标题】
java·开发语言
叫我一声阿雷吧2 小时前
【JS实战案例】实现图片懒加载（基础版）原生JS+性能优化，新手可直接复现
开发语言·javascript·性能优化·js图片懒加载
new_zhou2 小时前
Windows环境c++开发dump文件生成（优化方案）
c++·windows·qt
摇滚侠2 小时前
基于 session 的登录认证方式，基于 token 的登录认证方式，对比
java·开发语言·intellij-idea
北国1372 小时前
【Java】多线程输出滞后/错误解决&&线程创建方式与原理
java·开发语言
求真求知的糖葫芦2 小时前
巴伦学习（三.一）一种可以实现阻抗变换的平面Marchand巴伦的公式推导学习笔记（中）（自用）
笔记·学习·平面·射频工程
Coder_Boy_2 小时前
【Java核心】JVM核心知识清单
java·开发语言·jvm
努力学算法的蒟蒻2 小时前
day84（2.12）——leetcode面试经典150
算法·leetcode·面试
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03Zsh/Bash Conda设置延迟启动，启动速度优化04243 行 microGPT：把“训练 + 推理”拆到骨头里05openclaw配置教程（linux+局域网ollama）06MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法07openclaw 配置飞书 报错 应用未建立长连接08AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南09UV安装并设置国内源10冰达ROS机器人快速使用指南