一.十字链表和邻接多重表
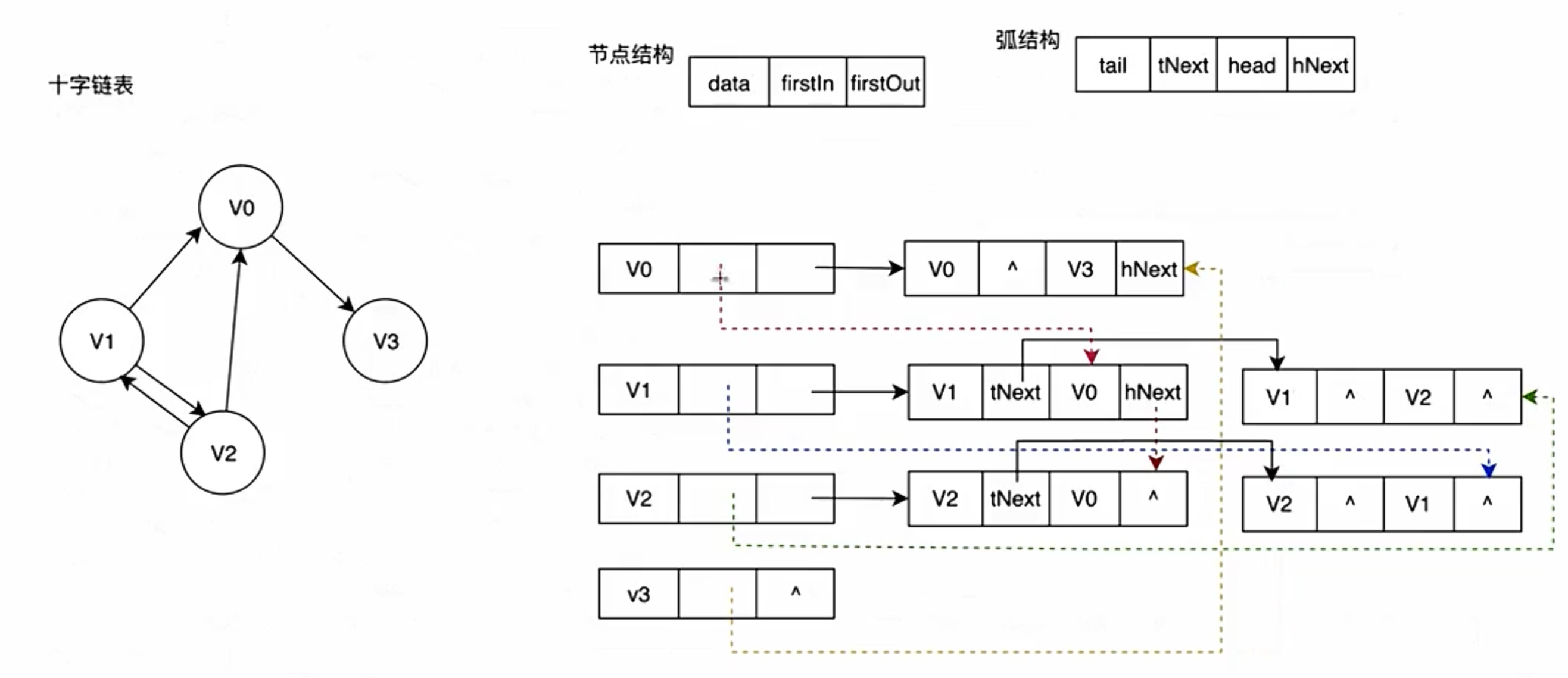
1.十字链表(专门优化有向图的邻接表)
核心问题:
普通邻接表存储有向图时,入边和出边分离------想查一个顶点的所有出度,直接查其邻接链表;想查所有入度,却需要遍历整个图的所有邻接链表,效率极低
设计逻辑:
将有向图的每一条边设计为一个独立的节点,节点中同时记录: 起点、终点、起点的下一条出边、终点的下一条入边;同时为每个顶点维护两个指针: 出度表头 (指向该顶点的第一条出度)、 入度表头 (指向该顶点的第一条入度)
核心优势:
出入度更方便,同时支持O(d)的出度和入度遍历,增删边时仅需修改相邻边节点的指针,无需遍历整个图,适配"频繁增删边、需要同时处理入度和出度"的有向图场景(如拓扑排序、关键路径的频繁操作)
十字链表相当于正邻接表逆邻接表的结合
但是空间利用率更高
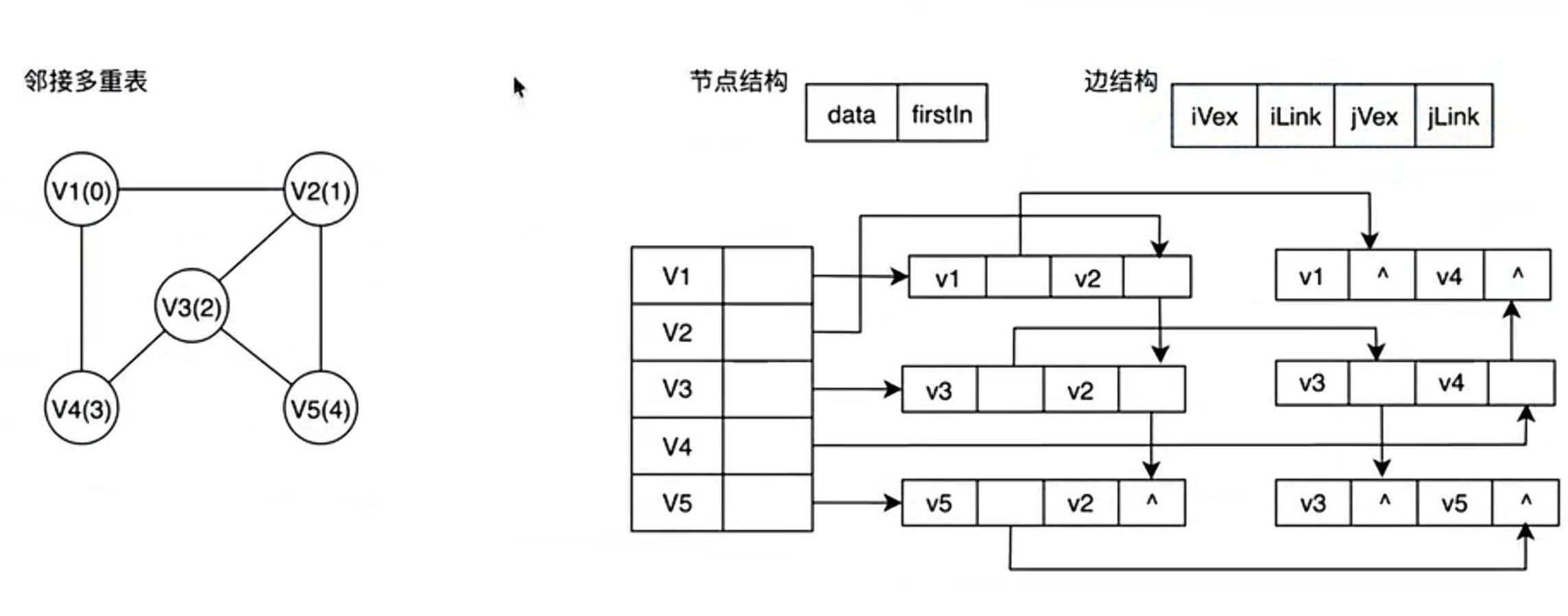
2.邻接多重表(专门优化无向图的邻接表)
核心问题:
普通邻接表存储无向图时,同一条边被存储两次(i的链表存j,j的链表存i)------增删边时,需要同时找到并修改两个节点,操作繁琐且容易出错
设计逻辑:
将无向图的每一条边设计为一个独立的节点,节点中记录: 边的两个顶点、顶点1的下一条邻接边、顶点2的下一条邻接边 ;每个顶点仅维护一个指针,指向其任意一条邻接边节点
核心优势:
一条边仅存储一次,增删边时仅需操作一个边节点,修改其指针即可,适配"频繁删边、边数较多"的无向图场景
存储结构的核心选择原则(使用场景)
看"顶点数n"和"边数e"的比例,本质是"空间"和"效率"的权衡:
(1) 当e ≈ n²(稠密图):选邻接矩阵,空间浪费少,查询边快;
(2) 当e ≈ n(稀疏图):选邻接表,空间利用率极高,遍历邻接顶点快;
(3)当需要频繁操作有向图的入边/出边:选十字链表;
(4)当需要频繁增删无向图的边:选邻接多重表
二.代码
1.十字链表
1.1要点
删除:(和多重邻接表删除思想一样,重点考虑一条边两个顶点,在那两层分别找到这两个顶点)
遍历顶点 u 的 出边链,找到 <u, v> 弧,从出链摘除
遍历顶点 v 的 入边链,找到 <u, v> 弧,从入链摘除
free(弧节点)
核心:
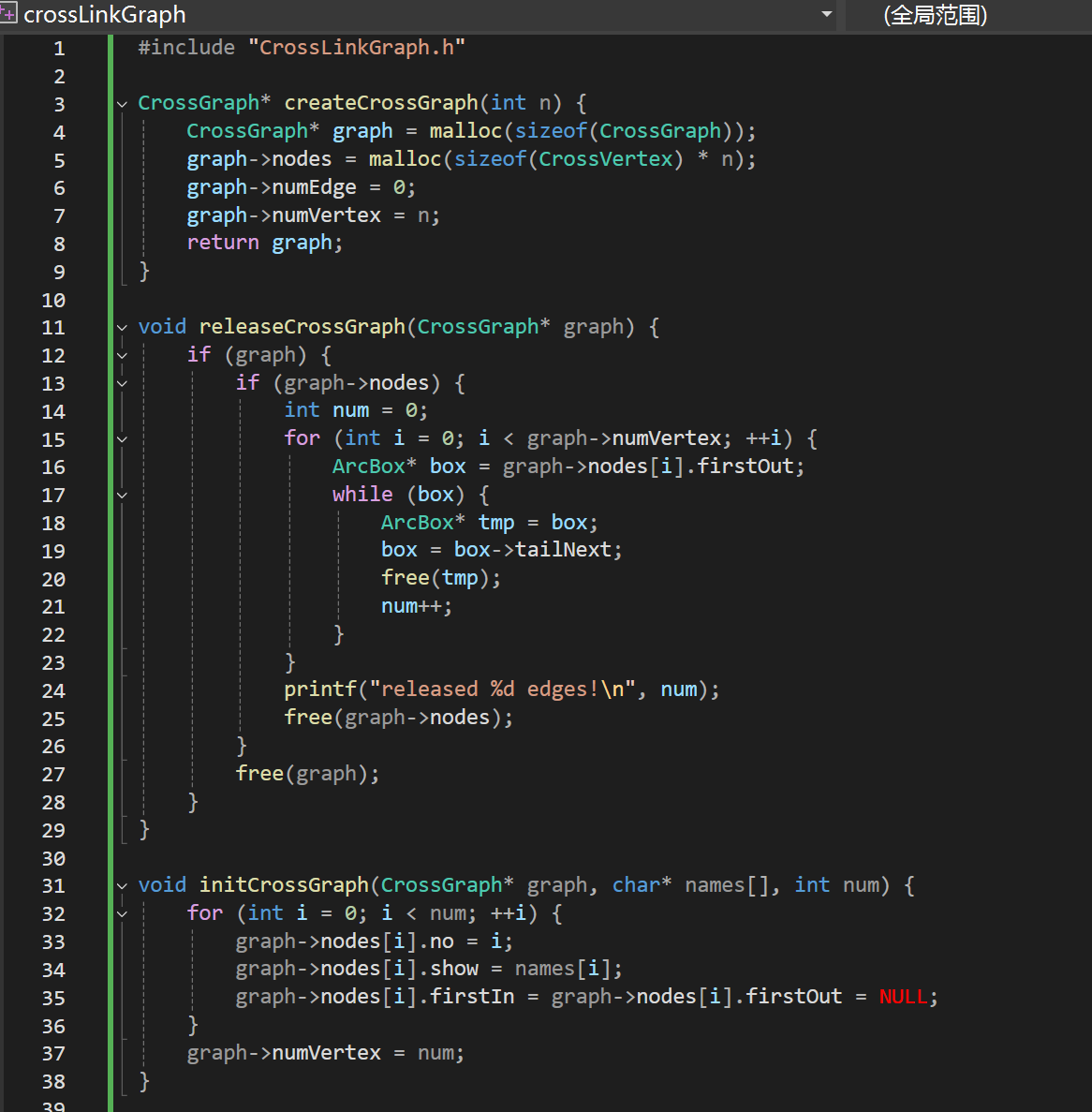
弧的结构定义:包含(弧尾)出度,(弧头)入度
顶点结构:序号,元素,入度/出度头节点
图头结构:定点结构,约束边,边总数
释放图时候,站在每一层顶点头出遍历删除释放,一层接着一层
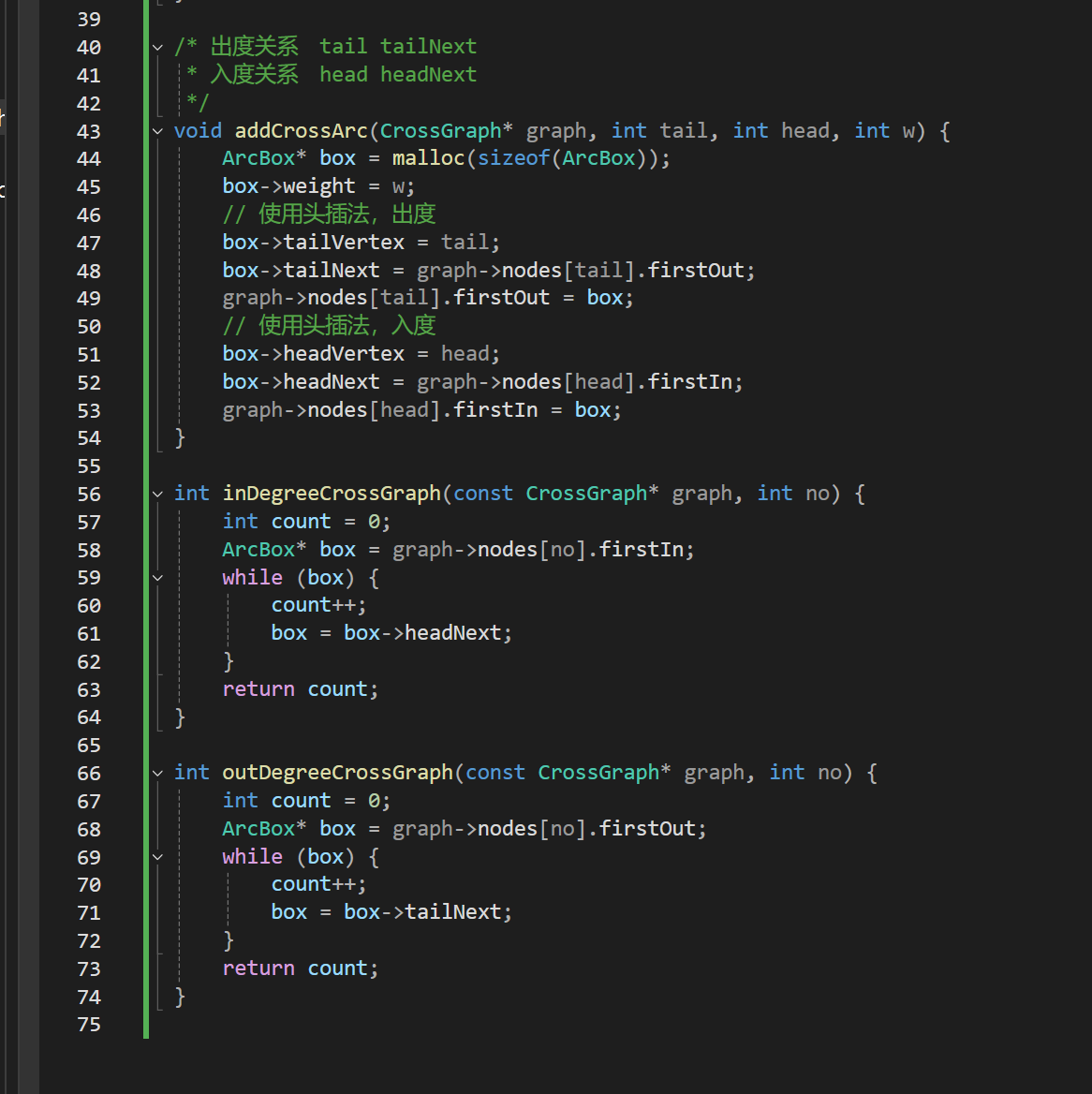
在添加边时候对入度出度同时进行头插法的操作,变会构成图中十字链表结构
no编号的出度入度的计算: 站在该节点的那一层上,分别看tailNext / headNext的节点数即可
1.2代码
.h
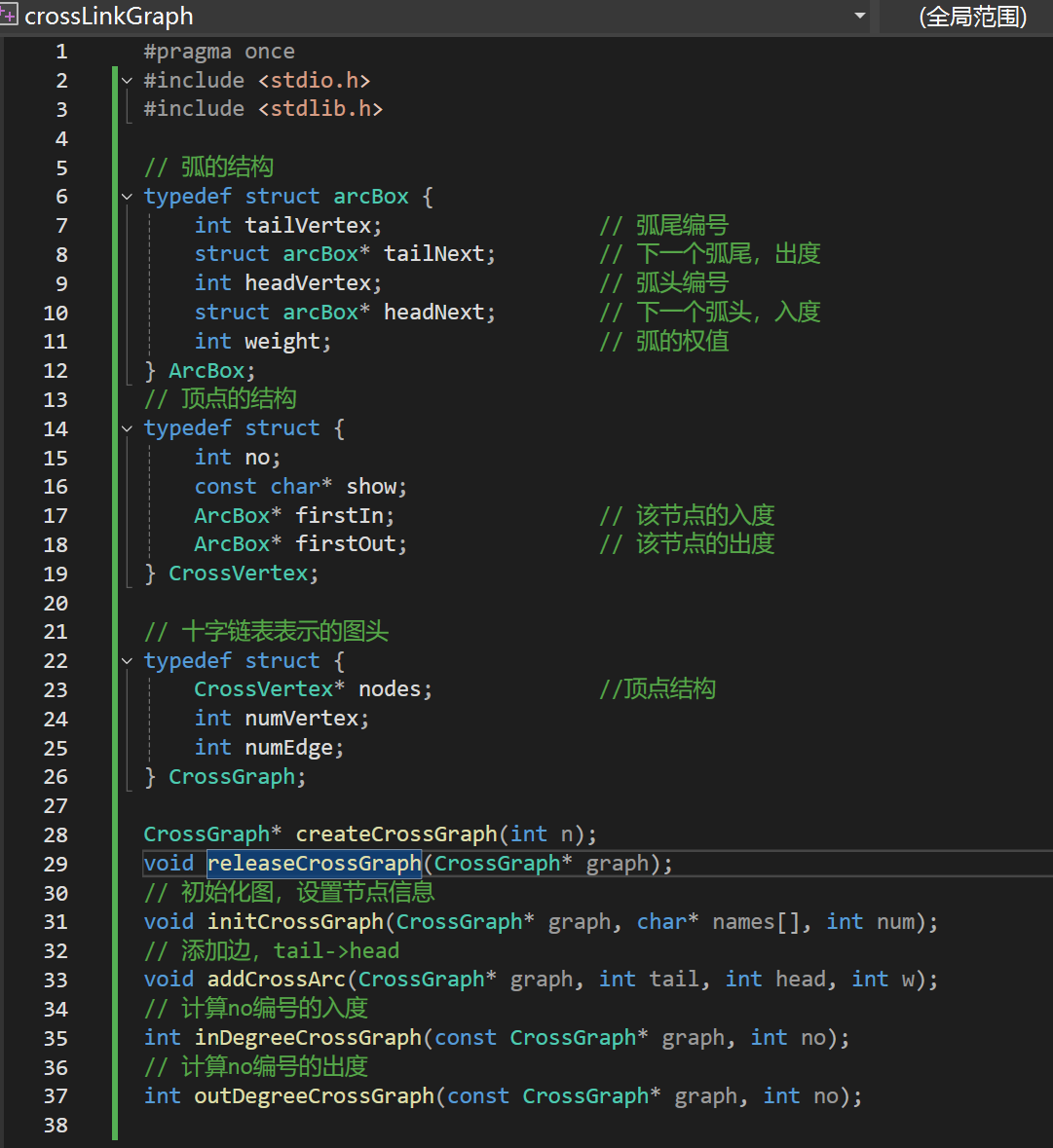
.c
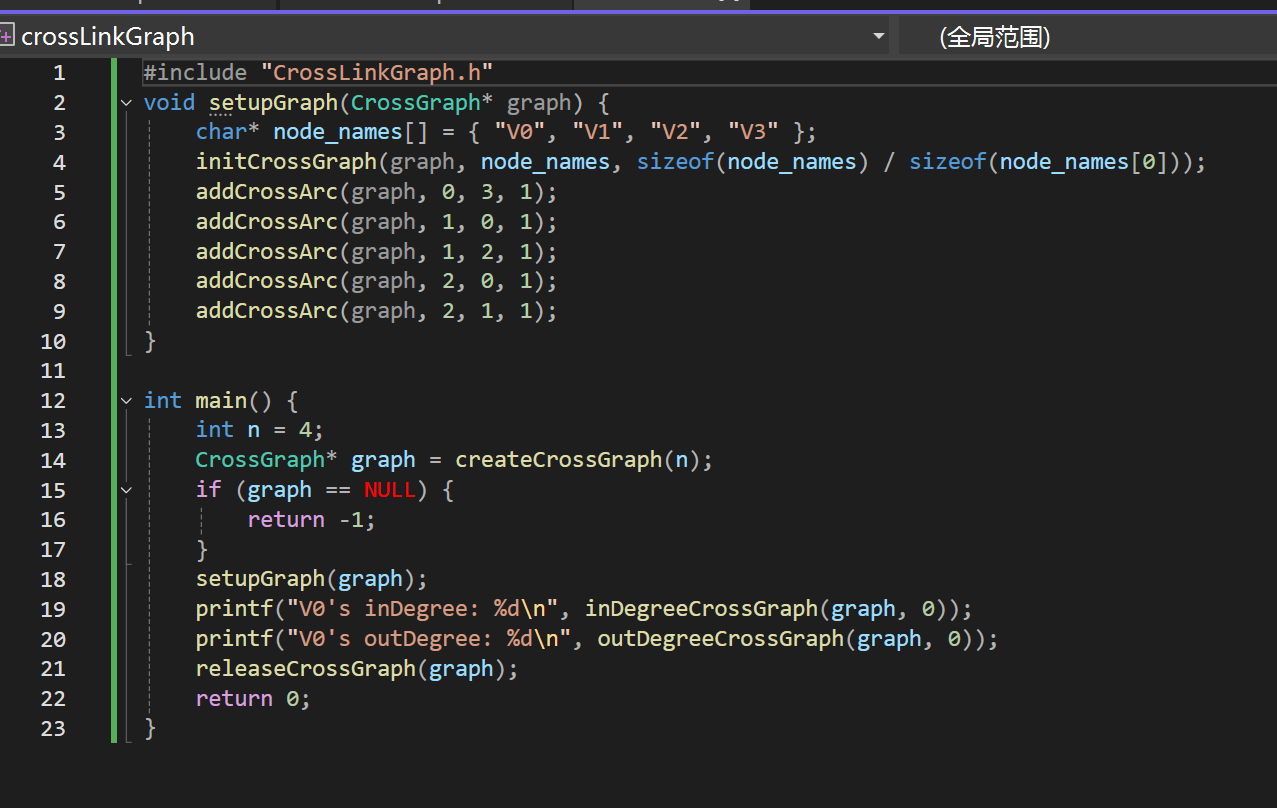
main.c
2.邻接多重表
2.1要点
删除操作:邻接多重表删除,找a,b节点,找到这个边,在释放
核心:
一条边,要找两个点;删除时,找到边,i不一定就是V1,j也不一定是V2
比如,从节点进来,V1在iLink上,就从iLink找,V1在jLink上就从jLink找; 提供找的方法 ;iLink链接的是以V1为起始(i)/终止(j)位置的下一个边
边的关系:以i为头节点往下走,以谁为节点到j
2.2代码
.h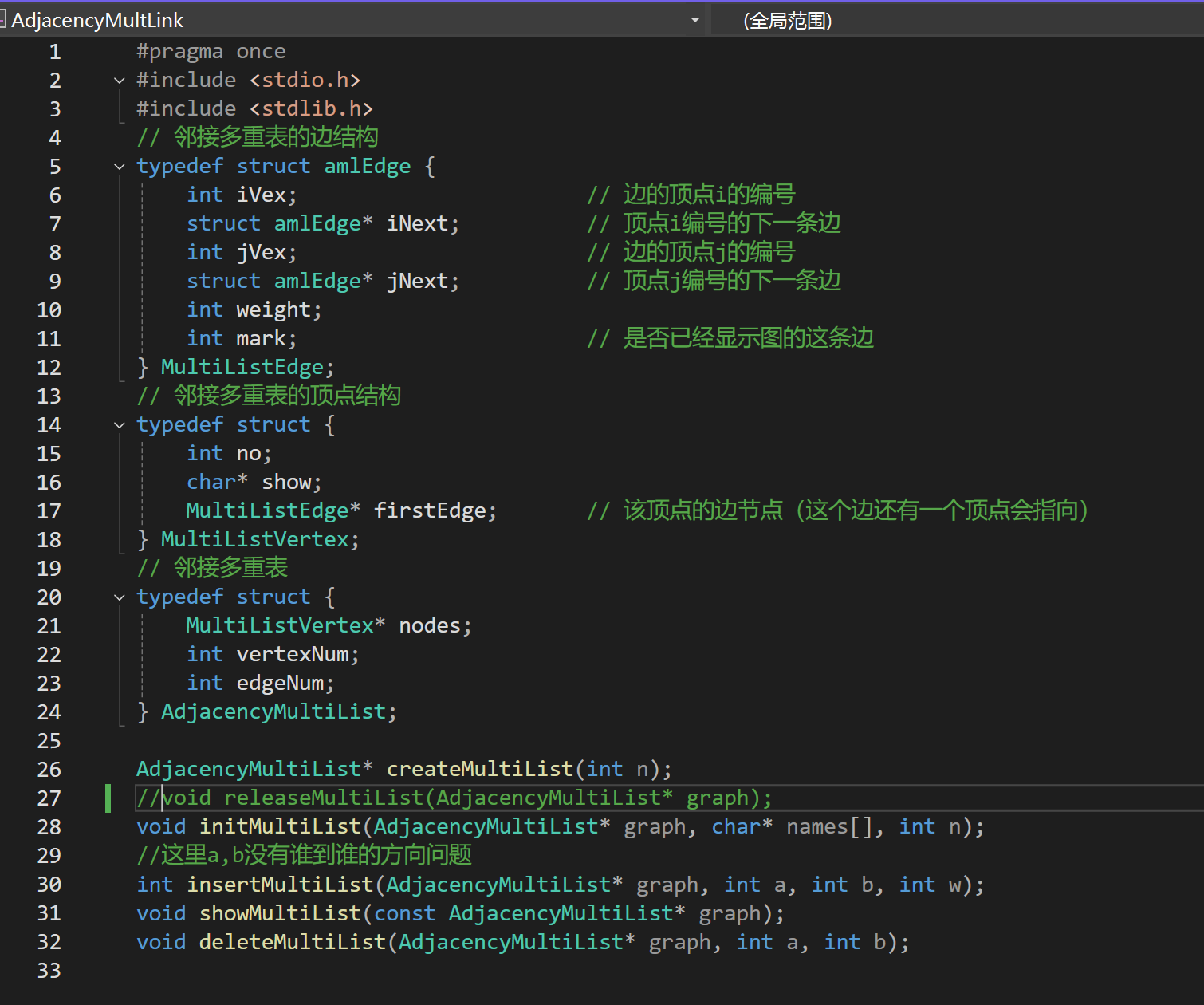
.c
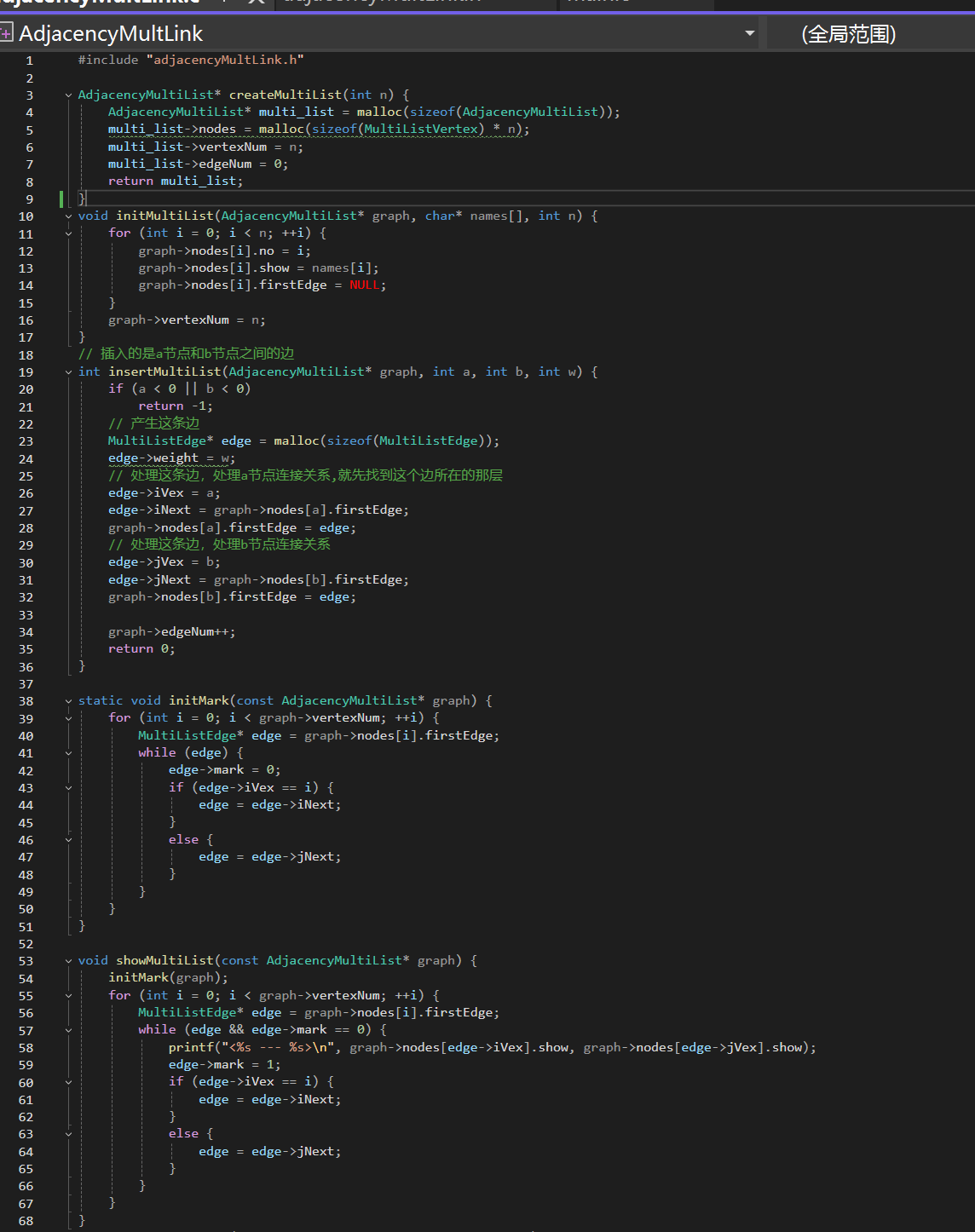
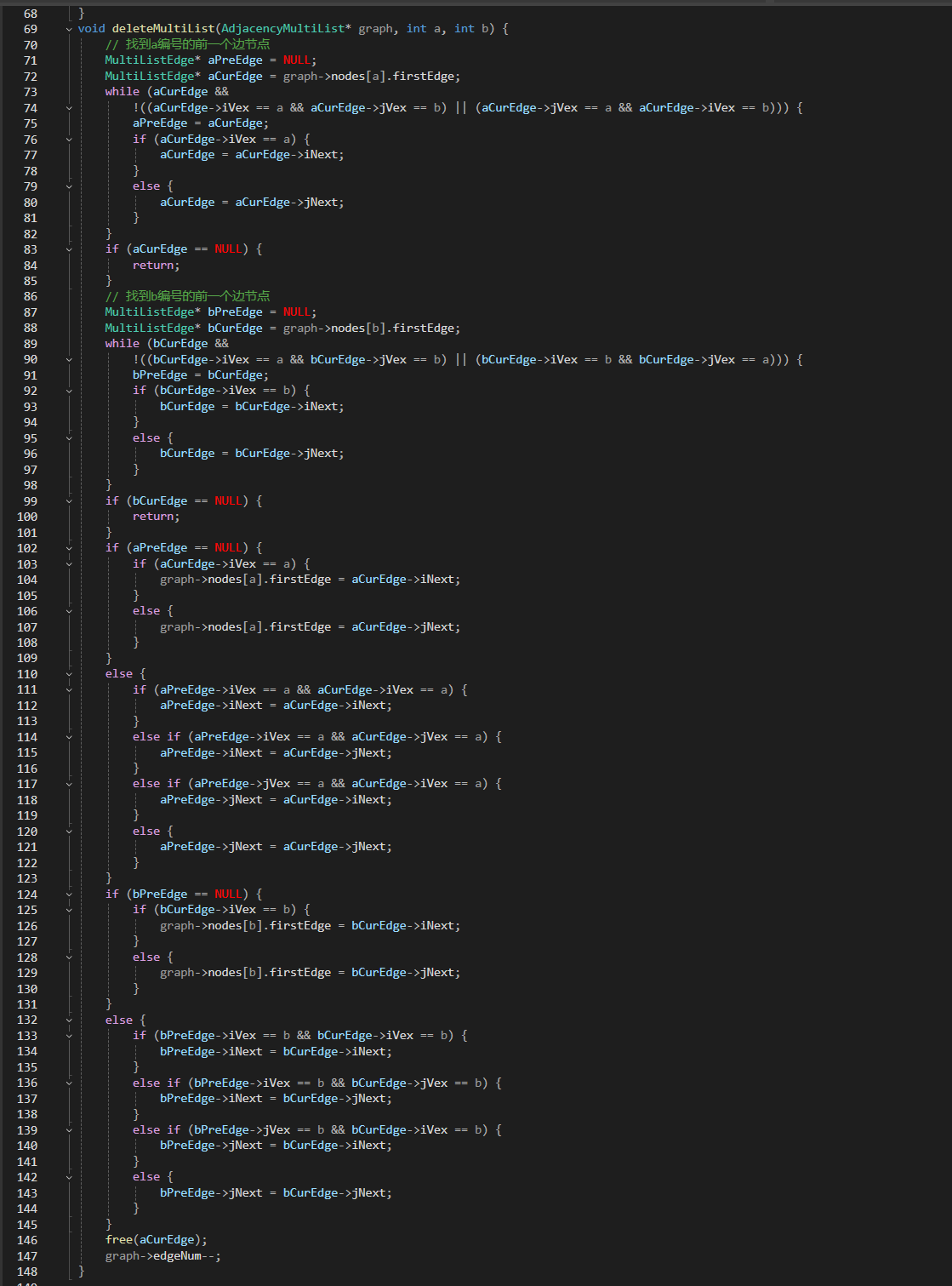
main.c