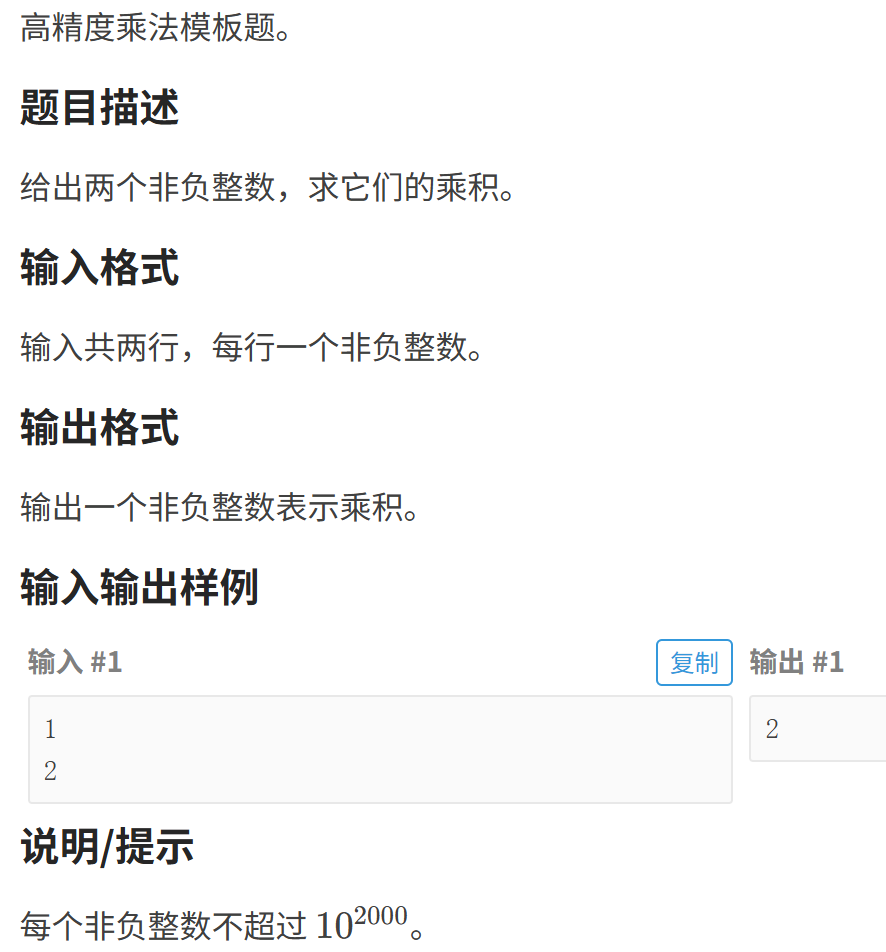
当数据的值特别大,各种类型都存不下的时候,此时就要用高精度算法来计算加减乘除:
1.先用字符串 读入这个数,然后用数组逆序存储该数的每一位。
注:①用字符串读取时,读取的是每一个'字符',而存入到数组中的是数字,因此要进行字符向数字的转变,eg:'2'->2,则应该'2'-'0'。
②数组逆序存储是因为我们一般计算都是从数字的个位算起,因此在数组中存储,先存个位、十位、百位...
2.利用数组,模拟加减乘除运算的过程。
高精度算法本质上还是模拟算法,用代码模拟小学列竖式计算加减乘除的过程。
一. 高精度加法
1.题目:
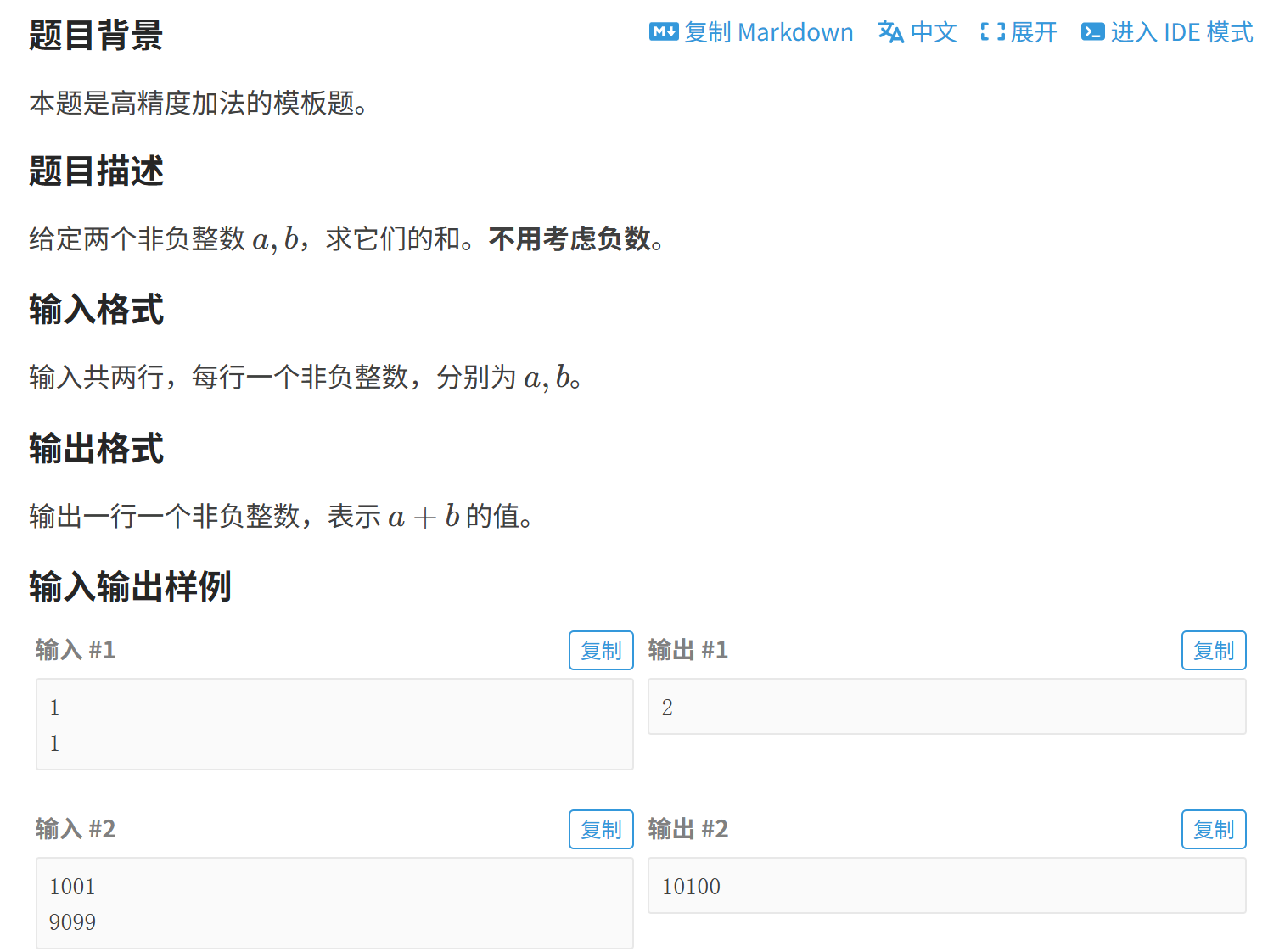
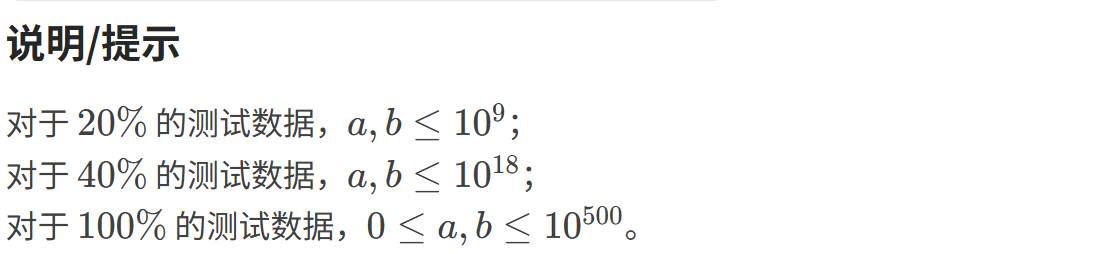
2.算法思路:
根据题目中的说明,"0<=a,b<=10^500",可看出a,b远远大于10^18,此时要用到高精度算法。
本题解题思路:模拟小学列竖式计算的过程。
①先用字符串读入,拆分每一位,逆序放在数组中。
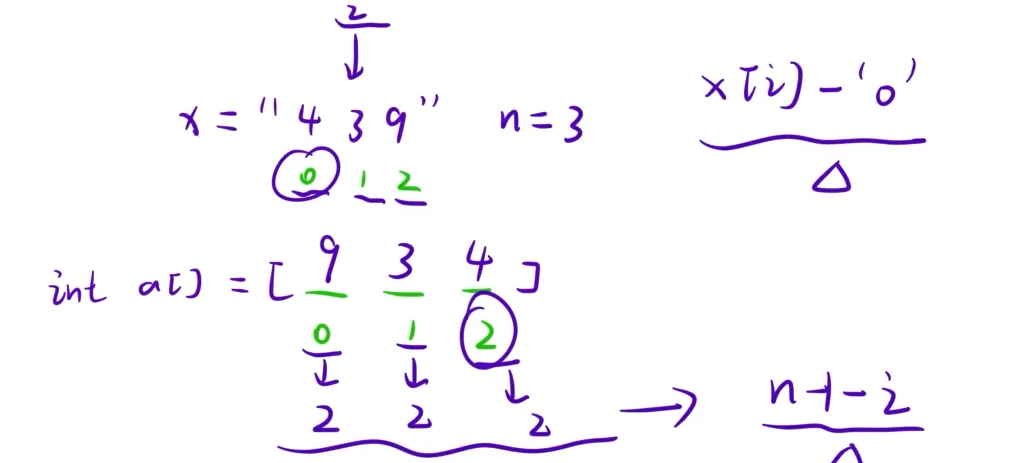
由上图可以看出,字符串与数组每一个对应位置的下标之和刚好等于,字符串的长度-1。
②利用数组,模拟小学列竖式计算加法的过程。
a.对应位相加,然后加上进位(设进位为x) b.处理进位(x/10) c.处理余数(x%10)。
用数组模拟计算过程:
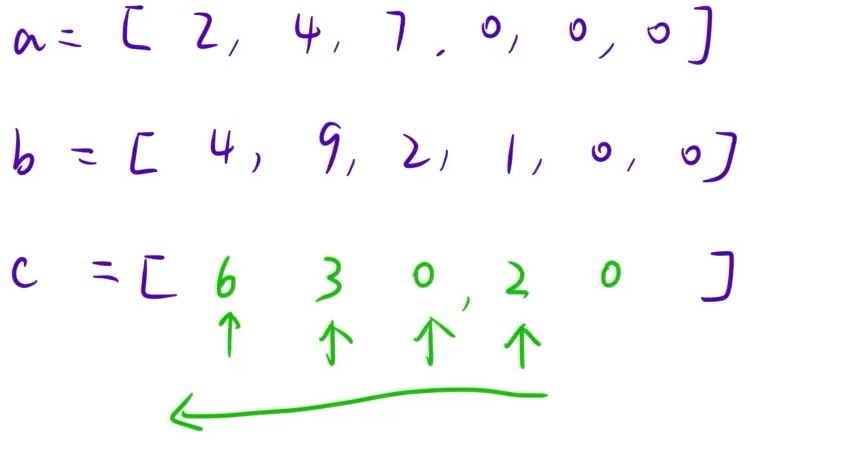
3.代码:
cpp
#include <iostream>
using namespace std;
const int N=1e6+10;
int a[N],b[N],c[N];
int la,lb,lc;
//高精度加法的模版
void add(int c[],int a[],int b[])
{
for(int i=0;i<lc;i++)
{
c[i]+=a[i]+b[i];//对应为相加,再加上进位
c[i+1]+=c[i]/10;//处理进位
c[i]%=10;//处理余数
}
if(c[lc])lc++;
}
int main()
{
string x,y;
cin>>x>>y;
//1.拆分每一位,逆序放在数组中
la=x.size();lb=y.size();lc=max(la,lb);
for(int i=0;i<la;i++)
{
a[la-1-i]=x[i]-'0';
}
for(int i=0;i<lb;i++)
{
b[lb-1-i]=y[i]-'0';
}
//2.模拟加法的过程
add(c,a,b);
//输出结果
for(int i=lc-1;i>=0;i--)
{
cout<<c[i];
}
return 0;
}二. 高精度减法
1.题目:
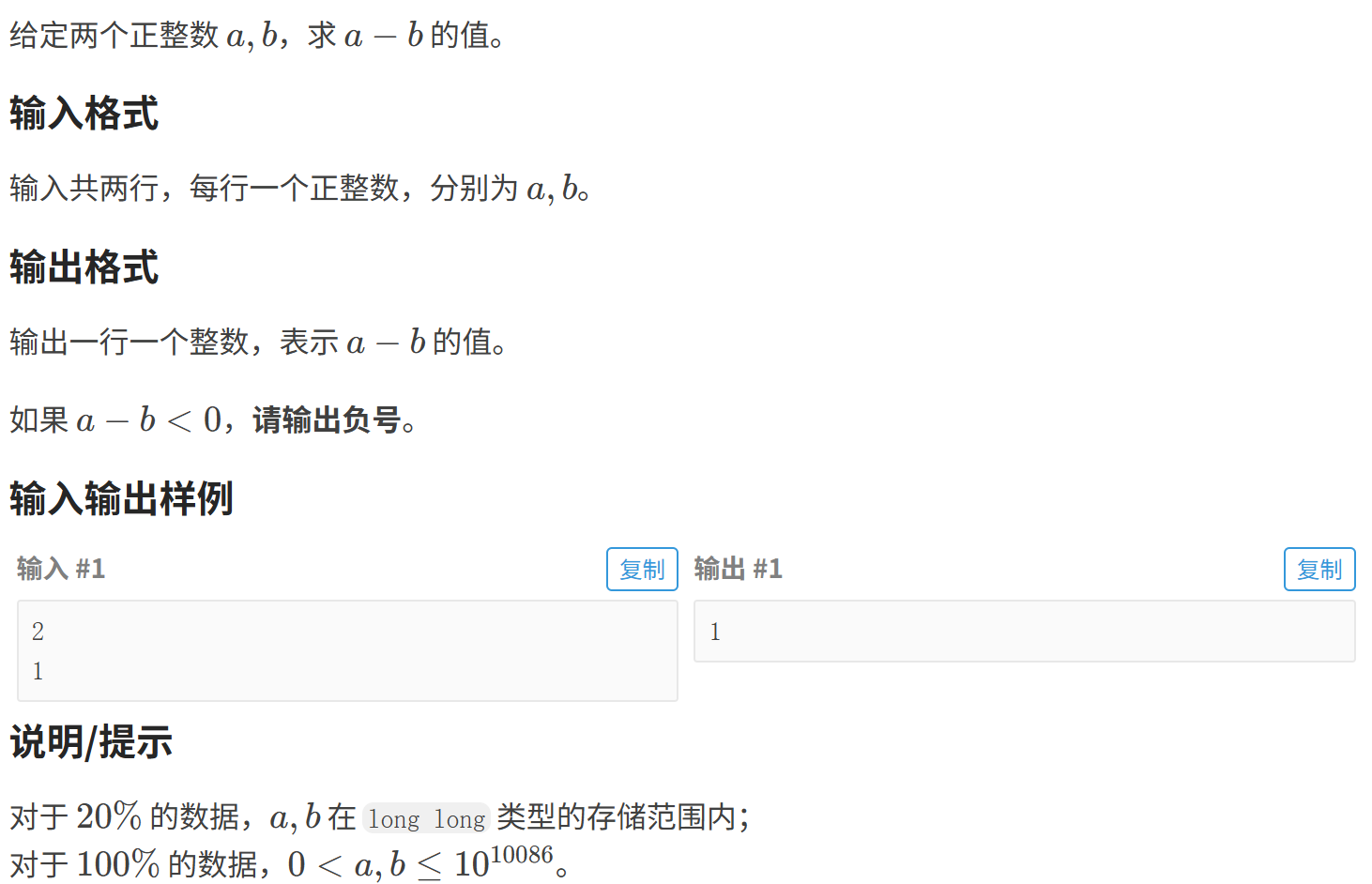
2.算法思路:
解法:模拟列竖式计算的过程
(1)先比较两数大小,用较大的数减去较小的数。
注:如果直接用字符串比较大小,是会出错的。注意"字符串比较"和"数的比较"的区别。
字典序VS数的大小: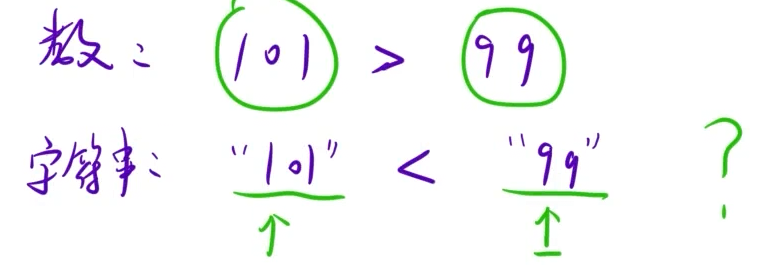
所以,用字符串比较之前,先比较一下字符串的长度。
(2)先将数以字符串的形式读取,然后拆分每一位,逆序放入数组中。
(3)利用数组,模拟减法列竖式的过程。
①先是对应位相减,然后处理借位。 ②如果对应位相减结果为负数,则往前借一位,再加上10。
3.代码:
cpp
#include <iostream>
using namespace std;
const int N=1e6+10;
int a[N],b[N],c[N];
int la,lb,lc;
//比较大小
bool cmp(string& x,string& y)//此处尽量加上取地址,如果不加,传入参数时会重新赋值
{
if(x.size()!=y.size())
{
return x.size()<y.size();
}
//字符串长度相等时,比较字典序大小
return x<y;
}
//高精度减法模版
void sub(int c[],int a[],int b[])
{
for(int i=0;i<lc;i++)
{
c[i]+=a[i]-b[i];
if(c[i]<0)
{
c[i+1]-=1;//借位
c[i]+=10;//处理当前位
}
}
//处理前导零
while(lc>1&&c[lc-1]==0) lc--;
}
int main()
{
string x,y;
cin>>x>>y;
//1.比较大小
if(cmp(x,y))
{
swap(x,y);
cout<<'-';
}
//2.将字符串每一位都逆序读入数组中
la=x.size(); lb=y.size(); lc=max(la,lb);
for(int i=0;i<la;i++) a[la-1-i]=x[i]-'0';
for(int i=0;i<lb;i++) b[lb-1-i]=y[i]-'0';
//3.模拟减法的过程
sub(c,a,b);
//4.逆序输出
for(int i=lc-1;i>=0;i--)
{
cout<<c[i];
}
return 0;
} 三. 高精度乘法
1.题目:
2.算法思路:
原理:模拟列竖式的过程
(1)先用字符串读入,然后拆分每一位,逆序放入数组中
(2)模拟列竖式乘法的过程(无进位相乘,然后相加,最后处理进位**(下图绿色大括号部分无需频繁处理进位)**)
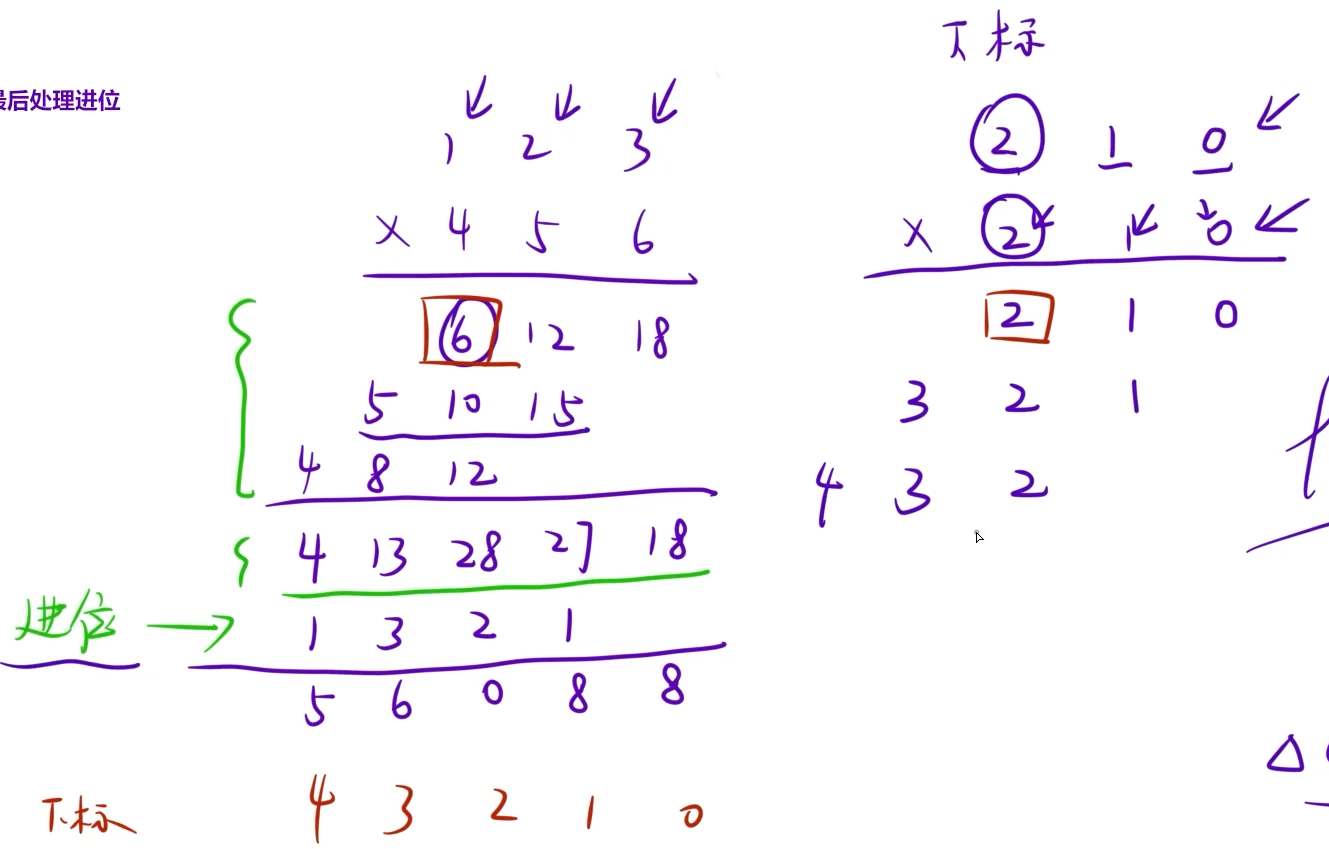
3.代码:
cpp
#include <iostream>
using namespace std;
const int N=1e6+10;
int a[N],b[N],c[N];
int la,lb,lc;
//高精度乘法的模版
int mul(int c[],int a[],int b[])
{
//1.无进位相乘,然后相加
for(int i=0;i<la;i++)
{
for(int j=0;j<lb;j++)
{
c[i+j]+=a[i]*b[j];
}
}
//2.处理进位
for(int i=0;i<lc;i++)
{
c[i+1]+=c[i]/10;
c[i]%=10;
}
//处理前导零
while(lc>1&&c[lc-1]==0) lc--;
}
int main()
{
string x,y; cin>>x>>y;
//1.拆分每一位,逆序放入数组中
la=x.size();lb=y.size();lc=la+lb;
for(int i=0;i<la;i++) a[la-1-i]=x[i]-'0';
for(int i=0;i<lb;i++) b[lb-1-i]=y[i]-'0';
//2.模拟乘法列竖式的过程最后处理进位
mul(c,a,b);
//3.输出
for(int i=lc-1;i>=0;i--)
{
cout<<c[i];
}
return 0;
} 四. 高精度除法
1.题目:
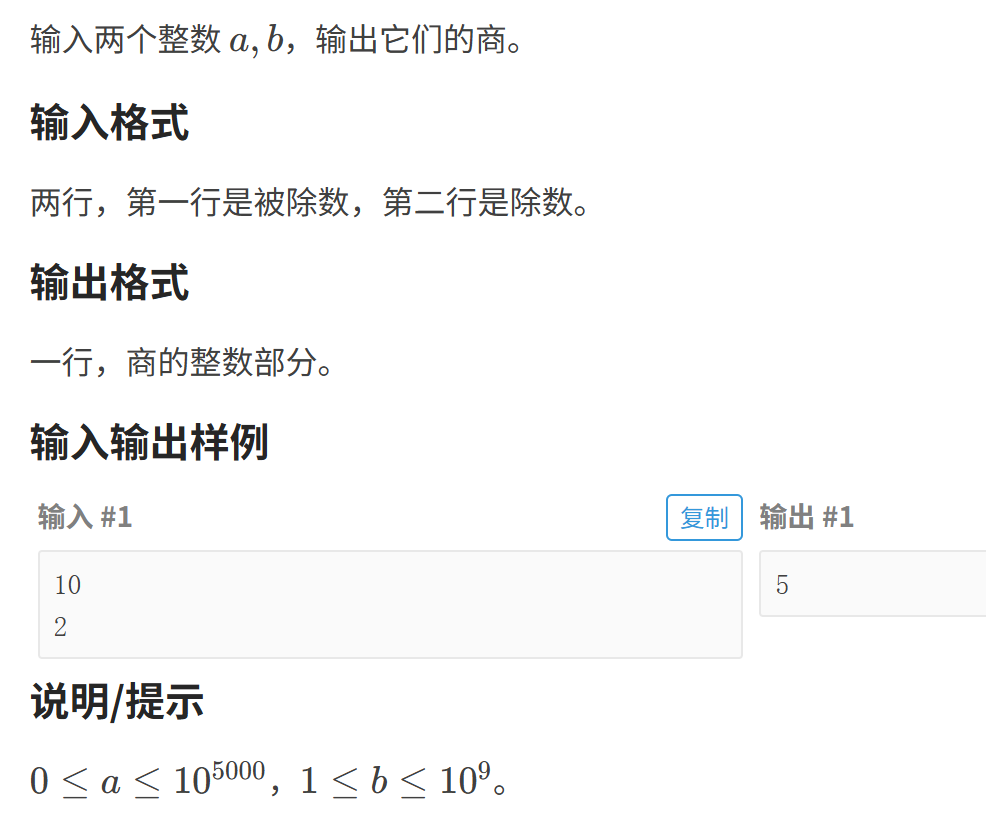
2.算法思路:
根据此题中 a,b的数据范围,可以看出这道题是"高精度除以低精度",模拟除法列式的过程。
(1)先用字符串读入一个数(除数),然后拆分每一位,逆序放入数组中
(2)模拟列竖式除法的过程
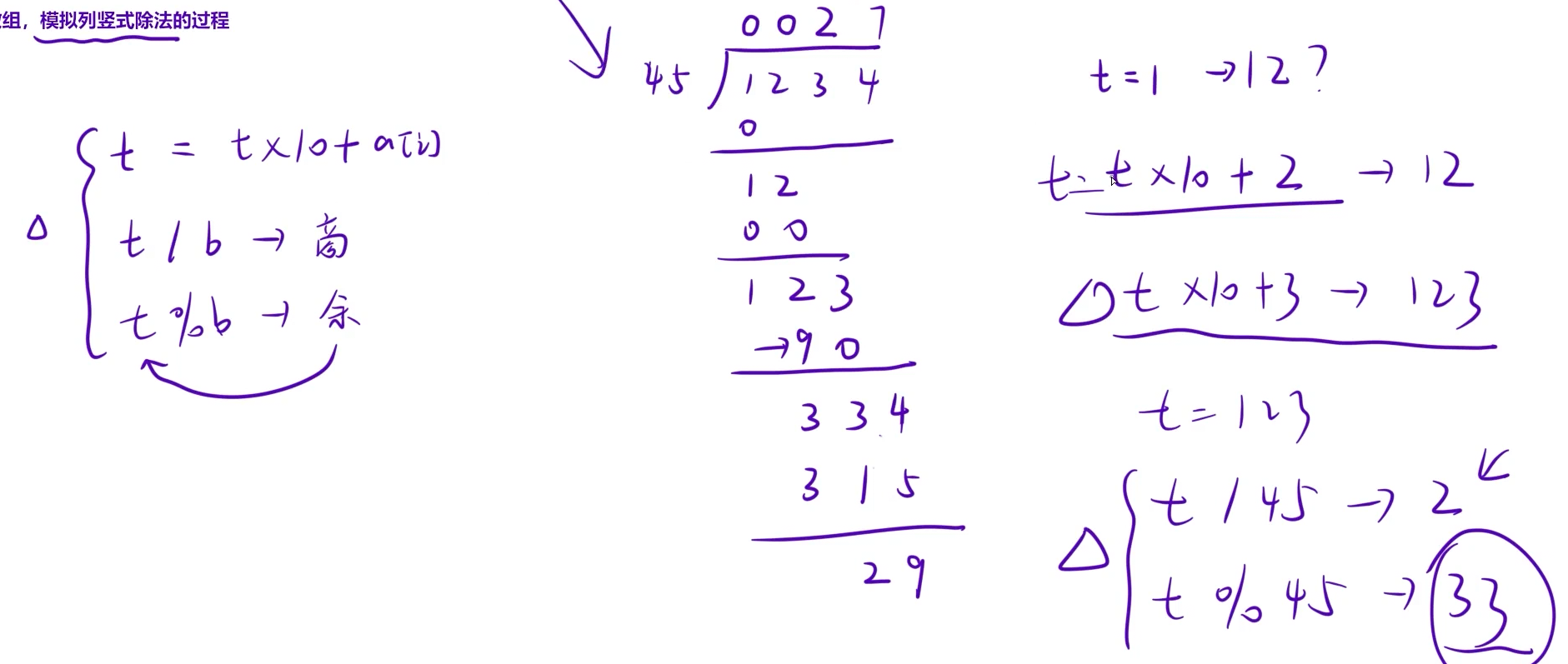
3.代码:
cpp
#include <iostream>
using namespace std;
const int N=1e6+10;
int a[N],b,c[N];
int la,lc;
typedef long long LL;
//高精度除法的模版 (高精度/低精度)
int sub(int c[],int a[],int b)
{
LL t=0;//标记每次出完之后的余数
for(int i=la-1;i>=0;i--)
{
//计算当前的被除数
t=t*10+a[i];
c[i]=t/b;
t%=b;
}
//处理前导0
while(lc>1&&c[lc-1]==0) lc--;
}
int main()
{
//1.先用字符串读入,然后拆分每一位,逆序放入数组中
string x;
cin>>x>>b;
la=x.size();
for(int i=0;i<la;i++) a[la-1-i]=x[i]-'0';
//2.模拟除法的过程
lc=la;
sub(c,a,b);
//3.输出
for(int i=lc-1;i>=0;i--)
cout<<c[i];
return 0;
} 以上就是今天的内容,感兴趣的大佬们可以一键三连哦~