230. 二叉搜索树中第 K 小的元素

230. 二叉搜索树中第 K 小的元素

中等

提示

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k小的元素（从 1 开始计数）。

示例 1：

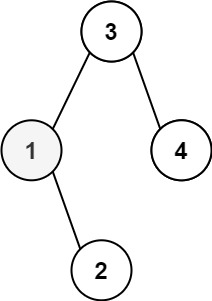
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

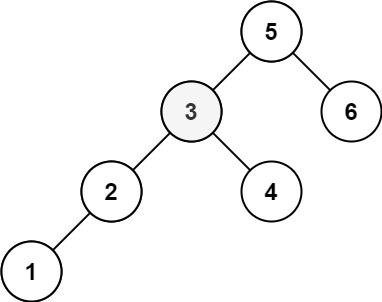
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

• 树中的节点数为 n 。
• 1 <= k <= n <= 104
• 0 <= Node.val <= 104

📝 核心笔记：二叉搜索树中第 K 小的元素 (Kth Smallest Element in a BST)

1. 核心思想 (一句话总结)

"在 BST 里走中序遍历，就等于在有序数组里数数。"

• 我们不需要真的把树转换成数组。
• 我们只需要一边走（左->根->右），一边倒数 k。
• 当 k 减到 0 时，脚下的那个节点就是答案。

2. 算法流程 (递归倒数)

1. 初始化 ：记录全局 k。
2. DFS (中序)：

• • Go Left：先去左子树找（因为最小的肯定在左边）。
  • Check Root：

• • • 每访问一个节点，k 减 1。
    • 判断：如果 k == 0，说明当前节点就是第 k 小的，记录 ans。

• • Go Right ：如果还没找到（k > 0），再去右子树找。

🔍 代码回忆清单

// 题目：LC 230. Kth Smallest Element in a BST
class Solution {
    // 全局变量，避免递归传参的麻烦
    private int ans;
    private int k;

    public int kthSmallest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return ans;
    }

    private void dfs(TreeNode node) {
        // 1. Base Case & 剪枝
        // 注意：这里建议写 k <= 0，防止 k 减成负数后绕过检查
        if (node == null || k <= 0) { 
            return;
        }
        
        // 2. 左
        dfs(node.left); 
        
        // 3. 根 (中序位置)
        // 每次从中序遍历中访问一个节点，就相当于在有序数组里划掉一个数
        if (--k == 0) {
            ans = node.val; // 找到了！
            return; // 找到后可以直接 return，不用去右边了 (小优化)
        }
        
        // 4. 右
        dfs(node.right); 
    }
}

⚡ 快速复习 CheckList (微调建议)

• 关于 k****变成负数的问题 (隐蔽 Bug)

• • 在您的原始代码中，if (--k == 0) 会让 k 继续减少变为 -1, -2...
  • 而开头检查的是 if (k == 0)。
  • 后果 ：当找到答案后，回溯到上层父节点时，--k 会让 k 变成负数，从而导致开头的 k == 0 拦截失效，程序会继续无意义地遍历右子树。
  • 修复 ：将 if (node == null || k == 0) 改为 if (node == null || k <= 0) 即可实现完美的提前终止。

• 迭代法 (Iterative) 怎么写？

• • 面试中如果要求非递归，还是用 栈 (Stack) 模拟中序遍历。
  • 一路向左 push，弹出一个就 k--，直到 k==0 返回当前值，否则转向右子树。迭代法的好处是可以控制 while 循环直接 return，不需要像递归那样等待栈逐层弹出。

🖼️ 数字演练

树：

      3
     / \
    1   4
     \
      2

Target: k = 2

1. dfs(3) -> Call dfs(1).
2. dfs(1) -> Call dfs(null) (Returns).
3. Process 1:

• • k becomes 1.
  • Not 0. Continue.

1. dfs(1) -> Call dfs(2) (Right child).
2. dfs(2) -> Call dfs(null).
3. Process 2:

• • k becomes 0.
  • Bingo! ans = 2.
  • (With optimization) Return logic starts unwinding.

---