(以下内容全部出自上述课程)
目录
- 最小生成树
-
- [1. 分类](#1. 分类)
-
- [1.1 广度优先生成树](#1.1 广度优先生成树)
- [1.2 深度优先生成树](#1.2 深度优先生成树)
- [1.3 最小生成树](#1.3 最小生成树)
- [2. 算法实现](#2. 算法实现)
-
- [2.1 Prim算法](#2.1 Prim算法)
- [2.2 Kruskal算法](#2.2 Kruskal算法)
- [2.3 对比](#2.3 对比)
- [3. 实现思想](#3. 实现思想)
-
- [3.1 Prim算法](#3.1 Prim算法)
- [3.2 Kruskal算法](#3.2 Kruskal算法)
- [4. 小结](#4. 小结)
- 最短路径问题
-
- [1. BFS算法](#1. BFS算法)
-
- [1.1 概念](#1.1 概念)
- [1.2 代码实现](#1.2 代码实现)
- [1.3 小结](#1.3 小结)
- [2. Dijkstra算法](#2. Dijkstra算法)
-
- [2.1 优化](#2.1 优化)
- [2.2 实现过程](#2.2 实现过程)
- [2.3 时间复杂度](#2.3 时间复杂度)
- [3. Floyd算法](#3. Floyd算法)
-
- [3.1 概念](#3.1 概念)
- [3.2 实现过程](#3.2 实现过程)
- [3.3 算法实例](#3.3 算法实例)
- [3.4 练习及小结](#3.4 练习及小结)
- 有向无环图(DAG图)
-
- [1. DAG描述表达式](#1. DAG描述表达式)
- [2. 解题方法](#2. 解题方法)
- 拓扑排序
-
- [1. AOV网](#1. AOV网)
- [2. 拓扑排序](#2. 拓扑排序)
- [3. 代码实现](#3. 代码实现)
- [4. 逆拓扑排序](#4. 逆拓扑排序)
- [5. 代码实现](#5. 代码实现)
- [6. 小结](#6. 小结)
- 关键路径
-
- [1. AOE网](#1. AOE网)
- [2. 关键路径](#2. 关键路径)
- [3. 实现步骤](#3. 实现步骤)
- [4. 特性](#4. 特性)
- [5. 小结](#5. 小结)
最小生成树
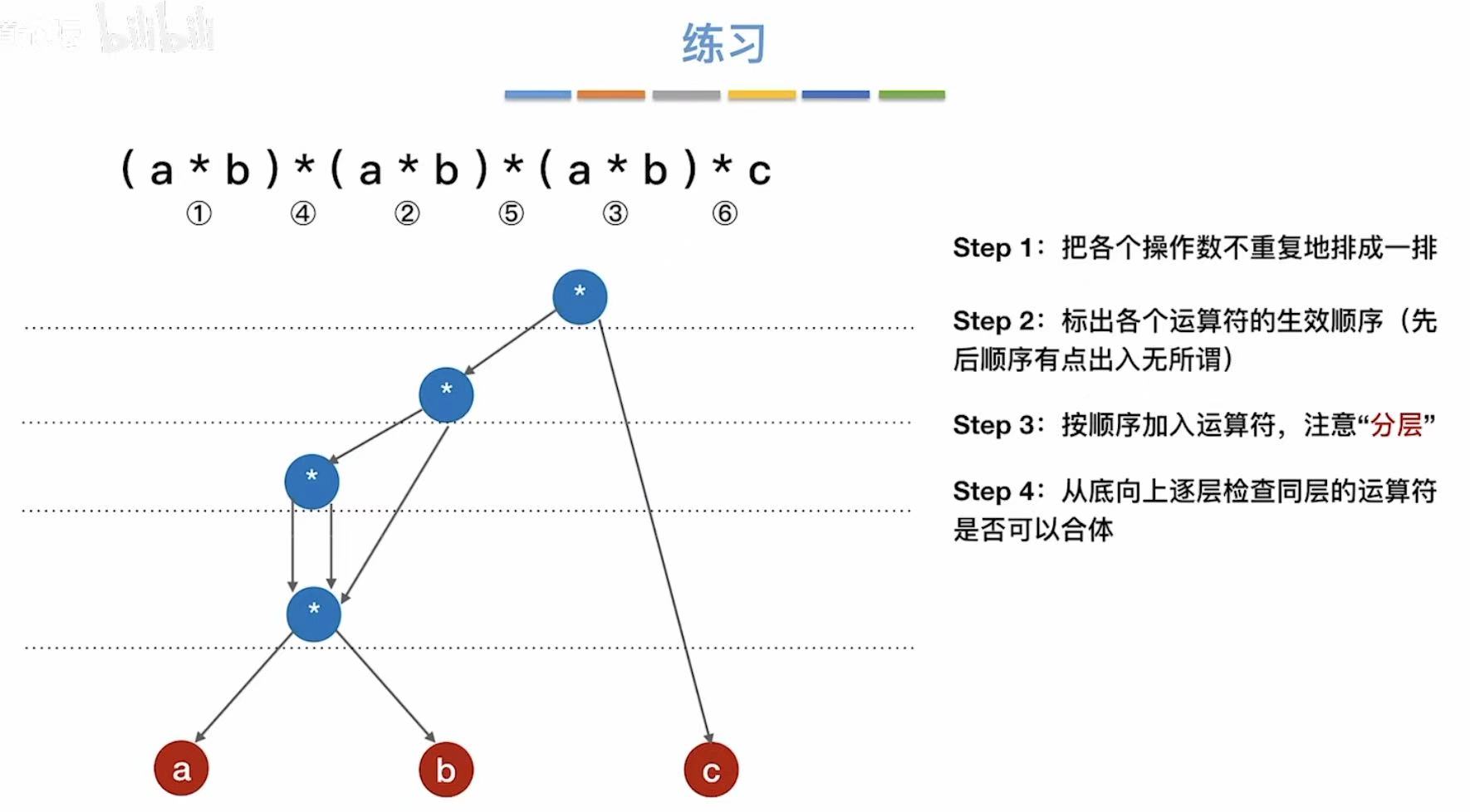
1. 分类
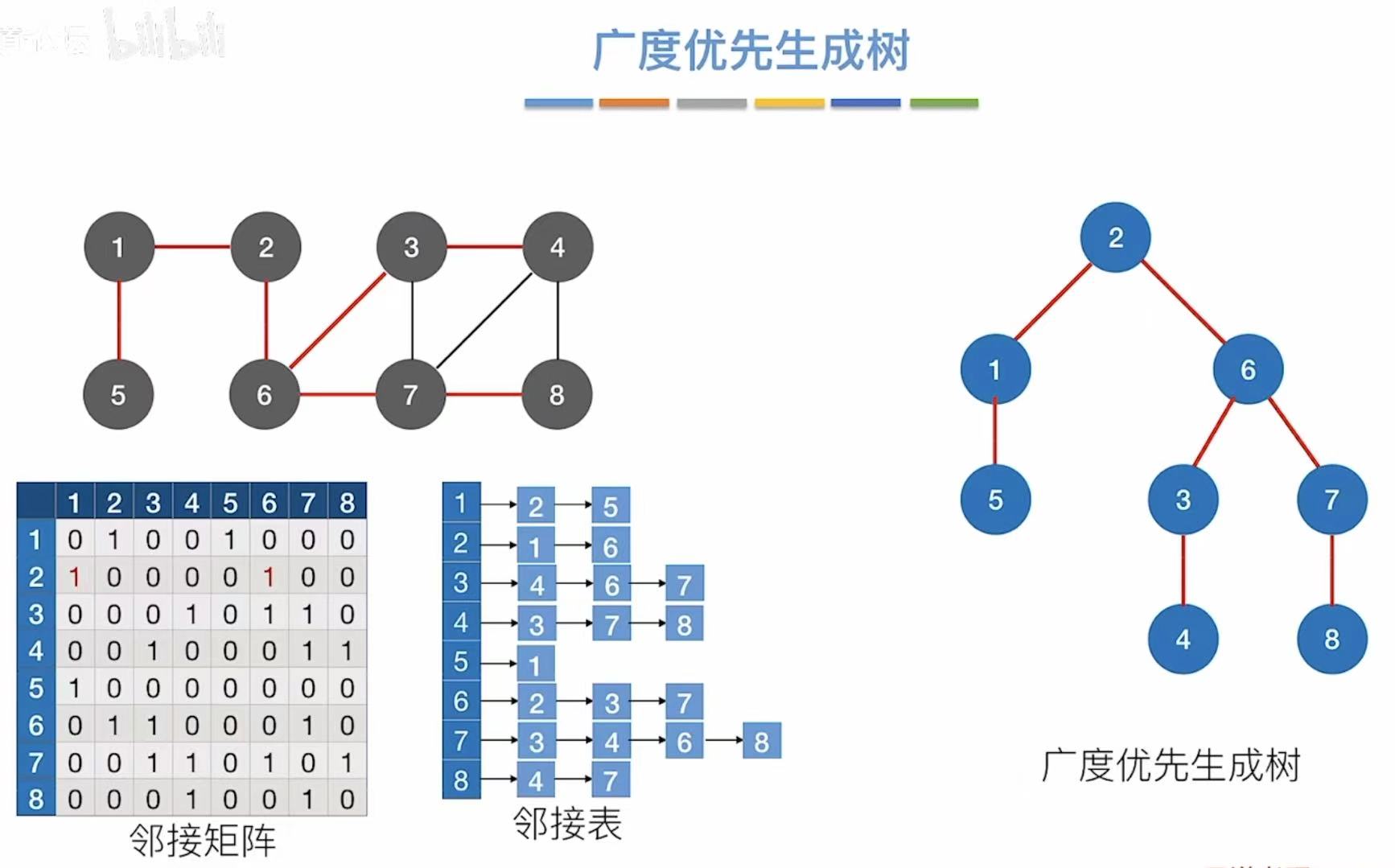
1.1 广度优先生成树
广度优先遍历可见:广度优先遍历(BFS)
1.2 深度优先生成树
深度优先遍历可见:深度优先遍历(DFS)
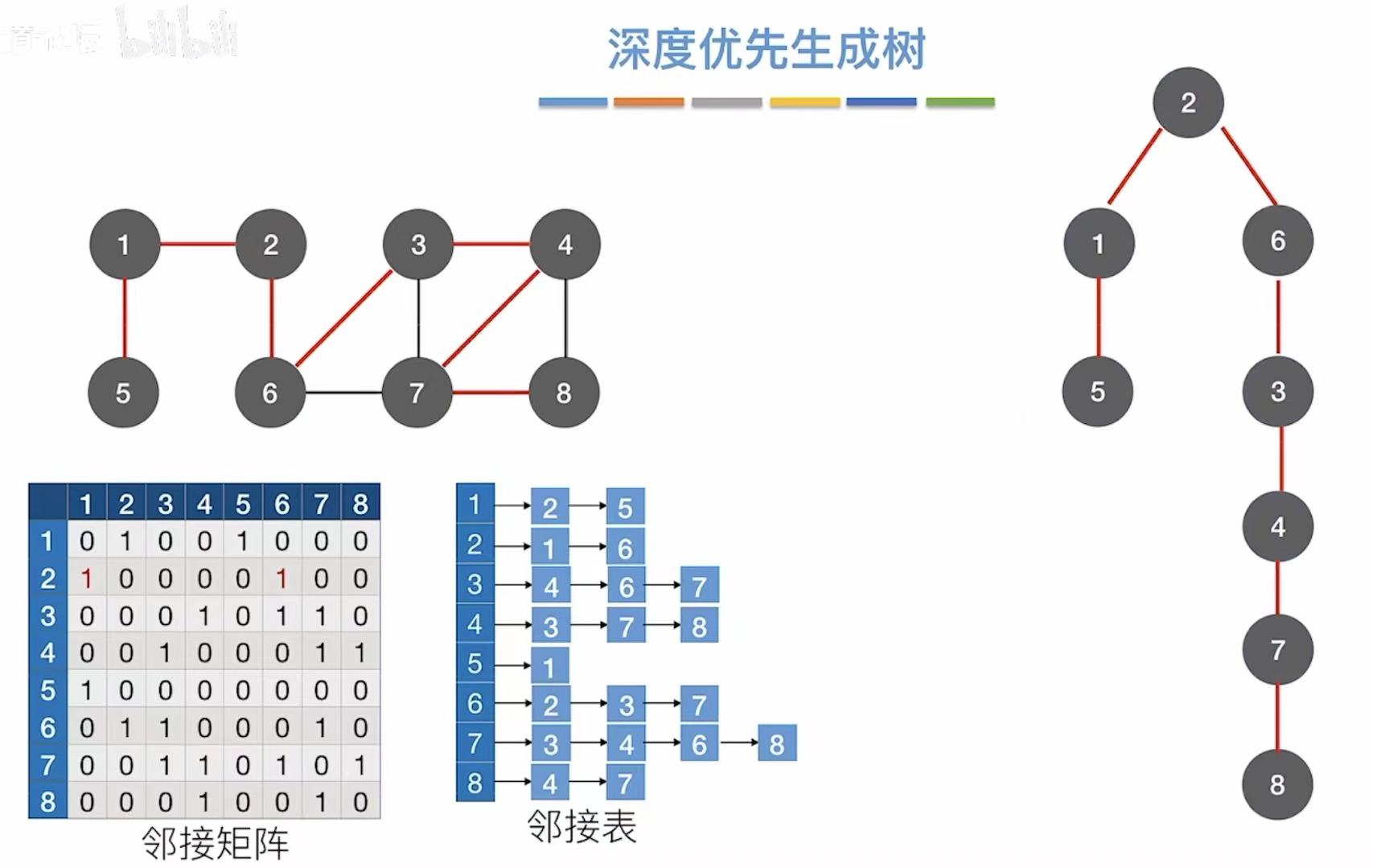
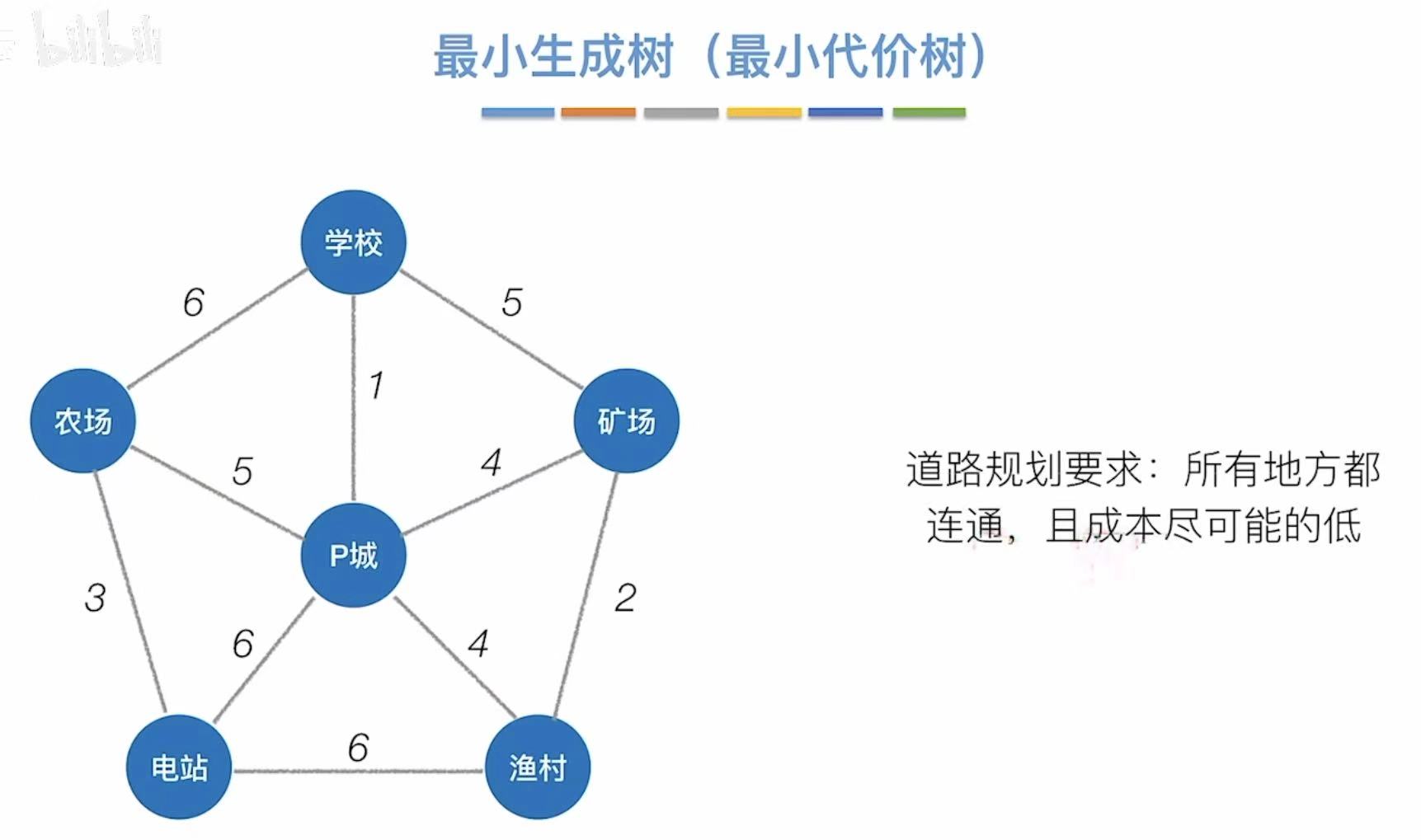
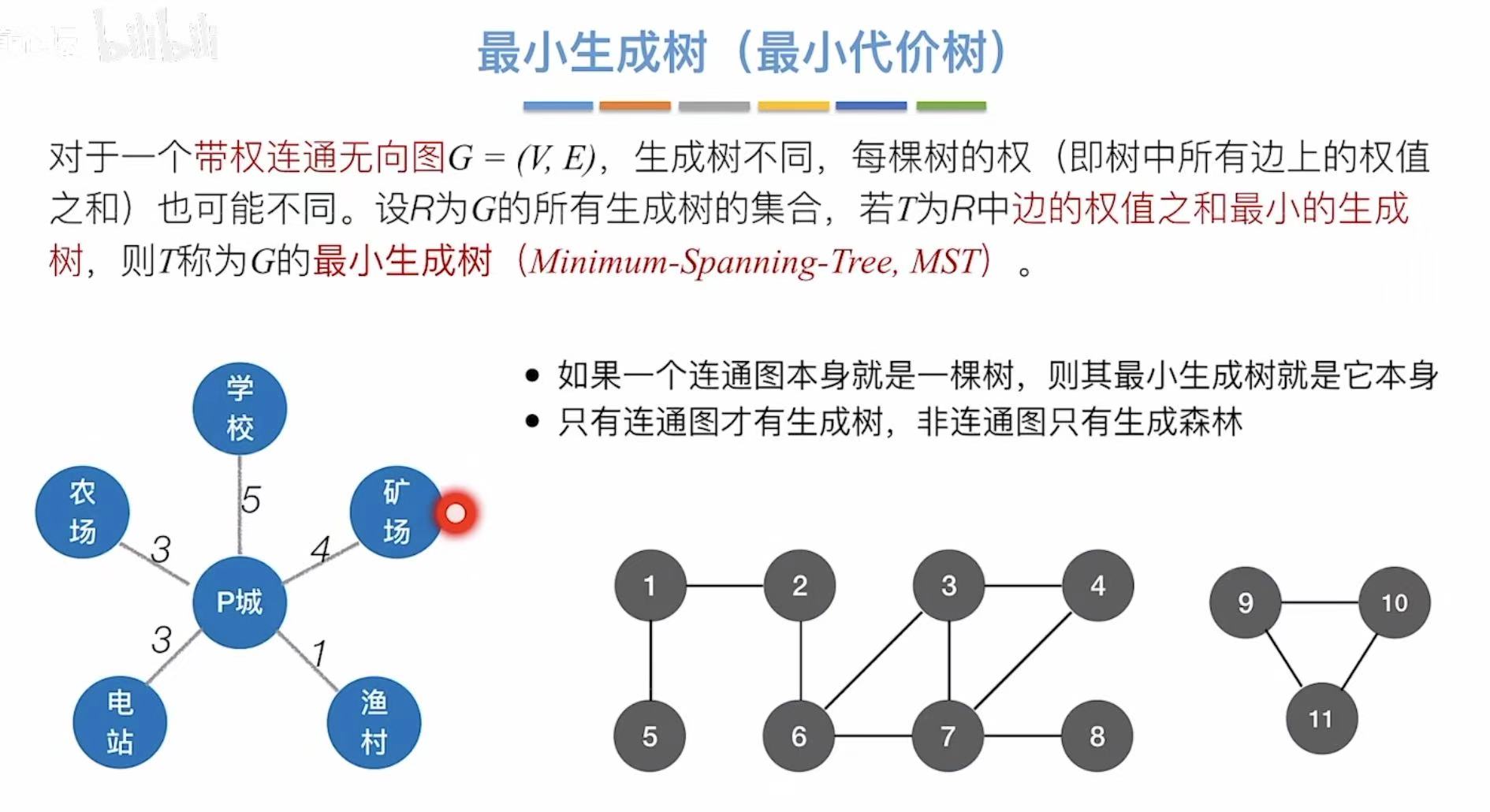
1.3 最小生成树
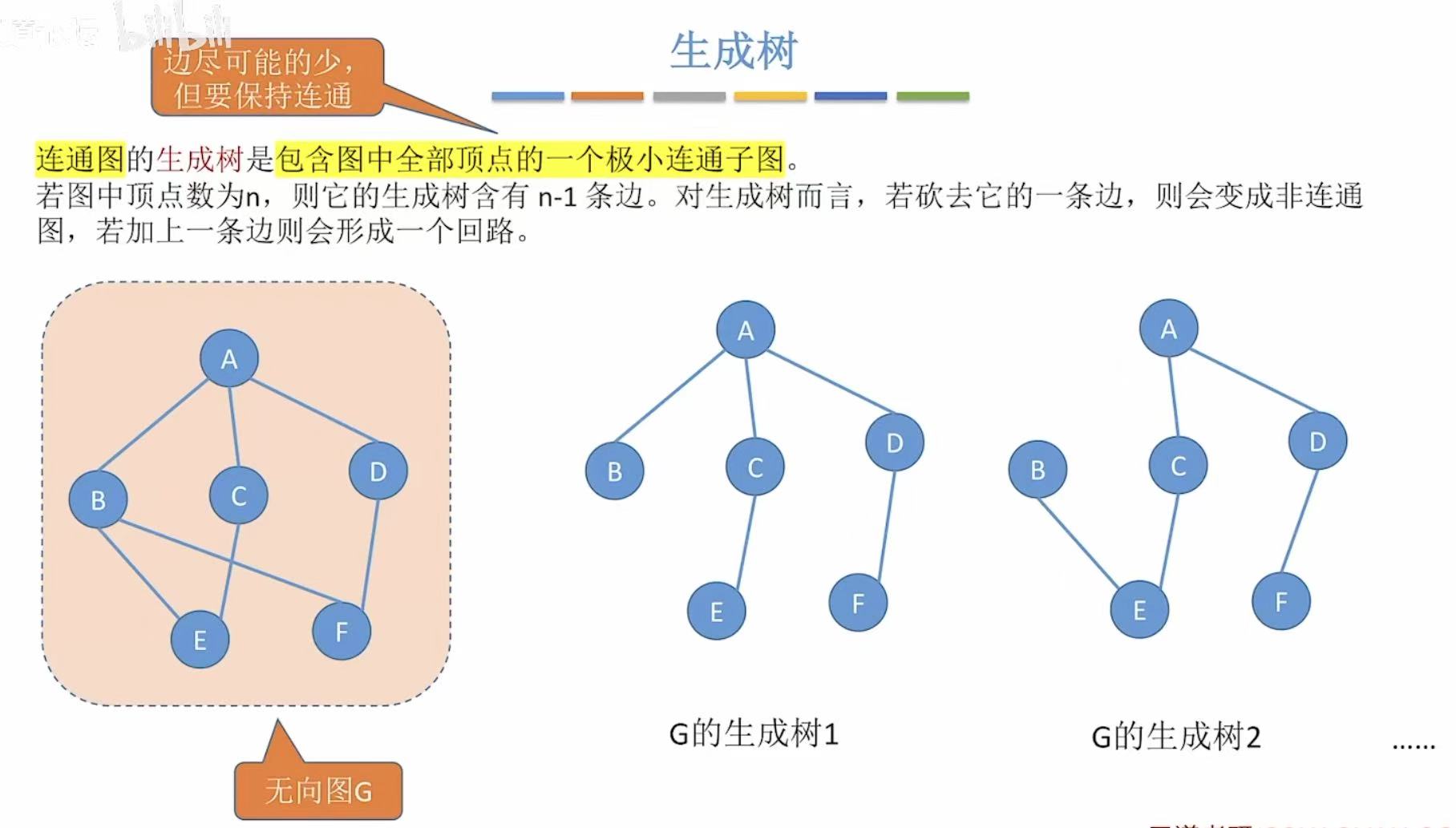
情景 :比如我们是一个铁路承包商,我们想在这几个地点中间修路,从一个地点可以随意到达另一个地点,那么怎么修我们的成本最低?
道路规划要求 :所有地方都连通,且成本尽可能的低。
如果我们随意地将所有地点与中间连通,如左图,我们就会付出19的代价-->权值
但如果是像右图一样,我们就可以减少需要付出的代价
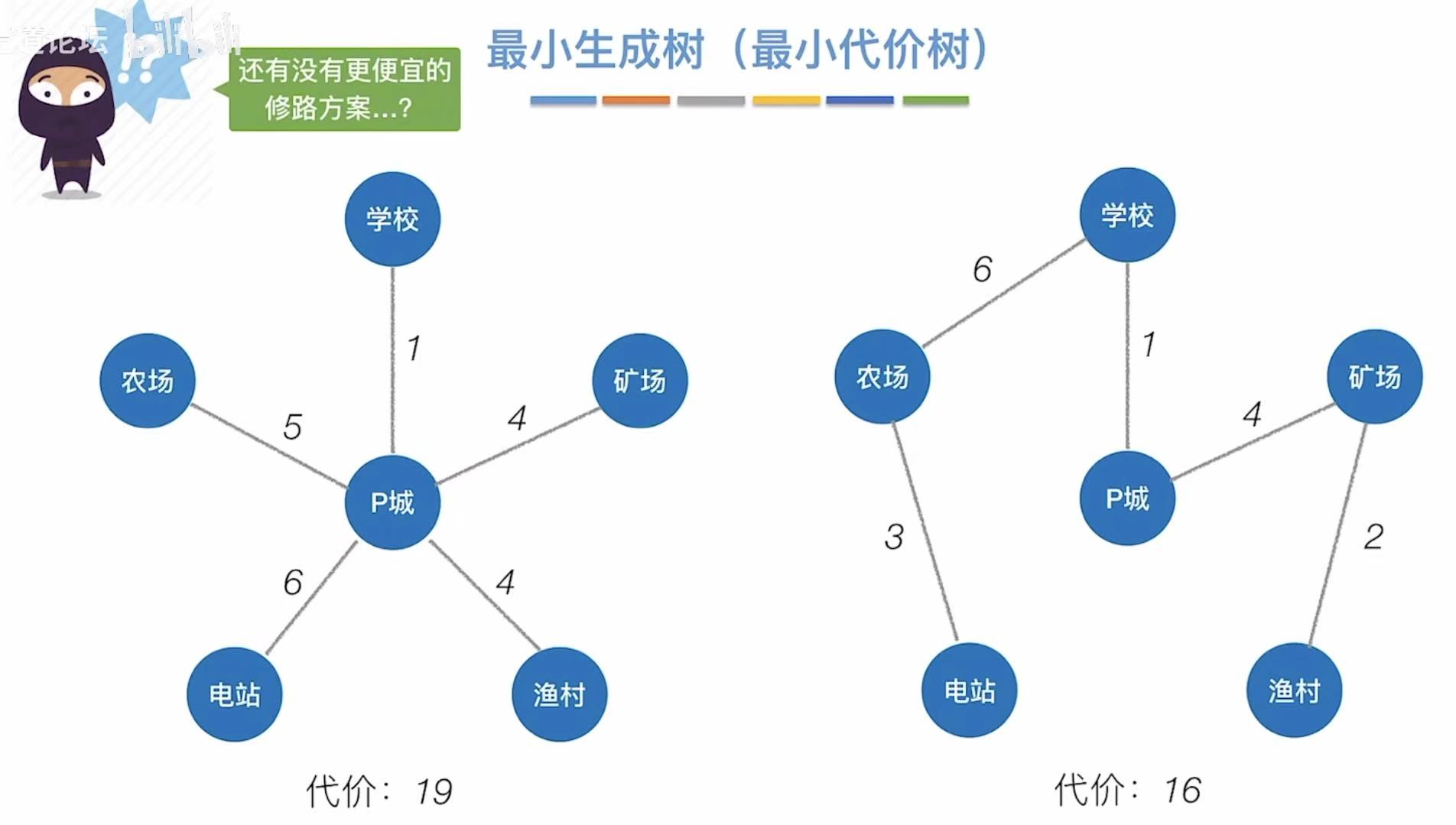
付出代价最小的树就是最小生成树。
- 最小生成树可能有很多个,但边的权值之和总是唯一且最小的。
- 最小生成树的边数=顶点数-1.砍掉一条则不连通,增加一条则会出现回路。
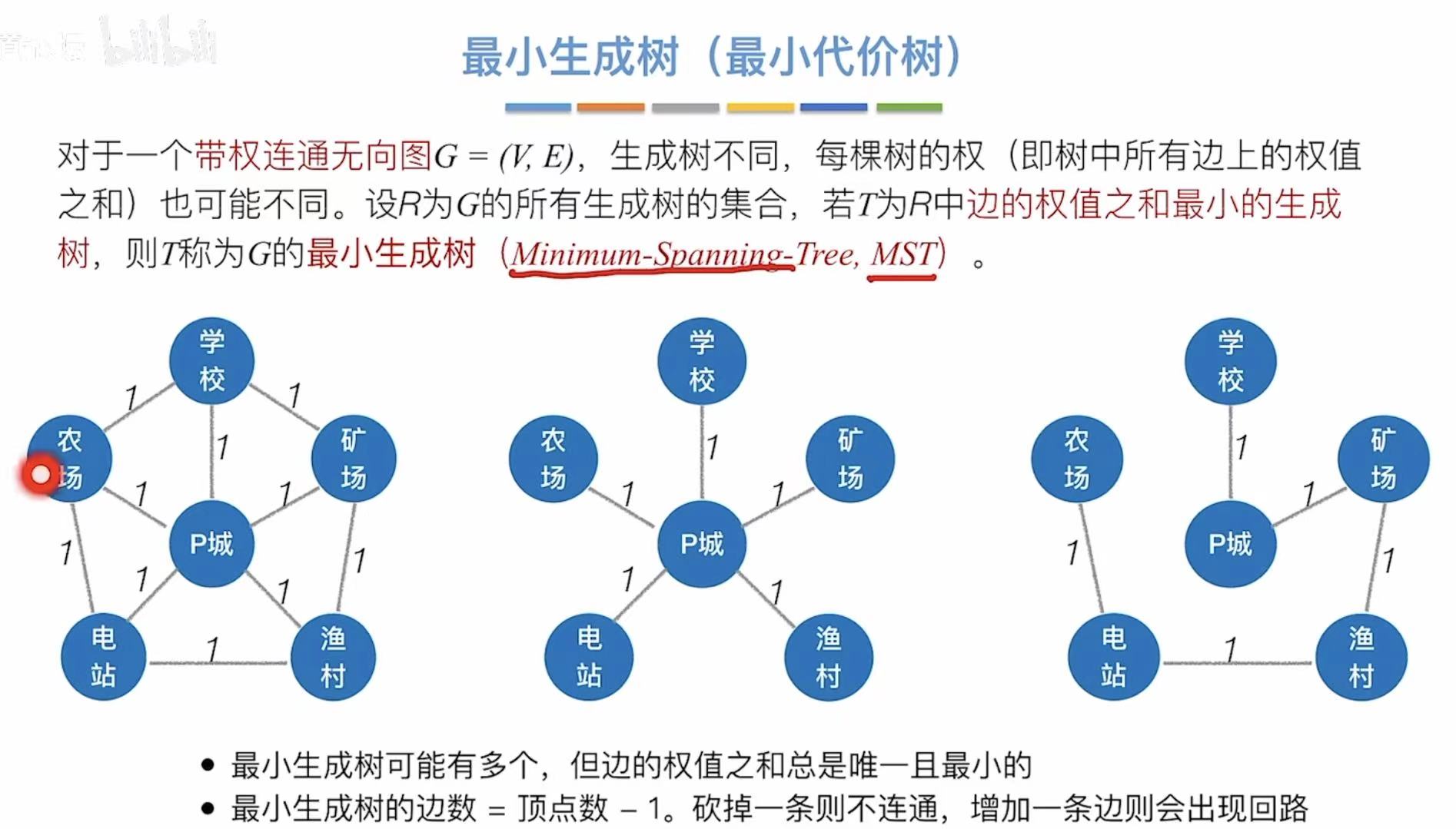
- 如果一个连通图本身就是一棵树,则其最小生成树就是它本身。
- 只有连通图才有生成树,非连通图只能生成森林。
小总结:

2. 算法实现
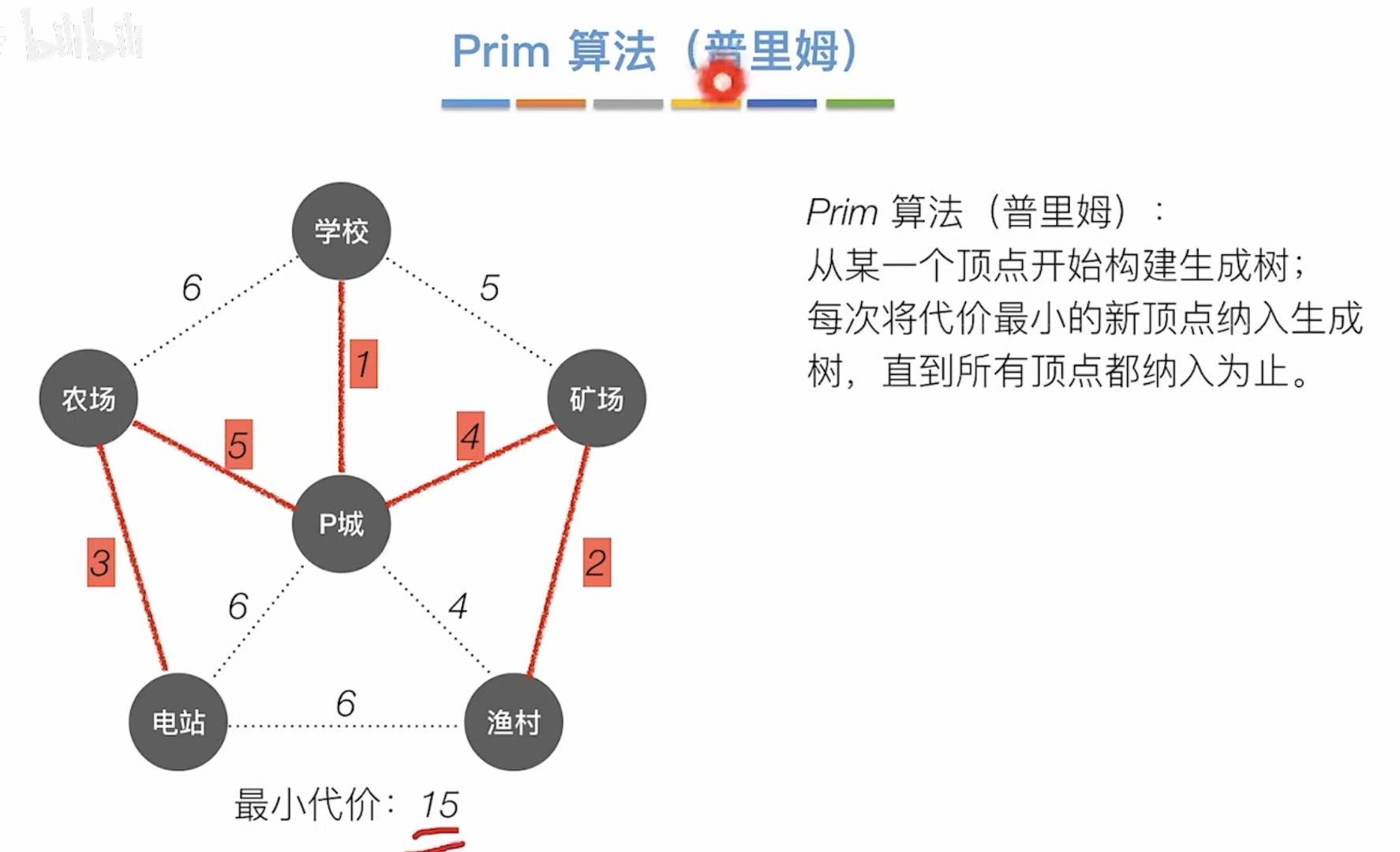
2.1 Prim算法
以顶点 为主要影响因素。
每纳入一个新的顶点,就把它加入之前的集合,然后一步一步找最小的权值的边。
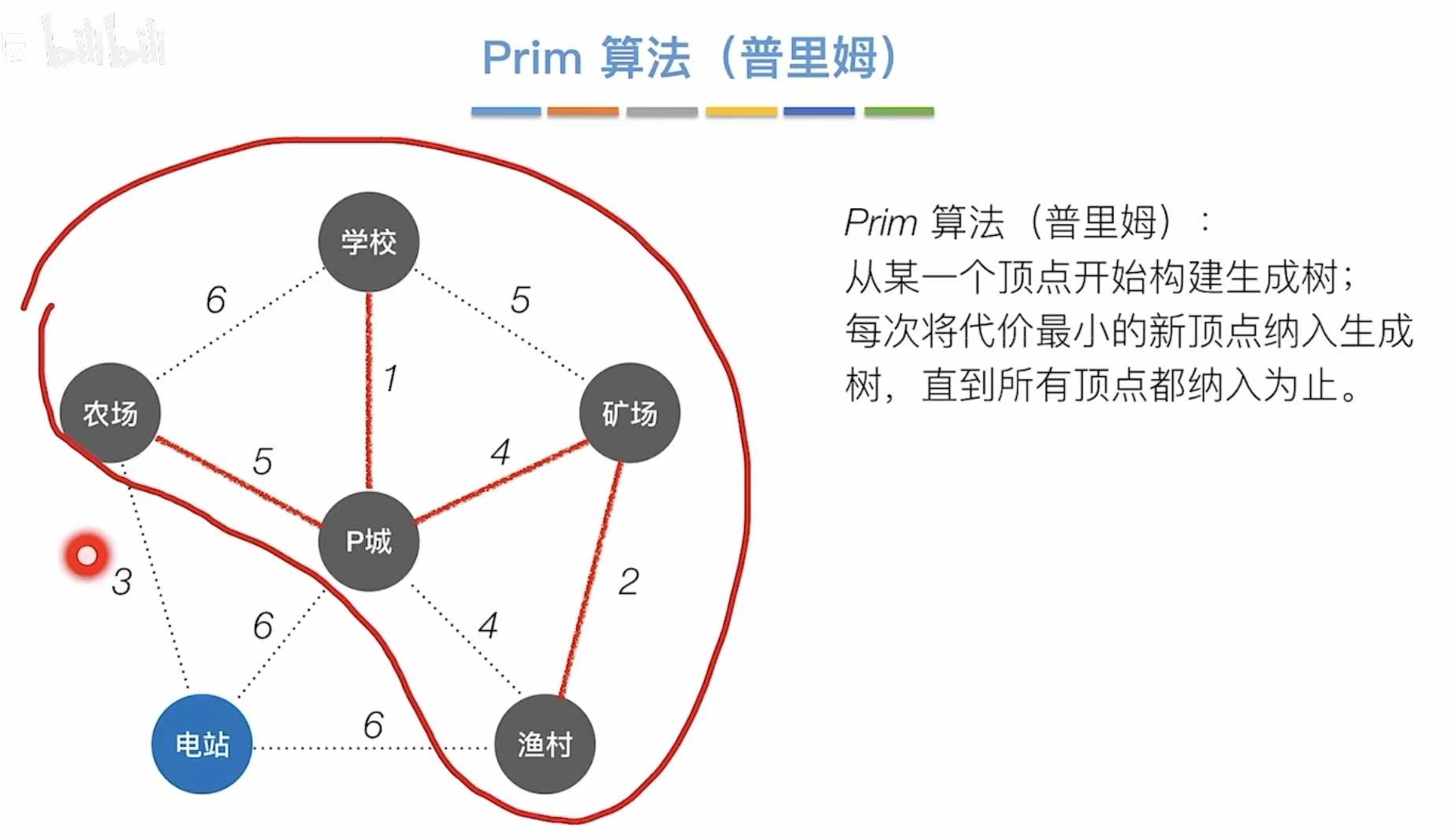
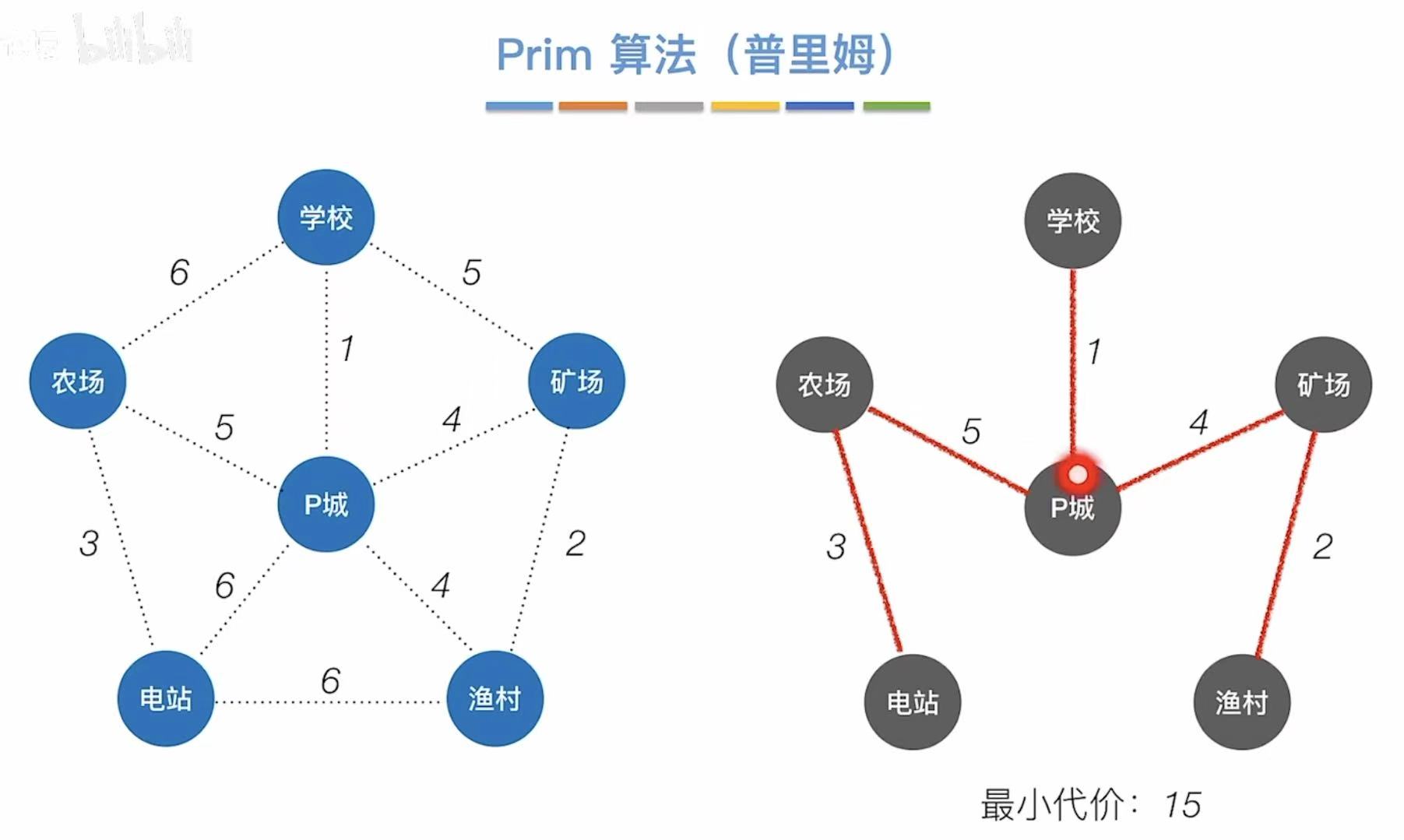
如右图就是最小生成树。
当然,最小生成树不唯一,下面的两个图也是最小生成树。
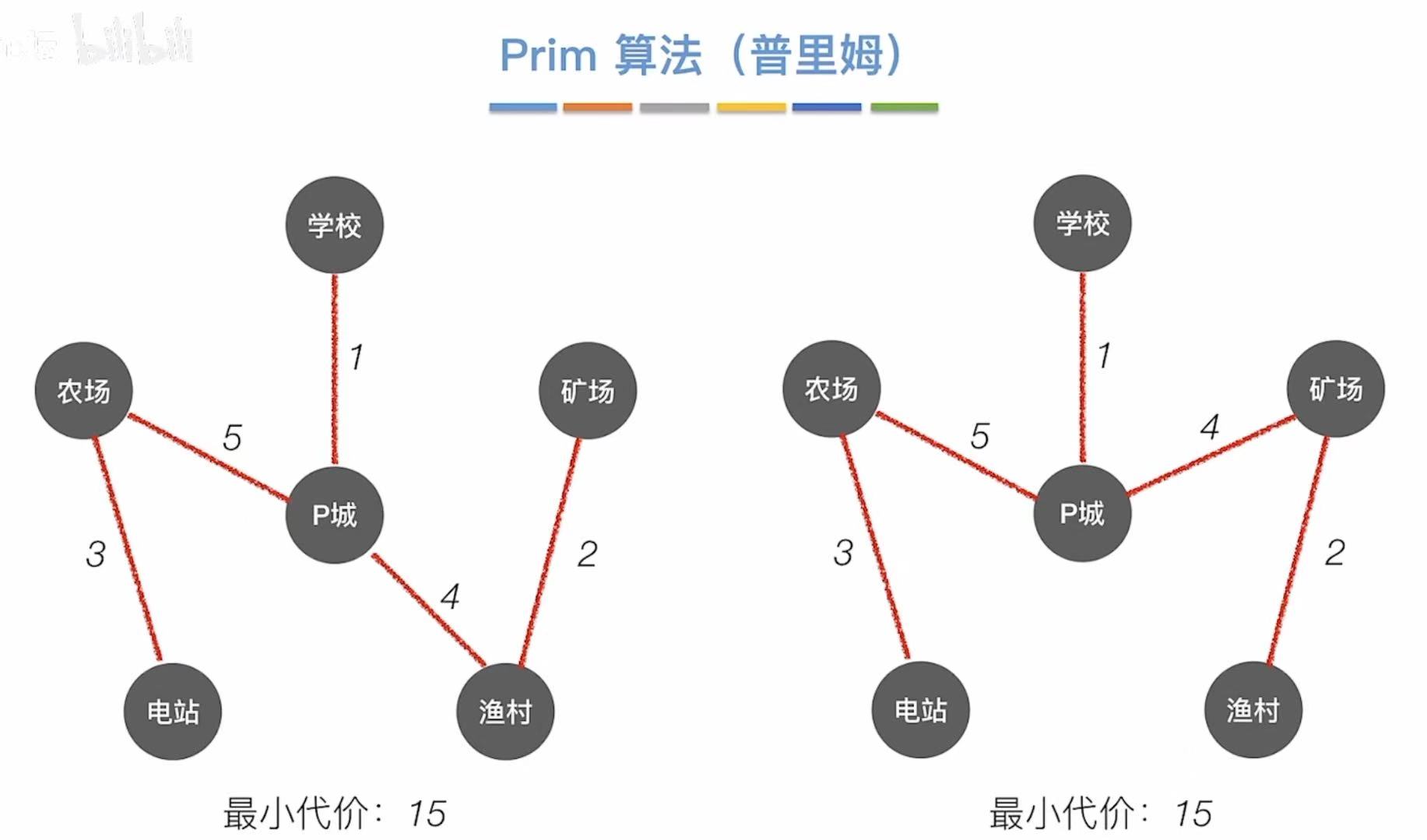
从学校开始:
- 学校、P城 最短:1
- 学校--1--P城、渔村 最短:4
- 学校--1--P城--4--渔村、矿场 最短:2
- 学校--1--P城--4--渔村--2--矿场、农场 最短:5
- 学校--1--P城--4--渔村--2--矿场--5--农场、电站 最短:3
- 总代价:1 + 4 + 2 + 5 + 3 = 15
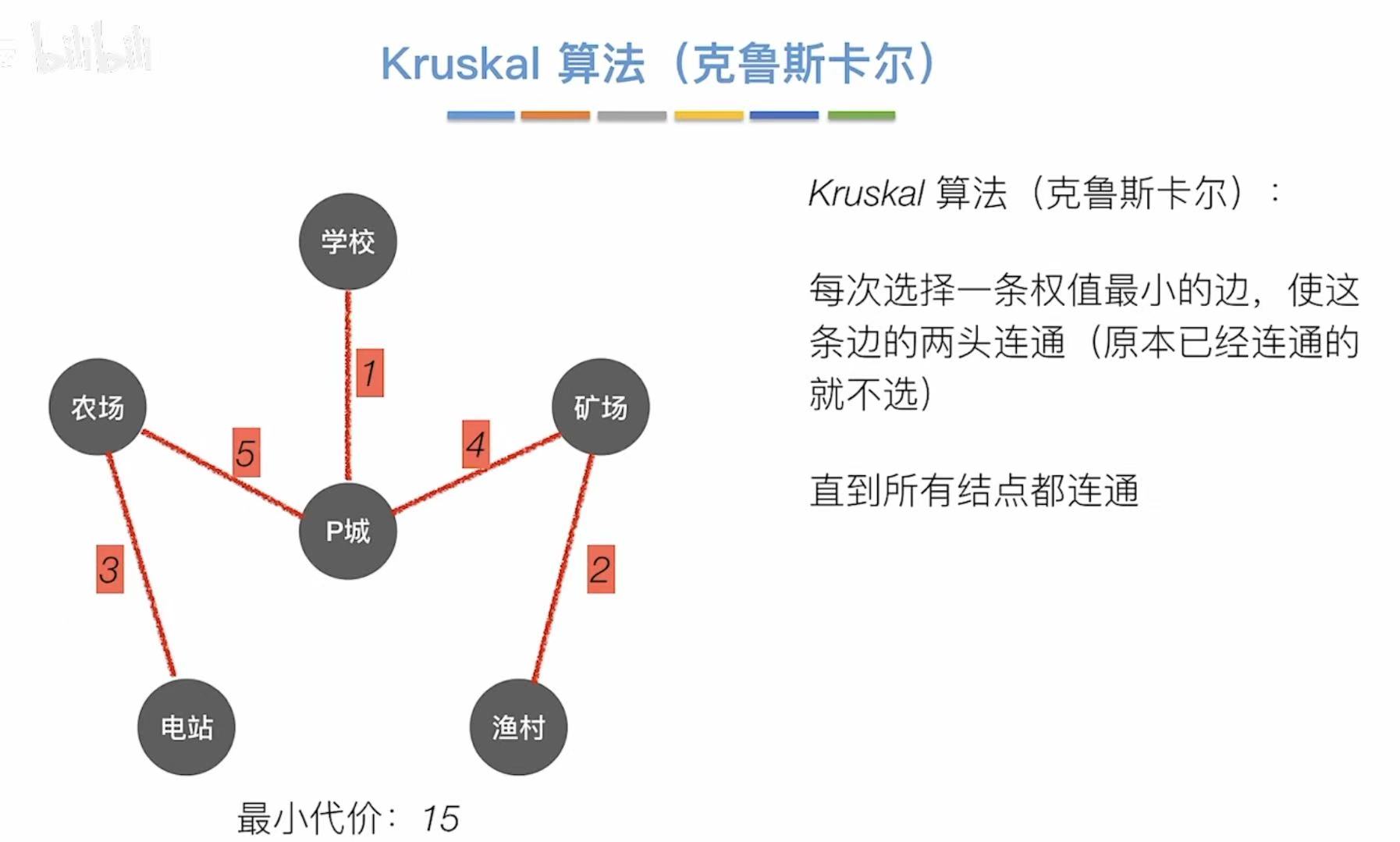
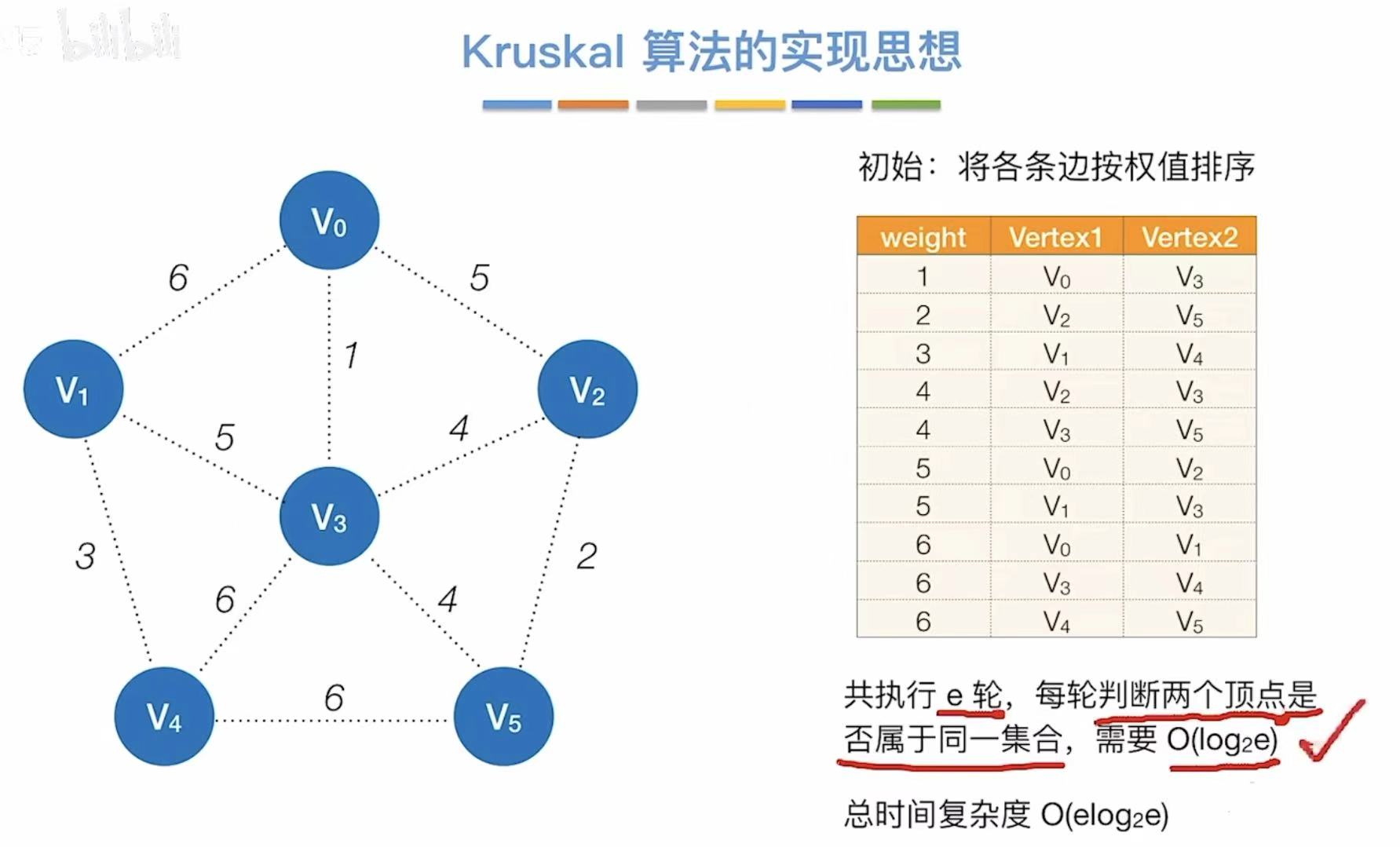
2.2 Kruskal算法
以边 为主要影响因素。
先挑边,再连的顶点。
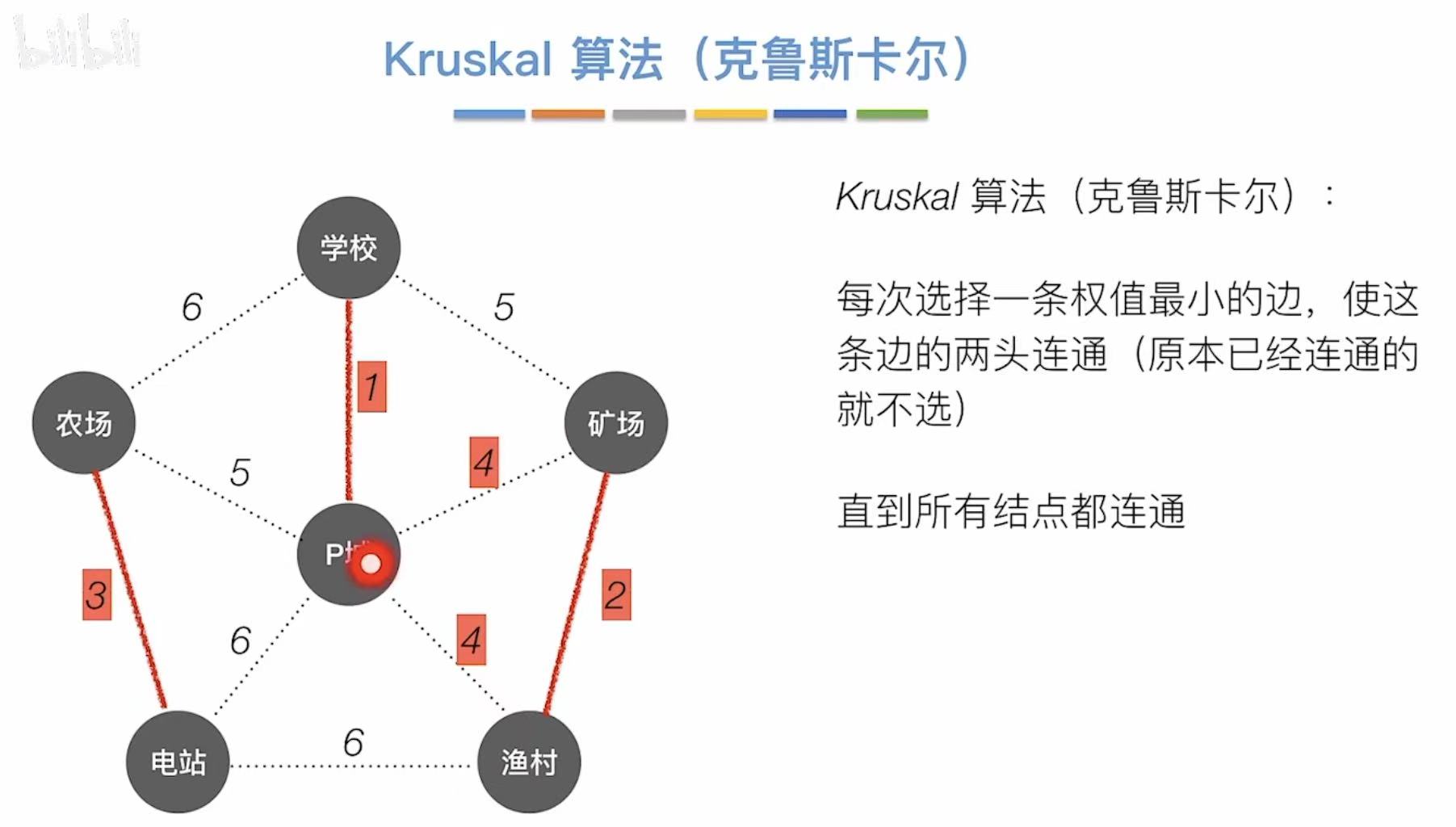
- 学校--P城(1)
- 渔村--矿场(2)
- 农场--电站(3)
- P城--矿场(4)
- 农场--P城(5)
- 总代价 = 1 + 2 + 3 + 4 + 5 = 15
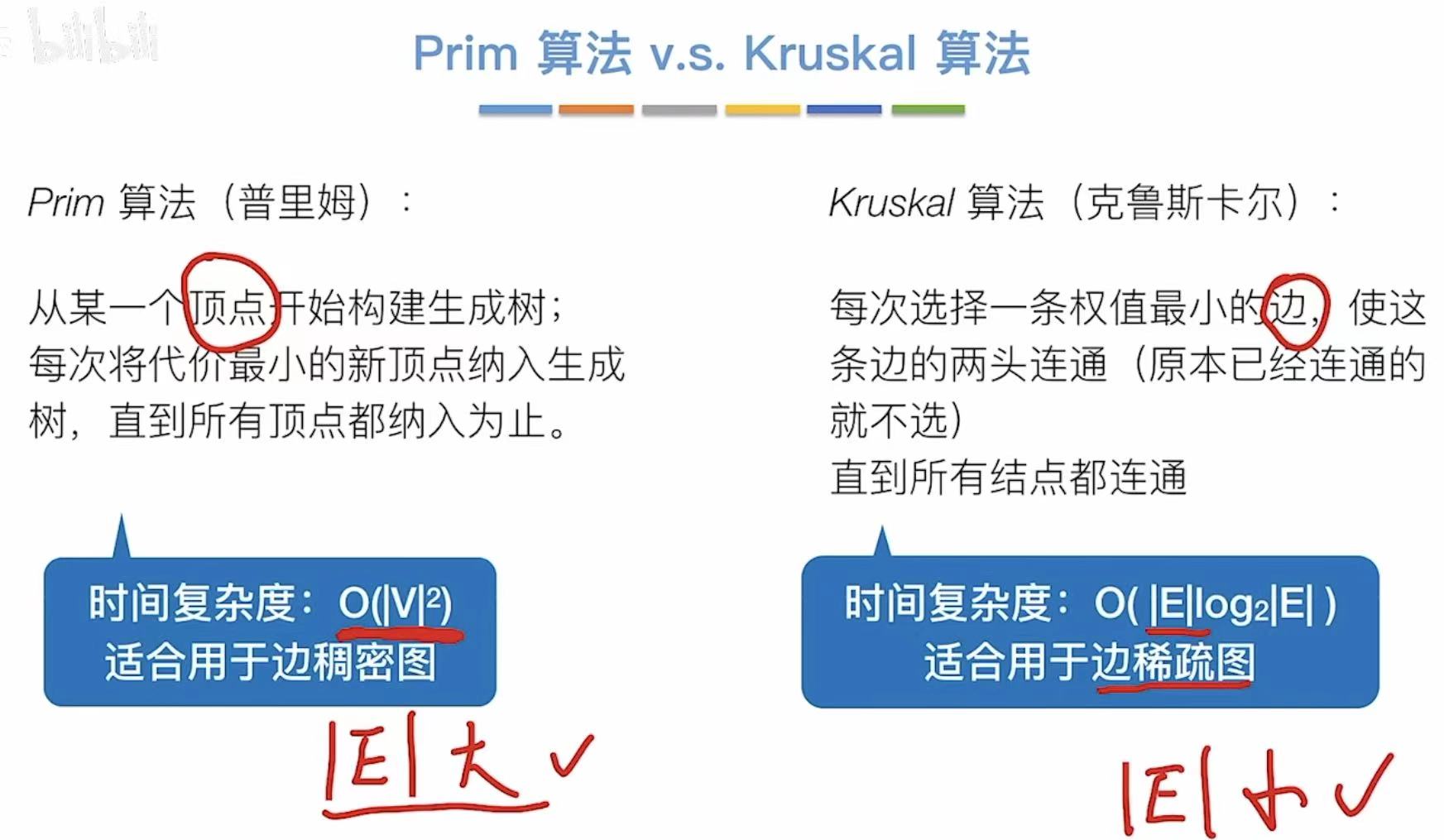
2.3 对比
- V:顶点
- E:边
- Prim算法先定顶点,顶点肯定是重要影响因素,因为边不影响什么,所以适合边多的稠密图。
- Kruskal算法先定边,边肯定是重要影响因素,所以适合边少的稀疏图。
3. 实现思想
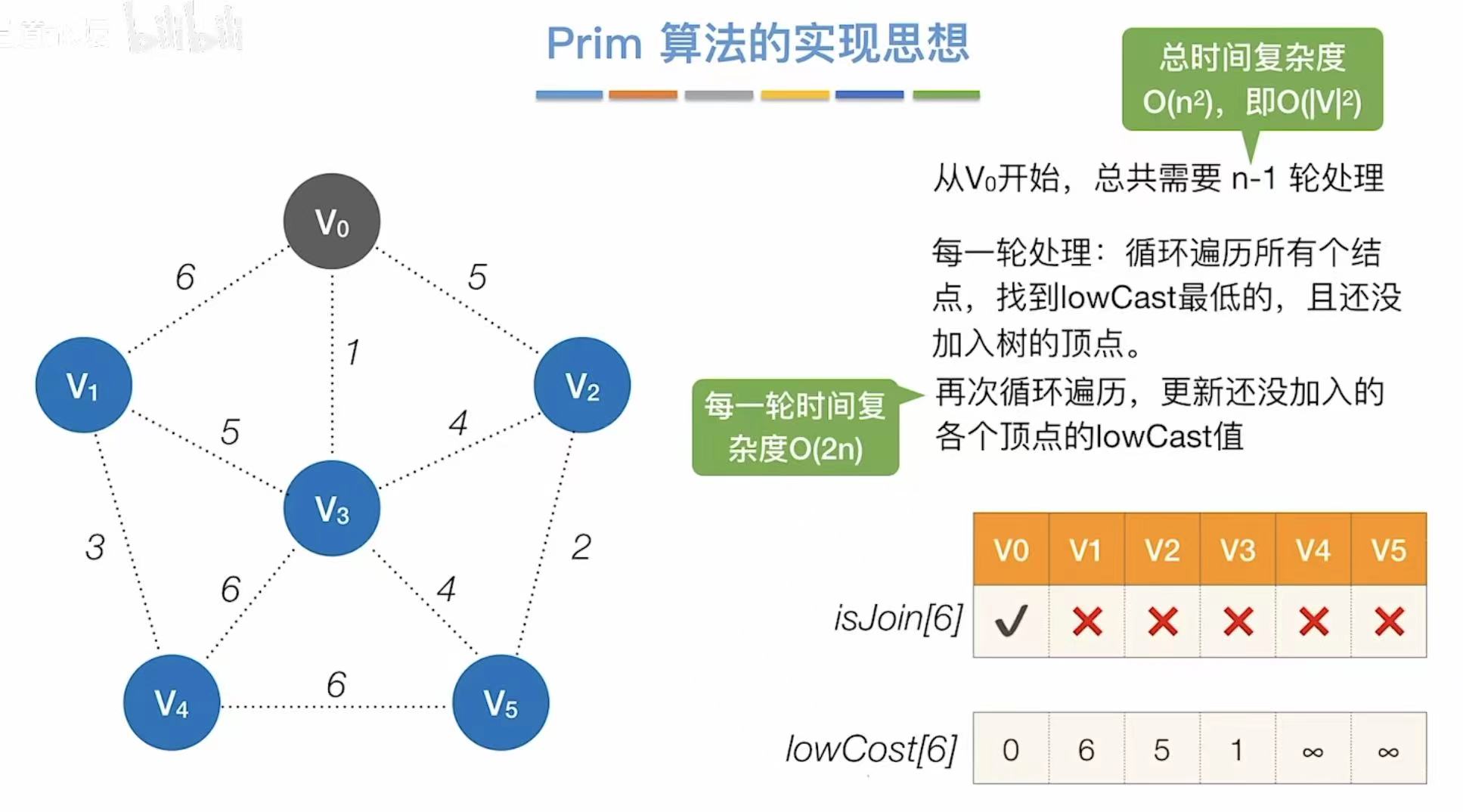
3.1 Prim算法
- v0√:v0已加入树
- ∞:v0没办法直接到v4、v5
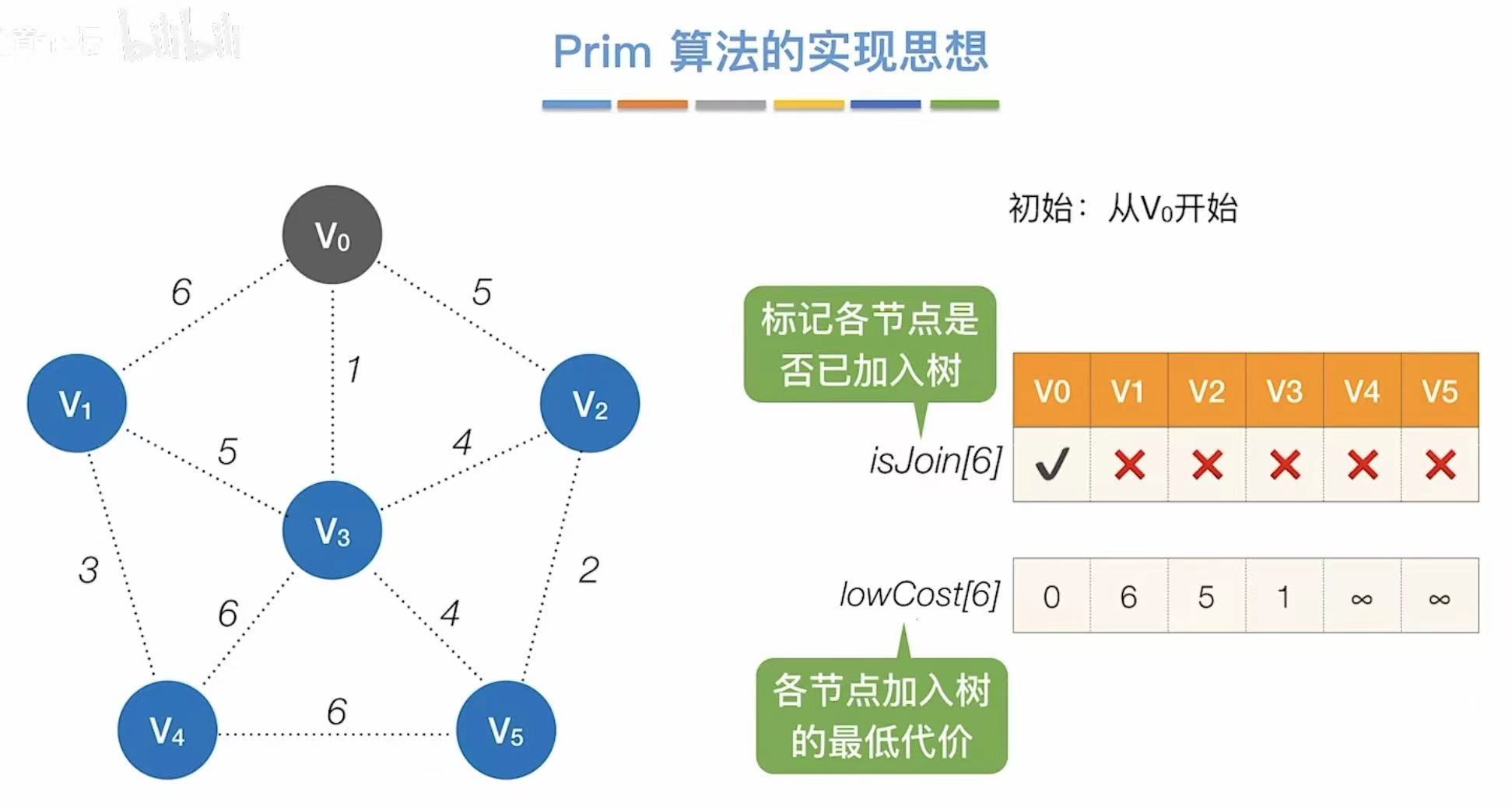
- 找到代价最低的1,则与v3相连
- 更新此时能够连通其他点的最低代价
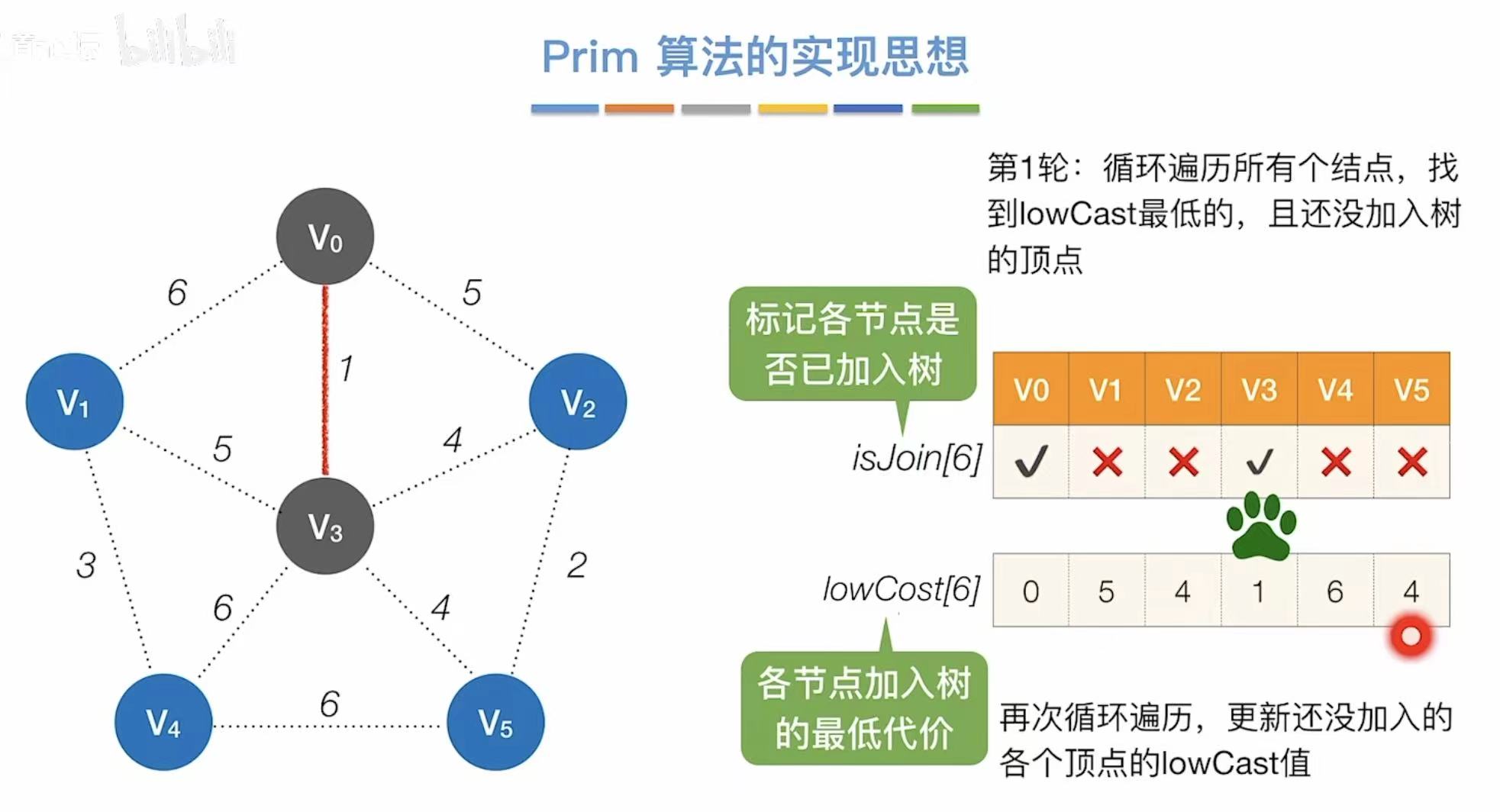
- 找到代价最低的2,则与v5相连
- 更新此时能够连通其他点的最低代价
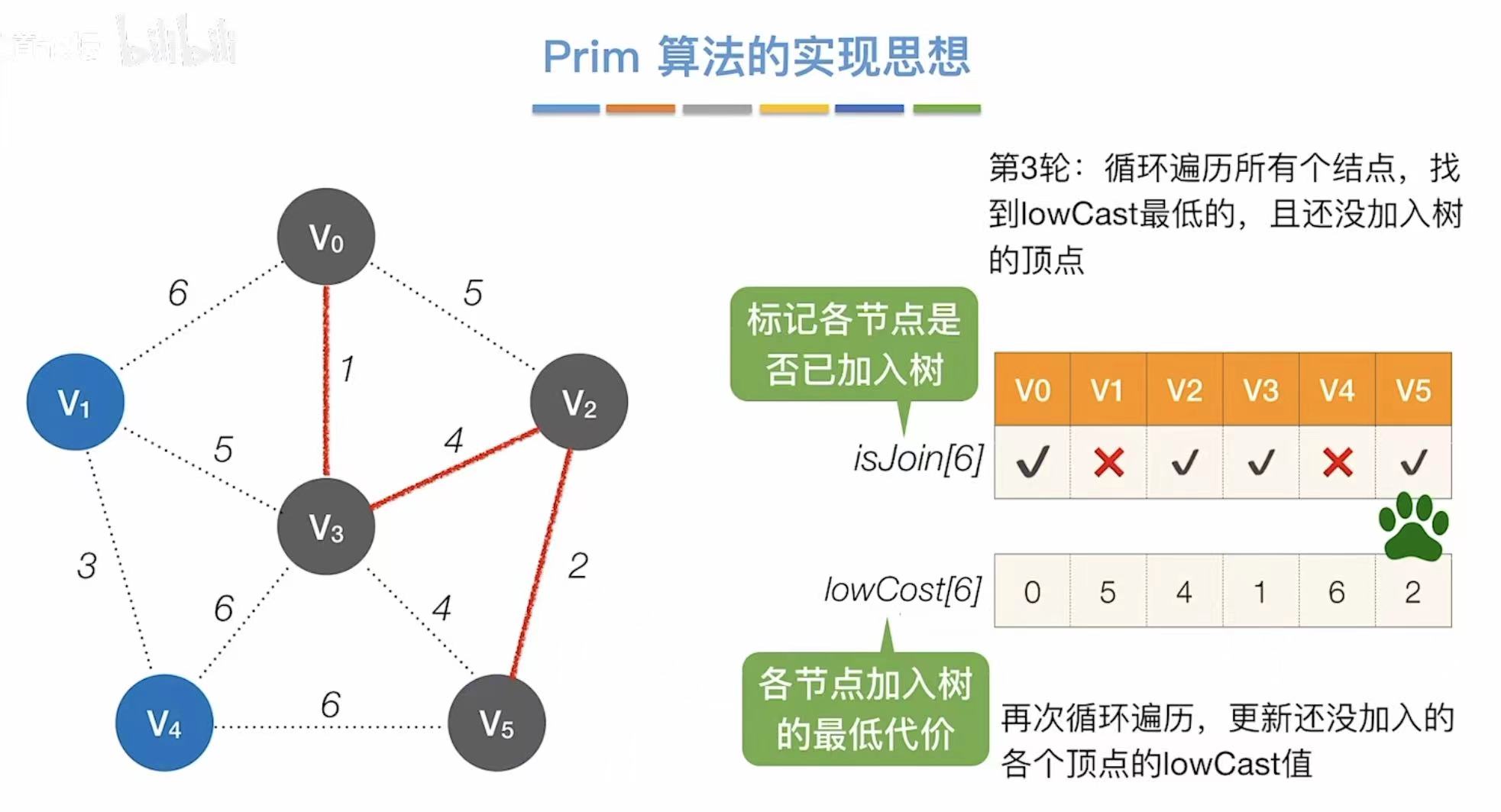
- 找到代价最低的5,则与v1相连
- 更新此时能够连通其他点的最低代价
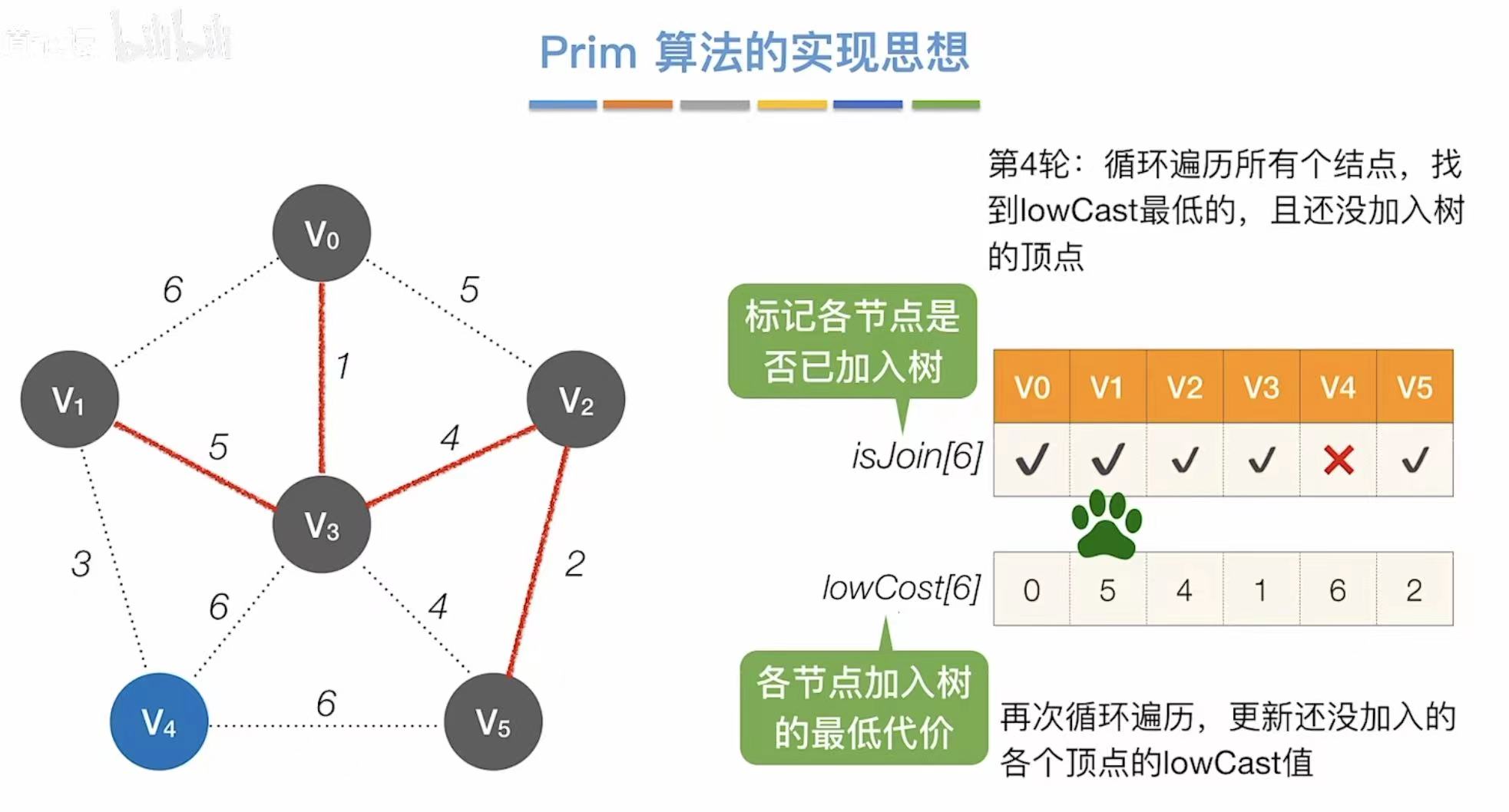
- 找到代价最低的3,则与v4相连
- 更新此时能够连通其他点的最低代价
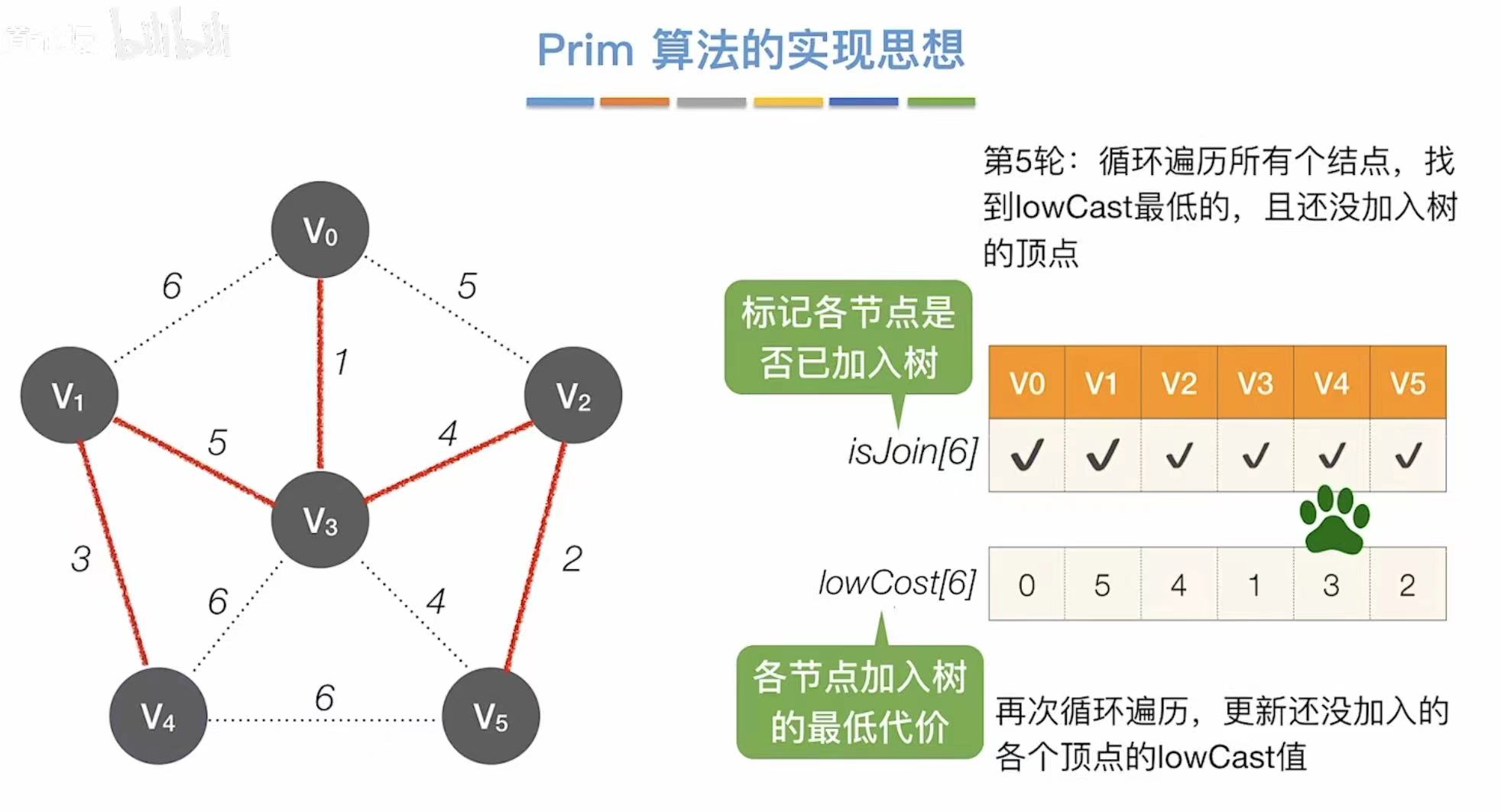
- 每轮时间复杂度:第一次遍历找最低代价,第二次遍历更新表格-->2n
- 总时间复杂度:需要重复n-1轮
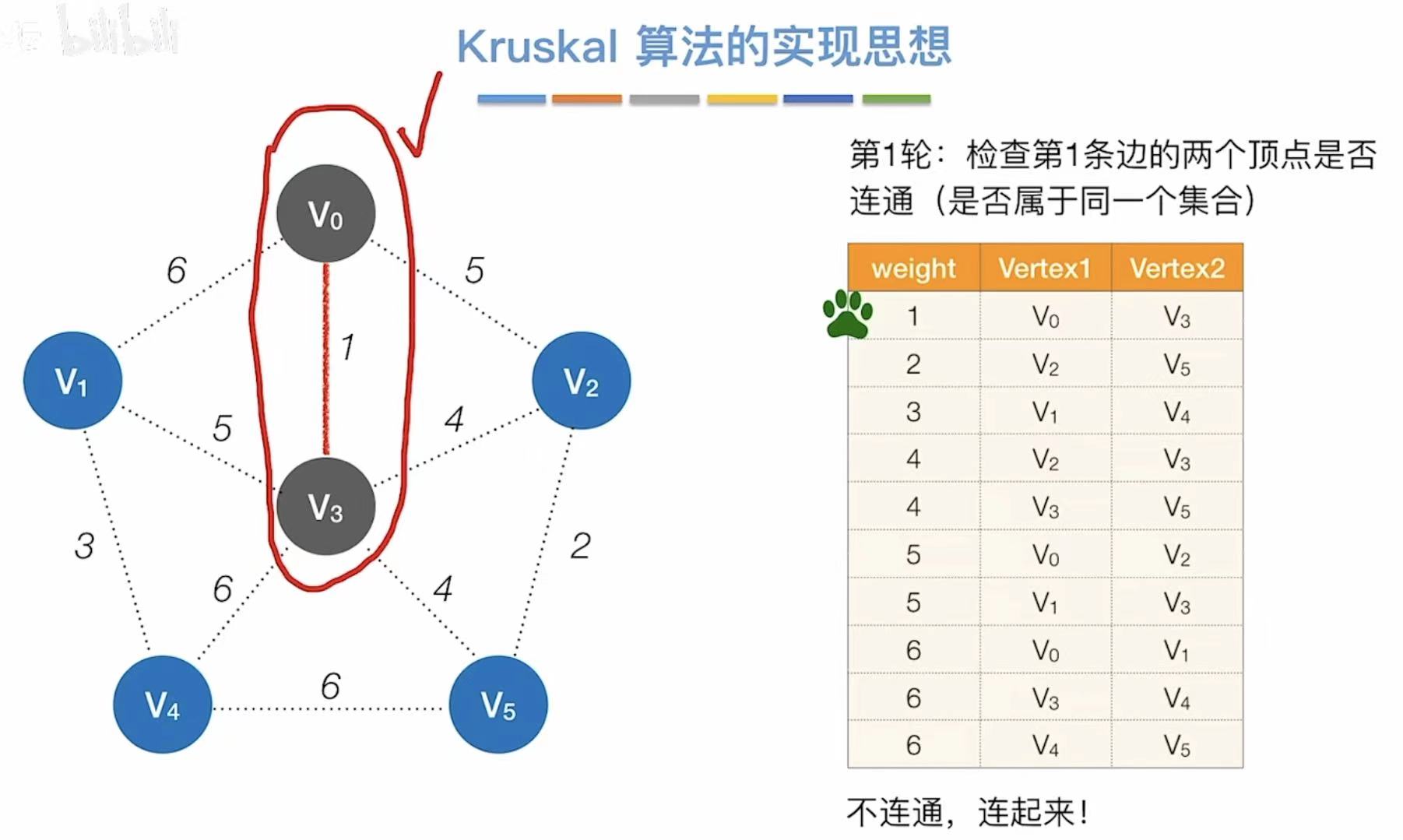
3.2 Kruskal算法
- 最开始就按照权值大小把表排好
- 从最小的开始,看两个顶点连通么
- 不连通就直接相连
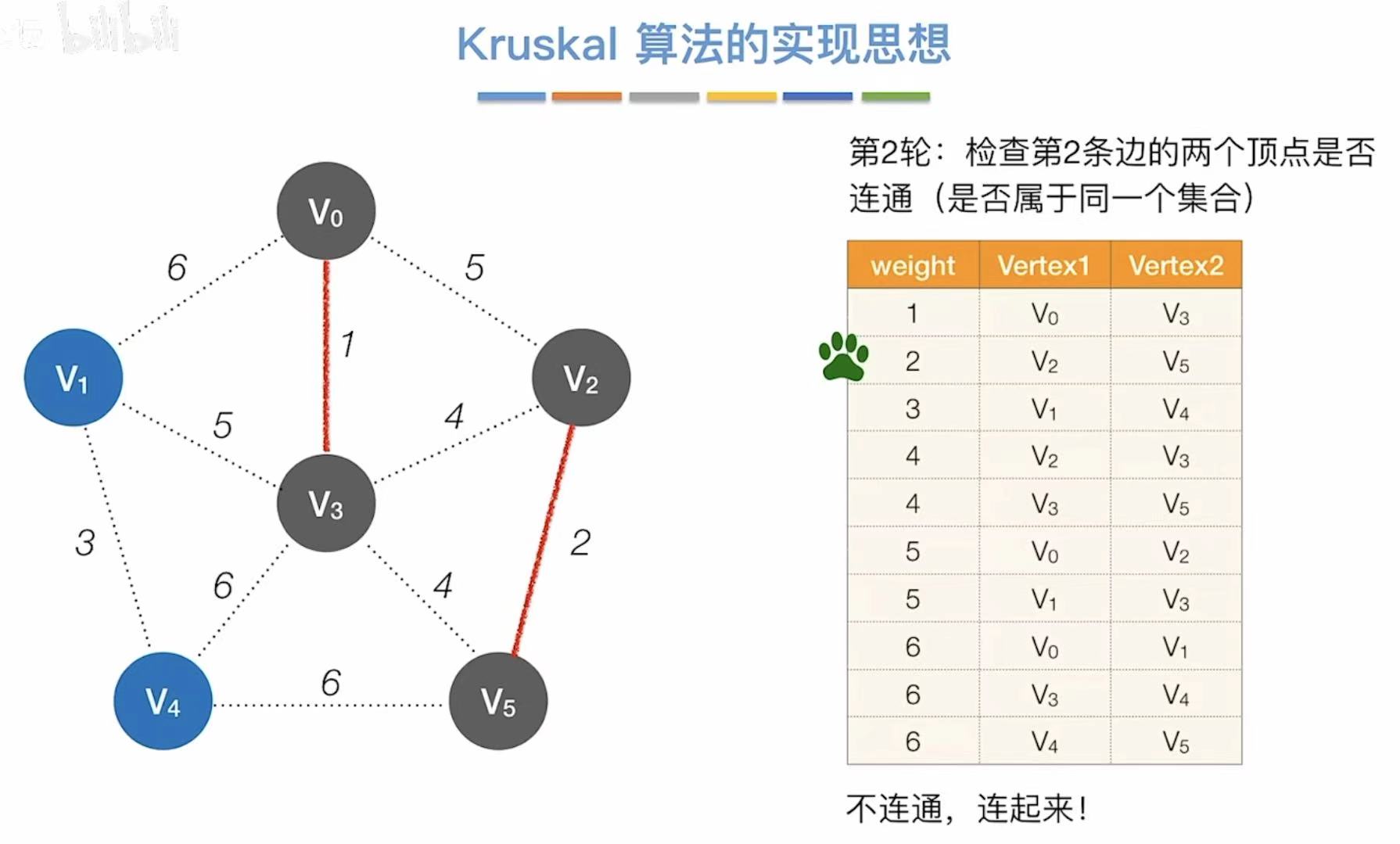
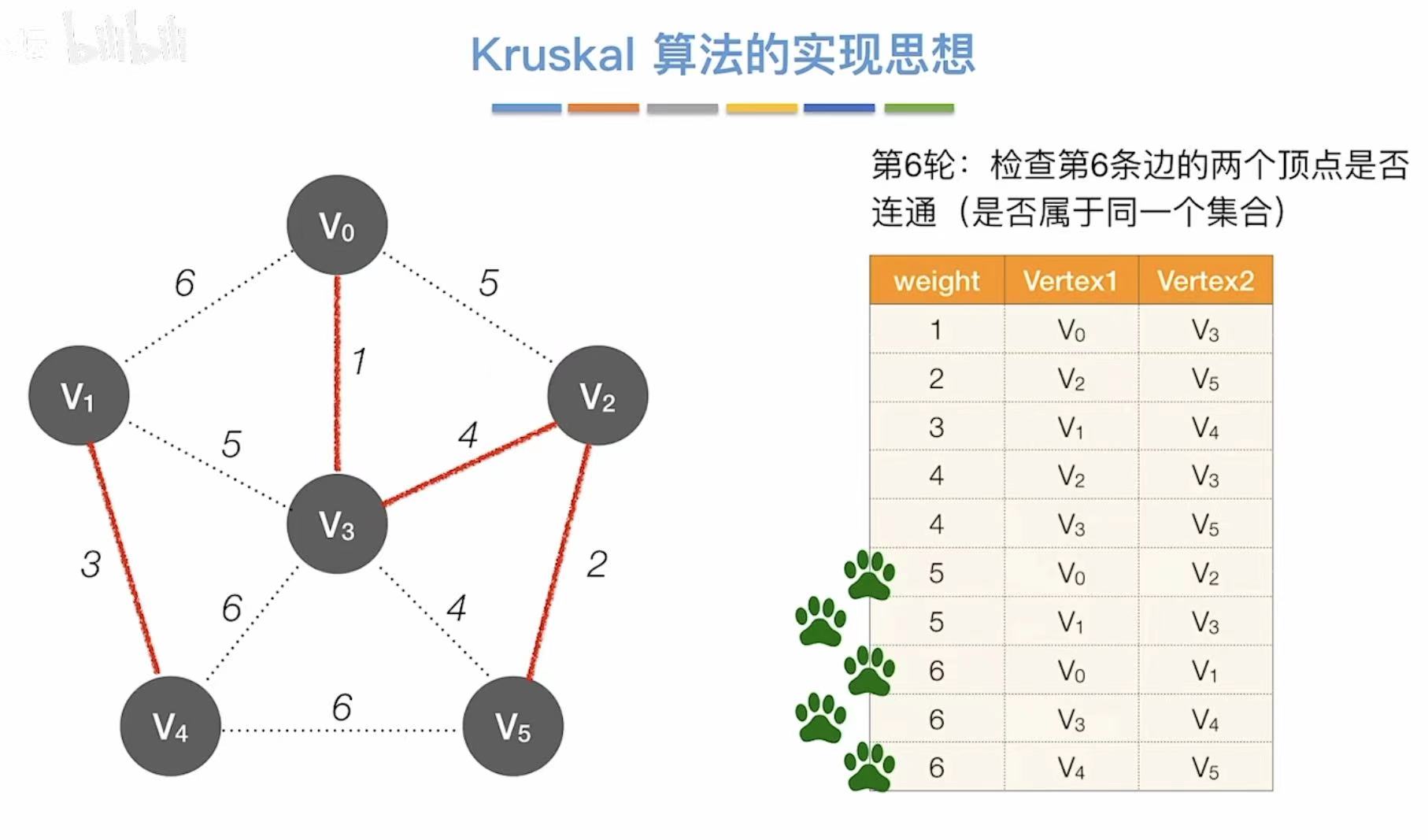
- 依次往后,看两个顶点连通么
- 不连通就直接相连
- 依次往后,看两个顶点连通么
- 不连通就直接相连
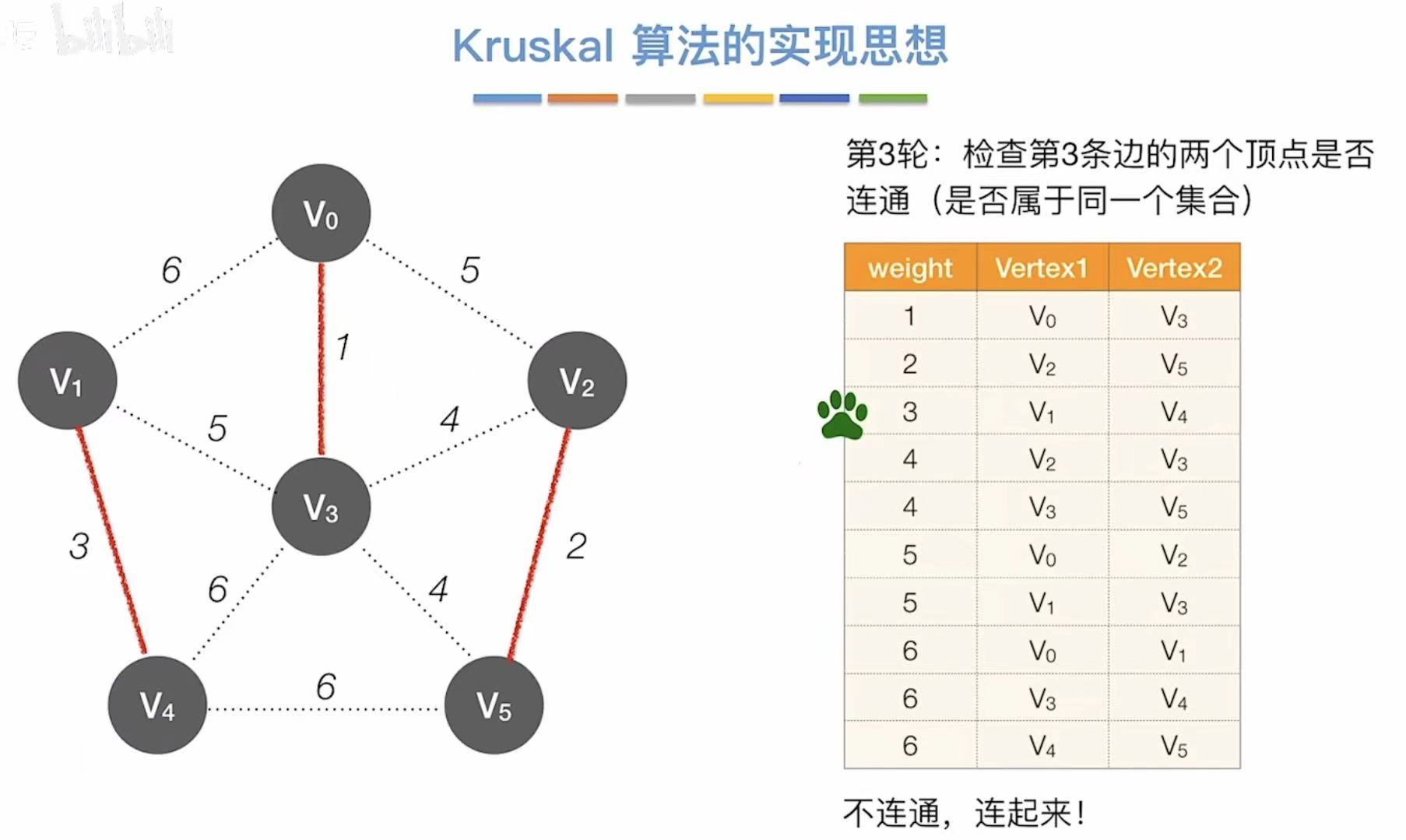
- 依次往后,看两个顶点连通么
- 不连通就直接相连
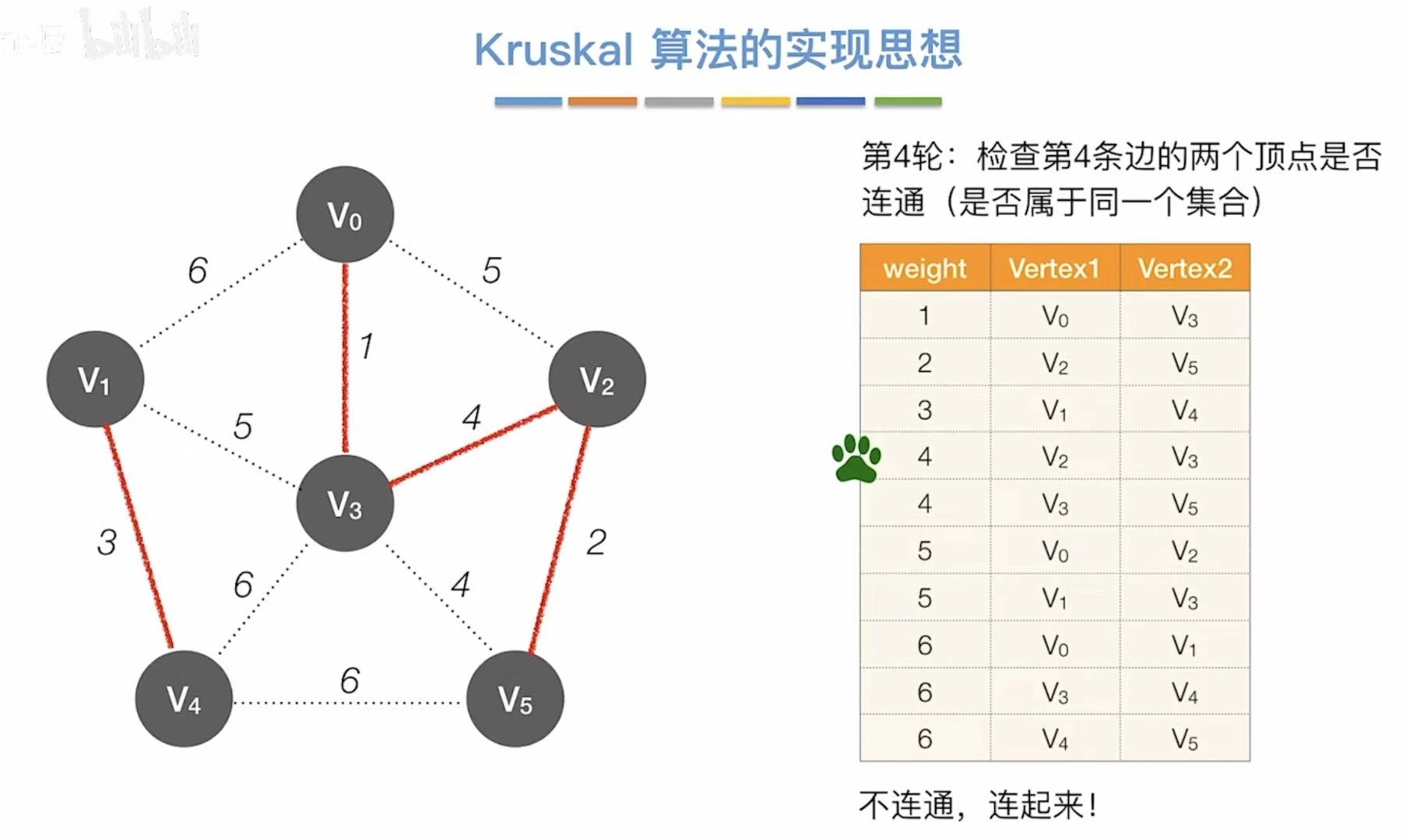
- 依次往后,看两个顶点连通么
- 已连通就直接跳过
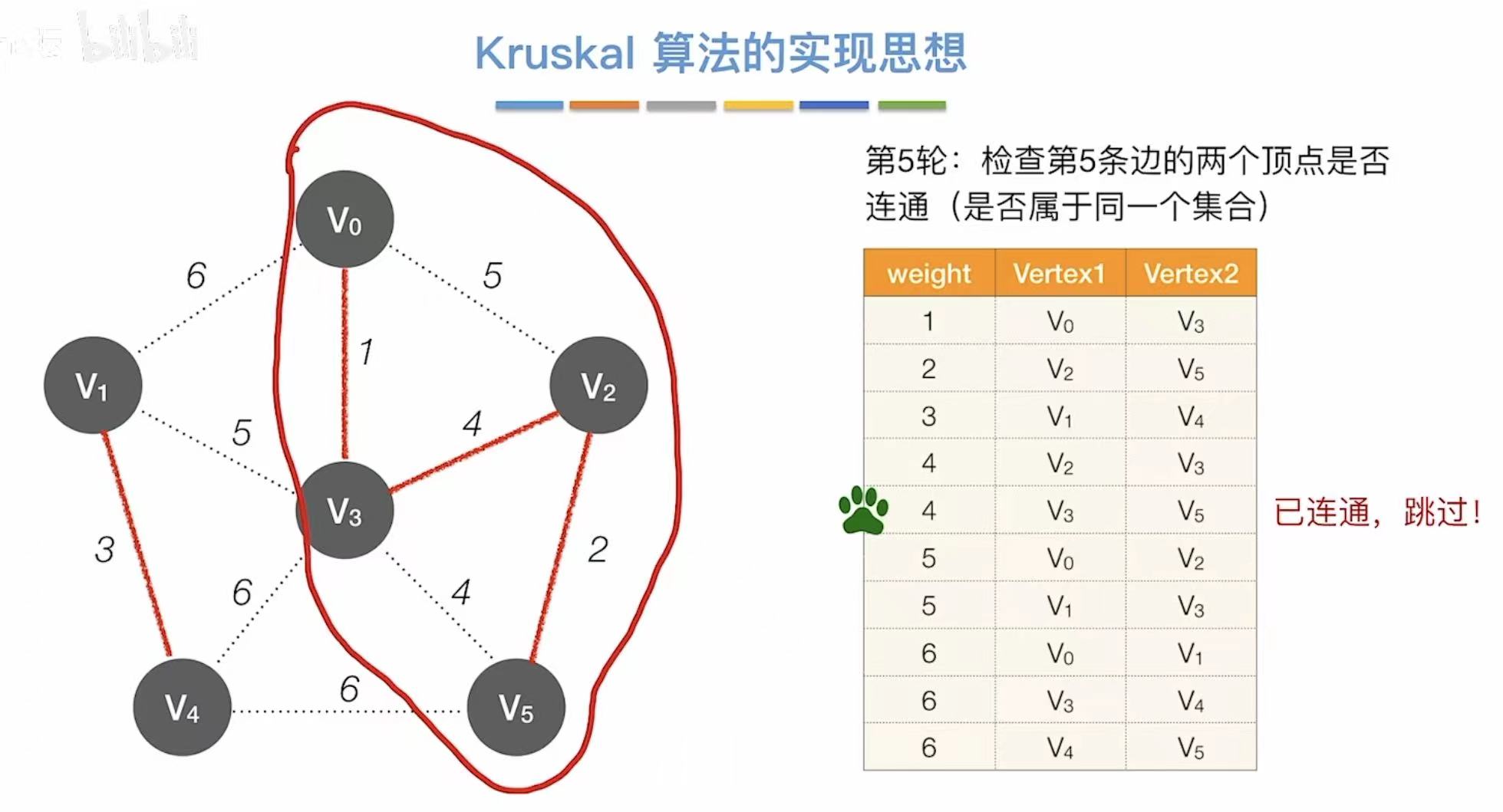
- 依次往后,看两个顶点连通么
- 不连通就直接相连
4. 小结

最短路径问题
1. BFS算法
1.1 概念
- 单源最短路径问题:只针对一个顶点,看其他顶点到它的最短路径。
- 每对顶点间的最短路径:谁到谁最方便不费力。
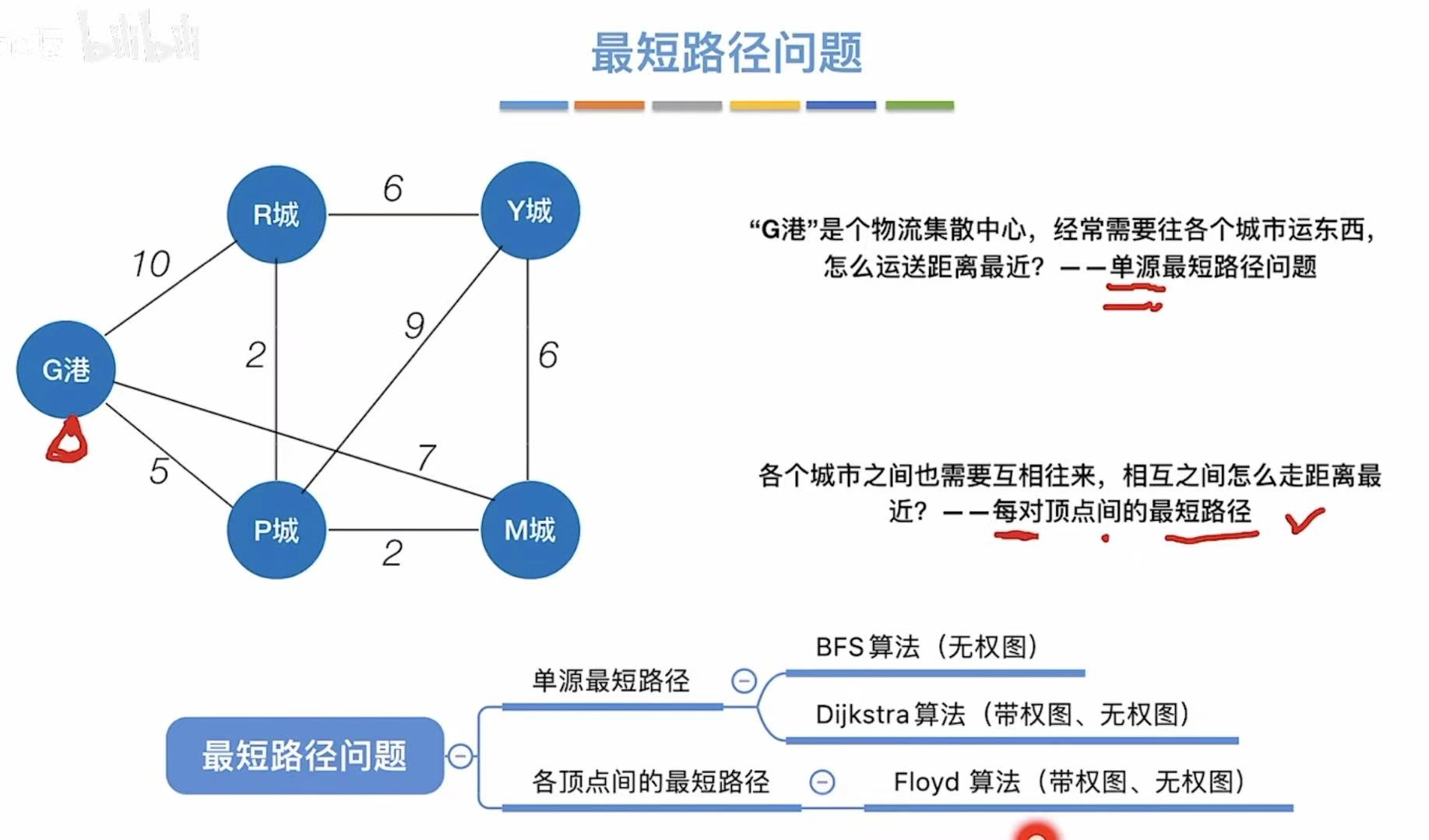
BFS,具体可见广度优先遍历
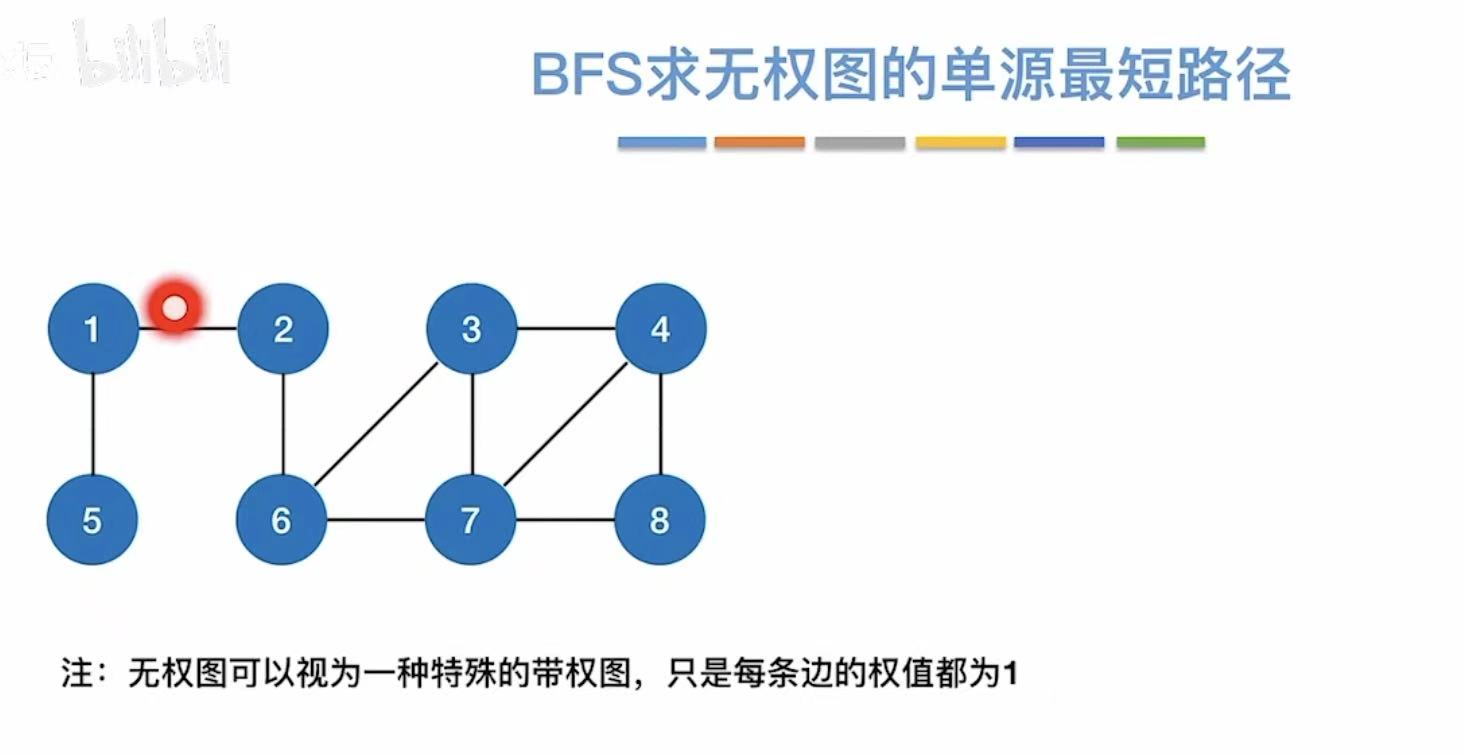
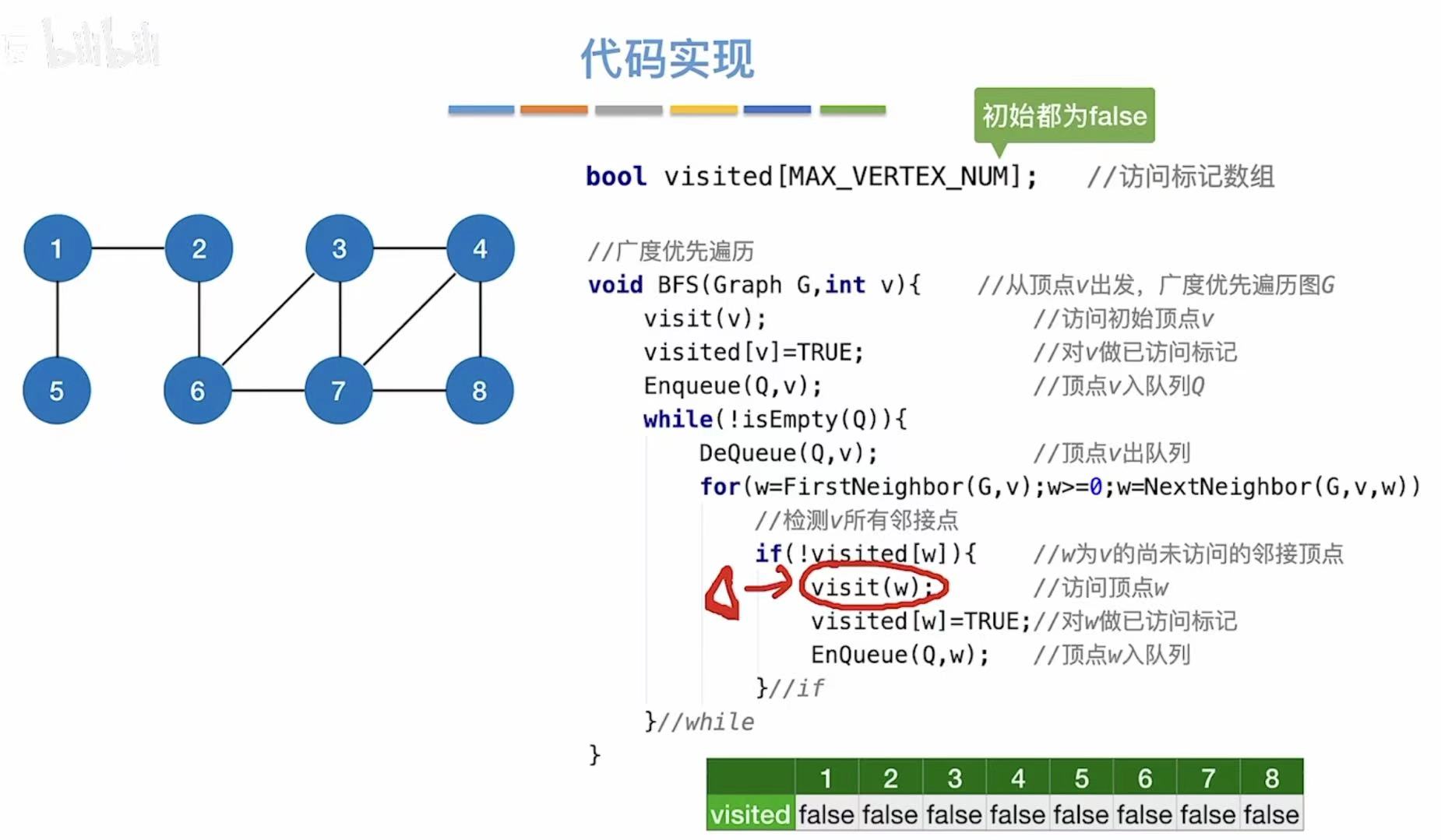
1.2 代码实现
java
// 访问标记数组:记录每个顶点是否已被访问过
// 初始时所有值都为 false(未访问)
bool visited[MAX_VERTEX_NUM]; // 访问标记数组
// 从顶点 v 出发,进行广度优先遍历的函数
void BFS(Graph G, int v) {
visit(v); // 访问起始顶点 v(如打印或处理数据)
visited[v] = TRUE; // 将顶点 v 标记为已访问,防止重复访问
Enqueue(Q, v); // 将顶点 v 入队列 Q,准备开始层序遍历
while (!IsEmpty(Q)) { // 当队列不为空时,继续遍历
DeQueue(Q, v); // 从队列头取出一个顶点 v(先进先出)
// 遍历当前顶点 v 的所有邻接点 w
for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
// 如果邻接点 w 还未被访问
if (!visited[w]) {
visit(w); // 访问该邻接点 w
visited[w] = TRUE; // 将 w 标记为已访问
Enqueue(Q, w); // 将 w 入队列,等待后续处理
}
}
}
}
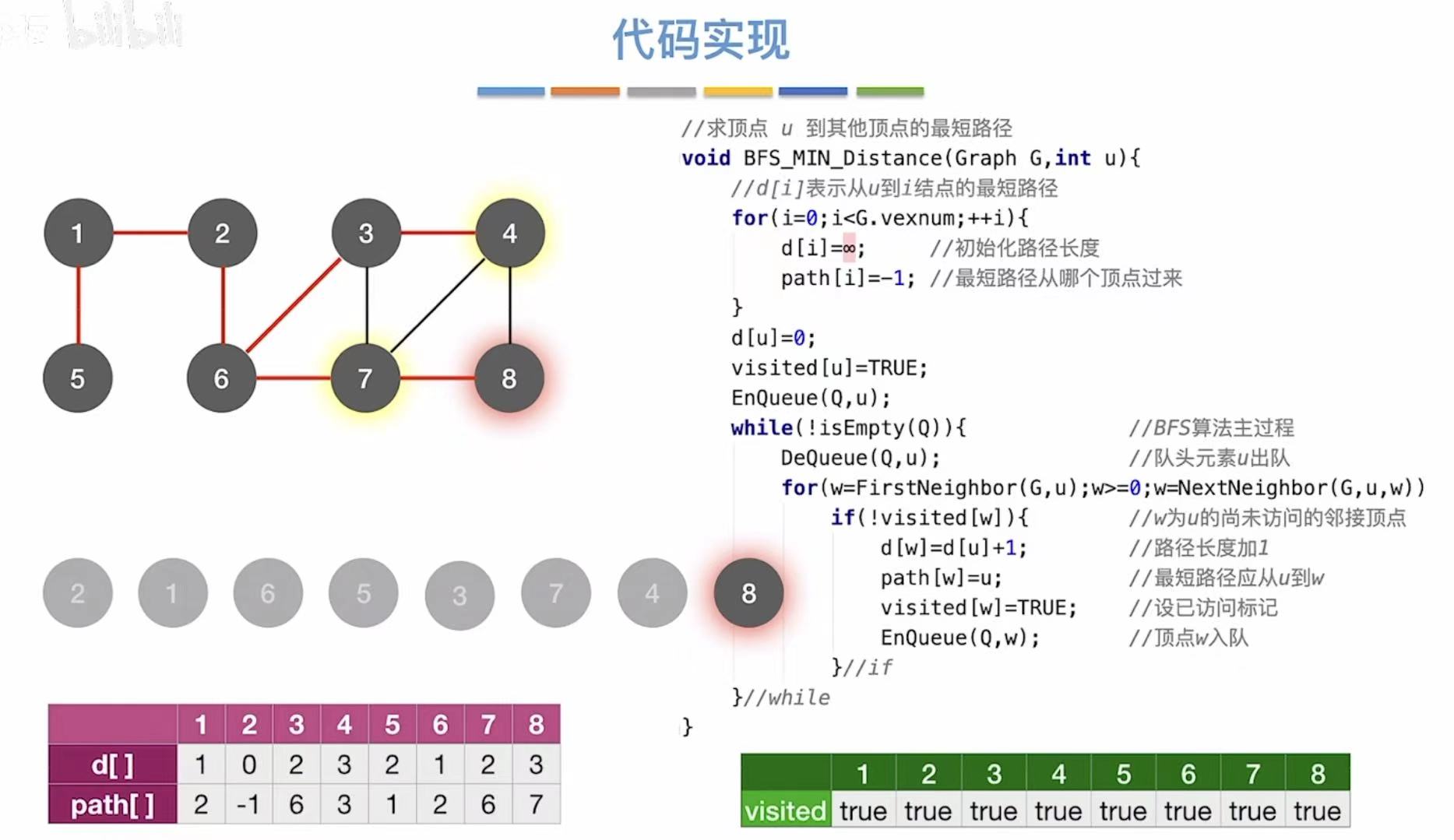
java
// 求顶点 u 到其他所有顶点的最短路径(适用于无权图)
void BFS_MIN_Distance(Graph G, int u) {
// d[i] 表示从起点 u 到顶点 i 的最短路径长度
int d[MAX_VERTEX_NUM]; // 路径长度数组
// path[i] 表示从起点 u 到顶点 i 的最短路径中,i 的前驱顶点
int path[MAX_VERTEX_NUM]; // 前驱数组(用于回溯路径)
// 初始化:所有顶点的最短路径长度设为 -1(表示未访问)
for (int i = 0; i < G.vexnum; ++i) {
d[i] = -1; // 初始距离为 -1(表示不可达或未访问)
path[i] = -1; // 初始前驱为 -1(表示无前驱)
}
// 起点 u 到自身的距离为 0
d[u] = 0;
// 标记起点 u 已访问
visited[u] = TRUE;
// 将起点 u 入队列,开始 BFS
Enqueue(Q, u);
// BFS 主循环:只要队列不空,就继续处理
while (!IsEmpty(Q)) {
DeQueue(Q, u); // 从队列头取出当前顶点 u
// 遍历 u 的所有邻接点 w
for (w = FirstNeighbor(G, u); w >= 0; w = NextNeighbor(G, u, w)) {
// 如果邻接点 w 尚未被访问
if (!visited[w]) {
// 更新 w 的最短路径长度:比 u 多走一步
d[w] = d[u] + 1;
// 记录 w 的前驱是 u(用于后续回溯路径)
path[w] = u;
// 标记 w 为已访问
visited[w] = TRUE;
// 将 w 入队列,等待后续处理
Enqueue(Q, w);
}
}
}
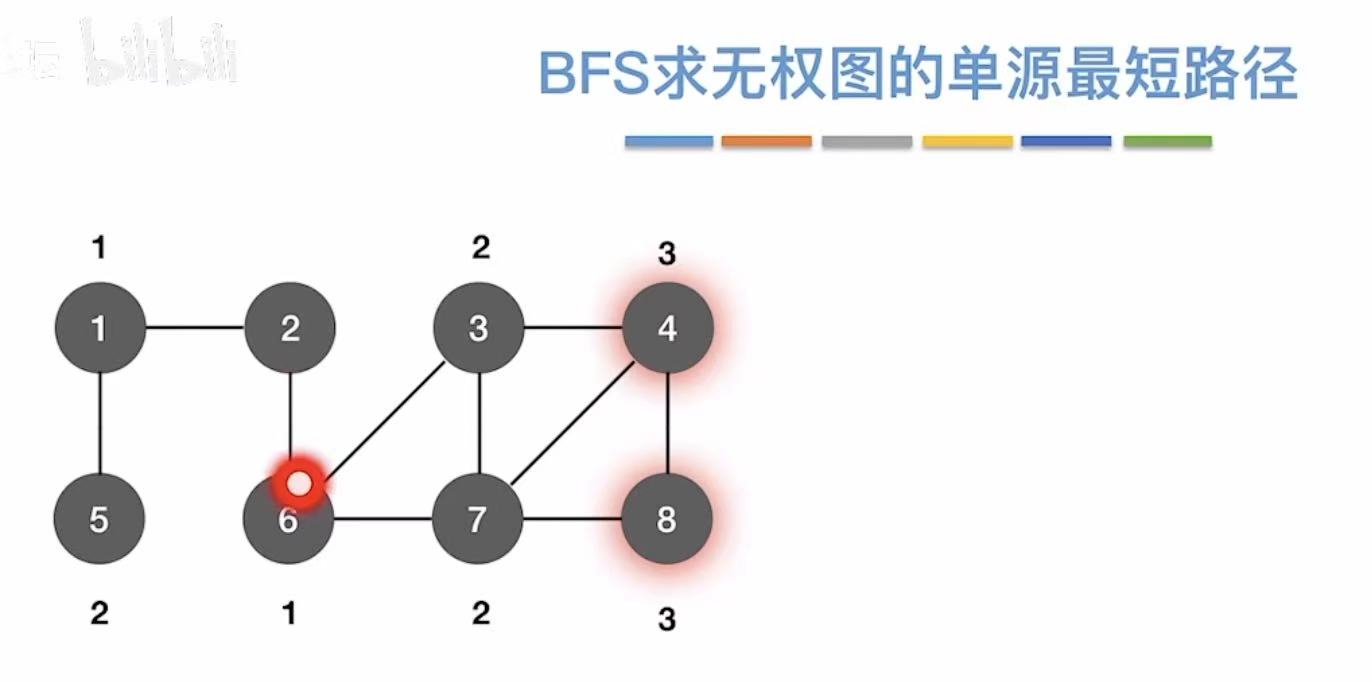
}| 步骤 | 操作 | d[] | path[] | 队列 Q |
|---|---|---|---|---|
| 1 | 初始化 | d[2]=0,其余=-1 | path[-1] | [2] |
| 2 | DeQueue(2) |
|||
| 3 | w=1,6 → 未访问 |
d[1]=1, d[6]=1 | path[1]=2, path[6]=2 | [1,6] |
| 4 | DeQueue(1) |
|||
| 5 | w=5 → 未访问 |
d[5]=2 | path[5]=1 | [6,5] |
| 6 | DeQueue(6) |
|||
| 7 | w=3,7 → 未访问 |
d[3]=2, d[7]=2 | path[3]=6, path[7]=6 | [5,3,7] |
| ... | 继续 | ... | ... | ... |
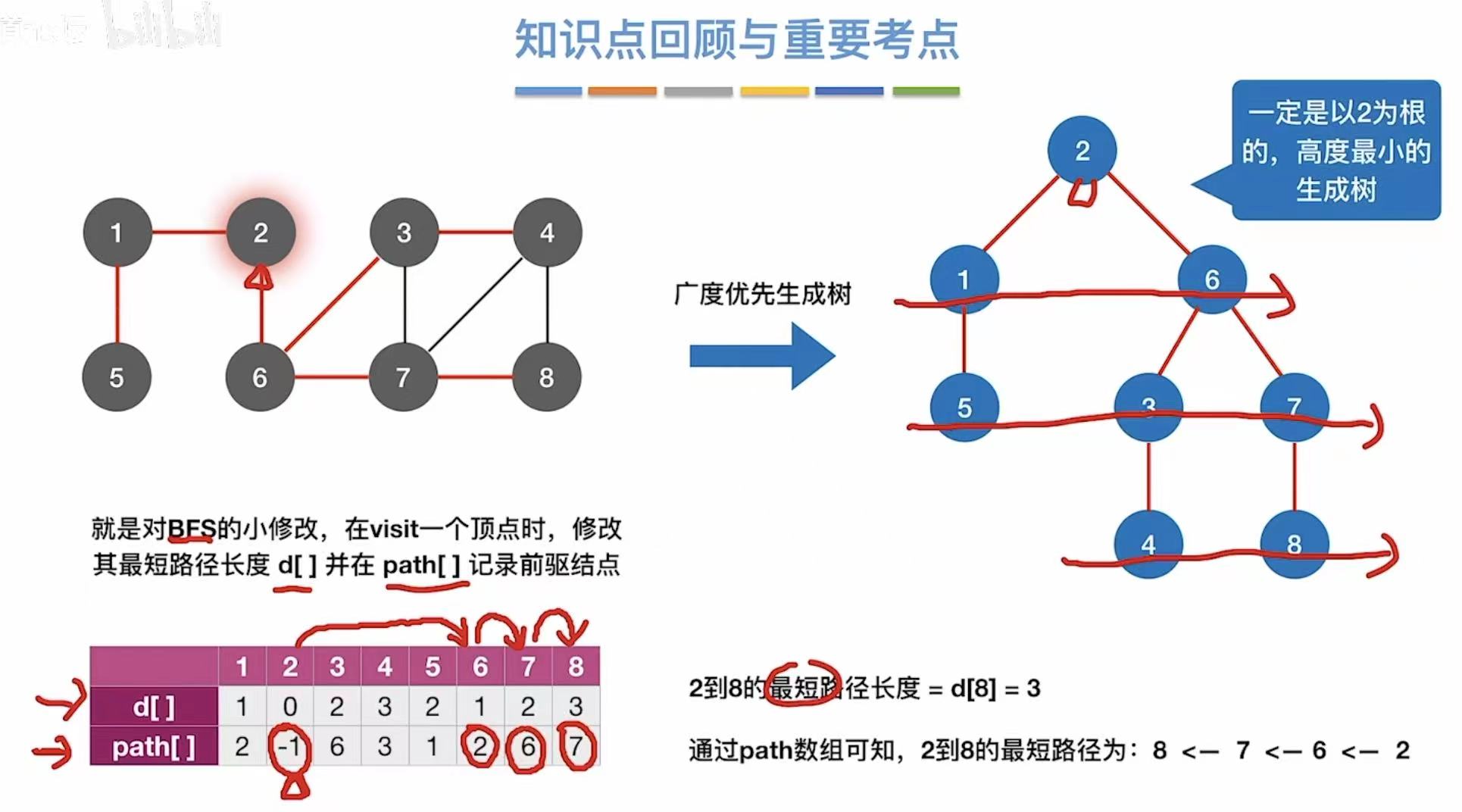
1.3 小结
2. Dijkstra算法
2.1 优化
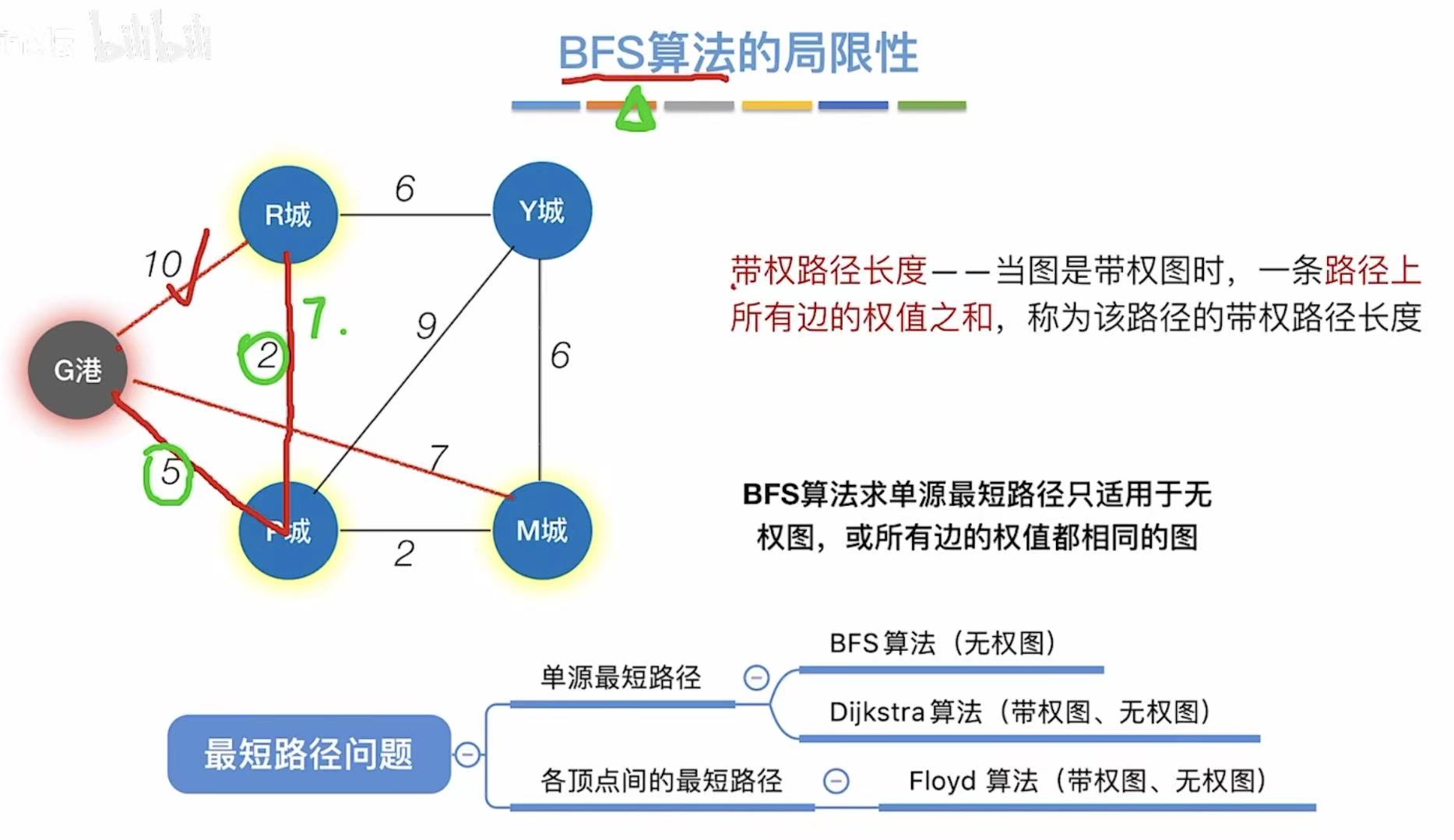
不限制有向无向,因为无向就相当于双向,比如下面两个图的右边是同一个图:
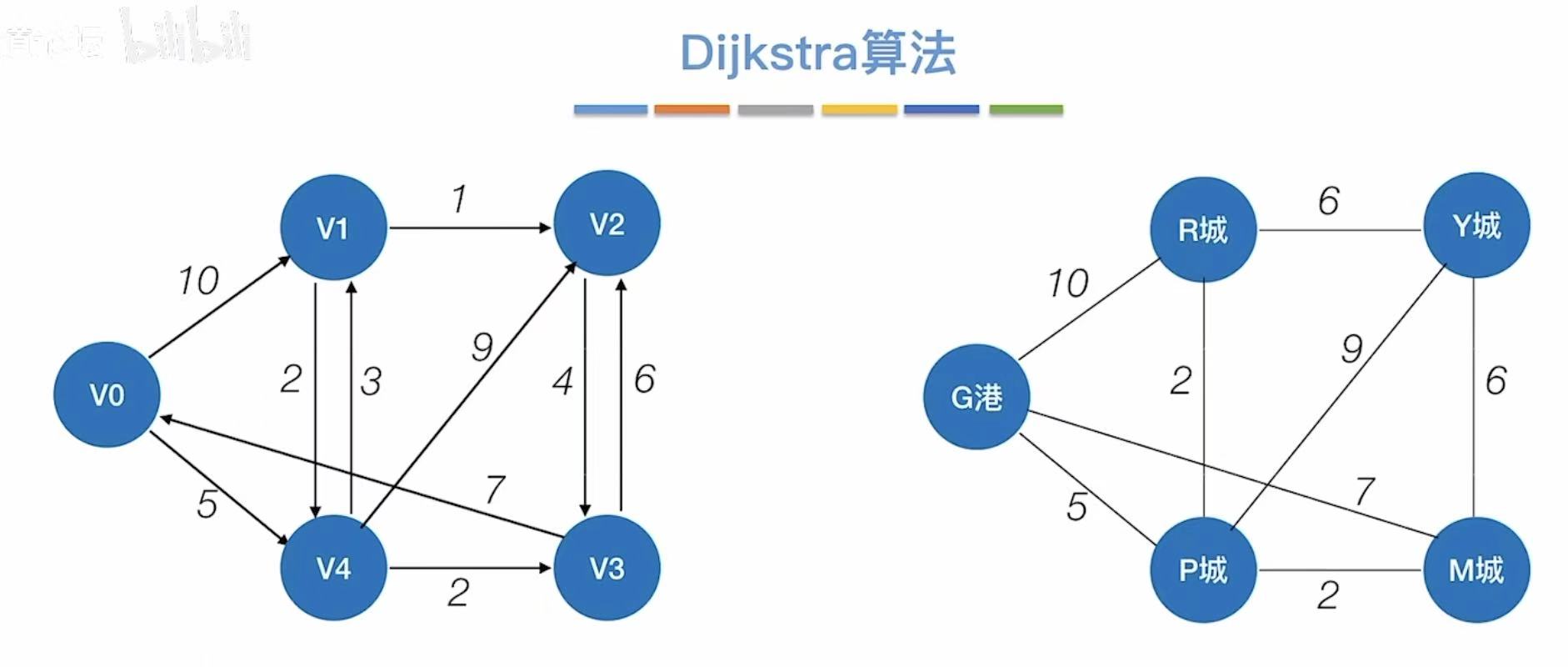
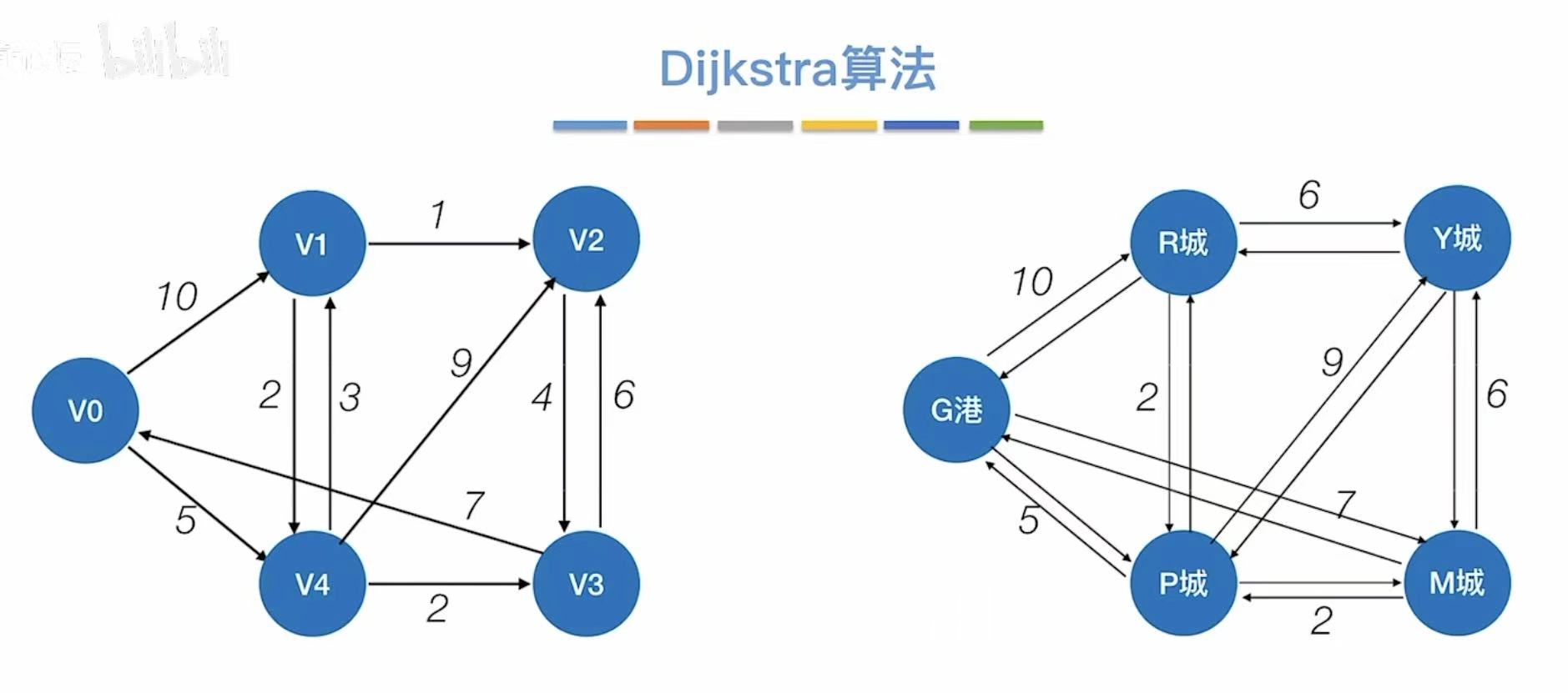
2.2 实现过程
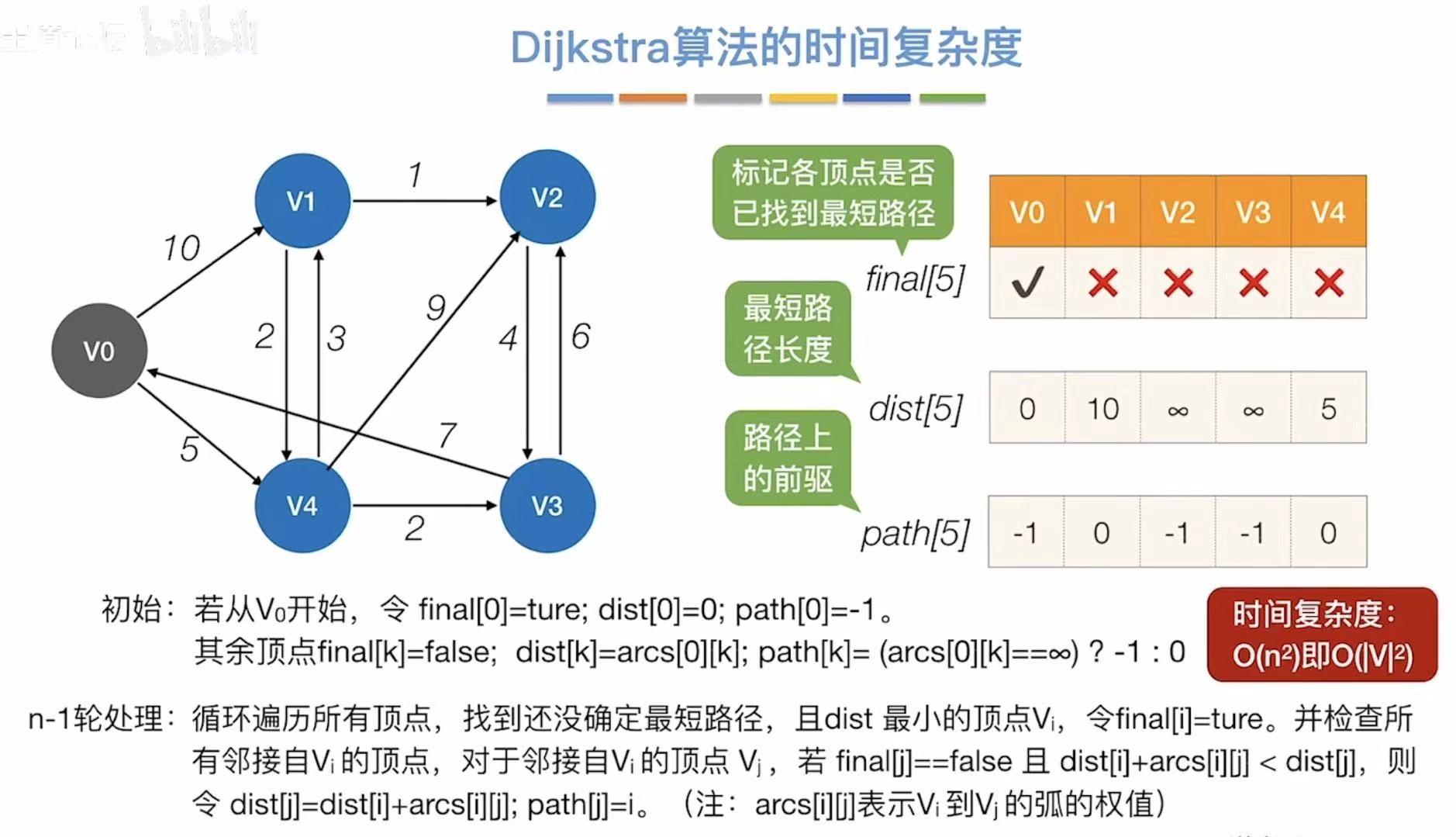
- v0√:从v0开始连通
- ∞:v0到v2、v3还没有直接连通的道路
- -1:还没办法到达v2、v3,因为v0是自己本身所以也无法到达
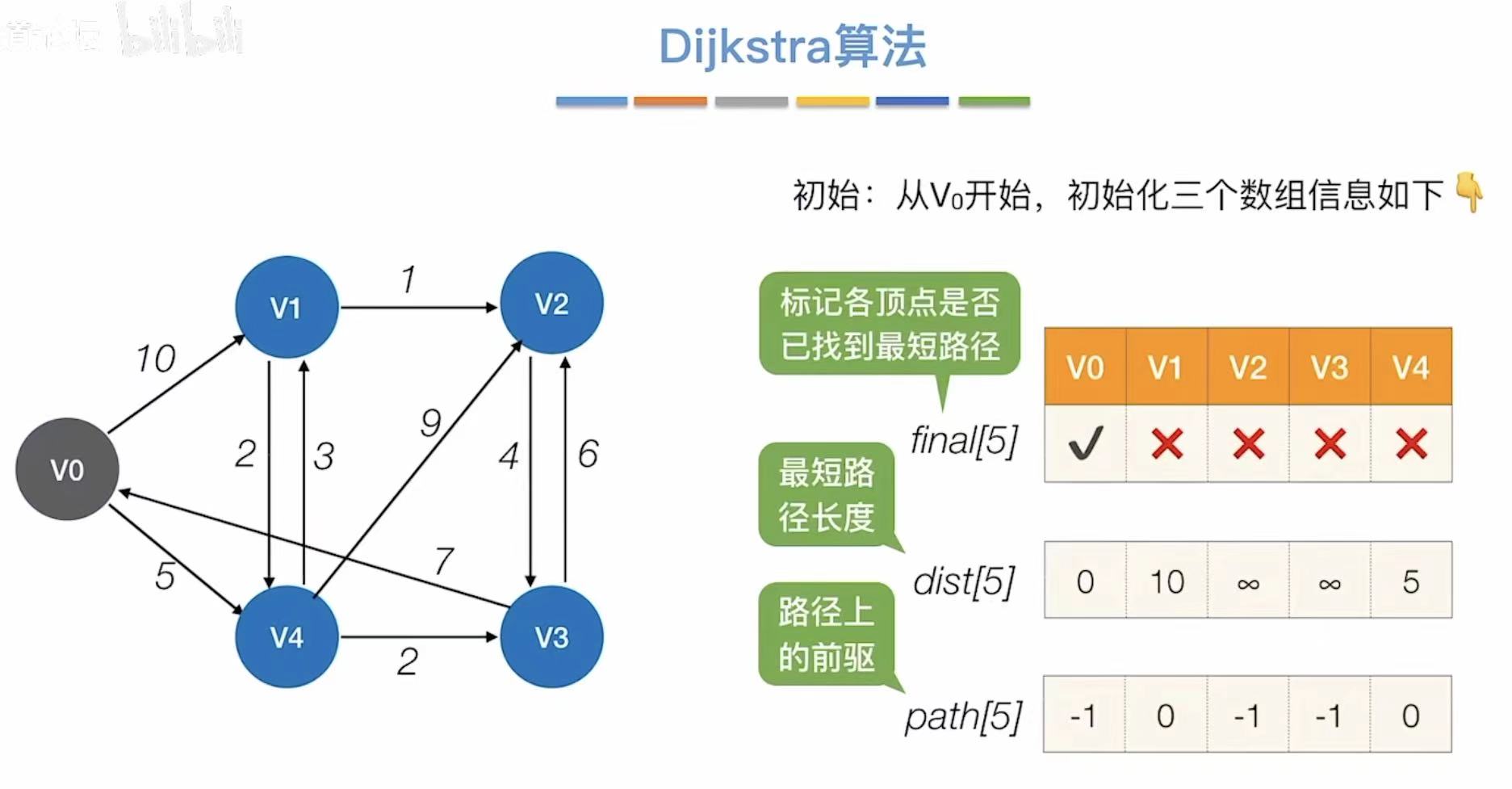
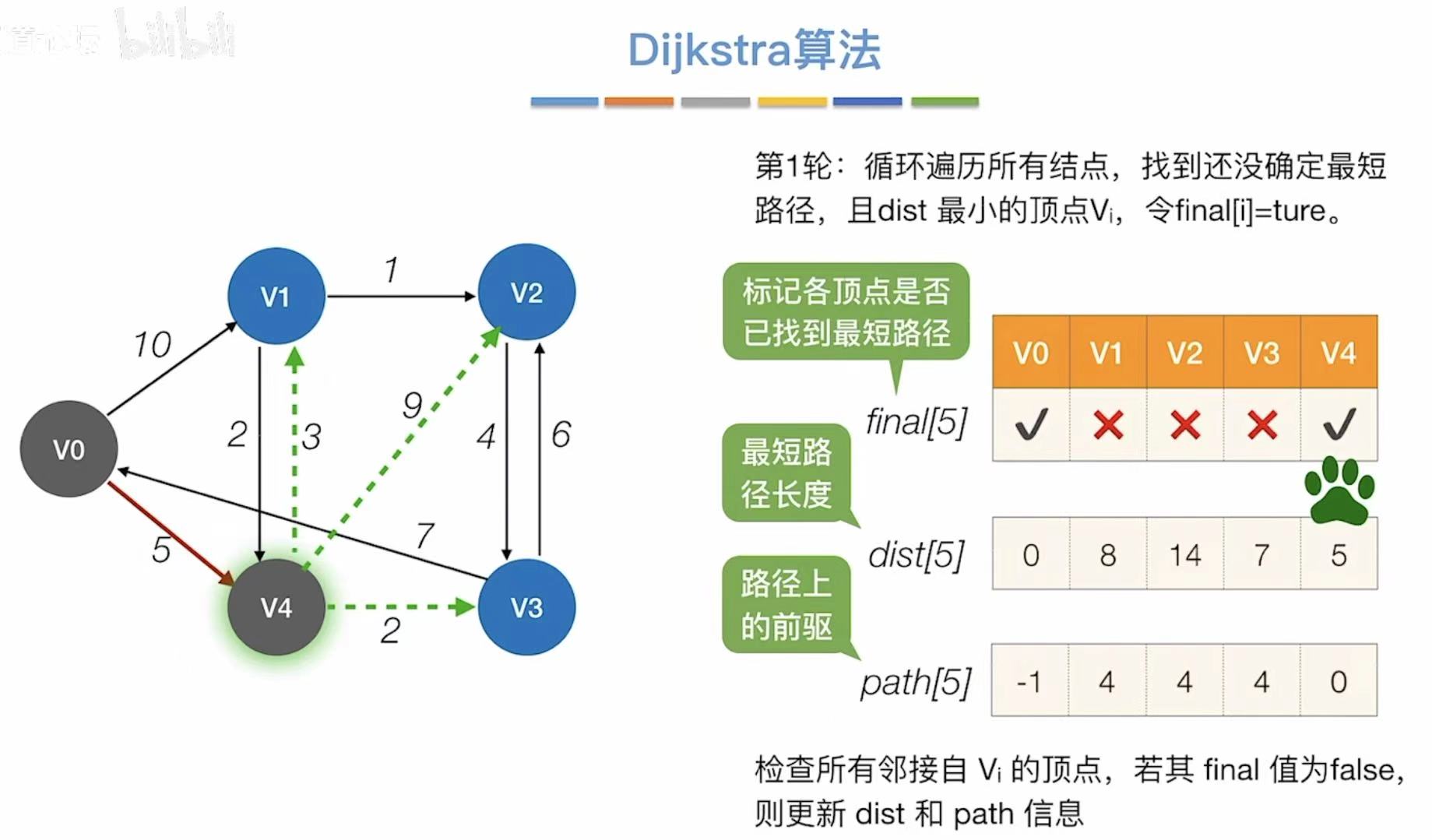
- 对比最短路径长度,选择最小的,可以直接到达v4
- 引入v4,更新能够连通的顶点和最短路径长度
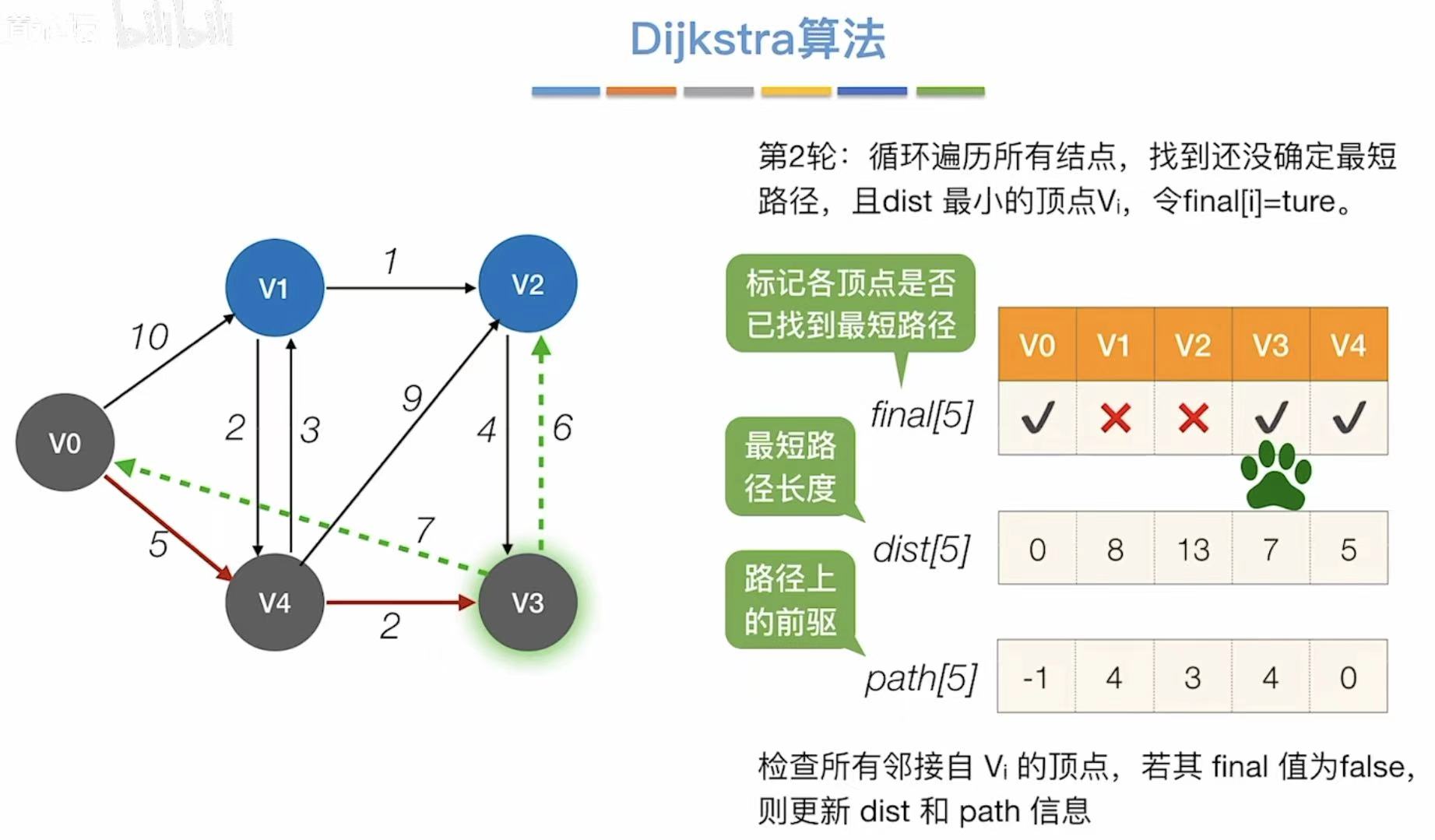
- 对比最短路径长度,选择最小的,可以直接到达v3
- 引入v3,更新能够连通的顶点和最短路径长度
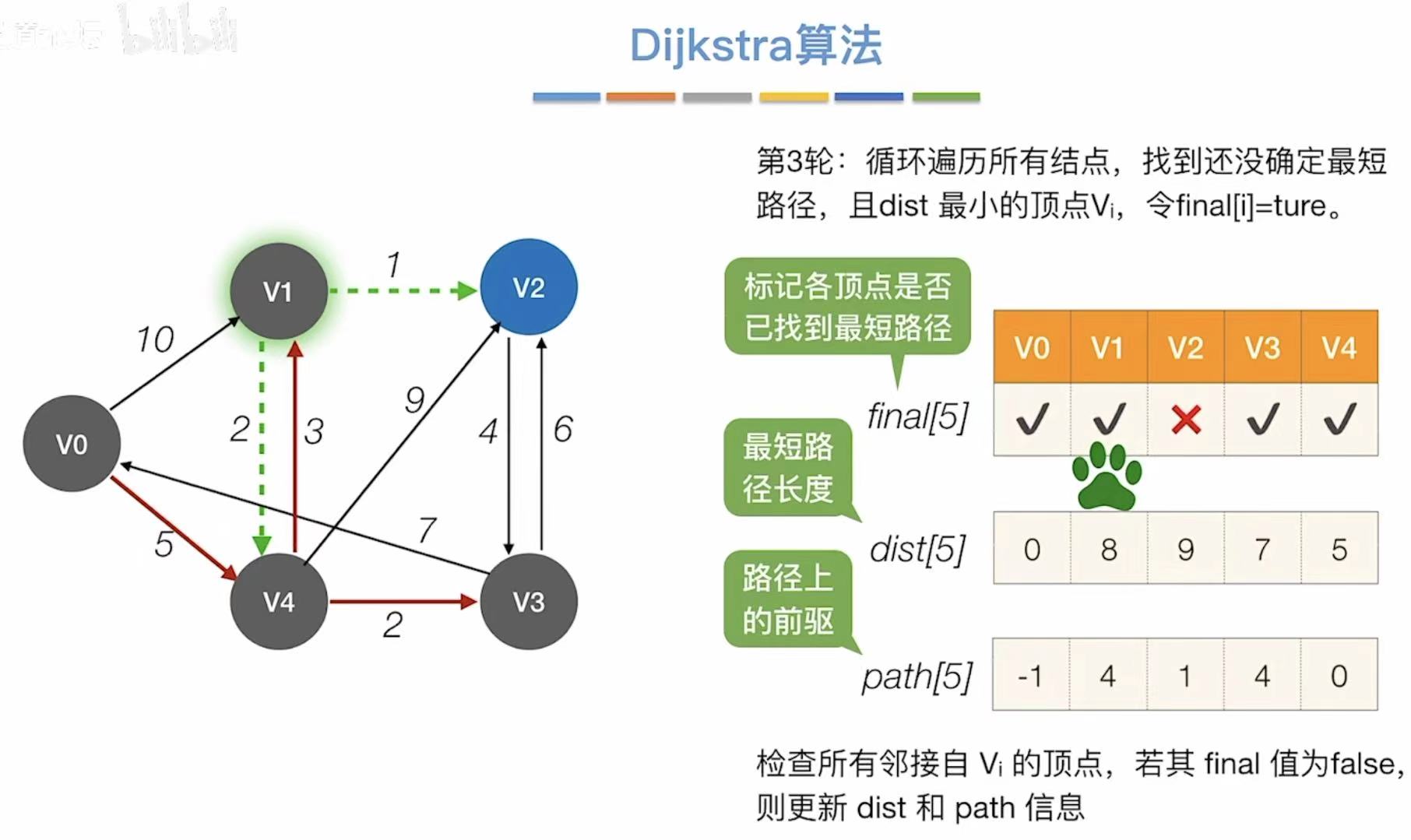
- 对比最短路径长度,选择最小的,可以直接到达v1
- 引入v1,更新能够连通的顶点和最短路径长度
- 对比最短路径长度,选择最小的,可以直接到达v2
- v2是最后一个顶点,所以就不需要更新了
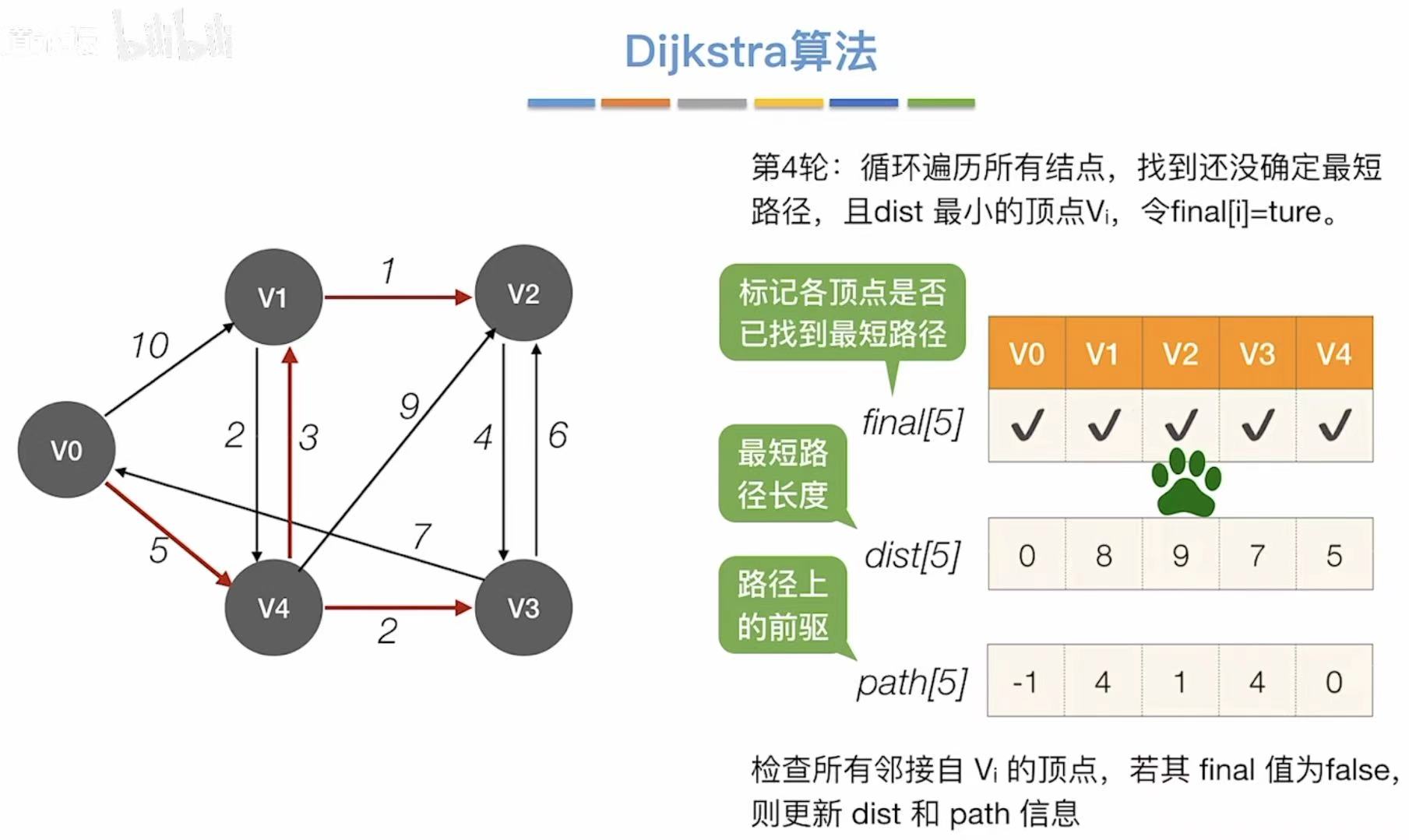
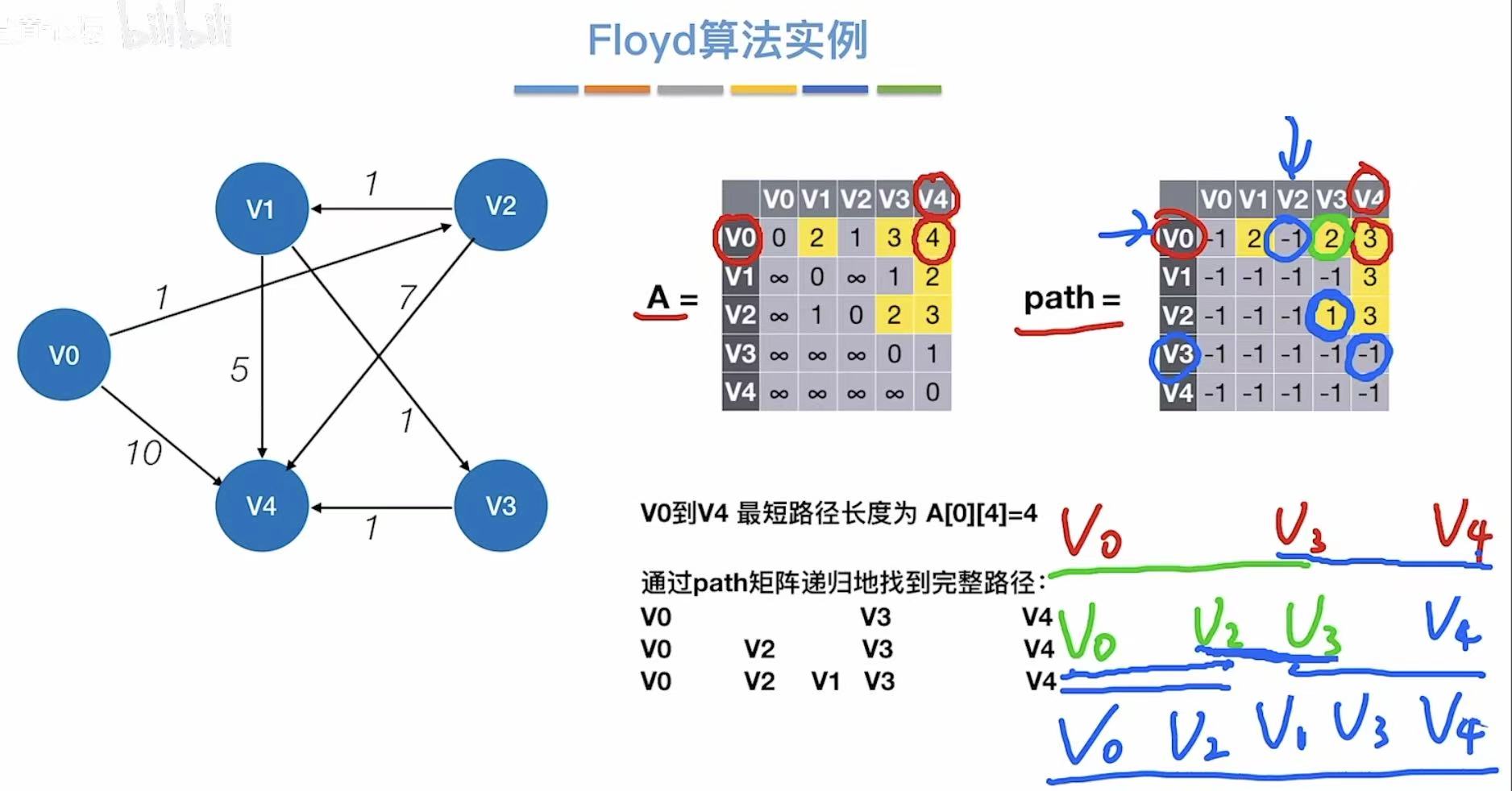
比如我们现在想从v0到达v2: - 观察v2的那一列
- 9:v0到v2的最短路径长度是9
- 1:v2需要经过v1;4:还要经过v4;0:最后成功到达v0
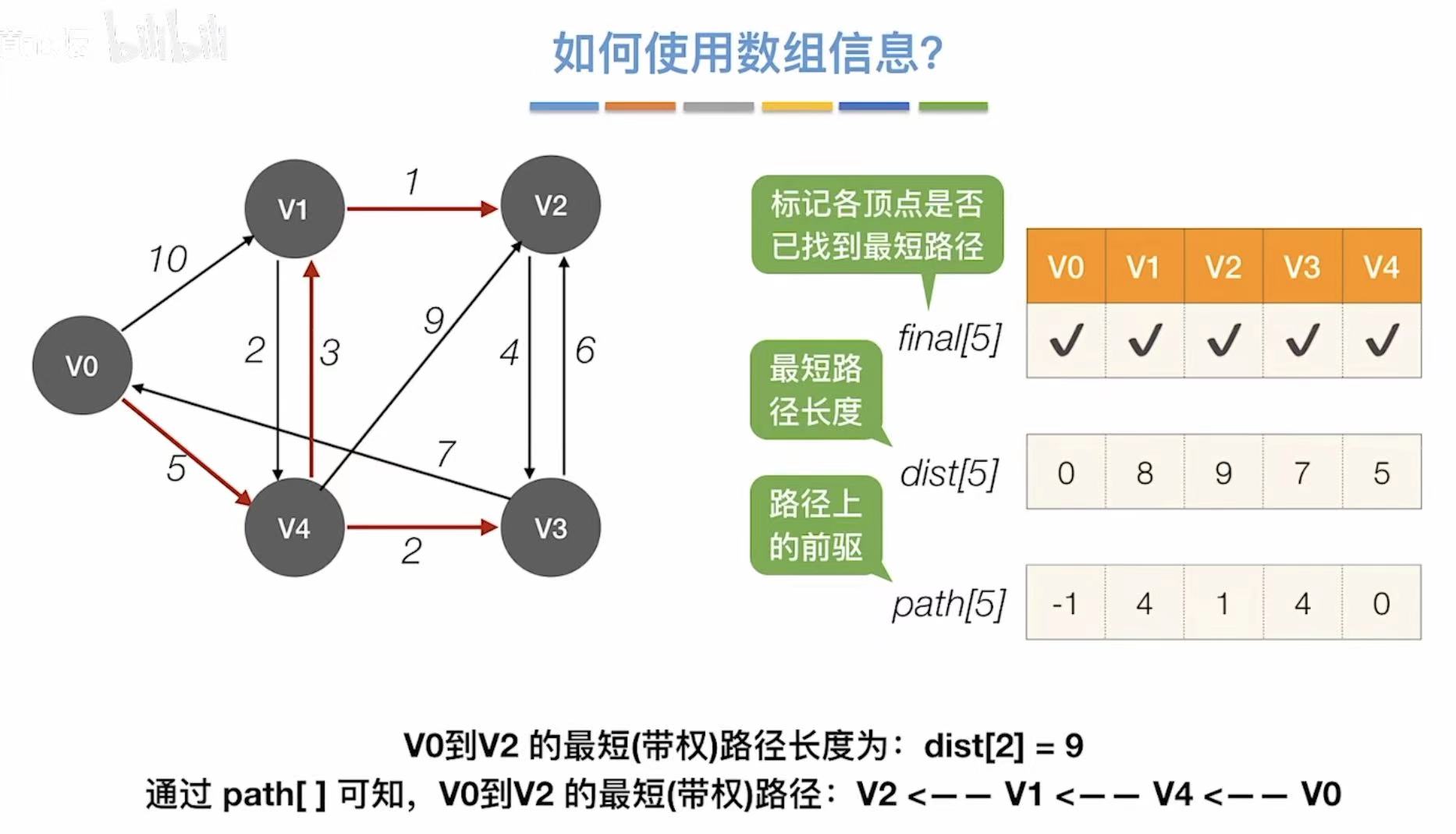
2.3 时间复杂度
因为每轮都需要检查更新n个顶点,需要检查更新n轮,所以时间复杂度是O(n2)
| 对比项 | Prim 算法 | Dijkstra 算法 |
|---|---|---|
| 目的 | 最小生成树 | 单源最短路径 |
| 图类型 | 无向图 | 有向/无向图(非负权) |
| 核心思想 | 连接最近的未连顶点 | 扩展最短的已知路径 |
| 更新规则 | dist[v] = min(dist[v], w(u,v)) |
dist[v] = min(dist[v], dist[u] + w(u,v)) |
| 结果依赖起点? | 否(MST 总权唯一) | 是 |
| 能否处理负权? | 可以(无向图) | 不可以 |
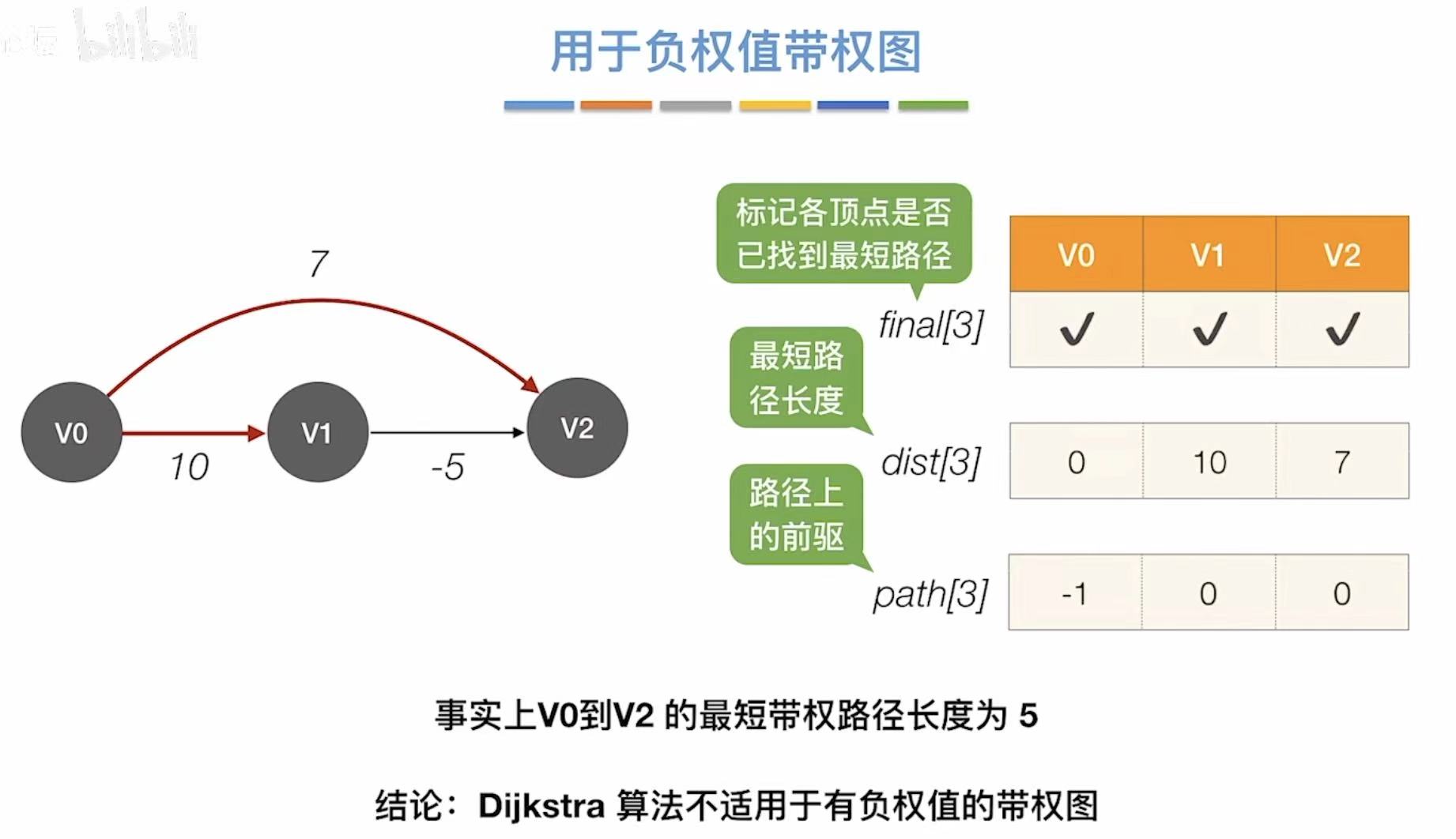
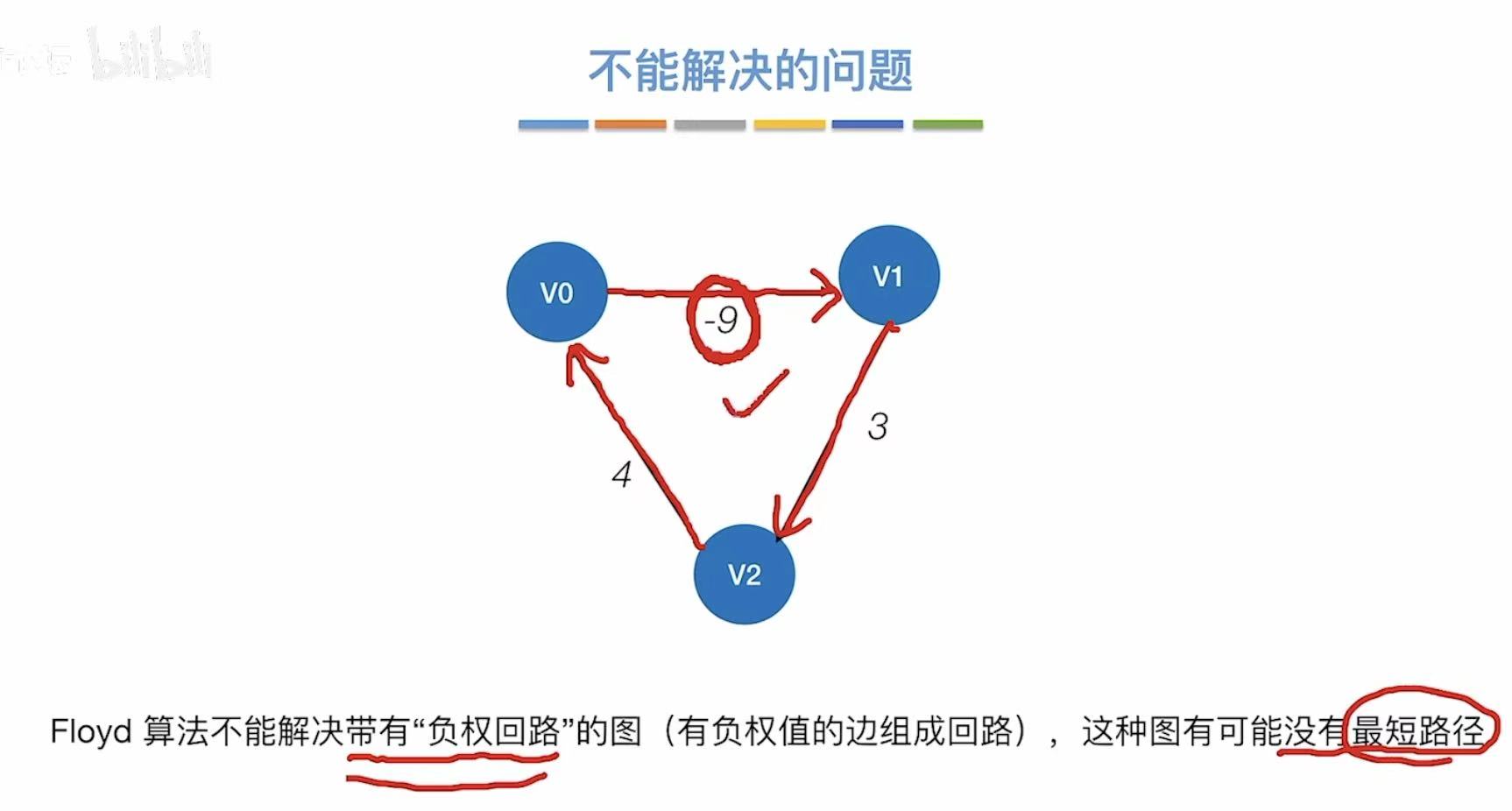
不适用负权值带权图!!!
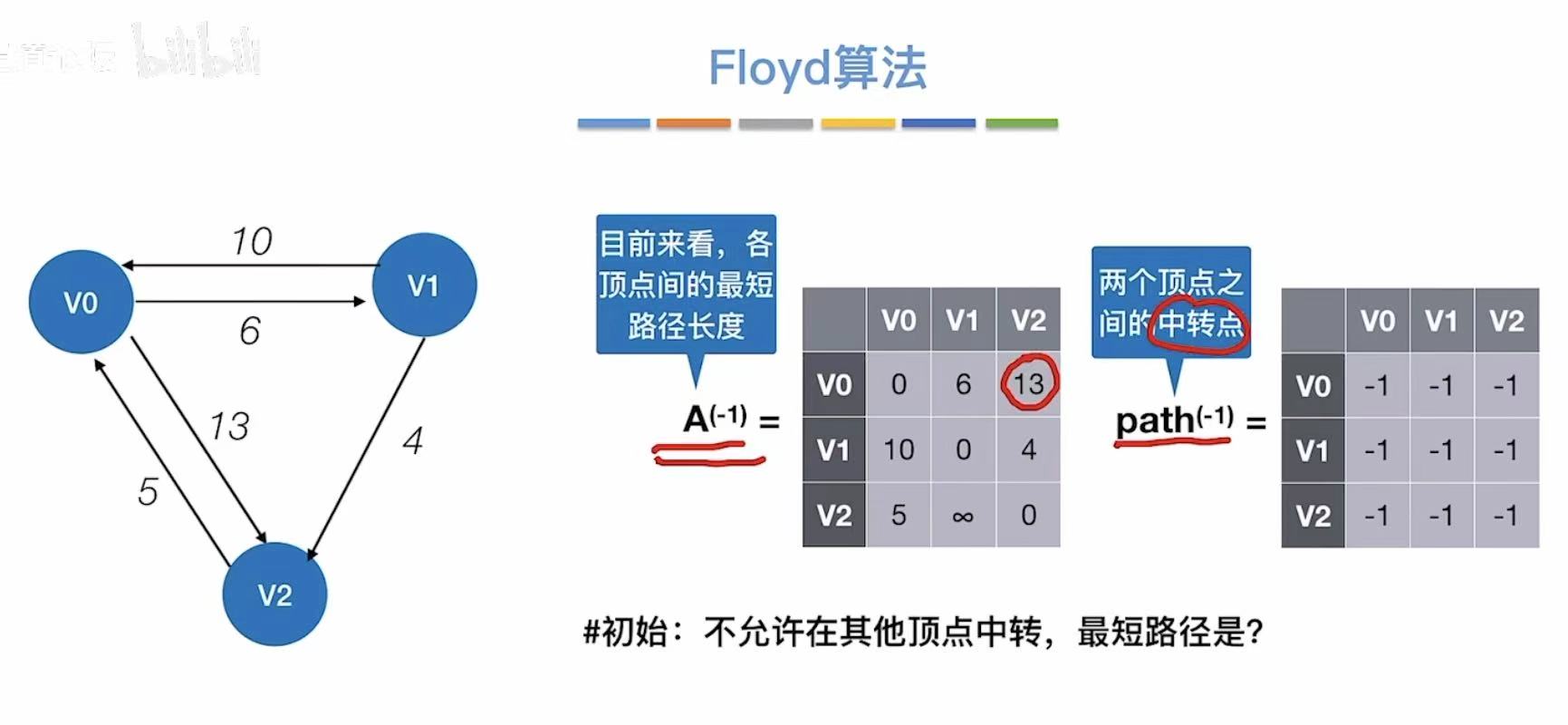
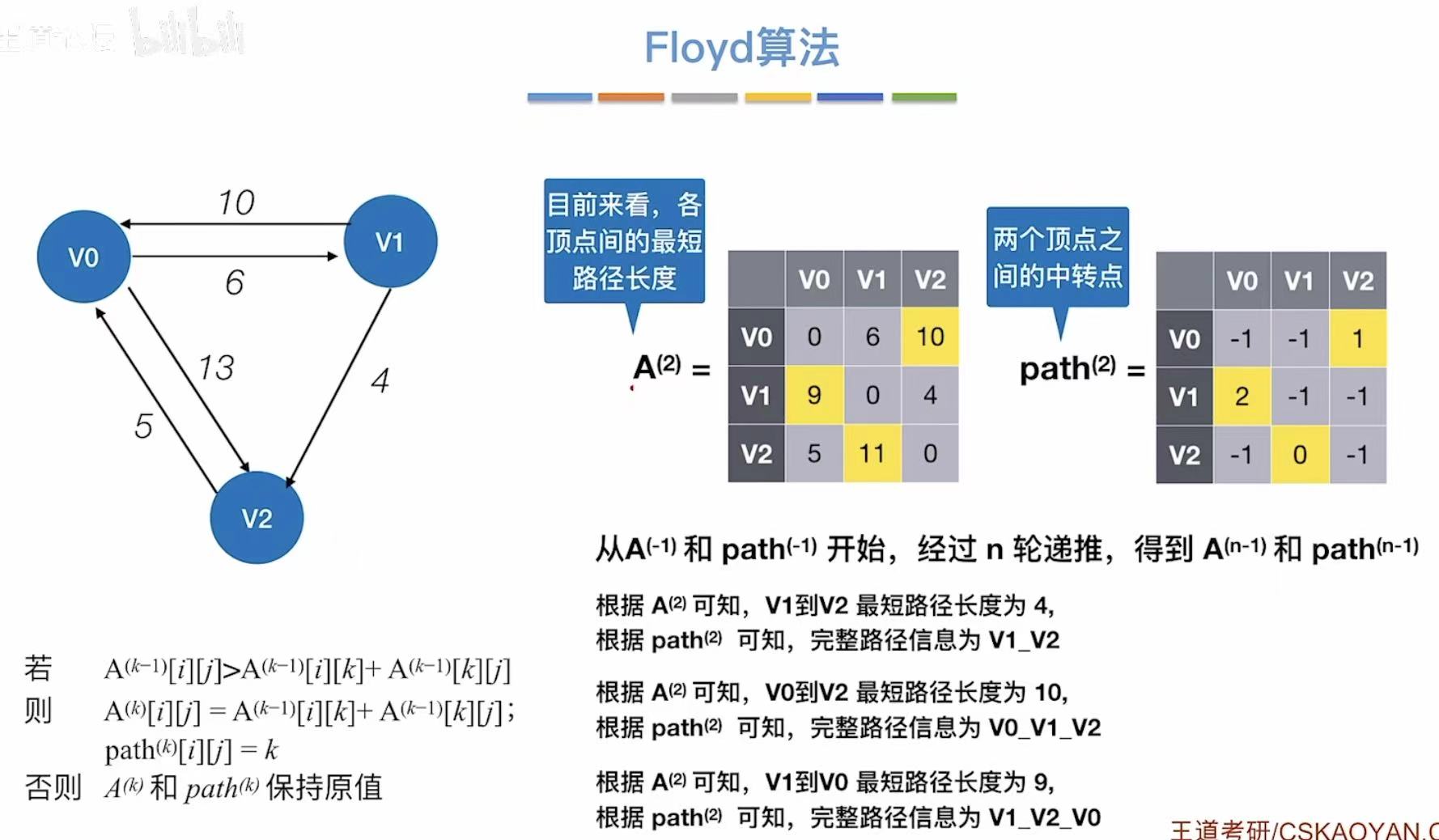
3. Floyd算法

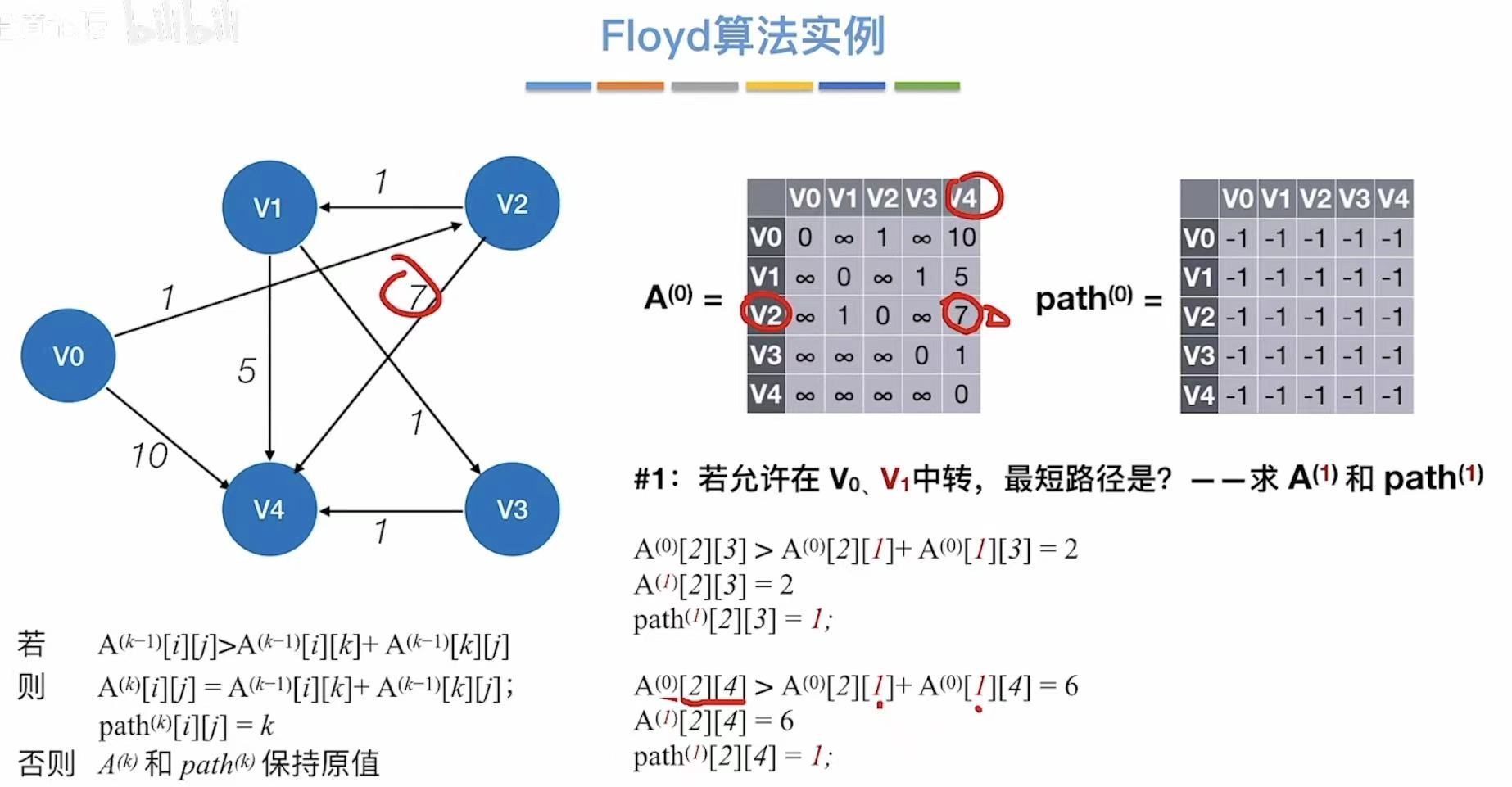
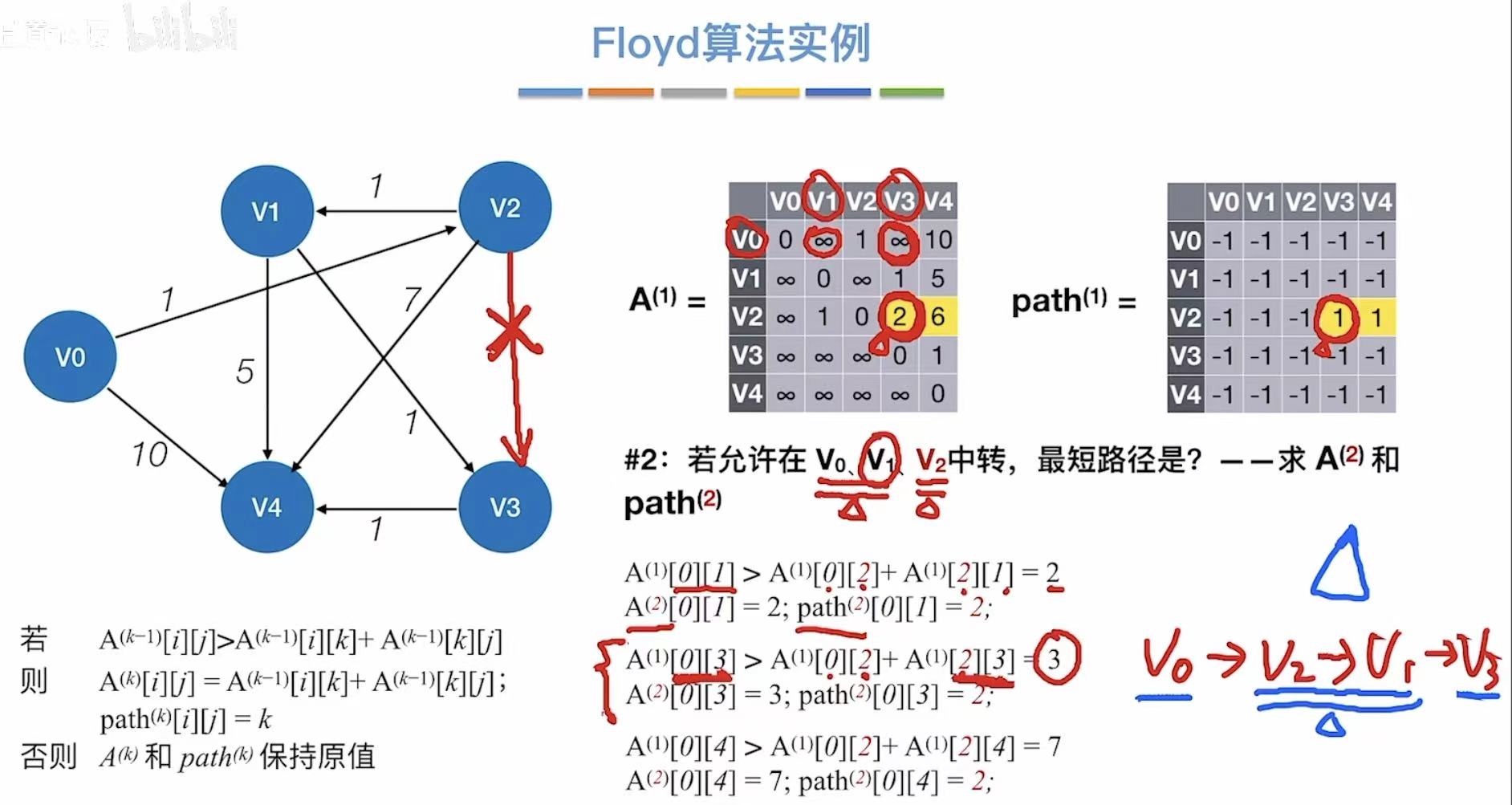
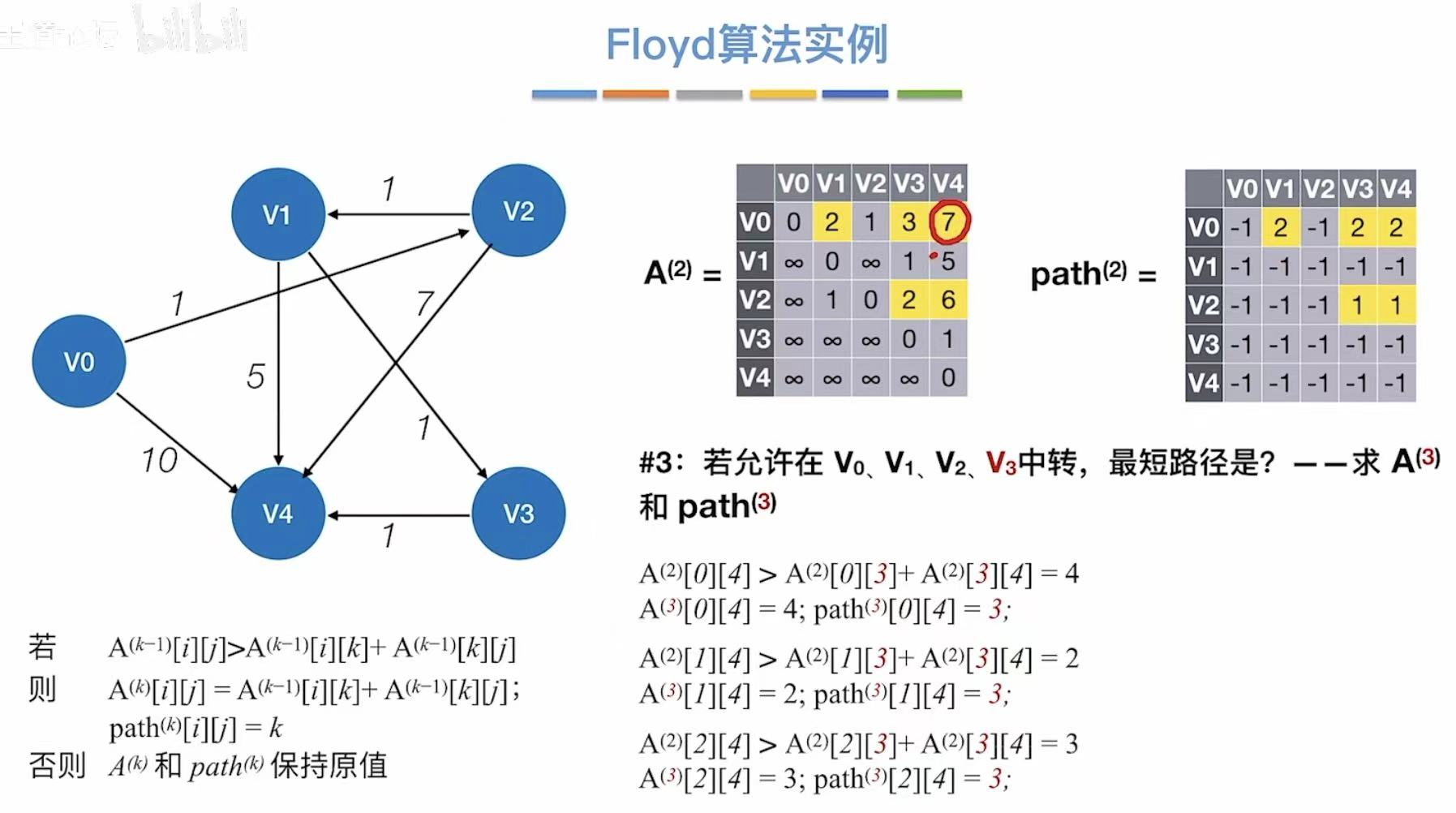
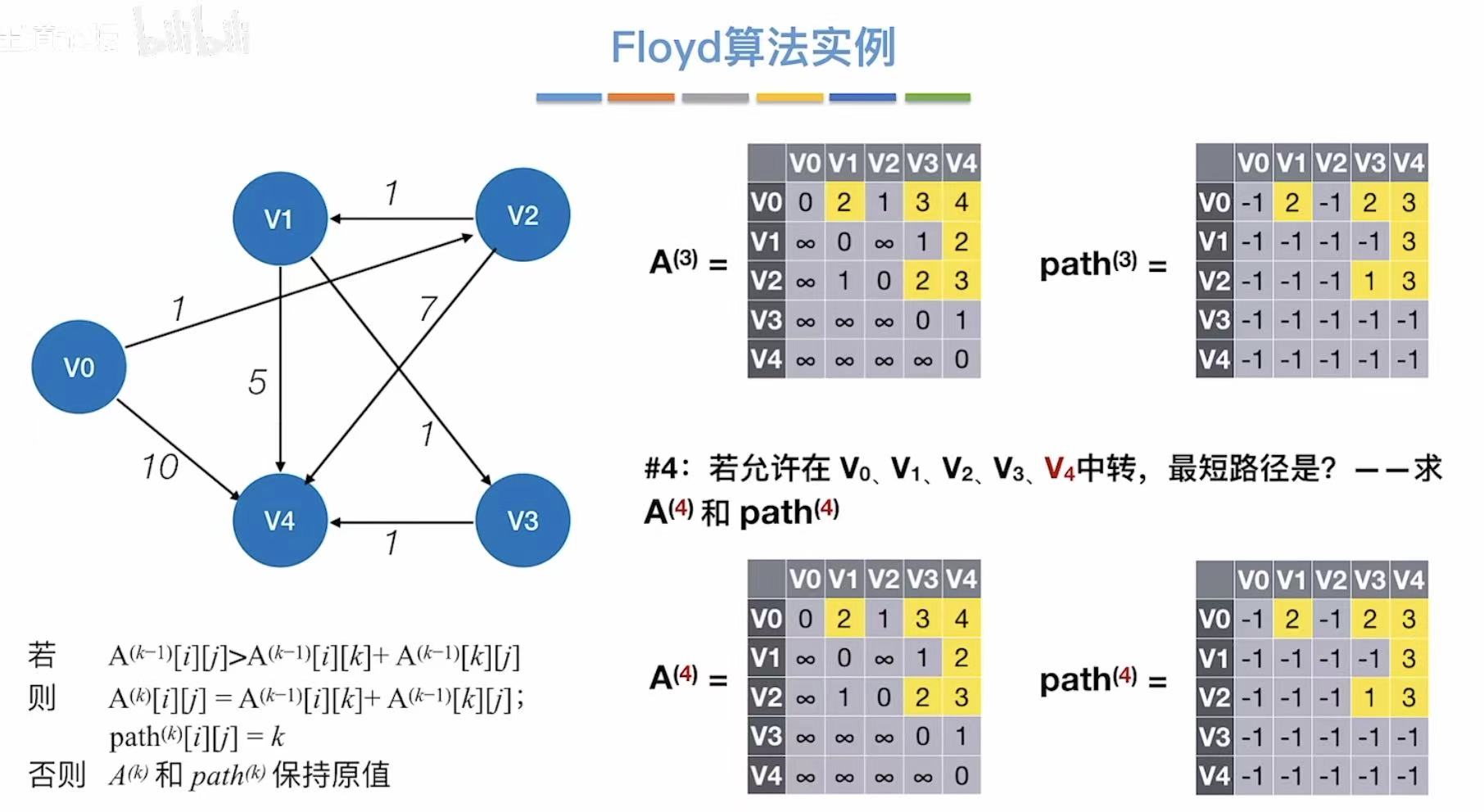
3.1 概念

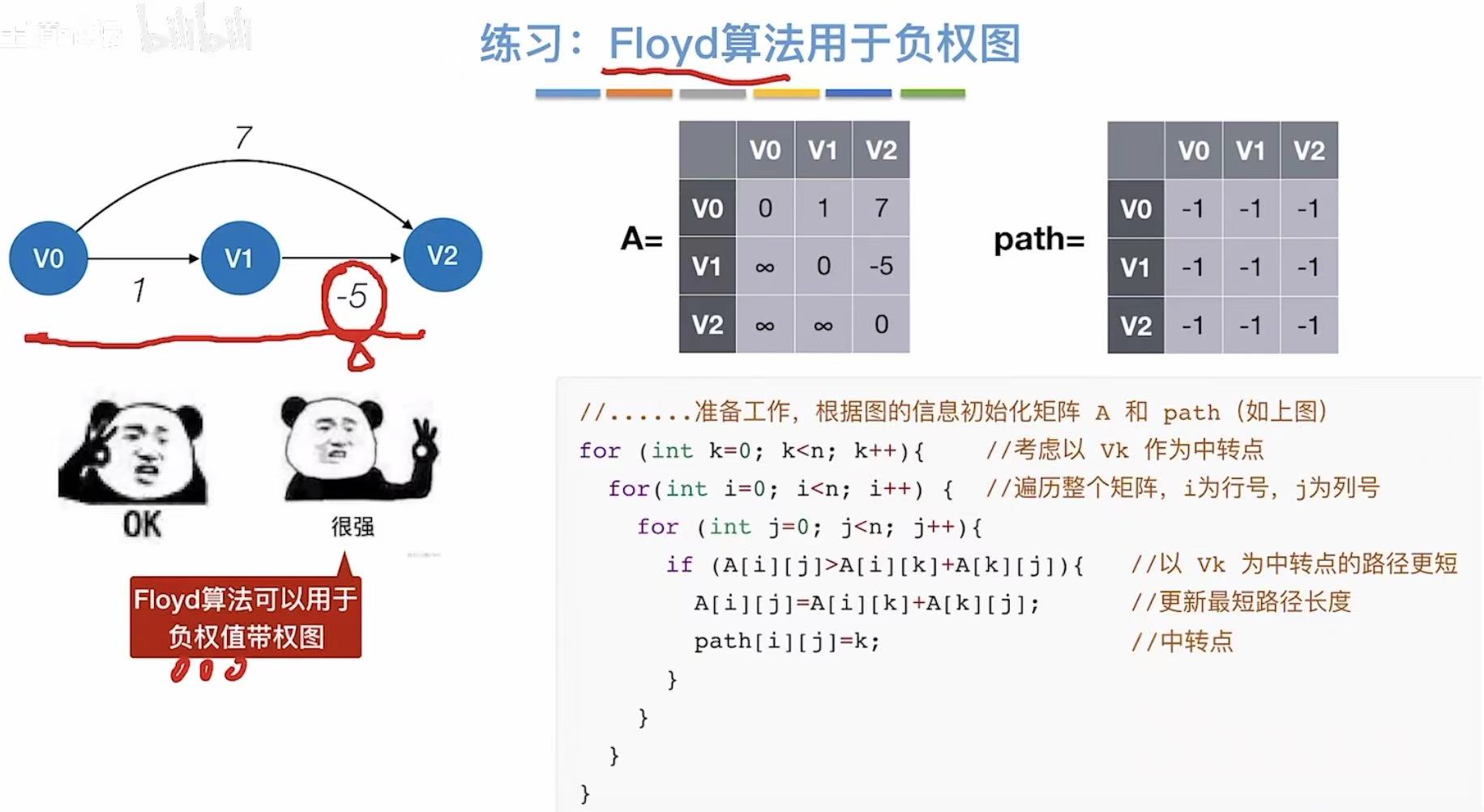
3.2 实现过程
初始:记录图上的无中转的真实数据
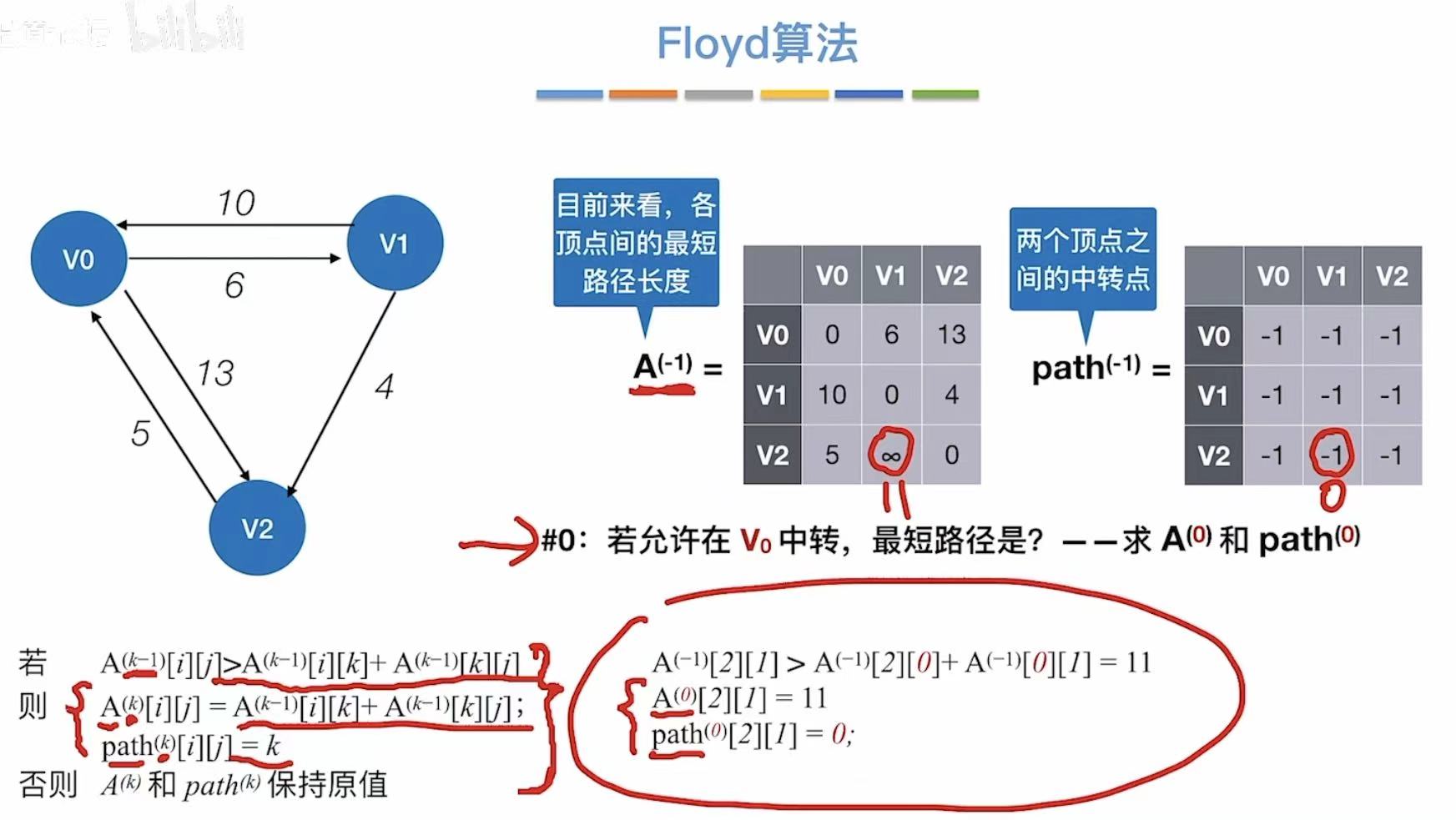
- 允许v0中转
- 更新两个表
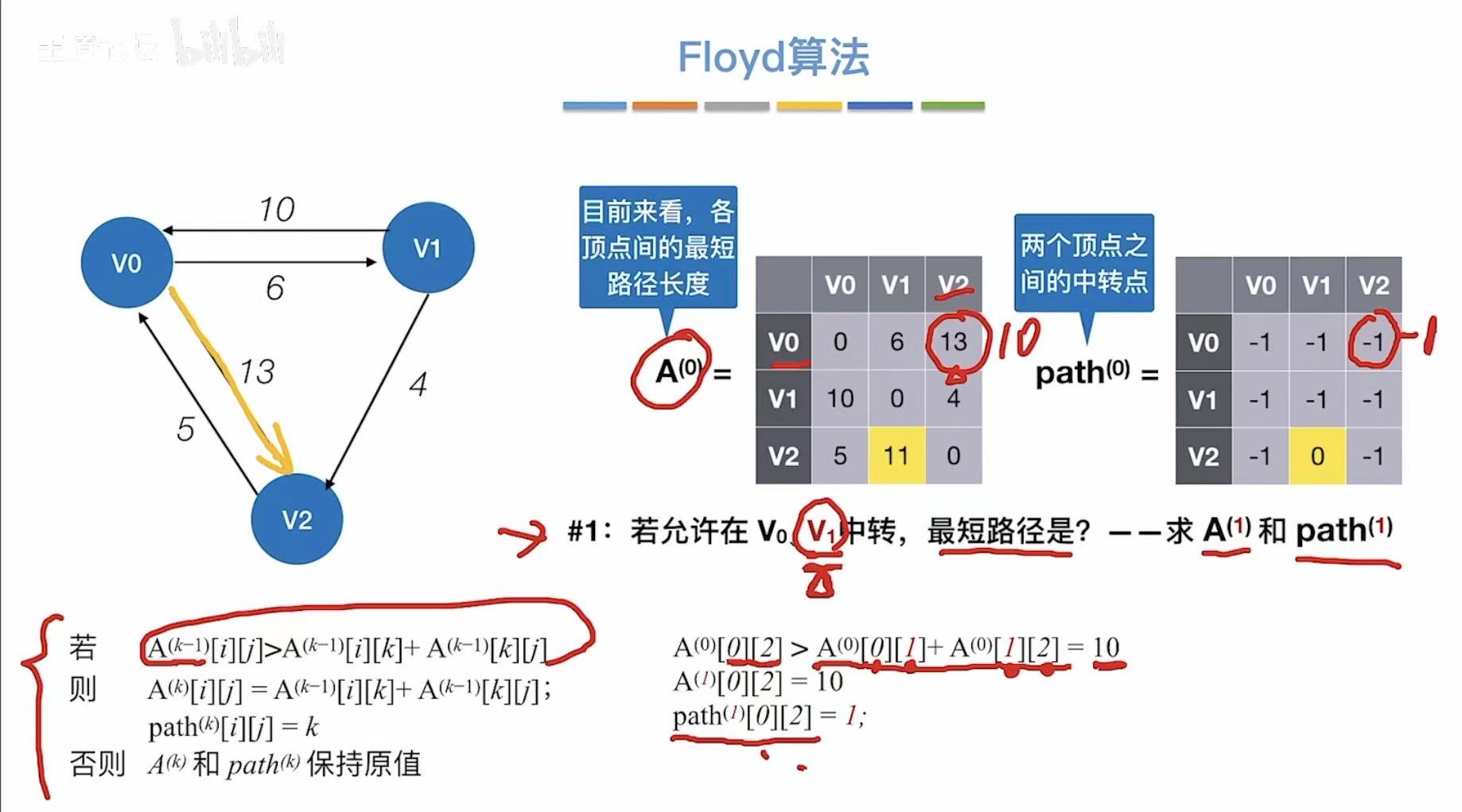
- 允许v1中转
- 更新两个表
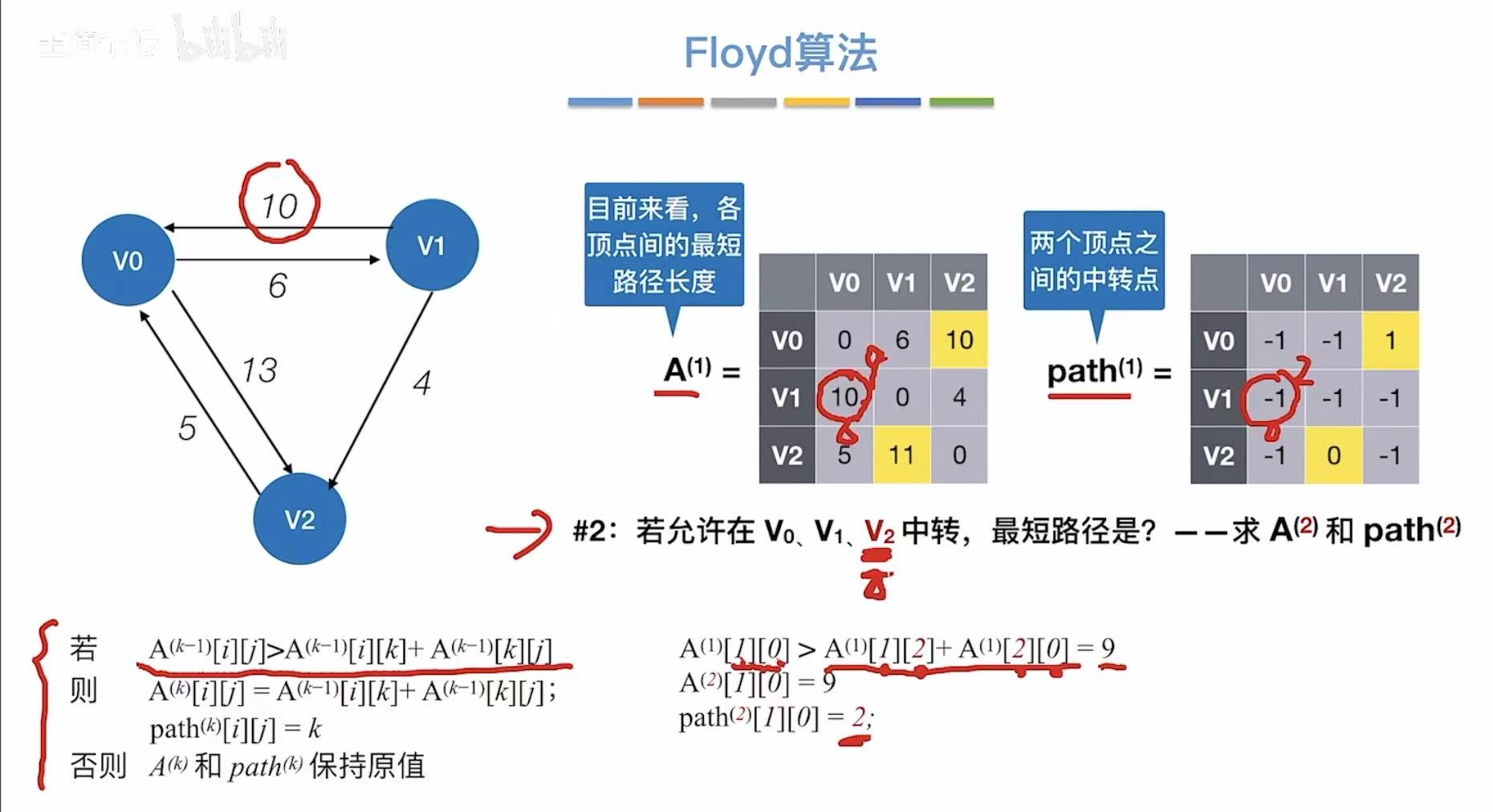
- 允许v2中转
- 更新两个表
- n轮之后
- 更新两个表
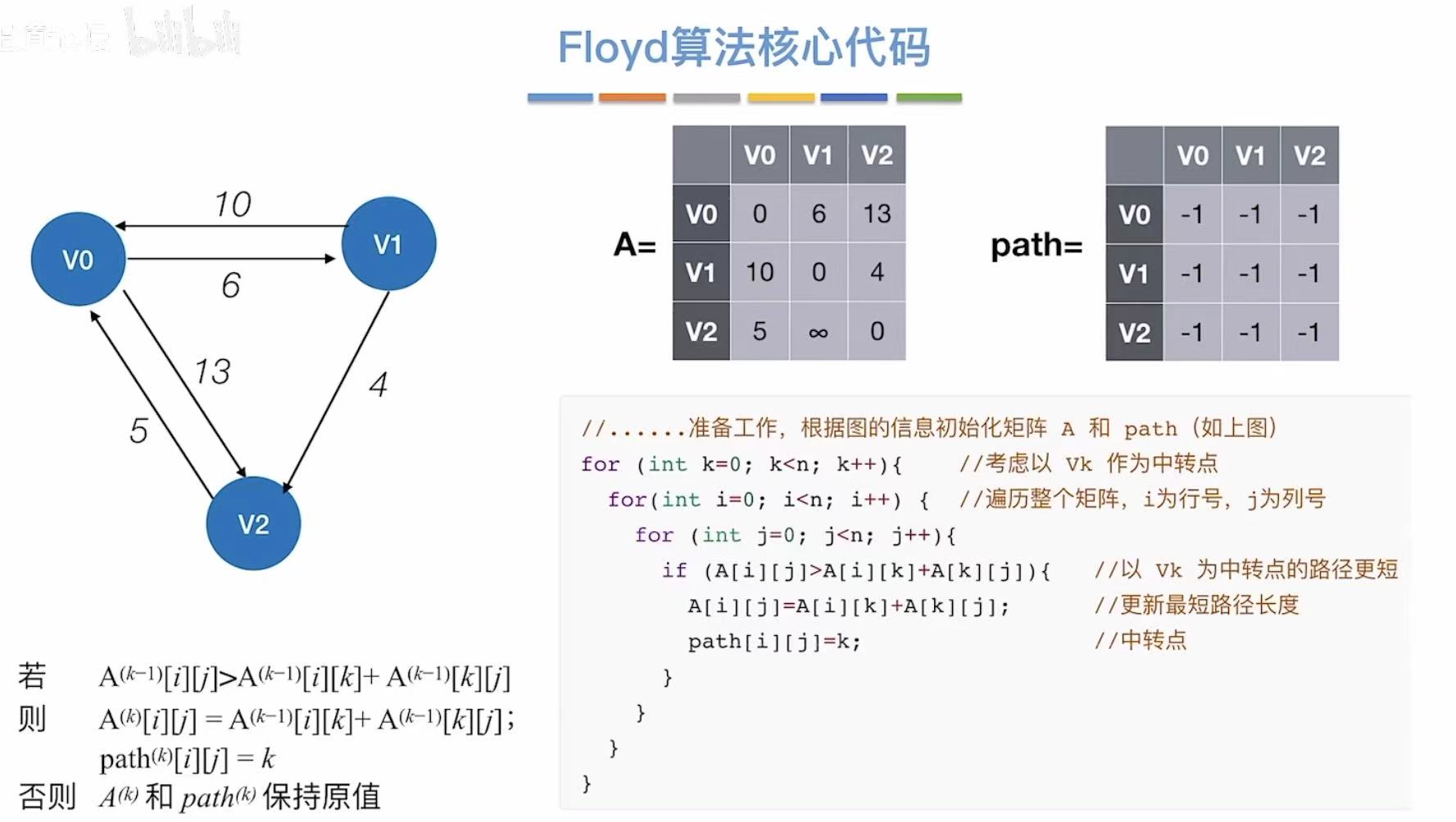
java
// Floyd 算法:求任意两点之间的最短路径(适用于带权有向图,允许负权边,但不能有负环)
// A[i][j] 表示从顶点 i 到顶点 j 的当前最短路径长度
// path[i][j] 表示从 i 到 j 的最短路径中,j 的前驱顶点(用于回溯路径)
// 初始化:根据图的信息构建初始距离矩阵 A 和路径矩阵 path
// 例如:A[i][j] = 边 (i,j) 的权重;若无边,则为 ∞(用一个大数表示)
// path[i][j] = -1 表示无直接路径或未定义
for (int k = 0; k < n; k++) { // 外层循环:枚举中间顶点 vk 作为"转点"
for (int i = 0; i < n; i++) { // 中层循环:遍历起点 i
for (int j = 0; j < n; j++) { // 内层循环:遍历终点 j
// 核心判断:是否通过顶点 k 能使 i→j 的路径更短?
if (A[i][j] > A[i][k] + A[k][j]) {
// 如果绕道 k 更短,则更新最短路径长度
A[i][j] = A[i][k] + A[k][j]; // 更新距离
// 同时更新路径记录:从 i 到 j 的路径现在经过 k
path[i][j] = k; // 记录 k 是 i→j 路径中的中转点
}
// 否则保持原值不变
}
}
}
3.3 算法实例
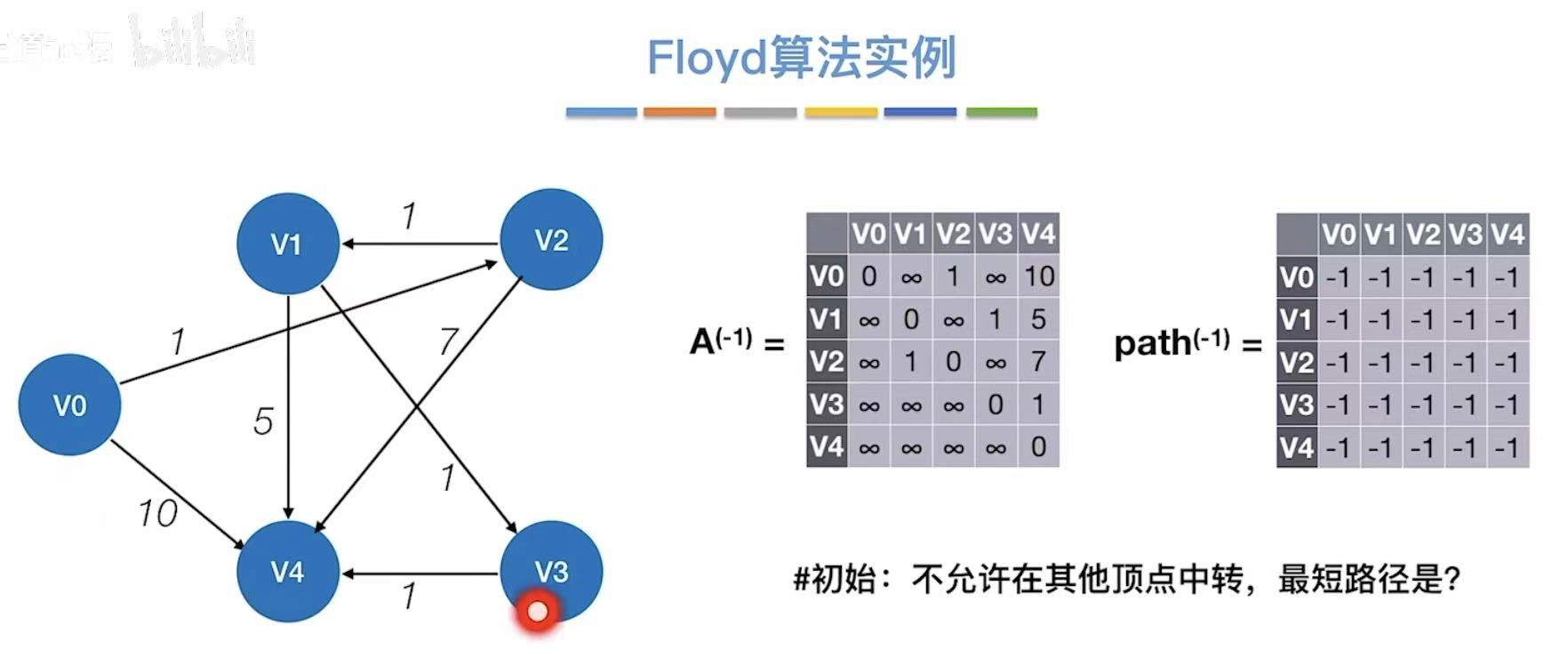
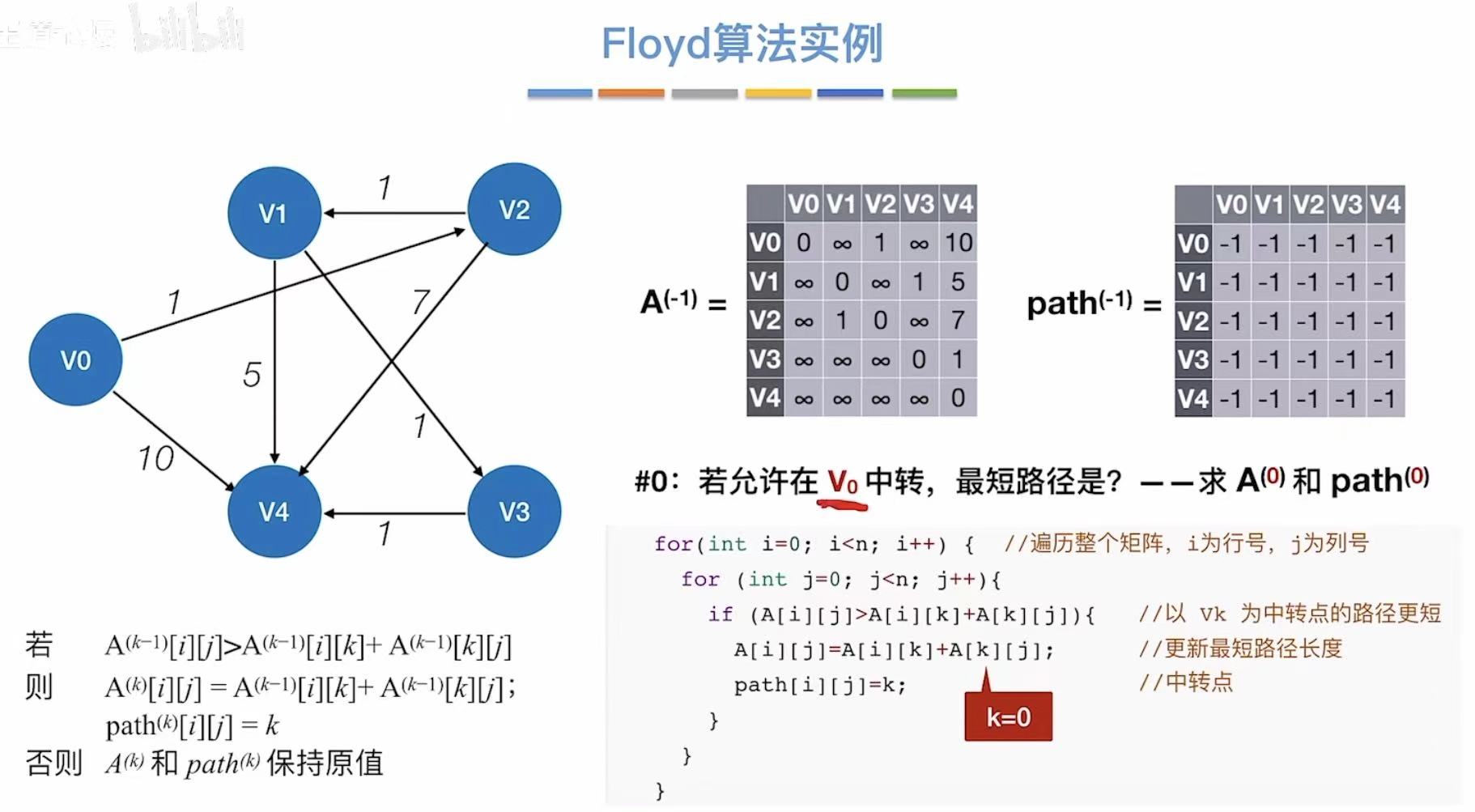
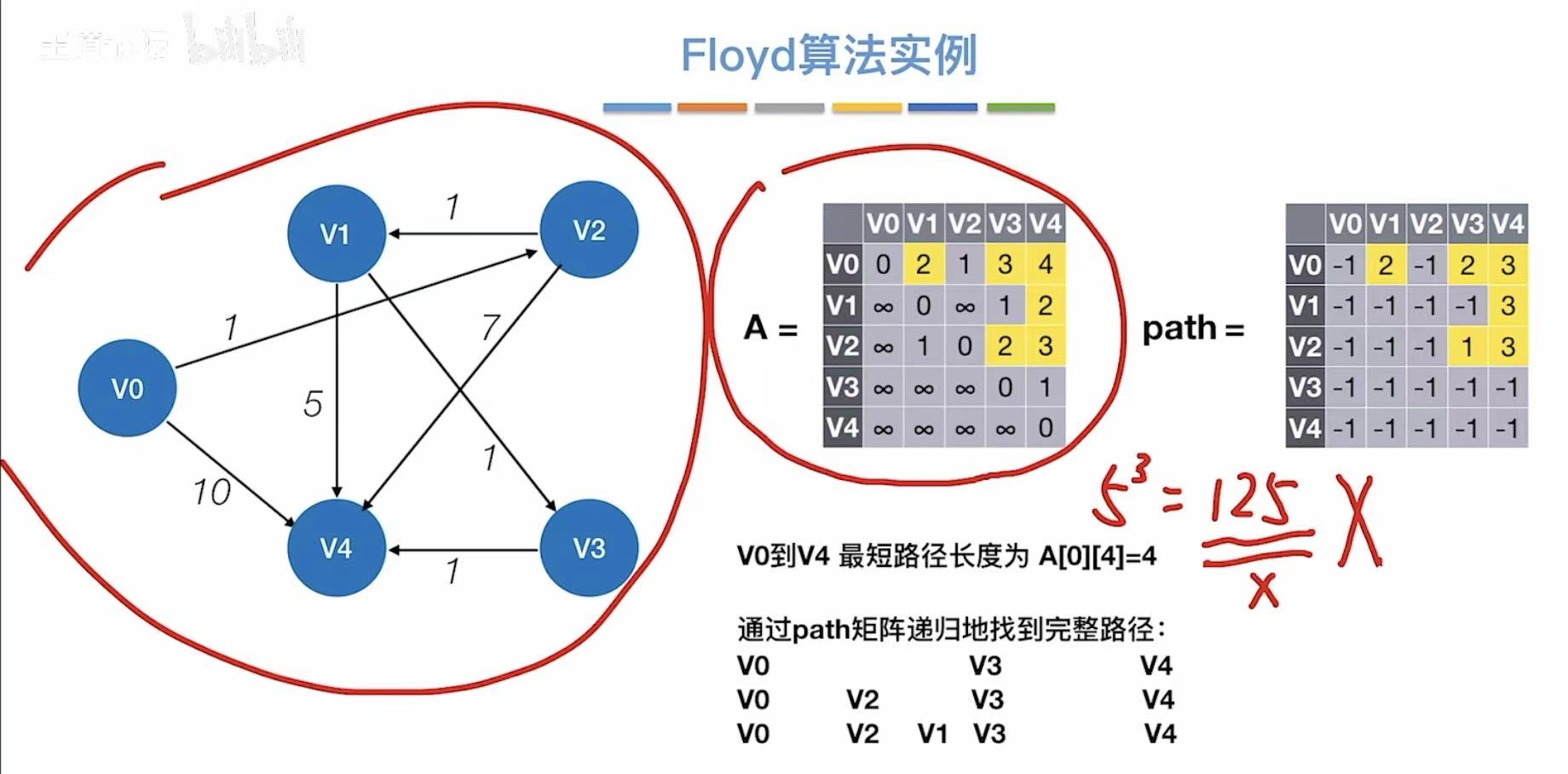
3.4 练习及小结
可以用于负权图
但是不可以用于带有负权回路的图。
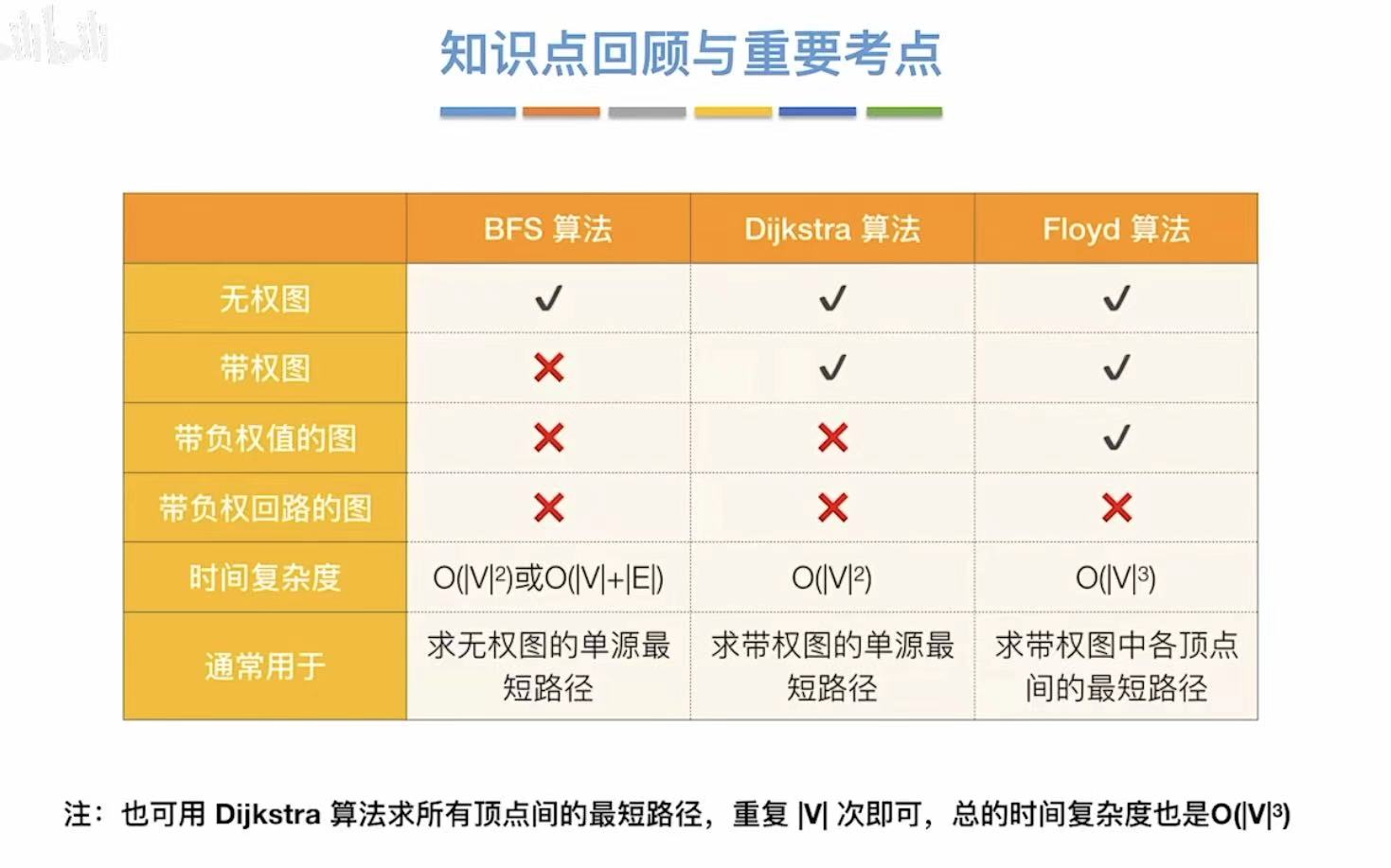
有向无环图(DAG图)
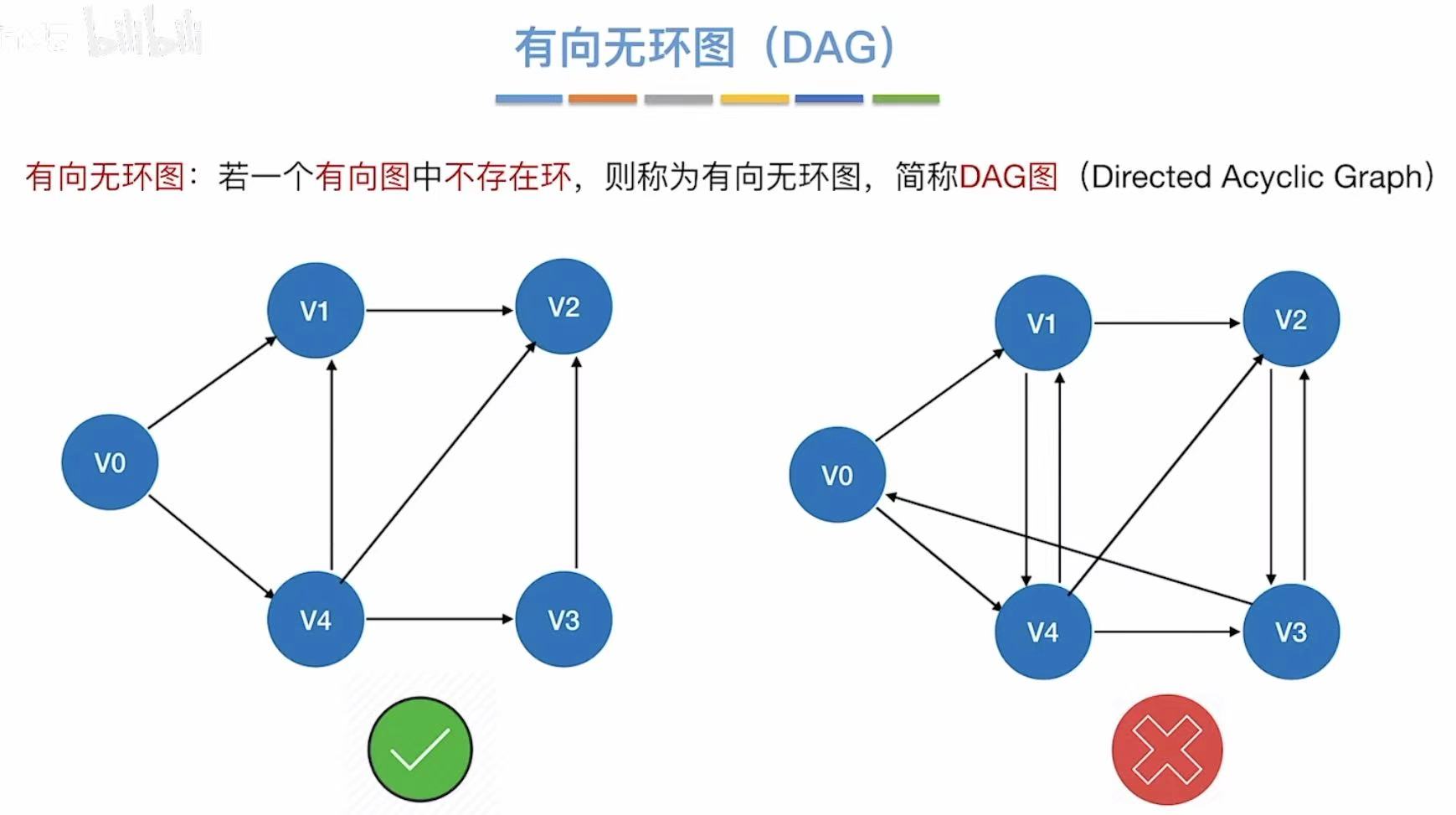
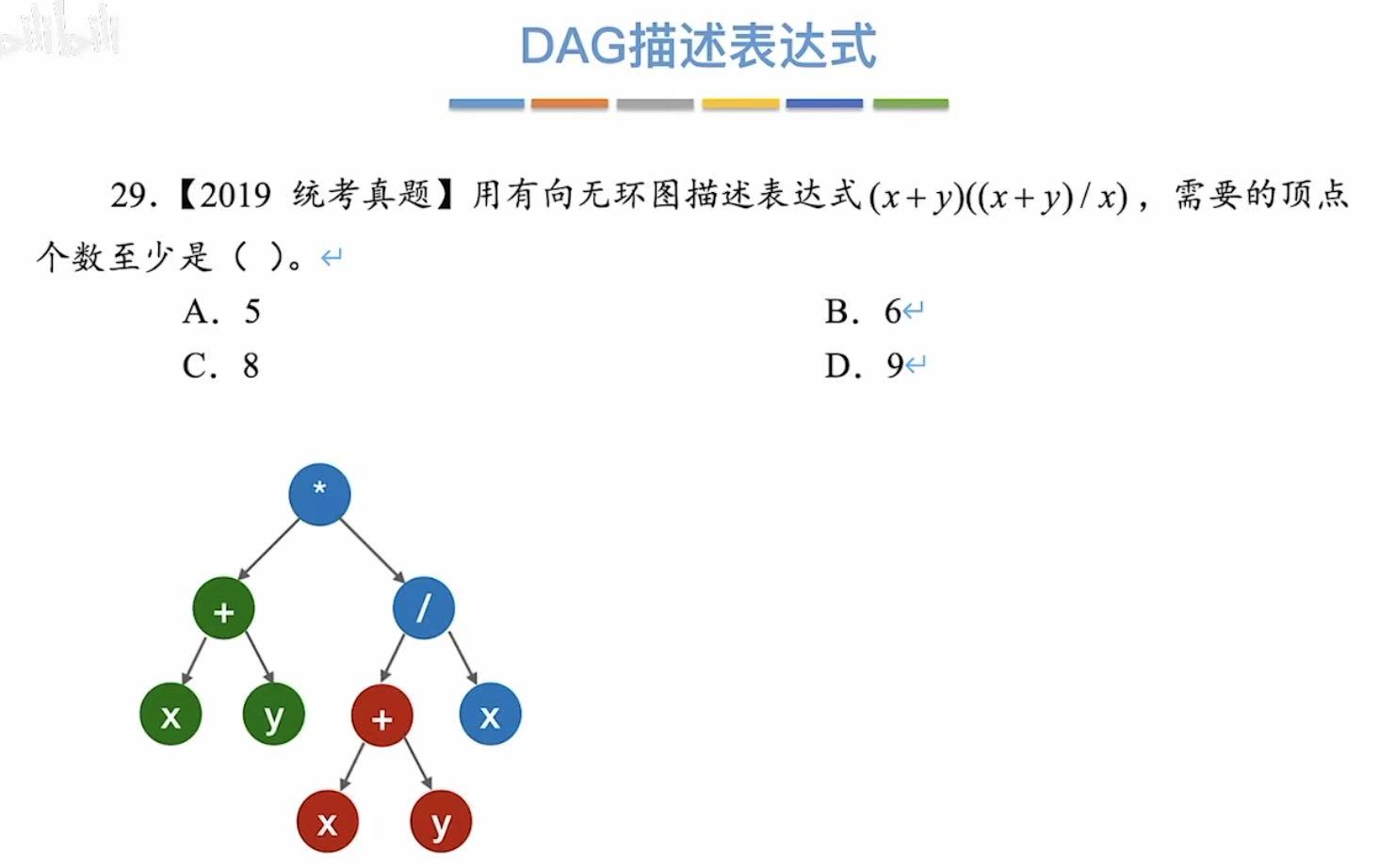
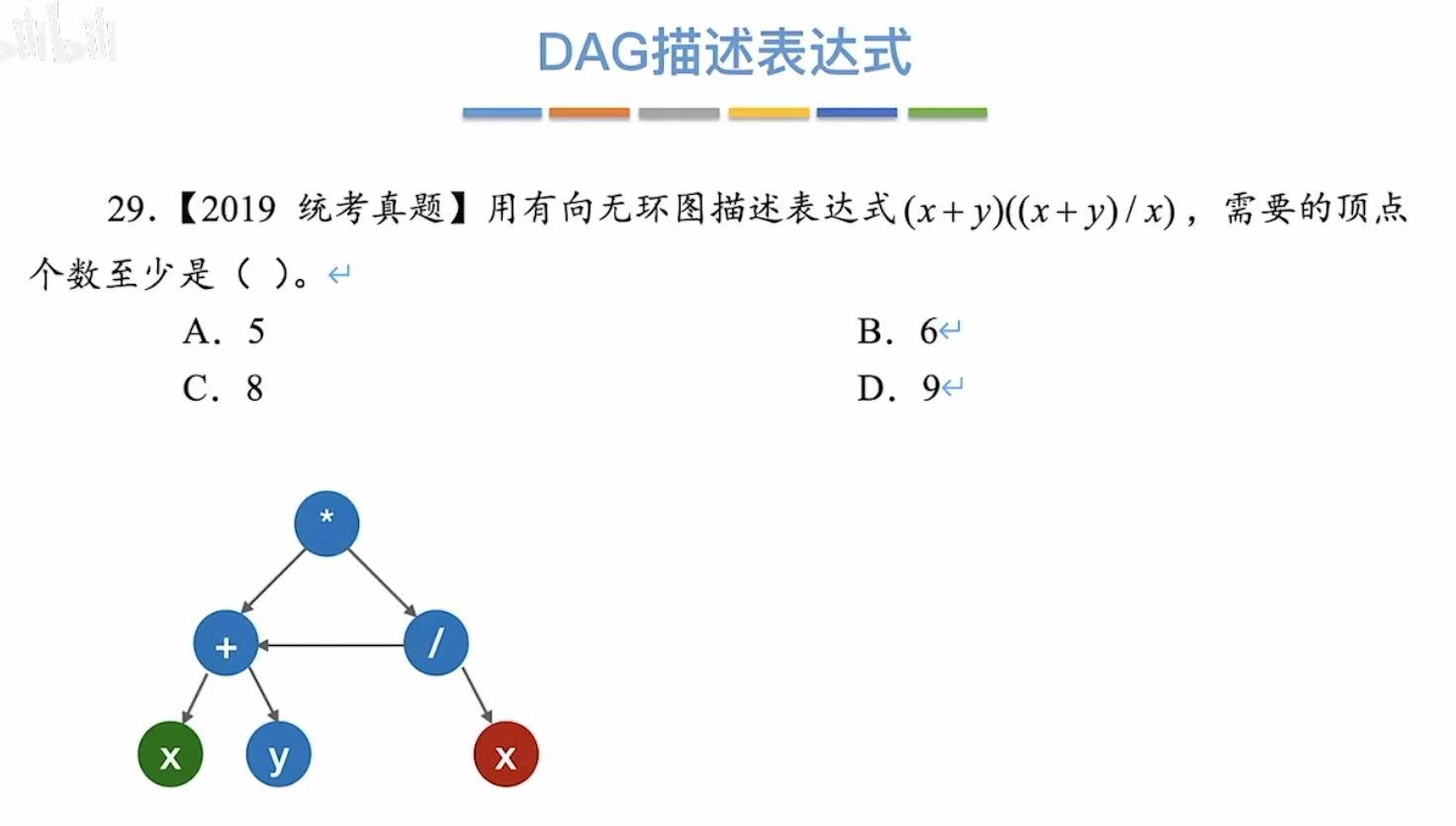
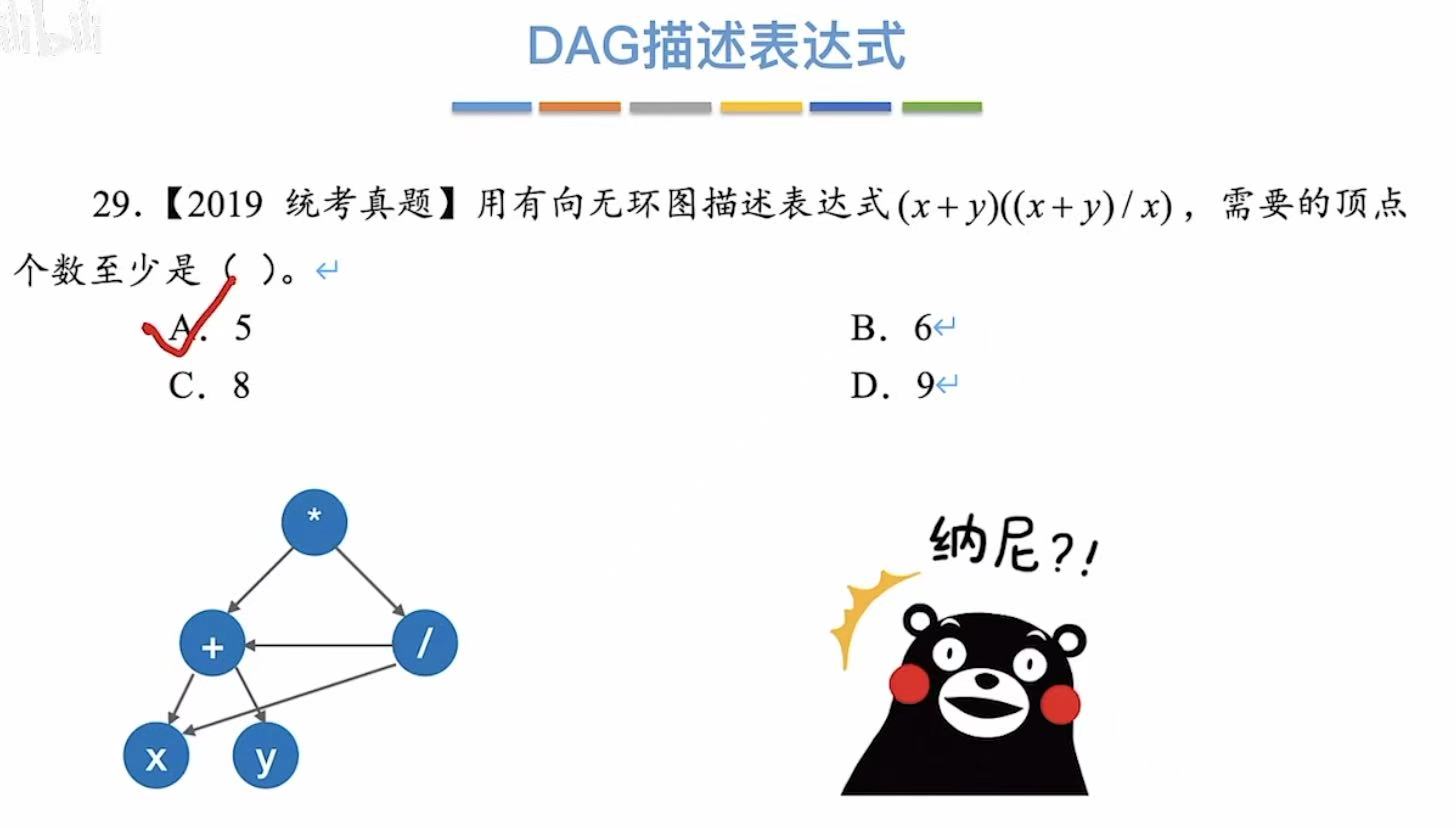
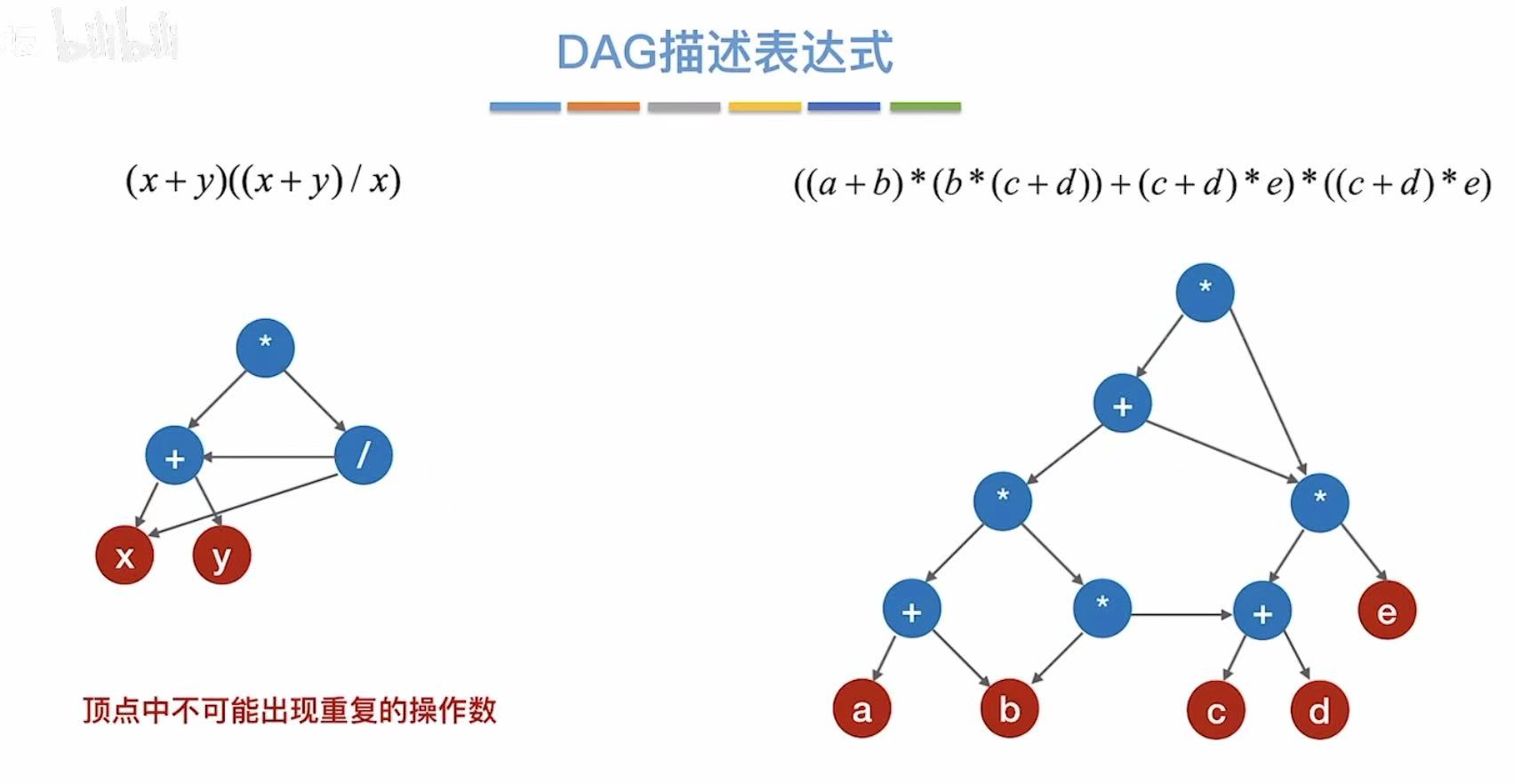
1. DAG描述表达式
两个重复的部分:
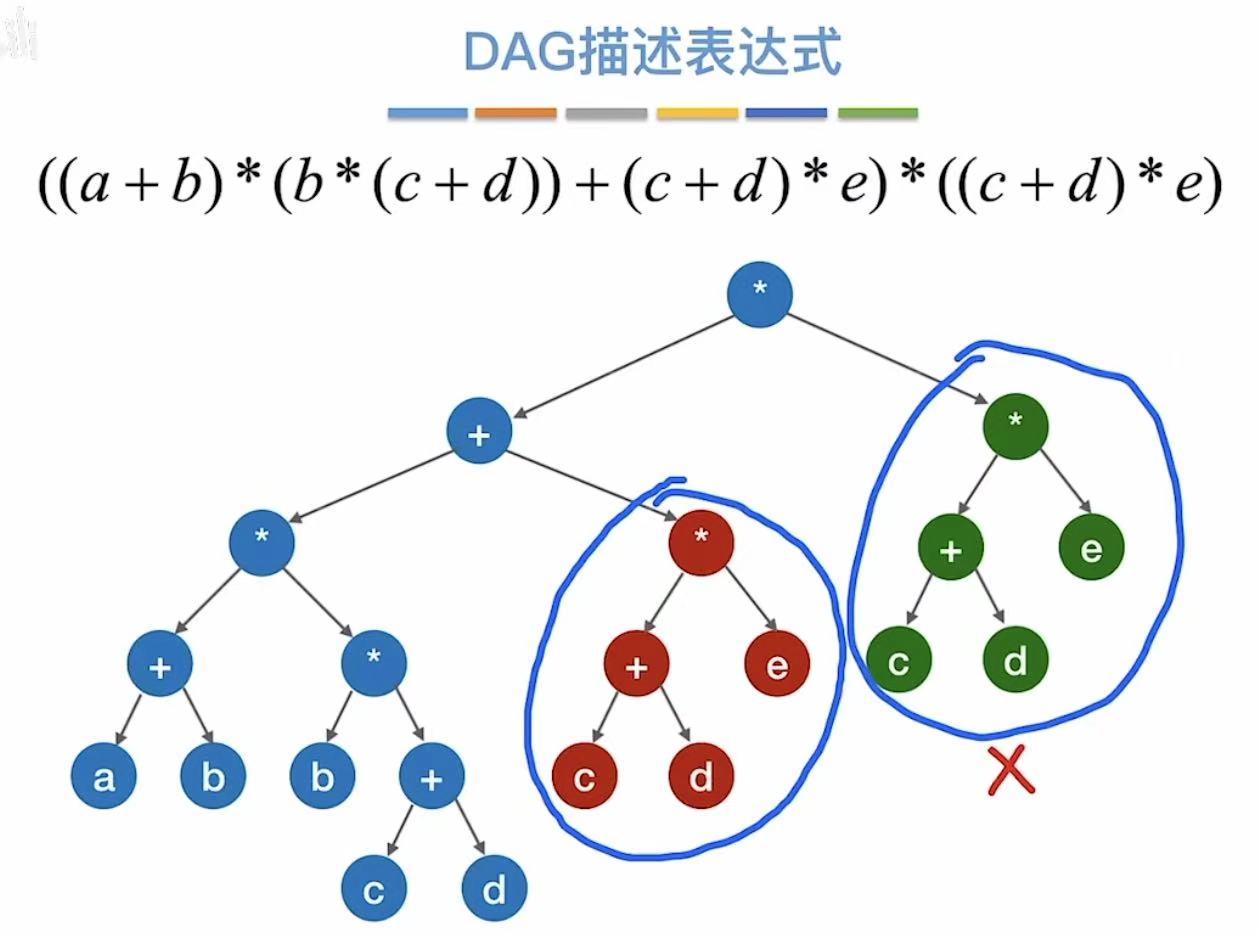
就可以合并成一个,由上面的顶点全部指向保留的这一个
红绿两个部分同样重复了,
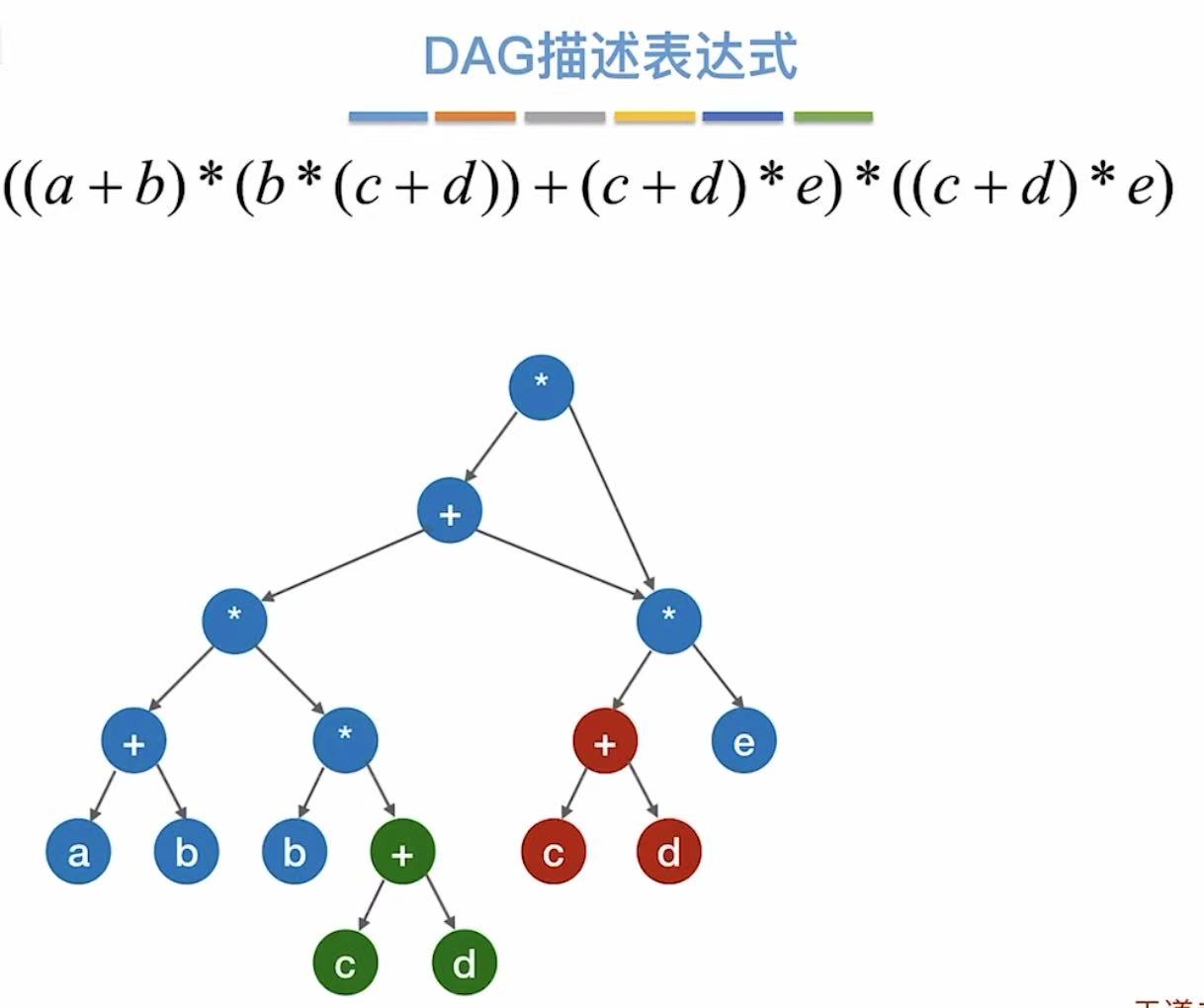
也可以保留其中一个,将另一边的指像这个重复的部分:
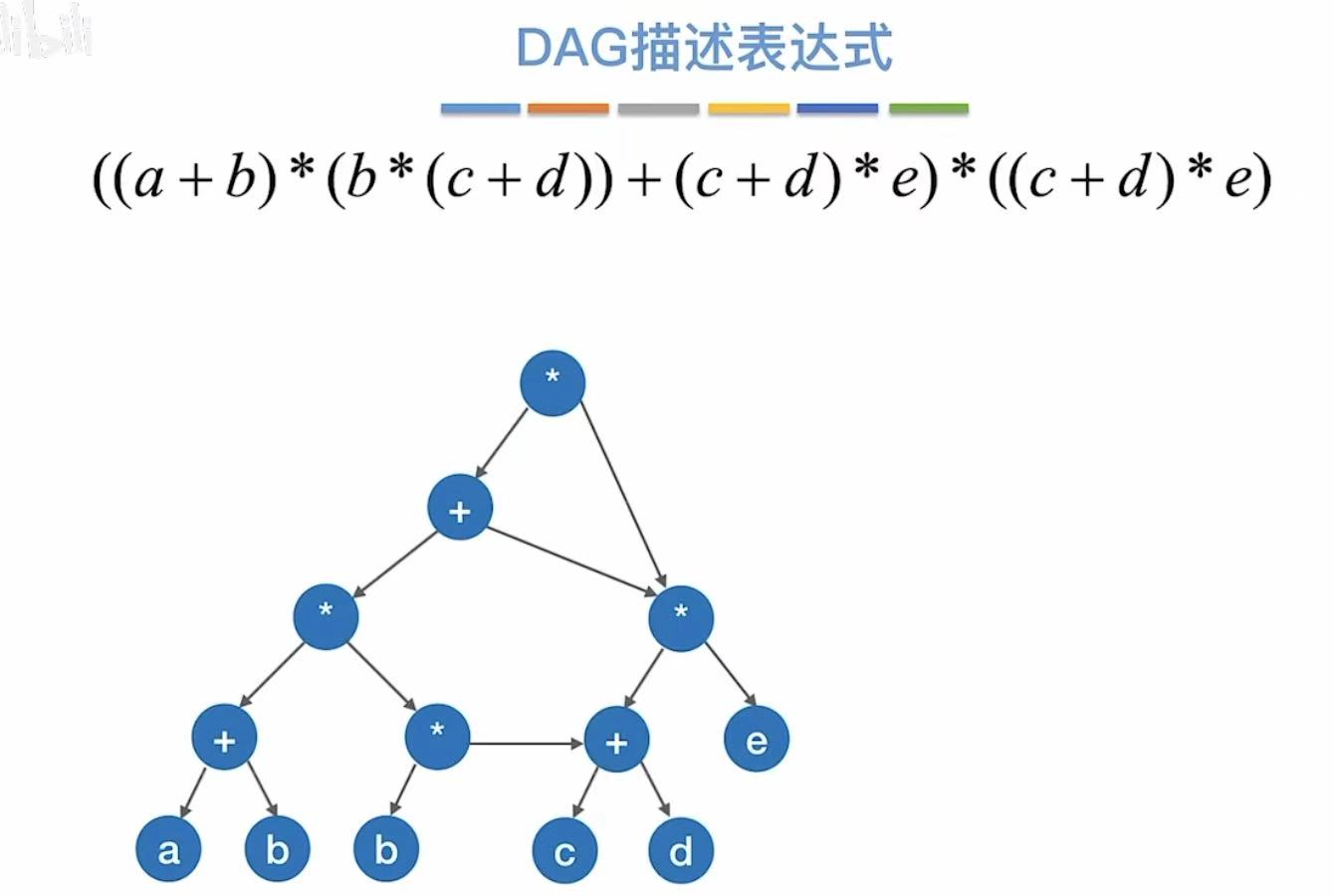
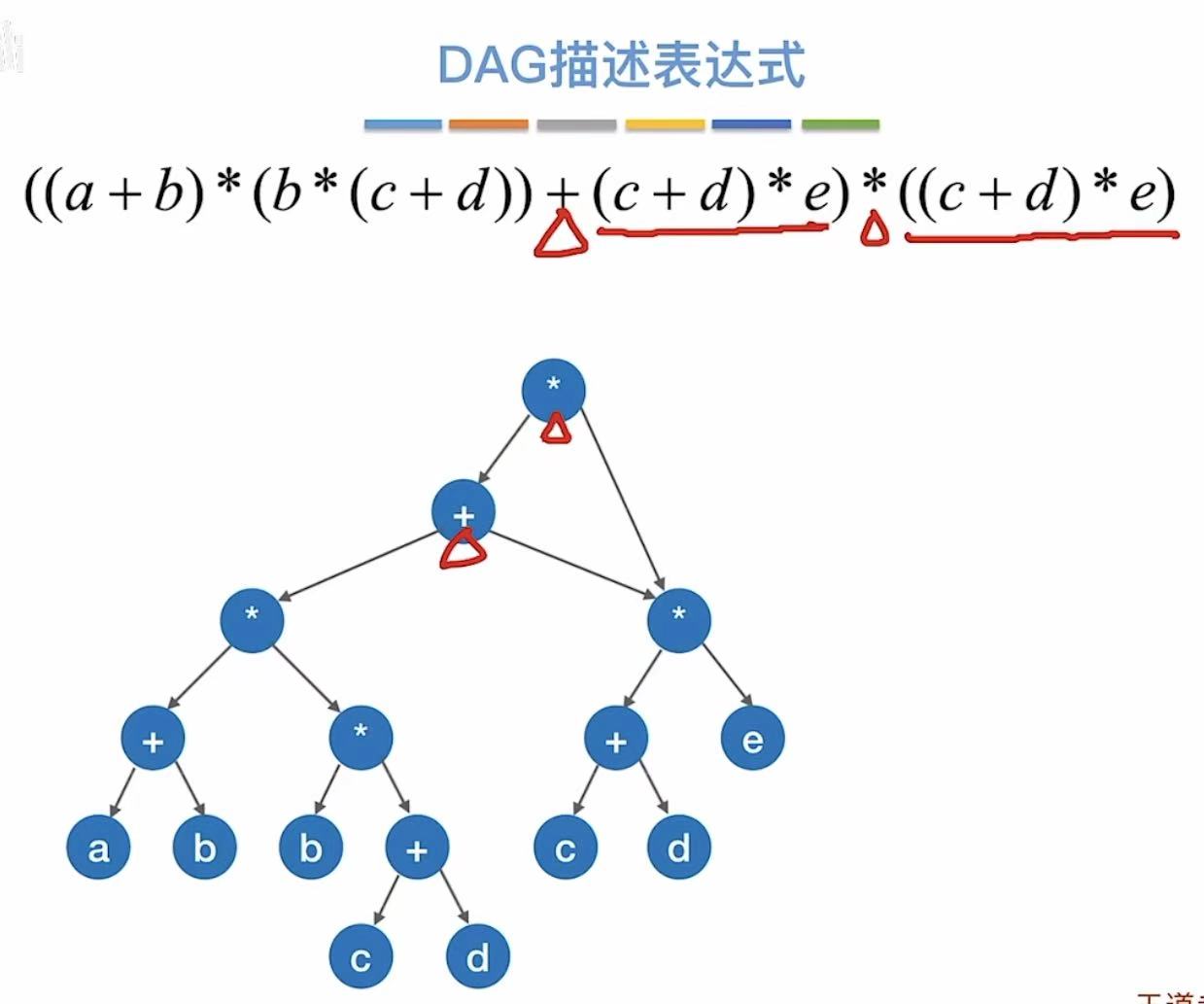
这两个b也重复了,
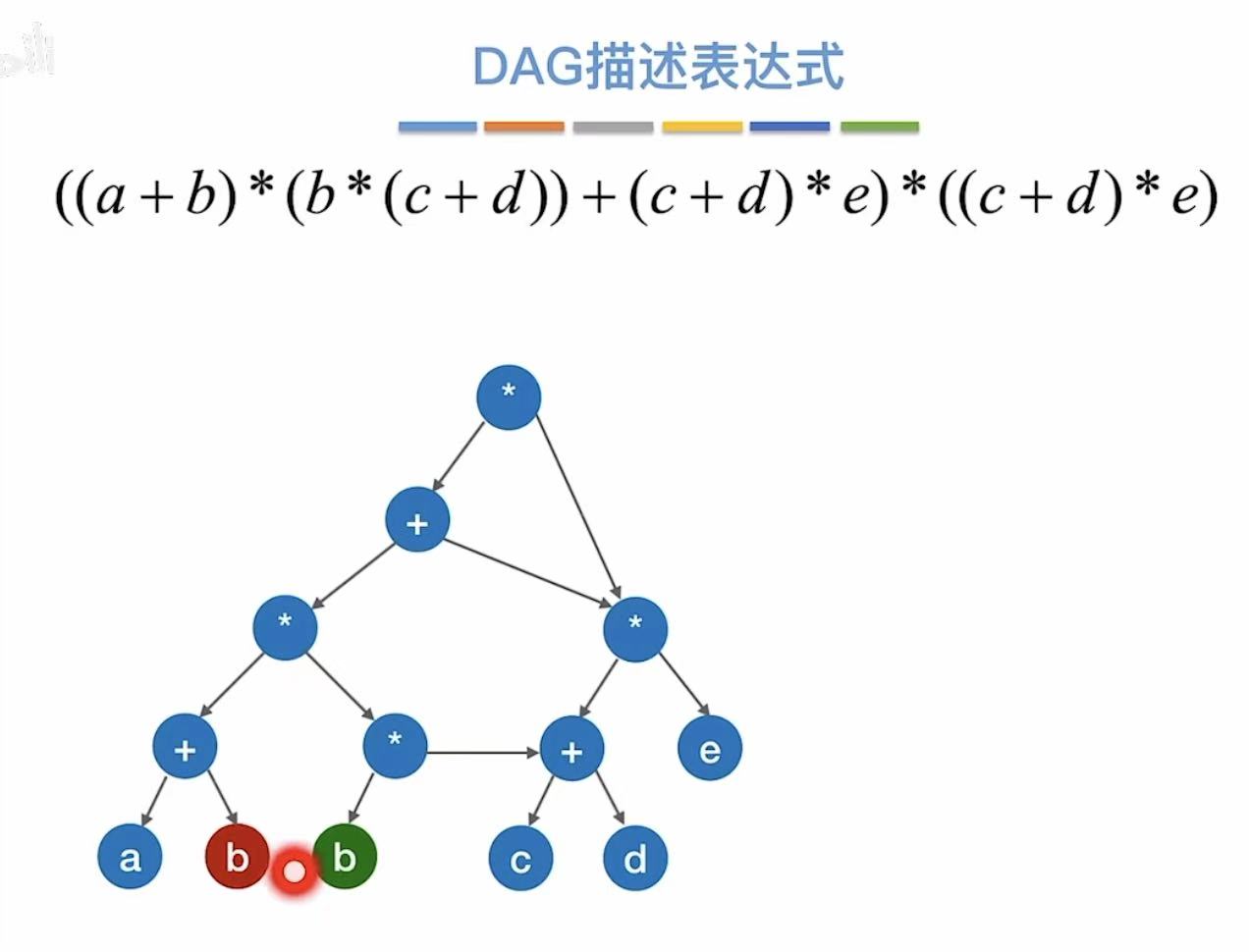
也可以合并成一个,然后上面的共同指向这一个:
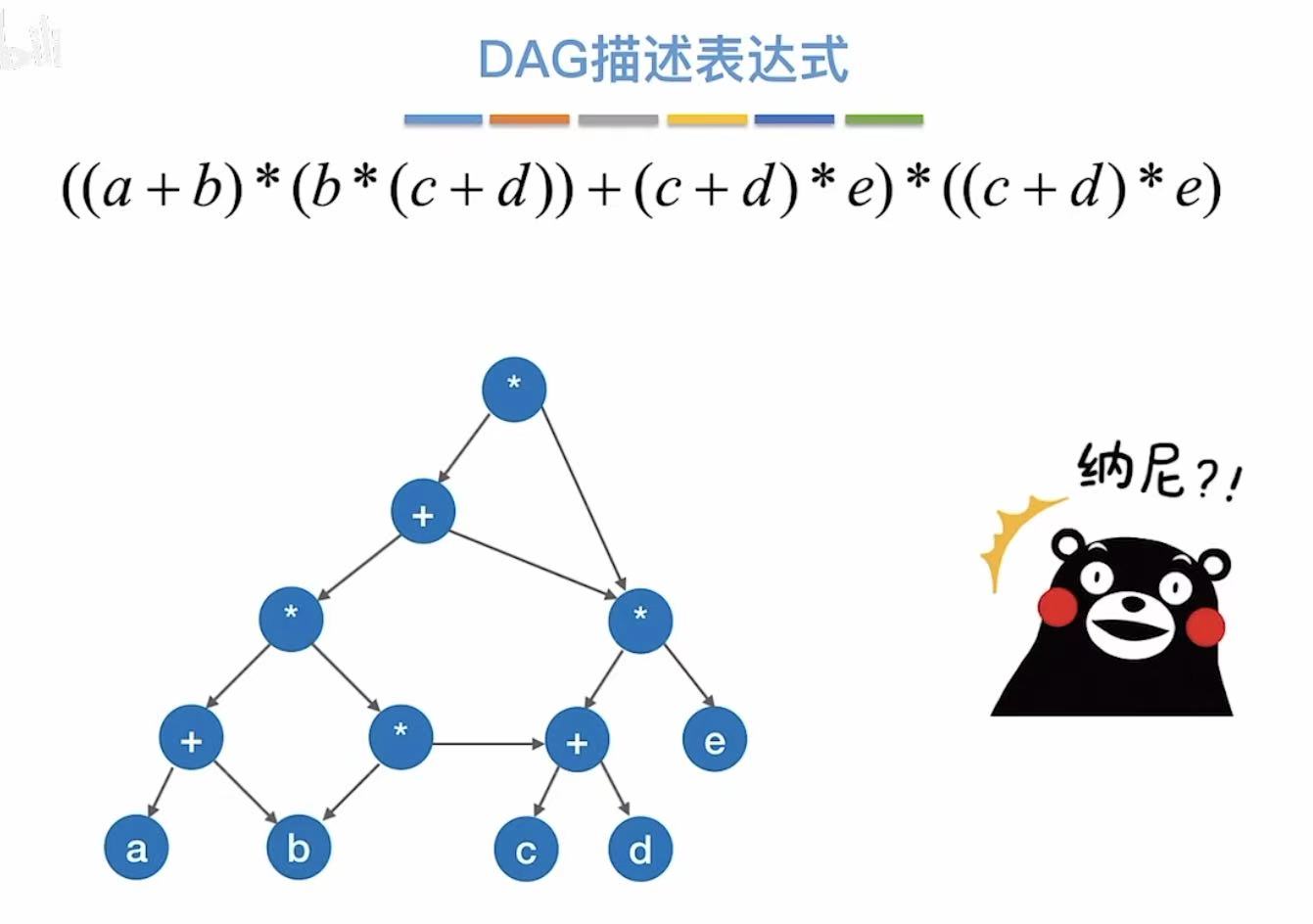
真题:
2. 解题方法
经过无数尝试及总结得出一个结论 :
顶点中不可能出现重复的操作数
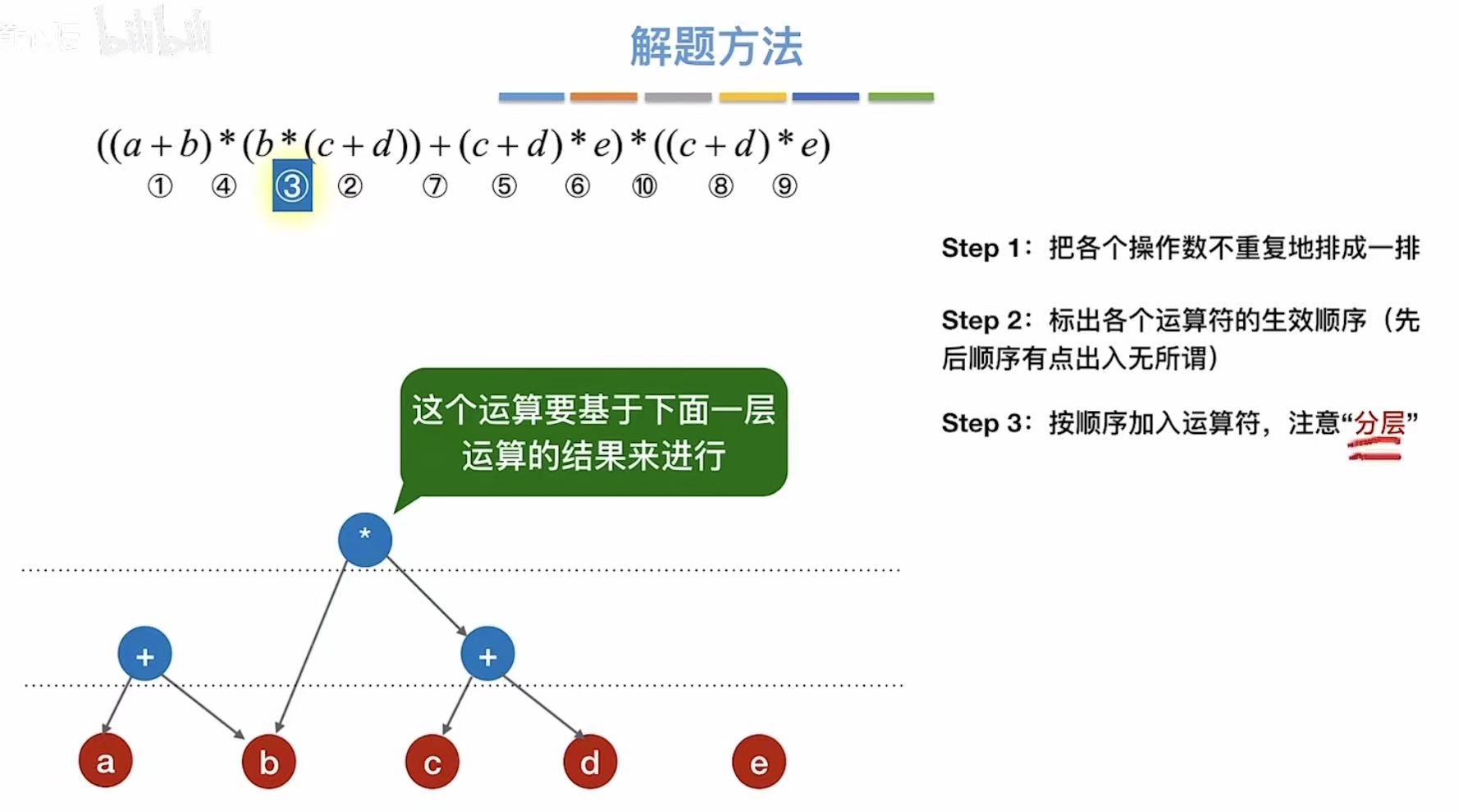
根据这一条结论,我们就可以得到如下的步骤:
- 最底层就是我们表达式中的所有元素
- 将表达式中的运算符标上序号,以防遗漏
- 按顺序把运算符加入到树中,注意分层
- 分层 :看清楚是谁与谁的运算,如果是与一个式子的运算,自然这个运算符就高人一等了
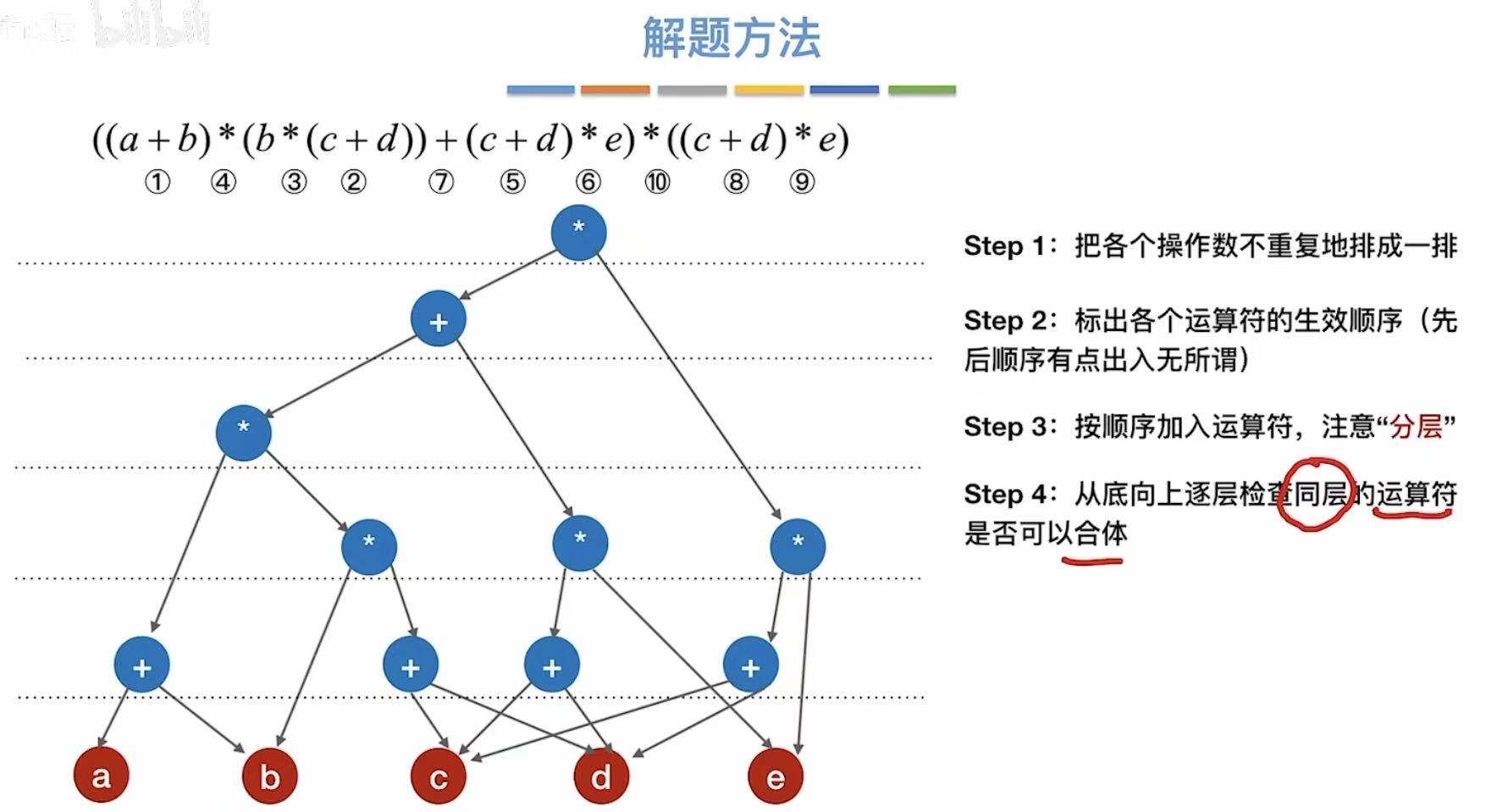
- 添加完所有的运算符,我们就可以来进行优化了
- 从底层向上逐层检查同层的运算符是否可以合体
- 比如c+d有3个,就可以合成一个
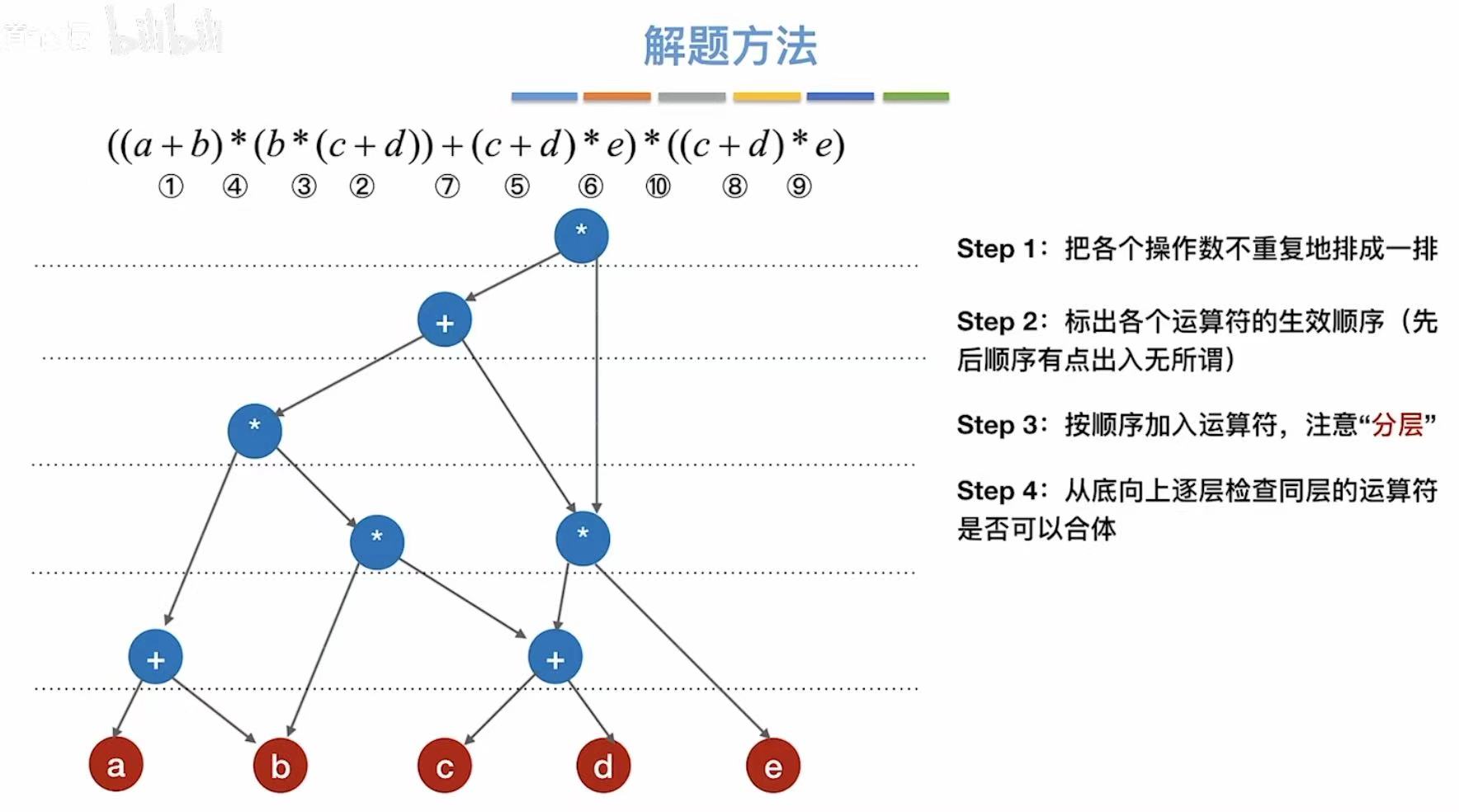
- 合体之后就是这个样子了:
小练习:
拓扑排序
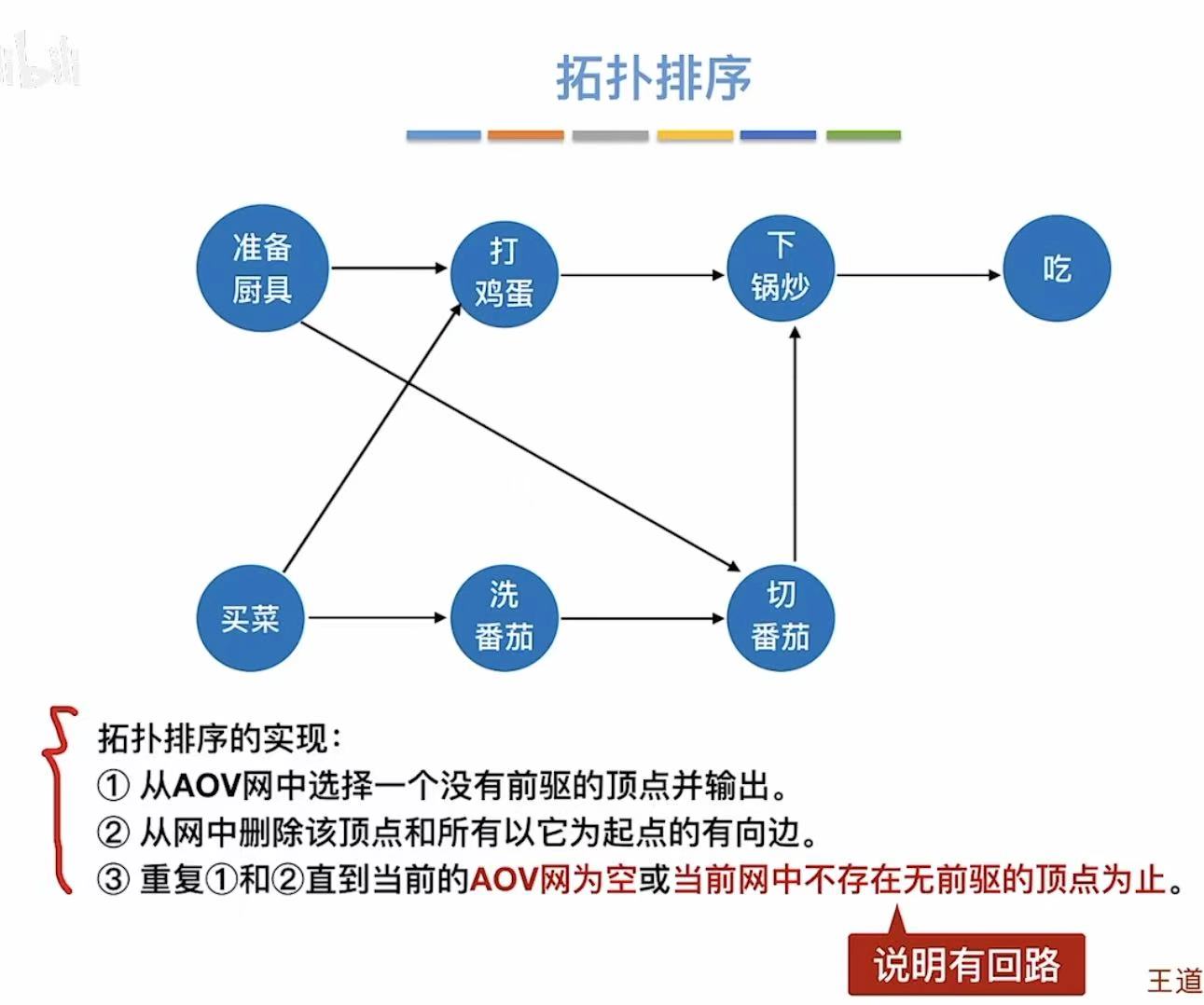
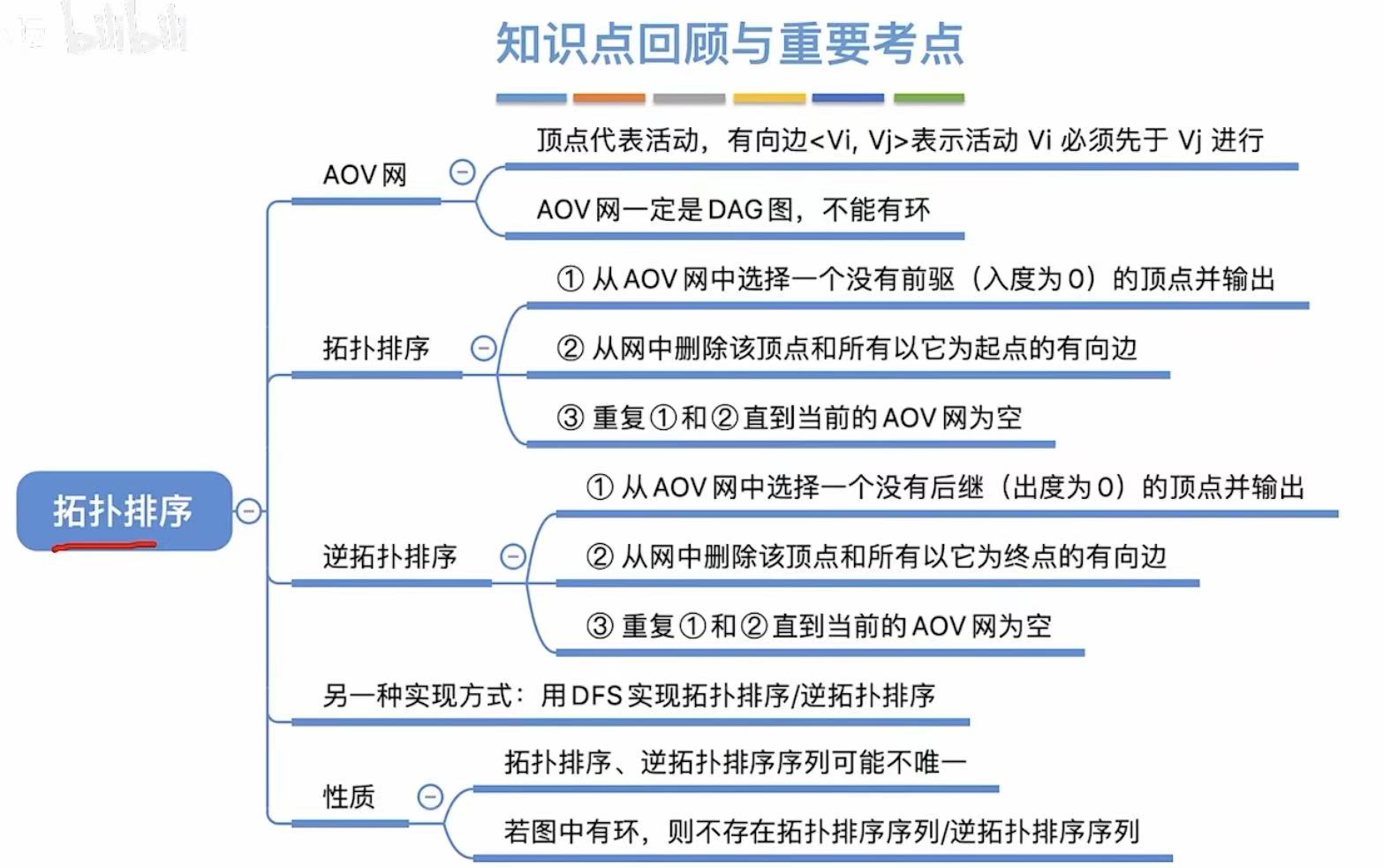
1. AOV网
用顶点表示活动
- A-->B:必须做完A才能执行B
- 被两个箭头指:必须完成前两个事件才能做接下来的事件
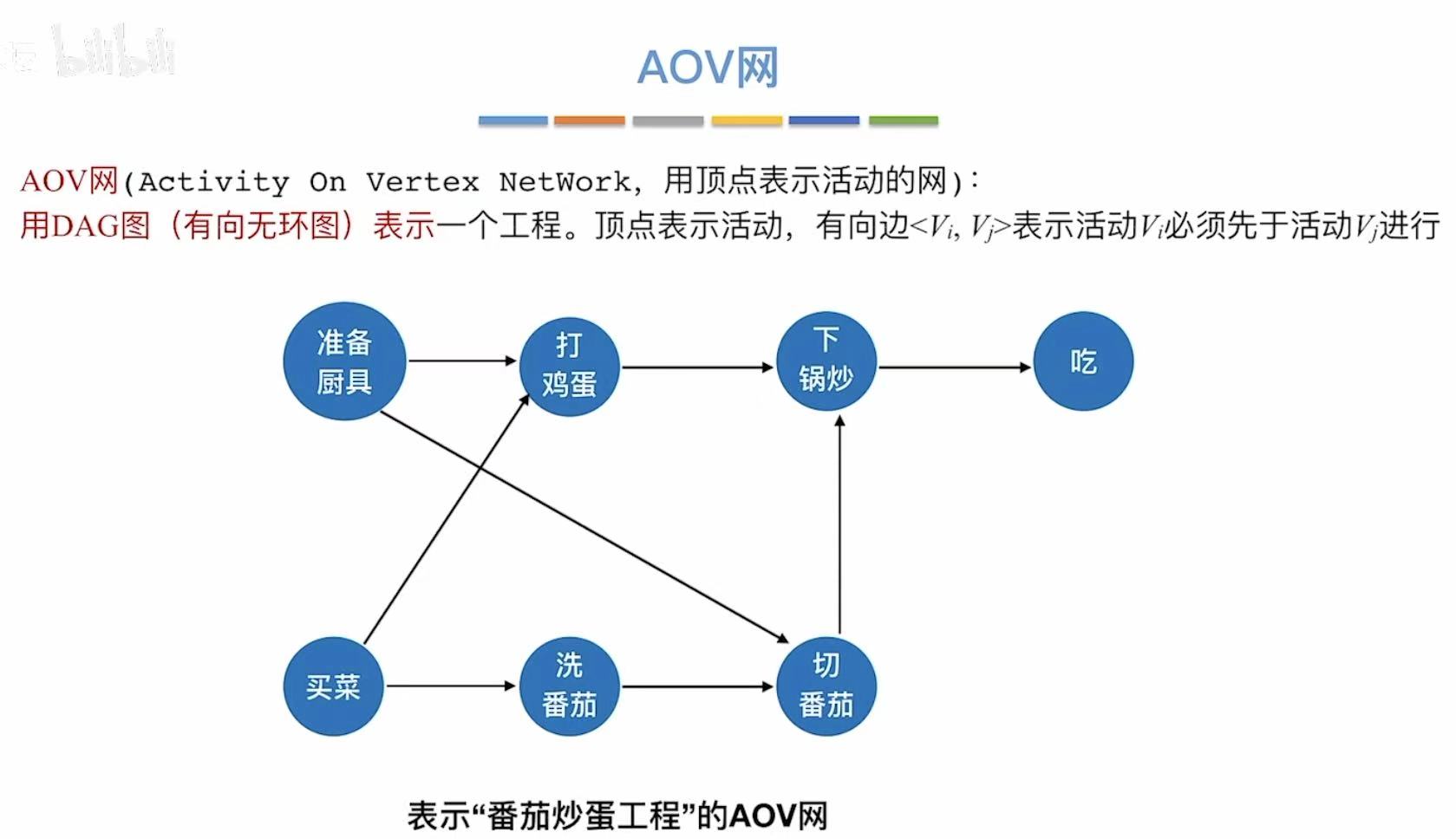
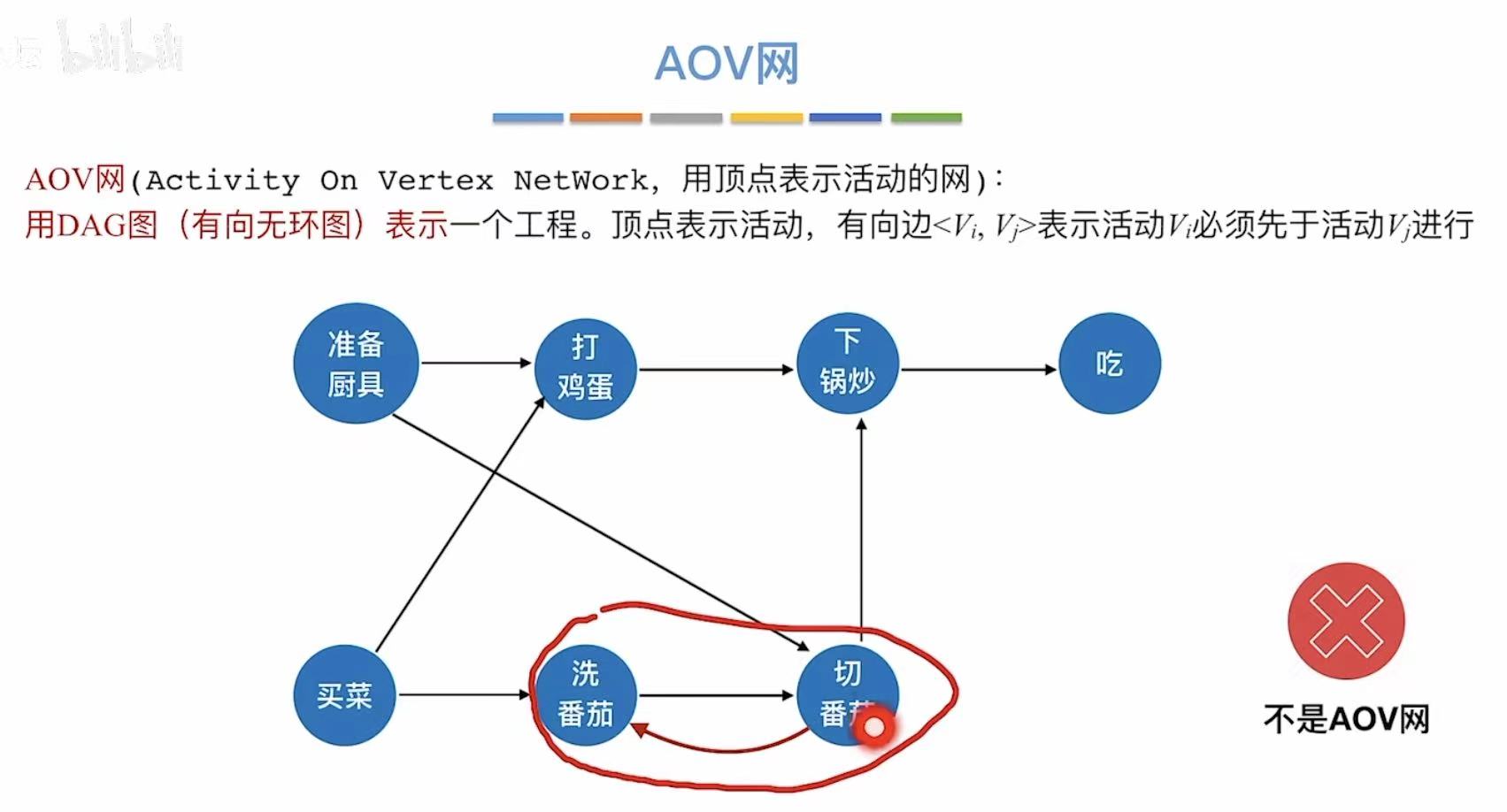
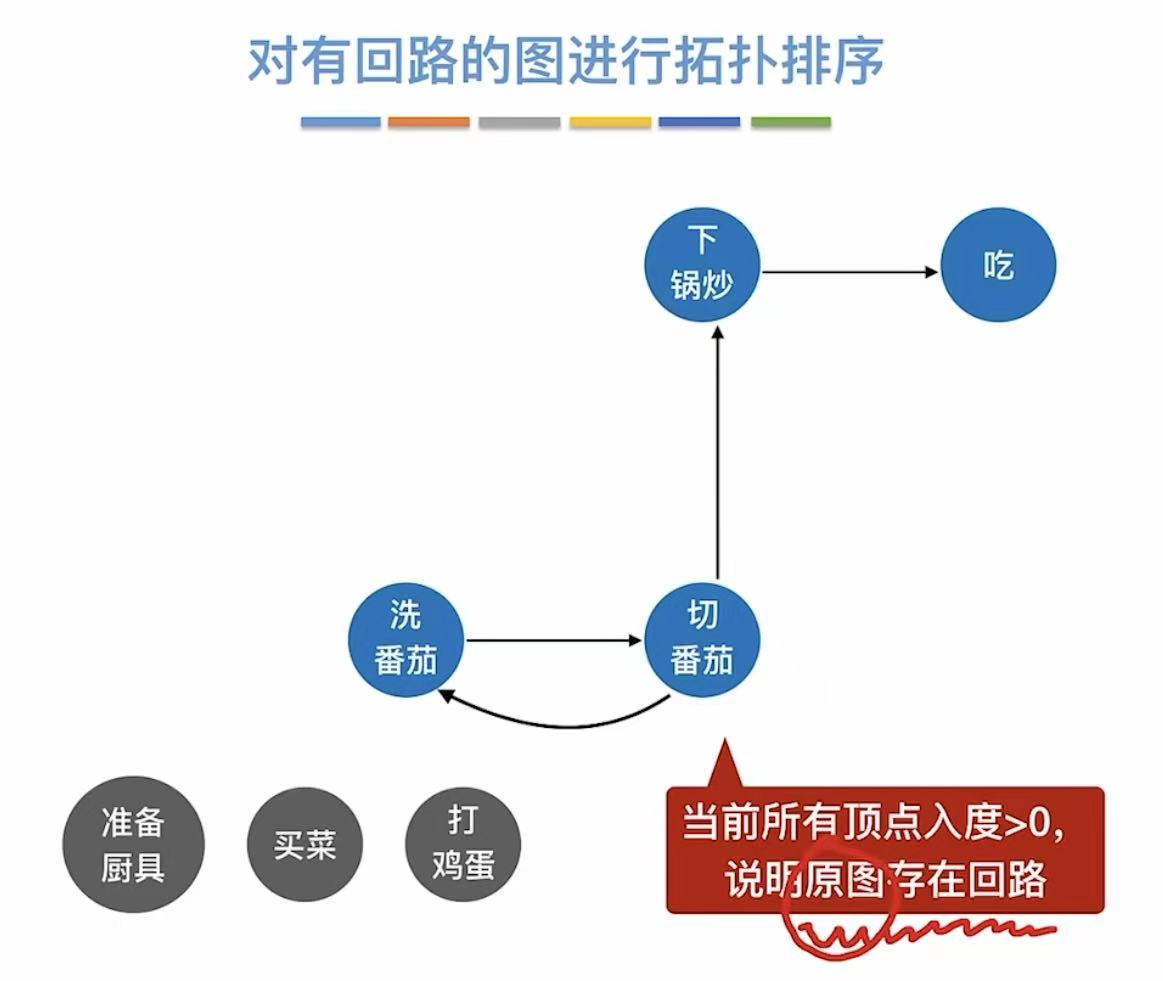
如果有环了,就不是AOV网了,因为AOV网本质上就是有向无环图(DAG)
2. 拓扑排序
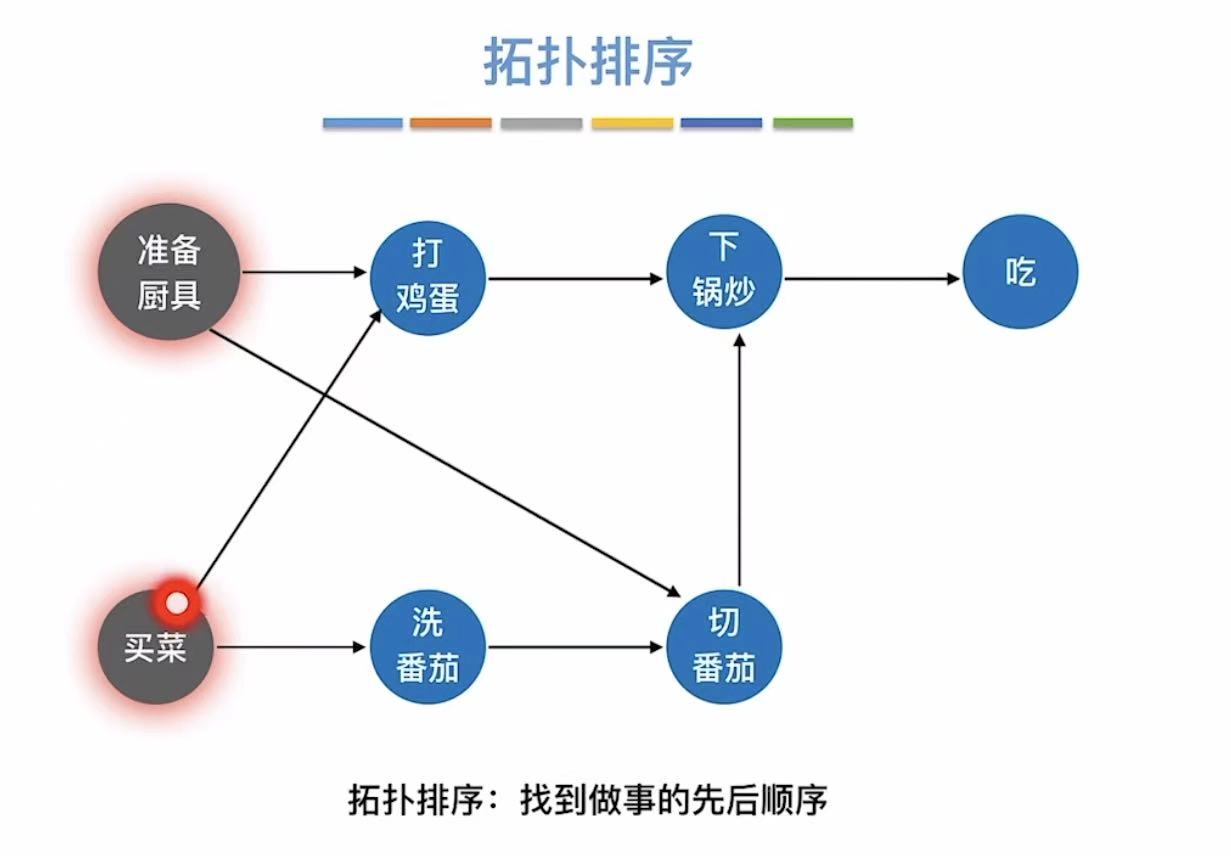
就是按照顺序把顶点写下来,先完成前提分支,然后切回主线继续进行

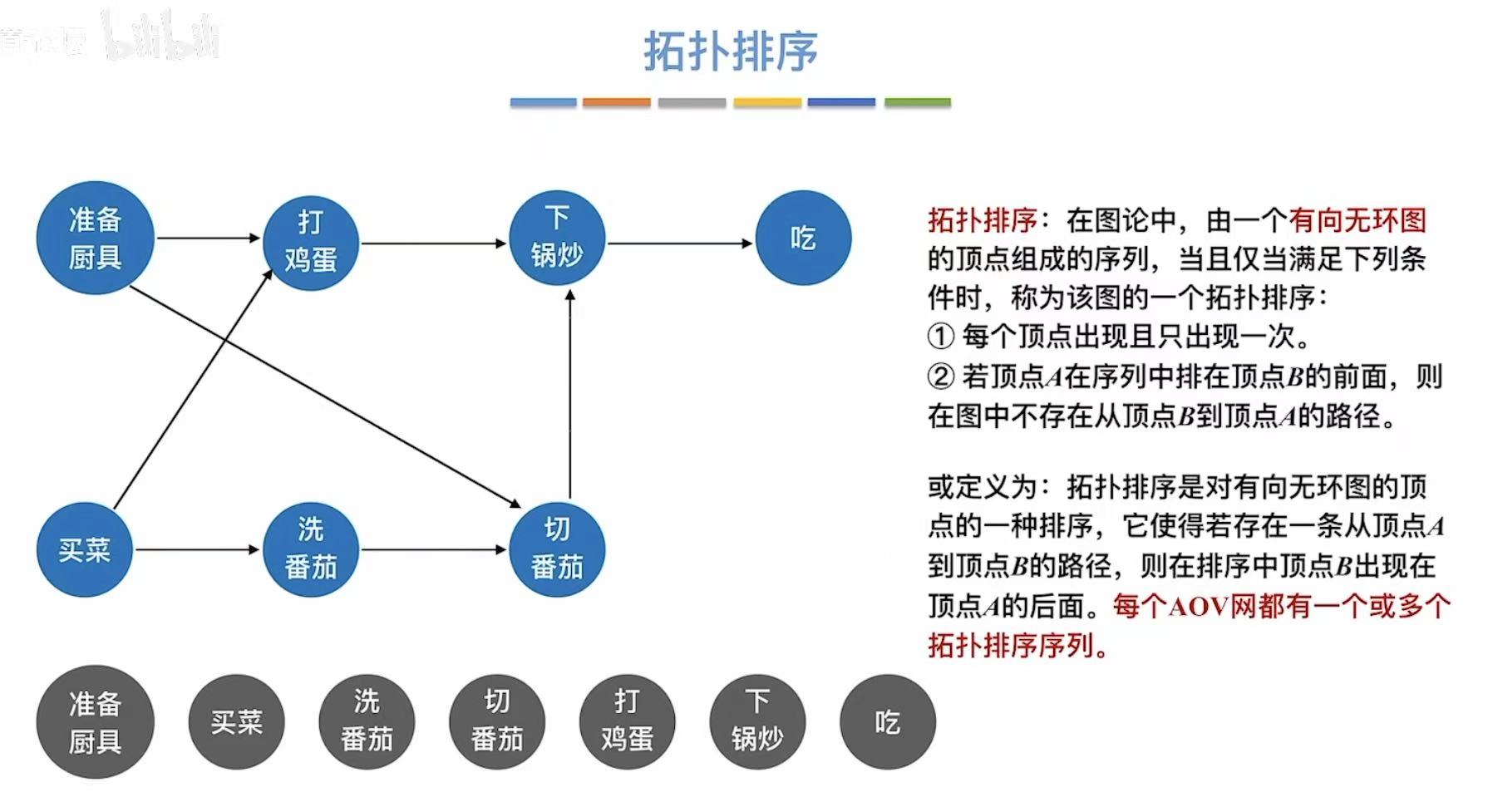
拓扑排序条件:
- 每个顶点出现且只出现一次
- 序列中A在B前-->图中无B到A的路径
3. 代码实现
定义:
java
#define MaxVertexNum 100 // 图中顶点数目的最大值
// 边(弧)结点结构体:用于存储有向边的信息
typedef struct ArcNode {
int adjvex; // 该弧指向的顶点在数组中的下标(即邻接点)
struct ArcNode *nextarc; // 指向下一条弧的指针(形成链表)
// InfoType info; // 可选:存储边的权值或其他信息
} ArcNode;
// 顶点结点结构体:用于存储顶点及其出边链表
typedef struct VNode {
VertexType data; // 存储顶点的数据(如字符、数字等)
ArcNode *firstarc; // 指向第一条依附于该顶点的弧(即邻接表头指针)
} VNode, AdjList[MaxVertexNum]; // VNode 是顶点类型,AdjList 是顶点数组
// 图的整体结构体:Graph(以邻接表存储)
typedef struct {
AdjList vertices; // 顶点数组:存储所有顶点和它们的邻接表
int vexnum, arcnum; // 图的当前实际顶点数和弧数
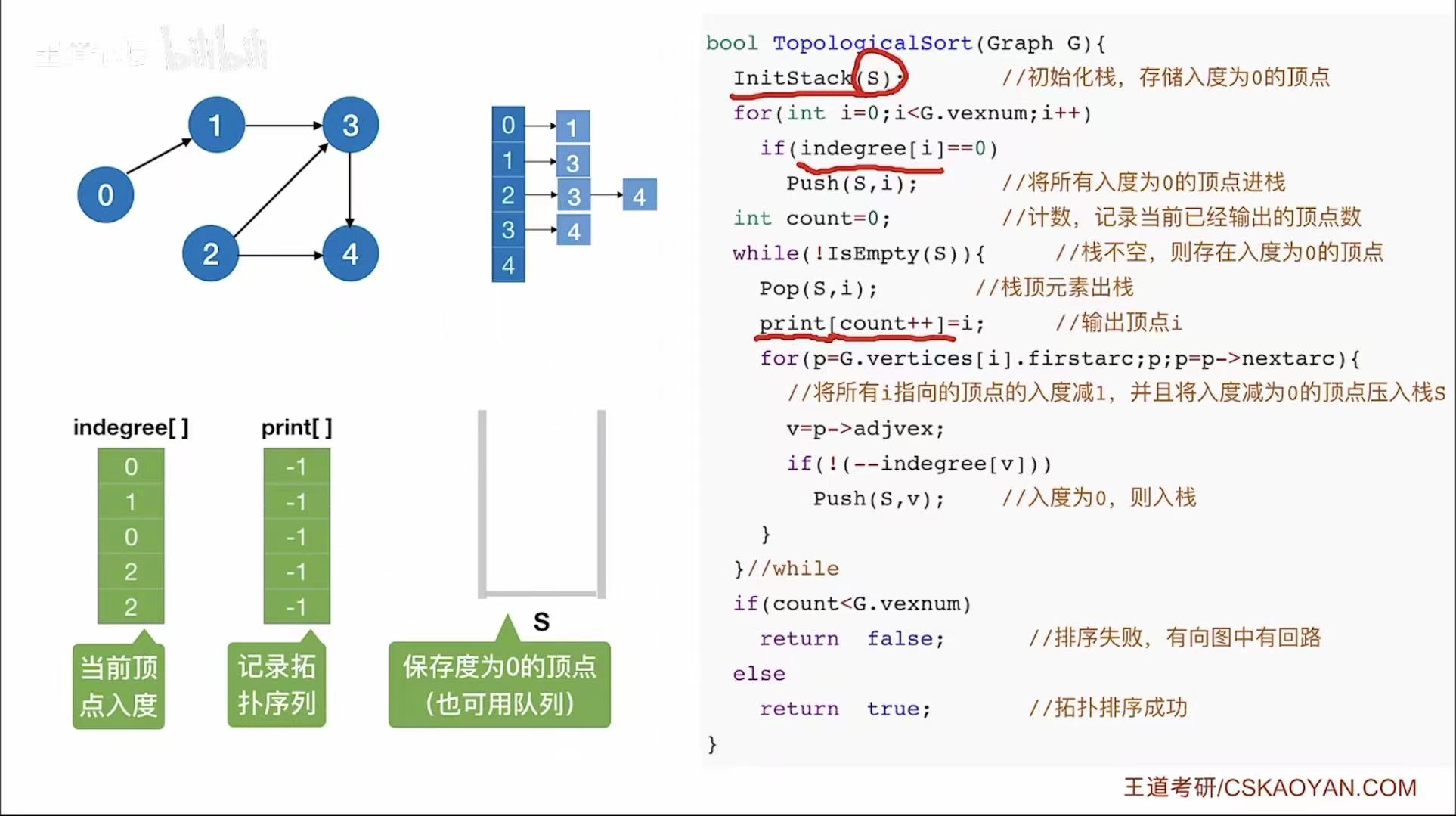
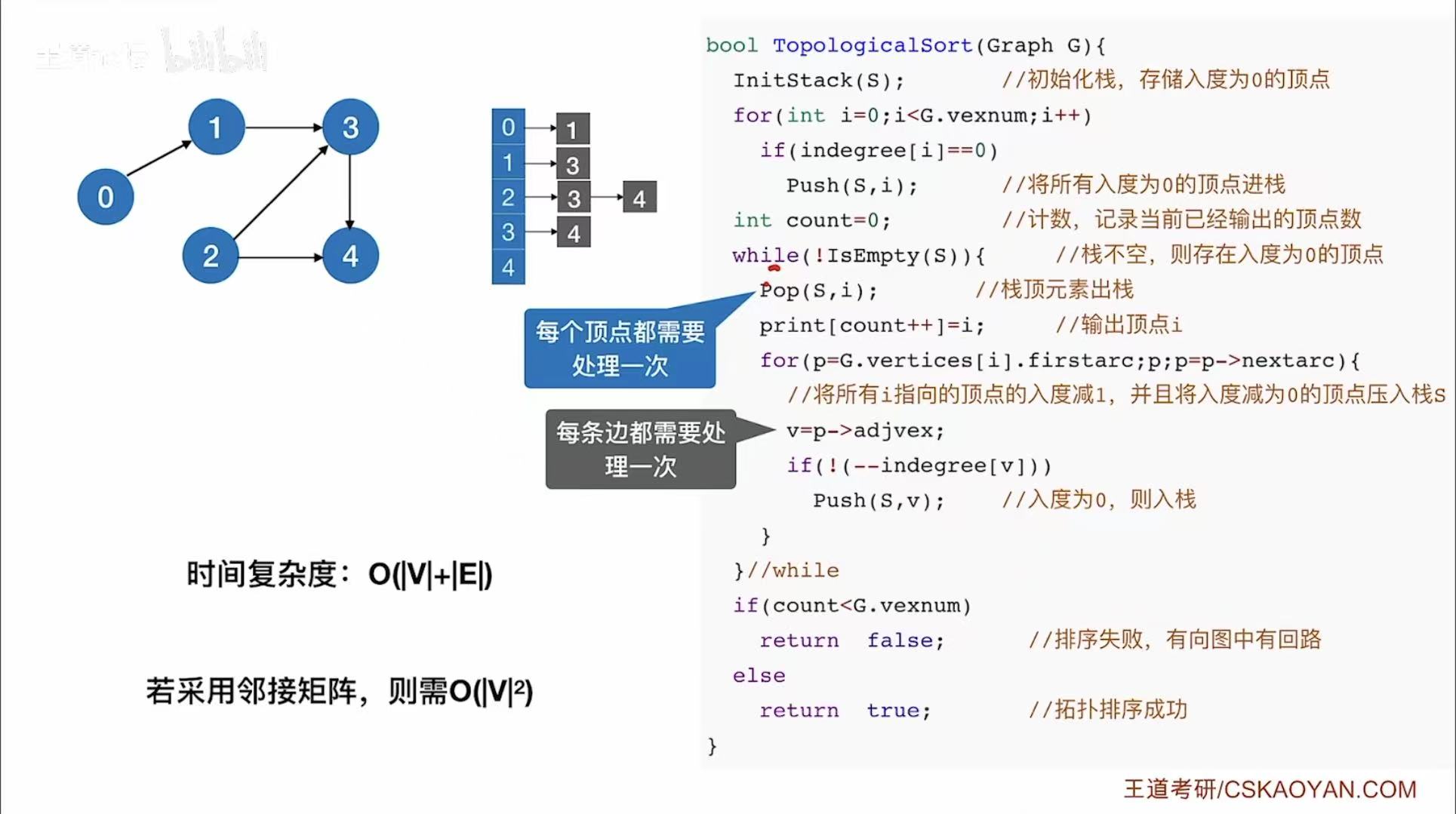
} Graph;拓扑排序函数实现:
java
bool TopologicalSort(Graph G) {
InitStack(S); // 初始化栈 S,用于存储入度为 0 的顶点
// 将所有入度为 0 的顶点压入栈中
for (int i = 0; i < G.vexnum; i++) {
if (indegree[i] == 0) // 如果顶点 i 的入度为 0
Push(S, i); // 将其压入栈 S
}
int count = 0; // 计数器:记录已经输出的顶点个数
while (!IsEmpty(S)) { // 当栈不为空时,继续处理
Pop(S, i); // 弹出栈顶元素 i(一个入度为 0 的顶点)
print[count++] = i; // 输出顶点 i,并计数
// 遍历顶点 i 的所有出边(即它指向的所有顶点)
for (p = G.vertices[i].firstarc; p != NULL; p = p->nextarc) {
v = p->adjvex; // 获取 i 指向的顶点 v
// 将 v 的入度减 1(因为 i 被移除,不再指向 v)
if (!(--indegree[v])) // 如果 v 的入度变为 0
Push(S, v); // 将 v 压入栈(准备输出)
}
}
// 判断是否成功完成拓扑排序
if (count < G.vexnum) // 如果输出的顶点数小于总顶点数
return false; // 说明图中有环,拓扑排序失败
else
return true; // 成功完成拓扑排序
}
栈的变化:
| 步骤 | 操作 | 栈 S 内容(从底 → 顶) | 入度数组 indegree[] |
输出 print[] |
说明 |
|---|---|---|---|---|---|
| 1 | 初始化 | [] |
[0,1,0,1,2] |
[-1,-1,-1,-1,-1] |
初始状态:入度已知,栈为空 |
| 2 | Push(0) |
[0] |
[0,1,0,1,2] |
[-1,-1,-1,-1,-1] |
顶点 0 入度为 0 → 压栈 |
| 3 | Push(2) |
[0, 2] |
[0,1,0,1,2] |
[-1,-1,-1,-1,-1] |
顶点 2 入度为 0 → 压栈 |
| 4 | Pop(S,i) → i=2 |
[0] |
[0,1,0,1,2] |
[2] |
弹出栈顶 2,输出 2 |
| 5 | 处理边 2→4 | [0] |
[0,1,0,1,1] |
[2] |
in[4] -=1 → 变为 1,不压栈 |
| 6 | Pop(S,i) → i=0 |
[] |
[0,1,0,1,1] |
[2,0] |
弹出栈顶 0,输出 0 |
| 7 | 处理边 0→1 | [] |
[0,0,0,1,1] |
[2,0] |
in[1] -=1 → 变为 0 → 压栈 |
| 8 | Push(1) |
[1] |
[0,0,0,1,1] |
[2,0] |
顶点 1 入度变为 0 → 压栈 |
| 9 | Pop(S,i) → i=1 |
[] |
[0,0,0,1,1] |
[2,0,1] |
弹出栈顶 1,输出 1 |
| 10 | 处理边 1→3 | [] |
[0,0,0,0,1] |
[2,0,1] |
in[3] -=1 → 变为 0 → 压栈 |
| 11 | Push(3) |
[3] |
[0,0,0,0,1] |
[2,0,1] |
顶点 3 入度变为 0 → 压栈 |
| 12 | Pop(S,i) → i=3 |
[] |
[0,0,0,0,1] |
[2,0,1,3] |
弹出栈顶 3,输出 3 |
| 13 | 处理边 3→4 | [] |
[0,0,0,0,0] |
[2,0,1,3] |
in[4] -=1 → 变为 0 → 压栈 |
| 14 | Push(4) |
[4] |
[0,0,0,0,0] |
[2,0,1,3] |
顶点 4 入度变为 0 → 压栈 |
| 15 | Pop(S,i) → i=4 |
[] |
[0,0,0,0,0] |
[2,0,1,3,4] |
弹出栈顶 4,输出 4 |
- 时间复杂度:因为每个顶点和边都需要处理一次。
4. 逆拓扑排序
就是把每个顶点反方向写出来。
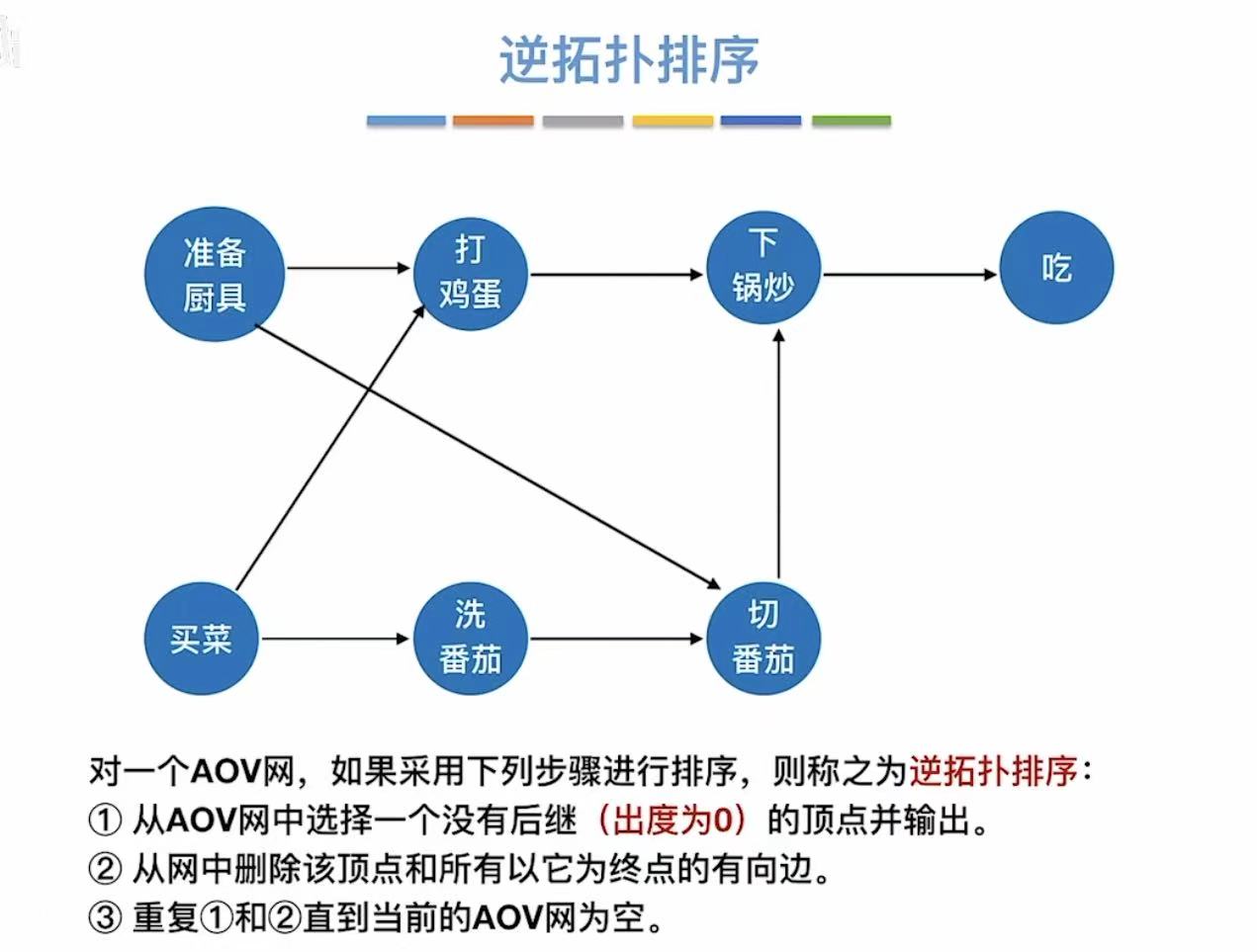
灰色就是逆拓扑排序后的样子:

5. 代码实现
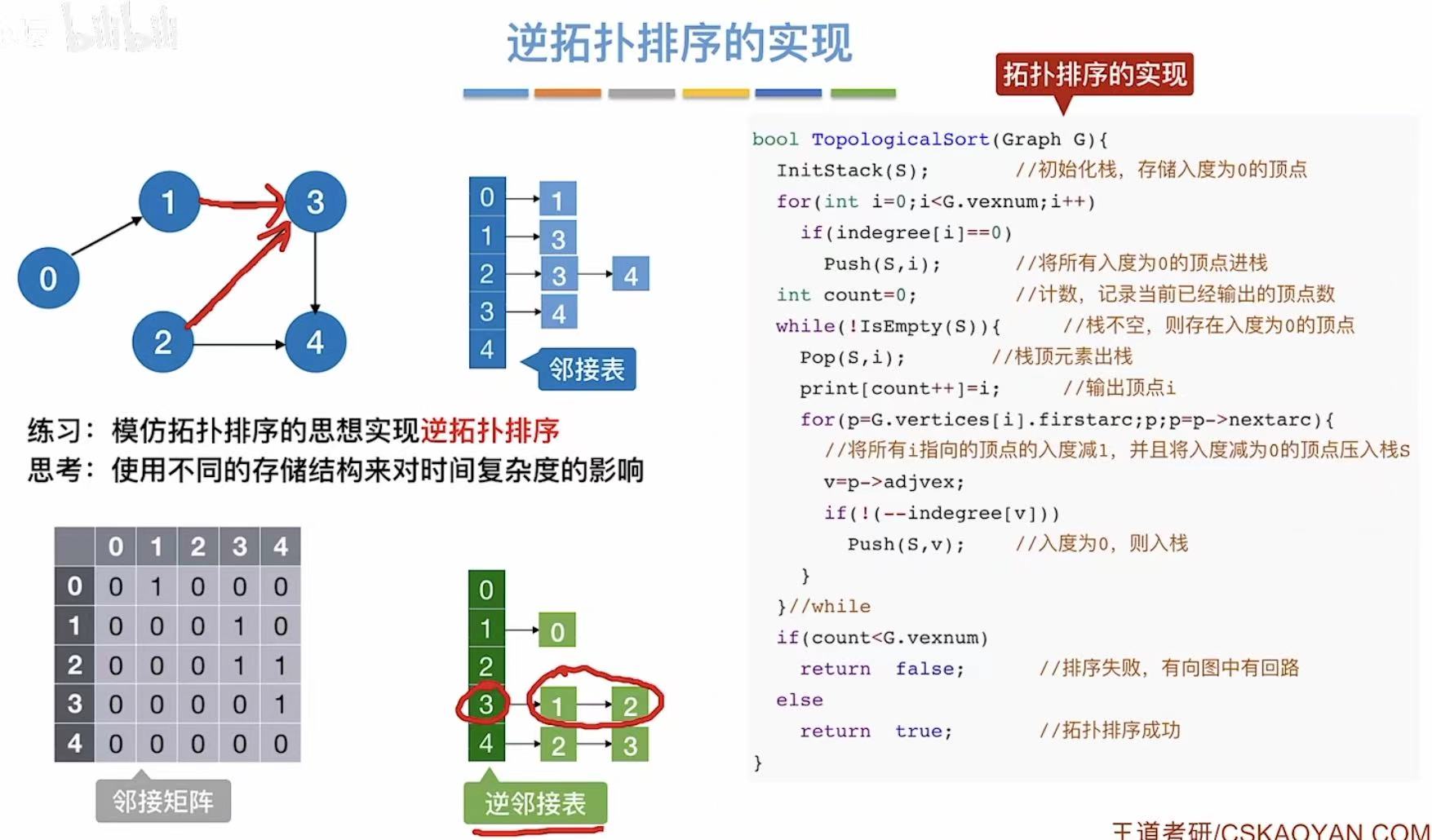
java
// 访问标记数组:记录每个顶点是否已被访问过
// 初始时所有值都为 false(未访问)
bool visited[MAX_VERTEX_NUM]; // 访问标记数组
// 对图 G 进行深度优先遍历的主函数
void DFSTraverse(Graph G) {
// 初始化访问标记数组:将所有顶点标记为"未访问"
for (v = 0; v < G.vexnum; ++v) {
visited[v] = FALSE; // 所有顶点初始状态为未访问
}
// 遍历图中的每一个顶点(处理非连通图)
for (v = 0; v < G.vexnum; ++v) {
// 如果当前顶点 v 尚未被访问
if (!visited[v]) {
// 从该顶点出发,进行一次 DFS 遍历
DFS(G, v); // 调用 DFS 函数,遍历以 v 为起点的连通分量
}
}
}
// 深度优先遍历函数(从顶点 v 开始)
void DFS(Graph G, int v) {
visited[v] = TRUE; // 将顶点 v 标记为已访问,防止重复访问
// 遍历当前顶点 v 的所有邻接点 w
// 使用 FirstNeighbor 和 NextNeighbor 枚举所有邻接点
for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
// 如果邻接点 w 还未被访问
if (!visited[w]) {
// 递归调用 DFS,从 w 开始继续深入遍历
DFS(G, w);
}
}
// ⭐ 关键:在顶点退栈前输出(即后序遍历)
print(v); // 输出当前顶点 v
}栈变化:
| 步骤 | 操作(函数调用/返回) | 递归栈内容(从底 → 顶) | 输出(print) | 说明 |
|---|---|---|---|---|
| 1 | DFS(0) 被调用 |
[0] |
--- | 访问顶点 0 |
| 2 | DFS(1) 被调用 |
[0, 1] |
--- | 0→1,访问 1 |
| 3 | DFS(3) 被调用 |
[0, 1, 3] |
--- | 1→3,访问 3 |
| 4 | DFS(4) 被调用 |
[0, 1, 3, 4] |
--- | 3→4,访问 4 |
| 5 | DFS(4) 返回 |
[0, 1, 3] |
4 | 4 无出边,输出 4 |
| 6 | DFS(3) 返回 |
[0, 1] |
4, 3 | 3 的邻接点处理完,输出 3 |
| 7 | DFS(1) 返回 |
[0] |
4, 3, 1 | 1 的邻接点处理完,输出 1 |
| 8 | DFS(0) 返回 |
[] |
4, 3, 1, 0 | 0 的邻接点处理完,输出 0 |
| 9 | DFS(2) 被调用 |
[2] |
4, 3, 1, 0 | 主循环继续,访问未访问的 2 |
| 10 | DFS(2) 返回 |
[] |
4, 3, 1, 0, 2 | 2→4(但 4 已访问),输出 2 |
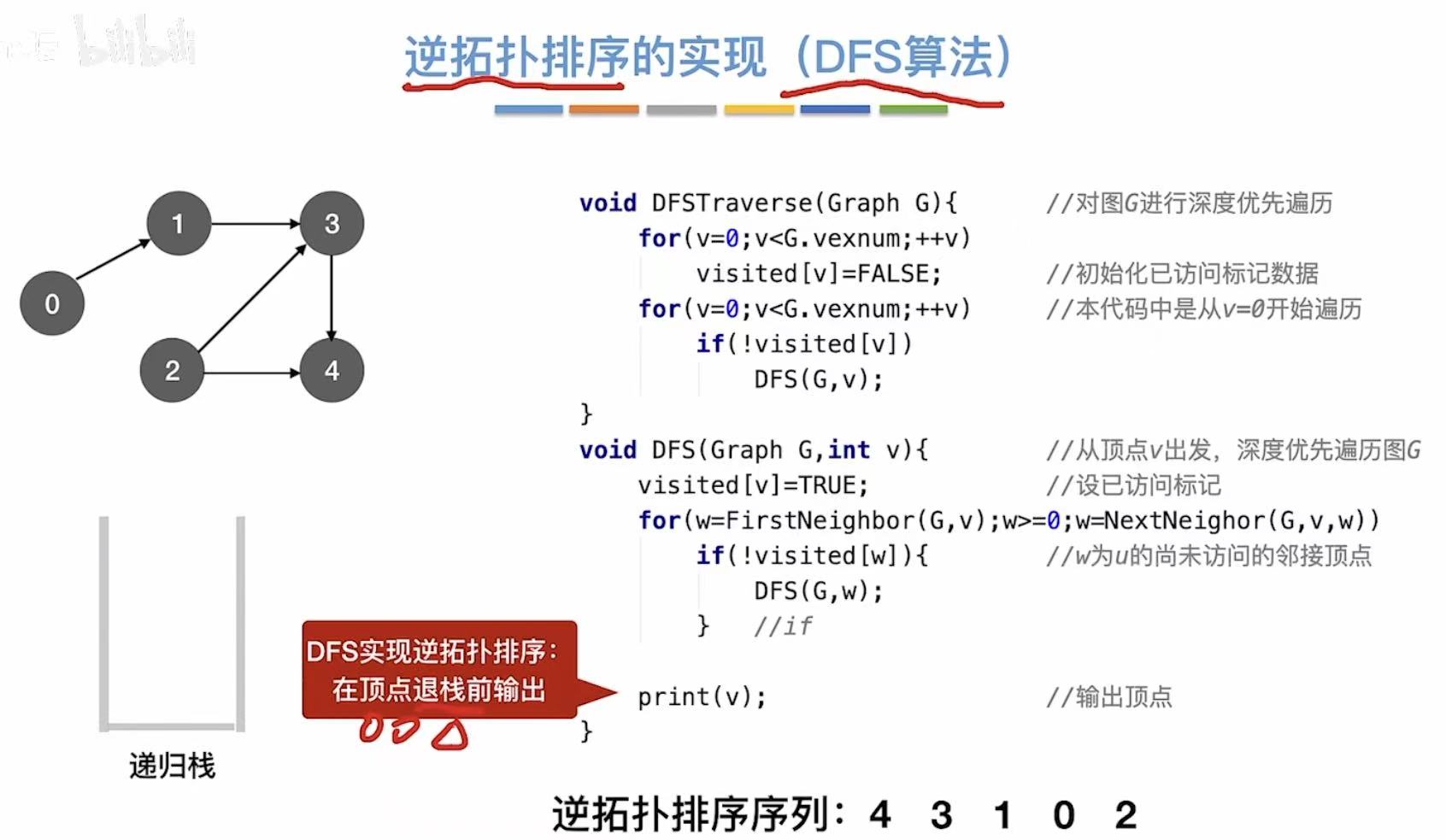
6. 小结
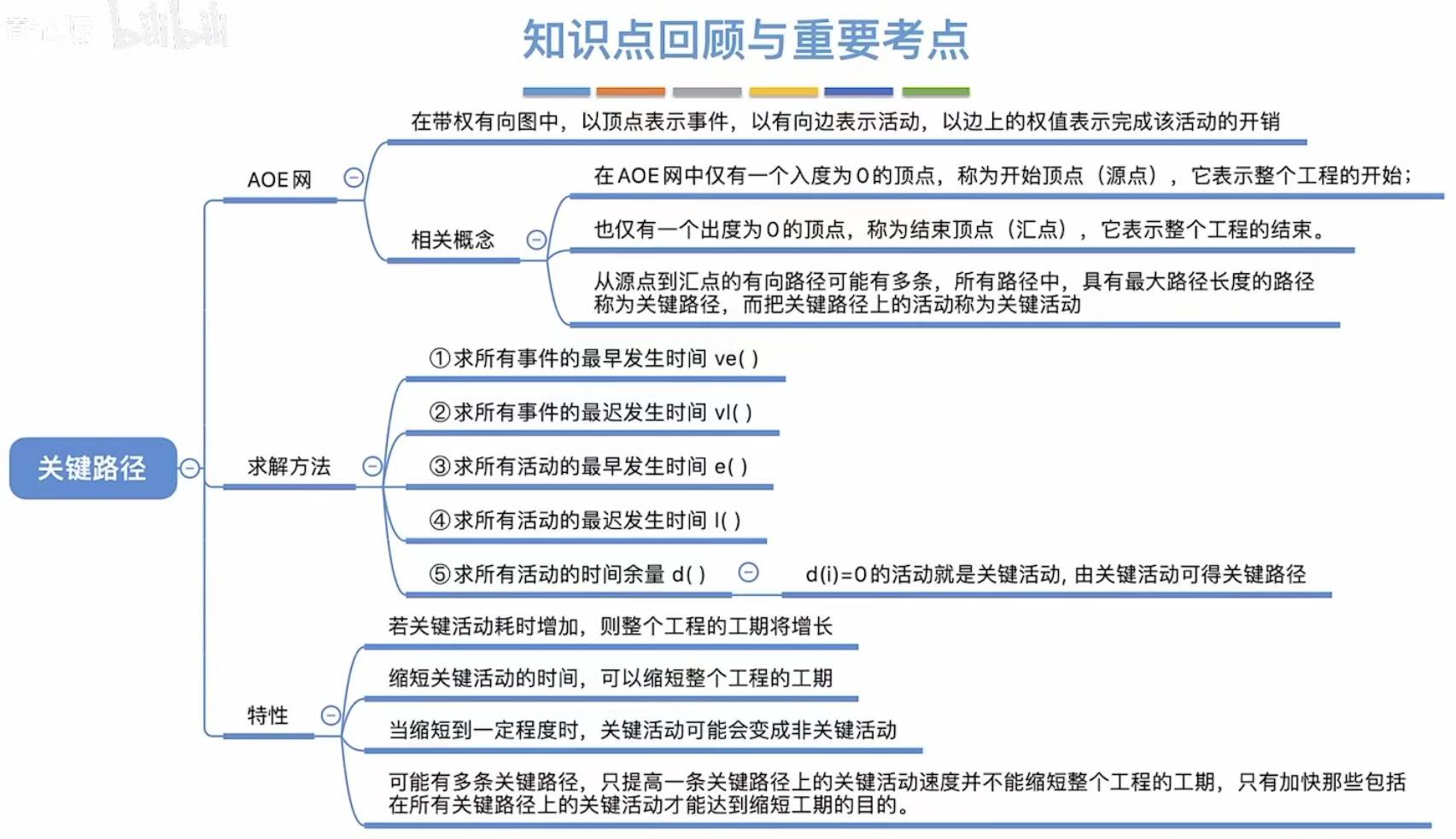
关键路径
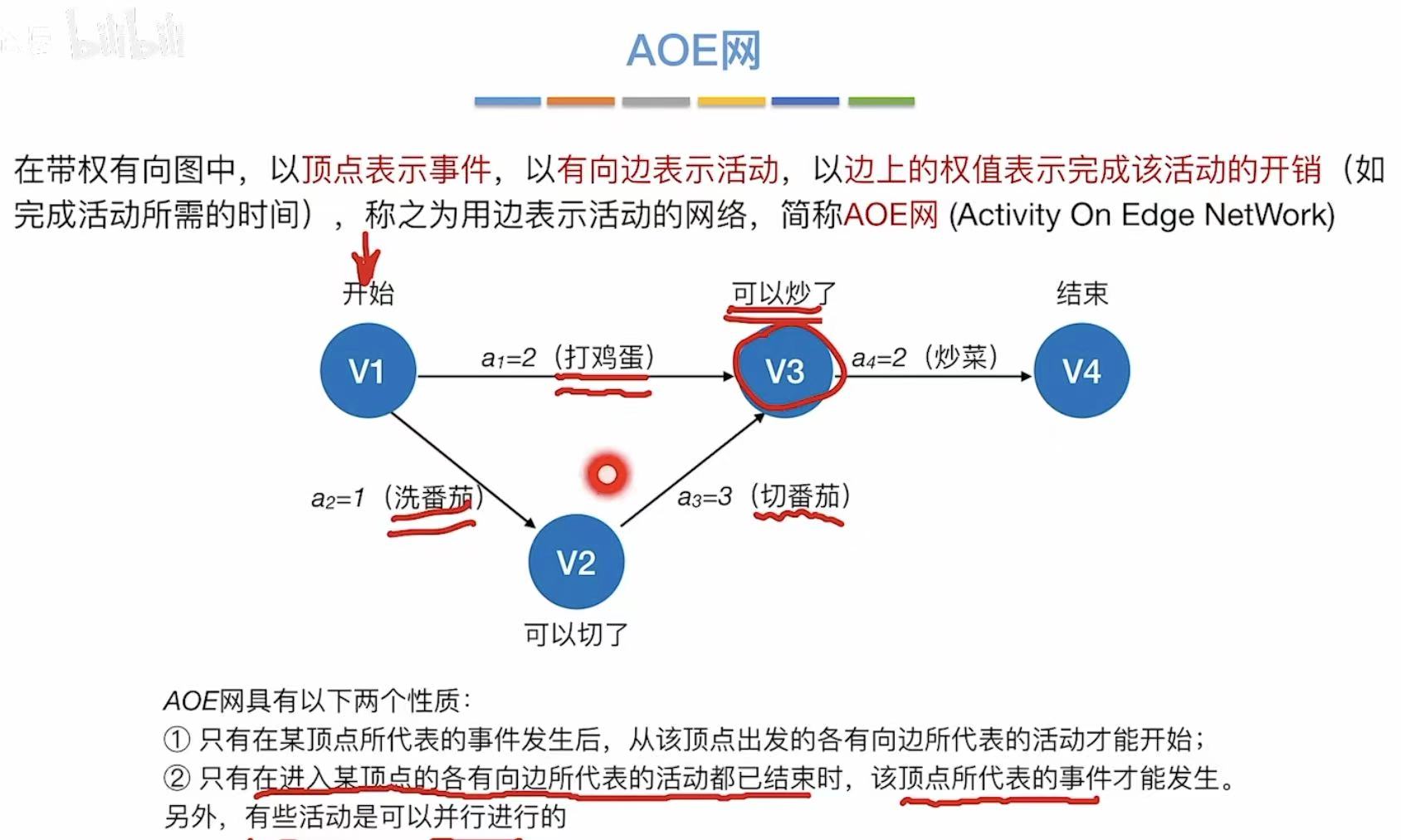
1. AOE网
用边来表示活动。
- 圈发生后-->边才能发生
- 边结束后-->圈才能发生
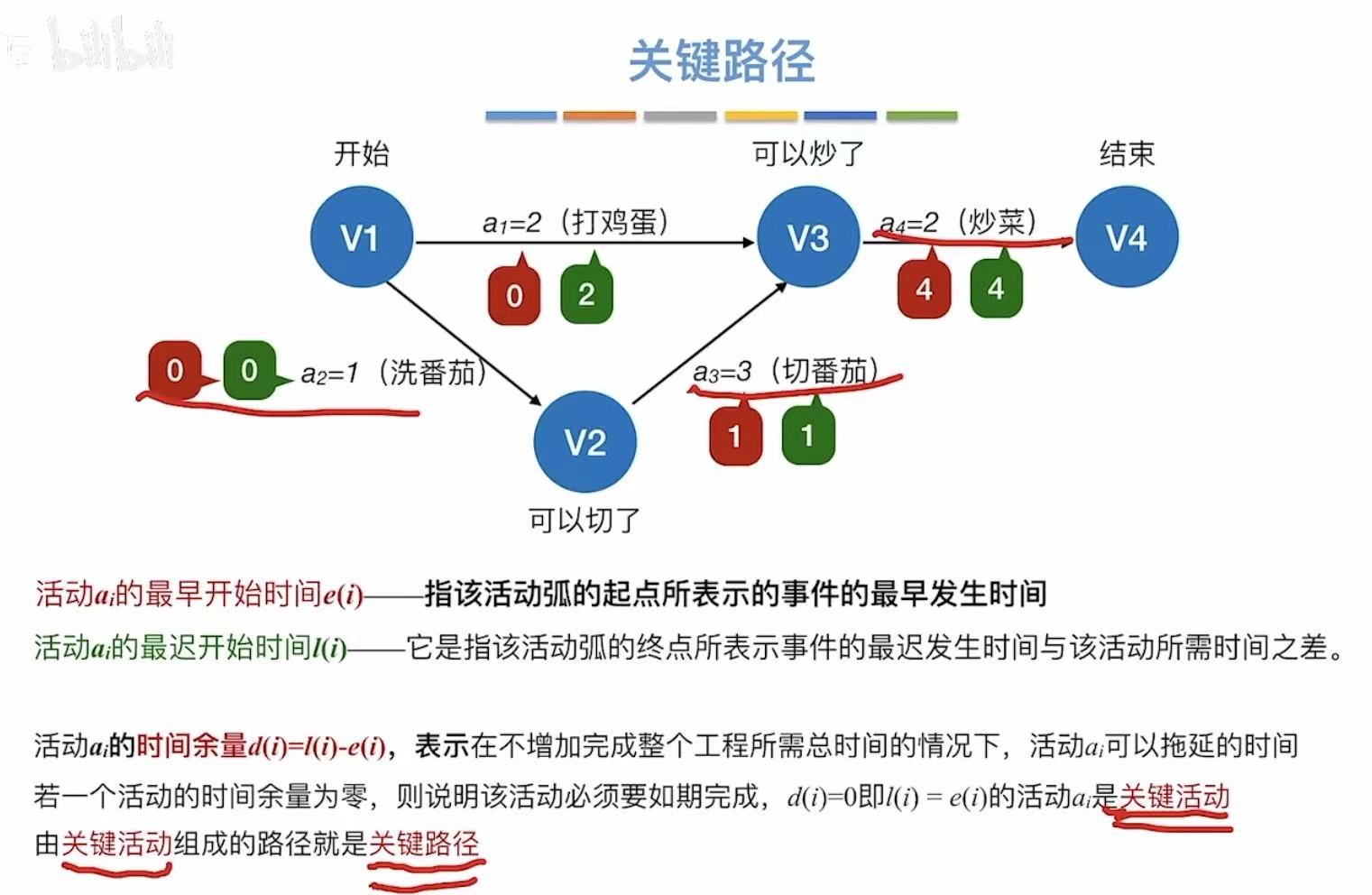
2. 关键路径
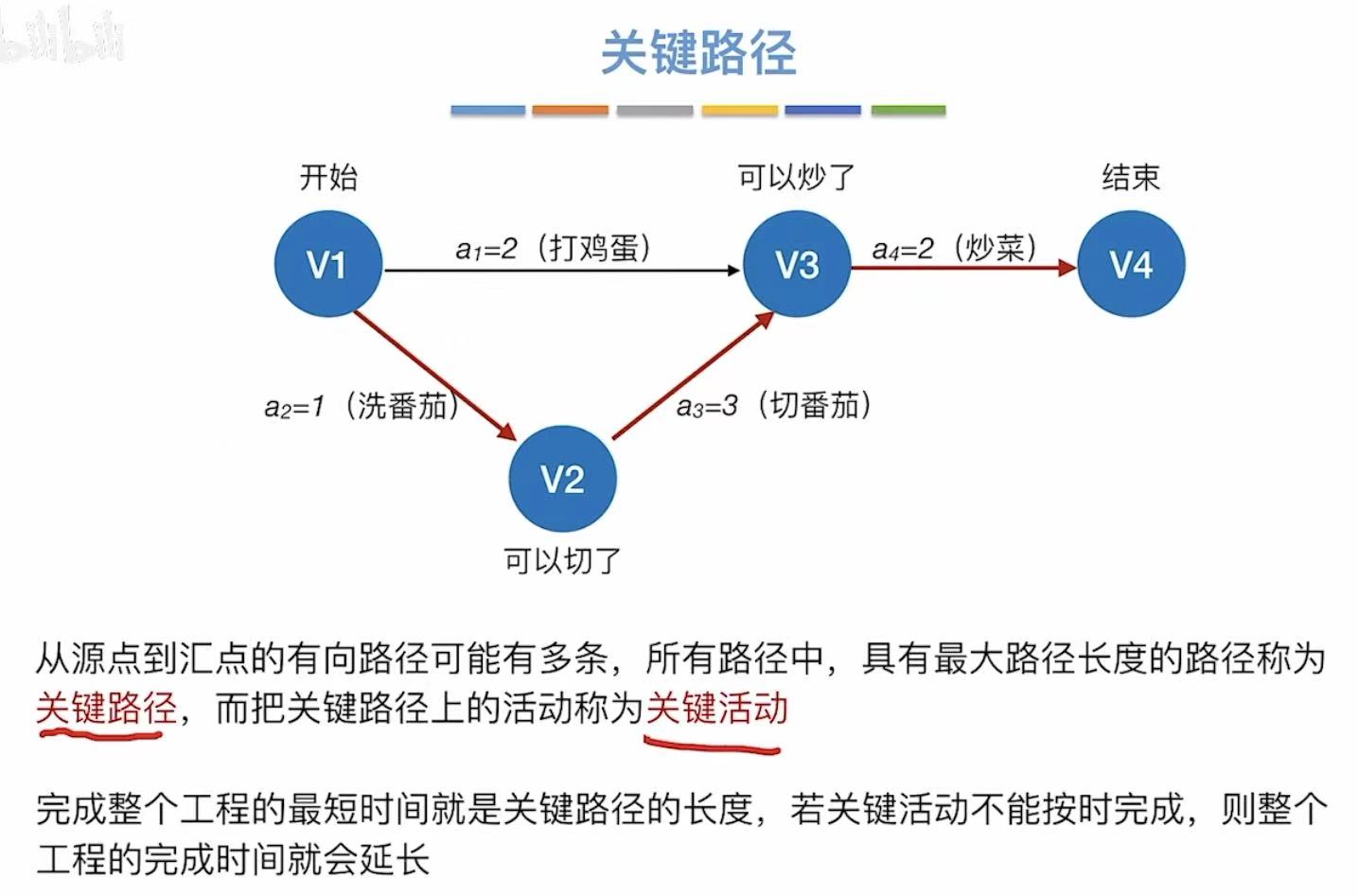
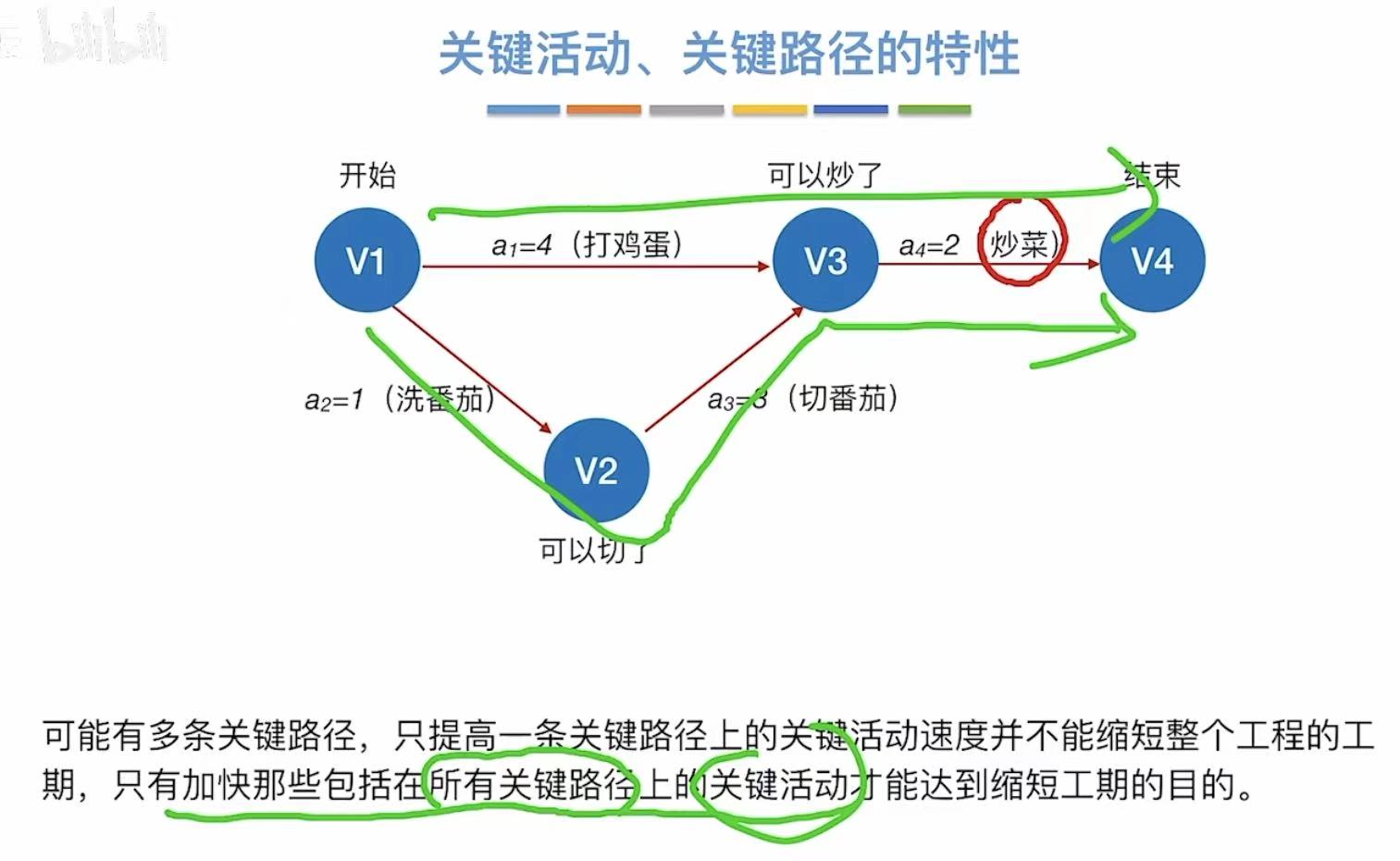
- 关键路径 :具有最大路径长度的路径
比如a2+a3+a4的路径长度为6,大于a1+a4的路径长度4,所以a2+a3+a4为关键路径 - 关键活动 :关键路径上的活动
a2+a3+a4对应的活动就是关键活动
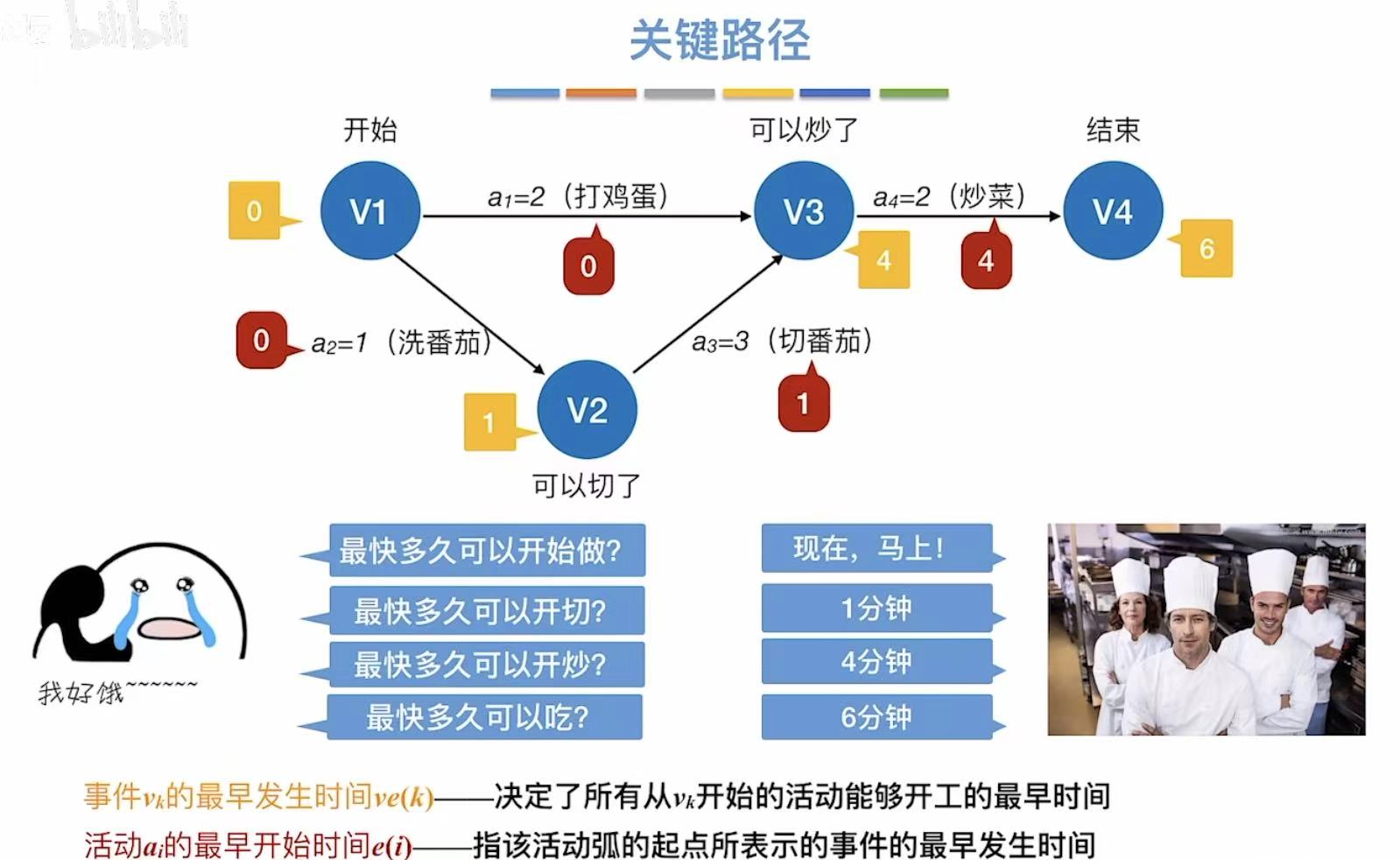
- 最早发生时间 :指顶点 ,活动的最早开始时间
比如:v3需要v1、v2连通的活动都必须结束,a1=2、a2=1 + a3=3 -->4;所以只能4的时候才能开工 - 最早开始时间 :指边 ,事件的最早开始时间
比如:0时v1发生了,a1和a2就可以紧跟着发生,所以它俩的最早发生时间是0
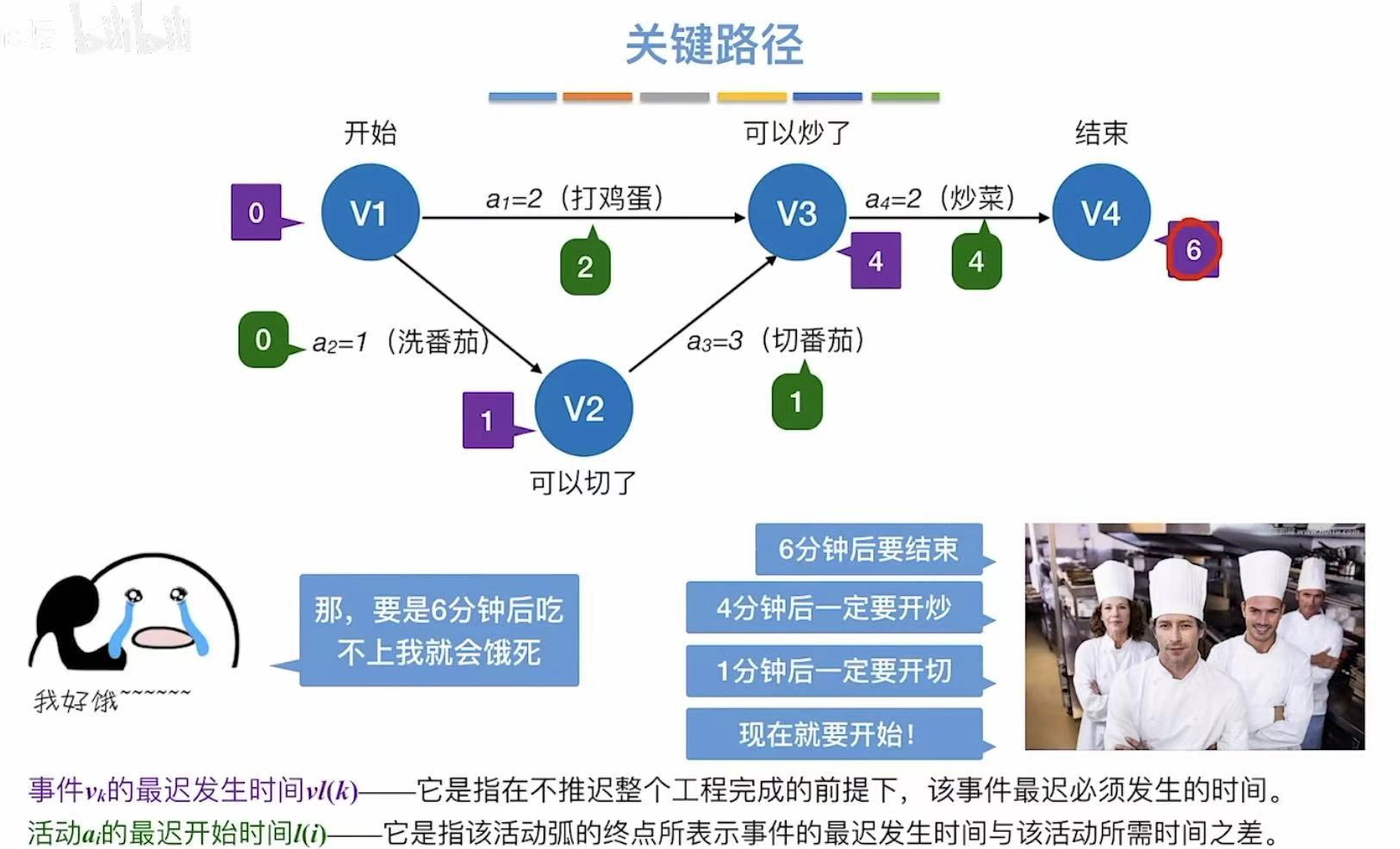
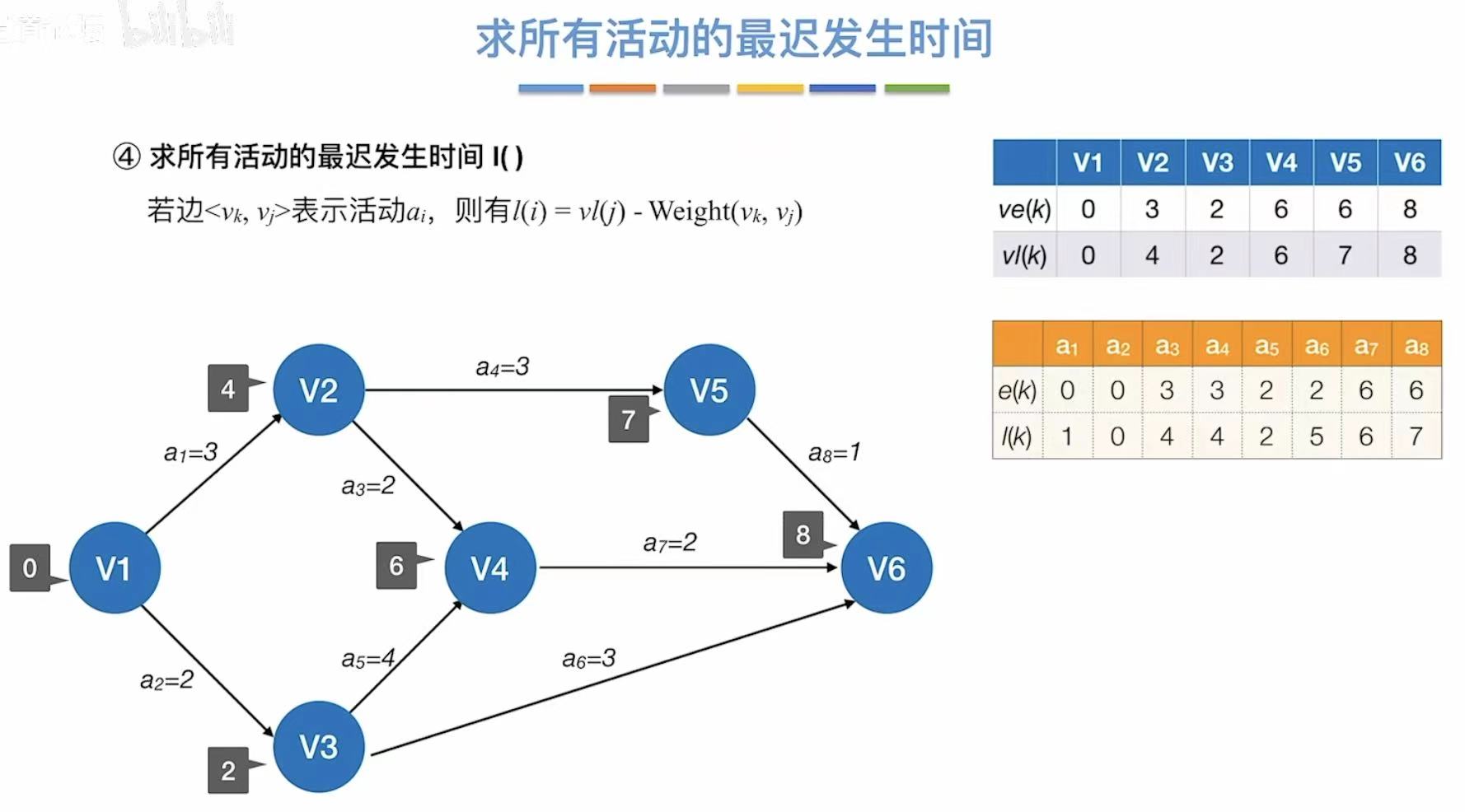
反向推,我已经知道6分钟可以做完番茄炒蛋,那我就要求6分钟后立马吃到: - 最迟发生时间 :指顶点,最晚6分钟就必须结束炒菜,然后依次向前推其他顶点的最迟发生时间
- 最迟开始时间 :指边 ,大部分都依赖于前一个顶点的最迟发生时间,但!
这里注意a1,因为a2和a3一共需要4分钟才能结束,而a2只需要两分钟,所以可以推迟在2时刻再开始a2
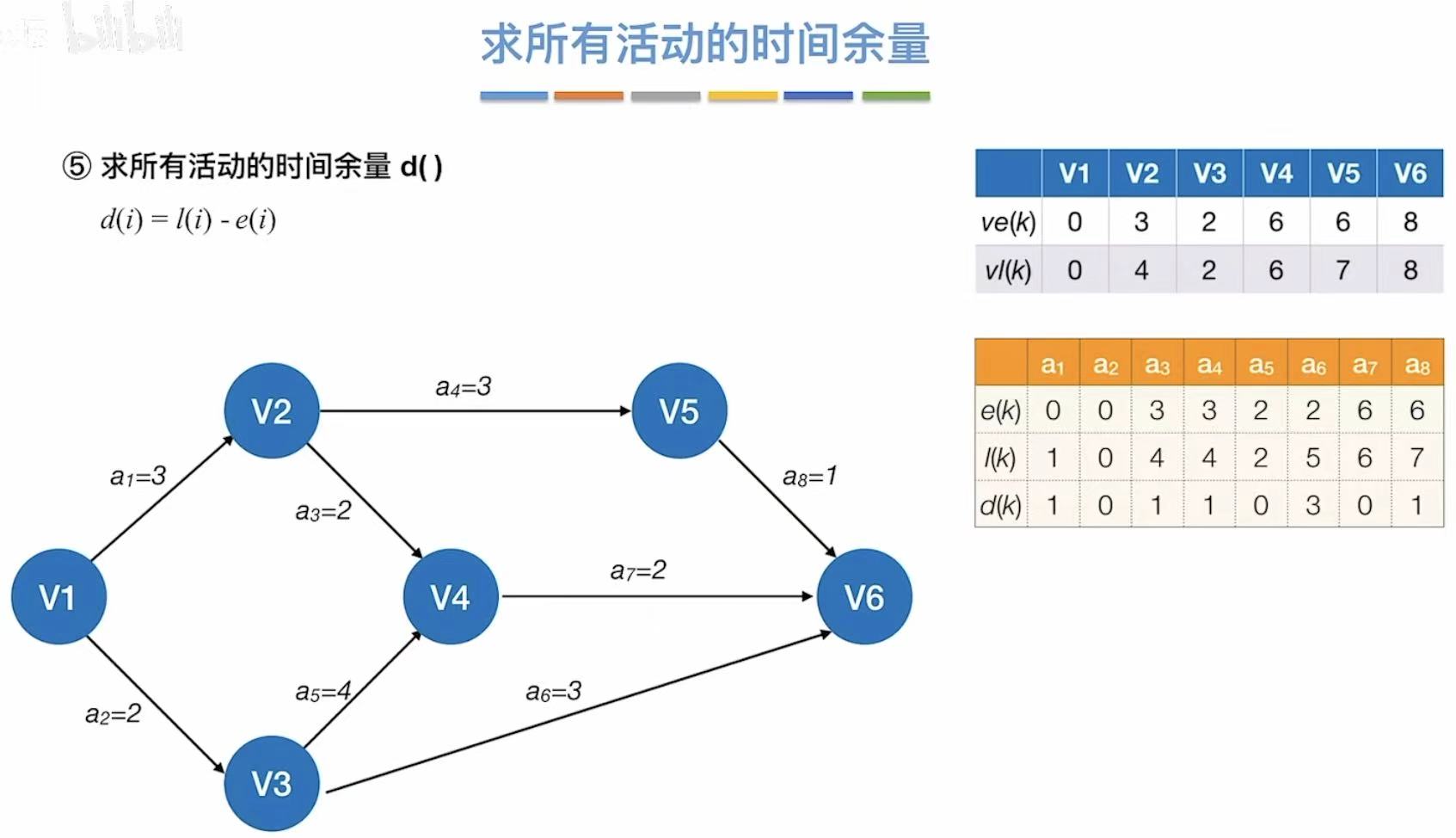
- 时间余量:就是看你能忙里偷闲偷多少
- 比如a1,最早可以0时刻开始,但是最晚可以2时刻开始,相减就代表你可以偷懒两分钟
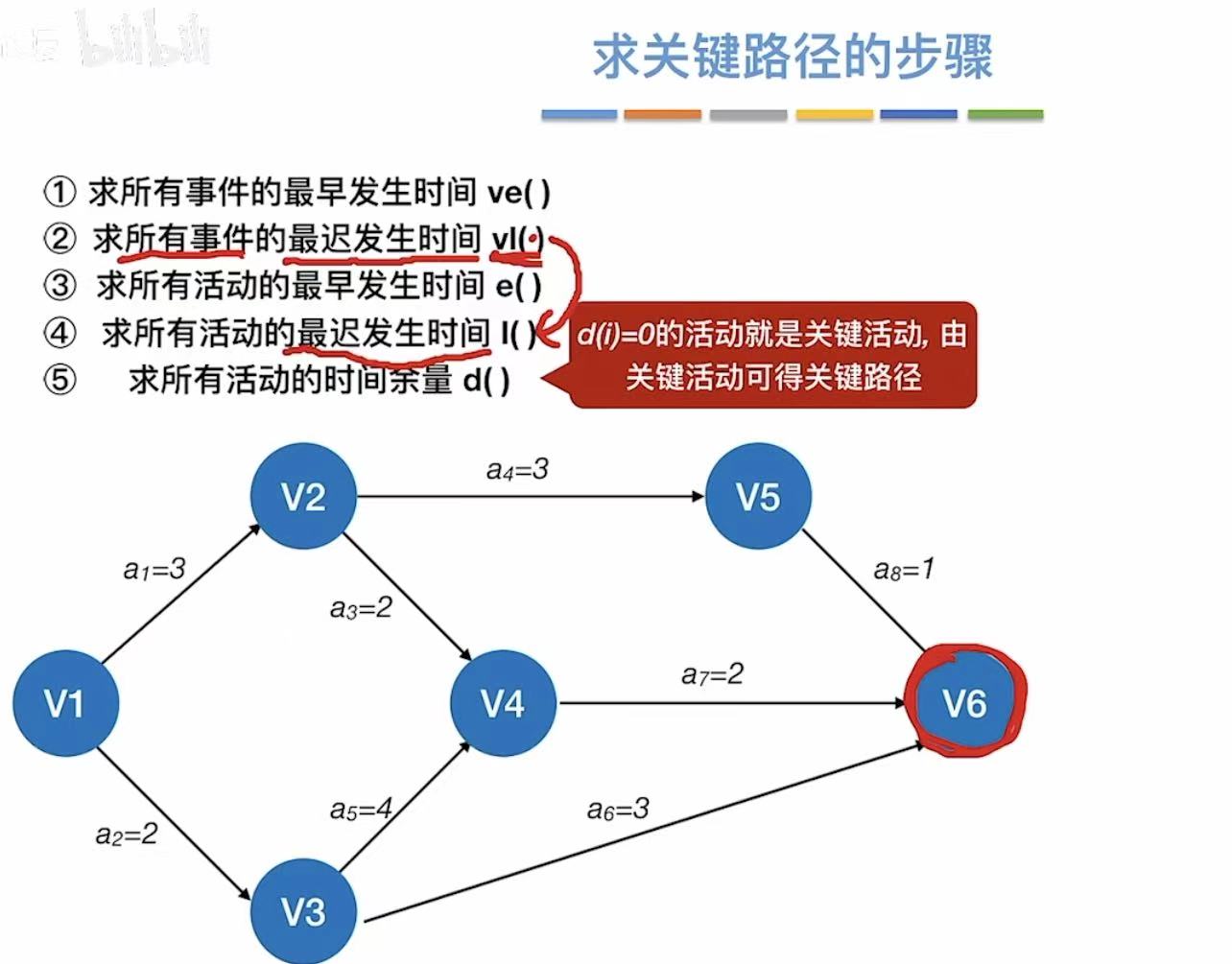
3. 实现步骤
就是上述介绍的概念全部算出来√
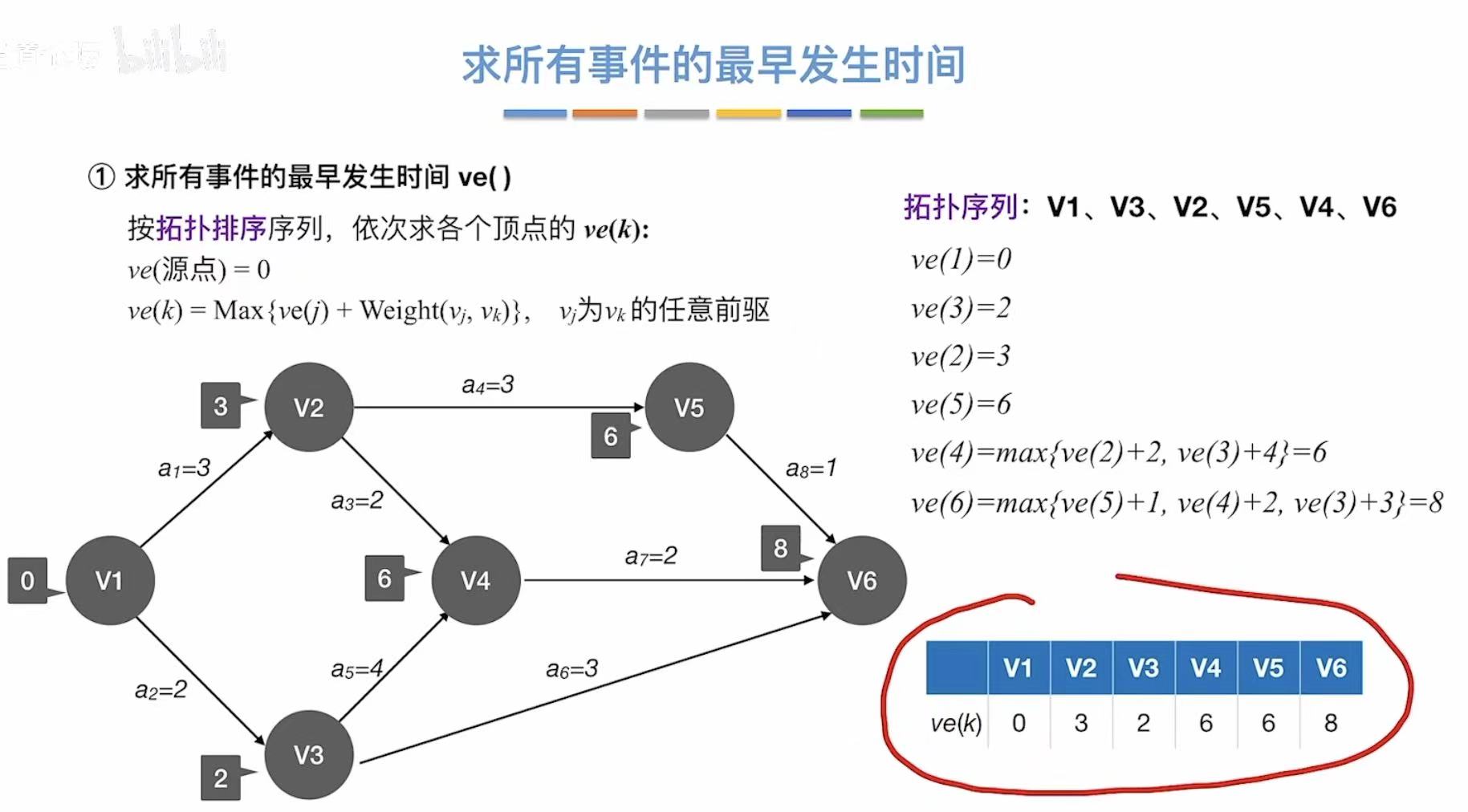
有两条路径的,就取值更大的那个
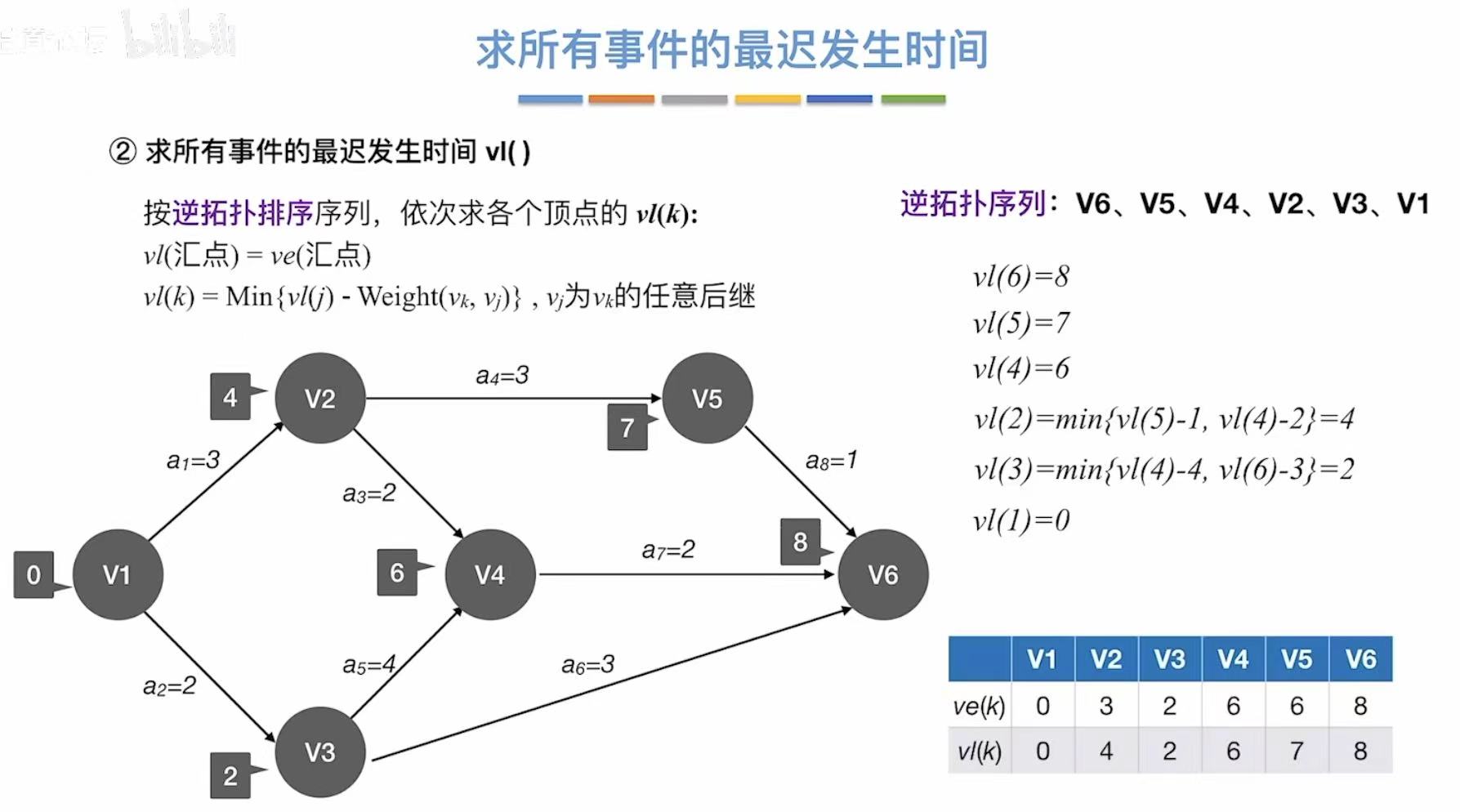
从上一步得到最后一个事件的最迟发生时间(就是它的最早发生时间),
然后逆推其余时间的最迟发生时间
看每个边的最早开始时间
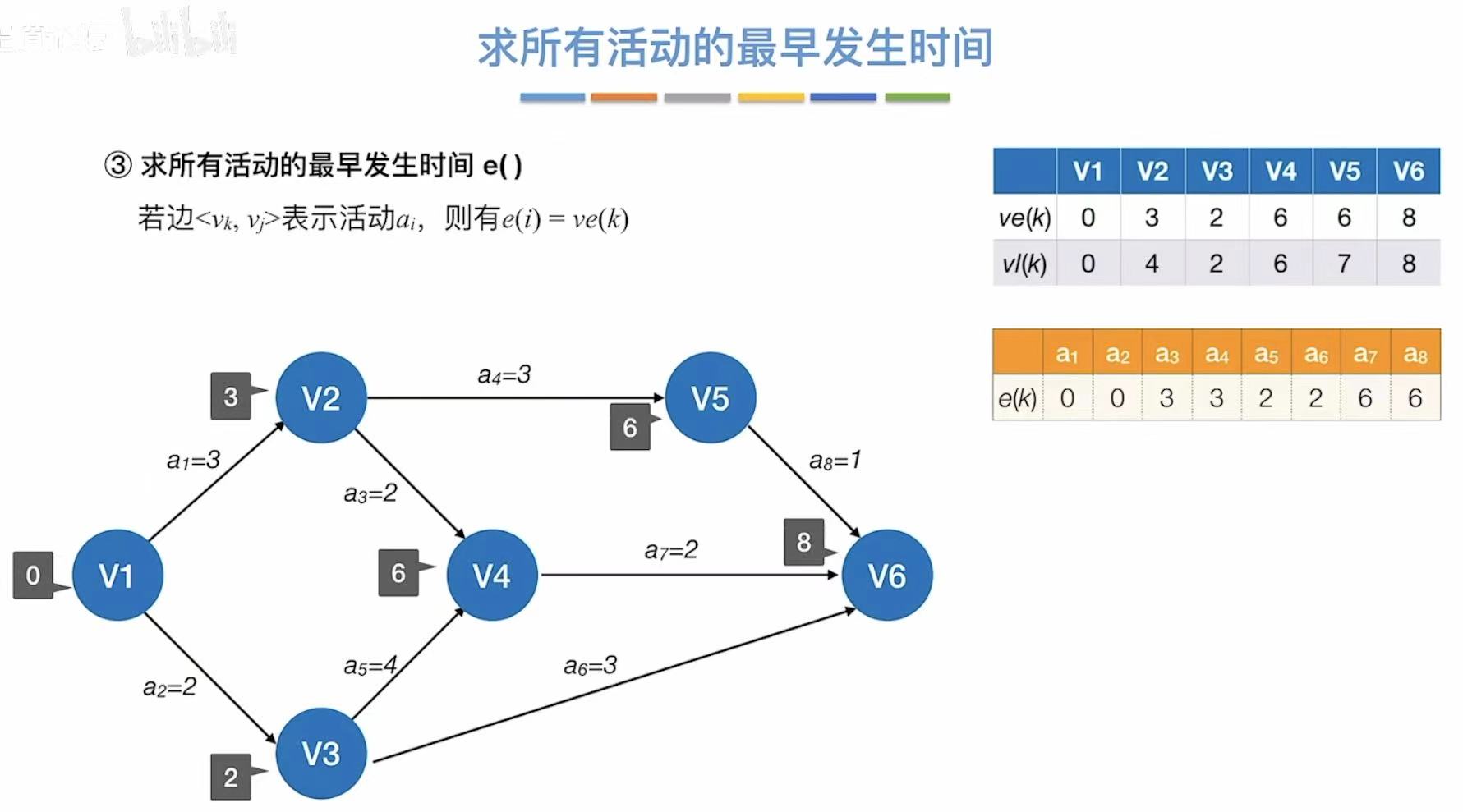
每个边最晚的发生时间
边的最晚发生时间-边的最早发生时间
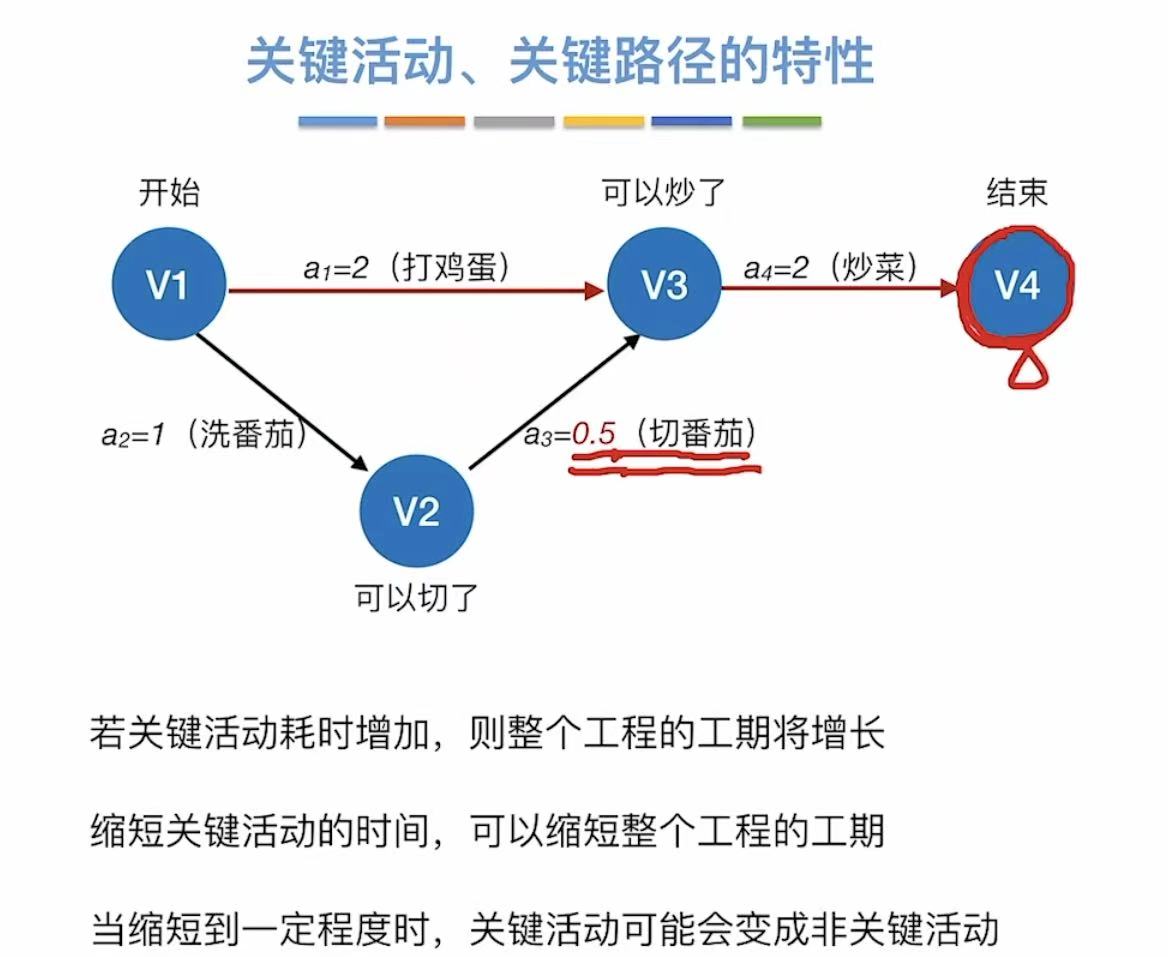
4. 特性
5. 小结