粒子群优化（PSO）改进算法在全局最优解搜索中的应用

一、PSO改进算法的核心逻辑

粒子群优化（PSO）是一种基于群体智能的全局优化算法，通过模拟鸟群觅食行为，利用粒子间的个体经验（pbest）和群体经验（gbest）引导搜索方向。标准PSO易出现 早熟收敛（陷入局部最优）和后期收敛缓慢 的问题，改进算法通过参数自适应调整 、混合策略等方式解决这些缺陷，提升全局搜索能力。

二、关键改进策略与实现细节

以下是针对全局最优解搜索的核心改进策略，结合MATLAB实现说明：

1. 参数自适应调整：平衡探索与开发

改进目标 ：在搜索初期保持全局探索 （大惯性权重），后期转向局部开发（小惯性权重），同时调整学习因子（c1、c2）以平衡个体与群体经验。

实现方法：

惯性权重（w） ：采用线性递减策略 ，从w_max（如0.9）逐渐减小到w_min（如0.4），公式为：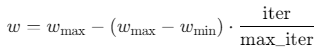
学习因子（c1、c2） ：c1（个体学习因子）从2.0递减到1.0，c2（社会学习因子）从1.0递增到2.0，公式为：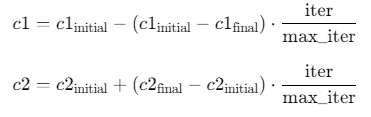

MATLAB代码示例：

matlab 复制代码

w_max = 0.9; w_min = 0.4;
c1_initial = 2.0; c1_final = 1.0;
c2_initial = 1.0; c2_final = 2.0;
for iter = 1:max_iter
    w = w_max - (w_max - w_min) * (iter/max_iter);
    c1 = c1_initial - (c1_initial - c1_final) * (iter/max_iter);
    c2 = c2_initial + (c2_final - c2_initial) * (iter/max_iter);
    % 更新粒子速度与位置（见下文）
end

2. 混合策略：融合其他算法的优势

改进目标 ：通过结合遗传算法（GA）、**模拟退火（SA）**等算法的优势，增强全局搜索能力，避免陷入局部最优。

常见混合方式：

PSO-GA混合 ：引入GA的交叉（crossover）和变异（mutation）操作，对粒子位置进行扰动，增加种群多样性。

MATLAB代码示例（交叉操作）：

matlab 复制代码

% 选择父代粒子（如最优粒子）
parents = select_parents(population, fitness, 2);
% 交叉生成子代
offspring = crossover(parents(1,:), parents(2,:), 0.8); % 0.8为交叉概率
% 变异操作
offspring = mutate(offspring, 0.1); % 0.1为变异概率
% 替换种群中的劣质粒子
population = replace_population(population, offspring, fitness);

PSO-SA混合 ：在迭代过程中加入模拟退火的"接受劣解"机制，当算法陷入局部最优时，以一定概率接受劣解，帮助跳出局部陷阱。

MATLAB代码示例（模拟退火接受准则）：
matlab 复制代码
```
T = initial_T * exp(-decay_rate * iter); % 温度衰减
delta_f = fitness(new_particle) - fitness(current_particle);
if delta_f < 0 || rand() < exp(-delta_f/T)
    current_particle = new_particle; % 接受新解
end
```

3. 拓扑结构优化：提升信息交流效率

改进目标 ：改变粒子间的通信方式（拓扑结构），避免"全连接"导致的群体思维固化，保留种群多样性。

常见拓扑结构：

环形拓扑：每个粒子仅与左右相邻的粒子通信，促进局部信息交换，适合高维问题。
随机拓扑：每次迭代随机调整粒子的邻域，增加种群多样性，避免早熟收敛。

MATLAB代码示例（环形拓扑的邻域选择）：

matlab 复制代码

neighborhood_size = 3; % 邻域大小为3（左右各1个粒子）
for i = 1:num_particles
    neighbors = [i-1, i, i+1]; % 环形邻域（首尾相连）
    neighbors(neighbors < 1) = num_particles;
    neighbors(neighbors > num_particles) = 1;
    % 计算邻域最优（lbest）
    lbest = find_best_particle(population(neighbors,:), fitness(neighbors));
    % 更新粒子速度（使用lbest代替gbest）
    v(i,:) = w*v(i,:) + c1*rand*(pbest(i,:)-x(i,:)) + c2*rand*(lbest - x(i,:));
end

三、MATLAB实现：改进的PSO算法框架

以下是带参数自适应调整和混合策略的PSO算法的MATLAB实现，用于寻找全局最优解：

1. 参数设置

matlab 复制代码

% 算法参数
num_particles = 50; % 粒子数量
max_iter = 200; % 最大迭代次数
dim = 10; % 问题维度（如10维优化问题）
w_max = 0.9; w_min = 0.4; % 惯性权重范围
c1_initial = 2.0; c1_final = 1.0; % 个体学习因子范围
c2_initial = 1.0; c2_final = 2.0; % 社会学习因子范围
v_max = 0.1; % 最大速度（避免粒子飞过最优解）
x_min = -5; x_max = 5; % 粒子位置范围

2. 初始化粒子群

matlab 复制代码

% 随机初始化粒子位置（x）和速度（v）
x = rand(num_particles, dim) * (x_max - x_min) + x_min;
v = rand(num_particles, dim) * 2*v_max - v_max;
% 初始化个体最优（pbest）和全局最优（gbest）
pbest = x;
pbest_fitness = arrayfun(@(i) fitness(x(i,:)), 1:num_particles);
[gbest_fitness, gbest_idx] = min(pbest_fitness);
gbest = x(gbest_idx,:);

3. 迭代优化

matlab 复制代码

for iter = 1:max_iter
    % 1. 参数自适应调整
    w = w_max - (w_max - w_min) * (iter/max_iter);
    c1 = c1_initial - (c1_initial - c1_final) * (iter/max_iter);
    c2 = c2_initial + (c2_final - c2_initial) * (iter/max_iter);
    
    % 2. 更新粒子速度与位置
    for i = 1:num_particles
        % 速度更新（带边界限制）
        v(i,:) = w*v(i,:) + c1*rand*(pbest(i,:)-x(i,:)) + c2*rand*(gbest - x(i,:));
        v(i,:) = max(min(v(i,:), v_max), -v_max); % 限制速度范围
        % 位置更新（带边界限制）
        x(i,:) = x(i,:) + v(i,:);
        x(i,:) = max(min(x(i,:), x_max), x_min); % 限制位置范围
    end
    
    % 3. 计算适应度，更新pbest和gbest
    for i = 1:num_particles
        current_fitness = fitness(x(i,:));
        if current_fitness < pbest_fitness(i)
            pbest(i,:) = x(i,:);
            pbest_fitness(i) = current_fitness;
        end
        if current_fitness < gbest_fitness
            gbest = x(i,:);
            gbest_fitness = current_fitness;
        end
    end
    
    % 4. 混合策略（如PSO-GA交叉变异）
    if mod(iter, 10) == 0 % 每10次迭代进行一次交叉变异
        % 选择父代（最优粒子）
        [~, sorted_idx] = sort(pbest_fitness);
        parents = pbest(sorted_idx(1:2), :);
        % 交叉生成子代
        offspring = crossover(parents(1,:), parents(2,:), 0.8);
        % 变异操作
        offspring = mutate(offspring, 0.1);
        % 替换劣质粒子
        [~, worst_idx] = max(pbest_fitness);
        pbest(worst_idx,:) = offspring;
        pbest_fitness(worst_idx) = fitness(offspring);
        % 更新gbest
        if fitness(offspring) < gbest_fitness
            gbest = offspring;
            gbest_fitness = fitness(offspring);
        end
    end
    
    % 5. 终止条件（可选）
    if gbest_fitness < 1e-5 % 达到目标精度
        break;
    end
end

4. 适应度函数（示例：Sphere函数）

matlab 复制代码

function f = fitness(x)
    % Sphere函数（单峰函数，全局最小值为0）
    f = sum(x.^2);
end

参考代码 pso的改进算法及其各种测试函数，用于寻找全局的最优解 www.youwenfan.com/contentcsr/100304.html

四、性能评估与优化建议

1. 性能评估指标

收敛速度：迭代次数或计算时间（如达到某一精度所需的迭代次数）。
全局最优性：找到的最优解与真实最优解的误差（如Sphere函数的误差）。
鲁棒性：多次运行结果的方差（如Rastrigin函数的成功率）。

2. 优化建议

参数调优 ：通过网格搜索 或贝叶斯优化 调整w_max、w_min、c1、c2等参数，提升算法性能。
并行计算 ：利用MATLAB的parfor循环加速粒子适应度计算，提升大规模问题的处理效率。
多目标优化 ：扩展PSO到多目标优化 （如同时优化收敛速度和全局最优性），采用帕累托支配 或加权求和方法处理多目标冲突。

五、应用场景

PSO改进算法广泛应用于高维、多峰、复杂约束的全局优化问题，如：

机器学习：神经网络权重优化、支持向量机（SVM）参数调优。
工程设计：结构优化、参数设计（如飞机机翼形状优化）。
电力系统：电网调度、新能源发电优化（如风电功率预测）。

结论

PSO改进算法通过参数自适应调整 、混合策略 等方式，有效解决了标准PSO的早熟收敛 和后期收敛缓慢问题，提升了全局搜索能力。在MATLAB中，通过合理设置参数、初始化粒子群、迭代优化，可实现高效的全局最优解搜索。实际应用中，需根据问题特性调整改进策略，以达到最佳性能。