- 第 169 篇 -
Date: 2026 - 02- 13 | 周五
Author: 郑龙浩(仟墨)
算法:图论 - 并查集
文章目录
-
- [2026-02-14 周六 | 算法打卡 day9](#2026-02-14 周六 | 算法打卡 day9)
2026-02-14 周六 | 算法打卡 day9
4-卡码网108-冗余连接
题目描述
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图,例如如图:
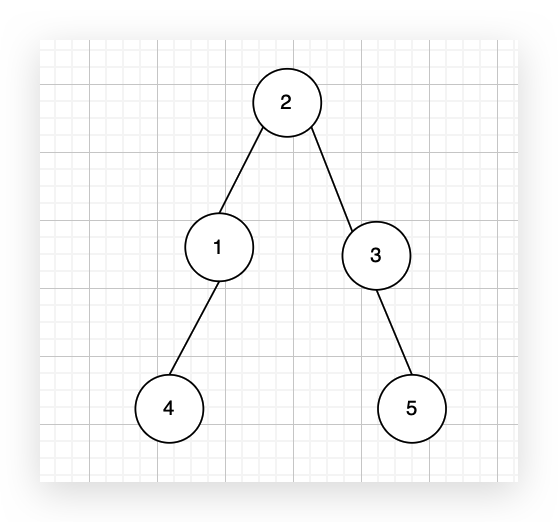
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图:
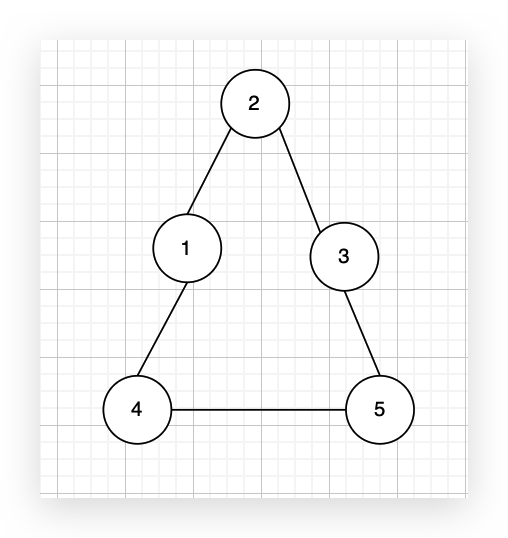
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
输入描述
第一行包含一个整数 N,表示图的节点个数和边的个数。
后续 N 行,每行包含两个整数 s 和 t,表示图中 s 和 t 之间有一条边。
输出描述
输出一条可以删除的边。如果有多个答案,请删除标准输入中最后出现的那条边。
输入示例
3
1 2
2 3
1 3输出示例
1 3提示信息
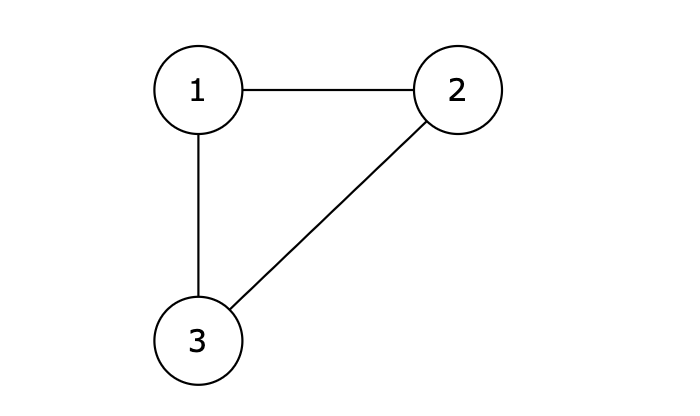
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边,所以输出结果为 1 3
数据范围:
1 <= N <= 1000.
cpp
// 3_卡码网107_寻找存在的路线_并查集.cpp
// Date: 2026-02-12 周四 Author:郑龙浩
// 算法:并查集 或者 DFS BFS
// 这就是个并查集的模版题
//
// 如果 x 与 y 是连接的(也就是x 与 y在一个集合),即x的根节点rootX 与 y的根节点rootY是相同的
// 用时:
#include "bits/stdc++.h"
using namespace std;
const int N = 1005;
int father[N];
// 初始化
void init(int n) {
for (int i = 1; i <= n; i++) father[i] = i;
}
// 查找i的根节点 + 路径压缩,让father[x]存储的一直是根节点
int find(int x) {
if (father[x] != x) { // 如果x不是根节点,就要让father[x] = find(father[x])
father[x] = find(father[x]);
}
return father[x];
}
// 将x 与 y放入同一个集合 --> 即让rootX 与 rootY处于同一个集合里
void join(int x, int y) {
int rootX = find(x); // x 的根节点
int rootY = find(y); // y 的根节点
if (rootX == rootY) return; // 如果x y指向同一个root节点,那么他俩是同一个集合,也就无需合并了
else father[rootX] = rootY; // 如果不是同一个集合,让他们的「根节点合并」,就相当于「集合的合并」
}
int main(void) {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
init(n); // 初始化集合
int s, t, rootX, rootY;
for (int i = 0; i < n; i++) {
cin >> s >> t;
rootX = find(s);
rootY = find(t);
if ( rootX == rootY) { // 如果 两个元素的根节点相同表示:则表示s t之间是连同的,也就是s 与 t之间是个连通图,那么这个边就一定是需要去掉的冗余之边
cout << s << ' ' << t;
return 0;
} else { // 如果s 与 t之间不构成连通图,也就是在同一个集合,或者不是指向同一个根节点的话,那么就将s 与 t连同起来
join(s, t);
}
}
return 0;
}