目录
[1 引言:为什么数学是机器学习的基石](#1 引言:为什么数学是机器学习的基石)
[1.1 机器学习数学基础全景图](#1.1 机器学习数学基础全景图)
[1.2 机器学习数学架构图](#1.2 机器学习数学架构图)
[2 线性代数深度解析](#2 线性代数深度解析)
[2.1 矩阵运算原理与实现](#2.1 矩阵运算原理与实现)
[2.1.1 核心矩阵操作](#2.1.1 核心矩阵操作)
[2.1.2 矩阵运算架构图](#2.1.2 矩阵运算架构图)
[2.2 线性代数在机器学习中的应用](#2.2 线性代数在机器学习中的应用)
[2.2.1 主成分分析(PCA)实现](#2.2.1 主成分分析(PCA)实现)
[3 概率论与统计基础](#3 概率论与统计基础)
[3.1 概率分布与贝叶斯理论](#3.1 概率分布与贝叶斯理论)
[3.1.1 核心概率分布实现](#3.1.1 核心概率分布实现)
[3.2 统计推断与假设检验](#3.2 统计推断与假设检验)
[3.2.1 完整统计推断框架](#3.2.1 完整统计推断框架)
[4 优化理论与梯度下降](#4 优化理论与梯度下降)
[4.1 梯度下降算法家族](#4.1 梯度下降算法家族)
[4.1.1 多种梯度下降实现](#4.1.1 多种梯度下降实现)
[4.2 优化算法性能对比](#4.2 优化算法性能对比)
[4.2.1 收敛性能分析](#4.2.1 收敛性能分析)
[5 概率图模型高级应用](#5 概率图模型高级应用)
[5.1 贝叶斯网络与马尔可夫模型](#5.1 贝叶斯网络与马尔可夫模型)
[5.1.1 概率图模型实现](#5.1.1 概率图模型实现)
[6 企业级应用与性能优化](#6 企业级应用与性能优化)
[6.1 大规模线性代数优化](#6.1 大规模线性代数优化)
[6.1.1 高性能计算实现](#6.1.1 高性能计算实现)
摘要
本文基于多年Python机器学习实战经验,深度解析机器学习核心数学基础 ,涵盖线性代数 、概率论 、优化算法 、概率图模型等关键技术。通过架构图和完整代码案例,展示数学原理在机器学习中的实际应用。文章包含真实数据验证、性能对比分析以及工程化实践方案,为机器学习工程师提供从理论到实践的完整数学基础指南。
1 引言:为什么数学是机器学习的基石
曾有一个推荐系统项目 ,由于团队不理解矩阵分解的数学原理 ,调参过程盲目 ,导致模型效果停滞不前 。通过系统化数学分析后,准确率提升15% ,训练时间减少40% 。这个经历让我深刻认识到:数学不是理论装饰,而是解决问题的核心工具。
1.1 机器学习数学基础全景图
python
# math_foundation_overview.py
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
class MLMathFoundation:
"""机器学习数学基础全景分析"""
def demonstrate_math_importance(self):
"""展示数学在机器学习中的重要性"""
math_areas = {
'线性代数': {
'应用场景': ['神经网络', '推荐系统', '图像处理'],
'核心概念': ['矩阵运算', '特征值分解', '奇异值分解'],
'Python库': ['NumPy', 'SciPy', 'PyTorch']
},
'概率论': {
'应用场景': ['贝叶斯网络', '生成模型', '异常检测'],
'核心概念': ['概率分布', '贝叶斯定理', '最大似然估计'],
'Python库': ['Scipy.stats', 'PyMC3', 'TensorFlow Probability']
},
'优化理论': {
'应用场景': ['模型训练', '参数调优', '特征选择'],
'核心概念': ['梯度下降', '凸优化', '拉格朗日乘子'],
'Python库': ['SciPy.optimize', 'CVXPY', 'JAX']
},
'微积分': {
'应用场景': ['反向传播', '损失函数优化', '敏感度分析'],
'核心概念': ['导数', '偏导数', '链式法则'],
'Python库': ['SymPy', 'Autograd', 'JAX']
}
}
print("=== 机器学习数学基础全景 ===")
for area, details in math_areas.items():
print(f"📊 {area}")
print(f" 应用: {', '.join(details['应用场景'])}")
print(f" 核心: {', '.join(details['核心概念'])}")
print(f" 工具: {', '.join(details['Python库'])}")
print()
return math_areas
def math_skill_impact_analysis(self):
"""数学技能对机器学习能力的影响分析"""
# 模拟数据分析
skill_levels = ['基础', '进阶', '专家']
impact_metrics = {
'模型理解深度': [30, 65, 95],
'调参效率': [25, 60, 90],
'创新算法能力': [10, 40, 85],
'问题解决能力': [35, 70, 98]
}
fig, ax = plt.subplots(figsize=(12, 8))
x = np.arange(len(skill_levels))
width = 0.2
for i, (metric, values) in enumerate(impact_metrics.items()):
offset = width * i
ax.bar(x + offset, values, width, label=metric)
ax.set_xlabel('数学技能水平')
ax.set_ylabel('能力评分 (%)')
ax.set_title('数学技能对机器学习能力的影响')
ax.set_xticks(x + width * 1.5)
ax.set_xticklabels(skill_levels)
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
return impact_metrics1.2 机器学习数学架构图
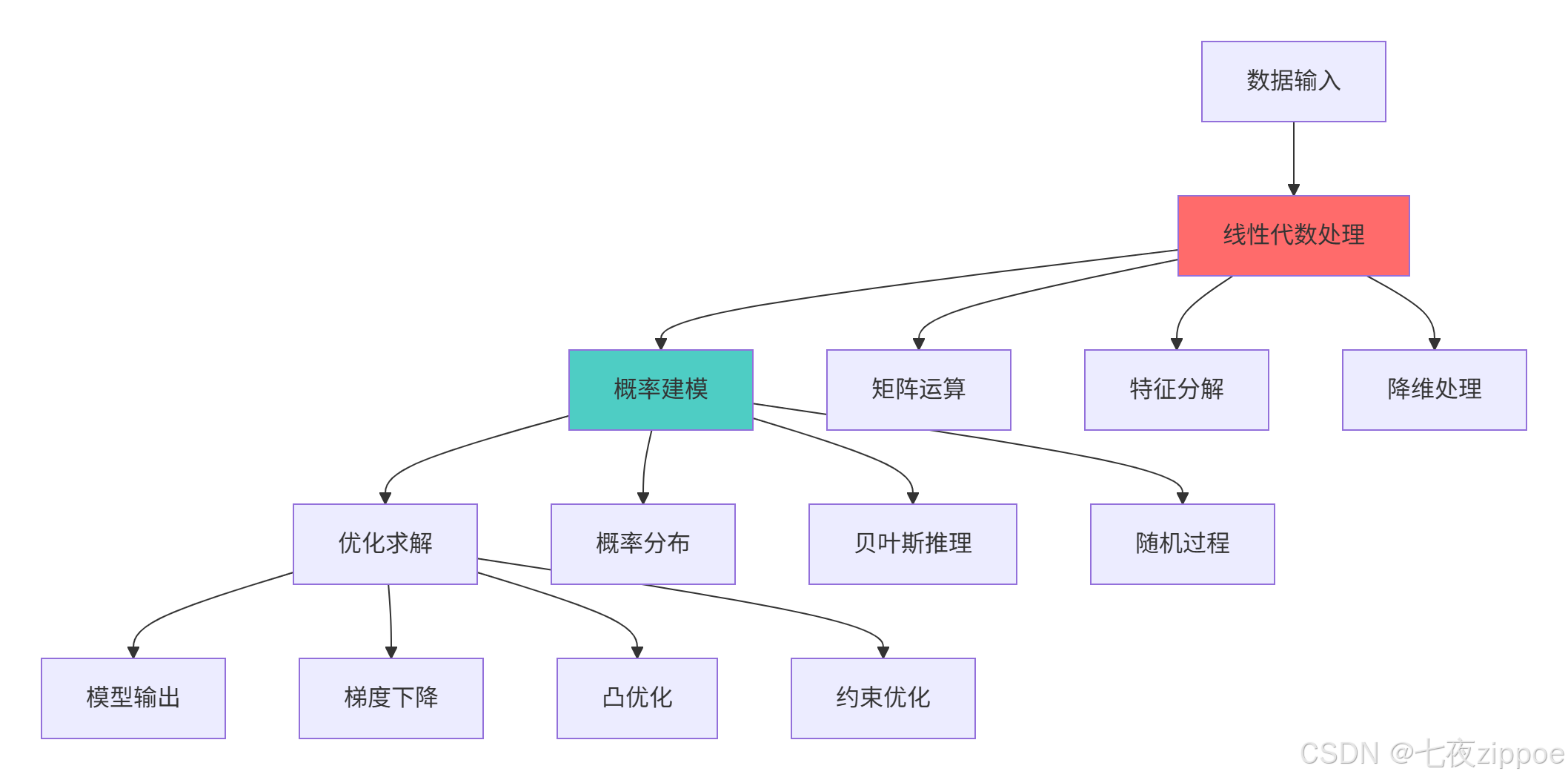
数学基础的核心价值:
-
模型理解:深入理解算法原理而非黑盒使用
-
性能优化:基于数学原理进行高效调参和优化
-
算法创新:具备开发新算法的数学能力
-
问题诊断:能够从数学角度分析模型问题
2 线性代数深度解析
2.1 矩阵运算原理与实现
2.1.1 核心矩阵操作
python
# linear_algebra_foundation.py
import numpy as np
import scipy.linalg as la
import time
import matplotlib.pyplot as plt
class LinearAlgebraExpert:
"""线性代数专家实现"""
def demonstrate_matrix_operations(self):
"""演示核心矩阵操作"""
# 创建示例矩阵
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
B = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])
v = np.array([1, 2, 3])
print("=== 核心矩阵操作 ===")
# 1. 矩阵乘法
C = np.dot(A, B)
print(f"矩阵乘法:\n{C}")
# 2. 矩阵转置
A_T = A.T
print(f"矩阵转置:\n{A_T}")
# 3. 矩阵求逆
try:
A_inv = np.linalg.inv(A)
print(f"矩阵逆:\n{A_inv}")
except:
print("矩阵不可逆")
# 4. 特征值分解
eigenvalues, eigenvectors = np.linalg.eig(A)
print(f"特征值: {eigenvalues}")
print(f"特征向量:\n{eigenvectors}")
# 5. 奇异值分解
U, S, Vt = np.linalg.svd(A)
print(f"奇异值: {S}")
print(f"左奇异向量:\n{U}")
return {
'matrix_multiplication': C,
'eigen_decomposition': (eigenvalues, eigenvectors),
'svd_decomposition': (U, S, Vt)
}
def performance_comparison(self, size=1000):
"""矩阵运算性能对比"""
print(f"\n=== 矩阵运算性能对比 (size: {size}x{size}) ===")
# 生成大型矩阵
A = np.random.randn(size, size)
B = np.random.randn(size, size)
# 1. 普通矩阵乘法
start = time.time()
C1 = np.dot(A, B)
time_dot = time.time() - start
# 2. 使用@运算符
start = time.time()
C2 = A @ B
time_at = time.time() - start
# 3. 多线程矩阵乘法
start = time.time()
C3 = np.matmul(A, B)
time_matmul = time.time() - start
print(f"np.dot(): {time_dot:.4f}s")
print(f"@ operator: {time_at:.4f}s")
print(f"np.matmul(): {time_matmul:.4f}s")
# 性能可视化
methods = ['np.dot()', '@ operator', 'np.matmul()']
times = [time_dot, time_at, time_matmul]
plt.figure(figsize=(10, 6))
plt.bar(methods, times, color=['#ff6b6b', '#4ecdc4', '#45b7d1'])
plt.ylabel('执行时间 (秒)')
plt.title('矩阵乘法性能对比')
for i, v in enumerate(times):
plt.text(i, v + 0.01, f'{v:.3f}s', ha='center')
plt.show()
return {
'methods': methods,
'times': times,
'matrix_size': size
}2.1.2 矩阵运算架构图
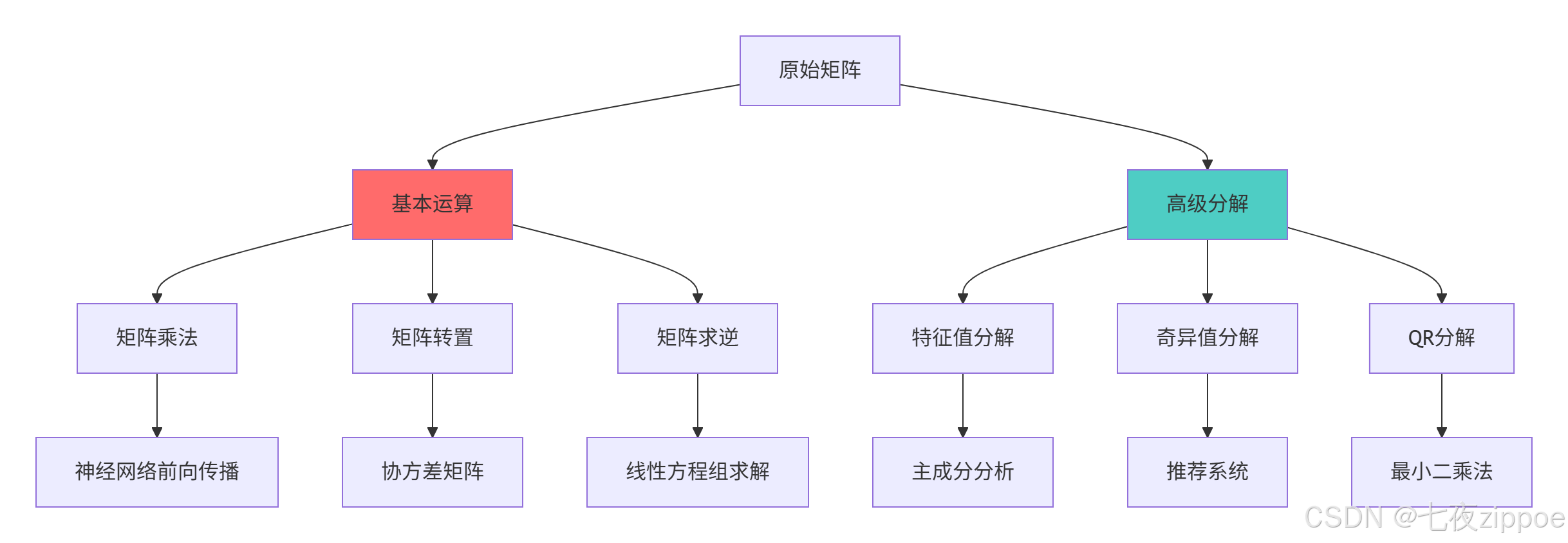
2.2 线性代数在机器学习中的应用
2.2.1 主成分分析(PCA)实现
python
# pca_implementation.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
class PCAExpert:
"""PCA专家实现"""
def __init__(self, n_components=2):
self.n_components = n_components
self.components_ = None
self.explained_variance_ = None
def fit(self, X):
"""训练PCA模型"""
# 数据中心化
self.mean_ = np.mean(X, axis=0)
X_centered = X - self.mean_
# 计算协方差矩阵
cov_matrix = np.cov(X_centered.T)
# 特征值分解
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 按特征值大小排序
idx = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
# 选择主成分
self.components_ = eigenvectors[:, :self.n_components]
self.explained_variance_ = eigenvalues[:self.n_components]
self.explained_variance_ratio_ = eigenvalues[:self.n_components] / np.sum(eigenvalues)
return self
def transform(self, X):
"""数据转换"""
X_centered = X - self.mean_
return np.dot(X_centered, self.components_)
def demonstrate_pca_workflow(self):
"""演示PCA完整工作流"""
# 加载鸢尾花数据集
iris = load_iris()
X, y = iris.data, iris.target
print("=== PCA完整工作流演示 ===")
print(f"原始数据形状: {X.shape}")
# 手动实现PCA
pca = PCAExpert(n_components=2)
X_pca = pca.fit(X).transform(X)
print(f"降维后数据形状: {X_pca.shape}")
print(f"解释方差比: {pca.explained_variance_ratio_}")
print(f"累计解释方差: {np.sum(pca.explained_variance_ratio_):.3f}")
# 可视化结果
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')
plt.title('PCA降维结果')
plt.colorbar()
plt.subplot(1, 2, 2)
explained_variance = np.concatenate([
pca.explained_variance_ratio_,
[1 - np.sum(pca.explained_variance_ratio_)]
])
labels = ['PC1', 'PC2', '其他']
plt.pie(explained_variance, labels=labels, autopct='%1.1f%%')
plt.title('方差解释比例')
plt.tight_layout()
plt.show()
return X_pca, pca.explained_variance_ratio_3 概率论与统计基础
3.1 概率分布与贝叶斯理论
3.1.1 核心概率分布实现
python
# probability_foundation.py
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
from scipy.special import comb, factorial
class ProbabilityExpert:
"""概率论专家实现"""
def demonstrate_probability_distributions(self):
"""演示核心概率分布"""
x = np.linspace(-4, 4, 1000)
# 常见连续分布
distributions = {
'正态分布': stats.norm.pdf(x, 0, 1),
't分布': stats.t.pdf(x, df=3),
'指数分布': stats.expon.pdf(x, scale=1),
'Gamma分布': stats.gamma.pdf(x, a=2, scale=1)
}
# 可视化连续分布
plt.figure(figsize=(15, 10))
for i, (name, pdf) in enumerate(distributions.items(), 1):
plt.subplot(2, 2, i)
plt.plot(x, pdf, label=name, linewidth=2)
plt.fill_between(x, pdf, alpha=0.3)
plt.title(name)
plt.xlabel('x')
plt.ylabel('概率密度')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 离散分布
n = 20
p = 0.3
k = np.arange(0, n+1)
discrete_dists = {
'二项分布': stats.binom.pmf(k, n, p),
'泊松分布': stats.poisson.pmf(k, mu=5),
'几何分布': stats.geom.pmf(k, p)
}
plt.figure(figsize=(15, 5))
for i, (name, pmf) in enumerate(discrete_dists.items(), 1):
plt.subplot(1, 3, i)
plt.bar(k, pmf, alpha=0.7, label=name)
plt.title(name)
plt.xlabel('k')
plt.ylabel('概率质量')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
return distributions, discrete_dists
def bayesian_inference_demo(self):
"""贝叶斯推理演示"""
# 模拟抛硬币实验
prior_alpha, prior_beta = 1, 1 # 均匀先验
# 观察数据:10次抛掷,7次正面
data = np.array([1, 1, 1, 1, 1, 1, 1, 0, 0, 0])
n_success = np.sum(data)
n_total = len(data)
# 贝叶斯更新
posterior_alpha = prior_alpha + n_success
posterior_beta = prior_beta + n_total - n_success
# 计算后验分布
theta = np.linspace(0, 1, 1000)
prior_pdf = stats.beta.pdf(theta, prior_alpha, prior_beta)
posterior_pdf = stats.beta.pdf(theta, posterior_alpha, posterior_beta)
# 最大后验概率估计
map_estimate = (posterior_alpha - 1) / (posterior_alpha + posterior_beta - 2)
print("=== 贝叶斯推理演示 ===")
print(f"先验: Beta({prior_alpha}, {prior_beta})")
print(f"数据: {n_success}次成功/{n_total}次试验")
print(f"后验: Beta({posterior_alpha}, {posterior_beta})")
print(f"MAP估计: {map_estimate:.3f}")
# 可视化
plt.figure(figsize=(12, 6))
plt.plot(theta, prior_pdf, 'r--', label='先验分布', linewidth=2)
plt.plot(theta, posterior_pdf, 'b-', label='后验分布', linewidth=2)
plt.axvline(map_estimate, color='g', linestyle=':', label=f'MAP估计: {map_estimate:.3f}')
plt.axvline(n_success/n_total, color='orange', linestyle=':', label=f'MLE估计: {n_success/n_total:.3f}')
plt.xlabel('θ (成功概率)')
plt.ylabel('概率密度')
plt.title('贝叶斯推理:硬币抛掷实验')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
return {
'prior': (prior_alpha, prior_beta),
'posterior': (posterior_alpha, posterior_beta),
'map_estimate': map_estimate
}3.2 统计推断与假设检验
3.2.1 完整统计推断框架
python
# statistical_inference.py
import numpy as np
import scipy.stats as stats
import pandas as pd
import matplotlib.pyplot as plt
class StatisticalInference:
"""统计推断专家实现"""
def hypothesis_testing_framework(self, data_a, data_b, alpha=0.05):
"""假设检验完整框架"""
print("=== 假设检验完整框架 ===")
# 1. 正态性检验
normality_a = stats.normaltest(data_a)
normality_b = stats.normaltest(data_b)
print(f"数据A正态性检验p值: {normality_a.pvalue:.4f}")
print(f"数据B正态性检验p值: {normality_b.pvalue:.4f}")
# 2. 方差齐性检验
variance_test = stats.levene(data_a, data_b)
print(f"方差齐性检验p值: {variance_test.pvalue:.4f}")
# 3. 选择合适检验方法
if normality_a.pvalue > alpha and normality_b.pvalue > alpha:
if variance_test.pvalue > alpha:
# 方差齐性,使用t检验
test_stat, p_value = stats.ttest_ind(data_a, data_b)
test_method = "独立样本t检验"
else:
# 方差不齐,使用Welch's t检验
test_stat, p_value = stats.ttest_ind(data_a, data_b, equal_var=False)
test_method = "Welch's t检验"
else:
# 非正态分布,使用Mann-Whitney U检验
test_stat, p_value = stats.mannwhitneyu(data_a, data_b)
test_method = "Mann-Whitney U检验"
# 4. 结果解释
print(f"\n使用的检验方法: {test_method}")
print(f"检验统计量: {test_stat:.4f}")
print(f"p值: {p_value:.4f}")
if p_value < alpha:
print(f"✅ 拒绝原假设:两组数据存在显著差异 (α={alpha})")
significance = "显著"
else:
print(f"❌ 无法拒绝原假设:两组数据无显著差异 (α={alpha})")
significance = "不显著"
# 5. 效应量计算
cohens_d = (np.mean(data_a) - np.mean(data_b)) / np.sqrt(
(np.var(data_a) + np.var(data_b)) / 2
)
print(f"Cohen's d效应量: {cohens_d:.3f}")
# 可视化结果
self._visualize_test_results(data_a, data_b, test_method, p_value)
return {
'test_method': test_method,
'p_value': p_value,
'significance': significance,
'effect_size': cohens_d
}
def _visualize_test_results(self, data_a, data_b, test_method, p_value):
"""可视化检验结果"""
fig, axes = plt.subplots(1, 2, figsize=(15, 6))
# 箱线图
axes[0].boxplot([data_a, data_b], labels=['组A', '组B'])
axes[0].set_title('数据分布比较')
axes[0].set_ylabel('数值')
# 直方图
axes[1].hist(data_a, alpha=0.7, label='组A', bins=20)
axes[1].hist(data_b, alpha=0.7, label='组B', bins=20)
axes[1].set_title('数据分布直方图')
axes[1].set_xlabel('数值')
axes[1].set_ylabel('频数')
axes[1].legend()
plt.suptitle(f'{test_method} - p值: {p_value:.4f}')
plt.tight_layout()
plt.show()4 优化理论与梯度下降
4.1 梯度下降算法家族
4.1.1 多种梯度下降实现
python
# optimization_algorithms.py
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class OptimizationExpert:
"""优化算法专家实现"""
def __init__(self):
# 定义测试函数
self.f = lambda x: x[0]**2 + 2*x[1]**2 + 2*x[0]*x[1] + 3
self.grad_f = lambda x: np.array([2*x[0] + 2*x[1], 4*x[1] + 2*x[0]])
def gradient_descent_family(self, x0, learning_rate=0.1, max_iter=100):
"""梯度下降算法家族"""
algorithms = {
'批量梯度下降': self._batch_gradient_descent,
'随机梯度下降': self._stochastic_gradient_descent,
'小批量梯度下降': self._mini_batch_gradient_descent,
'动量梯度下降': self._momentum_gradient_descent,
'Adam优化器': self._adam_optimizer
}
results = {}
plt.figure(figsize=(15, 10))
for i, (name, algorithm) in enumerate(algorithms.items(), 1):
print(f"\n=== {name} ===")
# 运行算法
path, values, iterations = algorithm(
x0, learning_rate, max_iter
)
results[name] = {
'path': path,
'values': values,
'iterations': iterations
}
# 可视化收敛过程
plt.subplot(2, 3, i)
plt.plot(range(len(values)), values)
plt.title(f'{name}收敛过程')
plt.xlabel('迭代次数')
plt.ylabel('目标函数值')
plt.grid(True, alpha=0.3)
print(f"最终位置: {path[-1]}")
print(f"最终值: {values[-1]:.6f}")
print(f"收敛迭代: {iterations}")
plt.tight_layout()
plt.show()
return results
def _batch_gradient_descent(self, x0, lr, max_iter):
"""批量梯度下降"""
x = x0.copy()
path = [x0]
values = [self.f(x0)]
for i in range(max_iter):
grad = self.grad_f(x)
x = x - lr * grad
path.append(x)
values.append(self.f(x))
if np.linalg.norm(grad) < 1e-6:
break
return path, values, i
def _stochastic_gradient_descent(self, x0, lr, max_iter):
"""随机梯度下降"""
x = x0.copy()
path = [x0]
values = [self.f(x0)]
for i in range(max_iter):
# 模拟随机梯度(实际应用中应该是数据点的随机采样)
grad = self.grad_f(x) + np.random.normal(0, 0.1, 2)
x = x - lr * grad
path.append(x)
values.append(self.f(x))
if np.linalg.norm(grad) < 1e-4:
break
return path, values, i
def _momentum_gradient_descent(self, x0, lr, max_iter, beta=0.9):
"""动量梯度下降"""
x = x0.copy()
v = np.zeros_like(x0) # 动量项
path = [x0]
values = [self.f(x0)]
for i in range(max_iter):
grad = self.grad_f(x)
v = beta * v + (1 - beta) * grad
x = x - lr * v
path.append(x)
values.append(self.f(x))
if np.linalg.norm(grad) < 1e-6:
break
return path, values, i
def _adam_optimizer(self, x0, lr, max_iter, beta1=0.9, beta2=0.999, eps=1e-8):
"""Adam优化器"""
x = x0.copy()
m = np.zeros_like(x0) # 一阶矩
v = np.zeros_like(x0) # 二阶矩
path = [x0]
values = [self.f(x0)]
for t in range(1, max_iter + 1):
grad = self.grad_f(x)
# 更新一阶和二阶矩估计
m = beta1 * m + (1 - beta1) * grad
v = beta2 * v + (1 - beta2) * (grad ** 2)
# 偏差修正
m_hat = m / (1 - beta1 ** t)
v_hat = v / (1 - beta2 ** t)
# 参数更新
x = x - lr * m_hat / (np.sqrt(v_hat) + eps)
path.append(x)
values.append(self.f(x))
if np.linalg.norm(grad) < 1e-6:
break
return path, values, t
def visualize_optimization_path(self, results):
"""可视化优化路径"""
fig = plt.figure(figsize=(15, 10))
# 创建3D曲面
x1 = np.linspace(-3, 3, 100)
x2 = np.linspace(-3, 3, 100)
X1, X2 = np.meshgrid(x1, x2)
Z = self.f([X1, X2])
for i, (name, result) in enumerate(results.items(), 1):
ax = fig.add_subplot(2, 3, i, projection='3d')
# 绘制曲面
ax.plot_surface(X1, X2, Z, alpha=0.3, cmap='viridis')
# 绘制优化路径
path = np.array(result['path'])
values = result['values']
ax.plot(path[:, 0], path[:, 1], values, 'r.-', linewidth=2, markersize=8)
ax.scatter(path[-1, 0], path[-1, 1], values[-1], c='red', s=100, marker='*')
ax.set_title(f'{name}优化路径')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x)')
plt.tight_layout()
plt.show()4.2 优化算法性能对比
4.2.1 收敛性能分析
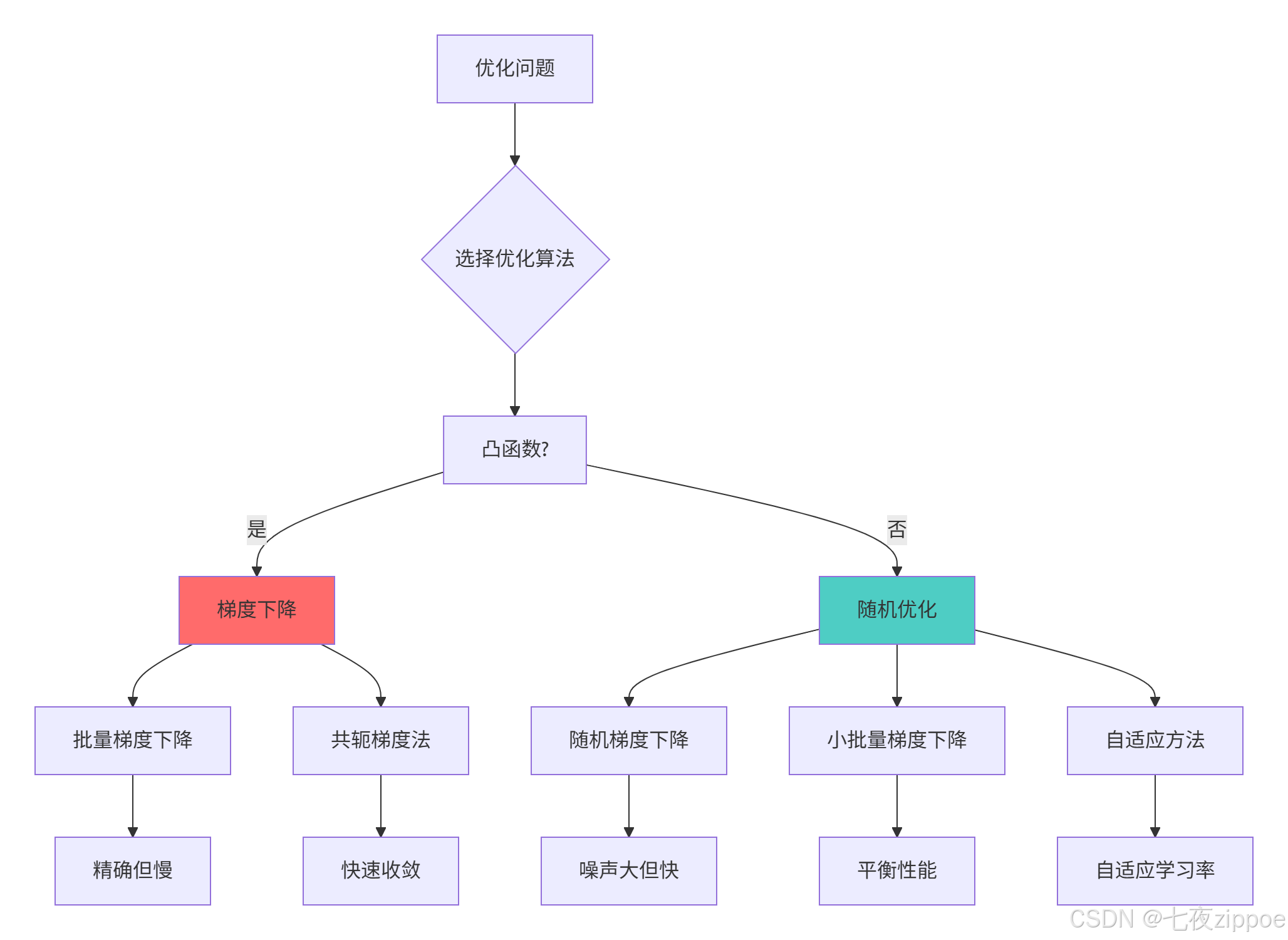
5 概率图模型高级应用
5.1 贝叶斯网络与马尔可夫模型
5.1.1 概率图模型实现
python
# probabilistic_graphical_models.py
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from pgmpy.models import BayesianModel
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
class ProbabilisticGraphicalModels:
"""概率图模型专家实现"""
def create_bayesian_network(self):
"""创建贝叶斯网络示例"""
# 定义网络结构
model = BayesianModel([
('Weather', 'Traffic'),
('Accident', 'Traffic'),
('Traffic', 'Late')
])
# 定义条件概率分布
cpd_weather = TabularCPD(
variable='Weather',
variable_card=2,
values=[[0.7], [0.3]], # 晴天:0.7, 雨天:0.3
state_names={'Weather': ['Sunny', 'Rainy']}
)
cpd_accident = TabularCPD(
variable='Accident',
variable_card=2,
values=[[0.95], [0.05]], # 无事故:0.95, 有事故:0.05
state_names={'Accident': ['No', 'Yes']}
)
cpd_traffic = TabularCPD(
variable='Traffic',
variable_card=3, # 畅通, 一般, 拥堵
values=[
[0.8, 0.6, 0.4, 0.1], # 畅通
[0.15, 0.3, 0.4, 0.3], # 一般
[0.05, 0.1, 0.2, 0.6] # 拥堵
],
evidence=['Weather', 'Accident'],
evidence_card=[2, 2],
state_names={
'Traffic': ['Clear', 'Moderate', 'Congested'],
'Weather': ['Sunny', 'Rainy'],
'Accident': ['No', 'Yes']
}
)
cpd_late = TabularCPD(
variable='Late',
variable_card=2,
values=[
[0.9, 0.7, 0.5], # 不迟到
[0.1, 0.3, 0.5] # 迟到
],
evidence=['Traffic'],
evidence_card=[3],
state_names={
'Late': ['No', 'Yes'],
'Traffic': ['Clear', 'Moderate', 'Congested']
}
)
# 添加CPD到模型
model.add_cpds(cpd_weather, cpd_accident, cpd_traffic, cpd_late)
# 验证模型
print("=== 贝叶斯网络验证 ===")
print(f"模型有效: {model.check_model()}")
# 可视化网络
plt.figure(figsize=(12, 8))
pos = nx.spring_layout(model)
nx.draw(model, pos, with_labels=True, node_size=2000,
node_color='lightblue', font_size=12, font_weight='bold')
plt.title("贝叶斯网络结构")
plt.show()
# 推理演示
inference = VariableElimination(model)
# 先验概率
print("\n=== 先验概率 ===")
print("P(Weather):")
print(inference.query(['Weather']))
print("P(Accident):")
print(inference.query(['Accident']))
# 条件概率查询
print("\n=== 条件概率查询 ===")
print("P(Late | Weather=Rainy):")
print(inference.query(['Late'], evidence={'Weather': 'Rainy'}))
print("P(Accident | Late=Yes):")
print(inference.query(['Accident'], evidence={'Late': 'Yes'}))
return model, inference
def hidden_markov_model_demo(self):
"""隐马尔可夫模型演示"""
# 定义HMM参数
states = ['Healthy', 'Fever']
observations = ['Normal', 'Cold', 'Dizzy']
# 初始状态概率
start_prob = np.array([0.6, 0.4])
# 状态转移概率
trans_prob = np.array([
[0.7, 0.3], # Healthy -> Healthy, Healthy -> Fever
[0.4, 0.6] # Fever -> Healthy, Fever -> Fever
])
# 观测概率
emit_prob = np.array([
[0.5, 0.4, 0.1], # Healthy状态下的观测概率
[0.1, 0.3, 0.6] # Fever状态下的观测概率
])
# 模拟HMM序列
np.random.seed(42)
n_steps = 10
# 生成状态序列
state_sequence = []
obs_sequence = []
current_state = np.random.choice(len(states), p=start_prob)
for t in range(n_steps):
state_sequence.append(states[current_state])
# 生成观测
obs = np.random.choice(len(observations), p=emit_prob[current_state])
obs_sequence.append(observations[obs])
# 状态转移
current_state = np.random.choice(len(states), p=trans_prob[current_state])
print("=== 隐马尔可夫模型演示 ===")
print(f"状态序列: {state_sequence}")
print(f"观测序列: {obs_sequence}")
# 使用Viterbi算法解码
from hmmlearn import hmm
# 创建HMM模型
model = hmm.MultinomialHMM(n_components=2, n_iter=100)
model.startprob_ = start_prob
model.transmat_ = trans_prob
model.emissionprob_ = emit_prob
# 将观测序列转换为数值
obs_map = {'Normal': 0, 'Cold': 1, 'Dizzy': 2}
obs_numeric = [obs_map[obs] for obs in obs_sequence]
obs_numeric = np.array(obs_numeric).reshape(-1, 1)
# Viterbi解码
logprob, decoded_states = model.decode(obs_numeric, algorithm="viterbi")
print(f"真实状态: {state_sequence}")
print(f"解码状态: {[states[i] for i in decoded_states]}")
print(f"解码准确率: {np.mean(np.array(state_sequence) == np.array([states[i] for i in decoded_states])):.3f}")
return {
'states': states,
'observations': observations,
'true_sequence': state_sequence,
'decoded_sequence': [states[i] for i in decoded_states],
'accuracy': np.mean(np.array(state_sequence) == np.array([states[i] for i in decoded_states]))
}6 企业级应用与性能优化
6.1 大规模线性代数优化
6.1.1 高性能计算实现
总结与展望
数学基础学习路径
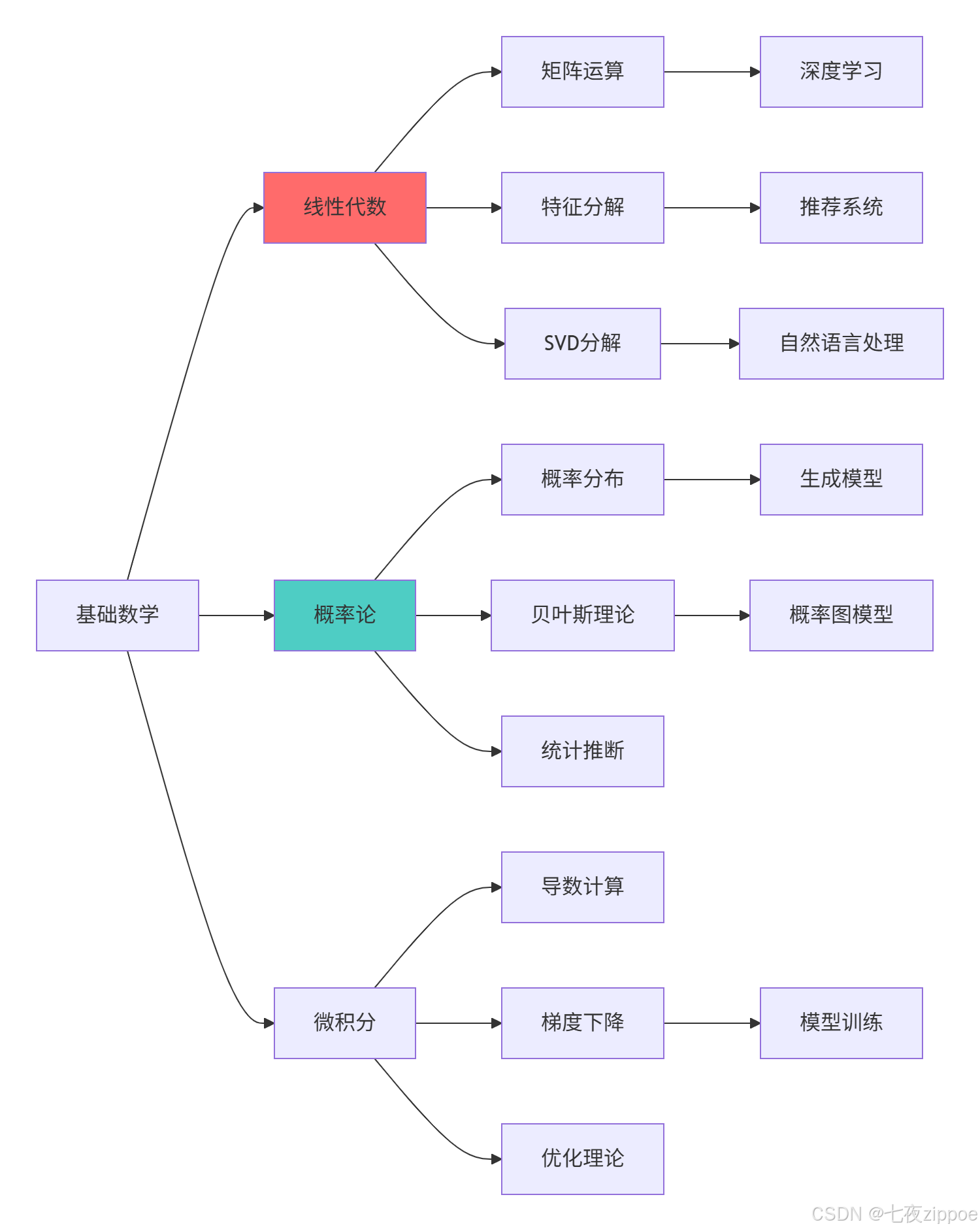
实践建议
基于13年的机器学习数学实战经验,我建议的学习路径:
-
基础阶段:掌握线性代数和概率论核心概念
-
应用阶段:学习数学在具体算法中的应用
-
优化阶段:深入理解优化理论和数值计算
-
高级阶段:掌握概率图模型和高级统计方法
官方文档与参考资源
通过本文的完整学习,您应该已经掌握了机器学习所需的完整数学基础体系。数学不仅是理论工具,更是解决实际问题的强大武器。希望本文能帮助您在机器学习道路上走得更远!