双指针法：从三道经典题看双指针的核心思想

双指针法是数组和链表问题中非常高效的一种策略，它通过两个指针在一次遍历中完成任务，将时间复杂度从暴力法的 O (n²) 优化到 O (n)。今天我们就通过 LeetCode 上的三道经典题目，深入理解双指针法的精髓。

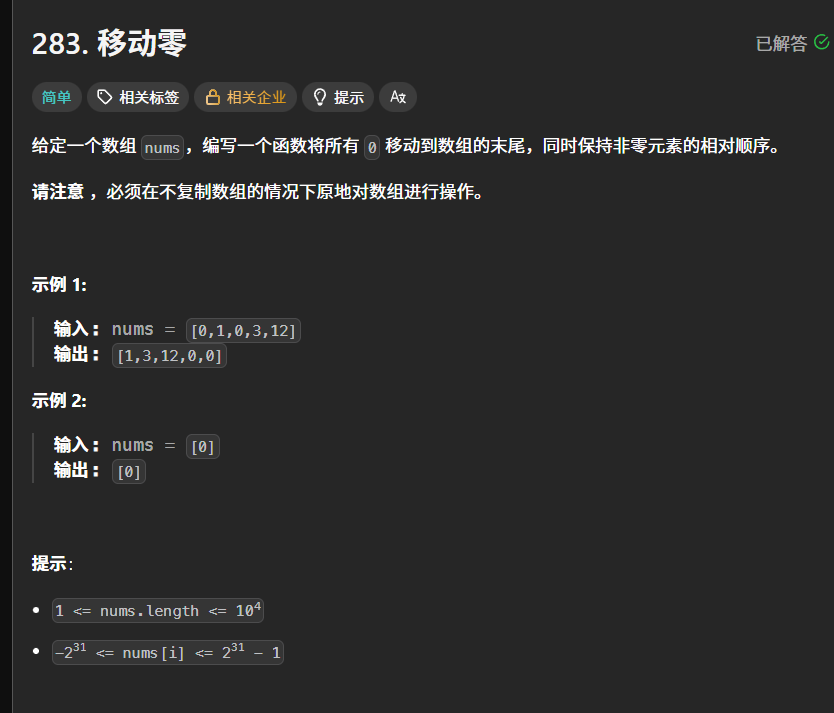
一、移动零（LeetCode 283）

283. 移动零 - 力扣（LeetCode）

这道题是双指针法中 "快慢指针" 的典型应用。我们可以把它理解为一个 "筛选" 和 "填充" 的过程：

慢指针 slow：指向当前需要填充非零元素的位置。
快指针 fast：遍历整个数组，寻找非零元素。

核心逻辑

快指针 fast 不断向前移动，遇到非零元素时，就将其赋值给慢指针 slow 指向的位置，然后慢指针 slow 也向前移动一步。
这样，慢指针之前的所有位置都被非零元素填满，并且保持了原有的相对顺序。
遍历结束后，从慢指针 slow 的位置开始，到数组末尾，所有位置都填充为 0。

快指针 fast 遍历了所有元素，保证了所有非零元素都被处理。
慢指针 slow 只在遇到非零元素时才移动，保证了非零元素按顺序填充到数组前面。
最后填充 0 的操作，将所有多余的位置清零，完成了 "移动零" 的目标。

代码实现

java 复制代码

class Solution {
    public void moveZeroes(int[] nums) {
        int slow = 0;
        // 第一遍遍历，将非零元素移动到数组前面
        for (int fast = 0; fast < nums.length; fast++) {
            if (nums[fast] != 0) {
                nums[slow] = nums[fast];
                slow++;
            }
        }
        // 第二遍遍历，将 slow 之后的元素全部置为 0
        for (int i = slow; i < nums.length; i++) {
            nums[i] = 0;
        }
    }
}

二、盛最多水的容器（LeetCode 11）

11. 盛最多水的容器 - 力扣（LeetCode）

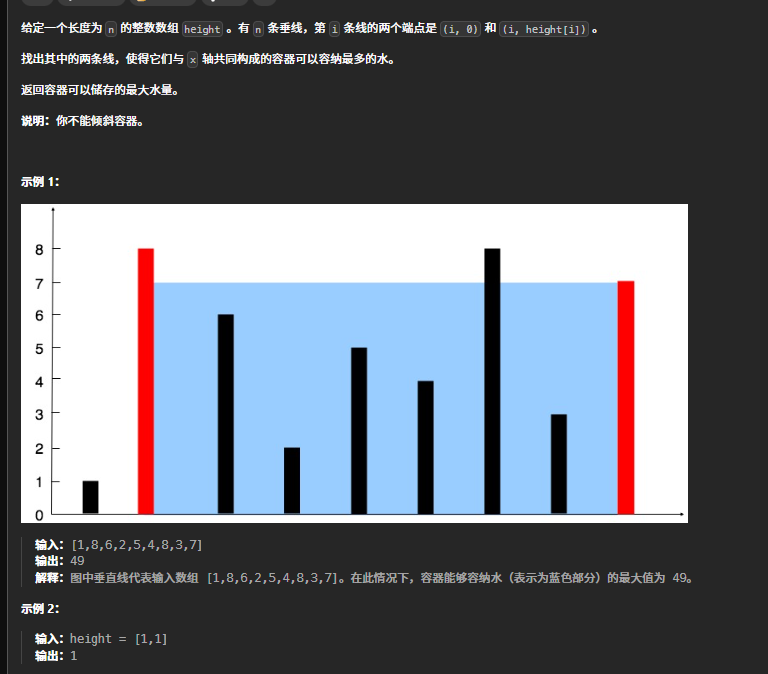
核心逻辑

容器的盛水量由两个因素决定：宽度（两指针之间的距离）和 有效高度（两个指针指向的高度中较小的那个）。
初始时，两个指针分别在数组两端，此时宽度最大。
每次移动较矮的那个指针(这是最关键的一步)：
想提高盛水量，要么增加高度要么增加宽度，而初始的时候，宽度是最大的(初始的时候两个指针分别位于数组的首和尾)
那么接下来我们只有想办法通过增加高度来提升水量，如果我们移动较高的指针，那么宽度是减小的，但是高度却一直被较矮的指针固定了，盛水量只会更小。
所以只有移动较矮的指针，才有可能会遇到更高的线，从而提高高度，得到更多的盛水量。

代码实现

java 复制代码

class Solution {
    public int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int result = 0;
        while (left < right) {
            // 计算当前指针的盛水量
            int cur = Math.min(height[left], height[right]) * (right - left);
            // 更新最大水量
            result = Math.max(result, cur);
            // 移动较矮的指针
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        return result;
    }
}

三、三数之和（LeetCode 15）

15. 三数之和 - 力扣（LeetCode）

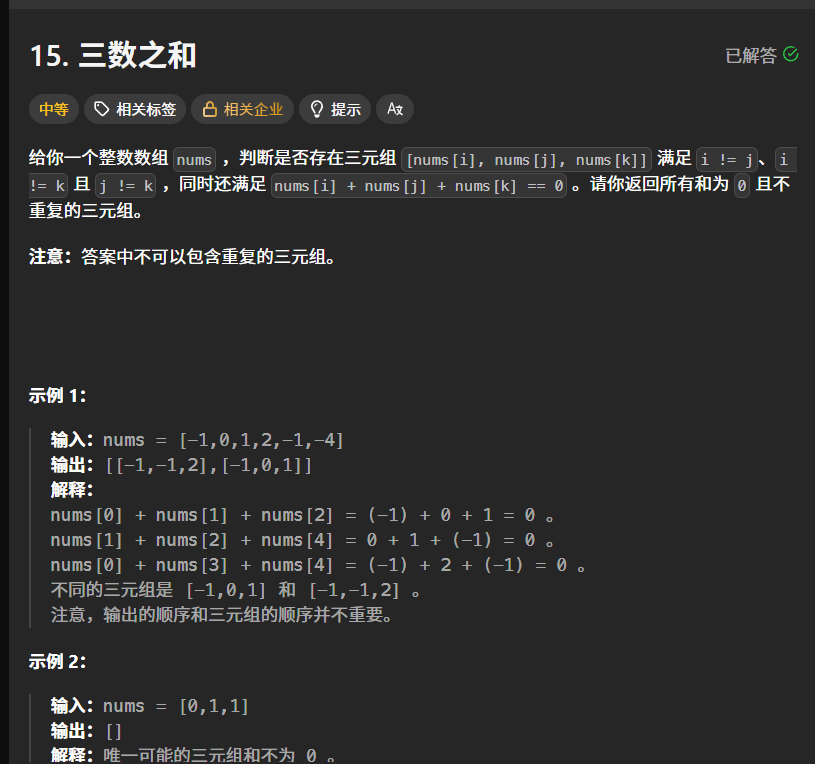
核心逻辑

排序：首先对数组进行从小到大的排序，这有两个好处：一是方便我们用双指针来寻找和为特定值的两个数，二是方便跳过重复元素，避免结果中出现重复的三元组。
固定一个数 ：遍历数组，将每个元素 nums[i] 作为三元组的第一个数。
利用双指针找另外两个数 ：在 i 之后的子数组中，用左指针 left = i+1 和右指针 right = n-1 来寻找和为 -nums[i] 的两个数。
- 如果 nums[left] + nums[right] < target，则 left++，增大和。
- 如果 nums[left] + nums[right] > target，则 right--，减小和。
- 如果 nums[left] + nums[right] == target，则记录三元组，并跳过所有重复的 nums[left] 和 nums[right]，避免重复结果。
跳过重复的第一个数：遍历过程中，如果当前元素和前一个元素相同，就跳过，避免生成重复的三元组。

代码实现

java 复制代码

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> retList = new ArrayList<>();
        // 先对数组排序
        Arrays.sort(nums);
        int n = nums.length;
        
        for (int i = 0; i < n; i++) {
            // 如果当前数大于0，后面的数都更大，不可能和为0
            if (nums[i] > 0) {
                break;
            }
            // 跳过重复的第一个数
            if (i > 0 && nums[i] == nums[i-1]) {
                continue;
            }
            
            int left = i + 1, right = n - 1;
            int target = -nums[i];
            
            while (left < right) {
                if (nums[left] + nums[right] < target) {
                    left++;
                } else if (nums[left] + nums[right] > target) {
                    right--;
                } else {
                    // 找到符合条件的三元组
                    retList.add(new ArrayList<>(Arrays.asList(nums[i], nums[left], nums[right])));
                    // 跳过重复的左指针元素
                    while (left < right && nums[left] == nums[left+1]) {
                        left++;
                    }
                    // 跳过重复的右指针元素
                    while (left < right && nums[right] == nums[right-1]) {
                        right--;
                    }
                    // 移动指针，寻找下一组解
                    left++;
                    right--;
                }
            }
        }
        return retList;
    }
}

结语

双指针法的魅力，在于它用一种极其简洁的方式，将时间复杂度大幅降低。通过这三道题，我们可以看到，双指针法的本质，就是用两个指针的协同移动，来替代原本需要多次嵌套遍历的逻辑。

无论是 "移动零" 中筛选填充，还是 "盛最多水的容器" 中从两端逼近最优解，亦或是 "三数之和" 中通过排序和指针移动来精准定位组合，其核心思想都是一致的：让指针的移动有明确的方向和目的，从而避免无意义的计算。

掌握双指针法，不仅是掌握了一种解题技巧，更是培养了一种高效思考问题的方式。希望通过这篇博客，你能在未来的算法学习中，更敏锐地发现可以用双指针法解决的问题，并能灵活运用，游刃有余。