2026年寒假牛客训练赛补题（五）

写在前面

笔者是大二acm选手，参加今年寒假的牛客训练赛，写这篇博客的时候六场已经全部打完了。

整体评价是第三场最简单，第四场最不友好（全是构造），第五场第六场难度跨度偏大

因为第四场实在是太过恶心，所以不想补了，一共只补五场，这篇博客记录第五场补的题。

这场我赛时开了四个题，赛后补两道题，一道是贪心+二分，一道是DP

注：本博客比赛题目来自牛客竞赛，题解参考牛客竞赛官方题解

比赛链接：https://ac.nowcoder.com/acm/contest/120565

E

题面

题意解释

给定一个数组，每个前缀和都对p取模，然后要求计算针对p取模的最大子段和

纠正一个可能出错的地方：取模是在计算前缀和时就已经取模的，而不是算出sum(r)-sum(l-1)之后才取模

思路

首先先关注一个地方：数组元素小于模数

由此我们可以得到，不会因为倍数的不同导致取模结果不同，当子段和是正时，p和998244353或1e9+7是一样的

要算最大子段和，先算前缀和

算出前缀和，[l,r]这一段的子段和就是sum(r)-sum(l-1)，若其为正，取模无所谓，若其为负，可能变成一个极大的数

若为正正常比较即可，若为负，因为结果在(-p,0)这个区间，所以取模就是结果+p

但是如果使用n^2遍历来算前缀和的差，就会出现这个结果

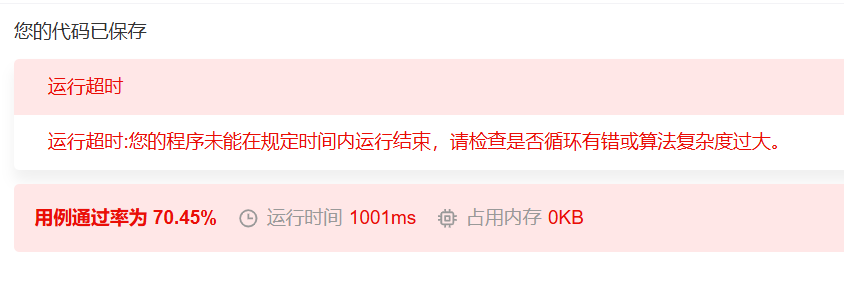
所以需要优化时间复杂度

我们先看sum(r)-sum(l-1)>0的情况，这种情况下由于数组元素规定非负，所以这个结果最大只能是sum(r)

再看sum(r)-sum(l-1)<0的情况，这种情况能创造的价值就更大了，所以我们重点偏重算这种情况，在r处找大于sum(r)的sum(l-1)，这里只需要找到符合条件的最小的sum(l-1)，毫无疑问sum(r)-sum(l-1)越接近-1得到的模数越大。因此这个地方可以直接使用二分查找

为了减轻代码量，可以直接使用set或者map

代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=1e9+7;

void solve() 
{
	ll n,p;
	cin>>n>>p;
	vector<ll>a(n);
	for (int i=0;i<n;i++) cin>>a[i];
	set<pair<ll,int>>s;
	s.insert({0, 0});
	ll current_sum = 0;
	ll max_mod = 0;
	int ans_l = 0, ans_r = 0; 
	for (int r=0;r<n;r++)
	{
		current_sum = (current_sum + a[r]) % p;	
		auto it = s.upper_bound({current_sum, -1}); 
		if (it != s.end()) 
		{
			ll candidate = (current_sum - it->first + p) % p;
			if (candidate > max_mod) 
			{
				max_mod = candidate;
				ans_l = it->second;   
				ans_r = r;          
			}
		}
		if (current_sum > max_mod) 
		{
			max_mod = current_sum;
			ans_l = 0;       
			ans_r = r;      
		}
		s.insert({current_sum, r + 1});
	}
	cout << ans_l << " " << ans_r << " " << max_mod << endl;
}

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	ll t=1;
	//cin>>t;
	while(t--) 
	{
		solve();
	}
	return 0;
}

F

题面

qcjj真可爱

题意解释

指定一句话的长度，给定"qcjjkkt"和"td"出现之后的贡献值，然后计算这句话最多能产生多少贡献值

可以注意到qcjjkktd，这样一个字符串既包括前者又包括后者，这是唯一需要关注的地方了

思路

这是一个背包问题的变式

我赛时想到的错误策略是：贡献值密度最大的越多越好，所以先算出三种句子的贡献值密度，然后一个劲堆这种句子

如果td最多直接堆td，堆到放不下；如果七个长度最多就堆七个长度的，剩下的全堆td；如果八个长度最多就堆八个长度的，剩下全堆td

但是这样只过了20%的样例

我感觉一方面是精度问题，可能算出来的密度精度有问题，并没有比较出谁密度最大

另一方面就是这种思路其实并不完全，如果密度差了0.0001这种类似情况，可能选另一个会更好

所以应该用DP这种更完全更全面的做法

如果句子长度是56*k，就可以完全放满，不留空隙这种情况就可以使用我赛时的策略，使用一种决策填满，然后取三种决策得到的最大值

如果长度不是56*k，那就先保证56*（k-1）能放满，然后剩下的再用背包问题的思路求解，尽量使贡献值最大

但是这里还有一个容易忽略的地方：当前这一段放满，下一段剩的特别少导致一点收益都没有；反而要比这一段留点位置给下一段放一个得到的收益更小。

代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

void solve() 
{
	ll n,a,b;
	cin>>n>>a>>b;
	ll max_56=max({56/7*a,56/2*b,56/8*(a+b)});
	ll k=n/56;
	ll r=n%56;
	auto dp_calc = [&](ll len) 
	{
		if (len==0) return 0LL;
		vector<ll>dp(len+1, 0); 
		for(int i=1;i<=len;i++)
		{
			if(i>=7) dp[i]=max(dp[i], dp[i-7] + a);
			if(i>=2) dp[i]=max(dp[i], dp[i-2] + b);
			if(i>=8) dp[i]=max(dp[i], dp[i-8] + (a+b));
		}
		return dp[len];
	};
	ll ans=0;
	if (k==0) 
	{
		ans=dp_calc(n);
	} 
	else
	{
		ll case1=k*max_56+dp_calc(r);
		ll case2=(k-1)*max_56+dp_calc(r+56);
		ans=max(case1,case2);
	}
	cout<<ans<<endl;
}

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	ll t=1;
	cin>>t;
	while(t--) 
	{
		solve();
	}
	return 0;
}

篇末总结

这场的难度确实有点高，六题也是六七百名的实力了，不过F的DP也足够好理解，对我这个水平还是很有帮助的，接下来再补完第六场，寒假的牛客任务就算完成了，接着学Java