人工智能数学基础——第二章 高等数学基础

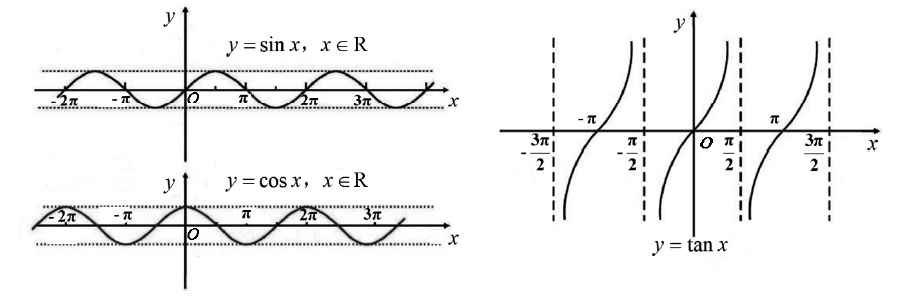
2.1函数

2.1.1函数的定义

设数集，则称映射为定义在D 上的函数，通常简记为。其中x 为自变量，y 为因变量，D 为定义域，记作。

对于每个，按对应法则f ，总有唯一确定的值y 与之对应，这个值成为函数f 在x 处的函数值，记为，即。函数值的全体构成的集合称为函数的值域，记作或。

2.1.2特殊函数的定义

1、分段函数：对于自变量x的不同取值范围，有不同的对应法则。

2、反函数：设函数是单射，则存在逆映射， 称此映射为函数的反函数。

3、显函数与隐函数：一个函数如果能用形如的解析式表示，其中x、y 分别是函数的自变量与因变量，则此函数成为显函数；如果由方程可确定y 是x 的函数，即x、y 在某个范围内存在函数，使，则这个函数是隐函数。

2.1.3函数的特性

1、函数的奇偶性

设函数的定义域D 关于原点对称。对于区间D 上任意点x ，若恒成立，则为奇函数，其图像在绕原点180°旋转后不会改变；若恒成立，则为偶函数，其图像在对y轴映射后不会改变。

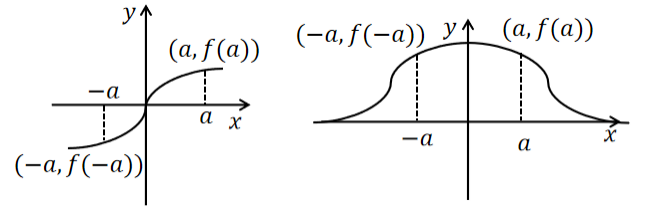
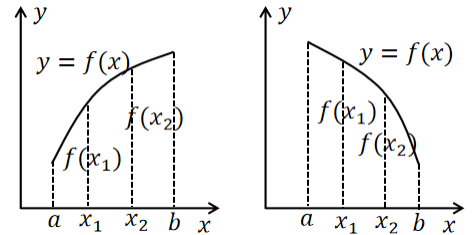
2、函数的单调性

设函数的定义域D，区间。假设区间I 上有任意两点及：当时，恒有，则称函数在区间I 上是单调递增的；当时，恒有，则称函数在区间I上是单调递减的。单调递增和单调递减的函数称为单调函数。

3、函数的周期性

设函数的定义域为D ，如果存在一个整数l ，使任意点有，且恒成立，则称为周期函数，l 称为的周期，通常说的周期函数是指最小正周期。