阵列
属于二维数组的内容
题目
-
问题描述
明明在上学的时候,参加数学兴趣班。在班上,老师介绍了一种非常有趣的阵列。
该阵列由n个正整数构成,阵列中的数字从1开始递增,数字的排序规则是从1开始由中间逆时针向外转出,2出现在1的下面,然后直至输出n为止。

明明回家后想自己动手构造这样的阵列。他从n=1开始构造,但是他发现当n越来越大时,阵列的复杂性就越高,然后构造出来的阵列就越容易出错。为了降低构造阵列的出错率,提高构造速度,明明就求助于你,请你帮他写一个程序,来构造这样的阵列。
明明的问题可以归结为:给你一个正整数n,请你按题目描述中所述的方法,构造出阵列。 -
输入说明
你写的程序要求从标准输入设备中读入测试数据作为你所写程序的输入数据。标准输入设备中有多组测试数据,每组测试数据仅占一行,每行仅有一个正整数n(1≤n≤99),即所要构造的阵列的大小。每组测试数据与其后一组测试数据之间没有任何空行,第一组测试数据前面以及最后一组测试数据后面也都没有任何空行。 -
输出说明
对于每一组测试数据,你写的程序要求计算出一组相应的运算结果,并将这一组运算结果作为你所写程序的输出数据依次写入到标准输出设备中。每组运算结果为一个大小为n的阵列,阵列中的数字用一个空格隔开,具体形式请参考输出样例: 当n为个位数时,输出的每个数占1位,当n为两位数时,两位数所在的列输出的每个数占2位(不足2位的左边补空格)。 每组运算结果与其后一组运算结果之间有一个空行,最后一组运算结果之后没有任何空行。 注:通常,显示屏为标准输出设备。 -
输入范例
5
45
10 -
输出范例
51 4
2 343 42 41 40 39 38 37
44 21 20 19 18 17 36
45 22 7 6 5 16 35
23 8 1 4 15 34
24 9 2 3 14 33
25 10 11 12 13 32
26 27 28 29 30 317 6 5
8 1 4
9 2 3
10
解题思路
- 本题思路是构造一个从中心开始逆时针向外扩展的螺旋矩阵。可以把问题理解为在一个 n×n 的二维数组中填入 1 到 n 的数字,起点是矩阵中心位置,1 放在中心,2 放在 1 的下方,然后按照"下 → 右 → 上 → 左"的顺序循环前进,并且每走两次方向后步数增加 1,例如先向下走 1 步,再向右走 1 步,然后向上走 2 步,再向左走 2 步,然后向下走 3 步、向右走 3 步,以此类推,直到填满 n 个数为止。实现时可以先创建一个足够大的 n×n 矩阵初始化为 0,确定中心坐标为 r=n/2,c=n/2(n 为奇数时正好在中间,偶数时按题意自动偏左上),然后用一个方向数组控制移动,依次填入数字,每填一个数就更新行列坐标,当数字填到 n 为止停止。最后按要求输出矩阵,输出时要注意对齐规则:当 n 为个位数时直接输出;当 n 为两位数时,所有数字按宽度 2 右对齐,可以用 setw(2) 控制格式,每组结果之间输出一个空行,最后一组不输出空行。
整体代码
cpp
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
bool first = true;
while(cin >> n){
if(!first) cout << endl;
first = false;
vector<vector<int>> a(n, vector<int>(n, 0));
int r = n / 2;
int c = n / 2;
a[r][c] = 1;
int num = 2;
int step = 1;
int dr[4] = {1, 0, -1, 0}; // 下 右 上 左
int dc[4] = {0, 1, 0, -1};
int dir = 0;
while(num <= n){
for(int t = 0; t < 2; t++){
for(int i = 0; i < step; i++){
if(num > n) break;
r += dr[dir];
c += dc[dir];
if(r >= 0 && r < n && c >= 0 && c < n){
a[r][c] = num++;
}
}
dir = (dir + 1) % 4;
}
step++;
}
int width = (n >= 10 ? 2 : 1);
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(width == 2)
cout << setw(2) << a[i][j];
else
cout << a[i][j];
if(j != n-1) cout << " ";
}
cout << endl;
}
}
return 0;
}注意事项
- 注意不要忘记了break。
饲料调配
属于二维数组的内容
题目
-
问题描述
农夫约翰从来只用调配得最好的饲料来为他的奶牛。
饲料用三种原料调配成:大麦,燕麦和小麦。他知道自己的饲料精确的配比,在市场上是买不到这样的饲料的。他只好购买其他三种混合饲料(同样都由三种麦子组成),然后将它们混合,来调配他的完美饲料。
给出三组整数,表示 大麦:燕麦:小麦 的比例,找出用这三种饲料调配 x:y:z 的饲料的方法。
例如,给出目标饲料 3:4:5 和三种饲料的比例:
1:2:3
3:7:1
2:1:2
你必须编程找出使这三种饲料用量最少的方案,要是不能用这三种饲料调配目标饲料,输出'NONE'。'用量最少'意味着三种饲料的用量(整数)的和必须最小。
对于上面的例子,你可以用8份饲料1,2份饲料2,和5份饲料3,来得到7份目标饲料: 8*(1:2:3) + 1*(3:7:1) + 5*(2:1:2) = (21:28:35) = 7*(3:4:5)
以上数字中,表示饲料比例的整数都是小于100(数量级)的非负整数,表示各种饲料的份数的整数都小于100。一种混合物的比例不会由其他混合物的比例直接相加得到。 -
输入说明
Line 1: 三个用空格分开的整数,表示目标饲料
Line 2...4: 每行包括三个用空格分开的整数,表示农夫约翰买进的饲料的比例 -
输出说明
输出文件要包括一行,这一行要么有四个整数,要么是'NONE'。前三个整数表示三种饲料的份数,用这样的配比可以得到目标饲料。第四个整数表示混合前三种饲料后得到的目标饲料的份数。 -
输入范例
3 4 5
1 2 3
3 7 1
2 1 2 -
输出范例
8 1 5 7
解题思路
- 本题思路是通过枚举三种饲料的使用份数来寻找满足比例关系的最优解。设目标饲料比例为 (x,y,z),三种已知饲料分别为 (a1,b1,c1)、(a2,b2,c2)、(a3,b3,c3),如果分别取 i、j、k 份三种饲料进行混合,则得到的新比例为 A=ia1+ja2+ka3,B=ib1+jb2+kb3,C=ic1+jc2+kc3,如果能够调配成功,那么一定存在一个正整数 t,使得 A=tx,B=ty,C=tz,也就是说三种成分必须同时是目标比例的同一个倍数,因此可以用三重循环枚举 i、j、k(范围 0 到 99,且不能全为 0),每次计算出 A、B、C,然后分别判断三个分量是否满足比例关系:如果目标某一项为 0,则对应混合结果也必须为 0;如果目标某一项不为 0,则混合结果必须能整除目标值,并且三个分量算出的倍数必须相同;只有在三项都满足且倍数 t>0 时才是合法方案。在所有合法方案中选择 i+j+k 最小的那个作为答案,因为题目要求"用量最少"即三种饲料份数之和最小。若最终没有找到任何满足条件的组合,则输出 NONE。
整体代码
cpp
#include <bits/stdc++.h>
using namespace std;
int main(){
int x,y,z;
cin >> x >> y >> z;
int a1,b1,c1;
int a2,b2,c2;
int a3,b3,c3;
cin >> a1 >> b1 >> c1;
cin >> a2 >> b2 >> c2;
cin >> a3 >> b3 >> c3;
int minSum = INT_MAX;
int ansI=0, ansJ=0, ansK=0, ansT=0;
for(int i=0;i<100;i++){
for(int j=0;j<100;j++){
for(int k=0;k<100;k++){
if(i==0 && j==0 && k==0) continue;
int A = i*a1 + j*a2 + k*a3;
int B = i*b1 + j*b2 + k*b3;
int C = i*c1 + j*c2 + k*c3;
int t = -1;
bool ok = true;
int target[3] = {x,y,z};
int mix[3] = {A,B,C};
for(int p=0;p<3;p++){
if(target[p] == 0){
if(mix[p] != 0){
ok = false;
break;
}
}else{
if(mix[p] % target[p] != 0){
ok = false;
break;
}
int temp = mix[p] / target[p];
if(t == -1) t = temp;
else if(t != temp){
ok = false;
break;
}
}
}
if(ok && t > 0){
if(i+j+k < minSum){
minSum = i+j+k;
ansI = i;
ansJ = j;
ansK = k;
ansT = t;
}
}
}
}
}
if(minSum == INT_MAX){
cout << "NONE";
}else{
cout << ansI << " " << ansJ << " " << ansK << " " << ansT;
}
return 0;
}注意事项
- 注意输出的格式。
求小数位数个数
属于字符串的内容
题目
-
问题描述
明明最近在一家软件公司实习,公司分配给他一个任务,要他写一个小程序,这个程序的功能是求出一个浮点数的小数部分的长度。例如程序输入1.1,则输出1,程序输入1.11,则输出2,明明觉得这个非常简单,花了不到5分钟的时间就把程序给写出来了,然后就把程序交给了测试员测试。但是没有想到的是,经过测试员的测试,发现了一大堆的错误,返回的结果很多都是不对的,这个令明明相当的不解,始终想不通自己的程序错在哪里。你是一名经验丰富的程序员,明明把这个问题来求助于你,明明和你说了他的想法,你一听就明白明明错在了哪里,原来明明使用double型来存放浮点数,但是由于double型的精度问题,不可能把所有的小数都精确的保存好,如果小数位数很长,就会出错。你发现了问题。现在请你写出正确的程序。 明明的问题可以归结为:给你一个浮点数,请你求出这个浮点数的小数位数。 -
输入说明
你写的程序要求从标准输入设备中读入测试数据作为你所写程序的输入数据。标准输入设备中有多组测试数据,每组测试数据仅占一行,每行仅包括一个浮点数数n,n的长度不超过100。每组测试数据与其后一组测试数据之间没有任何空行,第一组测试数据前面以及最后一组测试数据后面也都没有任何空行。 -
输出说明
对于每一组测试数据,你写的程序要求计算出一组相应的运算结果,并将这一组运算结果作为你所写程序的输出数据依次写入到标准输出设备中。每组运算结果为一个整数,即n的小数部分的位数。每组运算结果单独形成一行数据,其行首和行尾都没有任何空格,每组运算结果与其后一组运算结果之间没有任何空行,第一组运算结果前面以及最后一组运算结果后面也都没有任何空行。 注:通常,显示屏为标准输出设备。 -
输入范例
1.11
1.00000000000000001 -
输出范例
2
17
解题思路
- 本题思路是不能使用 double 存储浮点数,而是把输入当成字符串处理,因为题目中的数字长度可能达到 100 位,double 会产生精度误差。做法是每次读入一个字符串 s,然后在字符串中查找小数点的位置,如果不存在小数点,说明没有小数部分,直接输出 0;如果存在小数点,就用字符串总长度减去小数点位置再减 1,即 s.length() - pos - 1,得到小数部分的位数并输出即可。
整体代码
cpp
#include <bits/stdc++.h>
using namespace std;
int main(){
string s;
while(cin >> s){
size_t pos = s.find('.');
if(pos == string::npos){
cout << 0 << endl;
}else{
cout << s.length() - pos - 1 << endl;
}
}
return 0;
}注意事项
- 注意"=="和"="之分,不要忘记。
英文段落翻译
自己翻译
电子计算机
在第二次世界大战期间,工作在伦敦的北部的布莱切利园的由科学家和数学家组成的一支队伍创造了第一批全电子数字计算机之一的巨像。在1943年12月,包含了1500个真空管的巨像成为可运行的。他被由艾伦图灵领导的团队使用,在以恩尼格玛破译德国频道信息上有着巨大的贡献。
无独有偶,在英国,约翰阿塔纳索夫和克里福德贝里在早期的1939年建造了一个电子机器样机。这个样机和后来的实验完全沉寂了下来,并且与后来1945年的电子数字积分计算机相比显得相形见拙了。电子数字积分计算机被批准作为一项专利,但这个机器被揭示为含有第一次被使用在AB计算机的规则,它被几十年后在1973年推翻了。
电子积分计算机包含了1万8000个真空管,并且,拥有一个每分钟几百个乘法的速度,但是其程序最初是通过导线传送到处理器内的,并且不得不手动的交替。后来的机器都用了运行存储,并且以美籍匈牙利数学家约翰冯诺依曼呃思想为基础建造。这些指令例如数据都被存储在一个存储器中,把计算机从执行期间纸袋阅读器的速度限制中解放了并且允许没有阅读计算机的情况下解决问题。
AI翻译
3 . 电子计算机
第二次世界大战期间,一个由科学家和数学家组成的团队在位于伦敦北部的布莱切利园,创造了最早的全电子数字计算机之一:巨人计算机。到1943年12月,这台包含1500个真空管的巨人计算机投入使用。它被艾伦·图灵领导的团队用于破解德国用恩尼格玛密码加密的无线电信息,并取得了巨大的成功。
与此独立地,在美国,约翰·阿塔纳索夫和克利福德·贝里于1939年便在爱荷华州立学院研制出了一台电子计算机的原型机。这一原型机及后续研究均悄然完成,其后被1945年问世的电子数字积分计算机(ENIAC)的光芒所掩盖。ENIAC获得了相关专利,但数十年后的1973年,该专利被推翻,因其被证实采用了阿塔纳索夫-贝里计算机中首次使用的原理。
ENIAC(见图1A-1)包含18,000个真空管,运算速度达每分钟数百次乘法,但其程序最初是通过线路连接至处理器,必须手动进行更改。后来的计算机则基于匈牙利裔美国数学家约翰·冯·诺依曼的理念,实现了程序存储功能。指令与数据一同存储在"内存"中,使计算机在执行过程中摆脱了纸带阅读器的速度限制,也使得无需重新布线即可解决不同的问题。
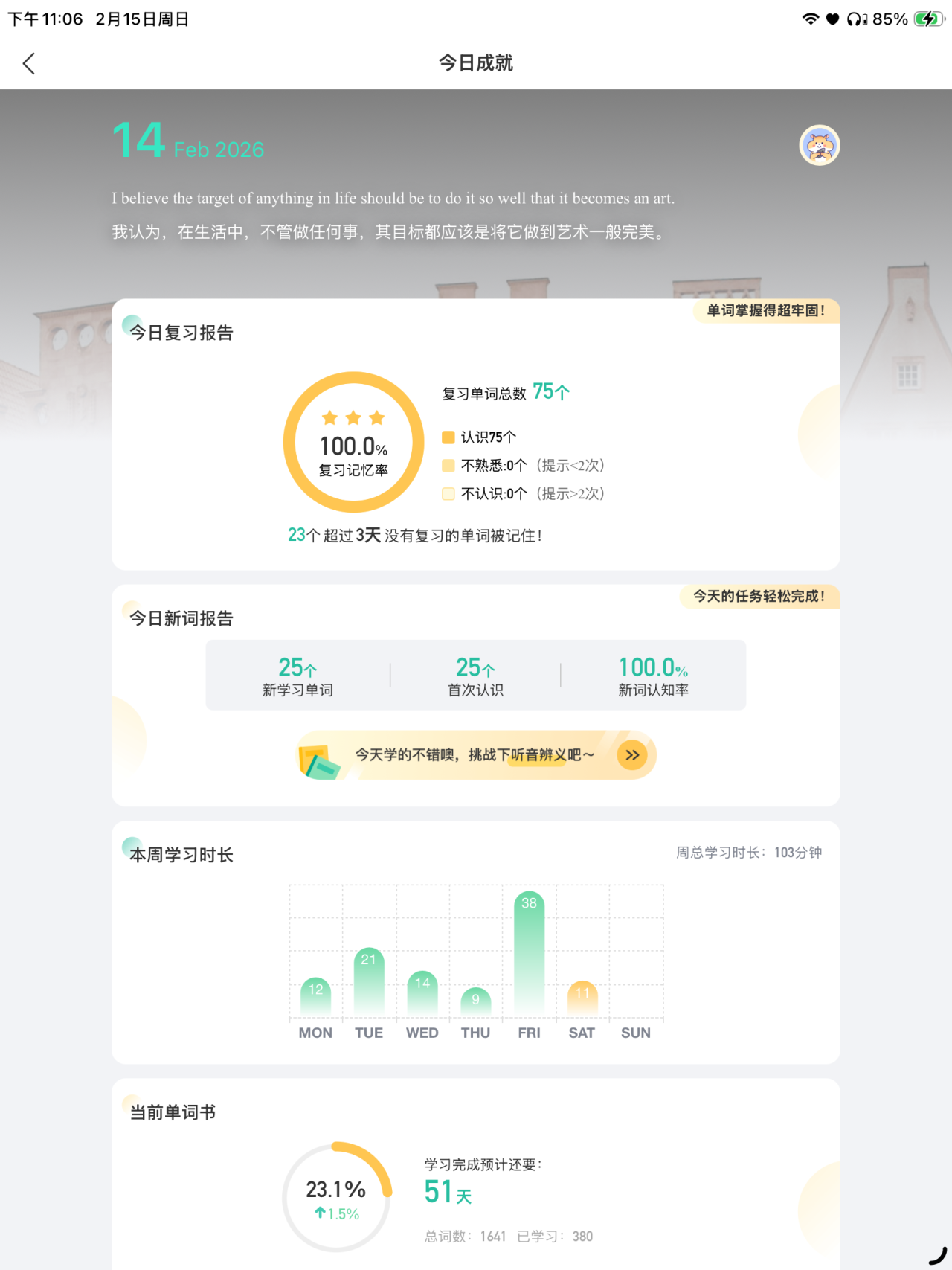
单词打卡
下一篇
待续