文章目录
- [1 串联PID控制原理](#1 串联PID控制原理)
- [2 问题描述](#2 问题描述)
- [3 Simulink仿真程序](#3 Simulink仿真程序)
- [4 Python仿真程序](#4 Python仿真程序)
1 串联PID控制原理
串联PID控制系统的典型结构如下图所示,系统中有两个PID控制器, G c 2 ( s ) G_{c2}(s) Gc2(s)称为副调节器传递函数,包围 G c 2 ( s ) G_{c2}(s) Gc2(s)的内环称为副回路。 G c 1 ( s ) G_{c1}(s) Gc1(s)称为主调节器的传递函数,包含 G c 1 ( s ) G_{c1}(s) Gc1(s)的外环称为主回路。主调节器的输出控制量 u 1 u_1 u1作为副回路的给定量 R 2 ( s ) R_2(s) R2(s)。
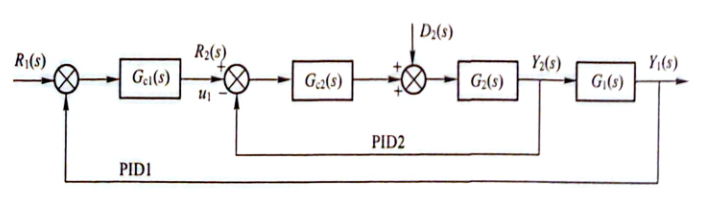
串联PID控制系统的计算顺序是先主回路(PID1),后副回路(PID2)。控制方式有两种:一种是异步采样控制,即主回路的采样控制周期 T 1 T_1 T1是副回路采样控制周期 T 2 T_2 T2的整数倍。这是因为一般串级控制系统中主控对象的响应速度慢、副控对象的响应速度快的缘故。另一种是同步采样控制,即主、副回路的采样控制周期相同。这时,应根据副回路选择采样周期,因为副回路的受控对象的响应速度较快。
PID串级控制的主要优点:
(1)将干扰加到副回路中,由副回路控制对其进行抑制;
(2)副回路中参数的变化,由副回路给于控制,对被控制量 G 1 G_1 G1的影响大为减弱;
(3)副回路的惯性由副回路给于调节,因而提高了整个系统的响应速度。
2 问题描述
设副对象特性为 G 2 ( s ) = 1 T 02 s + 1 G_2(s)=\frac{1}{T_{02}s+1} G2(s)=T02s+11,主对象特性为 G 1 ( s ) = 1 T 01 s + 1 G_1(s)=\frac{1}{T_{01}s+1} G1(s)=T01s+11, T 01 = T 02 = 10 T_{01}=T_{02}=10 T01=T02=10,采样时间为 2 s 2s 2s,外加干扰信号为一幅度为 0.01 0.01 0.01的随机信号 d 2 ( k ) = 0.01 rands ( 1 ) d_2(k)=0.01\text{rands}(1) d2(k)=0.01rands(1)。
3 Simulink仿真程序
按串级PID控制的基本原理,采用Simulink进行编程,在连续方式下进行仿真。主调节器采用PI控制,取 k p = 50 k_p=50 kp=50, k i = 5 k_i=5 ki=5,副调节器采用P控制,取 k p = 5 k_p=5 kp=5。
(1)当切换到单级PID时,控制效果如下:
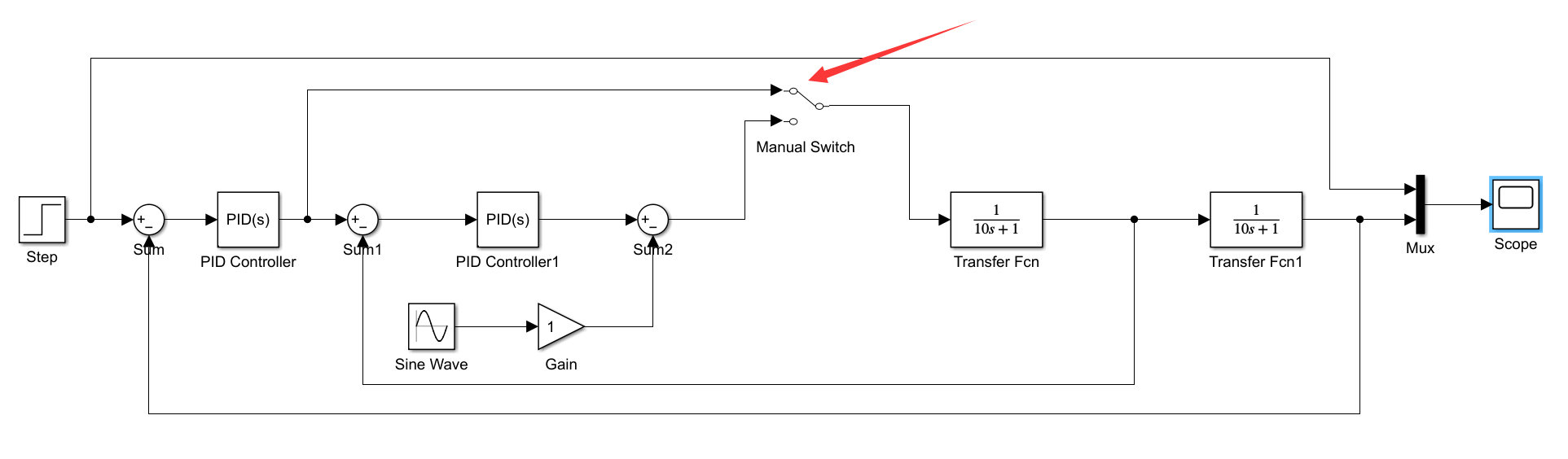
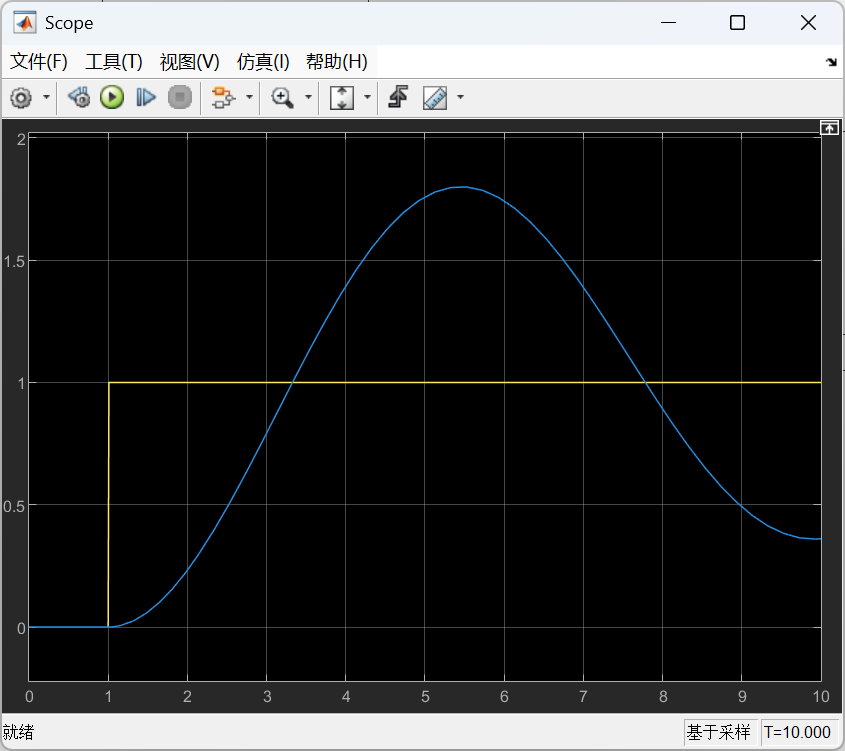
黄色线是理想输出,蓝色线是控制输出,蓝色线波动较大,控制效果较差。
(2)当切换到串级PID时,控制效果如下:
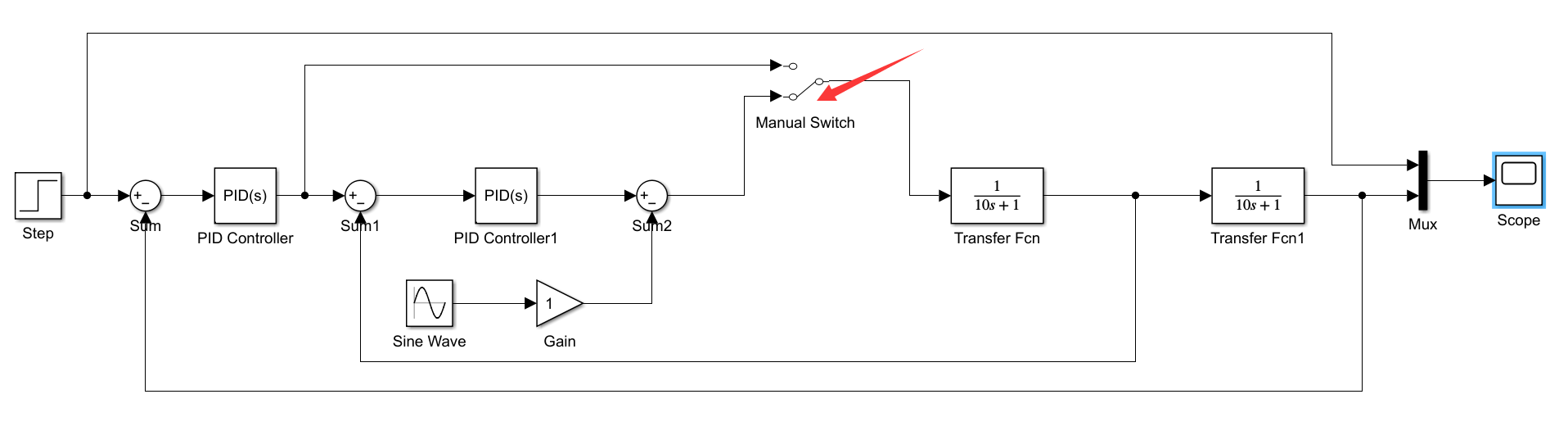
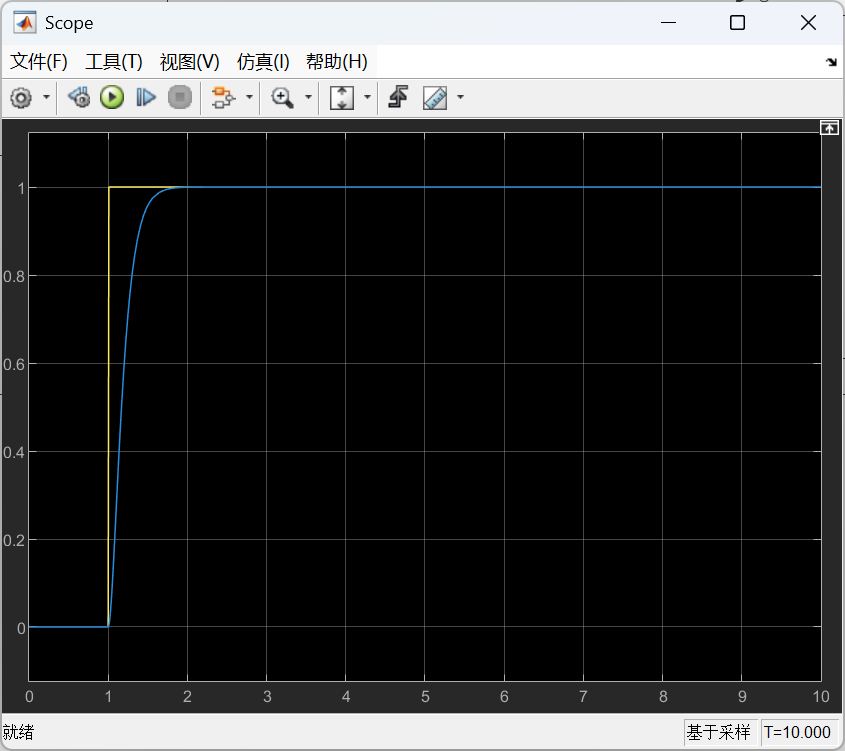
黄色线是理想输出,蓝色线是控制输出,蓝色线波动较小,控制效果较好。
4 Python仿真程序
(1)仿真结果
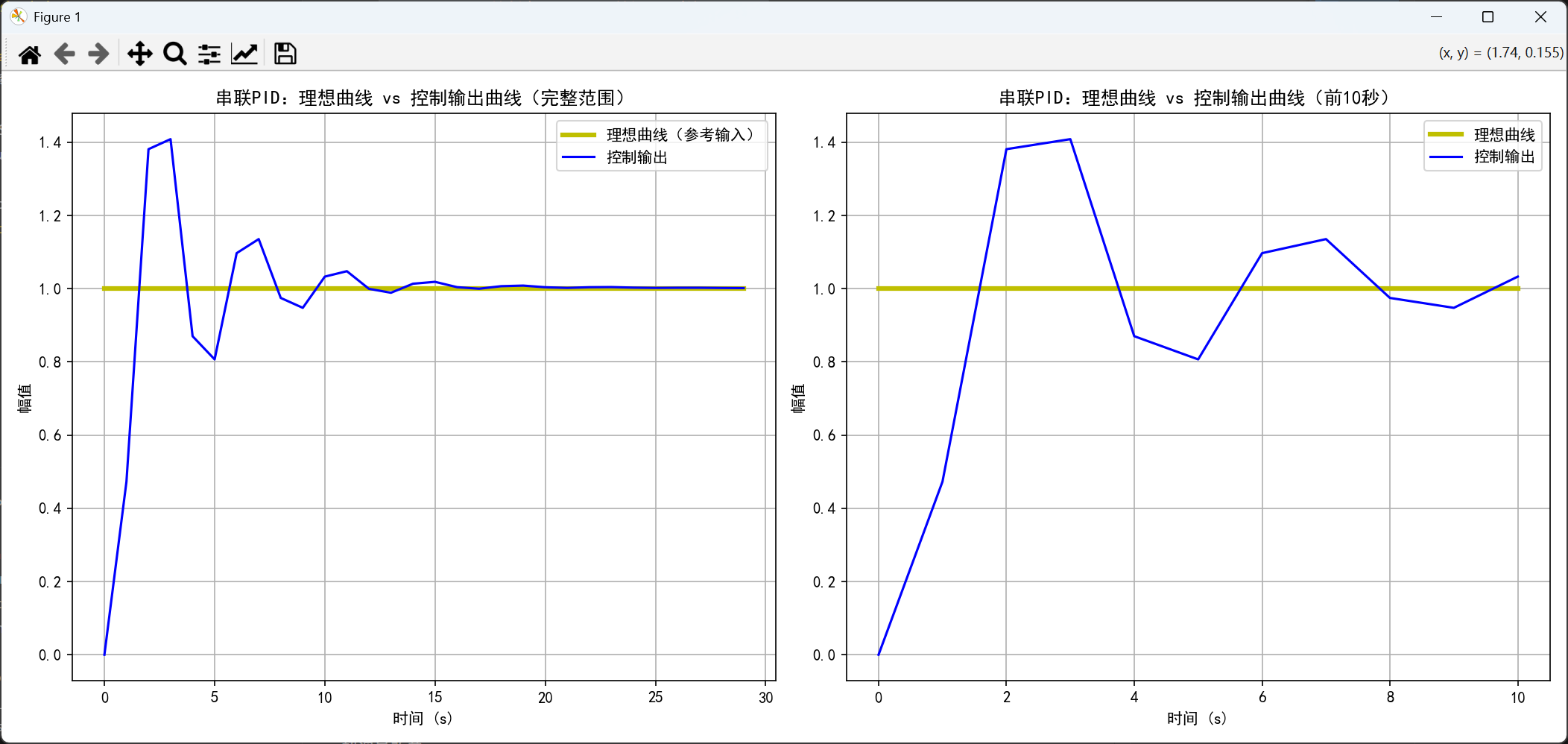
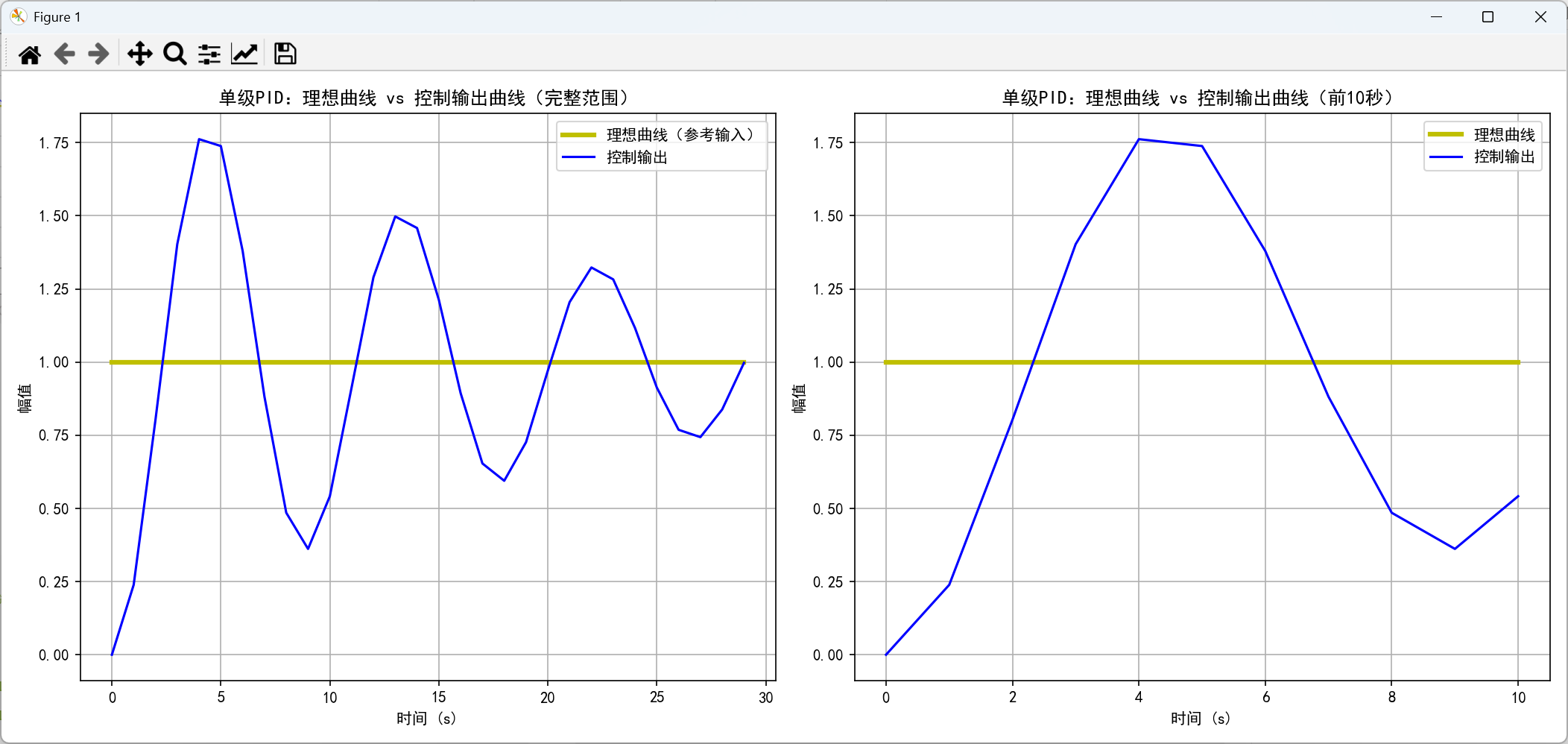
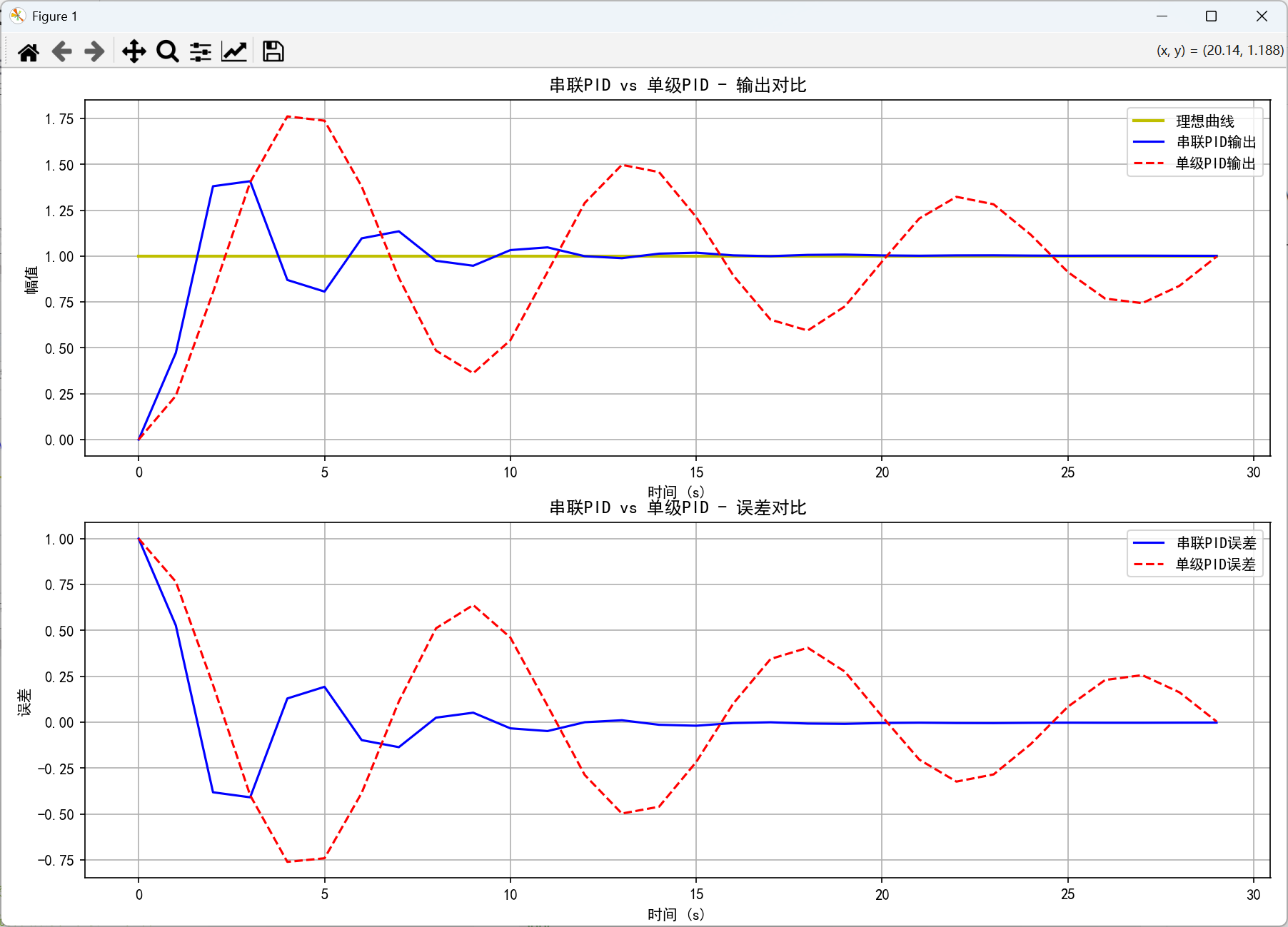

(2)仿真程序
python
"""
串联PID控制系统仿真 - 采样时间0.01秒完整版本
基于博客:Python控制系统仿真案例-串联PID控制
系统描述:
- 主对象:G1(s) = 1/(T01*s + 1), T01 = 10
- 副对象:G2(s) = 1/(T02*s + 1), T02 = 10
- 采样时间:0.01秒
- 干扰信号:d2(k) = 0.01 * random()
- 主调节器:PI控制,kp=50, ki=5
- 副调节器:P控制,kp=5
"""
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
class CascadePIDController:
"""串联PID控制器类"""
def __init__(self, kp_main=50, ki_main=5, kp_secondary=5):
"""
初始化串联PID控制器
参数:
kp_main: 主调节器比例系数
ki_main: 主调节器积分系数
kp_secondary: 副调节器比例系数
"""
self.kp_main = kp_main
self.ki_main = ki_main
self.kp_secondary = kp_secondary
# 主调节器积分项累积
self.integral_main = 0
# 存储历史数据用于绘图
self.time_history = []
self.reference_history = []
self.output_history = []
self.error_main_history = []
self.error_secondary_history = []
self.u_main_history = []
self.u_secondary_history = []
self.disturbance_history = []
def update(self, t, reference, output_primary, output_secondary, dt):
"""
更新控制器输出
参数:
t: 当前时间
reference: 主回路参考输入
output_primary: 主对象输出
output_secondary: 副对象输出
dt: 采样时间
返回:
u_secondary: 副调节器输出(最终控制量)
"""
# 1. 主回路计算
error_main = reference - output_primary
# 主调节器PI控制
self.integral_main += error_main * dt
# 积分限幅防止积分饱和(针对小采样时间调整)
integral_limit = 2.0
if self.integral_main > integral_limit:
self.integral_main = integral_limit
elif self.integral_main < -integral_limit:
self.integral_main = -integral_limit
u_main = self.kp_main * error_main + self.ki_main * self.integral_main
# 主调节器输出限幅
u_main_limit = 100.0
if u_main > u_main_limit:
u_main = u_main_limit
elif u_main < -u_main_limit:
u_main = -u_main_limit
# 2. 副回路计算
# 主调节器输出作为副回路的参考输入
reference_secondary = u_main
error_secondary = reference_secondary - output_secondary
# 副调节器P控制
u_secondary = self.kp_secondary * error_secondary
# 副调节器输出限幅
u_secondary_limit = 100.0
if u_secondary > u_secondary_limit:
u_secondary = u_secondary_limit
elif u_secondary < -u_secondary_limit:
u_secondary = -u_secondary_limit
# 存储历史数据(每100个点存储一次,避免数据量过大)
if len(self.time_history) == 0 or t - self.time_history[-1] >= 1.0: # 每秒存储一次
self.time_history.append(t)
self.reference_history.append(reference)
self.output_history.append(output_primary)
self.error_main_history.append(error_main)
self.error_secondary_history.append(error_secondary)
self.u_main_history.append(u_main)
self.u_secondary_history.append(u_secondary)
return u_secondary
def add_disturbance(self, disturbance, t):
"""添加干扰信号到历史记录"""
if len(self.disturbance_history) == 0 or t - self.time_history[-1] >= 1.0:
self.disturbance_history.append(disturbance)
def plot_ideal_vs_control(self, title="串联PID控制"):
"""绘制理想曲线和控制输出曲线的对比"""
time_array = np.array(self.time_history)
reference_array = np.array(self.reference_history)
output_array = np.array(self.output_history)
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# 1. 完整时间范围的对比
ax = axes[0]
ax.plot(time_array, reference_array, 'y-', linewidth=3, label='理想曲线(参考输入)')
ax.plot(time_array, output_array, 'b-', linewidth=1.5, label='控制输出')
ax.set_xlabel('时间 (s)')
ax.set_ylabel('幅值')
ax.set_title(f'{title}:理想曲线 vs 控制输出曲线(完整范围)')
ax.legend()
ax.grid(True)
# 2. 前10秒的放大对比(更清晰)
ax = axes[1]
# 找到前10秒的数据点索引
idx_10s = np.where(time_array <= 10)[0]
if len(idx_10s) > 0:
ax.plot(time_array[idx_10s], reference_array[idx_10s], 'y-', linewidth=3, label='理想曲线')
ax.plot(time_array[idx_10s], output_array[idx_10s], 'b-', linewidth=1.5, label='控制输出')
ax.set_xlabel('时间 (s)')
ax.set_ylabel('幅值')
ax.set_title(f'{title}:理想曲线 vs 控制输出曲线(前10秒)')
ax.legend()
ax.grid(True)
else:
# 如果仿真时间小于10秒,显示全部
ax.plot(time_array, reference_array, 'y-', linewidth=3, label='理想曲线')
ax.plot(time_array, output_array, 'b-', linewidth=1.5, label='控制输出')
ax.set_xlabel('时间 (s)')
ax.set_ylabel('幅值')
ax.set_title(f'{title}:理想曲线 vs 控制输出曲线')
ax.legend()
ax.grid(True)
plt.tight_layout()
plt.show()
return time_array, reference_array, output_array
class Plant:
"""被控对象类"""
def __init__(self, T01=10, T02=10):
"""
初始化被控对象
参数:
T01: 主对象时间常数
T02: 副对象时间常数
"""
self.T01 = T01
self.T02 = T02
# 状态变量
self.x1 = 0 # 主对象状态
self.x2 = 0 # 副对象状态
def update(self, u, disturbance=0, dt=0.01):
"""
更新对象状态
参数:
u: 控制输入
disturbance: 干扰信号
dt: 采样时间
返回:
x1: 主对象输出
x2: 副对象输出
"""
# 副对象:G2(s) = 1/(T02*s + 1)
# 离散化:使用前向欧拉法
dx2 = (u + disturbance - self.x2) / self.T02
self.x2 += dx2 * dt
# 主对象:G1(s) = 1/(T01*s + 1)
# 输入是副对象输出
dx1 = (self.x2 - self.x1) / self.T01
self.x1 += dx1 * dt
return self.x1, self.x2
def simulate_cascade_pid(simulation_time=30, dt=0.01, add_disturbance=True):
"""
运行串联PID仿真
参数:
simulation_time: 仿真时间
dt: 采样时间
add_disturbance: 是否添加干扰
返回:
controller: 控制器对象
plant: 被控对象对象
"""
# 初始化控制器和被控对象
controller = CascadePIDController(kp_main=50, ki_main=5, kp_secondary=5)
plant = Plant(T01=10, T02=10)
# 参考信号(阶跃信号)
reference = 1.0
# 仿真循环
step_count = int(simulation_time / dt)
for i in range(step_count):
t = i * dt
# 获取当前输出
output_primary, output_secondary = plant.x1, plant.x2
# 生成干扰信号
if add_disturbance:
disturbance = 0.01 * (2 * np.random.random() - 1) # 幅度0.01的随机信号
else:
disturbance = 0
# 更新控制器
u = controller.update(t, reference, output_primary, output_secondary, dt)
# 添加干扰到历史记录
controller.add_disturbance(disturbance, t)
# 更新被控对象
plant.update(u, disturbance, dt)
return controller, plant
def simulate_single_pid(simulation_time=30, dt=0.01, add_disturbance=True):
"""
运行单级PID仿真(用于对比)
参数:
simulation_time: 仿真时间
dt: 采样时间
add_disturbance: 是否添加干扰
返回:
controller: 控制器对象
"""
# 单级PID参数(使用主调节器参数)
kp = 50
ki = 5
# 创建控制器对象来存储结果
controller = CascadePIDController(kp_main=kp, ki_main=ki, kp_secondary=0)
# 初始化状态
integral = 0
x1 = 0
x2 = 0
T01 = 10
T02 = 10
# 参考信号
reference = 1.0
# 仿真循环
step_count = int(simulation_time / dt)
for i in range(step_count):
t = i * dt
# 计算误差
error = reference - x1
# PID控制(只有PI部分)
integral += error * dt
u = kp * error + ki * integral
# 生成干扰信号
if add_disturbance:
disturbance = 0.01 * (2 * np.random.random() - 1)
else:
disturbance = 0
# 更新被控对象
# 副对象
dx2 = (u + disturbance - x2) / T02
x2 += dx2 * dt
# 主对象
dx1 = (x2 - x1) / T01
x1 += dx1 * dt
# 存储历史数据(每秒存储一次)
if len(controller.time_history) == 0 or t - controller.time_history[-1] >= 1.0:
controller.time_history.append(t)
controller.reference_history.append(reference)
controller.output_history.append(x1)
controller.error_main_history.append(error)
controller.u_main_history.append(u)
controller.add_disturbance(disturbance, t)
return controller
def calculate_performance_metrics(time_array, output_array, reference=1.0):
"""计算性能指标"""
error_array = reference - output_array
# 稳态误差(最后5秒的平均值)
steady_start_idx = np.where(time_array >= time_array[-1] - 5)[0]
if len(steady_start_idx) > 0:
steady_error = np.mean(np.abs(error_array[steady_start_idx]))
else:
steady_error = np.mean(np.abs(error_array[-100:])) # 最后100个点
# 超调量
max_output = np.max(output_array)
overshoot = (max_output - reference) * 100 if max_output > reference else 0
# 调节时间(进入±2%误差带的时间)
error_band = 0.02
settling_idx = np.where(np.abs(error_array) <= error_band)[0]
if len(settling_idx) > 0:
settling_time = time_array[settling_idx[0]]
else:
settling_time = None
# 上升时间(从10%到90%)
idx_10 = np.where(output_array >= 0.1 * reference)[0]
idx_90 = np.where(output_array >= 0.9 * reference)[0]
if len(idx_10) > 0 and len(idx_90) > 0:
rise_time = time_array[idx_90[0]] - time_array[idx_10[0]]
else:
rise_time = None
return {
'steady_error': steady_error,
'overshoot': overshoot,
'settling_time': settling_time,
'rise_time': rise_time
}
def main():
"""主函数"""
print("串联PID控制系统仿真 - 采样时间0.01秒")
print("=" * 60)
# 运行串联PID仿真
print("运行串联PID仿真...")
cascade_controller, cascade_plant = simulate_cascade_pid(
simulation_time=30,
dt=0.01,
add_disturbance=True
)
# 显示理想曲线和控制输出曲线对比
print("绘制理想曲线 vs 控制输出曲线对比...")
cascade_time, cascade_ref, cascade_output = cascade_controller.plot_ideal_vs_control("串联PID")
# 运行单级PID仿真
print("\n运行单级PID仿真...")
single_controller = simulate_single_pid(
simulation_time=30,
dt=0.01,
add_disturbance=True
)
# 显示单级PID的理想曲线和控制输出曲线对比
single_time, single_ref, single_output = single_controller.plot_ideal_vs_control("单级PID")
# 绘制两种控制策略的对比图
print("\n绘制串联PID vs 单级PID对比图...")
fig, axes = plt.subplots(2, 1, figsize=(12, 10))
# 1. 输出对比
ax = axes[0]
ax.plot(cascade_time, cascade_ref, 'y-', linewidth=2, label='理想曲线')
ax.plot(cascade_time, cascade_output, 'b-', linewidth=1.5, label='串联PID输出')
ax.plot(single_time, single_output, 'r--', linewidth=1.5, label='单级PID输出')
ax.set_xlabel('时间 (s)')
ax.set_ylabel('幅值')
ax.set_title('串联PID vs 单级PID - 输出对比')
ax.legend()
ax.grid(True)
# 2. 误差对比
ax = axes[1]
cascade_error = np.array(cascade_controller.error_main_history)
single_error = np.array(single_controller.error_main_history)
ax.plot(cascade_time, cascade_error, 'b-', linewidth=1.5, label='串联PID误差')
ax.plot(single_time, single_error, 'r--', linewidth=1.5, label='单级PID误差')
ax.set_xlabel('时间 (s)')
ax.set_ylabel('误差')
ax.set_title('串联PID vs 单级PID - 误差对比')
ax.legend()
ax.grid(True)
plt.tight_layout()
plt.show()
# 计算性能指标
print("\n性能指标对比:")
print("-" * 50)
cascade_metrics = calculate_performance_metrics(cascade_time, cascade_output)
single_metrics = calculate_performance_metrics(single_time, single_output)
print(f"串联PID性能指标:")
print(f" 稳态误差: {cascade_metrics['steady_error']:.6f}")
print(f" 超调量: {cascade_metrics['overshoot']:.2f}%")
if cascade_metrics['settling_time']:
print(f" 调节时间(±2%): {cascade_metrics['settling_time']:.2f}s")
if cascade_metrics['rise_time']:
print(f" 上升时间: {cascade_metrics['rise_time']:.2f}s")
print(f"\n单级PID性能指标:")
print(f" 稳态误差: {single_metrics['steady_error']:.6f}")
print(f" 超调量: {single_metrics['overshoot']:.2f}%")
if single_metrics['settling_time']:
print(f" 调节时间(±2%): {single_metrics['settling_time']:.2f}s")
if single_metrics['rise_time']:
print(f" 上升时间: {single_metrics['rise_time']:.2f}s")
# 性能改进百分比
error_improvement = (single_metrics['steady_error'] - cascade_metrics['steady_error']) / single_metrics['steady_error'] * 100
overshoot_improvement = (single_metrics['overshoot'] - cascade_metrics['overshoot']) / single_metrics['overshoot'] * 100 if single_metrics['overshoot'] > 0 else 0
print(f"\n性能改进(串联PID相对于单级PID):")
print(f" 稳态误差改善: {error_improvement:.1f}%")
print(f" 超调量改善: {overshoot_improvement:.1f}%")
print("\n仿真完成!")
if __name__ == "__main__":
main()