一、K-means算法
聚类算法之一。
1、算法过程
- 随机猜测聚类中心位置
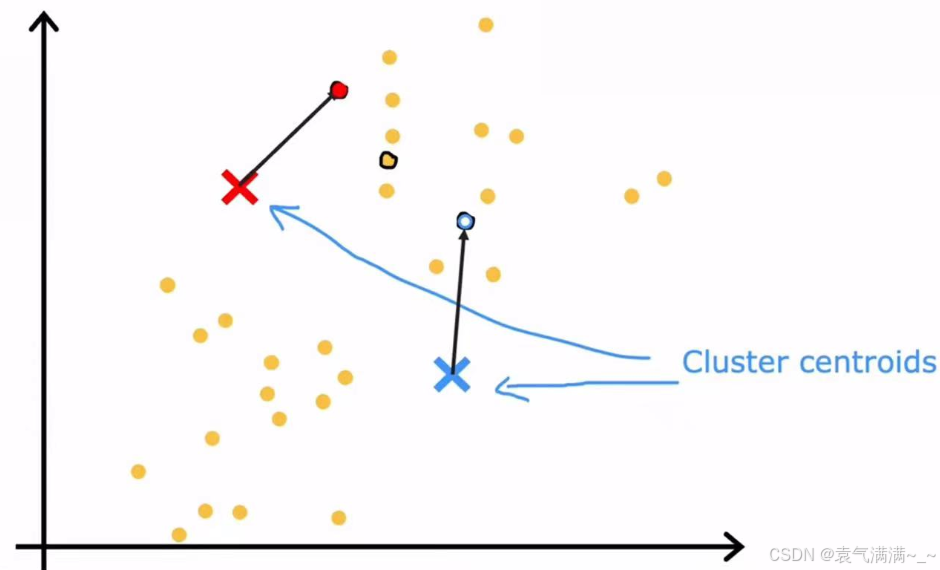
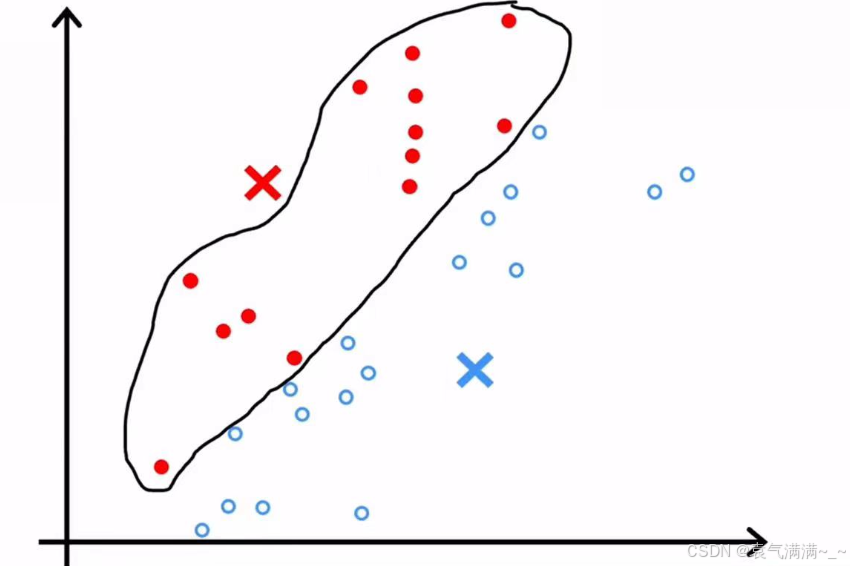
- 根据样本距离聚类中心的长度来分配样本
python
def find_closest_centroids(X, centroids):
K = centroids.shape[0]
idx = np.zeros(X.shape[0], dtype=int)
for i in range(X.shape[0]):
distance = []
for j in range(centroids.shape[0]):
norm_ij = np.linalg.norm(X[i] - centroids[j])
distance.append(norm_ij)
idx[i] = np.argmin(distance)
return idx- 查看聚类中心所分配的样本并取平均值,将该聚类中心移动至平均位置
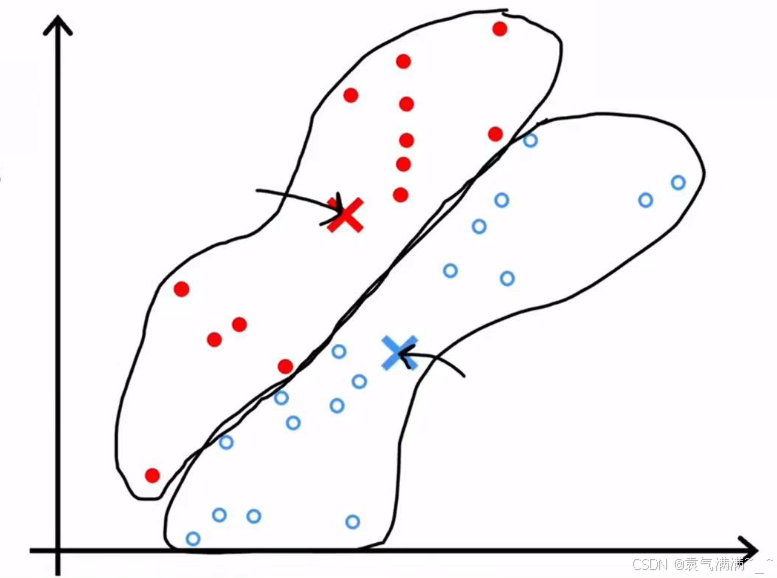
python
def compute_centroids(X, idx, K):
m, n = X.shape
centroids = np.zeros((K, n))
for k in range(K):
points = X[idx==k]
centroids[k] = np.mean(points,axis = 0)
return centroids- 重复2、3步直至聚类中心不在明显变化,表明该算法已收敛
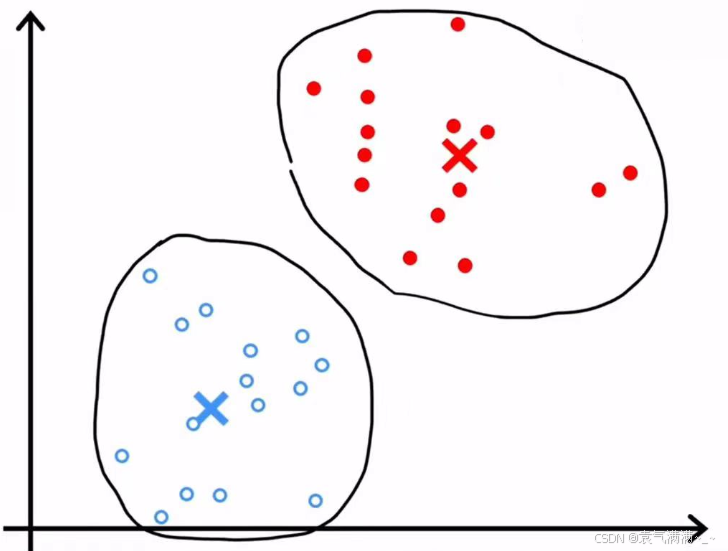
2、优化
K-means算法的迭代过程实际上是在优化一个特定的数学目标,即最小化代价函数。
2.1 K-means算法的代价函数(失真函数)
2.2 优化
- 分配:在保持聚类中心 μ 不变的情况下,通过调整每个样本点的归属
来最小化 J。
- 移动:在保持样本归属 c 不变的情况下,通过调整聚类中心
的位置来最小化 J。当
为该簇内所有点的平均值,可以使与该簇相关的平方和项最小。
K-means算法中一个常用的初始化方法是从 m 个训练样本中随机选择 K 个,并将这 K 个样本的位置作为初始的聚类中心位置。
python
def kMeans_init_centroids(X, K):
randidx = np.random.permutation(X.shape[0])
centroids = X[randidx[:K]]
return centroids由于不同的随机初始化可能会导致算法收敛到不同的聚类结果,其中一些可能不是全局最优解。
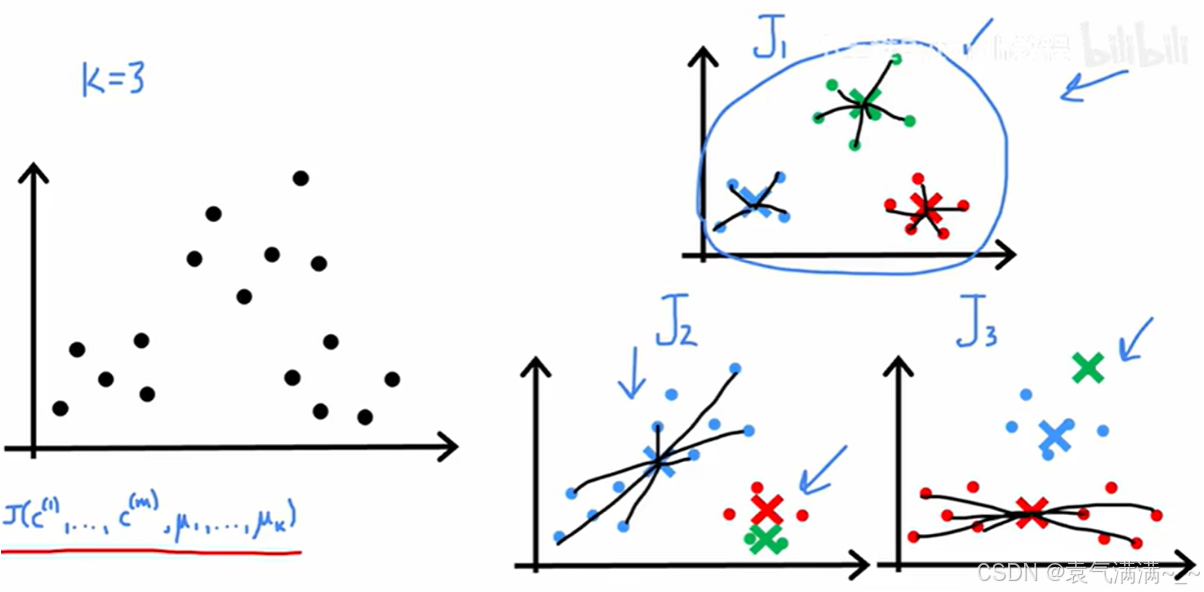
针对不是全局最优解,我们可以通过以下步骤来解决:
- 多次运行该算法(通常是50到1000次)
- 在每次运行中,都使用一组新的随机初始化的聚类中心
- 对每一次运行得到的聚类结果,计算其代价函数
J - 最后,选择所有运行中代价最小的那一组聚类结果作为最终答案。
选择最佳聚类数量K的方法:
- 肘部法则 (Elbow Method)
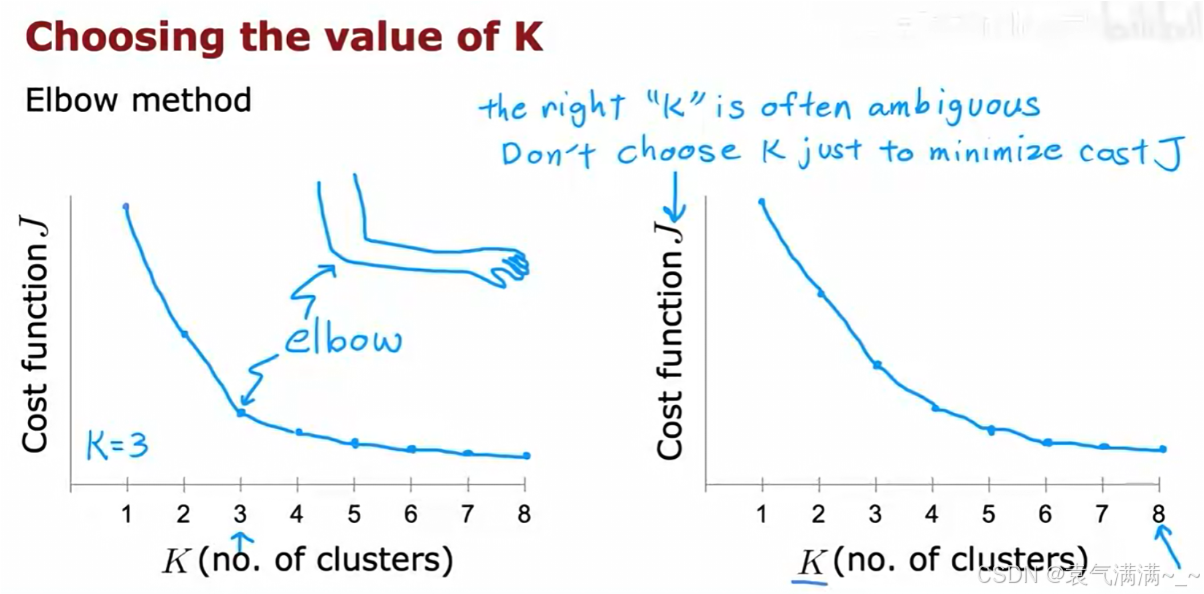
- 分别用不同的 K 值(例如从1到10)运行K-均值算法,并计算出每个 K 值对应的最低代价 J。然后,将 J 与 K 的关系绘制成图。
- 随着 K 的增加,代价 J 总是会下降。我们寻找的是图中的"肘部"(Elbow),即 J 值急剧下降后变得平缓的那个点。这个点通常被认为是 K 的一个合理选择。
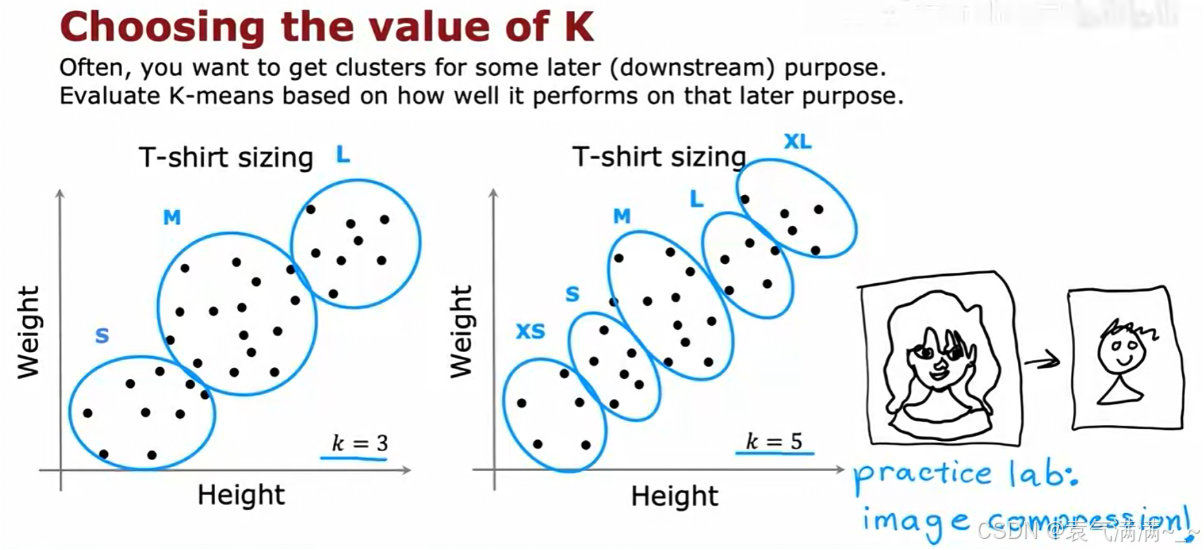
- 评估下游指标
- eg:在T恤尺码的例子中,可以看我们需要几个尺码,需要几个就让K等于几。
3、练习
python
# 使用K-means算法压缩图片
import numpy as np
import matplotlib.pyplot as plt
from utils import *
%matplotlib inline
def find_closest_centroids(X, centroids):
K = centroids.shape[0]
idx = np.zeros(X.shape[0], dtype=int)
for i in range(X.shape[0]):
distance = []
for j in range(centroids.shape[0]):
norm_ij = np.linalg.norm(X[i] - centroids[j])
distance.append(norm_ij)
idx[i] = np.argmin(distance)
return idx
def compute_centroids(X, idx, K):
m, n = X.shape
centroids = np.zeros((K, n))
for k in range(K):
points = X[idx==k]
centroids[k] = np.mean(points,axis = 0)
return centroids
def run_kMeans(X, initial_centroids, max_iters=10, plot_progress=False):
m, n = X.shape
K = initial_centroids.shape[0]
centroids = initial_centroids
previous_centroids = centroids
idx = np.zeros(m)
for i in range(max_iters):
print("K-Means iteration %d/%d" % (i, max_iters-1))
idx = find_closest_centroids(X, centroids)
if plot_progress:
plot_progress_kMeans(X, centroids, previous_centroids, idx, K, i)
previous_centroids = centroids
centroids = compute_centroids(X, idx, K)
plt.show()
return centroids, idx
def kMeans_init_centroids(X, K):
randidx = np.random.permutation(X.shape[0])
centroids = X[randidx[:K]]
return centroids
original_img = plt.imread('bird_small.png')
plt.imshow(original_img)
print("Shape of original_img is:", original_img.shape)
# 使所有的值在 0 - 1 之间
original_img = original_img / 255
X_img = np.reshape(original_img, (original_img.shape[0] * original_img.shape[1], 3))
K = 16
max_iters = 10
initial_centroids = kMeans_init_centroids(X_img, K)
centroids, idx = run_kMeans(X_img, initial_centroids, max_iters)
print("Shape of idx:", idx.shape)
print("Closest centroid for the first five elements:", idx[:5])
# 用索引表示图像
X_recovered = centroids[idx, :]
# 将恢复的图像重塑为合适的尺寸
X_recovered = np.reshape(X_recovered, original_img.shape)
# 原始图像
fig, ax = plt.subplots(1,2, figsize=(8,8))
plt.axis('off')
ax[0].imshow(original_img*255)
ax[0].set_title('Original')
ax[0].set_axis_off()
# 压缩图像
ax[1].imshow(X_recovered*255)
ax[1].set_title('Compressed with %d colours'%K)
ax[1].set_axis_off() 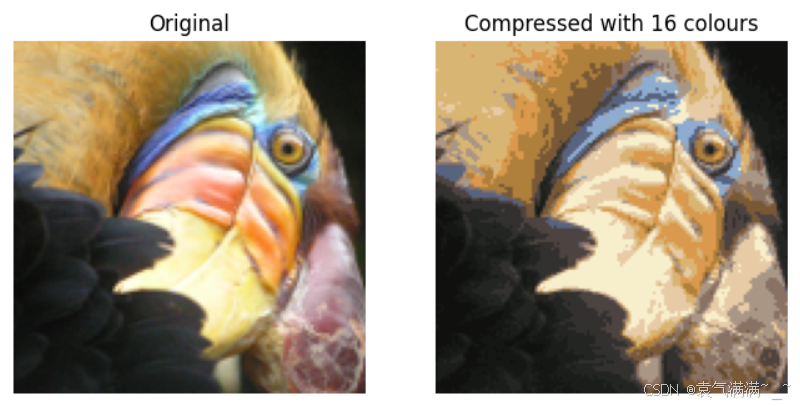
二、异常检测
1、算法过程
- 选择可能指示异常样本的特征
- 确定选择的特征后,为数据集的n个特征拟合参数
,相关公式如下:
python
def estimate_gaussian(X):
m, n = X.shape
mu = 1 / m * np.sum(X,axis=0)
var = 1 / m * np.sum((X-mu)**2,axis=0)
return mu, var # mu是所有特征的平均值,var是所有特征的方差- 计算新样本
的p(x),如果
,则标为异常
python
# 寻找最佳阈值
def select_threshold(y_val, p_val): # y_val验证集的真实值,p_val是验证集的预测结果
best_epsilon = 0
best_F1 = 0
F1 = 0
step_size = (max(p_val) - min(p_val)) / 1000
for epsilon in np.arange(min(p_val), max(p_val), step_size):
predictions = (p_val < epsilon)
tp = np.sum((predictions == 1) & (y_val == 1))
fp = np.sum((predictions == 1) & (y_val == 0))
fn = np.sum((predictions == 0) & (y_val == 1))
prec = tp / (tp +fp)
rec = tp / (tp + fn)
F1 = 2 * prec * rec / (prec + rec)
if F1 > best_F1:
best_F1 = F1
best_epsilon = epsilon
return best_epsilon, best_F1 # 最佳阈值,最佳阈值的F1分数2、算法评估
数据集划分:
- 训练集:包含大量的正常样本(
y=0),用于学习概率模型p(x)。 - 交叉验证集和测试集:包含大量的正常样本(
y=0),并混入一小部分已知的异常样本(y=1)。
评估:
- 精确率、召回率、F1分数
- 超参数调优:在训练集上拟合好
p(x)模型后,我们在交叉验证集上尝试不同的阈值ε,并选择那个能够使F1分数最高的ε作为最终的参数
3、对比
|-------------------|-------------------|
| 异常检测 | 监督学习 |
| 适合正样本(异常样本)数量少的 | 适合正负样本都充足的 |
| 适合异常类型多样的 | 适合正样本有共性的 |
| 应用案例:欺诈检测、数据中心监控等 | 应用案例:垃圾邮件分类、天气预测等 |
异常检测可以识别未来可能出现的新情况新异常,而监督学习没办法识别未来可能出现的新类别。
4、练习
python
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
X_train = np.load("data/X_part1.npy")
X_val = np.load("data/X_val_part1.npy")
y_val = np.load("data/y_val_part1.npy")
print ('The shape of X_train is:', X_train.shape)
print ('The shape of X_val is:', X_val.shape)
print ('The shape of y_val is: ', y_val.shape)
# 可视化初始数据
plt.scatter(X_train[:, 0], X_train[:, 1], marker='x', c='b')
plt.ylabel('Throughput (mb/s)')
plt.xlabel('Latency (ms)')
plt.axis([0, 30, 0, 30])
plt.show()
def estimate_gaussian(X):
m, n = X.shape
mu = 1 / m * np.sum(X,axis=0)
var = 1 / m * np.sum((X-mu)**2,axis=0)
return mu, var
mu, var = estimate_gaussian(X_train)
print("Mean of each feature:", mu)
print("Variance of each feature:", var)
def multivariate_gaussian(X, mu, var):
k = len(mu)
if var.ndim == 1:
var = np.diag(var)
X = X - mu
p = (2* np.pi)**(-k/2) * np.linalg.det(var)**(-0.5) * \
np.exp(-0.5 * np.sum(np.matmul(X, np.linalg.pinv(var)) * X, axis=1))
return p
p = multivariate_gaussian(X_train, mu, var)
def visualize_fit(X, mu, var):
X1, X2 = np.meshgrid(np.arange(0, 35.5, 0.5), np.arange(0, 35.5, 0.5))
Z = multivariate_gaussian(np.stack([X1.ravel(), X2.ravel()], axis=1), mu, var)
Z = Z.reshape(X1.shape)
plt.plot(X[:, 0], X[:, 1], 'bx')
if np.sum(np.isinf(Z)) == 0:
plt.contour(X1, X2, Z, levels=10**(np.arange(-20., 1, 3)), linewidths=1)
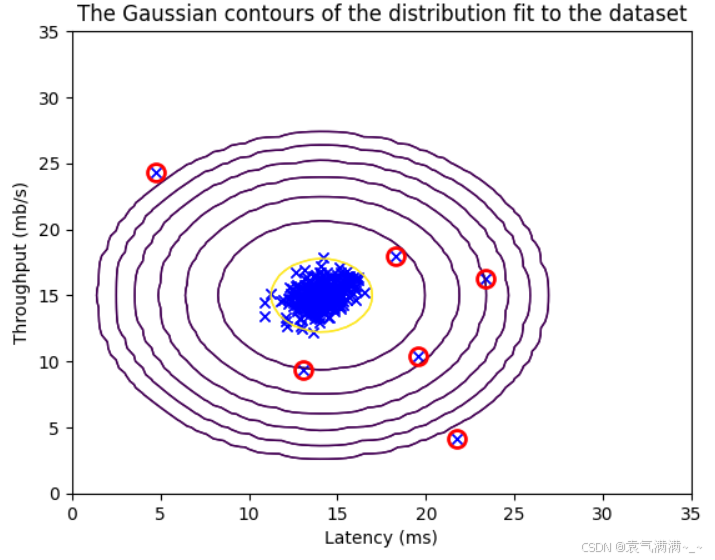
plt.title("The Gaussian contours of the distribution fit to the dataset")
plt.ylabel('Throughput (mb/s)')
plt.xlabel('Latency (ms)')
visualize_fit(X_train, mu, var)
def select_threshold(y_val, p_val):
best_epsilon = 0
best_F1 = 0
F1 = 0
step_size = (max(p_val) - min(p_val)) / 1000
for epsilon in np.arange(min(p_val), max(p_val), step_size):
predictions = (p_val < epsilon)
tp = np.sum((predictions == 1) & (y_val == 1))
fp = np.sum((predictions == 1) & (y_val == 0))
fn = np.sum((predictions == 0) & (y_val == 1))
prec = tp / (tp +fp)
rec = tp / (tp + fn)
F1 = 2 * prec * rec / (prec + rec)
if F1 > best_F1:
best_F1 = F1
best_epsilon = epsilon
return best_epsilon, best_F1
p_val = multivariate_gaussian(X_val, mu, var)
epsilon, F1 = select_threshold(y_val, p_val)
print('Best epsilon found using cross-validation: %e' % epsilon)
print('Best F1 on Cross Validation Set: %f' % F1)
outliers = p < epsilon
visualize_fit(X_train, mu, var)
plt.plot(X_train[outliers, 0], X_train[outliers, 1], 'ro', markersize= 10,markerfacecolor='none', markeredgewidth=2)
print("异常个数:%d" % np.sum(outliers))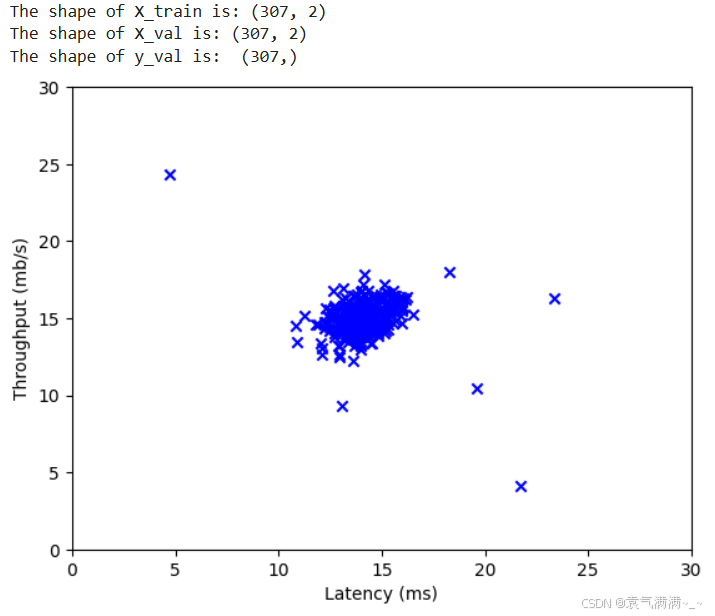

三、推荐系统
1、协同过滤算法
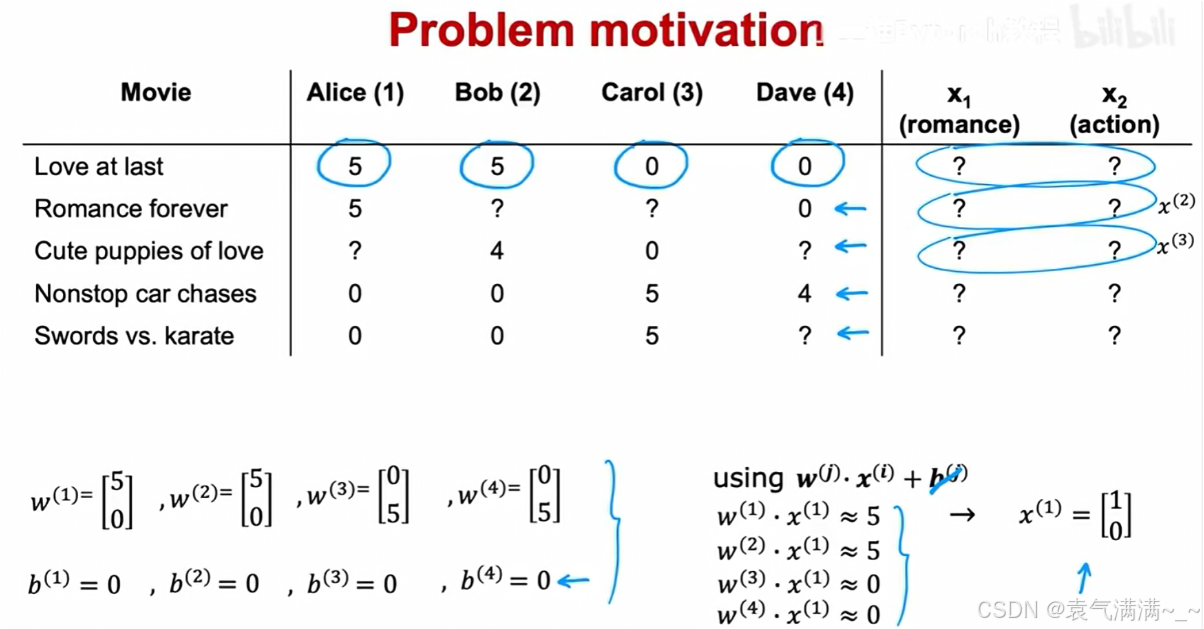
协同过滤算法就是同时学习电影特征x和用户参数w、b。
一个用户对多个电影预测w、b,多个用户对一个电影求x。
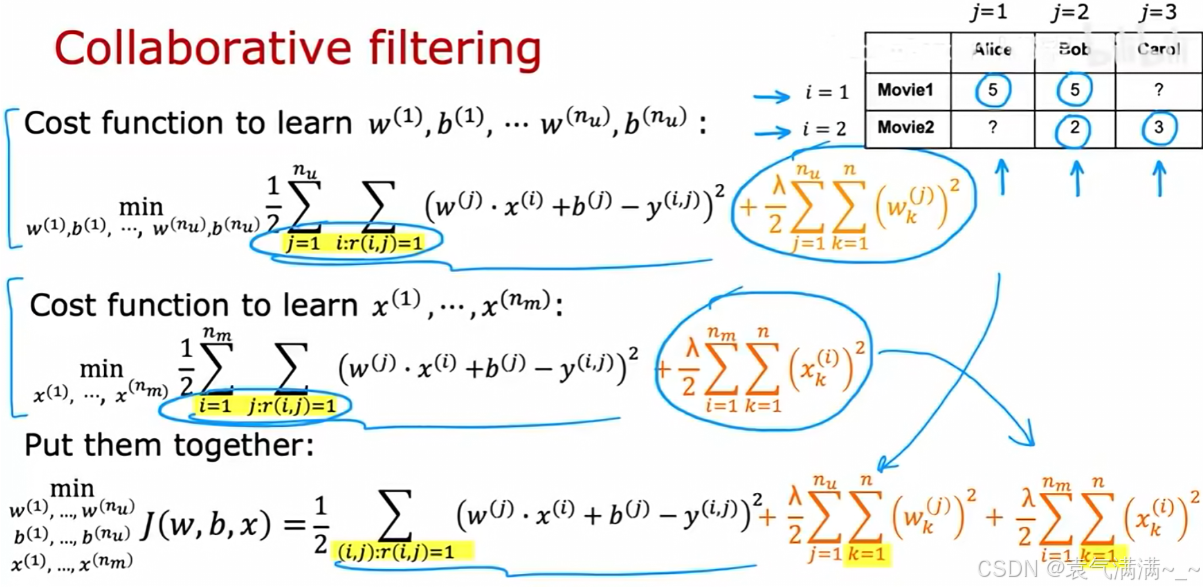
协同过滤代价函数:
- 它将 w, b, x 全部视为需要优化的参数
- 包含:对已知评分的预测误差、对用户参数的正则化、对电影特征的正则化
python
# 协同过滤代价函数
def cofi_cost_func(X, W, b, Y, R, lambda_):
nm, nu = Y.shape
J = 0
for j in range(nu):
w = W[j,:]
b_j = b[0,j]
for i in range(nm):
x = X[i,:]
y = Y[i,j]
r = R[i,j]
J += np.square(r * (np.dot(w,x) + b_j - y))
J += lambda_* (np.sum(np.square(W)) + np.sum(np.square(X)))
J = J/2
return J
# 矢量化实现协同过滤代价函数
def cofi_cost_func_v(X, W, b, Y, R, lambda_):
j = (tf.linalg.matmul(X, tf.transpose(W)) + b - Y)*R
J = 0.5 * tf.reduce_sum(j**2) + (lambda_/2) * (tf.reduce_sum(X**2) + tf.reduce_sum(W**2))
return J冷启动问题与均值归一化:
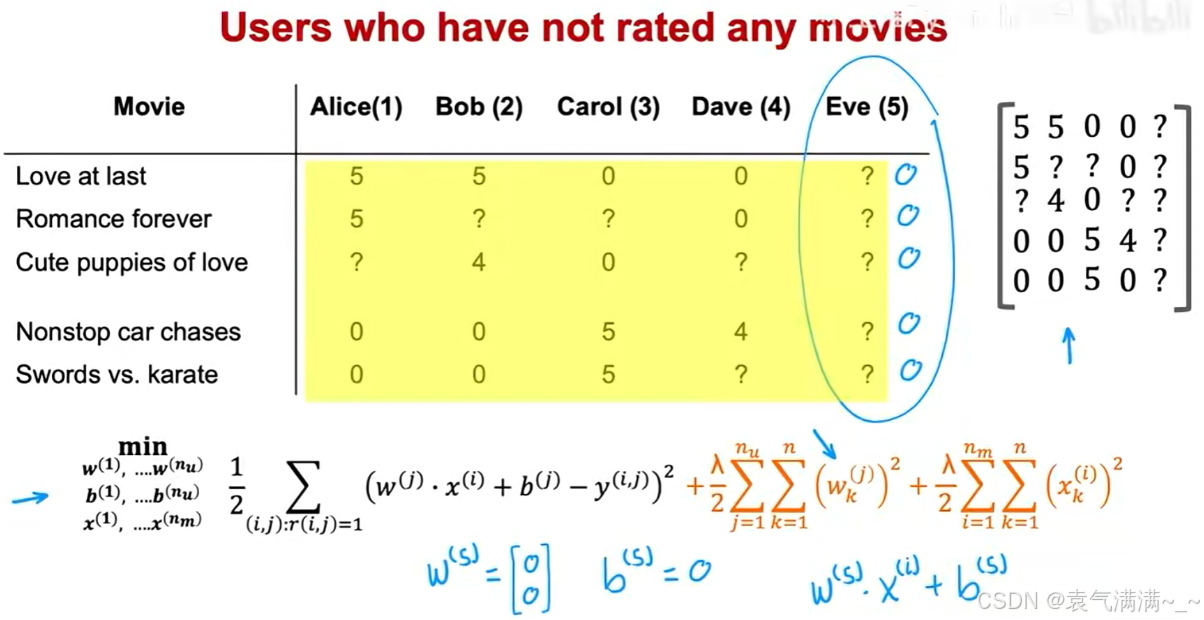
当一个新用户加入系统,他没有任何评分历史,会导致:
- 在使用协同过滤算法时,由于没有
的数据,代价函数中与该用户相关的预测误差项为0。
- 为了最小化总代价,正则化项会迫使该用户的参数
和
都变为0。
- 这导致对该用户的所有电影评分预测都为0,这是一个没有意义的推荐结果。

针对冷启动问题,可通过均值归一化来解决。
- 计算均值:对评分矩阵的每一行,计算所有已有评分的平均值 μ。
- 归一化:从每个电影的所有已有评分中,减去该电影的平均分,得到一个均值为0的归一化评分矩阵。
- 训练:在归一化的评分矩阵上运行协同过滤算法,学习参数 w, b 和特征 x。
- 预测:对于用户 j 和电影 i,进行预测时,在模型输出的基础上,必须将该电影的平均分加回来。
- 预测公式:
。对于新用户来说,其参数
和
仍然会是0。但现在的预测结果是
,即该用户对该电影的评分是2.5。这是一个远比预测0分更合理、更有意义的初始推荐。
2、PCA
PCA是一种无监督学习方法,旨在通过线性变换将原始的高维数据映射到低维空间,在减少数据特征的同时尽可能保留多的数据信息量。
核心思想:寻找一个新的坐标轴(或方向),称为主成分。
- 数据预处理(均值归一化、特征缩放)
- 寻找主成分
- 主成分的方向是能使原始数据投影到该轴上后,投影点的方差最大。
- 方差越大,意味着数据点在投影后散布得越开,这等同于保留了原始数据中最多的信息。如果投影后所有点都挤在一起,即方差小,则意味着大量原始信息丢失了。
- 计算新坐标
python
# 将2D数据转换为1D
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[3, 1], [1, 1], [1, 2],
[1, -1], [-2, -2], [-3, -2]])
# 初始化PCA模型,指定要降到的维度 n_components=1
pca = PCA(n_components=1)
# 拟合数据
pca.fit(X)
# 得到2D转换为1D的结果
X_trans = pca.transform(X)
print("Transformed data (1D):\n", X_trans)
# 从1D数据近似恢复为2D
X_reconstructed = pca.inverse_transform(X_trans)
print("Reconstructed data from 1D:\n", X_reconstructed)四、强化学习
1、相关术语
以火星车为例
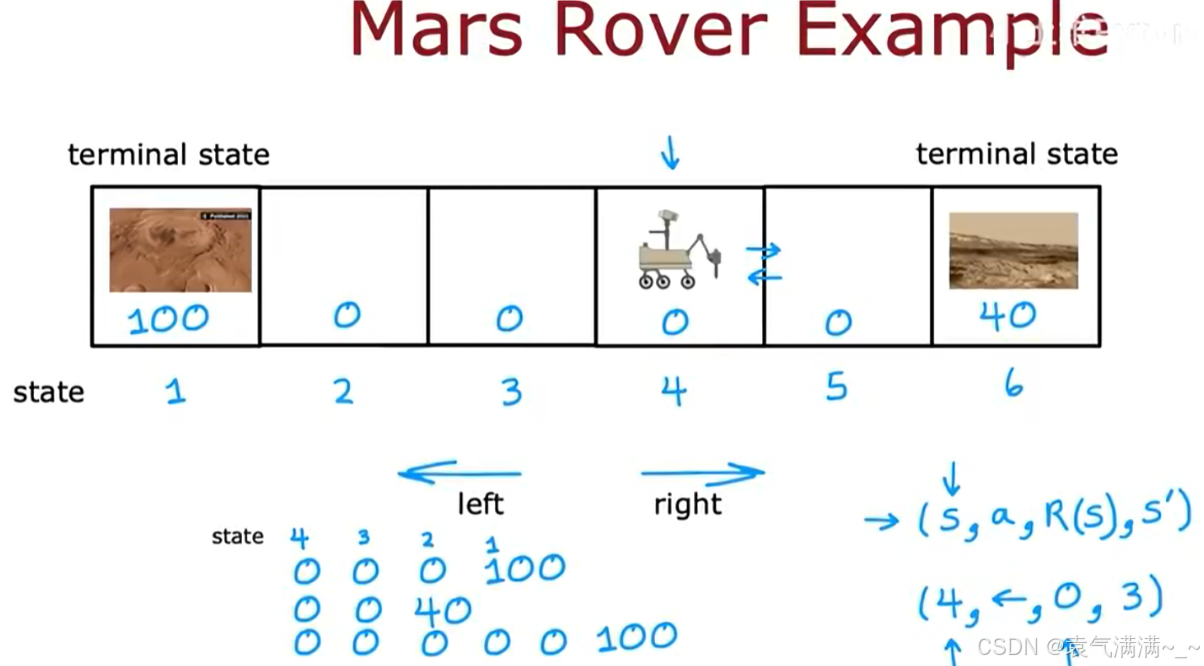
- 状态(States):火星车所在的位置格子。这个环境共有6个状态,标记为 s=1 到 s=6。状态1和状态6是终止状态,到达这些状态后,任务结束。
- 动作(Actions):在任何非终止状态下,火星车都可以选择向左(left)或向右(right)移动。
- 奖励 (Rewards): 奖励仅与到达的状态有关。
- 到达状态1,获得 +100 的奖励。
- 到达状态6,获得 +40 的奖励。
- 到达其他状态(2, 3, 4, 5),奖励为 0。
- (s, a, R(s), s'):在状态 s,采取行动 a,获得与状态s相关的奖励,并转移到新状态 s'。eg:(4, ←, 0, 3) 表示在状态4向左移动,获得0奖励,并到达状态3。
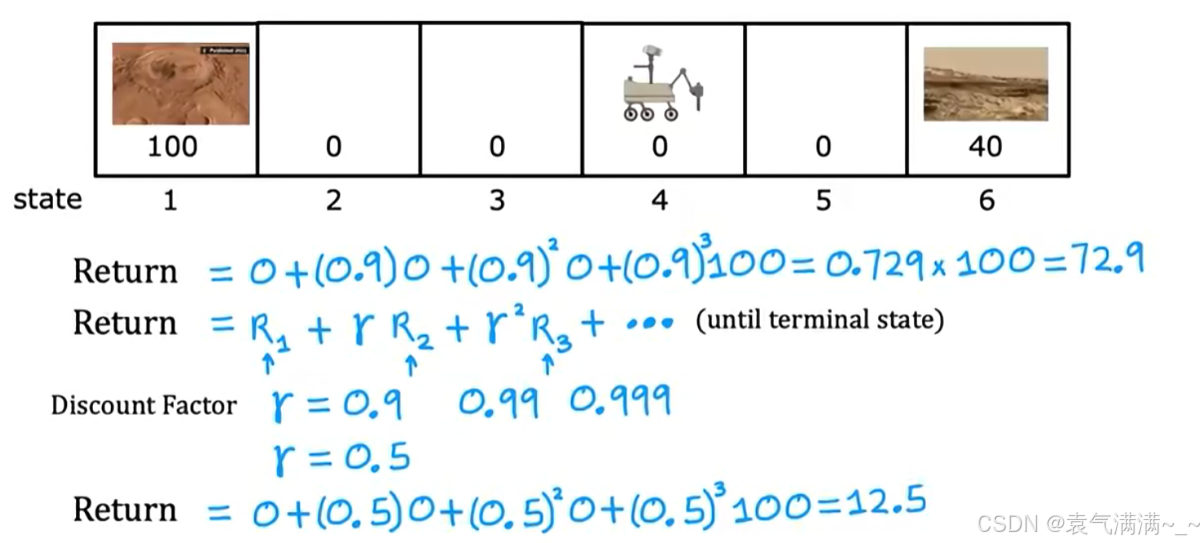
- 折扣因子(Discount Factor)
γ:一个介于0和1之间的数。γ值越接近0,智能体越"短视",只关心眼前的奖励。γ值越接近1,智能体越有"远见",会更多地考虑长远未来的奖励。
- 回报(Return):
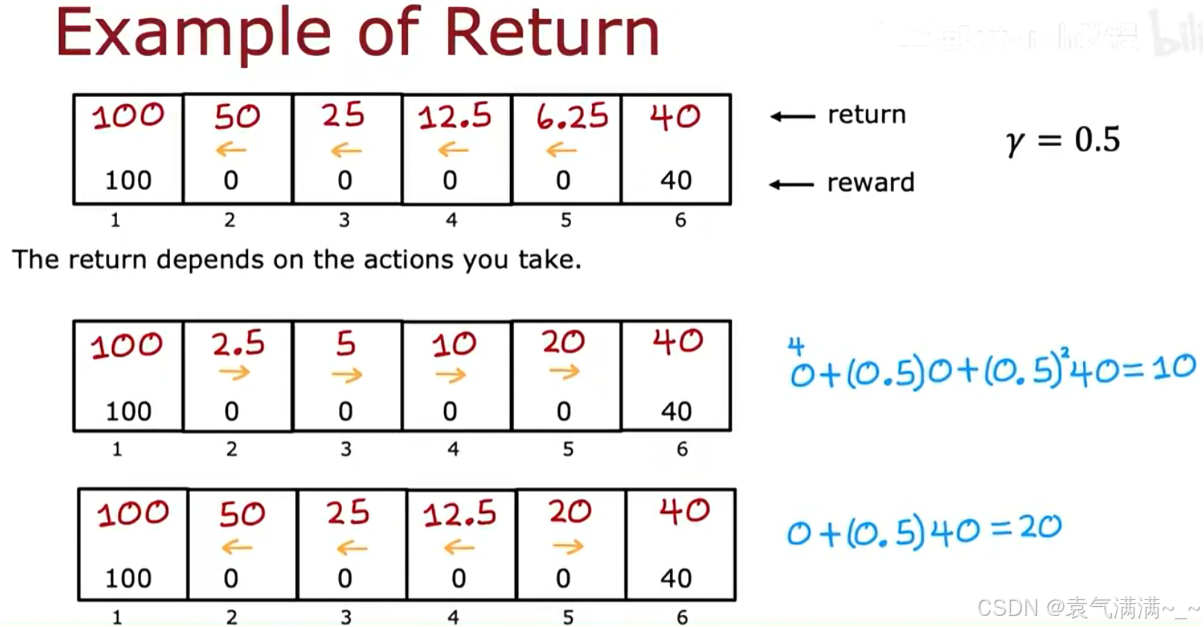
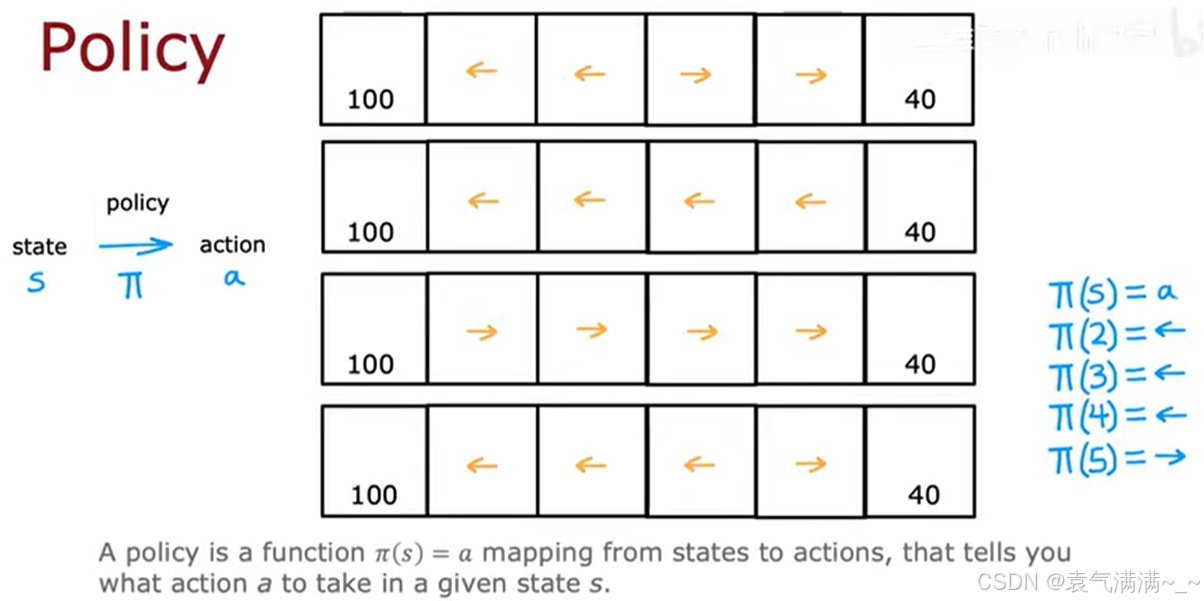
- 策略(Policy) π:一个函数,它告诉智能体,在给定的任何一个状态下,应该采取什么行动。eg:一个可能的策略是:在状态2, 3, 4都向左移动,在状态5向右移动。
2、Q-learning算法
2.1 状态-行动价值函数 (Q-function)

状态-行动价值函数 Q(s, a),简称Q函数。Q(s, a) 衡量了在状态 s 下,采取行动 a 的回报。
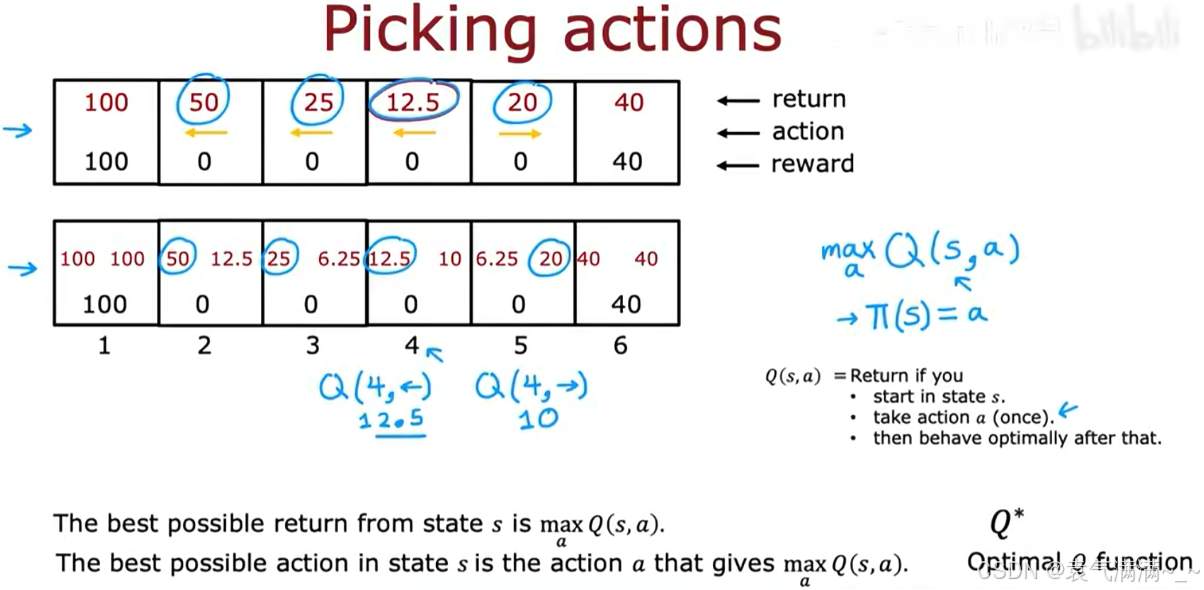
- 最优回报:
- 最优策略:在任何状态
s,选择那个能使Q(s, a)值最大的行动a
2.2 贝尔曼方程

通过回报公式推导贝尔曼方程:
