深度学习的数学原理（六）—— 梯度消失与激活函数

在深度学习中，激活函数是连接线性变换与非线性表达的核心，其设计合理性直接决定模型能否深度训练、精准拟合复杂数据。而梯度消失（或梯度爆炸）是深度神经网络训练过程中最经典、最棘手的问题之一------当模型层数加深时，反向传播的梯度会逐渐趋近于0（梯度消失）或趋于无穷大（梯度爆炸），导致浅层参数无法更新、模型收敛停滞或训练不稳定。本文将遵循"现象发现→原理拆解→解决方案"的逻辑，从直观例子切入，深入剖析梯度消失的数学本质，同时结合激活函数的进阶演进，给出对应的解决思路及底层原理，彻底搞懂这一核心难点。

一、从简单模型中发现梯度消失现象

为了避免复杂公式的堆砌，我们先构建一个极简的深度神经网络，通过手动计算梯度，直观感受梯度消失的过程。假设我们搭建一个3层全连接神经网络（输入层→隐藏层1→隐藏层2→输出层），各层结构及参数如下，重点观察反向传播时梯度的变化：

1.1 模型设定（极简版）

• 输入层：1个神经元，输入值 x=1x = 1x=1；

• 隐藏层1：1个神经元，权重 w1=0.5w_1 = 0.5w1=0.5，偏置 b1=0b_1 = 0b1=0，激活函数选用经典的Sigmoid函数；

• 隐藏层2：1个神经元，权重 w2=0.5w_2 = 0.5w2=0.5，偏置 b2=0b_2 = 0b2=0，激活函数同样为Sigmoid；

• 输出层：1个神经元，权重 w3=0.5w_3 = 0.5w3=0.5$，偏置 b3=0b_3 = 0b3=0，无激活函数（回归任务，输出 yhaty_{hat}yhat）；

• 损失函数：均方误差 L=12(y−yhat)2L = \frac{1}{2}(y - y_{hat})^2L=21(y−yhat)2，假设真实标签 y=1y = 1y=1（便于计算）。

1.2 前向传播计算（获取预测值）

前向传播的核心是"线性变换+激活"，逐步计算各层输出：

1. 隐藏层1的线性输出（未激活）：z1=w1x+b1=0.5×1+0=0.5z_1 = w_1 x + b_1 = 0.5 \times 1 + 0 = 0.5z1=w1x+b1=0.5×1+0=0.5；

2. 隐藏层1的激活输出：a1=σ(z1)=11+e−z1=11+e−0.5≈0.6225a_1 = \sigma(z_1) = \frac{1}{1 + e^{-z_1}} = \frac{1}{1 + e^{-0.5}} \approx 0.6225a1=σ(z1)=1+e−z11=1+e−0.51≈0.6225（Sigmoid函数计算）；

3. 隐藏层2的线性输出（未激活）：z2=w2a1+b2=0.5×0.6225+0≈0.31125z_2 = w_2 a_1 + b_2 = 0.5 \times 0.6225 + 0 \approx 0.31125z2=w2a1+b2=0.5×0.6225+0≈0.31125；

4. 隐藏层2的激活输出：a2=σ(z2)=11+e−0.31125≈0.5772a_2 = \sigma(z_2) = \frac{1}{1 + e^{-0.31125}} \approx 0.5772a2=σ(z2)=1+e−0.311251≈0.5772；

5. 输出层预测值：yhat=w3a2+b3=0.5×0.5772+0≈0.2886y_{hat} = w_3 a_2 + b_3 = 0.5 \times 0.5772 + 0 \approx 0.2886yhat=w3a2+b3=0.5×0.5772+0≈0.2886。

1.3 反向传播计算（求梯度，更新参数）

深度学习的参数更新依赖反向传播的梯度下降法，核心是通过链式法则，从输出层反向计算各层权重的梯度（即损失函数对权重的偏导数 ∂L∂w\frac{\partial L}{\partial w}∂w∂L），梯度越大，参数更新幅度越大；梯度趋近于0，参数几乎不更新（梯度消失）。

首先明确两个关键前提：

• 损失函数对输出层预测值的梯度：∂L∂yhat=yhat−y≈0.2886−1=−0.7114\frac{\partial L}{\partial y_{hat}} = y_{hat} - y \approx 0.2886 - 1 = -0.7114∂yhat∂L=yhat−y≈0.2886−1=−0.7114；

• Sigmoid函数的导数特性：σ′(z)=σ(z)(1−σ(z))\sigma'(z) = \sigma(z)(1 - \sigma(z))σ′(z)=σ(z)(1−σ(z))（这是后续梯度变化的核心关键，务必记住）。

接下来逐步计算各层权重的梯度：

1. 输出层权重 w3w_3w3 的梯度：∂L∂w3=∂L∂yhat×∂yhat∂w3=−0.7114×a2≈−0.7114×0.5772≈−0.4106\frac{\partial L}{\partial w_3} = \frac{\partial L}{\partial y_{hat}} \times \frac{\partial y_{hat}}{\partial w_3} = -0.7114 \times a_2 \approx -0.7114 \times 0.5772 \approx -0.4106∂w3∂L=∂yhat∂L×∂w3∂yhat=−0.7114×a2≈−0.7114×0.5772≈−0.4106（梯度较大，可正常更新）；

2. 隐藏层2权重 w2w_2w2 的梯度：∂L∂w2=∂L∂yhat×∂yhat∂a2×∂a2∂z2×∂z2∂w2\frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial y_{hat}} \times \frac{\partial y_{hat}}{\partial a_2} \times \frac{\partial a_2}{\partial z_2} \times \frac{\partial z_2}{\partial w_2}∂w2∂L=∂yhat∂L×∂a2∂yhat×∂z2∂a2×∂w2∂z2代入计算：∂yhat∂a2=w3=0.5\frac{\partial y_{hat}}{\partial a_2} = w_3 = 0.5∂a2∂yhat=w3=0.5，∂a2∂z2=σ(z2)(1−σ(z2))≈0.5772×(1−0.5772)≈0.2449\frac{\partial a_2}{\partial z_2} = \sigma(z_2)(1 - \sigma(z_2)) \approx 0.5772 \times (1 - 0.5772) \approx 0.2449∂z2∂a2=σ(z2)(1−σ(z2))≈0.5772×(1−0.5772)≈0.2449，∂z2∂w2=a1≈0.6225\frac{\partial z_2}{\partial w_2} = a_1 \approx 0.6225∂w2∂z2=a1≈0.6225。最终梯度：−0.7114×0.5×0.2449×0.6225≈−0.0547-0.7114 \times 0.5 \times 0.2449 \times 0.6225 \approx -0.0547−0.7114×0.5×0.2449×0.6225≈−0.0547（梯度明显变小）；

3. 隐藏层1权重 w1w_1w1 的梯度：∂L∂w1=∂L∂yhat×∂yhat∂a2×∂a2∂z2×∂z2∂a1×∂a1∂z1×∂z1∂w1\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial y_{hat}} \times \frac{\partial y_{hat}}{\partial a_2} \times \frac{\partial a_2}{\partial z_2} \times \frac{\partial z_2}{\partial a_1} \times \frac{\partial a_1}{\partial z_1} \times \frac{\partial z_1}{\partial w_1}∂w1∂L=∂yhat∂L×∂a2∂yhat×∂z2∂a2×∂a1∂z2×∂z1∂a1×∂w1∂z1新增项计算：∂z2∂a1=w2=0.5\frac{\partial z_2}{\partial a_1} = w_2 = 0.5∂a1∂z2=w2=0.5，∂a1∂z1=σ(z1)(1−σ(z1))≈0.6225×(1−0.6225)≈0.2350\frac{\partial a_1}{\partial z_1} = \sigma(z_1)(1 - \sigma(z_1)) \approx 0.6225 \times (1 - 0.6225) \approx 0.2350∂z1∂a1=σ(z1)(1−σ(z1))≈0.6225×(1−0.6225)≈0.2350，∂z1∂w1=x=1\frac{\partial z_1}{\partial w_1} = x = 1∂w1∂z1=x=1。最终梯度：−0.7114×0.5×0.2449×0.5×0.2350×1≈−0.0099-0.7114 \times 0.5 \times 0.2449 \times 0.5 \times 0.2350 \times 1 \approx -0.0099−0.7114×0.5×0.2449×0.5×0.2350×1≈−0.0099（梯度趋近于0，几乎无法更新）。

1.4 现象总结

仅3层的极简网络，使用Sigmoid作为激活函数时，反向传播的梯度从输出层到输入层（浅层）急剧衰减：w3w_3w3 梯度≈-0.4106，w2w_2w2梯度≈-0.0547，w1w_1w1 梯度≈-0.0099。若我们将网络层数增加到10层、20层，浅层权重的梯度会直接趋近于0，导致浅层参数无法更新------这就是典型的梯度消失。

反之，若我们将各层权重设为2.0（而非0.5），重复上述计算会发现：梯度会从输出层到浅层急剧增大（例如 w1w_1w1 梯度可能达到几十、上百），导致参数更新幅度过大，模型训练震荡、无法收敛------这就是梯度爆炸。两者本质是同一问题的两个极端，核心诱因一致。

二、梯度消失的数学根源

从上述例子可以看出，梯度消失的关键的是"反向传播时，链式法则的乘积项不断衰减"。结合数学推导，我们可以提炼出两个核心根源，其中激活函数的导数特性是直接诱因，权重初始化不当是辅助诱因，两者共同导致梯度消失/爆炸。

2.1 核心根源1：激活函数的导数取值范围（直接诱因）

反向传播的梯度计算，本质是"损失函数梯度 × 各层激活函数导数 × 各层权重"的链式乘积（如例子中 ∂L∂w1\frac{\partial L}{\partial w_1}∂w1∂L 的计算）。其中，激活函数的导数取值范围，直接决定了梯度的衰减/放大速度------这也是激活函数进阶的核心出发点。

（1）Sigmoid函数的致命缺陷

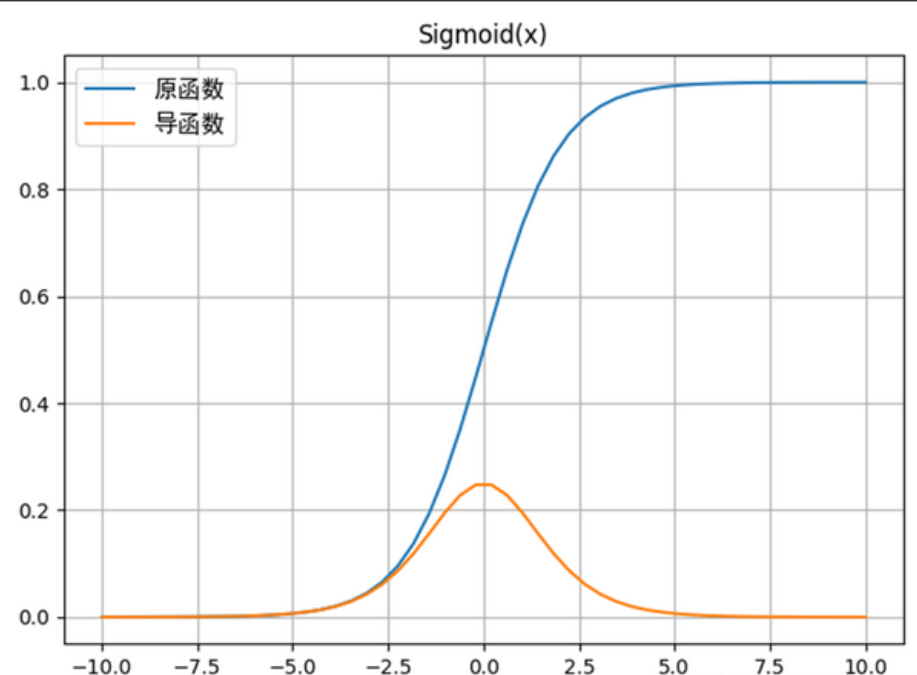
我们再深入分析Sigmoid函数的导数：σ′(z)=σ(z)(1−σ(z))\sigma'(z) = \sigma(z)(1 - \sigma(z))σ′(z)=σ(z)(1−σ(z))结合Sigmoid函数的图像（取值范围(0,1)），可得出两个关键结论：

• 导数的最大值：当 σ(z)=0.5\sigma(z) = 0.5σ(z)=0.5（即z=0z=0z=0）时，σ′(z)max=0.5×0.5=0.25\sigma'(z)_{max} = 0.5 \times 0.5 = 0.25σ′(z)max=0.5×0.5=0.25；

• 导数的衰减：当 ∣z∣>2|z| > 2∣z∣>2 时，σ(z)\sigma(z)σ(z) 趋近于0或1，此时σ′(z)\sigma'(z)σ′(z) 趋近于0（例如 z=3z=3z=3 时，σ(z)≈0.9526\sigma(z)≈0.9526σ(z)≈0.9526，σ′(z)≈0.0454\sigma'(z)≈0.0454σ′(z)≈0.0454；z=−3z=-3z=−3 时，σ(z)≈0.0474\sigma(z)≈0.0474σ(z)≈0.0474，σ′(z)≈0.0454\sigma'(z)≈0.0454σ′(z)≈0.0454）。

这意味着，无论输入 zzz 取何值，Sigmoid的导数都不会超过0.25。在深度网络中，反向传播的梯度需要乘以多个激活函数的导数（每层一个），假设网络有10层，即使每层导数都取最大值0.25，最终梯度会衰减为 0.2510≈9.5×10−70.25^{10} \approx 9.5 \times 10^{-7}0.2510≈9.5×10−7，几乎为0------这就是梯度消失的核心数学逻辑。

此外，Sigmoid函数还有一个缺陷：输出均值不为0（均值≈0.5），会导致反向传播时梯度出现"偏移"，进一步加剧梯度衰减。

（2）Tanh函数的改进与局限

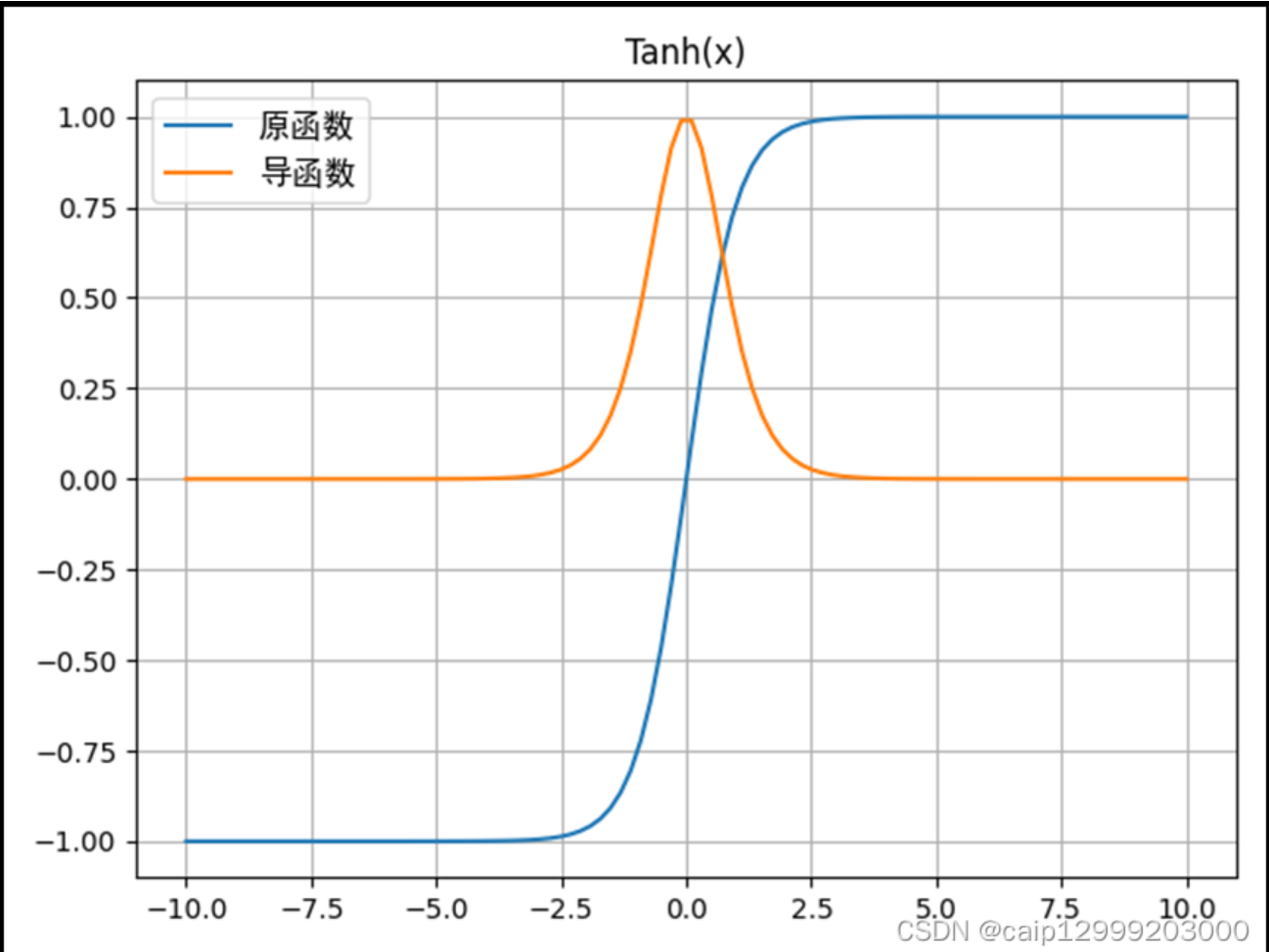
为了解决Sigmoid输出均值不为0的问题，人们提出了Tanh函数（双曲正切函数），其表达式为：tanh⁡(z)=ez−e−zez+e−z\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}tanh(z)=ez+e−zez−e−z

Tanh函数的导数为：tanh⁡′(z)=1−tanh⁡2(z)\tanh'(z) = 1 - \tanh^2(z)tanh′(z)=1−tanh2(z)，其取值范围为(0,1]，最大值为1（当 z=0z=0z=0 时），且输出均值为0（取值范围(-1,1)），确实缓解了梯度消失问题。但它的缺陷依然明显：当 ∣z∣>2|z| > 2∣z∣>2 时，tanh⁡(z)\tanh(z)tanh(z) 趋近于1或-1，此时 tanh⁡′(z)\tanh'(z)tanh′(z) 趋近于0，依然会导致梯度衰减。例如，10层网络使用Tanh函数，即使每层导数取0.5（中等水平），最终梯度会衰减为 0.510=0.00097660.5^{10} = 0.00097660.510=0.0009766，依然接近0------因此Tanh只能缓解，无法彻底解决梯度消失。

2.2 核心根源2：权重初始化不当（辅助诱因）

除了激活函数的导数，权重的初始值也会影响梯度的变化：

• 若权重初始化过大（如例子中设为2.0），则反向传播时，梯度会乘以多个大于1的权重，导致梯度呈指数级放大（梯度爆炸）；

• 若权重初始化过小（如例子中设为0.1），则梯度会乘以多个小于1的权重，结合激活函数导数的衰减，会进一步加速梯度消失；

• 若权重初始化为0或相同值，会导致"梯度同质化"，所有参数的梯度相同，无法有效更新（虽不是梯度消失，但属于初始化不当的衍生问题）。

这里补充一个关键结论：梯度消失/爆炸的本质，是"链式法则的乘积项（激活函数导数×权重）的绝对值乘积，随层数增加呈指数级衰减或放大"。当 ∣σ′(z)×w∣<1|\sigma'(z) \times w| < 1∣σ′(z)×w∣<1 时，梯度指数级衰减（梯度消失）；当 ∣σ′(z)×w∣>1|\sigma'(z) \times w| > 1∣σ′(z)×w∣>1 时，梯度指数级放大（梯度爆炸）。

三、解决方案及底层原理

针对上述两个核心根源，解决方案主要分为三类：优化激活函数（解决导数衰减问题）、优化权重初始化（解决乘积项放大/衰减问题）、其他辅助优化（缓解梯度传播障碍）。其中，激活函数的进阶是最直接、最核心的解决方案，我们重点拆解。

3.1 核心方案：激活函数进阶（彻底解决导数衰减）

进阶激活函数的核心设计思路是：让激活函数的导数在大部分区间内保持较大值（接近1），避免导数趋近于0，同时保证非线性表达能力。目前工业界最常用的是ReLU系列激活函数，我们从原理到应用，逐一拆解。

（1）ReLU函数（Rectified Linear Unit）------ 梯度消失的"终结者"

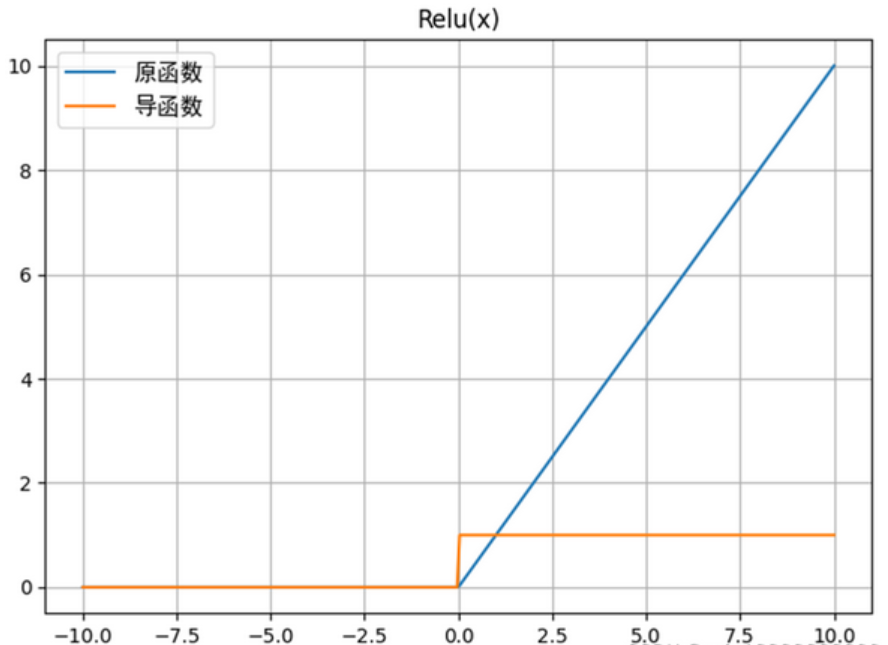
ReLU函数是目前最基础、最常用的进阶激活函数，表达式极其简单：ReLU(z)=max⁡(0,z)ReLU(z) = \max(0, z)ReLU(z)=max(0,z)。

底层原理（导数特性）

ReLU函数的导数为：ReLU′(z)={1,z>00,z≤0ReLU'(z) = \begin{cases} 1, & z > 0 \\ 0, & z \leq 0 \end{cases}ReLU′(z)={1,0,z>0z≤0

这个导数特性完美解决了Sigmoid和Tanh的缺陷：当z>0z > 0z>0 时，导数恒为1，不会出现导数衰减的情况------反向传播时，梯度可以通过"导数=1"的区间，无衰减地传递到浅层，彻底解决梯度消失问题。例如，10层网络使用ReLU函数，只要每层输入 z>0z > 0z>0，梯度就不会衰减（乘积项=1×权重，若权重初始化合理，可避免梯度爆炸）。

优势与局限

• 优势：计算简单（无需指数运算）、导数恒为1（无梯度衰减）、训练速度快，适配深度网络（如CNN、Transformer）；

• 局限：死亡ReLU问题------当 z≤0z \leq 0z≤0 时，导数为0，对应神经元的梯度为0，参数无法更新，最终成为"死亡神经元"（永久无法激活），导致模型表达能力下降。

（2）ReLU变种函数（解决死亡ReLU问题）

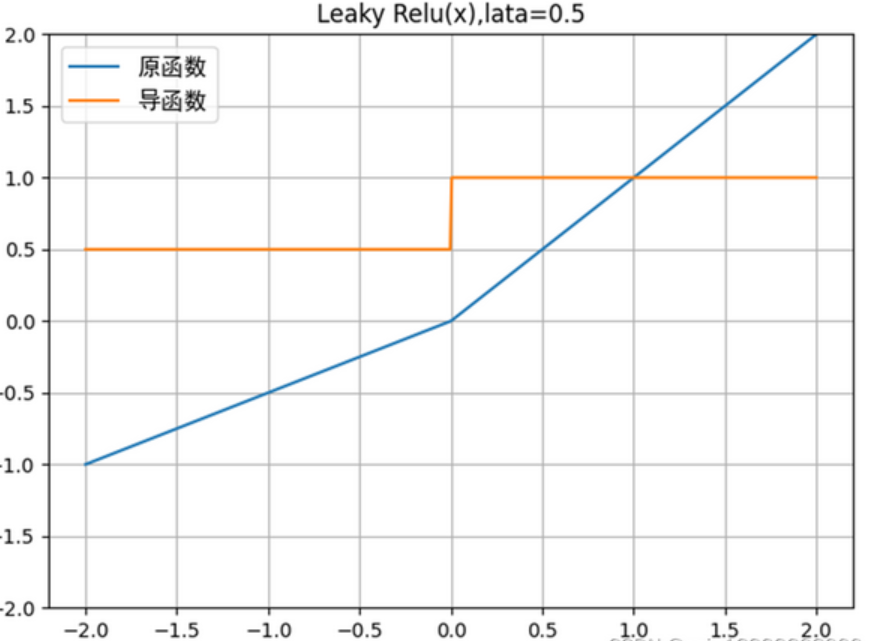
为了解决死亡ReLU问题，研究者在ReLU的基础上进行了微小修改，衍生出多个变种，核心思路是：z≤0z \leq 0z≤0在 时，让导数不为0，而是一个很小的正数，保证神经元即使被激活，也能缓慢更新参数。

① Leaky ReLU（带泄漏的ReLU）

表达式：LeakyReLU(z)={z,z>0αz,z≤0LeakyReLU(z) = \begin{cases} z, & z > 0 \\ \alpha z, & z \leq 0 \end{cases}LeakyReLU(z)={z,αz,z>0z≤0其中 α\alphaα 是一个很小的正数（通常取0.01）。

导数：LeakyReLU′(z)={1,z>0α,z≤0LeakyReLU'(z) = \begin{cases} 1, & z > 0 \\ \alpha, & z \leq 0 \end{cases}LeakyReLU′(z)={1,α,z>0z≤0

原理：当 z≤0z \leq 0z≤0 时，导数为α\alphaα（如0.01），而非0，这样即使神经元暂时未被激活，也能获得微小的梯度，避免成为死亡神经元。

② ELU（Exponential Linear Unit）

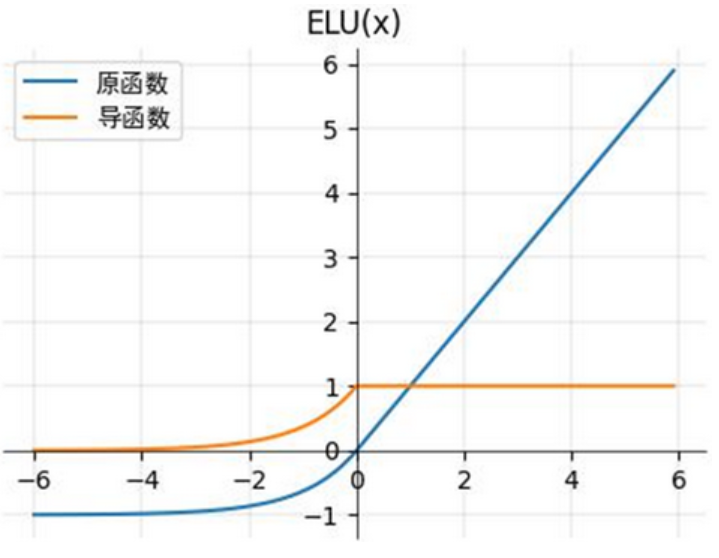
表达式：ELU(z)={z,z>0α(ez−1),z≤0ELU(z) = \begin{cases} z, & z > 0 \\ \alpha (e^z - 1), & z \leq 0 \end{cases}ELU(z)={z,α(ez−1),z>0z≤0其中α>0\alpha > 0α>0（通常取1）

导数：ELU′(z)={1,z>0αez,z≤0ELU'(z) = \begin{cases} 1, & z > 0 \\ \alpha e^z, & z \leq 0 \end{cases}ELU′(z)={1,αez,z>0z≤0。

原理：相比Leaky ReLU，ELU在 z≤0z \leq 0z≤0 时的输出是连续光滑的（导数随 zzz 变化，而非固定值），能进一步缓解梯度震荡，同时避免死亡神经元；但计算量略大于Leaky ReLU（需计算指数）。

③ Swish函数（Google提出，适配深层网络）

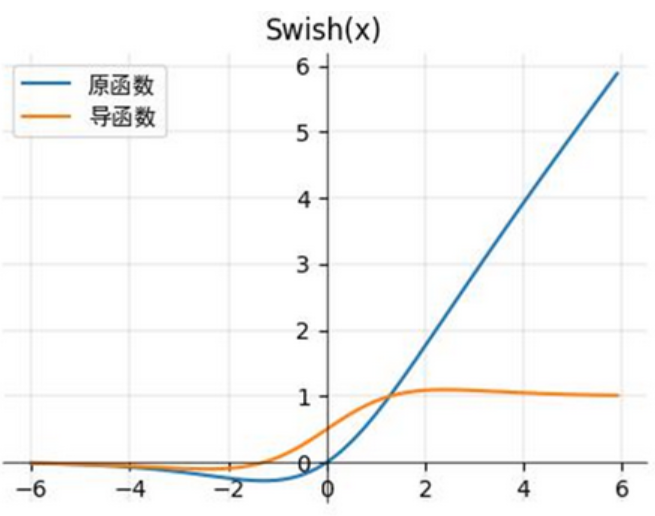
表达式：Swish(z)=z⋅σ(z)Swish(z) = z \cdot \sigma(z)Swish(z)=z⋅σ(z)（Sigmoid与线性项的乘积）

导数：Swish′(z)=σ(z)+z⋅σ′(z)Swish'(z) = \sigma(z) + z \cdot \sigma'(z)Swish′(z)=σ(z)+z⋅σ′(z)

原理：结合了Sigmoid的非线性和ReLU的梯度优势，导数在整个区间内都不为0（避免死亡神经元），且在 z>0z > 0z>0 时导数接近1（无梯度衰减），在深层网络（如Transformer、大模型）中表现优于ReLU。

当然，激活函数还有非常多中

3.2 权重初始化优化（避免梯度爆炸/加速衰减）

激活函数解决了"导数衰减"问题，而权重初始化则解决"乘积项放大/衰减"问题，两者结合才能彻底避免梯度消失/爆炸。常用的权重初始化方法，均基于"让 ∣σ′(z)×w∣≈1|\sigma'(z) \times w| \approx 1∣σ′(z)×w∣≈1"的核心原则，确保梯度稳定传递。

（1）Xavier初始化（适配Sigmoid/Tanh）

针对Sigmoid和Tanh函数（导数最大值分别为0.25和1），Xavier初始化的核心是：让权重的初始值服从均匀分布或正态分布，确保每层输入 zzz 的方差保持一致，从而让梯度不衰减、不爆炸。

均匀分布公式：w∼U(−6nin+nout,6nin+nout)w \sim U\left( -\frac{\sqrt{6}}{\sqrt{n_{in} + n_{out}}}, \frac{\sqrt{6}}{\sqrt{n_{in} + n_{out}}} \right)w∼U(−nin+nout 6 ,nin+nout 6 )其中 ninn_{in}nin 是输入神经元个数，noutn_{out}nout 是输出神经元个数。

（2）He初始化（适配ReLU系列）

ReLU系列函数（z>0z > 0z>0 时导数=1）的输入 zzz 有一半概率为正、一半为负（死亡神经元），因此He初始化在Xavier的基础上进行了调整，放大了权重的方差，确保有效梯度的传递。

均匀分布公式：w∼U(−6nin,6nin)w \sim U\left( -\frac{\sqrt{6}}{\sqrt{n_{in}}}, \frac{\sqrt{6}}{\sqrt{n_{in}}} \right)w∼U(−nin 6 ,nin 6 )仅依赖输入神经元个数 ninn_{in}nin。

注意：He初始化是ReLU系列激活函数的"黄金搭档"，工业界使用ReLU时，几乎都会搭配He初始化，避免梯度爆炸。

3.3 其他辅助优化（缓解梯度传播障碍）

除了激活函数和权重初始化，还有两种常用方法，可进一步缓解梯度消失/爆炸，尤其适配超深层网络（如100层以上）。

（1）批量归一化（Batch Normalization，BN）

核心原理：在每一层的线性变换之后、激活函数之前，对输入 zzz 进行归一化处理（让 zzz 的均值为0、方差为1），确保 zzz 始终处于激活函数的"梯度友好区间"（如ReLU的 z>0z > 0z>0 区间、Sigmoid的 ∣z∣<2|z| < 2∣z∣<2 区间）。

作用：避免输入zzz 过大或过小，导致激活函数导数趋近于0；同时加速训练收敛，减少权重初始化的敏感度------即使使用Sigmoid函数，搭配BN也能有效缓解梯度消失。

（2）残差连接（Residual Connection，ResNet核心）

核心原理：在深层网络中，新增"跳跃连接"，让浅层的输出直接传递到深层（即 al=σ(zl)+al−ka_l = \sigma(z_l) + a_{l-k}al=σ(zl)+al−k，kkk 是跳跃的层数），反向传播时，梯度可以通过跳跃连接"直接传递"到浅层，无需经过中间所有层的激活函数导数乘积。

作用：彻底打破"梯度必须经过所有层链式乘积"的限制，即使中间层出现梯度衰减，浅层也能通过跳跃连接获得足够大的梯度，适用于超深层网络（如ResNet-50、ResNet-101）。

残差链接及残差神经网络是非常重要的工作，后续会有专门的文章来介绍

四、总结

梯度消失的核心数学根源，是反向传播时，激活函数导数与权重的乘积项，随层数增加呈指数级衰减------其中Sigmoid/Tanh的导数衰减是直接诱因，权重初始化不当是辅助诱因。而激活函数的进阶，本质是通过"让导数保持较大值"，从根源上解决梯度衰减问题；再搭配权重初始化优化（Xavier/He）、批量归一化、残差连接等配套方法，即可彻底避免梯度消失/爆炸，支撑深层网络的稳定训练。

工业界实际应用中，建议优先选择：ReLU/ELU/Swish激活函数 + He初始化 + BN层；若网络层数超过50层，建议新增残差连接，确保梯度稳定传递。理解梯度消失的数学根源，不仅能帮助我们正确选择激活函数和优化方法，更能为后续的模型调优（如学习率调整、正则化）提供理论支撑。