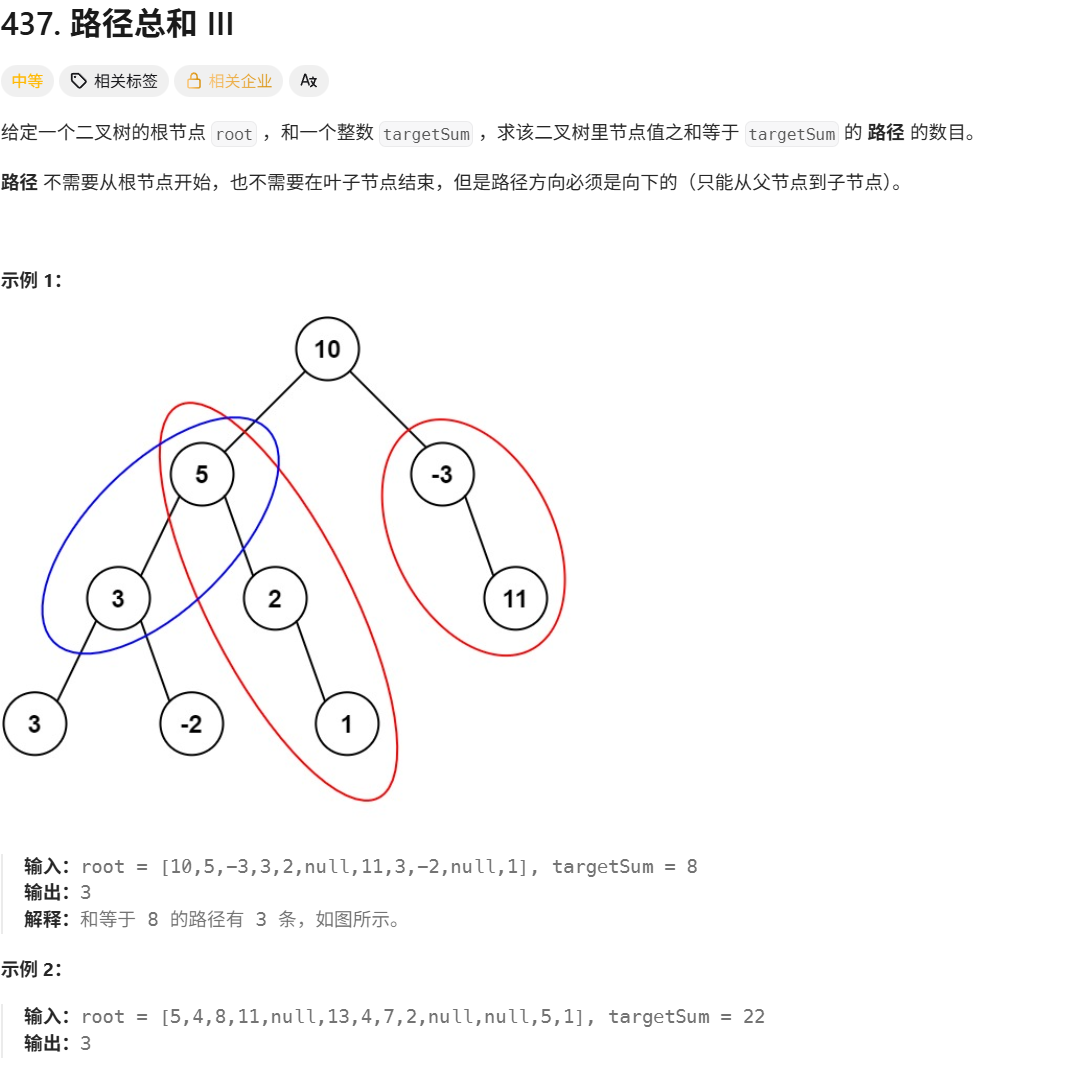
用前缀和来求区间和
在树 结构中,从根节点到当前节点 的路径也可以看作一个数组
方法:
- curSum:当前节点前缀和
- target:中间节点到当前节点的和
- curSum - target:中间节点前缀和
python
cursum
<--------------------------------------------------------------------------------------------------------------------------->
cursum-target target
|<------------------------------------------------------>|<------------------------------------------------------>|
---+--------------------+--------------------+----
根节点 中间节点 当前节点问题转换为:检查当前节点之前的节点的前缀和 ,有没有等于cursum-target的?
所以需要一个哈希表,记录:当前路径上所有出现过的前缀和,及其出现的次数
- 为什么要记录"当前路径上所有出现过的前缀和,及其出现的次数 ",只记录出没出现过不行吗?
不行,因为:路径上的前缀和可能会重复出现(尤其是当树中存在节点值为 0 或正负抵消的情况时)
python
# 假设 targetSum = 8
根节点
|
(A) 值: 3 [前缀和: 3]
|
(B) 值: 0 [前缀和: 3] <-- 重复出现了!
|
(C) 值: 5 [前缀和: 8]
|
(D) 值: 0 [前缀和: 8]
|
(E) 值: 0 [前缀和: 8] <-- 走到这里时,currSum = 8
# 走到节点 E 时, 前缀和 3 出现了 2次(节点 A 和节点 B)
# 这意味着,从节点 A 到 E 是一条和为 8 的路径;从节点 B 到 E 也是一条不同的和为 8 的路径。
# 如果只记录"出现过",就会丢掉其中一条路径,导致计数错误。如果树中全是正数,前缀和是严格递增的,确实不会重复。但题目没有这个限制:
- 节点值为 0:会导致前缀和原地踏步。
- 正负抵消:比如 5 -> -2 -> 2,前缀和会经历 5 -> 3 -> 5。
- 为什么要"销账"?在回溯时 "删除当前节点的前缀和"?
当前节点向下递归时,左右子节点需要当前节点的cursum
但递归结束,当前节点收到返回值时:- 如果当前节点是它的父节点的左子节点,则下次是向右递归,右子节点不需要左子节点的前缀和(题目要求:路径必须是垂直向下,不能跨越左右子树,不能先上再下)
- 如果当前节点是它的父节点的右子节点,则下次是向上回溯,那么父节点也可能是爷爷节点的左子树,当递归到爷爷节点的右子树时,右子树也不需要左子树的前缀和
- 即,销账是为了当当前节点去右子树递归时,不影响右子树;当当前节点作为上面某个根节点的左子树时,不影响上面某个根节点的右子树。
python
# targetSum =8
5 (root)
/ \
3 4
/ \
10 3 (node_X)- 沿着左边走:5 -> 3 -> 10。前缀和会出现 5, 8, 18
- 处理完 10 和 3 后,回溯。此时哈希表里的 18, 8 都被删除了,只剩下根节点的 5
- 进入右边:5 -> 4 -> 3
- 走到右下角的 3 (node_X) 时,currSum = 12
- 查账:找 12 - 8 = 4。哈希表里没有 4,路径数为 0。这是正确的。
哈希表记录:使用一个哈希表,存储当前路径上所有出现过的前缀和,及其出现的次数
python
# 哈希表存储:{前缀和: 出现的次数}
# 哈希表的初始值 {0: 1}:这是为了处理从根节点开始且路径和恰好等于 targetSum 的情况。此时 curr_sum - targetSum = 0,正好对应初始值。DFS 遍历这棵树
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import defaultdict
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
# 哈希表存储:{前缀和: 出现的次数}
cnt = defaultdict(int)
cnt[0] = 1
def dfs(node, curr_sum): # curr_sum 是从根节点到当前节点的值
if not node:
return 0
# # 1. 当前路径的前缀和
curr_sum += node.val
# 2.当前路径前缀和为 "curr_sum - targetSum"的中间节点(路径)个数
# 关键:先定义局部变量 count 并初始化,不然直接 count+=会报错
count = cnt[curr_sum - targetSum]
# 3. 当前节点前缀和 "curr_sum" 存入字典
cnt[curr_sum] += 1
# 递归,左右子树继续找
# 左右子树,都需要"当前节点的前缀和"
count += dfs(node.left, curr_sum)
count += dfs(node.right, curr_sum)
# 当前节点可能是它的父节点的左子节点
# 当前节点递归结束后,当前节点的父节点,要继续递归它的右子树,右边不需要左边的前缀和
cnt[curr_sum] -= 1
return count
# 直接返回根节点触发的递归结果
return dfs(root, 0)时间复杂度:O(N)O(N)O(N),每个节点仅遍历一次。
空间复杂度:O(N)O(N)O(N),哈希表在最坏情况下(树呈链状)需要存储 NNN 个前缀和。