【强化学习教程——01_强化学习基石】第06章_Q-Learning与SARSA

第 6 章：Q-Learning 与 SARSA

本章目标：理解 On-policy 与 Off-policy 的核心区别，掌握 SARSA 和 Q-Learning 算法，通过 Cliff Walking 案例深入理解两者的行为差异，学习 Expected SARSA 作为中间形态，并理解 Maximization Bias (最大化偏差) 问题及 Double Q-Learning 的解决方案。

---

📖 目录 (Table of Contents)

1. [On-policy vs Off-policy](#On-policy vs Off-policy)
2. SARSA (On-policy TD Control)
3. Q-Learning (Off-policy TD Control)
4. [Cliff Walking 案例分析](#Cliff Walking 案例分析)
5. [Expected SARSA](#Expected SARSA)
6. [Maximization Bias 与 Double Q-Learning](#Maximization Bias 与 Double Q-Learning)
7. 算法对比总结
8. 实战技巧：超参数衰减
9. 表格型方法的局限
10. 总结与预告

---

1. On-policy vs Off-policy

图解说明：

• On-policy：用什么策略采样，就用什么策略更新。吃自家菜。
• Off-policy：用一个行为策略 (Behavior Policy) 采样，同时优化另一个目标策略 (Target Policy)。可以吃别人家的菜学习做饭。

类型	定义	行为策略与目标策略	代表算法
On-policy	评估和改进同一策略	π b e h a v i o r = π t a r g e t \pi_{behavior} = \pi_{target} πbehavior=πtarget	SARSA
Off-policy	评估目标策略，使用行为策略采样	π b e h a v i o r ≠ π t a r g e t \pi_{behavior} \neq \pi_{target} πbehavior=πtarget	Q-Learning

---

2. SARSA (On-policy TD Control)

名称来源 ：State-Action-Reward-State-Action，即 ( S t , A t , R t + 1 , S t + 1 , A t + 1 ) (S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}) (St,At,Rt+1,St+1,At+1) 五元组。

更新公式：

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)−Q(St,At)]

关键特征：下一步动作 A t + 1 A_{t+1} At+1 由同一个 ϵ \epsilon ϵ-greedy 策略选取，因此更新值包含了探索行为带来的风险。

代码实现 (SARSA)

import numpy as np
from collections import defaultdict

def sarsa(env, num_episodes=5000, alpha=0.1, gamma=0.99, epsilon=0.1):
    """SARSA: On-policy TD Control"""
    Q = defaultdict(lambda: defaultdict(float))

    def epsilon_greedy(state):
        if np.random.random() < epsilon:
            return np.random.choice(env.get_actions())
        action_values = Q[state]
        if not action_values:
            return np.random.choice(env.get_actions())
        return max(action_values, key=action_values.get)

    for _ in range(num_episodes):
        state = env.reset()
        action = epsilon_greedy(state)

        while True:
            next_state, reward, done = env.step(state, action)
            next_action = epsilon_greedy(next_state)

            # SARSA 更新：使用实际选取的 next_action
            td_target = reward + gamma * Q[next_state][next_action] * (not done)
            td_error = td_target - Q[state][action]
            Q[state][action] += alpha * td_error

            state = next_state
            action = next_action

            if done: break

    return Q

---

3. Q-Learning (Off-policy TD Control)

更新公式：

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ max ⁡ a ′ Q ( S t + 1 , a ′ ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \max_{a'} Q(S_{t+1}, a') - Q(S_t, A_t) \right] Q(St,At)←Q(St,At)+α[Rt+1+γa′maxQ(St+1,a′)−Q(St,At)]

关键特征：无论实际采取什么动作，更新目标始终使用 max ⁡ a ′ Q ( S t + 1 , a ′ ) \max_{a'} Q(S_{t+1}, a') maxa′Q(St+1,a′)，即假设未来总是走最优路线。

代码实现 (Q-Learning)

def q_learning(env, num_episodes=5000, alpha=0.1, gamma=0.99, epsilon=0.1):
    """Q-Learning: Off-policy TD Control"""
    Q = defaultdict(lambda: defaultdict(float))

    def epsilon_greedy(state):
        if np.random.random() < epsilon:
            return np.random.choice(env.get_actions())
        action_values = Q[state]
        if not action_values:
            return np.random.choice(env.get_actions())
        return max(action_values, key=action_values.get)

    for _ in range(num_episodes):
        state = env.reset()

        while True:
            action = epsilon_greedy(state)
            next_state, reward, done = env.step(state, action)

            # Q-Learning 更新：使用 max 而非实际动作
            max_next_q = max(Q[next_state].values()) if Q[next_state] else 0
            td_target = reward + gamma * max_next_q * (not done)
            td_error = td_target - Q[state][action]
            Q[state][action] += alpha * td_error

            state = next_state
            if done: break

    return Q

---

4. Cliff Walking 案例分析

4.1 环境描述

Cliff Walking (悬崖漫步) 是 Sutton & Barto 教材中经典的 4x12 网格世界：

• 起点 ：左下角 ( 3 , 0 ) (3, 0) (3,0)
• 终点 ：右下角 ( 3 , 11 ) (3, 11) (3,11)
• 悬崖 ：底行中间位置 ( 3 , 1 ) (3, 1) (3,1) 到 ( 3 , 10 ) (3, 10) (3,10)，踩到立即回到起点并获得 − 100 -100 −100 奖励
• 每步奖励 ： − 1 -1 −1（鼓励尽快到达终点）

代码实现 (Cliff Walking Environment)

class CliffWalkingEnv:
    """4x12 Cliff Walking 环境"""
    def __init__(self):
        self.rows, self.cols = 4, 12
        self.start = (3, 0)
        self.goal = (3, 11)
        self.cliff = [(3, c) for c in range(1, 11)]

    def reset(self):
        self.state = self.start
        return self.state

    def get_actions(self):
        return [0, 1, 2, 3]  # 上、下、左、右

    def step(self, state, action):
        moves = {0: (-1, 0), 1: (1, 0), 2: (0, -1), 3: (0, 1)}
        dr, dc = moves[action]
        nr = max(0, min(self.rows - 1, state[0] + dr))
        nc = max(0, min(self.cols - 1, state[1] + dc))
        next_state = (nr, nc)

        if next_state in self.cliff:
            return self.start, -100, False
        elif next_state == self.goal:
            return next_state, -1, True
        else:
            return next_state, -1, False

4.2 更新机制对比

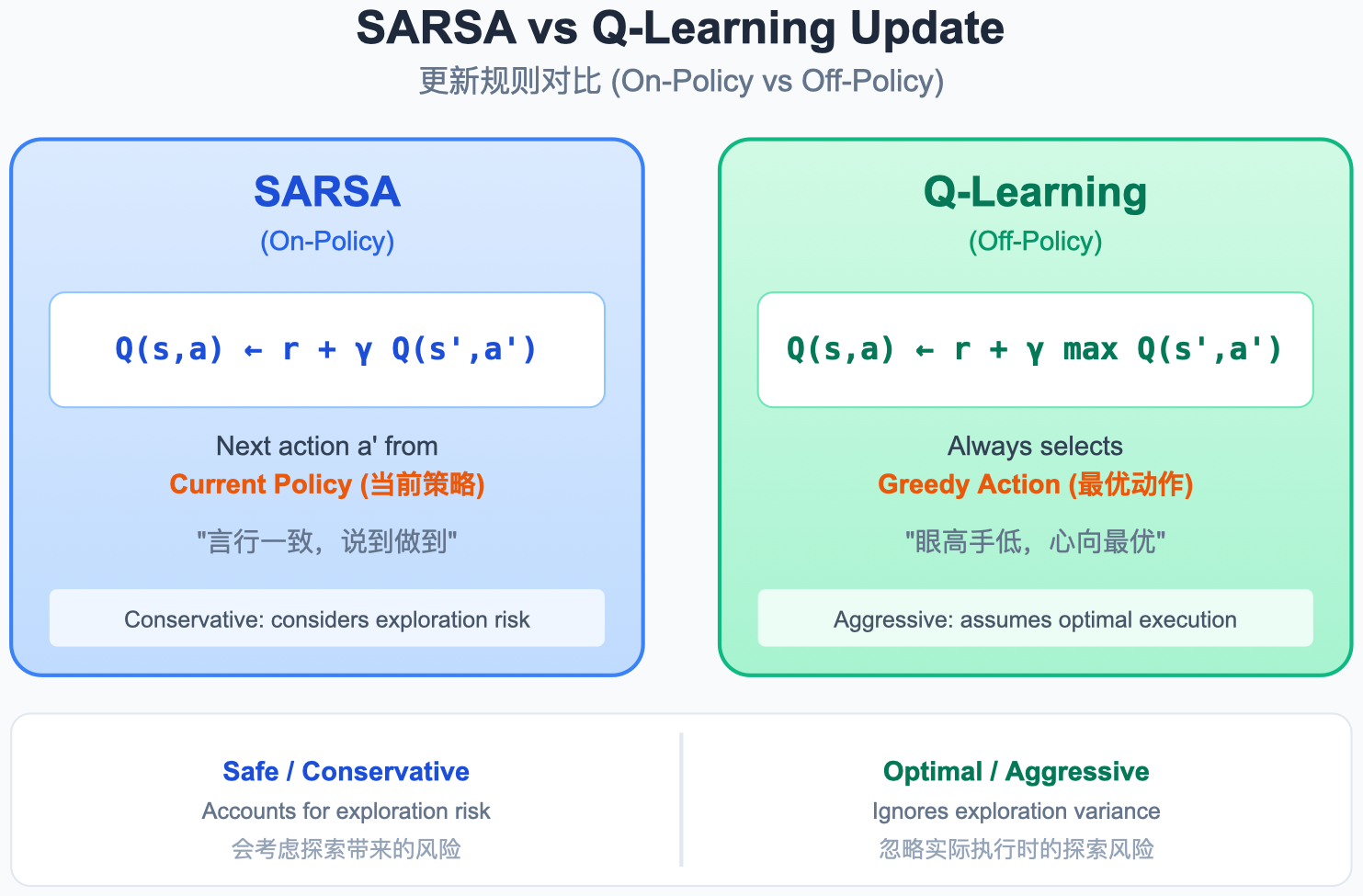
图解说明：

• SARSA 更新 ：使用实际采取的 A t + 1 A_{t+1} At+1，可能是探索性动作（随机走一步）。
• Q-Learning 更新 ：假设执行最优动作 max ⁡ a ′ Q \max_{a'} Q maxa′Q，与实际行为无关。

4.3 路径差异与直觉

图解说明：

• Q-Learning (乐观派)：学出紧贴悬崖的最短路径，因为更新目标假设未来总走最优动作，不会掉坑。
• SARSA (务实派) ：学出远离悬崖的安全路径，因为更新目标包含了 ϵ \epsilon ϵ-greedy 探索可能掉下悬崖的风险。

4.4 训练曲线观察

• Q-Learning：训练过程中频繁掉入悬崖（累积惩罚大），但最终收敛策略是最短路径。
• SARSA：训练过程中较少掉入悬崖（累积惩罚小），最终收敛策略是安全路径。

结论：在线控制场景（如机器人实时行走）优先用 SARSA；只关心最终最优解（如离线训练后部署）优先用 Q-Learning。

---

5. Expected SARSA

SARSA 与 Q-Learning 的中间形态：用策略的期望值替代单次采样。

更新公式：

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ ∑ a ′ π ( a ′ ∣ S t + 1 ) Q ( S t + 1 , a ′ ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \sum_{a'} \pi(a'|S_{t+1}) Q(S_{t+1}, a') - Q(S_t, A_t) \right] Q(St,At)←Q(St,At)+α[Rt+1+γa′∑π(a′∣St+1)Q(St+1,a′)−Q(St,At)]

• 当 π \pi π 是 ϵ \epsilon ϵ-greedy 策略时，Expected SARSA 是 On-policy 的
• 当 π \pi π 是 greedy 策略时，Expected SARSA 退化为 Q-Learning

代码实现 (Expected SARSA)

def expected_sarsa(env, num_episodes=5000, alpha=0.1, gamma=0.99, epsilon=0.1):
    """Expected SARSA: 使用期望值替代单次采样"""
    Q = defaultdict(lambda: defaultdict(float))

    for _ in range(num_episodes):
        state = env.reset()

        while True:
            # epsilon-greedy 行为策略
            if np.random.random() < epsilon:
                action = np.random.choice(env.get_actions())
            else:
                action = max(Q[state], key=Q[state].get) if Q[state] else np.random.choice(env.get_actions())

            next_state, reward, done = env.step(state, action)

            # 计算期望 Q 值
            actions = env.get_actions()
            n_actions = len(actions)
            expected_q = 0

            if Q[next_state]:
                best_action = max(Q[next_state], key=Q[next_state].get)
                for a in actions:
                    if a == best_action:
                        expected_q += (1 - epsilon + epsilon / n_actions) * Q[next_state][a]
                    else:
                        expected_q += (epsilon / n_actions) * Q[next_state][a]

            # 更新
            td_target = reward + gamma * expected_q * (not done)
            Q[state][action] += alpha * (td_target - Q[state][action])

            state = next_state
            if done: break

    return Q

---

6. Maximization Bias 与 Double Q-Learning

6.1 问题根源

Q-Learning 的更新目标使用 max ⁡ \max max 操作：

Y Q = R t + 1 + γ max ⁡ a ′ Q ( S t + 1 , a ′ ) Y^{Q} = R_{t+1} + \gamma \max_{a'} Q(S_{t+1}, a') YQ=Rt+1+γa′maxQ(St+1,a′)

根据 Jensen 不等式 (Jensen's Inequality)： E [ max ⁡ ( X ) ] ≥ max ⁡ ( E [ X ] ) E[\max(X)] \ge \max(E[X]) E[max(X)]≥max(E[X])

当 Q 值估计存在噪声时， max ⁡ \max max 操作会系统性地选中被高估的动作，导致正向偏差（过估计，Overestimation）。

6.2 数值示例

考虑一个状态 s s s，有 3 个动作，真实 Q 值均为 0：

动作	真实值 Q ∗ ( s , a ) Q^*(s,a) Q∗(s,a)	估计值 Q ^ ( s , a ) \hat{Q}(s,a) Q^(s,a)（含噪声）
a 1 a_1 a1	0	+0.3
a 2 a_2 a2	0	-0.2
a 3 a_3 a3	0	+0.5

• 真实最优值： max ⁡ a Q ∗ ( s , a ) = 0 \max_a Q^*(s,a) = 0 maxaQ∗(s,a)=0
• 估计最优值： max ⁡ a Q ^ ( s , a ) = + 0.5 \max_a \hat{Q}(s,a) = +0.5 maxaQ^(s,a)=+0.5（选中了噪声最大的 a 3 a_3 a3）
• 偏差 = + 0.5 − 0 = + 0.5 +0.5 - 0 = +0.5 +0.5−0=+0.5

这种正向偏差会在 Bootstrapping 过程中层层传递，导致 Q 值全面膨胀，严重时使策略退化。

6.3 解决方案：Double Q-Learning

核心思想：维护两个独立的 Q 表，将动作选择 和价值评估解耦。

Y D o u b l e Q = R t + 1 + γ Q 2 ( S t + 1 , arg ⁡ max ⁡ a ′ Q 1 ( S t + 1 , a ′ ) ) Y^{DoubleQ} = R_{t+1} + \gamma Q_2\left(S_{t+1},\ \arg\max_{a'} Q_1(S_{t+1}, a')\right) YDoubleQ=Rt+1+γQ2(St+1, arga′maxQ1(St+1,a′))

• Q 1 Q_1 Q1 负责选动作（哪个动作最好？）
• Q 2 Q_2 Q2 负责评估该动作的价值（这个动作到底值多少？）
• 每步随机选择更新 Q 1 Q_1 Q1 或 Q 2 Q_2 Q2，两者轮流充当选择者和评估者

代码实现 (Double Q-Learning)

def double_q_learning(env, num_episodes=5000, alpha=0.1, gamma=0.99, epsilon=0.1):
    """Double Q-Learning: 解耦动作选择与价值评估"""
    Q1 = defaultdict(lambda: defaultdict(float))
    Q2 = defaultdict(lambda: defaultdict(float))

    def epsilon_greedy(state):
        combined = defaultdict(float)
        for a in env.get_actions():
            combined[a] = Q1[state][a] + Q2[state][a]
        if np.random.random() < epsilon:
            return np.random.choice(env.get_actions())
        return max(combined, key=combined.get) if combined else np.random.choice(env.get_actions())

    for _ in range(num_episodes):
        state = env.reset()

        while True:
            action = epsilon_greedy(state)
            next_state, reward, done = env.step(state, action)

            # 随机选择更新 Q1 或 Q2
            if np.random.random() < 0.5:
                best_a = max(Q1[next_state], key=Q1[next_state].get) if Q1[next_state] else np.random.choice(env.get_actions())
                td_target = reward + gamma * Q2[next_state][best_a] * (not done)
                Q1[state][action] += alpha * (td_target - Q1[state][action])
            else:
                best_a = max(Q2[next_state], key=Q2[next_state].get) if Q2[next_state] else np.random.choice(env.get_actions())
                td_target = reward + gamma * Q1[next_state][best_a] * (not done)
                Q2[state][action] += alpha * (td_target - Q2[state][action])

            state = next_state
            if done: break

    # 返回合并后的 Q 表
    Q = defaultdict(lambda: defaultdict(float))
    for s in set(list(Q1.keys()) + list(Q2.keys())):
        for a in set(list(Q1[s].keys()) + list(Q2[s].keys())):
            Q[s][a] = (Q1[s][a] + Q2[s][a]) / 2
    return Q

---

7. 算法对比总结

7.1 更新公式对比

算法	更新目标 (TD Target)	类型
SARSA	R + γ Q ( S ′ , A ′ ) R + \gamma Q(S', A') R+γQ(S′,A′)，其中 A ′ ∼ π A' \sim \pi A′∼π	On-policy
Q-Learning	R + γ max ⁡ a ′ Q ( S ′ , a ′ ) R + \gamma \max_{a'} Q(S', a') R+γmaxa′Q(S′,a′)	Off-policy
Expected SARSA	R + γ ∑ a ′ π ( a ′ ∣ S ′ ) Q ( S ′ , a ′ ) R + \gamma \sum_{a'} \pi(a' \mid S') Q(S', a') R+γ∑a′π(a′∣S′)Q(S′,a′)	On/Off-policy
Double Q-Learning	R + γ Q 2 ( S ′ , arg ⁡ max ⁡ a ′ Q 1 ( S ′ , a ′ ) ) R + \gamma Q_2(S', \arg\max_{a'} Q_1(S', a')) R+γQ2(S′,argmaxa′Q1(S′,a′))	Off-policy

7.2 特性对比

特性	SARSA	Q-Learning	Expected SARSA
策略类型	On-policy	Off-policy	取决于 π \pi π
更新方差	较高（单次采样）	中等	较低（期望值）
过估计风险	低	高	中
安全性	高（考虑探索风险）	低（忽略探索风险）	中
收敛策略	ϵ \epsilon ϵ-greedy 最优	全局最优	ϵ \epsilon ϵ-greedy 最优
计算复杂度	O ( 1 ) O(1) O(1)	O ( 1 ) O(1) O(1)	O ( ∣ A ∣ ) O(|A|) O(∣A∣)

7.3 选型建议

• 在线安全敏感场景（机器人、自动驾驶）：优先 SARSA 或 Expected SARSA
• 离线训练、追求最优策略：优先 Q-Learning
• 需要低方差更新：优先 Expected SARSA
• Q 值过估计严重：使用 Double Q-Learning

---

8. 实战技巧：超参数衰减

8.1 探索率衰减 (Epsilon Decay)

GLIE 条件 (Greedy in the Limit with Infinite Exploration)：

1. 所有状态-动作对被访问无限次
2. 策略最终收敛到贪婪策略

常用指数衰减公式：

ϵ t = ϵ m i n + ( ϵ s t a r t − ϵ m i n ) ⋅ e − λ t \epsilon_t = \epsilon_{min} + (\epsilon_{start} - \epsilon_{min}) \cdot e^{-\lambda t} ϵt=ϵmin+(ϵstart−ϵmin)⋅e−λt

8.2 学习率衰减 (Alpha Decay)

Robbins-Monro 条件：

∑ t = 1 ∞ α t = ∞ , ∑ t = 1 ∞ α t 2 < ∞ \sum_{t=1}^\infty \alpha_t = \infty, \quad \sum_{t=1}^\infty \alpha_t^2 < \infty t=1∑∞αt=∞,t=1∑∞αt2<∞

第一个条件保证能克服初始偏差，第二个条件保证最终收敛。

---

9. 表格型方法的局限

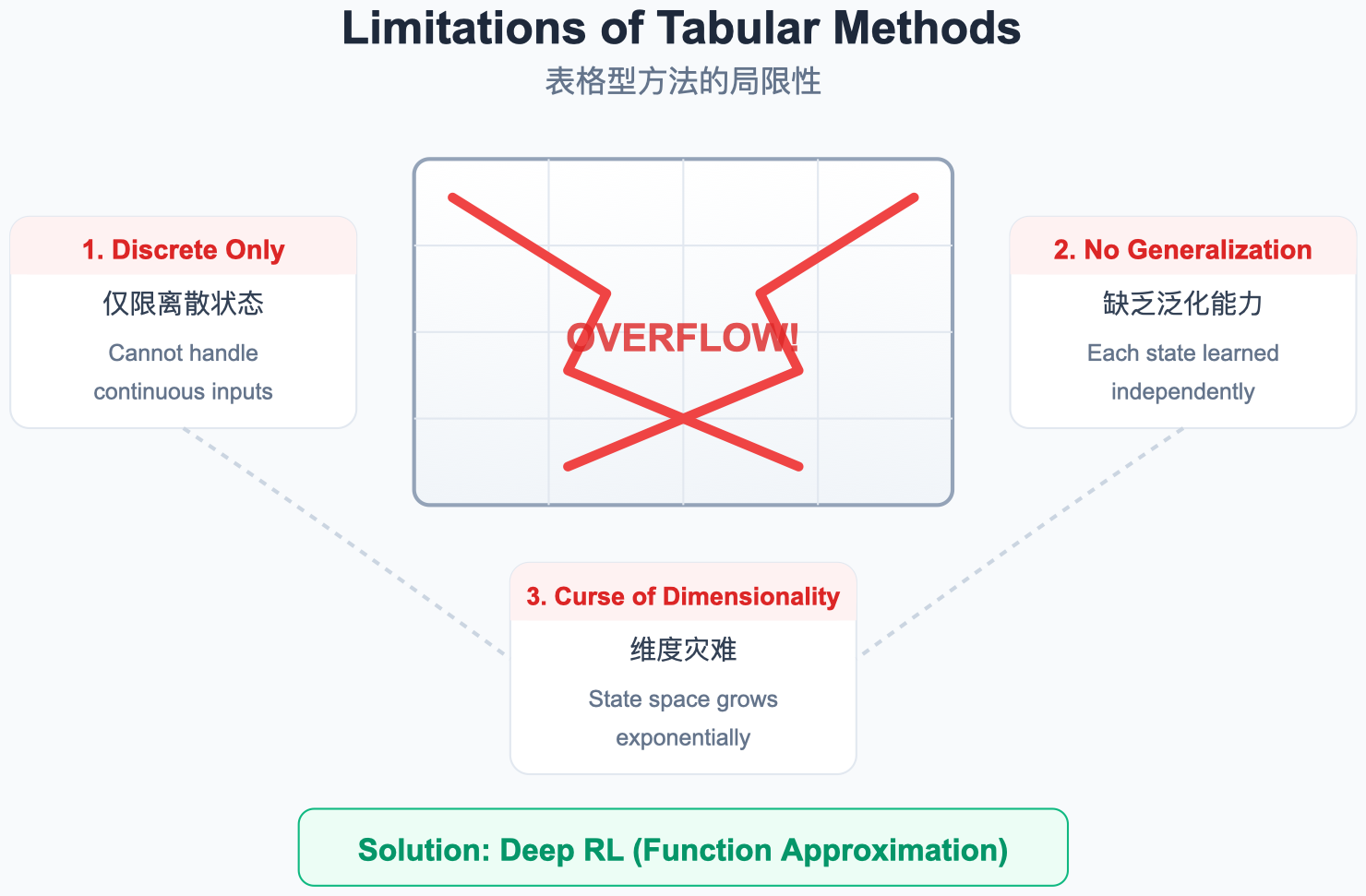
图解说明：

• 状态空间爆炸 ：围棋棋盘 19x19，状态数 ≈ 3 361 \approx 3^{361} ≈3361，表格无法存储。
• 连续状态：机械臂关节角度是连续值，无法枚举。
• 解决方案：用神经网络来近似 Q 函数，即深度 Q 网络 (Deep Q-Network, DQN)。

---

10. 总结与预告

本章核心：

• On-policy vs Off-policy：行为策略和目标策略是否是同一个，决定了算法的风格和适用场景。
• SARSA：On-policy TD 控制，学到的策略会把探索的风险考虑在内，更"谨慎"。
• Q-Learning：Off-policy TD 控制，直接朝全局最优走，不管当前怎么探索。
• Expected SARSA：用期望替代单次采样，兼具两者优点，方差更低。
• Double Q-Learning：解耦"选动作"和"评估动作"，解决 max 操作带来的系统性过估计。

下一章预告 ：

表格型方法在大规模或连续状态空间下彻底失效。下一章我们进入深度价值学习，看 DQN 如何用神经网络逼近 Q 函数，以及它背后的核心创新。

➡️ 下一章：第 7 章 - DQN 核心创新