目录
[二、环形链表 I](#二、环形链表 I)
[三、环形链表 II](#三、环形链表 II)
一、相交链表
(一)题目描述
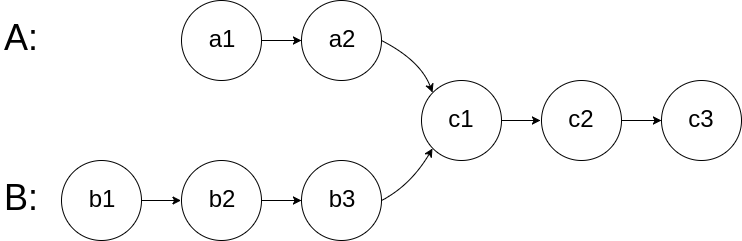
**1、题目简述:**给你两个单链表的头结点 headA 和 headB ,请你找出并返回两个单链表相交的起始结点。如果两个链表不存在相交结点,返回 null 。
**2、题目链接:**https://leetcode.cn/problems/intersection-of-two-linked-lists/description/
(二)解题思路
1、核心观察
**(1)相交特征:**两链表相交后,后续结点完全重合,因此尾结点地址必然相同(可用于初步判断是否相交)。
**(2)长度差问题:**若两链表长度不同,长链表需先移动 "长度差" 步,使两链表指针处于 "同一起跑线",再同步遍历找相交结点。
2、步骤拆解
(1)步骤 1:计算两链表长度
① 遍历 headA,计数 sizeA;遍历 headB,计数 sizeB。
②用 pa 和 pb 指针遍历,避免修改原头节点。
(2)步骤 2:计算长度差并移动长链表指针
①长度差 gap = abs(sizeA - sizeB)【abs函数取绝对值】。
②定义 longList(长链表头)和 shortList(短链表头)
若 sizeA > sizeB,longList = headA,shortList = headB;否则:longList = headB,shortList = headA。
③移动longList:循环gap次,longList = longList->next(消除长度差)。
(3)步骤 3:同步遍历找相交节点
**① 循环条件:**shortList != NULL(两指针此时长度相同,任一为空则不相交)。
②若shortList == longList(地址相同),返回当前节点(相交起始节点)。
③否则:shortList = shortList->next,longList = longList->next。
**(4)步骤 4:**处理不相交情况:循环结束未找到相交节点,返回null。
(三)代码实现
cpp
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
// 步骤1:计算两链表长度
ListNode* pa = headA;
ListNode* pb = headB;
int sizeA = 0, sizeB = 0;
while (pa != NULL) {
sizeA++;
pa = pa->next;
}
while (pb != NULL) {
sizeB++;
pb = pb->next;
}
// 步骤2:确定长/短链表,移动长链表指针消除长度差
int gap = abs(sizeA - sizeB);
ListNode* longList = headB;
ListNode* shortList = headA;
if (sizeA > sizeB) {
longList = headA;
shortList = headB;
}
while (gap--) {
longList = longList->next;
}
// 步骤3:同步遍历找相交节点
while (shortList != NULL) {
if (shortList == longList) {
return shortList;
}
shortList = shortList->next;
longList = longList->next;
}
// 不相交
return NULL;
}二、环形链表 I
(一)题目描述
**1、题目简述:**给定单链表的头结点head,判断链表中是否有环。若链表中存在环(尾节点next指针指向链表内任意节点,非null),返回true;否则返回false。
**2、题目链接:**https://leetcode.cn/problems/linked-list-cycle/description/
(二)解题思路
1、核心算法:快慢指针法
(1)原理
①若链表无环:快指针fast会率先到达null,循环终止。
②若链表有环:fast和slow最终会在环内相遇(fast速度快,会 "追上"slow)。
(2)步骤拆解
**① 指针初始化:**slow = head,fast = head(均从头节点出发)。
② 循环条件: fast != NULL && fast->next != NULL(确保不会出现空指针访问错误)。
**③ 指针移动:**slow = slow->next(1 步),fast = fast->next->next(2 步)。
**④ 相遇判断:**若slow == fast,返回true(有环)。
**⑤ 循环终止:**fast或fast->next为空,返回false(无环)。
2、关键证明:为何快慢指针必相遇
(1)假设条件
链表入环前长度为L,环周长为C。
当slow入环时,fast必然已在环内,两者距离为N(0 ≤ N < C)。
(2)追击过程
每次移动,fast 比 slow多走 1 步(2-1=1),因此两者距离每次缩减 1。距离变化:N → N-1 → N-2 → ... → 0,最终距离为 0 时相遇。
**(3)结论:**只要链表有环,快慢指针必在环内相遇。
Tip:如果快指针走的是任意步数,只有当快慢指针的速度差必须与环的长度互质,才能确保在循环链表中一定相遇。
(三)代码实现
cpp
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head)
{
// 处理空链表
if (head == NULL) {
return false;
}
// 初始化快慢指针
ListNode* slow = head;
ListNode* fast = head;
while (fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
// 相遇则有环
if (slow == fast) {
return true;
}
}
// 无环
return false;
}(四)易错点
**1、空链表未处理:**head为空时直接返回false,避免fast->next空指针异常。
**2、循环条件错误:**若仅判断fast != NULL,fast->next为空时,fast = fast->next->next会越界。
三、环形链表 II
(一)题目描述
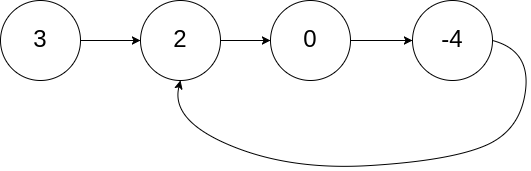
**1、题目简述:**给定单链表的头结点 head,返回链表开始入环的第一个结点。若链表无环,返回null。
**2、题目链接:**https://leetcode.cn/problems/linked-list-cycle-ii/description/
(二)解题思路
1、核心结论:快慢指针相遇点到入环起始结点的距离 = 头节点到入环起始结点的距离。
2、数学推导
(1)假设条件
头结点到入环点距离为L,入环点到相遇点距离为X,环周长为C。
相遇时,slow走了L + X步,fast走了L + X + nC步(n为fast在环内绕的圈数,n ≥ 1)。
(2)路程关系
因 fast 速度是 slow 的 2 倍,故 fast 路程 = 2×slow 路程 → L + X + nC = 2(L + X)。
化简得:L = nC - X → L = (n-1)C + (C - X)。
(3)结论
C - X 是相遇点到入环点的距离(环内剩余长度);(n-1)C表示绕环n-1圈,无实际影响(最终仍会回到入环点)。
因此,头节点到入环点的距离 = 相遇点到入环点的距离C,即 L = C - X。
3、步骤拆解
(1)步骤 1:快慢指针找相遇点(复用 "环形链表 I" 逻辑)
若未相遇(无环),返回null;若相遇,记录相遇点meetNode = slow(slow == fast)。
(2)步骤 2:双指针找入环点
**① 初始化指针:**pcur = head(从头节点出发),meet = meetNode(从相遇点出发)。
**② 循环条件:**pcur != meet。
**③ 指针移动:**pcur = pcur->next,meet = meet->next(均每次 1 步)。
**(3)步骤 3:返回结果 →**循环结束时,pcur(或meet)即为入环起始节点。
(三)代码实现
cpp
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head)
{
// 步骤1:快慢指针找相遇点
ListNode* slow = head;
ListNode* fast = head;
ListNode* meetNode = NULL;
while (fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
meetNode = slow;
break;
}
}
// 无环情况
// 这里一定要有,因为只有有环,上面才是找到了相遇点
// 否则就是无环退出了
if (fast == NULL || fast->next == NULL) {
return NULL;
}
// 步骤2:双指针找入环点
ListNode* pcur = head;
while (pcur != meetNode) {
pcur = pcur->next;
meetNode = meetNode->next;
}
return pcur;
}四、随机链表的复制
(一)题目描述
1、题目简述
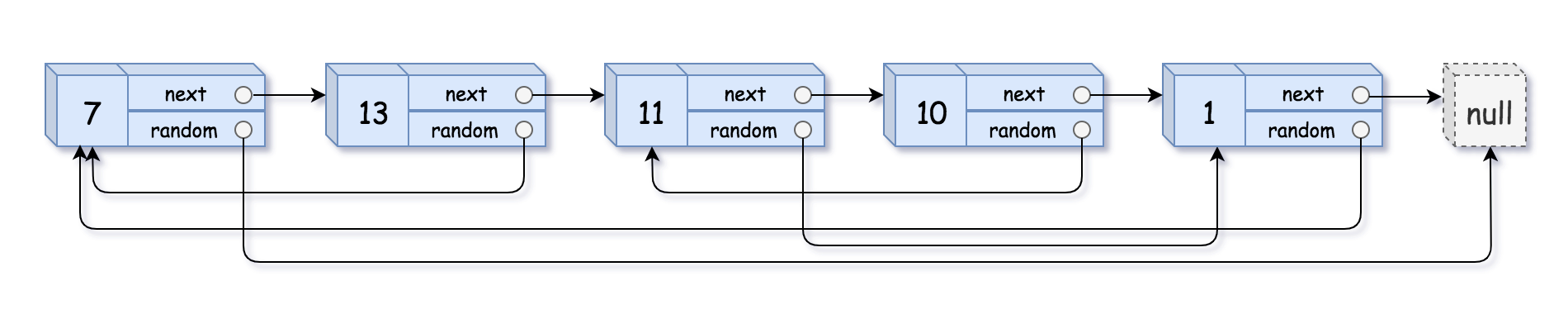
给定一个长度为 n 的链表,每个结点除了val(值)和next(指向下一节点)指针外,额外包含一个random指针。该指针可指向链表中任意结点或空结点,要求构造链表的深拷贝,返回复制链表的头结点。
**2、题目链接:**https://leetcode.cn/problems/copy-list-with-random-pointer/description/
3、 深拷贝 vs 浅拷贝
(1)浅拷贝: 仅复制结点值或指针地址,新指针与原指针指向同一块内存空间(如b=a仅复制值,指针repeat=pcur仅复制地址)。
(2)深拷贝: 为每个新结点分配独立内存空间,复制原节点的val、next和random指向逻辑,但新结点与原结点地址完全不同,相互独立。即 next 和 random 指针都不一样,同时,修改拷贝后的链表,不影响原来的链表。
4、深拷贝核心要求
复制链表由 n 个全新结点组成,结点值与原链表对应结点完全一致。新结点的 next 和 random 指针仅指向复制链表中的结点,不得指向原链表结点。
复制链表与原链表的指针指向逻辑完全一致,如原链表 x.random→y,则复制链表为 x'.random→y'。
5、难度分析
力扣难度:中等。原因是:
普通单链表复制仅需遍历一次,通过 next 指针即可串联新结点;但随机链表多了random 指针,其指向无规律(可指向任意结点或空),无法通过单次遍历直接定位,需特殊技巧处理,因此难度高于简单题。
(二)解题思路
1、在原链表中插入复制节点(核心铺垫)
**目标:**将复制结点插入原结点之后,形成 "原结点→复制结点→原结点→复制结点" 的交错结构,为后续random指针设置铺路。
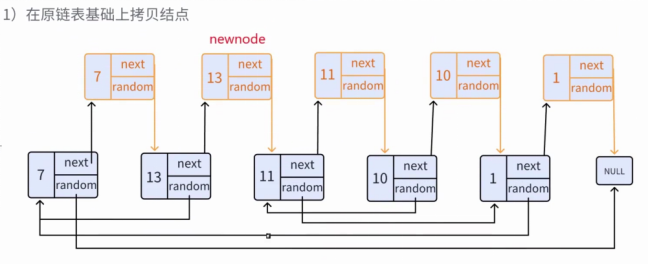
**(1)初始化遍历指针:**pcur = head(指向原链表头结点7)。
**(2)创建复制结点:**调用buyNode(pcur->val),创建值为7的复制结点copy_7,next和random初始化为NULL。
**(3)保存原结点的 next 指针:**next = pcur->next(保存13的地址,避免后续插入时丢失原链表连接)。
(4)插入复制结点
① copy_7->next = next(copy_7的next指向13)。
②pcur->next = copy_7(7的next指向copy_7),此时链表变为7→copy_7→13→11→10→1。
**(5)移动遍历指针:**pcur = next(pcur指向13,继续处理下一个原节点)。
**(6)循环执行:**重复步骤 2-5,直至pcur为空,最终形成交错链:7 → copy_7 → 13 → copy_13 → 11 → copy_11 → 10 → copy_10→ 1→ copy_1。如上图所示。
2、设置复制结点的 random 指针
**关键规律:**利用第一步的交错结构:原结点 pcur 的复制结点是 pcur->next,原结点 pcur->random 的复制结点是 pcur->random->next。
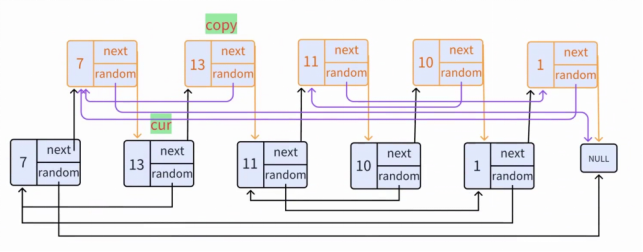
**(1)初始化指针:**pcur = head(指向原结点7),copy = pcur->next(指向复制结点copy_7)。
(2)分情况设置 random 指针
**① 情况 1:**原节点pcur->random == NULL(如7的random为空):
执行:copy -> random = NULL(copy_7的random也为空)。
**② 情况 2:**原节点pcur->random != NULL(如13的random指向7):
执行:copy->random = pcur->random->next(13的random是7,7的next是copy_7,因此copy_13的random指向copy_7)。
(3)移动指针
pcur = copy->next(pcur指向原节点13),copy = pcur->next(copy指向copy_13),重复步骤 2。
**(4)循环结束:**直至pcur为空,所有复制结点的random指针设置完成。
3、断开新旧链表(分离复制链表)
目标:从交错结构中拆分出独立的复制链表,原链表可恢复(可选,不影响复制结果)。
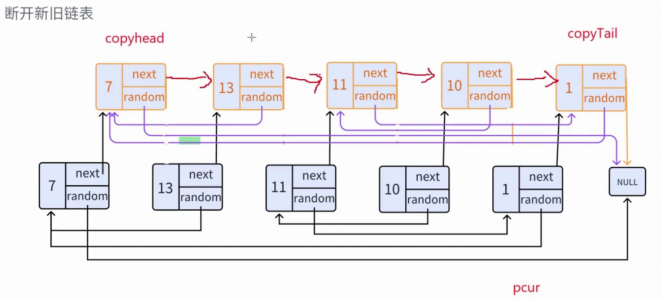
(1)初始化复制链表指针
①copyHead = head->next(复制链表头结点,指向copy_7)。
② copyTail = copyHead(复制链表尾结点,初始也指向copy_7)。
③ pcur = head(用于遍历原链表,辅助拆分)。
**(2)循环拆分:**当copyTail -> next != NULL(复制链表尾结点的下一个节点不为空,即还有未拆分的复制节点,此时继续遍历。):
①pcur = copyTail->next(pcur指向原节点13,因为copy_7的next是13)。
②copyTail->next = pcur->next(copy_7的next指向pcur->next即copy_13,而非原节点13)。
③ copyTail = copyTail->next(copyTail移动到copy_13,更新复制链表尾)。
**(3)拆分完成:**当copyTail -> next == NULL时,复制链表已完全独立,copyHead 即为复制链表的头结点。
(三)代码实现
cpp
// 结点结构体定义
struct Node {
int val;
struct Node *next;
struct Node *random;
};
// 创建新结点(封装函数)
struct Node* buyNode(int x)
{
struct Node* newnode = (struct Node*)malloc(sizeof(struct Node));
newnode->val = x;
newnode->next = NULL;
newnode->random = NULL;
return newnode;
}
// 第一步:在原链表中插入复制结点
void AddNode(struct Node* head)
{
struct Node* pcur = head;
while (pcur) {
struct Node* newnode = buyNode(pcur->val);
struct Node* next = pcur->next;
// 插入新结点
newnode->next = next;
pcur->next = newnode;
// 移动至原链表下一个结点
pcur = next;
}
}
// 第二步:设置复制节点的random指针
void setRandom(struct Node* head)
{
struct Node* pcur = head;
while (pcur) {
struct Node* copy = pcur->next;
// 按规则设置random指针
if (pcur->random) {
copy->random = pcur->random->next;
} else {
copy->random = NULL;
}
// 移动至原链表下一个结点
pcur = copy->next;
}
}
// 主函数:随机链表深拷贝
struct Node* copyRandomList(struct Node* head)
{
// 边界处理:空链表直接返回
if (head == NULL) {
return head;
}
// 第一步:插入复制节点
AddNode(head);
// 第二步:设置random指针
setRandom(head);
// 第三步:断开新旧链表
struct Node* pcur = head;
struct Node* copyHead = pcur->next;
struct Node* copyTail = copyHead;
while (copyTail->next) {
// 这里三步的前后顺序不能乱
pcur = copyTail->next;
copyTail->next = pcur->next;
copyTail = copyTail->next;
}
return copyHead;
}(四)易错点
1、空指针访问
**(1)错误原因:**未处理空链表,直接执行pcur->next(如head=NULL时)
**(2)解决方案:**在主函数开头增加 if (head == NULL) return head
2、random 指针设置错误
(1)错误原因: 未判断原节点random是否为空,直接执行pcur->random->next
**(2)解决方案:**在 setRandom 中增加 if (pcur->random) 的判断
(五)算法复杂度
**1、时间复杂度:**O(n),仅需 3 次遍历(插入结点 1 次、设置 random 1 次、拆分 1 次),每次遍历均为线性时间。
**2、空间复杂度:**O(1),仅使用常数个指针变量,同时内存开销与链表长度无关。